Estimation of Vehicle State Based on IMM-AUKF

Abstract

Establishing a symmetrical model of surrounding vehicles and accurately obtaining the driving state of the surrounding vehicles in the driving environment can improve the safety of driving, which is an important issue that needs to be considered in the automatic driving system or auxiliary driving system. Therefore, we propose an adaptive unscented Kalman filter algorithm based on Interacting Multiple Model (IMM) theory to estimate the state of target vehicle in the high-speed driving environment. To be specific, we use the Constant Turn Rate and Acceleration (CTRA) theory to establish the target vehicle kinematics model, simultaneously, in order to overcome the problem of estimator failure when the yaw rate is close to zero, a simplified version of the CTRA model is also introduced into the estimation process. In addition, the parameter adaptation strategy is added, so the proposed estimator can overcome the uncertainty of the noise model and improve its accuracy. Finally, the effectiveness of proposed state estimation algorithm is verified on the Carsim and Simulink co-simulation platform. The results of simulations and experiments show that the accuracy and stability of IMM-based algorithm is better than the single-model algorithm in different scenarios, and the parameter adaptation strategy brings performance improvement.

1. Introduction

Recently, owing to increasing demand for driving stability and safety, Advanced Driver Assistant Systems (ADAS) have developed rapidly in our daily life, which have significantly improved the safety, performance and efficiency of vehicles in various complex driving environments [1]. Additionally, accurate and stable estimation of vehicle driving state information such as the heading, yaw rate, absolute speed and acceleration of the target vehicle, as well as the relative position and relative speed of the target vehicle relative to the host vehicle, is essential for ADAS [2].

However, in practical applications, real-time acquisition of vehicle state usually requires expensive equipment, existing professional vehicle signal acquisition systems are very expensive and their installation is complicated, and some of the key states are hard to measure directly, making it difficult to popularize [3]. In addition, under different driving conditions such as straights and curves, if the state estimation methods cannot identify the real-time state of the target vehicle, the whole control process will be unstable [4,5]. Therefore, it is necessary to develop a low-cost and high precision online vehicle state estimation system that is applicable to real driving condition [6]. Current state estimation algorithm is mainly divided into two major categories: artificial intelligence (AI) and model-based.

Due to the development of high-performance computing hardware and the emergence of a large number of labeled datasets, the state estimation method based on AI has achieved great success. Ref. [7] used neural network method to detect and annotate vehicle for streaming video data with complex scenes, aiming to infer each vehicle’s pose, color and type. Lin et al. [8] presents an auto-masking neural network for vehicle detection and pose estimation. As proposed in [9], unsupervised convolutional neural network is adopted for vehicle type classification from frontal view images. Refs. [10,11,12,13] use Convolutional Neural Network (CNN) to estimate the actual state of the detected vehicles. Although the data-driven artificial intelligence method has achieved unprecedented success in state estimation, it requires a large amount of labeled data for training to prevent neural network parameters from overfitting.

The main research activities in the field of model-based state estimation concentrate on the choice of vehicle dynamics model and the application of filter theory. Ref. [14] presents a non-linear model-based observer which relies on an augmented Extended Kalman filter for combined estimation of motion states. Ref. [15] applies a particle filter (PF) and an unscented Kalman filter (UKF) to estimate the headway and velocity of a six-vehicle platoon system. However, due to the existence of various road conditions such as straights and curves in reality, the use of a single motion model-based approach often cannot accurately fit the state of the target vehicle. Therefore, the multiple-model structure is adopted. Ref. [16] proposes an interacting multiple model algorithm, using improved Markov process to describe the switching probability among the models. And a number of multiple-model techniques have been proposed [17,18,19,20,21,22,23]. Additionally, in order to improve the performance of the filter, the parameter adaptive process is introduced. Ref. [24] describes an adaptive interacting multiple-model algorithm that does not need predefined models for use in manoeuvring target tracking. To improve the robustness of the unscented Kalman filter when applied to highly nonlinear models, ref. [25] proposes a new method by modifying the main scaling parameter at every step using a self-adaptive algorithm.

In this paper, we propose an adaptive parameter Interacting Multiple Model unscented Kalman filter algorithm (IMM-AUKF) to achieve accurate real-time target vehicle state estimation performance. The remainder of the paper is organized as follows: In Section 2, vehicle coordinate, dynamics models and UKF algorithm procedure will be introduced. The structure and detailed design about IMM-AUKF algorithm is covered in Section 3. In Section 4, we use Carsim and Simulink co-simulation to verify the effectiveness of IMM-AUKF, in order to verify the algorithm we proposed, the experimental scene adopts flat road, only one and the same host car and one and the same target car, and set up two control experiments. Finally, in Section 5, we offer our conclusions.

2. Problem Formulation

2.1. Vehicle Coordinate

As shown in Figure 1, the research object of this paper is the vehicle in front of the host vehicle, and the target vehicle generally has no vertical movement, or the vertical movement speed is very small compared to the horizontal movement speed. Therefore, ignoring the movement of the vehicle in the vertical direction, the state estimation of the target vehicle can be simplified as the state estimation of the object on the plane in the radar coordinate system [26,27]. For the purpose of simplifying the problem, we set the on-board sensor as the origin of the coordinate system, the x-axis is parallel to the ground and points to the forward direction of the vehicle, the y-axis is parallel to the ground and points to the left of the driver. The output signal of the millimeter wave radar is given in the form of polar coordinates. In order to unify the radar coordinate system with the coordinate system defined above, we set the radar coordinate system as Figure 1: the center of the radar installation position is the pole, the polar axis coincides with the x-axis of the coordinate system and is positive in the counterclockwise direction.

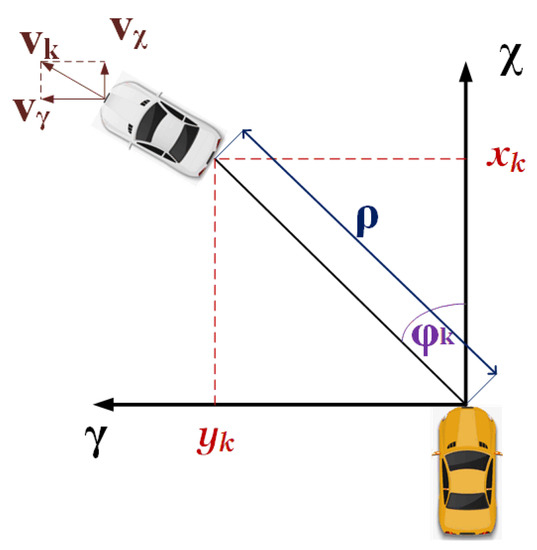
Figure 1. Vehicle Coordinate and Measurement model.

The state vector of the target vehicle at time $k$ is as follows:

$$X(k)={[x_k,y_k,v_k,a_k,{\phi }_k,{\omega }_k]}^T$$

(1)

where $x$ and $y$ are the components of polar coordinate distance between target vehicle and host vehicle $\rho$ on the x-axis and y-axis respectively. $v$ and $a$ are the velocity and acceleration of the target vehicle respectively. $\phi$ is the angle between the target vehicle and the x-axis in the vehicle coordinate system, and $\omega$ is yaw rate.

So, the conversion between the millimeter wave radar coordinate system and the vehicle body coordinate system is:

$$\left[\begin{array}{l}\rho \\ \varphi \end{array}\right]=\left[\begin{array}{c}\sqrt{{x_k}^2+{y_k}^2}\\ \mathrm{atan}2(y_k,x_k)\end{array}\right]$$

(2)

2.2. Construction of CTRA Model

CTRA model assumes that the tracked object is moving with a constant rate and a constant acceleration [28] from time $k$ to time $k+1$. Thus, the displacement of the object in the two axes is computed using the following equation:

$$X(k+1)=\left(\begin{array}{l}{x}_k+\frac{v_k\cdot (\sin ({\phi }_{k+1})-\sin ({\phi }_k))}{{\omega }_k}+\frac{a_k^{}\cdot (\cos ({\phi }_{k+1})-\cos ({\phi }_k))+a_k^{}\cdot {\omega }_k\cdot T\cdot \sin ({\phi }_{k+1})}{{\omega }_k^2}\\ y_k-\frac{v_k\cdot (\cos ({\phi }_{k+1})-\cos ({\phi }_k))}{{\omega }_k}+\frac{a_k^{}\cdot (\sin ({\phi }_{k+1})-\sin ({\phi }_k))-a_k^{}\cdot {\omega }_k\cdot T\cdot \cos ({\phi }_{k+1})}{{\omega }_k^2}\\ v_k+a_k^{}\cdot T\\ a_k^{}\\ {\phi }_k+{\omega }_k\cdot T\\ {\omega }_k\end{array}\right),\omega k\ne 0$$

(3)

where T is the time interval between two sequential scans.

This model can efficiently describe the true motion of a vehicle in the road, since the true trajectory can be considered that is consisted of segments where the turn rate and the acceleration remain constant. However, note this expression can be degenerated when the ${\omega }_k$-component of Equation (3) is close to zero, while this issue can be easily resolved by assuming that the vehicle keeps driving in a straight line, and then Equation (3) is simplified to Equation (4).

$$X(k+1)=\left(\begin{array}{l}{x}_k+(v_k\cdot T+\frac{1}{2}\cdot a_k^{}\cdot T^2)\cos (\phi )\\ y_k+(v_k\cdot T+\frac{1}{2}\cdot a_k^{}\cdot T^2)\sin (\phi )\\ v_k+a_k^{}\cdot T\\ a_k^{}\\ {\phi }_k\\ 0\end{array}\right),\omega k=0$$

(4)

2.3. Unscented Kalman Filter (UKF)

For nonlinear motion, we need to consider the interference of noise. For different time $k$, assume that nonlinear system contains the current state is $X(k)$ with white Gaussian noise $W(k)$ and measurements $Z$ with white Gaussian noise $V(k)$, integrates the interactive input result obtained in Equation (1), the system can be described by Equation (5).

$$\{\begin{array}{l}X(k+1)=f(X(k),W(k))\\ Z(k)=h(X(k),V(k))\end{array}$$

(5)

where $f(\cdot )$ is the nonlinear state equation function, determined by the motion model Equation (3) or Equation (4), and $h$ is the nonlinear observation equation function, determined by the observation model Equation (2).

Suppose $W(k)$ has a covariance matrix $Q$, and $V(k)$ has a covariance matrix $R$. According [29], the steps of the UKF algorithm for the state vector $X$ at different time $k$ are as follows:

(1) Use unscented transform to calculate 2n + 1 sigma points and corresponding weights, the superscript denotes i-th sigma point.

$$X^{(i)}(k|k)=\left[\widehat{X}(k|k)\widehat{X}(k|k)+(\sqrt{(n+\lambda )P(k|k)})\widehat{X}(k|k)-(\sqrt{(n+\lambda )P(k|k)})\right]$$

(6)

where $\widehat{\cdot }$ and P denote the mean and variance of the current state of the target vehicle respectively. Then use the nonlinear function Equation (3) to predict the 2n + 1 sigma point set obtained from Equation (6):

$$X^{(i)}(k+1|k)=f[k,X^{(i)}(k|k)],i=1,2,\cdots ,2n+1$$

(7)

And acquire the mean $\widehat{X}(k+1|k)$ and covariance $P(k+1|k)$ of the new distribution based on the weight $\omega m$ corresponding to each sigma point:

$$\{\begin{array}{l}\widehat{X}(k+1|k)={\displaystyle \sum _{i=0}^{2n}{\omega }_m^{(i)}{X}^{(i)}(k+1|k)}\\ P(k+1|k)={\displaystyle \sum _{i=0}^{2n}{\omega }_c^{(i)}([\hat{X}(k+1|k)-\stackrel{}{X^{(i)}}(k+1|k)]}\cdot {[\widehat{X}(k+1|k)-\stackrel{}{X^{(i)}}(k+1|k)]}^T)+Q\end{array}$$

(8)

(2) According to the predicted value, use Equation (6) again to generate a new sigma point set

$$\begin{array}{l}{X}^{(i)}(k+1|k)=[\widehat{X}(k+1|k)\widehat{X}(k+1|k)+(\sqrt{(n+\lambda )P(k+1|k)})]\\ \cdot [\widehat{X}(k+1|k)-(\sqrt{(n+\lambda )P(k+1|k)})]\end{array}$$

(9)

Then substitute the new sigma point set into the observation equation Equation (2) to get the predicted measurement:

$$Z^{(i)}(k+1|k)=h[X^{(i)}(k+1|k)]$$

(10)

Therefore, the mean and covariance matrix of the system prediction can be obtained by weighted summation:

$$\{\begin{array}{l}\overline{Z}(k+1|k)={\displaystyle \sum _{i=0}^{2n}{\omega }_m^{(i)}{Z}^{(i)}(k+1|k)}\\ P_{ZZ,k}={\displaystyle \sum _{i=0}^{2n}{\omega }_c^{(i)}[Z^{(i)}(k+1|k)}-\overline{Z}(k+1|k]{[Z^{(i)}(k+1|k)-\overline{Z}(k+1|k)]}^T+R\\ P_{XZ,k}={\displaystyle \sum _{i=0}^{2n}{\omega }_c^{(i)}[X^{(i)}(k+1|k)}-\widehat{X}(k+1|k)]{[Z^{(i)}(k+1|k)-\overline{Z}(k+1|k)]}^T\end{array}$$

(11)

(3) Finally, calculate the Kalman gain, update the state and covariance matrix of the system.

$$\{\begin{array}{l}K(k+1)=P_{XZ,k}{P}_{ZZ,k}^{-1}\\ \widehat{X}(k+1|k+1)=\widehat{X}(k+1|k)+K(k+1)[Z(k+1)-\overline{Z}(k+1|k)]\\ P(k+1|k+1)=P(k+1|k)-K(k+1)\cdot P_{ZZ,k}\cdot K^T(k+1)\end{array}$$

(12)

Traditional KF and EKF perform Taylor series expansion at the estimated point, and then perform n-order approximation. Different from them, UKF performs UT near the estimated point to match the mean and variance of the obtained sigma point set with the original statistical characteristics, and then directly performs nonlinear mapping on these sigma-point sets to obtain the state probability density by using statistical approximation methods [30].

3. Design of State Estimation Basing on IMM-AUKF

The main idea of the Interacting Multiple Model (IMM) algorithm is to realize automatic recognition and switching of multiple models based on Bayesian theory [31]. At any tracking moment, set multiple model filters for real-time motion model detection, and set the weight coefficient as well as model update probability for each filter, finally obtain the current optimal estimation state through weighted calculation, so as to achieve model adaptation track. The following Figure 2 is the flow chart of the IMM-AUKF algorithm:

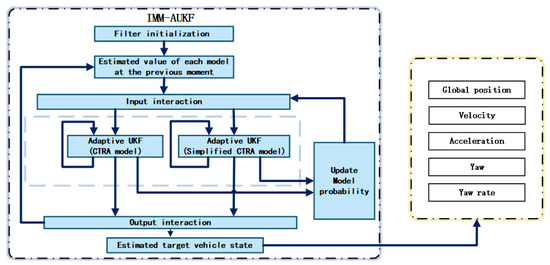
Figure 2. Block diagram of IMM-AUKF algorithm.

It is assumed that the target has $r$ motion states, corresponding to $r$ motion models, and the transition between the models is determined by the Markov probability transition matrix of Equation (13), where $p_{ij}$ indicates that the target is transferred from the $i-\mathrm{th}$ motion model to the probability of the $j-\mathrm{th}$ motion model [32].

$$P=\left[\begin{array}{l}{p}_{11}\dots p_{1r}\\ \dots \dots \dots \\ p_{r1}\dots p_{rr}\end{array}\right]$$

(13)

IMM-AUKF algorithm are used to achieve recursive estimation, each recursion is mainly divided into the following four steps.

3.1. Input Interaction

Assuming that the current moment is $k$, take model $j$ as an example. According to the optimal state estimation ${\widehat{X}}_j(k-1|k-1)$, the covariance matrix $P_i(k-1|k-1)$ and the probability model of each filter ${\mu }_i(k-1)$ obtained by using the IMM-UKF algorithm at the last state estimation process, the hybrid state estimation and covariance are obtained. And the mixed estimation is used as the initial state of the current cycle, the parameter calculation process is as follows:

The predicted probability of model $j$ (normalized constant) is

$${\overline{c}}_j={\displaystyle \sum _{i=1}^r{p}_{ij}{\mu }_i(k-1)}$$

(14)

Then we propagate the hybrid probability from model $i$ to model $j$ based on output hybrid probability from last scan:

$${\mu }_{ij}(k-1|k-1)={\displaystyle \sum _{i=1}^r{p}_{ij}{\mu }_i(k-1)/{\overline{c}}_j}$$

(15)

Finally, the output estimated state and covariance of model $j$ is

$$\{\begin{array}{l}{\widehat{X}}_{0j}(k-1|k-1)={\displaystyle \sum _{i=1}^r{\widehat{X}}_i(k-1|k-1)}{\mu }_{ij}(k-1|k-1)\\ P_{0j}(k-1|k-1)={\displaystyle \sum _{i=1}^r{\mu }_{ij}(k-1|k-1)}\{P_i(k-1|k-1)\\ +[{\widehat{X}}_i(k-1|k-1)-{\widehat{X}}_{0j}(k-1|k-1)]\\ \cdot {[{\widehat{X}}_i(k-1|k-1)-{\widehat{X}}_{0j}(k-1|k-1)]}^{\mathrm{T}}\}\}\end{array}$$

(16)

3.2. Adaptive Parameter UKF

When the vehicle-mounted sensor tracks the state of the preceding vehicle, due to the interference of various factors, the data filtered by the UKF may contain other noise values, which will inevitably increase the error of the filtering and noise reduction. In order to solve this problem, the AUKF algorithm is implemented by combining the UKF and Sage-Husa filtering algorithms [33]. The Sage-Husa adaptive filter enables colleagues who use the original data to filter and reduce noise, and correct the system noise variance in real time, which greatly improves the filtering. Combining Equation (17), the adaptive parameter process is as follows:

$$\{\begin{array}{l}{\epsilon }_{k+1}=Z(k+1)-Z(k+1|k)\\ d_{k+1}=\frac{1-b}{1-b^{k+1}}\\ R_{k+1}=(1-d_{k+1})R_k+d_{k+1}\cdot {\epsilon }_{k+1}\cdot {\epsilon }_{k+1}^T\\ Q_{k+1}=(1-d_{k+1})Q_k+d_{k+1}({\epsilon }_{k+1}\cdot {\epsilon }_{k+1}^T\cdot k_{k+1}^T+P_{k+1})\end{array}$$

(17)

where $b$ is the forgetting factor, which is generally $0.95\le b\le 0.99$.

Use Equations (16) and (17) and millimeter-wave radar measurement values $Z(k)$ as input to the UKF mentioned in Section 2.3, then use the adaptive parameters mentioned above to update the prediction state ${\widehat{X}}_j(k|k)$ and filter covariance $P_j(k|k)$.

3.3. Update Model Probability

Use the maximum likelihood function to update the model probability, and the likelihood function of model $j$ is:

$${\Lambda }_j(k)=\frac{1}{{(2\pi )}^{n/2}|S_j(k){|}^{1/2}}\exp \{-\frac{1}{2}{\nu }_j^T{S}_j^{-1}(k){\nu }_j\}$$

(18)

where:

$$\{\begin{array}{l}{\nu }_j(k)=Z(k)-H(k){\widehat{X}}_j(k|k-1)\\ S_j(k)=H(k)P_j(k|k-1)H{(k)}^T+R(k)\end{array}$$

(19)

Now, the probability of model $j$ can be parameterized as:

$${\mu }_j(k)={\Lambda }_j(k)\cdot {\overline{c}}_j/c$$

(20)

where $c$ is the normalization constant:

$$c={\displaystyle \sum _{j=1}^r{\Lambda }_j(k)\cdot {\overline{c}}_j}$$

(21)

3.4. Output Interaction

Based on Equations (14)–(21), the estimation results of each filter are weighted and combined to obtain a comprehensive state estimation and covariance estimation. Total estimated state and covariance is as Equation (22) shown

$$\{\begin{array}{l}\widehat{X}(k|k)={\displaystyle \sum _{j=1}^r{\widehat{X}}_j(k|k)}{\mu }_j(k)\\ P(k|k)={\displaystyle \sum _{j=1}^r{\mu }_j(k)\{P_j(k|k)}\stackrel{}{+[{\widehat{X}}_j(k|k)-X}(k|k)]\cdot {[{\widehat{X}}_j(k|k)-\widehat{X}(k|k)]}^{\mathrm{T}}\text{}}\end{array}$$

(22)

The above is a filtering derivation process of the IMM-UKF tracking algorithm. Each time, the previous interactive output is used as the next interactive input value, thereby completing the entire filter tracking process loop.

4. Testing and Analyzing

4.1. Experiment Introduction and Evaluation Indicators

In order to test the effectiveness of proposed IMM-AUKF algorithm, we use Carsim to set up a road as shown in Figure 3. The road contains straights, left turns, and right turns and other elements, which are used to simulate the four driving environments in our daily life: the target vehicle (t) and host vehicle (h) are all in a straight road, t enters a turn and h is still in the straight road, both cars are in a curve, and t leaves a turn and h is still in the curve.

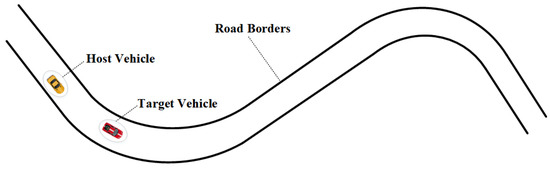
Figure 3. Schematic diagram of the experimental scene.

In the four scenarios, the virtual radar obtains the relative motion information of the target vehicle, and transmits it to the IMM-AUKF estimator established in the Simulink environment in real time through the interface to realize joint simulation. The criteria that are used to evaluate the performance of each filter are based in the calculation of the estimation errors of the actual distance. The best filter is the one that minimize the mean of filtering error $\overline{e_x(k)}$ and the standard deviation ${\sigma }_{\stackrel{⌢}{x}}$.

$$\{\begin{array}{l}\overline{e_x(k)}=\frac{1}{M}{\displaystyle \sum _{i=1}^M[x_i(k)-{\widehat{x}}_i(k|k)]}\\ {\sigma }_{\stackrel{⌢}{x}}=\sqrt{\frac{1}{M}{\displaystyle \sum _{i=1}^M{[x_i(k)-{\widehat{x}}_i(k|k)]}^2}-{[\overline{e_x(k)}]}^2}\end{array}$$

(23)

where $M$ is the number of MonteCarlo simulations, it is $k=1,2,\dots ,n$, n is sampling times, we take n = 50.

4.2. Results Analysis

Figure 4 is the trajectory estimated by IMM-AUKF, and Figure 5 is the speed, acceleration, yaw and the yaw rate estimated by IMM-AUKF. It can be seen from the simulation results that whether the target vehicle is driving in a straight line or a curve, the filtering outputs are all small fluctuations near the actual value.

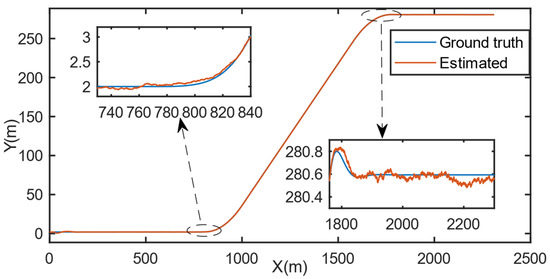
Figure 4. Global position estimated by IMM-AUKF.

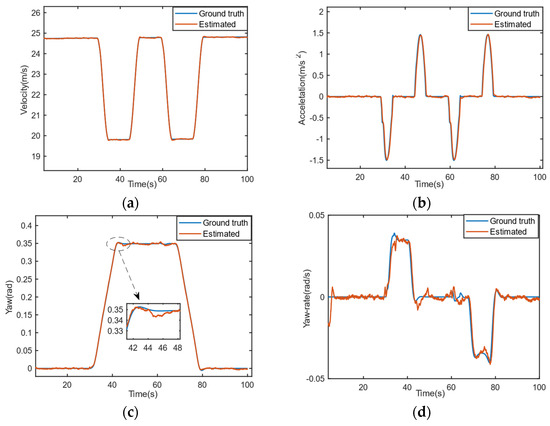
Figure 5. Target vehicle state estimated by IMM-AUKF. (a) velocity, (b) acceleration, (c) yaw, (d) yaw rate.

Figure 6 and Figure 7 shows the estimation error and standard deviation estimation error for each state respectively. It can be seen from the curve that because there are two turns, there are four large fluctuations in the error before and after the turn. When the trajectory of the target becomes a uniform motion, the error curve returns to zero with small fluctuations.

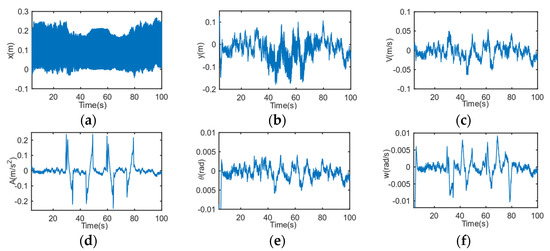
Figure 6. Estimation error of IMM-AUKF for multi-states. (a) x-direction, (b) y-direction, (c) velocity, (d) acceleration, (e) yaw, (f) yaw rate.

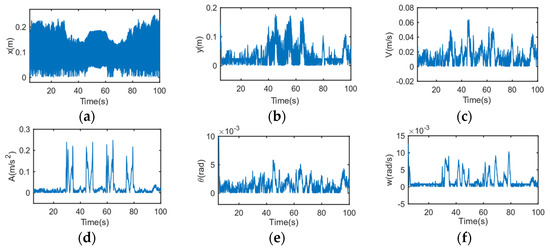
Figure 7. Standard deviation estimation error of IMM-AUKF for multi-states. (a) x-direction, (b) y-direction, (c) velocity, (d) acceleration, (e) yaw, (f) yaw rate.

4.3. Ablation Experiment

4.3.1. Comparative Analysis of Multi-model and Single-Model Estimation

It can be seen from Figure 8 and Figure 9 that the IMM-UKF algorithm performs better than the CTRA-UKF/simplified CTRA-UKF algorithm when the target vehicle is traveling in a straight line; when the target vehicle is traveling on a curve, the IMM-UKF model performs better than the Simplified CTRA-UKF/simplified CTRA-UKF algorithm. This is because the IMM algorithm in this paper uses two models to describe the possible state of the target vehicle during driving, and then uses effective weighted fusion to estimate the system state, which overcomes the single-model state estimation in different motion modes (straight roads, Corners) poor performance when switching.

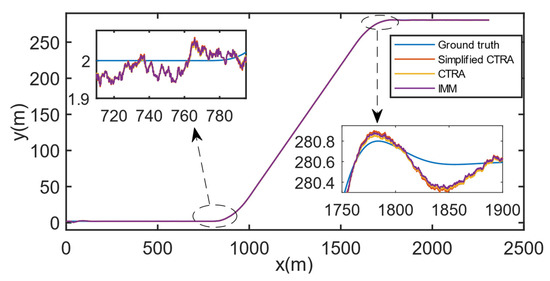
Figure 8. The performance of different estimation methods on global position.

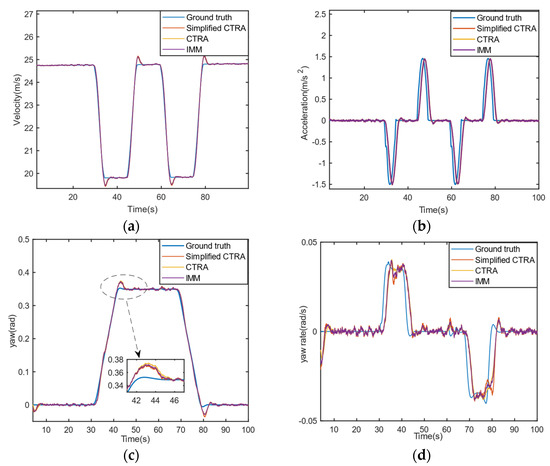
Figure 9. The performance of different estimation methods on multi-states. (a) velocity, (b) acceleration, (c) yaw, (d) yaw rate.

4.3.2. Comparison of AUKF and UKF Based on Multi-Model

Figure 10 and Figure 11 are comparisons results of IMM-UKF with IMM-AUKF. It can be seen that after the step of parameter adaptation is added, the filtering result is closer to the real value, and the problem of large delay in state estimation in filtering is eliminated.

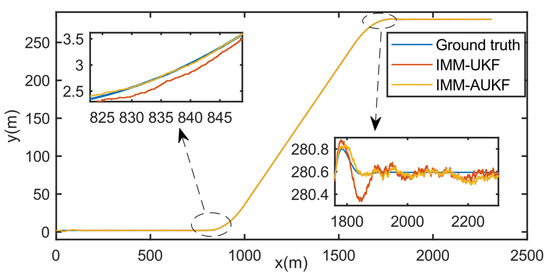
Figure 10. The performance of different estimation methods on global position.

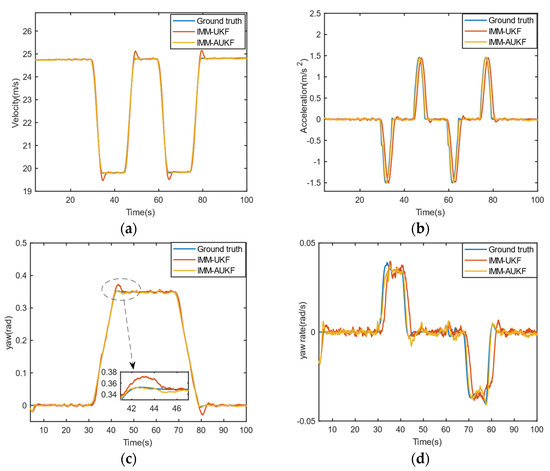
Figure 11. The performance of IMM-UKF and IMM-AUKF on multi-states. (a) velocity, (b) acceleration, (c) yaw, (d) yaw rate.

Table 1 shows the mean value of the standard deviation of 4 models. It can be seen that the state estimation filtered by IMM-AUKF is closer to the actual states of the tracked object, and its performance is more stable when switching between different states.

Table 1. The STD error of different estimation methods on different driving environment.

Motion	CTRA	Simplified CTRA	IMM-UKF	IMM-AUKF
Drive straight	0.0461	0.0464	0.0459	0.0379
Cornering	0.1480	0.1325	0.1387	0.0411

5. Conclusions and Future Work

In this paper, based on Interacting Multiple Model theory and parameter adaptation strategy, a real-time target vehicle state estimation algorithm is proposed. We use the Constant Turn Rate and Acceleration (CTRA) theory to establish the target vehicle kinematics model, and add its simplified version combine with IMM algorithm to improve the estimator performance in dealing with different driving environments. Additionally, in order to enhance the stability of the proposed algorithm, we add parameter adaptation process to the UKF algorithm to overcome the uncertainty of the noise model. Carsim and Simulink co-simulation results show that our proposed algorithm performs better than the single-model state estimation algorithm on accuracy and stability.

In the future, we will use public datasets to validate our proposed algorithm, and consider applying multi-sensor fusion algorithm to enhance the robustness of the algorithm.