An Enhanced Localization Approach for Energy Conservation in Wireless Sensor Network with Q Deep Learning Algorithm

Abstract

Wireless Sensor Networks (WSN) have distributed a collection of tiny sensor nodes deployed randomly in the given symmetry environment to sense natural phenomena. The sensed data are disseminated symmetrically to the control station using multi-hop communication. In WSN, the energy conservation during node coverage plays a major role in detecting node failure and providing efficient and symmetrical data transmission to the nodes of WSN. Using the cluster method and efficient localization techniques, the nodes are grouped and the precise location of the nodes is identified to establish the connection with the nearby nodes in the case of node failure. The location accuracy is achieved using the localization estimation of the anchor nodes and the nearest hop node distance estimation using the received signal strength measurement. The node optimization can be performed efficiently by the accurate estimation of the localization of the node. To optimize the node coverage and provide energy efficient and symmetrical localization among the nodes, in this paper, a cluster-based routing protocol and a novel bio-inspired algorithm, namely, Modified Bat for Node Optimization ($MB-NO$), to localize and optimize the unknown nodes along with the reinforcement-based Q learning algorithm is proposed with the motive of increasing the accuracy estimation between anchor nodes and the other neighbor nodes, with the objective function to optimize and improve the nodes’ coverage among the network’s nodes in order to increase the nodes’ localization accuracy. The distance metrics between the anchor nodes and other neighbor nodes have an estimated symmetry with three node positions, namely C-shape, S-shape and H-shape, using the Q learning algorithm. The proposed algorithm is implemented using the NS3 simulator. The simulation results show that the accuracy and precision of the proposed algorithm are achieved at 98% in the node coverage optimization with reduced Mean Localization Error (MLE) and computational process time compared with other bio-inspired algorithms, such as Artificial Bee Colony optimization and Genetic Algorithms.

1. Introduction

A Wireless Sensor Network (WSN) is a distributed collection of tiny sensor nodes which are assumed to be the self-operating and esteemed networks which can process the communication, sensing and distance estimation between the nodes in the network. Node coverage and localization are two of the main concerns involved in WSN for energy-efficient data communication [1]. In many wireless sensor network applications, the location information from which the data were obtained is necessary. As a result, the location of sensor nodes affects WSN performance. Compared to other methods, the original bat optimization technique has a lower mean localization error and takes less time to compute, but its localization efficiency is lower than 100% and it tends to get stuck at a local ideal value [2]. Most of the existing systems’ node coverage optimization and localization algorithms fail to accurately estimate the location of the nodes. Moreover, they fail to optimize node coverage, which will result in partitioning the network into disjointed segments. Therefore, providing efficient node coverage with accurate node location estimation in the network is needed to establish the connectivity among the nodes in the network [3]. The node coverage optimization and localization identification of the nodes are addressed by using the various algorithms in soft computing and Bio-inspired models. Particle Swarm Optimization (PSO) is a straightforward bio-inspired algorithm that finds the optimal solution; this algorithm is different from the other, following optimization techniques because it is not dependent on any gradient or any differential form of objectives, it needs only objective function. In addition, less hyper parameters are in use [4]. Various PSO and evolutionary algorithms have been applied to the WSN to provide an efficient solution to network node optimization, node localization, node clustering and node segmentation. The PSO algorithms work on the node with the node coverage problem to enhance the network lifetime and the coverage rate among the nodes in the network [5]. In WSN, PSO algorithms have been used to estimate the localizations of the nodes based on the angle measurement between the sensor nodes and the anchor node. Metrics such as the packet delivery ratio between the nodes are used to determine the angle measurement of the nodes in sensor nodes, time of arrival of the packets and range of the received signal strength [6].

Moreover, the PSO algorithms have been applied to WSNs to enhance the quality of service and provide energy-efficient data dissemination in a wireless sensor network. The bio-inspired algorithms have an efficient proposal for predicting the unknown nodes in the localization area and enhancing the various optimum node estimation parameters [7]. For the node coverage optimization challenges, the Bat Algorithm has been used to simulate the echolocation behavior of a bat. The Bat Algorithm has been employed, along with the various evolutionary algorithms, to provide the optimal solution to the node coverage and node localization problems in WSN. The node localization is estimated with the received signal strength; hence, the data are assumed to be from the proper location [8]. The unknown nodes near the sensor nodes are estimated with the analysis of the unknown sensor nodes, which are closer to the neighbor nodes and are taken into account in the known locations. While estimating the location of the unknown node using the node coverage parameters, it is essential to monitor the computational cost, and the received signal should not accumulate the data inferred in the optimal allocation [9]. The optimal constraint is analyzed with the hop node communication, and the distance is measured with hop-1 parameters multiplied by the total distance estimation. The PSO, Ant Colony Optimization algorithm (ACO) and The Artificial Bee Colony (ABC) algorithm are the estimation algorithms which identify the node localization using the received signal strength for the unknown node address. All these algorithms have been proposed to estimate a better accuracy in the proposed node analysis parameters. However, all these algorithms are not accurate in detecting the location of the unknown nodes and fail to optimize the node’s coverage in the WSN [10]. Motivated by all these observations, a novel bio-inspired algorithm, namely, the Bat Algorithm (BA), is based on the way the microbats use echolocation. In terms of accuracy and efficiency, BA is far better than other current usage algorithms. Due to a bat’s inability to thoroughly search every direction in the search area, the BA has an extremely low success rate. In order to solve this issue, the algorithm is modified as the Modified Bat for Node Optimization (MB-NO) algorithm to reduce the energy conservation. This is proposed, along with the Q learning method proposed in this paper, to optimize the node coverage and accurately estimate the sensor nodes’ proposed localization. Q learning is one of the reinforcement learning algorithms which is not dependent on any data model, i.e., model free learning; reinforcement learning is the subfield of Machine Learning that develops a model’s ability to solve issues at their best on its own. Moreover, the proposed method provides energy conservation during node coverage and localization of the nodes in WSN [11]. The layer-wise assumption in the node segments of the proposed system is shown in Figure 1 along with the node-based cluster creation.

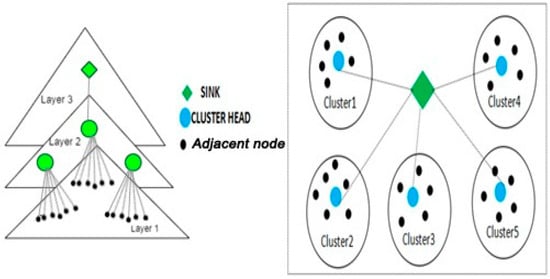
Figure 1. Node-based optimization using cluster in WSN.

The major research contributions are:

• This paper outlines the node coverage optimization in WSN using the Modified Bat for Node Optimization$\left(MB-NO\right)$algorithm to enhance the node coverage and reduce energy consumption to provide efficient sensor node localization.
• A novel $MB-NO$ algorithm, along with Q learning, has been proposed to widely analyze the accuracy of the node localization and the sensor node precision coverage with the shortest hop distance nodes estimation.
• The precision estimation is enhanced for the node coverage in WSN with the help of the received signal strength in the sensor nodes using the novel bio-inspired $MB-NO$ algorithm.
• The objective function used is the number of nodes and the transmission time (ms), that is defined as:

$$O_f=\mathsf{\Sigma } N\left(i\right)\ast Tt$$

The Q learning approach to segment the sensor nodes and the localization accuracy is optimized in the proposed system.

The paper has been organized as follows: Section 1 outlines the “Introduction”, Section 2 covers the “Related Works”, and Section 3 proposes the “Network Model and Problem Formulation” with energy optimization to perform the node optimization. Section 4 proposes the “Modified Bat for Node Optimization ($MB-NO$)” algorithm-based node optimization with secure Q learning-based communication. Section 5 performs the “Performance Evaluation and Results”. Section 6 includes the “Conclusion and Future Work”.

2. Related Works

Various authors have proposed methods to optimize node coverage and accurate location estimation in WSN. Some of the methods proposed in the literature include the following: Neng et al. [12] has proposed joint node selection, flow routing and cell coverage optimization for network sum-rate maximization in wireless sensor networks. In their approach, the authors have proposed joint node selection for routing packets in the network. Moreover, the authors have proposed cell coverage optimization using sum rate maximization in WSN to enhance node coverage optimization. Their method’s limitations are less accurate in detecting the nodes’ location, and there is a network coverage problem. Lenka et al. [13] and Ghosh et al. have proposed remote sensor systems which play a crucial role in incalculable applications. The fundamental capacity of WSN is to measure extricated information and to communicate it to distant areas. The inclusion and availability issues of the node’s lifetime are the primary concerns to be considered in this paper [14].

Eleni et al. [15] has outlined that Wireless Sensor Networks (WSNs) comprise an Fe battery-controlled sensor hub. The detecting inclusion of the Field of Interest (FoI) is a significant capacity of the sensor hubs in associated WSNs. An FoI is supposed to be canvassed if each point in the FoI is checked by any event. Due to the small size and battery power, there are limited connectivity and coverage issues addressed in the paper by Choudhary et al. [16], who has proposed a smart Bat Algorithm in WSN to optimize the connectivity in WSN. The smart Bat Algorithm has been applied to the 3D environment to optimize the network coverage and connectivity in WSN. The limitations of their approach are the connectivity exit and connection issues in their system. Shen et al. [17] have proposed an ant colony optimization approach for maximizing the lifetime of heterogeneous wireless sensor networks. The advantage of their approach is its energy conservation, and the limitations are their network connectivity and node coverage. Singh et al. [18] have proposed a system where the grid-based deployment of sensor nodes is used to quantify the connectivity issue in WSN. In their system, the sensor nodes are organized as grids so that the distance between the deployed modes is uniform. The limitation of their approach is that there is no coverage optimization, and, hence, it consumes more energy during the network node’s connectivity. Mohar et al. [19] has investigated a productive network based on the organization anticipating the availability of the network when sensors are situated and influenced by arbitrarily limited blunders around their comparative lattice vertices. They have proposed another way to assess the normal availability level of the sent sensor hubs. They have applied pragmatic 3D arrangement situations to form the cubic framework based on an organization with limited uniform irregular mistakes. The normal availability rate is registered mathematically and confirmed by broad reenactment results. Nieoleseu et al. [20] has proposed a system where the arrangement of remote sensor nodes is exceptionally reliable, based on the objective condition. When the attributes of the ideal territory are known, the subject of system size emerges. Elements such as transmission power level, cost of system organization and the inclusion territory legitimately influence the size of the system. This paper dissects the conduct of an average multi-bounce remote sensor that arranges it to work in an outside situation.

Poongudi et al. [21] has proposed Q learning-based two-tier data dissemination in WSN. In their system, the network is organized into two tiers. The first tier is responsible for node coverage, and the second is used for data dissemination in WSN. The limitations are that it suffers from scalability and node coverage optimization in WSN. Zidong et al. [22] have proposed a reliable routing infrastructure for green IoT. The proposed system’s major aim is to conserve energy during data communication. The limitation of their approach is that they only focus on energy conservation and not on localization and node optimization in IoT networks. Rimpy et al. [23] have studied Medium Access Control (MAC) for remote sensor systems (WSNs) under the Irregular Repetition Slotted ALOHA (IRSA) convention. Specifically, they upgrade the degree conveyance utilized by IRSA for limited casing sizes. Their model employs IRSA as a Decentralized Partially Observable Markov Decision Process (Dec-POMDP). The proposed system results are nonexclusive regarding node coverage optimization in WSN. F. Anwar et al. [24] has proposed Distance Vector based node localization in WSN. Their system estimates the location of the nodes precisely by using the distance vector calculation of the nodes in the network. The limitation of their system is that the DV calculation is not accurate. Therefore, it leads to the node coverage optimization problem in WSN. Poongudi et al. [25] has proposed the indoor localization algorithm for WSN in an NLOS environment. The proposed system provides an efficient method to locate the nodes and optimize the node coverage in WSN. This method’s limitations are exiting node coverage and an optimization problem in WSN.

J. Wang et al. presented that in the misfortune situations, dynamic sensors are regularly utilized for localization in WSNs. Be that as it may, many of the current localization calculations are intended for the static hubs in WSNs. This paper presents an overview of localization calculations in versatile remote sensor systems: mechanical technology localization calculations, Monte Carlo-based portable localization calculations and without-range-based portable localizations. This paper leads to an examination of cutting-edge portable localization calculations [26]. The author proposed that executing situating frameworks for indoor conditions is famously troublesome. The immense range of communicating boundaries, for example, furniture, room shape and materials, imply that the reenactment of such a situation is of restricted worth. We present results from an observational examination regarding the feasible precision of a Radio Frequency (RF) situating framework, dependent on signal quality. Techniques to improve certainty, for example, recurrence averaging and bi-directional going, are investigated. At last, we introduce and assess a novel technique for adjusting the channel engendering type with no earlier information on the sensor organize format or room shape [27]. In remote sensor systems, sensor position vulnerability debases the precision of the vitality-based objective confinement, accomplished utilizing the Maximum Likelihood Estimation (MLE) techniques. In this paper, we built up another MLE approach that fuses a model of sensor position vulnerability. Recreations showed that our new MLE approach outflanked an MLE approach that does not represent sensor position vulnerability. Root–Mean–Square (RMS) assessment mistakes for target confinement were near the Cramer-Rao lower bound (CRLB).

Sivagami et al. [28] proposed a novel mixture enhancement calculation, a molecule swarm streamlining the counterfeit honey bee province (PSO-ABC), given the PSO and ABC calculations. The ABC calculation can counterbalance the PSO calculation that effectively falls into a nearby advancement; consolidating the calculations can somewhat improve the PSO calculation’s enhancement capacity. Along these lines, this paper applied the PSO-ABC mixture calculation and the limited component technique to methodically enhance the mechanical presentation of the plate rotor of a bicycle and confirmed the mathematical calculation model through the remote sensor arrange innovation. The exploratory test was finished with remote sensor arrange innovations. The calculation contrasted the conventional PSO and ABC models to confirm the advanced impacts of the proposed PSO-ABC cross-breed calculation after boundary choice. The PSO, ABC and PSO-ABC models received a similar populace to direct a multi-target advancement for vibration-increasing velocities of the circle rotor. The outcomes from these models demonstrated that the proposed PSO-ABC technique is prevalent for advancing the vibration qualities of the circle rotors.

Per M. L. Bharathi et al. [29]., remote sensor systems are outstanding systems that include organized gadgets in enormous numbers and spatial dissemination. They have distinctive detecting limits and take an interest in completing basic undertakings. It is recorded as a hard copy outline where thickness matrix-based bunching in WSN has improved the execution of the WSNs by using social event-based data collection. Regardless, no improvement strategy is considered for the effective course determination in thickness matrix-based bunching. This paper proposes two new methodologies. For example, fake honey bee province is a multitude-based enhancement procedure for vitality proficient steering calculation, and compressive detecting is, likewise, used to expand the vitality rate or execution. The proposed procedure has demonstrated very critical improvement over accessible ones [30]. In a paper by F. Anwar et al., in vitality constrained remote sensor system WSNs, the methods to perform strong direction are among the fundamental core interests. A respectable methodology of insect state advancement ACO calculation for finding the ideal course in the WSNs for information transmission is proposed here for improvement and streamlining, considering the method by which to arrive at the hubs. Utilizing the proposed ACO calculation and considering both the hub portability and the current vitality of the hubs, an ideal course and the best expense from the starting hub to the objective hub is identified. The proposed calculation has been reproduced and confirmed using MATLAB. The reenactment results show that a new subterranean insect province enhancement-based calculation can accomplish better execution and quicker assembly by which to decide on the best cost course [31].

An intelligent Distance–Vector (DV-Hop) [32] calculation for finding hubs has been developed to address the problem of the helpless finding execution in unique DV-Hop calculations. One of the without-range computations in Wireless Sensor Networks (WSN) was proposed in this paper. Considering the impact of dynamic geography, the self-versatile fake honey bee province calculation was discovered by gauging the obscure hub area. Recreation results show that the new calculation has better finding execution exactness and accuracy steadiness than DV-Hop calculation with no extra gadgets and correspondence overhead. Therefore, it is an additionally encouraging finding plan in WSNs, with irregular dispersing hubs and dynamic geography.

Satinder Singh Mohar et al. [33] proposed a work to improve the localization efficiency with a decrease in error. The simulation result showed that the performance of the proposed algorithm produced an efficient result when compared with other algorithms, but the demerits are that it produced the best result for a short distance only, and cannot provide a proper response over a large geographical area.

3. Network Model and Problem Formulation

Let $N=\left\{N_1,N_2,N_3,\dots N_n\right\}$ be the set of sensor nodes, and each node is assumed to have constant transmission parameters and also to have equal participation in the deployed environment. Let $U=\left\{U_{N1},U_{N2},U_{N3}\dots U_{Nn}\right\}$be the set of unknown nodes, set where the location of the nodes is not known. The unknown set of nodes may be operating with the sensor nodes to estimate the sensor pair in the neighbor nodes, determined as $N_{SN}=\left\{N_{SN1}, N_{SN2}, N_{SN3},\dots \dots N_{SN},\right\}.$ Hence, the sensor node is united to form a parametric assumption $N=U{\displaystyle \cup }$$N_{SN}$. By combining the operating parameters with the unknown locations and the coverage, the node coverage optimization is calculated [2]. The node coverage is estimated using the N pairs N (Xm, Yn), where the adjacent nodes are marked with $U=m-1,m-2,m-3$ and the nearest hop nodes are estimated using the $U=n-1,n-2,n-3$. The hop distance is estimated using the distance between the N pairs of the sensor nodes and hop = N$U\cup$. In addition, the distance denoted as $h{d}_{m, n}^{est}$ and the probable actual attained distance are estimated using the $h{d}_{m,n}^{act}$.

In order to enhance network coverage among the nodes in a wireless sensor network (WSN), the position of the sensor nodes is determined using the hop distance. The error variation in the received signal strength is assumed to be minimal in count in the determined place. The number of sensor nodes increases when the hops are increased with the sensor pairs. The distance metrics between the different sensor nodes and the adjacent nodes have been obtained using the formula $U=n-1,n-2,n-3$ estimated nodes. The proposed localization and node optimization have been applied to WSN using the bat and the Q learning algorithms. In the proposed system, the received signal strength is used to enhance the localization of the unknown nodes. The average error distance between the sensor nodes and neighbor nodes is estimated using the sensor nodes. The shortest distance between the sensor and unknown nodes is estimated by measuring the distance in the reception parameters. Nm is assumed to be of the ‘m’ segments in the measurable distance, and the segment is completed with the localization values. The estimation accuracy of the proposed method is estimated with the Est_Am for the m-segment sensor nodes in the WSN. The average distance error AVG _disterror is the error where the process of the sensor nodes and the unknown nodes estimation is performed using the anchor sensor nodes to estimate the localization of unknown nodes in the network. Table 1 outlines the list of notations used in the proposed system.

Table 1. Notations used in the proposed system.

Parameters	Details
N	Sensor nodes group
{N1,N2,N3,…Nn}	Set of sensor nodes
U	Unknown nodes
NSN	Neighbor nodes
$N=U{\displaystyle \cup }$$N_{SN}$	Coverage optimization
N (Xm, Yn)	Node coverage
X	Adjacent nodes coverage parameter
Yn	Nearest hop nodes
U = m−1, m−2, m−3	Adjacent node
U = n−1, n−2, n−3	Nearest hop node estimation
hop = N$U\cup$	Hop distance
$h{d}_{m, n}^{est}$	Nearest hop distance estimation
$h{d}_{m,n}^{act}$	Nearest hop distance actual
EA	The average error in distance between the sensor and adjacent nodes
SD	Shortest distance between the sensor and unknown nodes
Nm	Sensor nodes in the m segments
EstAm	Estimation accuracy of the sensor nodes
AN	Set of the unknown nodes in the coverage area
AVG disterror	Average of the distance in the estimated and the actual
TSN(i)	Threshold values of sensor network
ED	Euclidean distance
Pr ch	Probability of percentage in cluster head
Psn	Probability of sensor nodes
Es	Sensor node energy
Esrc,dest	Energy of source node and destination node
RXE	Received energy
Tn	Total number of nodes
Rt	Range of transmission nodes

3.1. Node Clustering Using LEACH Protocol

WSN is susceptible to energy conservation, which depends on the network model and will affect the network’s lifetime. The network life depends on the routing protocol used in the network. The deployment of nodes takes place in the network and plays a major role where the network nodes can obtain the maximum coverage. In the proposed system, the LEACH routing protocol has been used to deploy the moving nodes to optimize the route parameters based on the signal strength with the sensing domain. The node deployment involves a setup phase, where the clustering of the sensor nodes is formed, and all the information is communicated from the cluster head to the corresponding cluster nodes via the sink node. The cluster head collects the information from the nodes and sends it to the various anchors and the adjacent nodes in the network. The energy consumption in each node is assumed to be under control in each phase of the sensor selection. The energy consumption is assumed to be off in the cluster assumptions in the threshold values attained using balance analysis. The energy monitoring is conducted using the LEACH protocol with the interval range threshold value [1, 0]. The threshold value of the network is computed by using Equation (1):

$$TSN\left(i\right)=\{\begin{array}{c}\frac{probability of percentage in cluster head\left(p{r}_{ch}\right) }{1-probability of percentage in cluster head \left(p{r}_{ch}\right)} if m\in N\\ 0\end{array}$$

(1)

where $TSN\left(i\right)$ denotes the threshold values of the network.

The $probability of percentage in cluster head\left(p{r}_{ch}\right)$ is where ‘m’ denotes the number of nodes possible within the internal cluster communication, and ‘N’ denotes the set of sensor nodes possibly used within the framework estimation of the sensor nodes.

3.2. Energy Estimation for Node Coverage Optimization

In the proposed system, the Euclidean distance is used to compute the distance between the sensor nodes and the adjacent nodes by using the LEACH routing protocol. Equation (2) gives the Euclidean distance formula used in the proposed system.

$$E_D\left(N_i,D_j\right)=\sqrt{\left({\left(X_{i ,}{D}_{j }\right)}^2-{\left(Y_{i ,}{Y}_{j }\right)}^2\right)}$$

(2)

The distance measurement is computed with the obstruction of values analyzed with probability estimation using the sensor nodes and the adjacent nodes. Euclidean distance (E_D) is calculated using (X_i, D_j), (Y_i, Y_j), which are the two different coordinates. The nodes are aligned with the task of predicting the defined modelling using the LEACH protocol, which is shown in Equation (3).

$${\mathrm{Pr}}_{\mathrm{ch}} \left(N_i,D_j\right)=\{\begin{array}{c}0 I_{ri}\le E_{D }\left(N_i,D_j\right)\\ e^{-\gamma }\frac{E_{D }\left(N_i,D_j\right)-I_{ri}-I_{re}}{I_{ri}-E_{D }\left(N_i,D_j\right)} I_{ri}-I_{re}\le E_{D }\left(N_i,D_j\right)<I_{re} \\ 1 I_{ri}-I_{re}\ge E_{D }\left(N_i,D_j\right)\end{array}$$

(3)

The sensing error is identified in the sensor node using the $I_{re}$, and the radius is determined using the I_ri. The γ illustrates the sensing parameter and attenuation coefficient. The target coefficient is obscured with the sensor network using the assumptions in the probability evaluation, defined as Porch $\left(N_i,D_j\right)$, which is shown in Equation (4).

$$P_{sn }=1-{\displaystyle \prod }_{i=1}^N\mathrm{Prch} \left(N_i,D_j\right)$$

(4)

Figure 2 represents the formation of the cluster nodes between the nodes to monitor the energy conservation before the application of Bat implementation.

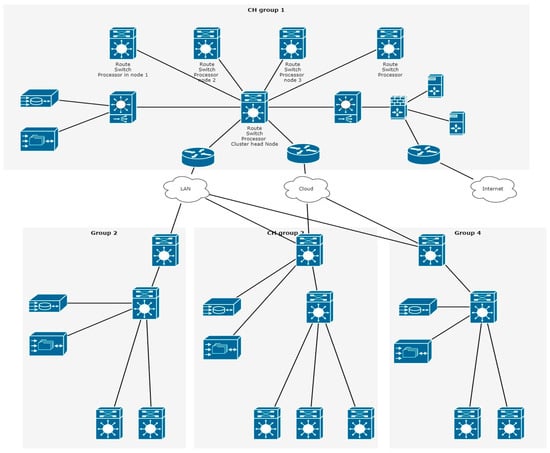
Figure 2. CH formation for node optimization with energy conservation.

The node coverage of the sensor node is illustrated by using the parameters in the received signal strength in each node of clusters, which is given in Equation (5):

$$E_{S\left(i\right)}=\left({\displaystyle \sum }_{i=1}^{Num}{\displaystyle \sum }_{Src\in CH}{E}_{Source} S{N}_{ch}+E_{RSSI}+E_{DA}\right)+{\displaystyle \sum }_{i=1}^{num}{E}_{dest} S{N}_{ch}+E_{Final}$$

(5)

Equation (5) shows the assumptions used in the network’s sensor node energy prediction using the LEACH protocol. Let $E_{Source}$ be the source node energy for the sensor nodes in clusters. $E_{RSSI}$ also predicts the energy of the received signal strength, and $E_{DA}$ is the data predicting the node in the transmission range. E_dest is the destination node energy. The destination is assumed to be within the mean values, and E_final is the final energy of the nodes that are assumed with the num values of the cluster head selection in the predetermined evaluation. The sensor nodes have been classified according to the metrics given in Table 2 for implementing the $MB-NO$ algorithm and Q learning parameters.

Table 2. Assumptions in energy monitoring using the cluster for $MB-NO$ algorithm.

Values	Estimations
−1	The sensor node and the route are assumed to be non-alive
0	The sensor node and the route are assumed to be of static or ideal mode
1	The sensor node and the route are assumed to be in the cluster head assumption
>1	A node acting as cluster head

The energy consumed in the proposed work can be estimated using the optimum coverage. The parameters for the optimum coverage are given in Equation (6):

$$E_{\mathit{Src},\mathit{dest}}=\{\begin{array}{c}{E}_{\mathit{consum} } X Z+E_{\mathit{dissip}}X Z X E_{D }\left(N_i,D_j\right) if E_{D }\left(N_i,D_j\right)<E_{D0} \\ E_{\mathit{consum} } X Z+E_{\mathit{utilised}}X Z X E_{D }\left(N_i,D_j\right) if E_{D }\left(N_i,D_j\right)\ge E_{D0}\end{array}$$

(6)

Let $E_{\mathit{Src},\mathit{dest}}$ be the energy consumption from the source node to the destination nodes in the network. Let the $E_{\mathit{consum} }$ be the consumed energy for all the sensor nodes, and the dissipation nodes for a neighbourhood with ‘z’ bits of data are transferred in the wireless communication environment. The Euclidean distance measures are used to identify the estimations using the forecasting model of the data in wireless communication. $E_{D0 }=\sqrt{\frac{E_{\mathit{dissip}}}{E_{\mathit{utilised}}}}$ shows the distance estimated with the Euclidean assumption in energy dissipated with the energy utilized. The data can be transmitted using the analysis below; hence, the sensor nodes are utilized in the data transmission.

3.3. Node Coverage Rate and Localization Optimization

The received energy is estimated based on the node energy dissipated and the energy utilized in the estimation. Hence, the utilized energy is obtained with the ‘z’ number of bits having the received signal strength in terms of ‘z’ bits forming a reception of node positioning in the WSN given in Equation (7):

$$R{X}_E=E_{utilised}X Z=\frac{E_{dissip}X Z }{E_{RSSI}}$$

(7)

The sensor nodes and the corresponding nodes utilize the maximum amount of reception in the node strength. Equation (7) satisfies the allocated energy for utilization in the node optimization using cluster analysis.

$$E_{Final}={\displaystyle \sum }{E}_{IN }+S{N}_a$$

(8)

The final average energy is assumed to be of inactive node energy consumption and active sensor nodes’ energy consumption, which is given in Equation (8). The falls are from the final sensor nodes in the active zones for the nodes to be perfect in the active region, as is shown in Equation (9):

$$S{N}_a=\{\begin{array}{l}1, if E_{Src,dest}\in Sr{c}_{CH} or E_{Src,dest}\in Sr{c}_{nonCH} \\ 0, otherwise\end{array}$$

(9)

The possible energy outcome has determined the node coverage rate, and the energy consumption is assumed to be of the sensor nodes in the adjacent node’s enhancement. The node process with the coverage accuracy is estimated using Equation (10). The target node coverage rate is estimated using the coverage node having the target of $\left({\mathit{SN}}_i\right) \mathrm{with} \mathrm{parameter}$s given in Equation (10):

$$T\left(i\right)={{\displaystyle \sum }}_{i=}^m{T}_c\left(S{N}_i\right)$$

(10)

The average task performed in each node is assumed to be in the highest coverage area of the sensor nodes, as given in Equation (11):

$$S{N}_i=\{\begin{array}{c}0 if E_{D }\in S{N}_{inactive} and E_{D }\le r_i\\ 1 otherwise\end{array}$$

(11)

The coverage rate is assumed to be of the active sensor nodes’ parameters and the nodes’ inactive assumption. The radius r_i assumes to be off the sensor node pairs in the segment. The final energy is assumed to be of the equilibrium-based energy options that prevail in the independent nodes. The energy equilibrium is used to obtain the final derivate of the sensor nodes’ active region coverage, as shown in the Equation (12):

$$E{N}_{equilibirum}=\frac{{{\displaystyle \sum }}_{i=1}^{n}E S{N}_{active}}{n}$$

(12)

3.3.1. Axiom 1

The energy maximization is obtained with the energy equilibrium in the network if the number of target nodes is assumed to be minimal, as given in the Equation (13):

$$E{N}_{equilibirum}\left(i\right)=\mathrm{Max} \left(S{N}_i\right)$$

(13)

3.3.2. Axiom 2

The energy minimization is obtained with the energy equilibrium if the number of target nodes is assumed to be correlated with the sensor node coverage, as given in Equation (14):

$$E{N}_{equilibirum}\left(i\right)=\mathrm{Min} (S{N}_i)$$

(14)

3.4. Node Localization Error

Identify the coordinates of the nodes to find the average localization error (Avg.LE), the coordinates of neighbor nodes (S_i, N_i) and the sensor nodes (s_i, n_i), which is outlined as below:

$$\mathrm{Avg}. \mathrm{LE}=\frac{1}{\mathrm{Tn}}{{\displaystyle \sum }}_{i=1}^{Tn}\sqrt{{\left(Si-si \right)}^2+{\left(Ni-ni\right)}^2}$$

(15)

Tn is the entire number of nodes.

The node localization is improved by inclined values of Avg. LE at Equation (15) and Unknown node (U) using optimization approaches. It is calculated as:

U = Sn − Tn

(16)

Sn—Sensor Nodes and Tn—Total nodes available.

Mean Localization Error (LE) is calculated by the normalized Average LE and the range of sensor nodes transmission (Rt).

$$\mathrm{Mean}. \mathrm{LE}=\frac{\frac{1}{\mathrm{Tn}}{{\displaystyle \sum }}_{i=1}^{Tn}\sqrt{{\left(Si-si \right)}^2+{\left(Ni-ni\right)}^2}}{Rt}$$

(17)

4. Modified Bat for Node Optimization ($MB-NO$)

The Bat Algorithm (BA) is a bio-inspired algorithm used as an optimization algorithm for checking the node essentials in the WSN. The network is formed using the sensor nodes, adjacent nodes and anchor nodes. Besides the problem incurred, energy-constrained localization and node optimization are the major perspectives in the proposed work. The Bat Algorithm works on the principle of echolocation, which emits a wave to find the nearest food source. The nearest location is obtained through bat sense power, even though the network is complicated. The ultrasound waves emitted by bats observe the reflection sound to obtain the nearest locations. The capacity of the bat is obtained using the velocity and position it travels. A bat is unable to investigate every route in the search arena; the BA has a relatively low success rate. Therefore, the present BA is updated to Modified Bat for Node Optimization ($MB-NO$) to address this issue. The proposed sensor nodes adjust the frequency. When the source node is identified, the Bat’s loudness decreases with increased frequency. The value of the fitness function determines the choice of bat movement and the effective search space exploration in the MB-NO algorithm. It outperforms the original Bat Algorithm in terms of computational time and the success rate of localized nodes.

Algorithm 1 represents the $MB-NO$ algorithm-based node classifications, and the optimization has been applied in the node source. The energy equilibrium is maintained throughout the big source of the network. The ultrasound waves emitted by bats observe the reflection sound to obtain the nearest locations. The capacity of the bat is obtained using the velocity and position it travels. The proposed sensor nodes adjust the frequency. When the source node is identified, the bat’s loudness decreases with increased frequency. The $MB-NO$ algorithm provides good comfort compared to the other GA algorithm; the energy equilibrium is assumed to be higher when dealing with the sensor nodes using Algorithm 1. The proposed algorithm focuses on the nearest neighborhood node in the $MB-NO$ nearest food locator. For the nearest node, once established, the $MB-NO$ will work on the node to establish communication using the frequent frequency estimation. The node optimizer may support the process using the SN_i. The objective function is obtained in the search space using the node estimator. The fitness function is applied to identify the nodes which establish secure communication. The search space will provide the best communication using the algorithm, and the optimization needs to be retrieved using the $MB-NO$ module in the WSN. The generated solution was established with the node observation’s storage solution. The energy in the node optimization is acquired using the various sensor nodes established. The step-up process of implementing the $MB-NO$ algorithm for the sensor nodes process is shown in Figure 3.

Algorithm 1: Adjacent node formation and node optimization using MB-NO algorithm

1. initialize ${\mathrm{SN}}_i\in N//$Set of Nodes 2. for all j $\in T\left(i\right)\mathrm{do}$ 3.    if ${\mathrm{SN}}_a\ne \varnothing$, then 4.     Optimization Bat $\forall {\mathrm{SN}}_i\left\{\mathrm{Freq},\mathrm{Node} \mathrm{location},\mathrm{Node} \mathrm{energy} \mathrm{limits}\right\}$ 5.     Select ${\mathrm{SN}}_{\mathrm{CH}}$ with cluster head formation for node optimization 6.    else 7.   ANj is selected according to the $P_{\mathrm{sn} }=$ ${\mathrm{SN}}_a\in$ ${\mathrm{SN}}_i$//Adjacent Node pair se lection from cluster 8.   do the process repeatedly 9.    ${\mathrm{SN}}_{i }\left\{\mathrm{Freq},\mathrm{Node} \mathrm{location},\mathrm{Node} \mathrm{energy} \mathrm{limits}\right\}$=$(\left\{{\mathrm{SN}}_i\right\}, i\in m,$ ${\mathrm{SN}}_a\ne \varnothing$) 10.    for all i $\in P_{\mathrm{sn} }\mathrm{do}$ 11. if ${\mathrm{SN}}_a\ne \varnothing$ then//Nearest optimal Node is obtained 12.    a collects the active nodes using the MB-NO algorithm $\forall i\in {\mathrm{SN}}_i$ 13.        ${\mathrm{EN}}_{\mathrm{equilibirum}}$ = $\varnothing$ 14.        for all [ i $\in \left[{\mathrm{SN}}_a\in N\right]$ N$\ne \varnothing$] do 15.            if ${\mathrm{EN}}_{\mathrm{equilibirum}} ,{\mathrm{SN}}_a$ $\ne \varnothing$ then 16.            N= Min $({\mathrm{SN}}_i$) 17.            else//energy is not conservator, and localization failed 18.            ${\displaystyle \sum }_{i=}^m{T}_c\left({\mathrm{SN}}_i\right)$//The energy equilibrium is obtained 19.        $\forall j\in N,{\mathrm{SN}}_i$ = $\left\{i\right\}$//Node optimised with conservative energy 20.        else 21.    ${\mathrm{EN}}_{\mathrm{equilibirum}}\left(i\right)$ = Max $({\mathrm{SN}}_i$)//Maximum energy utilised and node fails. 22. end if 23. {freq, veloci } increase in the number of nodes and reduce the computation time.//calculate using the formula (15), (16) $25$.   if (current algo. mean error < existing algo. mean error)//connect the nodes $26$.   else $27$.   change the frequency and node location. $28$. end if

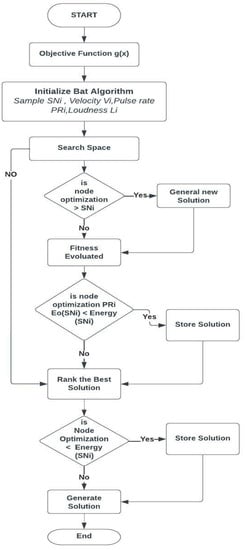
Figure 3. Implementation of $MB-NO$ algorithm to estimate the node optimization and energy conservation.

Q Learning-Based Secure Communication

Reinforcement Learning uses the original neighbor nodes to behave in the way of predicting the sensor node pair using the trustable nodes when there is a lack of secure nodes in wireless communication. The Q learning algorithm is used in the WSN, where the agent ‘a’ performs an action based on the environment’s current working ‘s’ state. The action is used to analyze the node behavior in the WSN environment. The state of the WSN behaves in such a way that the state may change from one state to a new state ‘$s_1$’. The WSN employs the Bat Algorithm for the node optimization where the node can be performed. The learning policy, which is assumed to be of Q learning, proposes the mapping context.

Moreover, Q learning is an open structured Algorithm 2 that allows the below axioms.

(a)

The WSN has various sensor nodes operating in a different obscured environment; here, the sensor nodes are mapped with the agent for the RL process and the environment with the RL-based learning approaches.

(b)

The action space and state space are compared with the agent task and the working state of the corresponding sensor nodes in the working environment.

(c)

The task set of the sensor nodes and the working set of the anchor nodes is obscured by the nature of the state space. The applications of the WSN are mapped with the task set of the RL algorithm. The sensor nodes and the related nodes have a working set environment in the proposed modelling. This mapping may help analyze the data persistently in the nodes to map with the current setup.

(d)

The task set activates the agent, and the operating environment is learned using the proposed RL model.

The three metrics for the WSN approach are the event space, reward and the network result. The WSN process events represent the jamming in the node communication. The reward helps analyze the proposed model’s prospectus growth in communication. The move taken within the prescribed service establishes the agent modelling; hence, each state is subject to $S_{t \in }{S}_j$, where $S_{t }$represents the state value in the $‘t’$ parameters. The $S_j$ represents the analysis in the assumptions for the neighbor values for $j$ states. The environment will be working for the key model in the state space. The action and task space are consumed based on the node selection parameters. The Q learning is estimated using the $Q_{m+1}\left(S_{t },A{C}_{t }\right)$, representing that the estimation is completed with the state space $S_{t }$and $A{C}_{t }$ action spaces in the working environment. The agent is assumed to be in the processing control of the sensor nodes, and the learning policy is obtained using the space which is given in Equation (15):

$$Q_{m+1}\left(S_t,A{C}_t\right)=\left(1-\alpha \right) Q_t\left(S_t,A{C}_t\right)+\alpha [ {\beta }_{t }+\gamma \max Q_m\left(S_{t+1},{\alpha }_{t+1}\right)]$$

(18)

The updated information regarding the Q learning aspects will be working on the nodes with the range of $\alpha \in \left[0,1\right]$ and the $\gamma ϵ\left[0,1\right]$. The ranges specify the action space and the state space of the action in the working sensor model. The Q value is obtained using the maximum positive reward that can help analyze the node with the neighborhood nature and the adjacent neighbor nature.

Axiom 1

(a)

Analyze the sensor node operating environment with the agent space in $En{v}_t$;

(b)

The nature of the working environment for the present space state has been assumed to be in the space control for the sensor as exploration;

(c)

The best action is assumed as the collective reward from the node $S{N}_i$ for the set of action spaces.//implemented from $MB-NO$;

(d)

The action has been determined using the $A{C}_{t }$in the state space of the sensor deployed nodes of cluster head group 1;

(e)

The reward will be collected from $S_{t }$at time $S_{t+1 }$ to estimate the $\gamma \max Q_m\left(S_{t+1},{\alpha }_{t+1 }\right)$ in the predetermined energy estimation.

Algorithm 2: Reinforcement learning algorithm

1. Initialize the parameters (a) Assume the initial learning policy with a rate of $\alpha$, the reward factor as $\beta$and $\gamma .$ (b) The time-space at $S_{t }$= 0. (c) For all state space, the $S_{t }\in a^1, a^2,\dots \dots \dots ,a^n$ and where the working sensor nodes are assumed in a single cluster. (d) Let $Q_{t }\left(S_{t }\in a^1, a^2,\dots \dots \dots ,a^n \right)=0$//Initial assignment in all sensor nodes. (e) $\delta \left(S_{t, }a\right)=\frac{1}{\frac{1}{\left|A^i\right|} } {\left(S_{t+1, }{a}_{t }\right)}^n$where the $\frac{1}{\left|A^i\right|}$ is the assumption of state space having similar agent pairs. (f) The cluster formation is supported in the state space control CHs$\left(S_{t, }a\right)$ = $\frac{1}{\frac{1}{\left|A^i\right|} } {\left(S_{t+1, }{a}_{t }\right)}^{n+1}$ 2. Do the following (a) Execute the action of the search space in the state with $a^1, a^2,\dots \dots \dots , a^n$. (b) The event reward is assumed to be off in the state as $r{s}^1,r{s}^2,r{s}^3\dots \dots r{s}^n$. (c) Estimate the values of Q $Q_{m+1}\left(S_{t },A{C}_{t }\right)=\left(1-\alpha \right) Q_t\left(S_{t },A{C}_{t }\right)$ +$\alpha [ {\beta }_{t }+\gamma \max Q_m\left(S_{t+1 },{\alpha }_{t+1 }\right)$. (d) ${\mathrm{SN}}_i\left\{\mathrm{Freq},\mathrm{Node} \mathrm{location},\mathrm{Node} \mathrm{energy} \mathrm{limits}\right\}$ = $(\left\{{\mathrm{SN}}_i\right\}, i\in m,$ ${\mathrm{SN}}_a\ne \varnothing$) =$\frac{1}{\frac{1}{\left|A^i\right|} } {\left(S_{t+1, }{a}_{t }\right)}^n$. (d) Update $\frac{1}{\frac{1}{\left|A^i\right|} } {\left(S_{t+1, }{a}_{t }\right)}^n$. (e) Predict the next set of actions with the energy-constrained node mechanism for $Q_{m+1}\left(S_{t },A{C}_{t }\right)$. 3. End Do

5. Performance Evaluation and Results

In this section, the simulation has been performed using the $MB-NO$ algorithm for energy conserved node optimization, and the results are compared with ACO and ABC optimization. The simulation coverage has been conducted with the below experimental setup for various C-shaped, H-shaped and S-shaped networks, as shown in Table 3.

Table 3. Simulation settings.

Simulation Parameters	C-, H-, S-Shaped Networks
Simulation area	250 × 250 m
Frequency band	700 MHz
Sensor nodes	30
Anchor and other unknown nodes	250
Channel bandwidth	4 MHz
Packet size (Control)	150 bit
Packet size (Data)	4 Kbytes
Energy during transmission	0.1
Transmitter energy	40 × 10−8
Receiver energy	40 × 10−8
Maximum lifetime	6 × 10−8

In both Figure 4 and Figure 5 the original BOA and the suggested BOA versions, the initial deployment of target nodes and anchor nodes is arbitrary, Therefore, each BOA and BOA variation 1 algorithm is performed 50 times in order to lessen the impact of randomness, and the best value for computation time, number of localised nodes, and other mistakes is chosen [33]. The simulation has been performed with the three types of networks: C-shaped, H-shaped and S-shaped. To accomplish the objective of energy conservation and node optimization, two objective functions are used, including number of sensor nodes and the transmission time (time stamp measured in ms), which is defined in session 1. The experimental results demonstrated that the MB-NO is more effective at cutting overall power usage when compared to three other optimization techniques. Figure 6 estimates the Objective Function for the C-shaped network with optimized nodes. The estimation shows that the Bat Algorithm establishes a good optimal solution with better energy conservation with the optimized sensor and the adjacent nodes maintained throughout. Table 4 shows the conservative energy analysis using the above metrics, and the parameters are established within the conservative column. The Bat performs the best approach in energy conservation using the 30 sensor nodes with 250 adjacent nodes. The 30 sensor nodes use the best efficiency for the summarized time stamp. The $MB-NO$ outperform when compared with the ACO and ABC optimization.

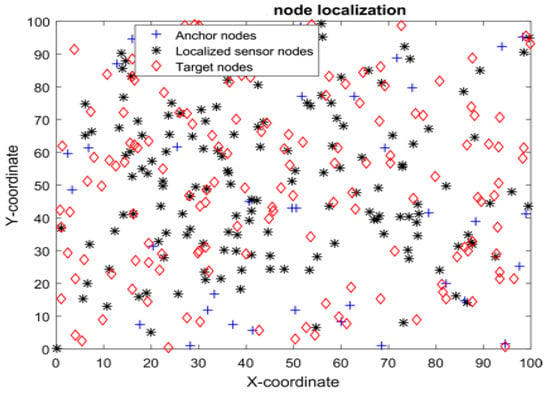
Figure 4. Node localization.

Figure 5. Variant 1 based node localization.

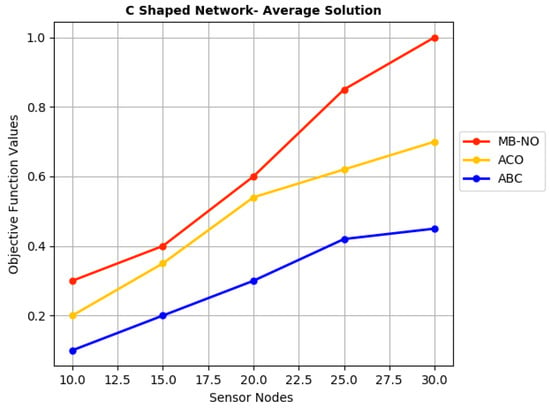
Figure 6. Objective function estimation for a C-shaped network with optimized nodes.

Table 4. Objective function estimation for a C-shaped network with optimized sensor nodes.

Nodes	Objective Function Values (ms)
	$\mathit{M}\mathit{B}-\mathit{N}\mathit{O}$	ACO	ABC
10	0.3	0.2	0.1
15	0.4	0.35	0.2
20	0.6	0.54	0.3
25	0.85	0.62	0.42
30	1	0.7	0.45

Figure 7 estimates the objective function for an H-shaped network with optimized nodes. The estimation shows that the Bat Algorithm establishes a good optimal solution with proper energy conservation, with the optimized sensor and the adjacent nodes maintained throughout. Table 5 shows the conservative energy analysis using the above metrics, and the parameters are established within the conservative column. The $MB-NO$ performs the best approach in energy conservation using the 30 sensor nodes with 250 adjacent nodes. The 30 sensor nodes use the best efficiency for the summarized time stamp. The $MB-NO$ outperforms when compared with the ACO and ABC optimization. In the H-shaped network, the performance measurement is estimated with the rise in transmission time in ms. The H-shaped network is subject to parallel communication estimation in the fixed sensor nodes. The optimal values suggest that the efficient node optimization performs well with the H-shape based on the energy equilibrium, and the average solution attained here works well for the H-shaped network.

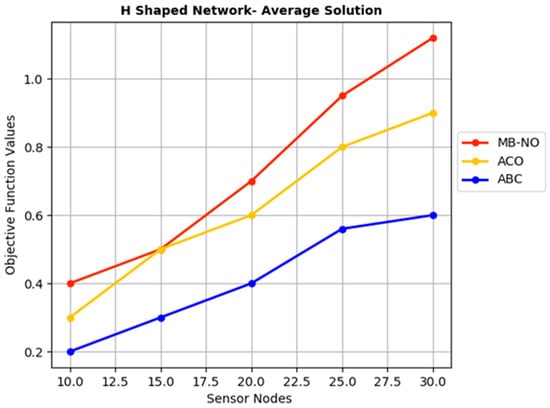
Figure 7. Objective function estimation for an H-shaped network with optimized nodes.

Table 5. Objective function estimation for an H-shaped network with optimized sensor node.

Nodes	Objective Function Values (ms)
	$\mathit{M}\mathit{B}-\mathit{N}\mathit{O}$	ACO	ABC
10	0.4	0.3	0.2
15	0.5	0.5	0.3
20	0.7	0.6	0.4
25	0.95	0.8	0.56
30	1.12	0.9	0.6

Figure 8 estimates the objective function for an S-shaped network with optimized nodes. The estimation shows that the Bat Algorithm establishes a good optimal solution with proper energy conservation, with the optimized sensor and the adjacent nodes maintained throughout. Table 6 shows the conservative energy analysis using the above metrics, and the parameters are established within the conservative column. The $MB-NO$ performs the best approach in energy conservation using the 30 sensor nodes with 250 adjacent nodes. The 30 sensor nodes use the best efficiency for the summarized time stamp. The $MB-NO$ outperforms when compared with the ACO and ABC optimization. In an S-shaped network, the performance measurement is estimated with the raise in transmission time in ms compared to the H- and C-shaped networks. The optimal values suggest that the efficient node optimization performs well with the S-shape based on the energy equilibrium, and the average solution attained here works well for the S-shaped network. At the offset, all the H- and C-shaped networks are assumed to be off, with the best solution, even in compressed mode transmission. Comparatively, the average solution implies a node estimation in the proper assumptions for the sensor and adjacent node communication using the $MB-NO$ algorithm.

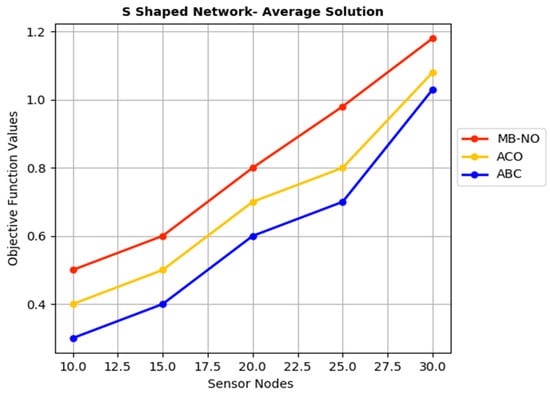
Figure 8. Objective function estimation for an S-shaped network with optimized nodes.

Table 6. Objective function estimation for an S-shaped network with optimized sensor nodes.

Nodes	Objective Function Values (ms)
	$\mathit{M}\mathit{B}-\mathit{N}\mathit{O}$	ACO	ABC
10	0.5	0.4	0.3
15	0.6	0.5	0.4
20	0.8	0.7	0.6
25	0.98	0.8	0.7
30	1.18	1.08	1.03

In Figure 9, the number of iterations is increased with the sensor nodes in the node optimization. The $MB-NO$ algorithm proposes maximum energy conservation, as shown in Table 7; the maximum conservation is obtained with the energy measured, assuming that the other algorithms propose the values with the least energy level equilibrium.

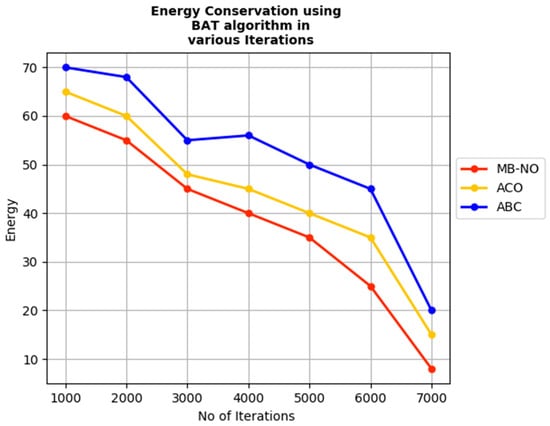
Figure 9. Iterations vs. energy conservation using Bat Algorithm.

Table 7. Energy conservation using Bat Algorithm in various iterations.

Iterations	$\mathit{M}\mathit{B}-\mathit{N}\mathit{O}$	ACO (J)	ABC (J)
1000	60	65	70
2000	55	60	68
3000	45	48	55
4000	40	45	56
5000	35	40	50
6000	25	35	45
7000	8	15	20

In Figure 10, the number of iterations is increased with the sensor nodes in the node optimization. The number of iterations is measured with the network lifetime process; hence, the network may be compared in a higher lifetime using the $MB-NO$ algorithm. Hence, the energy parameters, node optimization and the increased secure transmission through Q learning assumed substantial outcomes.

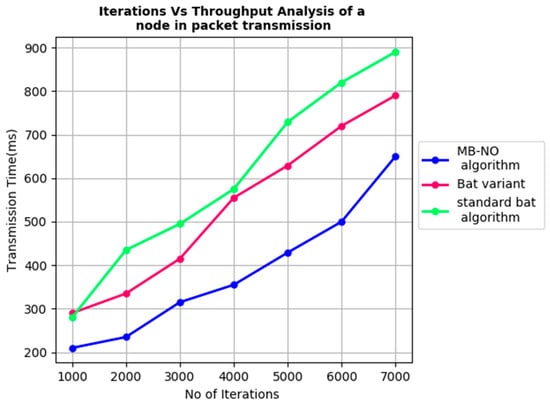
Figure 10. Iterations vs. throughput analysis of a node in packet transmission using Bat Algorithm.

Table 8 depicts the comparison of the computational time, mean localization error and localization nodes. These metrics are evaluated with 10 to 50 nodes where the computational time is given as $T\left(s\right),$ mean localization error is provided as (MLE) and the localization nodes are provided as $N_L.$ The computational time ranges from 0.95 s to 1.04 s, the node location of the proposed MB-NO ranges from 132 to 152 and the mean localization error ranges from 0.47 to 0.31. Mean localization error (MLE) is achieved in the proposed algorithm and more in both bat variants and standard Bat Algorithm; moreover, the computational time is less in MB-NO and the number of nodes more than the other two algorithms. Due to this, the proposed algorithm is very efficient, with improved concurrence and producing a higher success rate (See Figure 11, Figure 12 and Figure 13). From the analysis, it is proven that the model works well compared to other approaches to fulfill the research requirements.

Table 8. Comparison of computational time, mean localization error and localization nodes.

Anchor Node	MB−NO Algorithm			Bat Variant			Standard Bat Algorithm
	T(s)	$N_L$	MLE	T(s)	$N_L$	MLE	T(s)	$N_L$	MLE
10	0.29	146	0.3	0.34	145	0.44	0.95	132	0.32
15	0.31	150	0.31	0.35	148	0.40	0.96	135	0.32
20	0.31	151	0.3	0.36	151	0.37	0.97	144	0.31
25	0.31	151	0.26	0.36	151	0.34	0.99	146	0.31
30	0.31	152	0.29	0.37	151	0.33	1	149	0.30
35	0.31	153	0.26	0.37	151	0.32	1.01	150	0.29
40	0.32	153	0.25	0.37	151	0.32	1.02	151	0.28
45	0.33	153	0.24	0.37	151	0.32	1.03	151	0.28
50	0.33	154	0.23	0.37	151	0.30	1.04	152	0.27

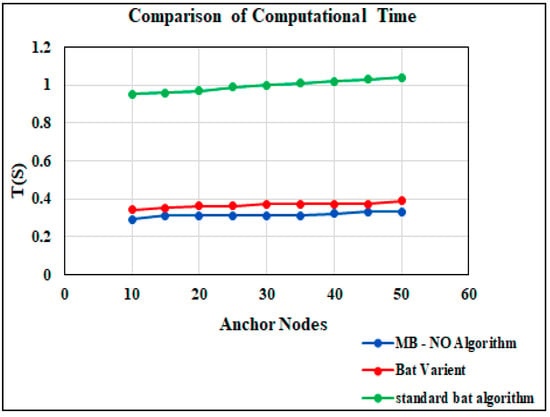
Figure 11. Comparison of computational time.

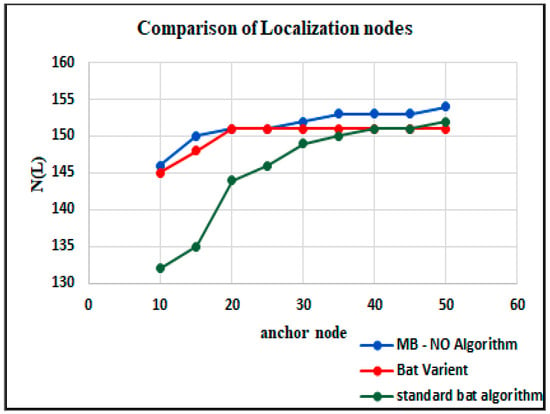
Figure 12. Comparison of localization node.

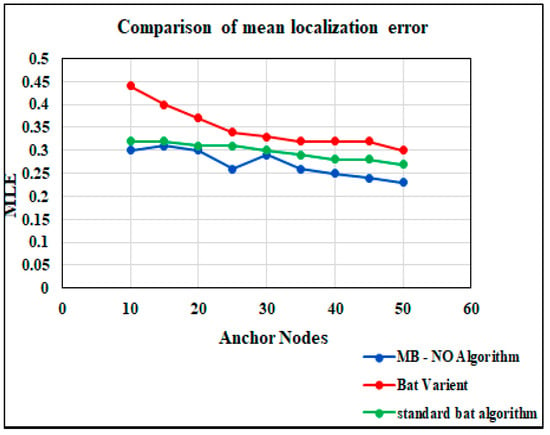
Figure 13. Comparison of mean localization error.

6. Conclusions

In this paper, a proposal has been made with the node optimization enhancement with the localized sensor nodes and other node clusters. The received signal strength is observed in various environments. The proposed model outreached a fine-tuned node optimization; hence, the network has been tested under three network structures: C-shaped, H-shaped and S-shaped. The proposed $MB-NO$ algorithm works on the sensor nodes as it identifies the best optimal solution for node optimization. The results substantially outperformed better results than the ACO and the ABC optimization. The Q learning performs a secure communication with the optimized nodes to enhance the secured connectivity based on the working environment. The $MB-NO$ and Q learning algorithms develop a good network solution in the proposed node optimization and energy conservation in those nodes. All the shaped networks’ energy conservation improves by 10% around the ACO and ABC. The node optimization increases with the proposed $MB-NO$ algorithm and reduces the mean localization error (MLE). Future research enhances secure communication, with a timestamp and protocol estimation having limited power transmission, and enlarges the area coverage.