The Singularity of Four Kinds of Tricyclic Graphs

Abstract

A singular graph G, defined when its adjacency matrix is singular, has important applications in mathematics, natural sciences and engineering. The chemical importance of singular graphs lies in the fact that if the molecular graph is singular, the nullity (the number of the zero eigenvalue) is greater than 0, then the corresponding chemical compound is highly reactive or unstable. By this reasoning, chemists have a great interest in this problem. Thus, the problem of characterization singular graphs was proposed and raised extensive studies on this challenging problem thereafter. The graph obtained by conglutinating the starting vertices of three paths $P_{s_1}$, $P_{s_2}$, $P_{s_3}$ into a vertex, and three end vertices into a vertex on the cycle $C_{a_1}$, $C_{a_2}$, $C_{a_3}$, respectively, is denoted as $\gamma (a_1,a_2,a_3,s_1,s_2,s_3)$. Note that $\delta (a_1,a_2,a_3,s_1,s_2)=\gamma (a_1,a_2,a_3,s_1,1,s_2)$, $\zeta (a_1,a_2,a_3,s)=\gamma (a_1,a_2,a_3,1,1,s)$, $\phi (a_1,a_2,a_3)=\gamma (a_1,a_2,a_3,1,1,1)$. In this paper, we give the necessity and sufficiency that the $\gamma -$graph, $\delta -$graph, $\zeta -$graph and $\phi -$graph are singular and prove that the probability that a randomly given $\gamma -$graph, $\delta -$graph, $\zeta -$graph or $\phi -$graph being singular is equal to $\frac{325}{512},\frac{165}{256},\frac{43}{64}$, $\frac{21}{32}$, respectively. From our main results, we can conclude that such a $\gamma -$graph($\delta -$graph, $\zeta -$graph, $\phi -$graph) is singular if at least one cycle is a multiple of 4 in length, and surprisingly, the theoretical probability of these graphs being singular is more than half. This result promotes the understanding of a singular graph and may be promising to propel the solutions to relevant application problems.

1. Introduction

This paper considers only finite undirected simple graphs. Let G be a graph with order n, and the $adjacencymatrix$ is defined as: $A\left(G\right)={\left(a_{ij}\right)}_{n\times n}$

$$a_{ij}=\left\{\begin{array}{cc}1\hfill & \mathrm{if}i\sim j,\hfill \\ 0\hfill & \mathrm{others}.\hfill \end{array}\right.$$

where $i\sim j$ denotes that the vertices i and j are adjacent. Obviously, $A\left(G\right)$ is a real symmetric matrix where all the diagonal elements are 0 and the other elements are 0 or 1 with all real eigenvalues. These n eigenvalues of $A\left(G\right)$ are called the eigenvalues of the graph G and form the spectrum of this graph. The number of nonzero and zero eigenvalues in the spectrum of G are called the $rank$ and $nullity$ of the graph G, denoted by $r\left(G\right)$ and $\eta \left(G\right)$, respectively, and it is apparent $r\left(G\right)+\eta \left(G\right)=n$.

The graph G is said to be singular if and only if 0 is an eigenvalue of $A\left(G\right)$. In other words, the graph G is singular if and only if $\eta \left(G\right)>0$.

In chemistry, for a molecule, we can obtain a molecular graph by representing the atoms by vertices and the bonds by edges (see [1]). The nullity of a molecular graph has many important applications (see [1,2,3,4,5,6,7]). For example, the nullity of a graph is equal to zero is a necessary condition for the chemical property stability of the molecule it represents (see [6]). In 1957, Collatz and Sinogowitz proposed the problem of characterizing all graphs whose nullity is greater than zero in [2], in other words, the problem of characterizing all singular graphs, which is a very difficult problem. So far, only some special results are known (see [8,9,10,11,12,13,14,15,16,17]). This problem encourages people to study the structural characteristics of singular graphs, and many authors have studied the interaction between the nullity and the structure of a graph (see [18,19,20,21,22]). A system of linear homogeneous equations $Ax=0$ yields non-trivial solutions $x\ne 0$ when the linear transformation A is not invertible. Such a matrix A is singular. The solutions have many direct applications, for instance, to networks in computer science and electrical circuits, to financial models in economics, to biological models in genetics and bioinformatics as well as to the understanding of non-bonding orbitals in carbon unsaturated molecules [23,24,25]. The nullity of a graph is also important in mathematics because it is relevant to the rank of the adjacency matrix. Recent studies have also shown that singular graphs are related to other fields of mathematics, such as the representation theory of finite groups [26,27,28,29] combinatorial mathematics, algebraic geometry and so on (see [26,30,31,32]).

It is well known that a graph G is singular if and only if the determinant $det\left(A\right(G\left)\right)$ of its adjacency matrix $A\left(G\right)$ equals 0. However, only a few studies describe singular graphs from the perspective of the determinant and also very limited literature studies the necessity and sufficiency of the singular of a class of graph. In this paper, by using the determinant of the adjacency matrix, we give the necessity and sufficiency that $\gamma -$graph, $\delta -$graph, $\zeta -$graph and $\phi -$graph are singular, and the probability values of these graph singulars are given.

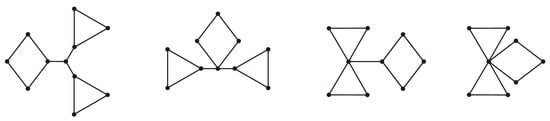
For the positive integer n, $K_n$, $P_n$ and $C_n$ denote the complete graph, the path and the cycle on n vertices, respectively. The graph obtained by conglutinating three starting vertices of three paths $P_{s_1}$, $P_{s_2}$, $P_{s_3}$ into a vertex, and three end vertices into a vertex on the cycle $C_{a_1}$, $C_{a_2}$, $C_{a_3}$, respectively, is denoted as $\gamma$($a_1$,$a_2$,$a_3$,$s_1$,$s_2$,$s_3$) (see Figure 1). Note that $\delta$($a_1$,$a_2$,$a_3$,$s_1$,$s_2$) = $\gamma$($a_1$,$a_2$,$a_3$,$s_1$,1,$s_2$) (see Figure 2), $\zeta$($a_1$,$a_2$,$a_3$,s) = $\gamma$($a_1$,$a_2$,$a_3$,1,1,s) (see Figure 3) and $\phi$($a_1$,$a_2$,$a_3$) = $\gamma$($a_1$,$a_2$,$a_3$,1,1,1) (see Figure 4). Let $G\cup H$ denote the union of G and H. The undefined concepts and notations will follow [7]. In this paper, we give the necessity and sufficiency that $\gamma -$graph, $\delta -$graph, $\zeta -$graph and $\phi -$graph are singular and prove that the probability that a randomly given $\gamma -$graph, $\delta -$graph, $\zeta -$graph or $\phi -$graph being singular is equal to $\frac{325}{512},\frac{165}{256},\frac{43}{64}$, $\frac{21}{32}$, respectively.

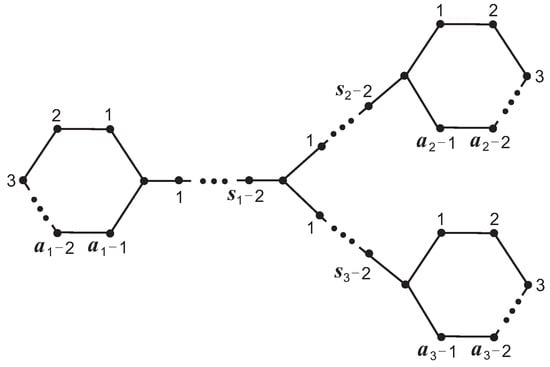
Figure 1. Graph $\gamma (a_1,a_2,a_3,s_1,s_2,s_3)$.

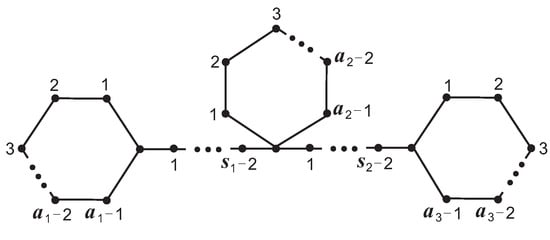
Figure 2. Graph $\delta (a_1,a_2,a_3,s_1,s_2)$.

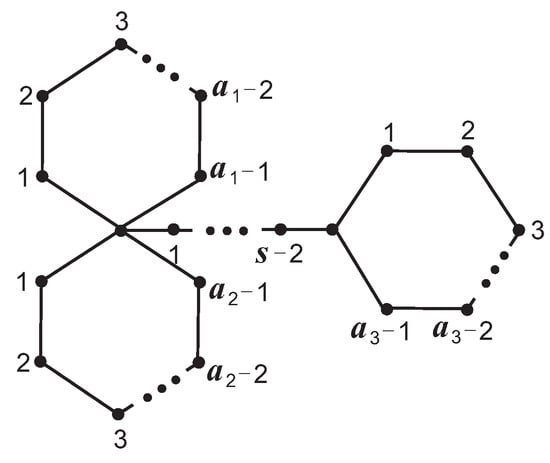
Figure 3. Graph $\zeta (a_1,a_2,a_3,s)$.

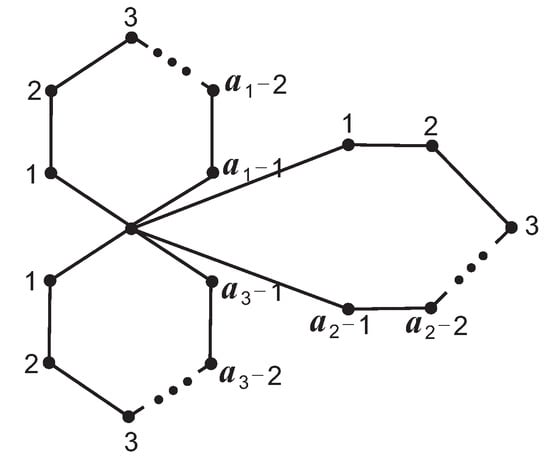
Figure 4. Graph $\phi (a_1,a_2,a_3)$.

We call $a_1,a_2,a_3$ three a, and call $s_1,s_2,s_3$ three s. The main conclusions are the following two theorems:

Theorem 1. 

$G=\gamma (a_1,a_2,a_3,s_1,s_2,s_3)$ (see Figure 1) is singular if and only if one of the following holds:

$\left(i\right)$ There is at least one cycle whose length is a multiple of 4;

$\left(ii\right)$ There are exactly three even cycles, and at least two s are odd or three s are even;

$\left(iii\right)$ There are exactly two even cycles, and two s connected with these two even cycles are odd;

$\left(iv\right)$ There is exactly one even cycle, and the s connected with this even cycle is even, and the length of two odd cycles is not congruent with respect to module 4 and the parity of two s connected with these two odd cycles is the same.

From Theorem 1, it is easy to derive the following corollaries:

Corollary 1. 

$G=\delta (a_1,a_2,a_3,s_1,s_2)$ (see Figure 2) is singular if and only if one of the following holds:

$\left(i\right)$ There is at least one cycle whose length is a multiple of 4.

$\left(ii\right)$ There are exactly three even cycles, and at least one s is odd.

$\left(iii\right)$ There are exactly two even cycles:

(1) The middle cycle is an even cycle, and the s connected with another even cycle is odd;

(2) The middle cycle is an odd cycle, and two s are odd.

$\left(iv\right)$ There is exactly one even cycle at each end, and the s connected with this even cycle is even, the length of two odd cycles is not congruent with respect to module 4 and the s connected with another odd cycle is odd.

Corollary 2. 

$G=\zeta (a_1,a_2,a_3,s)$ (see Figure 3) is singular if and only if one of the following holds:

$\left(i\right)$ There is at least one cycle whose length is a multiple of 4.

$\left(ii\right)$ There are exactly three even cycles.

$\left(iii\right)$ There are exactly two even cycles, and two even cycles have a common vertex or the s connected with two even cycles is odd.

$\left(iv\right)$ There is exactly one even cycle that has no common vertex with the other two cycles, s is even and the length of two odd cycles is not congruent with respect to module 4.

Corollary 3. 

$G=\phi (a_1,a_2,a_3)$ (see Figure 4) is singular if and only if one of the following holds:

$\left(i\right)$ There is at least one cycle whose length is a multiple of 4;

$\left(ii\right)$ There are at least two even cycles.

Theorem 2. 

The probability that a randomly given $\gamma -$graph, $\delta -$graph, $\zeta -$graph or $\phi -$graph being singular is equal to $\frac{325}{512},\frac{165}{256},\frac{43}{64}$, $\frac{21}{32}$, respectively.

Example 1. 

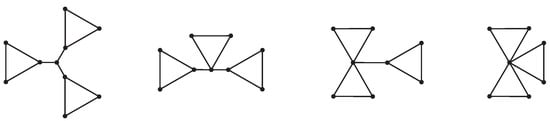
From Theorem 1, Corollaries 1–3, we know that the graph $G=\gamma (a_1,a_2,a_3$, $s_1,s_2,s_3)$ ($\delta (a_1,a_2,a_3,s_1,s_2)$, $\zeta (a_1,a_2,a_3,s)$ or $\phi (a_1,a_2,a_3)$) is singular if the length of a cycle on the graph G is a multiple of 4. The smallest singular graph of the number of vertices in $\gamma -$($\delta -$, $\zeta -$, $\phi -$) graphs is $\gamma (4,3,3,2,2,2)$($\delta (3,4,3,2,2)$, $\zeta (3,3,4,2)$, $\phi (4,3,3)$), and it has 11 (10, 9, 8) vertices (see Figure 5). The smallest non-singular graphs of the number of vertices in $\gamma -$($\delta -$, $\zeta -$, $\phi -$) graphs is $\gamma (3,3,3,2,2,2)$($\delta (3,3,3,2,2)$, $\zeta (3,3,3,2)$, $\phi (3,3,3)$), and it has 10 (9, 8, 7) vertices (see Figure 6). From Theorem 2, we were surprised to find that more than half of the $\gamma -$($\delta -$, $\zeta -$, $\phi -$) graphs were singular.

Figure 5. The smallest singular graph of the number of vertices in $\gamma -$($\delta -$, $\zeta -$, $\phi -$): $\gamma (4,3,3,2,2,2)$, $\delta (3,4,3,2,2)$, $\zeta (3,3,4,2)$ and $\phi (4,3,3)$.

Figure 6. The smallest non-singular graphs of the number of vertices in $\gamma -$($\delta -$, $\zeta -$, $\phi -$): $\gamma (3,3,3,2,2,2)$, $\delta (3,3,3,2,2)$, $\zeta (3,3,3,2)$ and $\phi (3,3,3)$.

2. Some Lemmas

Lemma 1.

([11]). Let $G=G_1\cup G_2\cup \cdots \cup G_t$, where $G_i(i=1,2,\dots ,t)$ is a connected component of the graph G, then $\eta \left(G\right)={\displaystyle \sum _{i=1}^t}\eta \left(G_i\right)$. Equivalently, G is non-singular if and only if each $G_i(i=1,2,\dots ,t)$ is non-singular.

A vertex with degree 1 is called a pendant vertex, and a vertex adjacent to the pendant vertex is called a quasi-pendant vertex.

Lemma 2. 

([11]). Let G have a pendant vertex, and H is the graph obtained by deleting the pendant vertex and the quasi-pendant vertex from G, then $\eta \left(G\right)=\eta \left(H\right)$.

According to Lemma, H is the graph obtained by deleting the pendant vertex and the quasi-pendant vertex from G when G contents pendant or quasi-pendant vertex, in fact, the adjacency matrix $A\left(G\right)$ of G is congruent to $\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]\oplus A\left(H\right)$, where $A\left(H\right)$ is the adjacency matrix of H and ⊕ is the direct sum of matrices. From this, it is easy to know that $r\left(G\right)=r\left(H\right)+2$, $\eta \left(G\right)=\eta \left(H\right)$.

A graph G is singular if and only if the determinant $detA\left(G\right)=0$; however, the determinant of the adjacency matrix is related to a so-called spanning elementary subgraph on this graph. The subgraph of the graph G whose every component is an isolated edge or a cycle is called an $elementarysubgraph$ or $Sachssubgraph$ of G. An elementary subgraph of G containing all vertices is called a $spanningelementarysubgraph$ or $spanningSachssubgraph$. The spanning elementary subgraph composed only of isolated edges is called the perfect matching of graph G. Of course, a graph with the perfect matching must have an even number of vertices.

Lemma 3. 

([11]). Let G be a graph with n vertices and its adjacency matrix be $A\left(G\right)$, then

$$det\left(A\left(G\right)\right)={(-1)}^n\sum _{H\in \mathcal{H}}{(-1)}^{p\left(H\right)}{2}^{c\left(H\right)},$$

where $\mathcal{H}$ denotes the set of all spanning Sachs subgraphs of graph G, $p\left(H\right)$ denotes the number of components in graph H and $c\left(H\right)$ denotes the number of cycles in graph H.

By Lemma 3, if a graph has no spanning Sachs subgraph, then it is singular. A spanning Sachs subgraph of a tree can only be a perfect matching. According to this, it is easy to know that a tree is singular if and only if it does not have a perfect matching. For a cycle $C_n$, if n is odd, its spanning Sachs subgraph has only $C_n$, so $C_n$ is singular if and only if $det\left(A\left(C_n\right)\right)={(-1)}^{n+1}\times 2=0,$ but that is impossible. If n is even, its spanning Sachs subgraph has $C_n$ and two perfect matchings, so $C_n$ is singular if and only if $det\left(A\left(C_n\right)\right)={(-1)}^n[{(-1)}^1\times 2+{(-1)}^{\frac{n}{2}}\times 2]=0,$ if and only if $4|n$. The proof of our main result is derived from Lemma 3.

3. Proofs of Theorems 1 and 2

Proof of Theorem 1. 

$\left|V\left(G\right)\right|=a_1+a_2+a_3+s_1+s_2+s_3-5$. According to the number of even numbers in $\{a_1,a_2,a_3\}$⇒ the number of even numbers in $\{s_1,s_2,s_3\}$ (combined with the symmetry of graph $\gamma (a_1,a_2,a_3,s_1,s_2,s_3)$), the following four cases are classified.

Case 1 There are three a that are even.

Subcase 1.1 There are three s that are even, where G has no spanning Sachs subgraph, G is singular.

Subcase 1.2 There are exactly two s that are even. Suppose that $s_1,s_2$ are even, $s_3$ is odd. Where the spanning Sachs subgraph of G with three cycles is: $C_{a_1}\cup C_{a_2}\cup C_{a_3}\cup \frac{s_1+s_2+s_3-5}{2}{P}_2$ (one); the spanning Sachs subgraph of G with two cycles is: $C_{a_1}\cup C_{a_2}\cup \frac{a_3+s_1+s_2+s_3-5}{2}{P}_2$ (two), $C_{a_1}\cup C_{a_3}\cup \frac{a_2+s_1+s_2+s_3-5}{2}{P}_2$ (two), $C_{a_2}\cup C_{a_3}\cup \frac{a_1+s_1+s_2+s_3-5}{2}{P}_2$ (two); and the spanning Sachs subgraph of G with one cycle is: $C_{a_1}\cup \frac{a_2+a_3+s_1+s_2+s_3-5}{2}{P}_2$ (four), $C_{a_2}\cup \frac{a_1+a_3+s_1+s_2+s_3-5}{2}{P}_2$ (four), $C_{a_3}\cup \frac{a_1+a_2+s_1+s_2+s_3-5}{2}{P}_2$ (four); there are 8 perfect matchings.

By Lemma 3, G is singular if and only if

$${(-1)}^{\frac{s_1+s_2+s_3-5}{2}+3}\times 2^3+{(-1)}^{\frac{a_3+s_1+s_2+s_3-5}{2}+2}\times 2^3+{(-1)}^{\frac{a_2+s_1+s_2+s_3-5}{2}+2}\times 2^3$$

$$+{(-1)}^{\frac{a_1+s_1+s_2+s_3-5}{2}+2}\times 2^3+{(-1)}^{\frac{a_2+a_3+s_1+s_2+s_3-5}{2}+1}\times 2^3+{(-1)}^{\frac{a_1+a_3+s_1+s_2+s_3-5}{2}+1}\times 2^3$$

$$+{(-1)}^{\frac{a_1+a_2+s_1+s_2+s_3-5}{2}+1}\times 2^3+{(-1)}^{\frac{a_1+a_2+a_3+s_1+s_2+s_3-5}{2}}\times 8=0,$$

multiply both sides by ${(-1)}^{\frac{a_1+a_2+a_3+s_1+s_2+s_3-5}{2}}$, and we obtain

$${(-1)}^{\frac{a_1+a_2+a_3}{2}+3}+{(-1)}^{\frac{a_1+a_2}{2}+2}+{(-1)}^{\frac{a_1+a_3}{2}+2}+{(-1)}^{\frac{a_2+a_3}{2}+2}$$

$$+{(-1)}^{\frac{a_1}{2}+1}+{(-1)}^{\frac{a_2}{2}+1}+{(-1)}^{\frac{a_3}{2}+1}+1=0,$$

if and only if

$$({(-1)}^{\frac{a_1}{2}}-1)({(-1)}^{\frac{a_2}{2}}-1)({(-1)}^{\frac{a_3}{2}}-1)=0,$$

if and only if $4|a_1$, $4|a_2$ or $4|a_3$.

Subcase 1.3 There is exactly one s that is even. Suppose that $s_1$ is even, $s_2,s_3$ are odd, where G has no spanning Sachs subgraph, G is singular.

Subcase 1.4 There is no s that is even, where G has no spanning Sachs subgraph, G is singular.

Case 2 There are exactly two a that are even. Suppose that $a_1$, $a_2$ are even and $a_3$ is odd.

Subcase 2.1 There are three s that are even. Where there is no spanning Sachs subgraph of G with three cycles; the spanning Sachs subgraph of G with two cycles is: $C_{a_1}\cup C_{a_2}\cup \frac{a_3+s_1+s_2+s_3-5}{2}{P}_2$ (one); the spanning Sachs subgraph of G with one cycle is: $C_{a_1}\cup \frac{a_2+a_3+s_1+s_2+s_3-5}{2}{P}_2$ (two), $C_{a_2}\cup \frac{a_1+a_3+s_1+s_2+s_3-5}{2}{P}_2$ (two); there are 4 perfect matchings.

By Lemma 3, G is singular if and only if

$${(-1)}^{\frac{a_3+s_1+s_2+s_3-5}{2}+2}\times 2^2+{(-1)}^{\frac{a_2+a_3+s_1+s_2+s_3-5}{2}+1}\times 2^2$$

$$+{(-1)}^{\frac{a_1+a_3+s_1+s_2+s_3-5}{2}+1}\times 2^2+{(-1)}^{\frac{a_1+a_2+a_3+s_1+s_2+s_3-5}{2}}\times 4=0,$$

multiply both sides by ${(-1)}^{\frac{a_1+a_2+a_3+s_1+s_2+s_3-5}{2}}\times \frac{1}{4}$, and we obtain

$${(-1)}^{\frac{a_1+a_2}{2}+2}+{(-1)}^{\frac{a_1}{2}+1}+{(-1)}^{\frac{a_2}{2}+1}+1=0,$$

that is

$${(-1)}^{\frac{a_1+a_2}{2}}-{(-1)}^{\frac{a_1}{2}}-{(-1)}^{\frac{a_2}{2}}+1=0,$$

if and only if

$$({(-1)}^{\frac{a_1}{2}}-1)({(-1)}^{\frac{a_2}{2}}-1)=0,$$

if and only if $4|a_1$ or $4|a_2$.

Subcase 2.2 There are exactly two s that are even.

Subcase 2.2.1 Suppose that $s_1,s_2$ are even, $s_3$ is odd. Where the spanning Sachs subgraph of G with three cycles is: $C_{a_1}\cup C_{a_2}\cup C_{a_3}\cup \frac{s_1+s_2+s_3-5}{2}{P}_2$ (one); the spanning Sachs subgraph of G with two cycles is: $C_{a_1}\cup C_{a_3}\cup \frac{a_2+s_1+s_2+s_3-5}{2}{P}_2$ (two), $C_{a_2}\cup C_{a_3}\cup \frac{a_1+s_1+s_2+s_3-5}{2}{P}_2$ (two); and the spanning Sachs subgraph of G with one cycle is: $C_{a_3}\cup \frac{a_1+a_2+s_1+s_2+s_3-5}{2}{P}_2$ (four); there is no perfect matching.

By Lemma 3, G is singular if and only if

$${(-1)}^{\frac{s_1+s_2+s_3-5}{2}+3}\times 2^3+{(-1)}^{\frac{a_2+s_1+s_2+s_3-5}{2}+2}\times 2^3$$

$$+{(-1)}^{\frac{a_1+s_1+s_2+s_3-5}{2}+2}\times 2^3+{(-1)}^{\frac{a_1+a_2+s_1+s_2+s_3-5}{2}}\times 2^3=0,$$

multiply both sides by ${(-1)}^{\frac{a_1+a_2+s_1+s_2+s_3-5}{2}}$, and we obtain

$${(-1)}^{\frac{a_1+a_2}{2}+3}+{(-1)}^{\frac{a_1}{2}+2}+{(-1)}^{\frac{a_2}{2}+2}+1=0,$$

if and only if

$$({(-1)}^{\frac{a_1}{2}}-1)({(-1)}^{\frac{a_2}{2}}-1)=0,$$

if and only if $4|a_1$ or $4|a_2$.

Subcase 2.2.2 Suppose that $s_1,s_3$ are even, $s_2$ is odd. Where the spanning Sachs subgraph of G with three cycles is: $C_{a_1}\cup C_{a_2}\cup C_{a_3}\cup \frac{s_1+s_2+s_3-5}{2}{P}_2$ (one); the spanning Sachs subgraph of G with two cycles is: $C_{a_1}\cup C_{a_3}\cup \frac{a_2+s_1+s_2+s_3-5}{2}{P}_2$ (two), $C_{a_2}\cup C_{a_3}\cup \frac{a_1+s_1+s_2+s_3-5}{2}{P}_2$ (two); and the spanning Sachs subgraph of G with one cycle is: $C_{a_3}\cup \frac{a_1+a_2+s_1+s_2+s_3-5}{2}{P}_2$ (four); there is no perfect matching.

Similar to Subcase 2.2.1, we obtain G is singular if and only if $4|a_1$ or $4|a_2$.

Subcase 2.3 There is exactly one s that is even.

Subcase 2.3.1 Suppose that $s_1$ is even, $s_2,s_3$ are odd. Where there is no spanning Sachs subgraph of G with three cycles; the spanning Sachs subgraph of G with two cycles is: $C_{a_1}\cup C_{a_2}\cup \frac{a_3+s_1+s_2+s_3-5}{2}{P}_2$ (one); the spanning Sachs subgraph of G with one cycle is: $C_{a_1}\cup \frac{a_2+a_3+s_1+s_2+s_3-5}{2}{P}_2$ (two), $C_{a_2}\cup \frac{a_1+a_3+s_1+s_2+s_3-5}{2}{P}_2$ (two); there are 4 perfect matchings.

Similar to Subcase 2.1, we obtain G is singular if and only if $4|a_1$ or $4|a_2$.

Subcase 2.3.2 Suppose that $s_3$ is even, $s_1,s_2$ are odd. Where there is no spanning Sachs subgraph of G, G is singular.

Subcase 2.4 There is no s that is even. Where there is no spanning Sachs subgraph of G, G is singular.

Case 3 There is exactly one a that is even. Suppose that $a_1$ is even and $a_2$, $a_3$ are odd.

Subcase 3.1 There are three s that are even. Where there is no spanning Sachs subgraph of G with three cycles; the spanning Sachs subgraph of G with two cycles is: $C_{a_1}\cup C_{a_2}\cup \frac{a_3+s_1+s_2+s_3-5}{2}{P}_2$ (one), $C_{a_1}\cup C_{a_3}\cup \frac{a_2+s_1+s_2+s_3-5}{2}{P}_2$ (one); the spanning Sachs subgraph of G with one cycle is: $C_{a_2}\cup \frac{a_1+a_3+s_1+s_2+s_3-5}{2}{P}_2$ (two), $C_{a_3}\cup \frac{a_1+a_2+s_1+s_2+s_3-5}{2}{P}_2$ (two); there is no perfect matching.

By Lemma 3, G is singular if and only if

$${(-1)}^{\frac{a_3+s_1+s_2+s_3-5}{2}+2}\times 2^2+{(-1)}^{\frac{a_2+s_1+s_2+s_3-5}{2}+2}\times 2^2$$

$$+{(-1)}^{\frac{a_1+a_3+s_1+s_2+s_3-5}{2}+1}\times 2^2+{(-1)}^{\frac{a_1+a_2+s_1+s_2+s_3-5}{2}+1}\times 2^2=0,$$

multiply both sides by ${(-1)}^{\frac{s_1+s_2+s_3}{2}}$, and we obtain

$${(-1)}^{\frac{a_3-5}{2}}+{(-1)}^{\frac{a_2-5}{2}}-{(-1)}^{\frac{a_1+a_3-5}{2}}-{(-1)}^{\frac{a_1+a_2-5}{2}}=0,$$

if and only if

$$({(-1)}^{\frac{a_1}{2}}-1)({(-1)}^{\frac{a_2-5}{2}}+{(-1)}^{\frac{a_3-5}{2}})=0,$$

if and only if $4|a_1$, or $a_2\not\equiv a_3$ (mod 4).

Subcase 3.2 There are exactly two s that are even.

Subcase 3.2.1 Suppose that $s_1,s_2$ are even, $s_3$ is odd. Where the spanning Sachs subgraph of G with three cycles is: $C_{a_1}\cup C_{a_2}\cup C_{a_3}\cup \frac{s_1+s_2+s_3-5}{2}{P}_2$ (one); the spanning Sachs subgraph of G with two cycles is: $C_{a_2}\cup C_{a_3}\cup \frac{a_1+s_1+s_2+s_3-5}{2}{P}_2$ (two); the spanning Sachs subgraph of G with one cycle is: $C_{a_1}\cup \frac{a_2+a_3+s_1+s_2+s_3-5}{2}{P}_2$ (one); there are 2 perfect matchings.

By Lemma 3, G is singular if and only if

$${(-1)}^{\frac{s_1+s_2+s_3-5}{2}+3}\times 2^3+{(-1)}^{\frac{a_1+s_1+s_2+s_3-5}{2}+2}\times 2^3$$

$$+{(-1)}^{\frac{a_2+a_3+s_1+s_2+s_3-5}{2}+1}\times 2+{(-1)}^{\frac{a_1+a_2+a_3+s_1+s_2+s_3-5}{2}}\times 2=0,$$

multiply both sides by ${(-1)}^{\frac{a_1+a_2+a_3+s_1+s_2+s_3-5}{2}}$, and we obtain

$$-{(-1)}^{\frac{a_1+a_2+a_3}{2}}\times 4+{(-1)}^{\frac{a_2+a_3}{2}}\times 4-{(-1)}^{\frac{a_1}{2}}+1=0,$$

if and only if

$$({(-1)}^{\frac{a_1}{2}}-1)({(-1)}^{\frac{a_2+a_3}{2}}\times 4+1)=0,$$

if and only if $4|a_1$.

Subcase 3.2.2 Suppose that $s_2,s_3$ are even, $s_1$ is odd. Where the spanning Sachs subgraph of G with three cycles is: $C_{a_1}\cup C_{a_2}\cup C_{a_3}\cup \frac{s_1+s_2+s_3-5}{2}{P}_2$ (one); the spanning Sachs subgraph of G with two cycles is: $C_{a_2}\cup C_{a_3}\cup \frac{a_1+s_1+s_2+s_3-5}{2}{P}_2$ (two); there is no spanning Sachs subgraph of G with one cycle; there is no perfect matching.

By Lemma 3, G is singular if and only if

$${(-1)}^{\frac{s_1+s_2+s_3-5}{2}+3}\times 2^3+{(-1)}^{\frac{a_1+s_1+s_2+s_3-5}{2}+2}\times 2^3=0,$$

if and only if $4|a_1$.

Subcase 3.3 There is exactly one s that is even.

Subcase 3.3.1 Suppose that $s_1$ is even, $s_2,s_3$ are odd. Where there is no spanning Sachs subgraph of G with three cycles; the spanning Sachs subgraph of G with two cycles is: $C_{a_1}\cup C_{a_2}\cup \frac{a_3+s_1+s_2+s_3-5}{2}{P}_2$ (one), $C_{a_1}\cup C_{a_3}\cup \frac{a_2+s_1+s_2+s_3-5}{2}{P}_2$ (one); the spanning Sachs subgraph of G with one cycle is: $C_{a_2}\cup \frac{a_1+a_3+s_1+s_2+s_3-5}{2}{P}_2$ (two), $C_{a_3}\cup \frac{a_1+a_2+s_1+s_2+s_3-5}{2}{P}_2$ (two); there is no perfect matching.

Similar to Subcase 3.1, we obtain G is singular if and only if $4|a_1$ or $a_2\not\equiv a_3$ (mod 4).

Subcase 3.3.2 Suppose that $s_3$ is even, $s_1,s_2$ are odd. Where there is no spanning Sachs subgraph of G with three cycles; the spanning Sachs subgraph of G with two cycles is: $C_{a_1}\cup C_{a_3}\cup \frac{a_2+s_1+s_2+s_3-5}{2}{P}_2$ (one); the spanning Sachs subgraph of G with one cycle is: $C_{a_3}\cup \frac{a_1+a_2+s_1+s_2+s_3-5}{2}{P}_2$ (two); there is no perfect matching.

By Lemma 3, G is singular if and only if

$${(-1)}^{\frac{a_2+s_1+s_2+s_3-5}{2}+2}\times 2^2+{(-1)}^{\frac{a_1+a_2+s_1+s_2+s_3-5}{2}+1}\times 2^2=0,$$

if and only if $4|a_1$.

Subcase 3.4 There is no s that is even. Where there is no spanning Sachs subgraph of G with three cycles; there is no spanning Sachs subgraph of G with two cycles; the spanning Sachs subgraph of G with one cycle is: $C_{a_1}\cup \frac{a_2+a_3+s_1+s_2+s_3-5}{2}{P}_2$ (one); there are 2 perfect matchings.

By Lemma 3, G is singular if and only if

$${(-1)}^{\frac{a_2+a_3+s_1+s_2+s_3-5}{2}+1}\times 2+{(-1)}^{\frac{a_1+a_2+a_3+s_1+s_2+s_3-5}{2}}\times 2=0,$$

if and only if $4|a_1$.

Case 4 There is no a that is even.

Subcase 4.1 There are three s that are even. There is no spanning Sachs subgraph of G with three cycles; the spanning Sachs subgraph of G with two cycles is: $C_{a_1}\cup C_{a_2}\cup \frac{a_3+s_1+s_2+s_3-5}{2}{P}_2$ (one), $C_{a_1}\cup C_{a_3}\cup \frac{a_2+s_1+s_2+s_3-5}{2}{P}_2$ (one), $C_{a_2}\cup C_{a_3}\cup \frac{a_1+s_1+s_2+s_3-5}{2}{P}_2$ (one); there is no spanning Sachs subgraph of G with one cycle; there is no perfect matching.

By Lemma 3, G is singular if and only if

$${(-1)}^{\frac{a_3+s_1+s_2+s_3-5}{2}+2}\times 2^2+{(-1)}^{\frac{a_2+s_1+s_2+s_3-5}{2}+2}\times 2^2+{(-1)}^{\frac{a_1+s_1+s_2+s_3-5}{2}+2}\times 2^2=0,$$

multiply both sides by ${(-1)}^{\frac{s_1+s_2+s_3}{2}}$, and we obtain

$${(-1)}^{\frac{a_3-5}{2}}+{(-1)}^{\frac{a_2-5}{2}}+{(-1)}^{\frac{a_1-5}{2}}=0.$$

However, that is impossible, so G is non-singular.

Subcase 4.2 There are exactly two s that are even. Suppose that $s_1,s_2$ are even, $s_3$ is odd. Where the spanning Sachs subgraph of G with three cycles is: $C_{a_1}\cup C_{a_2}\cup C_{a_3}\cup \frac{s_1+s_2+s_3-5}{2}{P}_2$ (one); there is no spanning Sachs subgraph of G with two cycles; the spanning Sachs subgraph of G with one cycle is: $C_{a_1}\cup \frac{a_2+a_3+s_1+s_2+s_3-5}{2}{P}_2$ (one), $C_{a_2}\cup \frac{a_1+a_3+s_1+s_2+s_3-5}{2}{P}_2$ (one); there is no perfect matching.

By Lemma 3, G is singular if and only if

$${(-1)}^{\frac{s_1+s_2+s_3-5}{2}+3}\times 2^3+{(-1)}^{\frac{a_2+a_3+s_1+s_2+s_3-5}{2}+1}\times 2+{(-1)}^{\frac{a_1+a_3+s_1+s_2+s_3-5}{2}+1}\times 2=0,$$

multiply both sides by ${(-1)}^{\frac{s_1+s_2+s_3-5}{2}}$, and we obtain

$$-4-{(-1)}^{\frac{a_2+a_3}{2}}+{(-1)}^{\frac{a_1+a_3}{2}}=0.$$

However, that is impossible, so G is non-singular.

Subcase 4.3 There is exactly one s that is even. Suppose that $s_1$ is even, $s_2,s_3$ are odd. Where there is no spanning Sachs subgraph of G with three cycles; the spanning Sachs subgraph of G with two cycles is: $C_{a_1}\cup C_{a_2}\cup \frac{a_3+s_1+s_2+s_3-5}{2}{P}_2$ (one), $C_{a_1}\cup C_{a_3}\cup \frac{a_2+s_1+s_2+s_3-5}{2}{P}_2$ (one); there is no spanning Sachs subgraph of G with one cycle; there is 1 perfect matching.

By Lemma 3, G is singular if and only if

$${(-1)}^{\frac{a_3+s_1+s_2+s_3-5}{2}+2}\times 2^2+{(-1)}^{\frac{a_2+s_1+s_2+s_3-5}{2}+2}\times 2^2+{(-1)}^{\frac{a_1+a_2+a_3+s_1+s_2+s_3-5}{2}}=0.$$

However, that is impossible, so G is non-singular.

Subcase 4.4 There is no s that is even. Where there is no spanning Sachs subgraph of G with three cycles; there is no spanning Sachs subgraph of G with two cycles; the spanning Sachs subgraph of G with one cycle is: $C_{a_1}\cup \frac{a_2+a_3+s_1+s_2+s_3-5}{2}{P}_2$ (one), $C_{a_2}\cup \frac{a_1+a_3+s_1+s_2+s_3-5}{2}{P}_2$ (one), $C_{a_3}\cup \frac{a_1+a_2+s_1+s_2+s_3-5}{2}{P}_2$ (one); there is no perfect matching.

By Lemma 3, G is singular if and only if

$${(-1)}^{\frac{a_2+a_3+s_1+s_2+s_3-5}{2}+1}\times 2+{(-1)}^{\frac{a_1+a_3+s_1+s_2+s_3-5}{2}+1}\times 2+{(-1)}^{\frac{a_1+a_2+s_1+s_2+s_3-5}{2}+1}\times 2=0.$$

However, that is impossible, so G is non-singular. □

Proof of Theorem 2. 

Let X be a random event and $P\left(X\right)$ denote the probability that the event X will occur.

Let U denote a random event: graph $\gamma (a_1,a_2,a_3,s_1,s_2,s_3)$ (see Figure 1) is singular. In order to make Theorem 1 (i)–(iv) mutually incompatible, the even cycle in (ii)–(iv) is restricted to the cycle whose length is module 4 plus 2.

Let A denote a random event: there is at least one cycle whose length is a multiple of 4.

Let $B_1$ denote a random event: there are three a that satisfy $a\equiv 2\left(mod4\right)$, and at least two s are odd or three s are even (the opposite is: exactly one s is odd).

Let $B_2$ denote a random event: there are exactly two a that satisfy $a\equiv 2\left(mod4\right)$, and the other $a\equiv 1\left(mod2\right)$, and the s connected with these two even cycles are all odd.

Let $B_3$ denote a random event: there is exactly one a that satisfies $a\equiv 2\left(mod4\right)$, and the other two $a\equiv 1\left(mod2\right)$, and the s connected with this even cycle is even, and the length of two odd cycles is not congruent with respect to module 4 and the parity of two s connected with these two odd cycles is the same. Then,

$$p\left(A\right)=1-{\left(\frac{3}{4}\right)}^3=\frac{37}{64},p\left(B_1\right)={\left(\frac{1}{4}\right)}^3(1-\left(\genfrac{}{}{0pt}{}{3}{1}\right){\left(\frac{1}{2}\right)}^3)=\frac{5}{512},$$

$$p\left(B_2\right)=\left(\genfrac{}{}{0pt}{}{3}{2}\right){\left(\frac{1}{4}\right)}^2\times {\left(\frac{1}{2}\right)}^3=\frac{3}{128},p\left(B_3\right)=\left(\genfrac{}{}{0pt}{}{3}{1}\right)\frac{1}{4}\times {\left(\frac{1}{2}\right)}^5=\frac{3}{128},$$

by Theorem 1, we obtain

$$p\left(U\right)=p(A\cup B_1\cup B_2\cup B_3)=p\left(A\right)+p\left(B_1\right)+p\left(B_2\right)+p\left(B_3\right)$$

$$=\frac{37}{64}+\frac{5}{512}+\frac{3}{128}+\frac{3}{256}=\frac{325}{512}.$$

Let V denote a random event: graph $\delta (a_1,a_2,a_3,s_1,s_2)$ (see Figure 2) is singular. In order to make Corollary 1 (i)–(iv) mutually incompatible, the even cycle in (ii)–(iv) is restricted to the cycle whose length is module 4 plus 2.

Let A denote a random event: there is at least one cycle whose length is a multiple of 4.

Let $B_1^{\prime }$ denote a random event: there are three a that satisfy $a\equiv 2\left(mod4\right)$, and at least one s is odd.

Let $C_1$ denote a random event: $a_2\equiv 2\left(mod4\right)$, in the remaining a, one $a\equiv 2\left(mod4\right)$, the other a is odd and the s connected with the even cycle is odd.

Let $C_2$ denote a random event: $a_1,a_3\equiv 2\left(mod4\right)$, $a_2$ is odd, and two s are odd.

Let $B_2^{\prime }=C_1\cup C_2$.

Let $B_3^{\prime }$ denote a random event: $a_2$ is odd, in the remaining a, one $a\equiv 2\left(mod4\right)$, the other a is odd, and the s connected with the even cycle is even, the length of two odd cycles is not congruent with respect to module 4 and the s connected with another odd cycle is odd. Then,

$$p\left(A\right)=1-{\left(\frac{3}{4}\right)}^3=\frac{37}{64},p\left(B_1^{\prime }\right)={\left(\frac{1}{4}\right)}^3(1-{\left(\frac{1}{2}\right)}^2)=\frac{3}{256},$$

$$p\left(C_1\right)=\frac{1}{4}\times \left(\genfrac{}{}{0pt}{}{2}{1}\right)\frac{1}{4}\times {\left(\frac{1}{2}\right)}^2=\frac{1}{32},p\left(C_2\right)={\left(\frac{1}{4}\right)}^2\times {\left(\frac{1}{2}\right)}^3=\frac{1}{128},$$

$$p\left(B_2^{\prime }\right)=p(C_1\cup C_2)=p\left(C_1\right)+p\left(C_2\right)=\frac{5}{128},p\left(B_3^{\prime }\right)=\frac{1}{2}\times \left(\genfrac{}{}{0pt}{}{2}{1}\right)\frac{1}{4}\times {\left(\frac{1}{2}\right)}^4=\frac{1}{64},$$

$$p\left(V\right)=p(A\cup B_1^{\prime }\cup B_2^{\prime }\cup B_3^{\prime })=p\left(A\right)+p\left(B_1^{\prime }\right)+p\left(B_2^{\prime }\right)+p\left(B_3^{\prime }\right)$$

$$=\frac{37}{64}+\frac{3}{256}+\frac{5}{128}+\frac{1}{64}=\frac{165}{256}.$$

Let W denote a random event: graph $\zeta (a_1,a_2,a_3,s)$ (see Figure 3) is singular. In order to make Corollary 2 (i)–(iv) mutually incompatible, the even cycle in (ii)–(iv) is restricted to the cycle whose length is module 4 plus 2.

Let A denote a random event: there is at least one cycle whose length is a multiple of 4.

Let $B_1^{″}$ denote a random event: there are three a that satisfy $a\equiv 2\left(mod4\right)$.

Let $C_1^{\prime }$ denote a random event: $a_1,a_2\equiv 2\left(mod4\right)$, $a_3$ is odd.

Let $C_2^{\prime }$ denote a random event: $a_3\equiv 2\left(mod4\right)$, in the remaining a, one $a\equiv 2\left(mod4\right)$, the other a is odd and s is odd.

Let $B_2^{″}=C_1^{\prime }\cup C_2^{\prime }$.

Let $B_3^{″}$ denote a random event: $a_3\equiv 2\left(mod4\right)$, $a_1,a_2$ are odd and s is even; the length of two odd cycles is not congruent with respect to module 4. Then,

$$p\left(A\right)=1-{\left(\frac{3}{4}\right)}^3=\frac{37}{64},p\left(B_1^{″}\right)={\left(\frac{1}{4}\right)}^3=\frac{1}{64},$$

$$p\left(C_1^{\prime }\right)={\left(\frac{1}{4}\right)}^2\times \frac{1}{2}=\frac{1}{32},p\left(C_2^{\prime }\right)=\left(\genfrac{}{}{0pt}{}{2}{1}\right){\left(\frac{1}{4}\right)}^2\times {\left(\frac{1}{2}\right)}^2=\frac{1}{32},$$

$$p\left(B_2^{″}\right)=p(C_1^{\prime }\cup C_2^{\prime })=p\left(C_1^{\prime }\right)+p\left(C_2^{\prime }\right)=\frac{1}{16},p\left(B_3^{″}\right)=\frac{1}{4}\times {\left(\frac{1}{2}\right)}^4=\frac{1}{64},$$

$$p\left(W\right)=p(A\cup B_1^{″}\cup B_2^{″}\cup B_3^{″})=p\left(A\right)+p\left(B_1^{″}\right)+p\left(B_2^{″}\right)+p\left(B_3^{″}\right)$$

$$=\frac{37}{64}+\frac{1}{64}+\frac{1}{16}+\frac{1}{64}=\frac{43}{64}.$$

Let Y denote a random event: graph $\phi (a_1,a_2,a_3)$ (see Figure 4) is singular. In order to make Corollary 3 (i)–(ii) mutually incompatible, the even cycle in (ii) is restricted to the cycle whose length is module 4 plus 2.

Let A denote a random event: there is at least one cycle whose length is a multiple of 4.

Let D denote a random event: there are three a that satisfy $a\equiv 2\left(mod4\right)$, or two a satisfy $a\equiv 2\left(mod4\right)$, the other a is odd. Then,

$$p\left(A\right)=1-{\left(\frac{3}{4}\right)}^3=\frac{37}{64},p\left(D\right)={\left(\frac{1}{4}\right)}^3+\left(\genfrac{}{}{0pt}{}{2}{1}\right){\left(\frac{1}{4}\right)}^2\times \frac{1}{2}=\frac{5}{64},$$

$$p\left(Y\right)=p(A\cup D)=\frac{37}{64}+\frac{5}{64}=\frac{21}{32}.$$

□

4. Discussion

We know that a connected graph G is a tree, unicyclic graph, bicyclic graph and tricyclic graph if and only if $\left|E\right(G\left)\right|=\left|V\right(G\left)\right|-1,\left|V\right(G\left)\right|,\left|V\right(G\left)\right|+1$ and $\left|V\right(G\left)\right|+2$, respectively. When the starting vertices of three paths $P_{b_1}$, $P_{b_2}$ and $P_{b_3}$ are conglutinated into a vertex and the end vertices are conglutinated into a vertex, the resulting graph is called a $\theta -$graph and is denoted as $\theta (b_1,b_2,b_3)$. The graph formed by the two end vertices of a path $P_s$ conglutinating into a vertex on the cycle $C_a$ and $C_b$ is called a $\infty -$graph, denoted as $\infty (a,s,b)$ (see Figure 7).

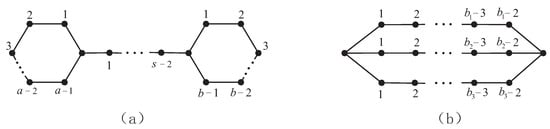
Figure 7. Two bicyclic graphs $\infty (a,s,b)$ and $\theta (b_1,b_2,b_3)$. Bicyclic graphs can be divided into two kinds: one is (a) ∞-graph as its induced subgraph, the other is (b) $\theta$-graph as its induced subgraph.

Every unicyclic graph contains a cycle $C_n$ as its induced subgraph. Meanwhile, the cycle $C_n$ is singular if and only if $4|n$. Bicyclic graphs can be divided into two kinds: one is ∞-graph as its induced subgraph, the other is $\theta$-graph as its induced subgraph. Below, we list two theorems that we will not prove.

Theorem 3. 

$\theta (b_1,b_2,b_3)$ is singular if and only if one of the following holds:

$\left(i\right)$ There are three b that are odd.

$\left(ii\right)$ The parity of three b is not all the same, and the length of the cycle formed by two paths with the same parity is a multiple of 4.

Theorem 4. 

$\infty (a,s,b)$ is singular if and only if one of the following holds:

$\left(i\right)$ There is at least one of two cycles whose length is a multiple of 4, that is, $4|a$ or $4|b$.

$\left(ii\right)$ s is odd:

(1) Both cycles are even cycles;

(2) Both cycles are odd cycles, and their lengths are not congruent with respect to module 4.

By Theorem 3, the probability that $\theta (b_1,b_2,b_3)$ is a singular graph is $\frac{1}{2}$. By Theorem 4, the probability that $\infty (a,s,b)$ is a singular graph is $\frac{17}{32}$.

The tricyclic graphs can be divided into 15 kinds, according to the induced subgraphs it contains. The tricyclic graphs containing $\gamma -$ graph, $\delta -$ graph, $\zeta -$ graph and $\phi -$ graph are denoted as $\mathcal{T}\left(\gamma \right)$, $\mathcal{T}\left(\delta \right)$, $\mathcal{T}\left(\zeta \right)$ and $\mathcal{T}\left(\phi \right)$, respectively. Suppose G has a pendant vertex, and $G^{\prime }$ is the graph obtained by deleting the pendant vertex and the quasi-pendant vertex from G, by Lemma 2, graphs G and $G^{\prime }$ have the same singularity. Similarly, if graph $G^{\prime }$ also has a pendant vertex, and $G^{″}$ is the graph obtained by deleting the pendant vertex and the quasi-pendant vertex from $G^{\prime }$, by Lemma 2, the graphs $G^{\prime }$ and $G^{″}$ therefore have the same singularity. By repeating the procedure above, that is, deleting in sequence the pendant vertices and quasi-pendant vertices from the graph, these graphs share the same singularity. Combined with Lemma 1, Theorem 1, Theorem 3, Theorem 4 and Corollaries 1–3, we can determine that singular graphs in $\mathcal{T}\left(\gamma \right)$, $\mathcal{T}\left(\delta \right)$, $\mathcal{T}\left(\zeta \right)$ and $\mathcal{T}\left(\phi \right)$.

5. Conclusions

By using the following results, a graph G with n vertices singularity if and only if its determinant $det\left(A\right(G)$ of adjacency matrix $A\left(G\right)$ equals 0, and combined with $det\left(A\left(G\right)\right)={(-1)}^n{\sum }_{H\in \mathcal{H}}{(-1)}^{p\left(H\right)}{2}^{c\left(H\right)},$ where $\mathcal{H}$ denotes the set of all the spanning Sachs subgraphs of graph G, $p\left(H\right)$ denotes the number of components in graph H and $c\left(H\right)$ denotes the number of cycles in graph H. We give the necessity and sufficiency that four kinds of tricyclic graphs, $\gamma -$graph, $\delta -$graph, $\zeta -$graph and $\phi -$graph, are singular and prove that the probability that a randomly given $\gamma -$graph, $\delta -$graph, $\zeta -$graph or $\phi -$graph being singular is equal to $\frac{325}{512},\frac{165}{256},\frac{43}{64}$, $\frac{21}{32}$, respectively. These results shine light upon the understanding of certain singular graphs and may be promising to solve its relevant problems.