Integrable Coupling of Expanded Isospectral and Non-Isospectral Dirac Hierarchy and Its Reduction

Abstract

In this paper, we first generalize the Dirac spectral problem to isospectral and non-isospectral problems and use the Tu scheme to derive the hierarchy of some new soliton evolution equations. Then, integrable coupling is obtained by solving the isospectral and non-isospectral zero curvature equations.We find that the obtained hierarchy has the bi-Hamiltonian structure of the combined form. In particular, one of the integrable soliton hierarchies is reduced to be similar to the coupled nonlinear Schördinger system in the AKNS hierarchy. Next, the strict self-adjointness of the reduced equation system is verified, and conservation laws are constructed with the aid of the Ibragimov method. In addition, we apply the extended Kudryashov method to obtain some exact solutions of this reduced equation system.

1. Introduction

Integrable systems are an important research field in nonlinear science and have important application backgrounds in the fields of optical fiber communication, superconductivity, shallow water waves, and plasma. The famous Lax pair method proposed by Magri [1] can generate a large number of integrable hierarchies of evolutionary equations. Tu [2] constructed the Lax pair or isospectral problem by using the Lie algebra of square matrix and its corresponding loop algebra, derived the soliton hierarchy from its compatibility, and determined the Hamiltonian structure of the soliton hierarchy by the trace identity, which is called the Tu scheme by Ma [3]. Many interesting isospectral integrable hierarchies and their properties can be obtained using the Tu scheme, as shown in Refs. [4,5,6,7,8,9,10,11,12,13]. The above integrable hierarchies are proposed in the case of isospectral problems. As a result, Zhang et al. [14,15,16] proposed a method for generating a nonisospectral integrable hierarchy on the basis of the assumption that ${\lambda }_t={\sum }_{i=0}^m{k}_i\left(t\right){\lambda }^{m-i}$.

With the introduction of the integrable coupling problem, there have been more methods to construct integrable coupling, such as the perturbation method, the generalization method of new loop algebra, and the non-semisimple Lie algebra method. Among them, Ma et al. [17], for the first time, put forward the use of the non-semisimple Lie algebra method to find integrable coupling. Based on this, experts and scholars worldwide have obtained meaningful conclusions, which have greatly promoted the development of integrable coupling [18,19,20,21,22].

In this paper, we first consider the application of the Tu scheme to the Dirac spectral problem and derive some new isospectral–non-isospectral soliton equation hierarchies. In Section 3, we construct a new Lie algebra $\overline{g}$ and its corresponding loop algebra $\tilde{g}$ and obtain the nonisospectral integrable coupling of Dirac by solving the zero curvature equation.

In Section 4, we use the method proposed by Tu [2] to generate integrable Hamiltonian hierarchies by using trace identities, as well as the Tu scheme to obtain some properties of integrable systems and Hamiltonian structures, such as the works [23,24,25]. In Section 5 and Section 6, we focus on Equation (12) that is reduced from the new isospectral–non-isospectral soliton equation hierarchies in Section 2, which are similar to the coupled nonlinear Schördinger system in the AKNS hierarchy; then, we study the self-adjointness and conservation laws of this equation system using the method proposed by Ibragimov [26] and find some exact solutions to the equation system by improving the methods in Refs. [27,28,29].

2. An Isospectral–Non-Isopectral Dirac Equation Integrable Hierarchy

Firstly, we show a classical algebra $A_1=h,e,f$, where

$$h=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right), e=\left(\begin{array}{cc}0& 1\\ 0& 0\end{array}\right), f=\left(\begin{array}{cc}0& 0\\ 1& 0\end{array}\right),$$

given a loop algebra

$${\overline{A}}_1=\{h\left(n\right),e\left(n\right),f\left(n\right)\},h\left(n\right)=h{\lambda }^n,f\left(n\right)=f{\lambda }^n,e\left(n\right)=e{\lambda }^n,$$

along with the commutators

$$\left[h\right(m),e(n\left)\right]=2e(m+n),\left[h\right(m),f(n\left)\right]=-2f(m+n),\left[e\right(m),f(n\left)\right]=h(m+n).m,n\in \mathrm{Z}.$$

Consider the following Dirac spectral problem

$${\phi }_x=U\phi ,U=ph\left(0\right)+qe\left(0\right)+qf\left(0\right)+e\left(1\right)-f\left(1\right),$$

(1)

$${\phi }_t=V_1\phi +V_2\phi =:V\phi ,$$

(2)

where

$$\begin{array}{c}\hfill V=V_1+V_2,V_1=Ch\left(0\right)+(A+B)e\left(0\right)+(A-B)f\left(0\right),\\ \hfill V_2=\overline{C}h\left(0\right)+(\overline{A}+\overline{B})e\left(0\right)+(\overline{A}-\overline{B})f\left(0\right),\\ \hfill A=\sum _{i\ge 0}{a}_i{\lambda }^{-i},B=\sum _{i\ge 0}{b}_i{\lambda }^{-i},C=\sum _{i\ge 0}{c}_i{\lambda }^{-i},\\ \hfill \overline{A}=\sum _{j\ge 0}{\overline{a}}_j{\lambda }^{-j},\overline{B}=\sum _{j\ge 0}{\overline{b}}_j{\lambda }^{-j},\overline{C}=\sum _{j\ge 0}{\overline{c}}_j{\lambda }^{-j}.\end{array}$$

Taking the spectral evolution ${\lambda }_t={\sum }_{j\ge 0}{k}_j\left(t\right){\lambda }^{-j}$, the compatibility condition of (1) and (2) reads

$$\frac{\partial U}{\partial u}{u}_t+\frac{\partial U}{\partial \lambda }{\lambda }_t-V_x+[U,V]=0.$$

(3)

According to the generalized Tu scheme, we first solve the stationary zero curvature equation for V:

$$\frac{\partial U}{\partial \lambda }{\lambda }_t+[U,V]=V_x,$$

(4)

which gives rise to

$$\left\{\begin{array}{c}{a}_{i+1}=\frac{1}{2}{c}_{i,x}+q{b}_i,\hfill \\ c_{i+1}=-\frac{1}{2}{a}_{i,x}+p{b}_i,\hfill \\ b_{i+1,x}=-2q{c}_{i+1}+2p{a}_{i+1},\hfill \\ {\overline{a}}_{j+1}=\frac{1}{2}{\overline{c}}_{j,x}+q{\overline{b}}_j,\hfill \\ {\overline{c}}_{j+1}=-\frac{1}{2}{\overline{a}}_{j,x}+p{\overline{b}}_j,\hfill \\ {\overline{b}}_{j+1,x}=-2q{\overline{c}}_{j+1}+2p{\overline{a}}_{j+1}+2k_{j+1}\left(t\right),\hfill \end{array}\right.$$

(5)

Taking $a_0=c_0=0,b_0=\alpha \left(t\right),{\overline{a}}_0={\overline{c}}_0=0,$ and ${\overline{b}}_0=k_0\left(t\right)$ into (5), we have

$$\begin{array}{cc}\hfill & a_1=q{\alpha }_0,c_1=p{\alpha }_0,b_1=0,a_2=\frac{{\alpha }_0}{2}{p}_x,\hfill \\ \hfill & c_2=-\frac{{\alpha }_0}{2}{q}_x,b_2=\frac{{\alpha }_0}{2}(p^2+q^2),a_3=-\frac{{\alpha }_0}{4}{q}_{xx}+\frac{{\alpha }_0}{2}q(p^2+q^2),\hfill \\ \hfill & c_3=-\frac{{\alpha }_0}{4}{p}_{xx}+\frac{{\alpha }_0}{2}p(p^2+q^2),b_3=\frac{{\alpha }_0}{2}(q{p}_x-p{q}_x),\hfill \\ \hfill & {\overline{a}}_1=q{k}_0,{\overline{c}}_1=p{k}_0,{\overline{b}}_1=2k_{1}x,{\overline{a}}_2=\frac{1}{2}{p}_x{k}_0+2q{k}_{1}x,\hfill \\ \hfill & {\overline{c}}_2=-\frac{1}{2}{k}_0{q}_x+2p{k}_{1}x,{\overline{b}}_2=\frac{k_0}{2}(p^2+q^2)+2k_{2}x,\hfill \\ \hfill & {\overline{a}}_3=-\frac{k_0}{4}{q}_{xx}+\frac{k_0}{2}q(p^2+q^2)+2q{k}_{2}x+p_x{k}_{1}x+p{k}_1,\hfill \\ \hfill & {\overline{c}}_3=-\frac{k_0}{4}{p}_{xx}+\frac{k_0}{2}p(p^2+q^2)+2p{k}_{2}x-q_x{k}_{1}x-q{k}_1,\hfill \\ \hfill & {\overline{b}}_3={\partial }^{-1}[\frac{k_0}{2}(q{p}_{xx}-p{q}_{xx})+2k_1(p^2+q^2+q{q}_{x}x+p{p}_{x}x)].\hfill \end{array}$$

Note that

$$\begin{array}{cc}\hfill V_{+}^{\left(n\right)}=& \sum _{i=0}^n(c_{i}h(n-i)+(a_i+b_i)e(n-i)+(a_i-b_i)f(n-i))\hfill \\ \hfill & +\sum _{j=0}^m({\overline{a}}_{j}h(m-j)+({\overline{a}}_j+{\overline{b}}_j)e(m-j)+({\overline{a}}_j-{\overline{b}}_j)f(m-j)),\hfill \\ \hfill {\lambda }_{t,+}^{\left(m\right)}=& \sum _{j=0}^m{k}_j\left(t\right){\lambda }^{m-j};\hfill \end{array}$$

then, a direct calculation reads

$$\begin{array}{cc}\hfill & -{(V_{1,+}^{(n)})}_x+[U,V_{1,+}^{(n)}]+\frac{\partial U}{\partial \lambda }{\lambda }_{t,+}^{(m)}-{(V_{2,+}^{(m)})}_x+[U,V_{2,+}^{(m)}]\hfill \\ \hfill & =-2a_{n+1}h(0)+2c_{n+1}e(0)+2c_{n+1}f(0)-2{\overline{a}}_{m+1}h(0)+2{\overline{c}}_{m+1}e\left(0\right)+2{\overline{c}}_{m+1}f\left(0\right).\hfill \end{array}$$

Set $V^n=V_{+}^{\left(n\right)}$; then, by the compatibility condition of non-isospectral Lax pairs, we have

$${\phi }_x=U\phi ,{\phi }_t=V^{\left(n\right)}\phi ,$$

which admits an isospectral–non-isospectral integerable hierarchy of evolution equations

$${\left(\begin{array}{c}p\\ -q\end{array}\right)}_t=\left(\begin{array}{c}2a_{n+1}+2{\overline{a}}_{m+1}\\ 2c_{n+1}+2{\overline{c}}_{m+1}\end{array}\right)=2\left(\begin{array}{c}{a}_{n+1}\\ c_{n+1}\end{array}\right)+2\left(\begin{array}{c}{\overline{a}}_{m+1}\\ {\overline{c}}_{m+1}\end{array}\right).$$

(6)

From (5) we find

$$\left(\begin{array}{c}{a}_{n+1}\\ c_{n+1}\end{array}\right)=\left(\begin{array}{cc}2q{\partial }^{-1}p& \frac{1}{2}\partial -2q{\partial }^{-1}q\\ -\frac{1}{2}\partial +2p{\partial }^{-1}p& -2p{\partial }^{-1}q\end{array}\right)\left(\begin{array}{c}{a}_n\\ c_n\end{array}\right)=:L\left(\begin{array}{c}{a}_n\\ c_n\end{array}\right).$$

(7)

Similarly, it can be inferred from (5) that

$$\left(\begin{array}{c}{\overline{a}}_{m+1}\\ {\overline{c}}_{m+1}\end{array}\right)=L\left(\begin{array}{c}{\overline{a}}_m\\ {\overline{c}}_m\end{array}\right)+2k_m\left(t\right)\left(\begin{array}{c}qx\\ px\end{array}\right).$$

(8)

Therefore, (6) can be written, using (7) and (8), as

$${\left(\begin{array}{c}p\\ -q\end{array}\right)}_{t_{n,m}}=2L[\left(\begin{array}{c}{a}_n\\ c_n\end{array}\right)+\left(\begin{array}{c}{\overline{a}}_m\\ {\overline{c}}_m\end{array}\right)]+4K_m\left(t\right)\left(\begin{array}{c}qx\\ px\end{array}\right).$$

(9)

Obviously, when $K_i\left(t\right)=0,i=0,1,\cdots ,m,{\overline{c}}_i={\overline{b}}_i=0$, (9) reduces to a hierarchy of the Dirac systems

$${\left(\begin{array}{c}p\\ -q\end{array}\right)}_t={\left(2L\right)}^n\left(\begin{array}{c}{\alpha }_{0}q\\ {\alpha }_{0}p\end{array}\right).$$

(10)

When $n=2,$ and $m=0$, we obtain from (9)

$$\left\{\begin{array}{cc}\hfill & p_t=-\frac{{\alpha }_0}{2}{q}_{xx}+{\alpha }_{0}q{p}^2+{\alpha }_0{q}^3+4k_{0}qx,\hfill \\ \hfill & q_t=\frac{{\alpha }_0}{2}{p}_{xx}-{\alpha }_0{q}^{2}p-{\alpha }_0{p}^3-4k_{0}px.\hfill \end{array}\right.$$

(11)

Taking ${\alpha }_0=1,k_0=0$, (11) becomes

$$\left\{\begin{array}{c}{p}_t=-\frac{1}{2}{q}_{xx}+q{p}^2+q^3,\hfill \\ q_t=\frac{1}{2}{p}_{xx}-q^{2}p-p^3.\hfill \end{array}\right.$$

(12)

This system is similar to the coupled nonlinear Schördinger system in the AKNS hierarchy.

When $n=0,$ and $m=2$, we obtain from (9)

$$\left\{\begin{array}{c}{p}_t=-\frac{1}{2}{k}_0{q}_{xx}+k_0{q}^3+k_{0}q{p}^2+2k_{1}x{p}_x+2k_{1}p+4k_{2}qx,\hfill \\ q_t=\frac{1}{2}{k}_0{p}_{xx}-k_0{p}^3-k_0{q}^{2}p+2k_{1}x{q}_x+2k_{1}q-4k_{2}px.\hfill \end{array}\right.$$

(13)

3. Integrable Coupling of the Nonisospectral Dirac Hierarchy

We quote a Lie algebra $g=span\left\{g_i,i=1,2,\cdots ,6\right\}$ [30], which has a set of bases,

$$\begin{array}{c}\hfill g_1=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& -1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& -1\end{array}\right),g_2=\left(\begin{array}{cccc}0& 1& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 1\\ 0& 0& 0& 0\end{array}\right),g_3=\left(\begin{array}{cccc}0& 0& 0& 0\\ 1& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 1& 0\end{array}\right),\\ \hfill g_4=\left(\begin{array}{cccc}0& 0& ϵ& 0\\ 0& 0& 0& -ϵ\\ 1& 0& 0& 0\\ 0& -1& 0& 0\end{array}\right),g_5=\left(\begin{array}{cccc}0& 0& 0& ϵ\\ 0& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 0\end{array}\right),g_6=\left(\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& ϵ& 0\\ 0& 0& 0& 0\\ 1& 0& 0& 0\end{array}\right),\end{array}$$

with the commuting relations

$$\begin{array}{cc}\hfill & [g_1,g_2]=2g_2,[g_1,g_3]=-2g_3,[g_1,g_4]=0,[g_1,g_5]=2g_5,[g_1,g_6]=-2g_6,[g_2,g_3]=g_1,\hfill \\ \hfill & [g_2,g_4]=-2g_5,[g_2,g_5]=0,[g_2,g_6]=g_4,[g_3,g_4]=2g_6,[g_3,g_5]=-g_4,[g_3,g_6]=0,\hfill \\ \hfill & [g_4,g_5]=2ϵg_2,[g_4,g_6]=-2ϵg_3,[g_5,g_6]=ϵg_1.\hfill \end{array}$$

The corresponding loop alegbra is taken by

$$\tilde{g}=span\left\{g_i\left(n\right),i=1,2,\dots ,6,n=1,2,\cdots \right\},g_i\left(n\right)=g_i{\lambda }^n,$$

along with the commutator

$$\begin{array}{cc}\hfill & [g_1\left(m\right),g_2\left(n\right)]=2g_2(m+n),[g_1\left(m\right),g_3\left(n\right)]=-2g_3(m+n),[g_1\left(m\right),g_5\left(n\right)]=2g_5(m+n),\hfill \\ & [g_1\left(m\right),g_6\left(n\right)]=-2g_6(m+n),[g_2\left(m\right),g_3\left(n\right)]=g_1(m+n),[g_2\left(m\right),g_4\left(n\right)]=-2g_5(m+n),\hfill \\ & [g_2\left(m\right),g_6\left(n\right)]=g_4(m+n),[g_3\left(m\right),g_4\left(n\right)]=2g_6(m+n),[g_3\left(m\right),g_5\left(n\right)]=-g_4(m+n),\hfill \\ & [g_4\left(m\right),g_5\left(n\right)]=2ϵg_2(m+n),[g_4\left(m\right),g_6\left(n\right)]=-2ϵg_3(m+n),[g_5\left(m\right),g_6\left(n\right)]=ϵg_1(m+n),\hfill \\ & [g_1\left(m\right),g_4\left(n\right)]=0,[g_2\left(m\right),g_5\left(n\right)]=0,[g_3\left(m\right),g_6\left(n\right)]=0.\hfill \end{array}$$

Based on the loop algebra $\tilde{g}$, we consider the spectral problem

$$\left\{\begin{array}{c}{\Phi }_x=U(\overline{u},\lambda )\Phi ,\hfill \\ U=p{g}_1\left(0\right)+g_2\left(1\right)-g_3\left(1\right)+q{g}_2\left(0\right)+q{g}_3\left(0\right)+r{g}_4\left(0\right)+g_5\left(1\right)-g_6\left(1\right)+s{g}_5\left(0\right)+s{g}_6\left(0\right),\hfill \\ {\Phi }_t=W\Phi ,\hfill \\ W=c{g}_1\left(0\right)+(a+b)g_2\left(0\right)+(a-b)g_3\left(0\right)+e{g}_4\left(0\right)+(f+g)g_5\left(0\right)+(f-g)g_6\left(0\right),\hfill \\ {\lambda }_t=\sum _{i\ge 0}{k}_i\left(t\right){\lambda }^{-i},\hfill \end{array}\right.$$

(14)

where $\overline{u}={(p,q,r,s)}^{\mathsf{T}}$ is the potential, $\Phi ={({\Phi }_1,{\Phi }_2,{\Phi }_3,{\Phi }_4)}^{\mathsf{T}}$ is the eigenfunction, and

$$a=\sum _{i\ge 0}{a}_i{\lambda }^{-i},b=\sum _{i\ge 0}{b}_i{\lambda }^{-i},c=\sum _{i\ge 0}{c}_i{\lambda }^{-i},e=\sum _{i\ge 0}{e}_i{\lambda }^{-i},f=\sum _{i\ge 0}{f}_i{\lambda }^{-i},g=\sum _{i\ge 0}{g}_i{\lambda }^{-i}.$$

In terms of the steps of the Tu scheme, the non-isospectral stationsry zero curvature equation

$$W_x=[U,W]+\frac{\partial U}{\partial \lambda }{\lambda }_t,$$

(15)

admits that

$$\left\{\begin{array}{c}{c}_{n,x}=2a_{n+1}-2q{b}_n+2ϵf_{n+1}-2ϵs{g}_n,\hfill \\ a_{n+1}+ϵf_{n+1}=\frac{1}{2}{c}_{n,x}+q{b}_n+ϵs{g}_n,\hfill \\ c_{n+1}+ϵe_{n+1}=-\frac{1}{2}{a}_{n.x}+p{b}_n+ϵr{g}_n,\hfill \\ e_{n,x}=2a_{n+1}-2s{b}_n+2f_{n+1}-2q{g}_n,\hfill \\ a_{n+1}+f_{n+1}=\frac{1}{2}{e}_{n,x}+s{b}_n+q{g}_n,\hfill \\ c_{n+1}+e_{n+1}=-\frac{1}{2}{f}_{n,x}+r{b}_n+p{g}_n,\hfill \end{array}\right.$$

(16)

which has an equivalent form

$$\left\{\begin{array}{c}{b}_{n,x}=2p{a}_n-2q{c}_n+2ϵr{f}_n-2ϵs{e}_n+k_n\left(t\right),\hfill \\ g_{n,x}=2r{a}_n-2s{c}_n+2p{f}_n-2q{e}_n+k_n\left(t\right),\hfill \\ a_{n+1}=\frac{1}{ϵ-1}(\frac{1}{2}ϵe_{n,x}+ϵs{b}_n+ϵq{g}_n-\frac{1}{2}{c}_{n,x}-q{b}_n-ϵs{g}_n),\hfill \\ f_{n+1}=\frac{1}{ϵ-1}(\frac{1}{2}{c}_{n,x}+q{b}_n+ϵs{g}_n-\frac{1}{2}{e}_{n,x}-s{b}_n-q{g}_n),\hfill \\ c_{n+1}=\frac{1}{ϵ-1}(-\frac{1}{2}ϵf_{n,x}+ϵr{b}_n+ϵp{g}_n+\frac{1}{2}{a}_{n,x}-p{b}_n-ϵr{g}_n),\hfill \\ e_{n+1}=\frac{1}{ϵ-1}(-\frac{1}{2}{a}_{n,x}+p{b}_n+ϵr{g}_n+\frac{1}{2}{f}_{n,x}-r{b}_n-p{g}_n).\hfill \end{array}\right.$$

(17)

Set

$$a_0=c_0=e_0=f_0=0,b_0=g_0=1,$$

and

$$a_m{|}_{u=0}=b_m{|}_{u=0}=c_m{|}_{u=0}=e_m{|}_{u=0}=f_m{{|}_{u=0}=g_m|}_{u=0}=0,m\ge 0;$$

then, the first two sets are written as:

$$\begin{array}{cc}\hfill & a_1=q,f_1=s,c_1=p,e_1=r,b_1=k_1(t)x,g_1=k_1(t)x,\hfill \\ \hfill & a_2=\frac{1}{2(ϵ-1)}(ϵr_x-p_x)+q{k}_{1}x,f_2=\frac{1}{2(ϵ-1)}(p_x-r_x)+s{k}_{1}x,\hfill \\ \hfill & e_2=\frac{1}{2(ϵ-1)}(s_x-q_x)+r{k}_{1}x,c_2=\frac{1}{2(ϵ-1)}(q_x-ϵs_x)+p{k}_{1}x,\hfill \\ \hfill & b_2=\frac{1}{ϵ-1}[(-\frac{1}{2}(p^2+q^2+ϵr^2+ϵs^2)+ϵpr+ϵqs)]+k_{2}x,\hfill \\ \hfill & f_2=\frac{1}{ϵ-1}[(\frac{1}{2}(p^2+q^2+ϵr^2+ϵs^2)-pr-qs)]+k_{2}x,\hfill \\ \hfill & \cdots \hfill \end{array}$$

Denote that

$$\begin{array}{cc}\hfill W_{+}^{[m]}=& \sum _{i=0}^m[c_i{g}_1(m-i)+(a_i+b_i)g_2(m-i)+(a_i-b_i)g_3(m-i)\hfill \\ & +e_i{g}_4(m-i)+(f_i+g_i)g_5(m-i)+(f_i-g_i)g_6(m-i)],\hfill \\ \hfill W_{-}^{[m]}=& \sum _{i=m+1}^{\infty }[c_i{g}_1(m-i)+(a_i+b_i)g_2(m-i)+(a_i-b_i)g_3(m-i)\hfill \\ & +e_i{g}_4(m-i)+(f_i+g_i)g_5(m-i)+(f_i-g_i)g_6(m-i)],\hfill \\ \hfill {\lambda }_{t,+}^{[m]}=& \sum _{i=0}^{m-1}{k}_i\left(t\right){\lambda }^{m-i}={\lambda }^m\sum _{i\ge 0}{k}_i\left(t\right){\lambda }^{-i}-\sum _{i\ge n}{k}_i\left(t\right){\lambda }^{m-i}={\lambda }^m{\lambda }_t-{\lambda }_{t,-}^{[m]}.\hfill \end{array}$$

(18)

Then, Equation (15) can be written as

$$-W_{+,x}^{[m]}+[U,W_{+}^{[m]}]+\frac{\partial U}{\partial \lambda }{\lambda }_{t,+}^m=W_{-,x}^{[m]}-[U,W_{-}^{[m]}]-\frac{\partial U}{\partial \lambda }{\lambda }_{t,-}^{[m]}.$$

(19)

By taking (18) into (19) and taking these terms of gradation 0, we can obtain

$$\begin{array}{cc}\hfill -W_{+,x}^{[m]}+[U,W_{+}^{[m]}]+\frac{\partial U}{\partial \lambda }{\lambda }_{t,+}^{[m]}=& 2(a_{m+1}+ϵf_{m+1})g_1\left(0\right)+2(-c_{m+1}-ϵe_{m+1})(g_2\left(0\right)+g_3\left(0\right))\hfill \\ & +2(a_{m+1}+f_{m+1})g_4\left(0\right)+2(-c_{m+1}-e_{m+1})(g_5\left(0\right)+g_6\left(0\right)).\hfill \end{array}$$

(20)

Then, the zero curvature equation

$$\frac{\partial U}{\partial u}{u}_t+\frac{\partial U}{\partial \lambda }{\lambda }_t-W_x^{[m]}+[U,W^{[m]}]=0$$

(21)

gives rise to the non-isospectral Dirac integrable coupling hierarchy as follows:

$$u_{t_m}={\left[\begin{array}{c}p\\ q\\ r\\ s\end{array}\right]}_{t_m}=2\left[\begin{array}{c}{a}_{m+1}+ϵf_{m+1}\\ -c_{m+1}-ϵe_{m+1}\\ a_{m+1}+f_{m+1}\\ -c_{m+1}-e_{m+1}\end{array}\right].$$

(22)

The first two nonlinear examples as:

$$\left\{\begin{array}{c}{p}_{t_1}=p_x+2(q+ϵs)k_1\left(t\right)x,\hfill \\ q_{t_1}=q_x-2(p+ϵr)k_1\left(t\right)x,\hfill \\ r_{t_1}=r_x+2(q+s)k_1\left(t\right)x,\hfill \\ s_{t_1}=s_x-2(p+r)k_1\left(t\right)x.\hfill \end{array}\right.$$

(23)

and

$$\left\{\begin{array}{cc}{p}_{t_2}=\hfill & \frac{1}{ϵ-1}[\frac{1}{2}(q_{xx}-ϵs_{xx})+(ϵs-q)(p^2+q^2+ϵr^2+ϵs^2)+2ϵpqr+2ϵq^{2}s-2ϵpsr-2ϵq{s}^2]\hfill \\ \hfill & +(p+p_{x}x)k_1\left(t\right)+2(ϵs+q)x{k}_2\left(t\right),\hfill \\ q_{t_2}=\hfill & \frac{1}{ϵ-1}[\frac{1}{2}(ϵr_{xx}-p_{xx})-(ϵr-p)(p^2+q^2+ϵr^2+ϵs^2)+2ϵp{r}^2+2ϵqrs-2ϵp^{2}r-2ϵpqs]\hfill \\ \hfill & +(q+q_{x}x)k_1\left(t\right)-2(ϵr+p)x{k}_2\left(t\right),\hfill \\ r_{t_2}=\hfill & \frac{1}{ϵ-1}[\frac{1}{2}(s_{xx}-q_{xx})+(q-s)(p^2+q^2+ϵr^2+ϵs^2)+2ϵpsr+2ϵq{s}^2-2pqr-2q^{2}s]\hfill \\ \hfill & +(p+p_{x}x)k_1\left(t\right)+2(s+q)x{k}_2\left(t\right),\hfill \\ s_{t_2}=\hfill & \frac{1}{ϵ-1}[\frac{1}{2}(p_{xx}-r_{xx})-(p-r)(p^2+q^2+ϵr^2+ϵs^2)+2ϵp^{2}r+2ϵpqs-2ϵp{r}^2-2ϵqrs]\hfill \\ \hfill & +(s+s_{x}x)k_1\left(t\right)-2(r+p)x{k}_2\left(t\right).\hfill \end{array}\right.$$

(24)

4. Hamiltonian Structure of the Dirac Integrable Coupling

In this section, we focus on the Hamiltonian structure of the hierarchy (22) by using the trace identity proposed by Tu [2]. We denote the trace of the square matrices A and B by $<A,B>=tr\left(AB\right)$.

From (14), let

$$U_1=\left[\begin{array}{cc}p& \lambda +q\\ -\lambda +q& -p\end{array}\right],U_2\left[\begin{array}{cc}r& \lambda +s\\ -\lambda +s& -r\end{array}\right],W_1=\left[\begin{array}{cc}c& a+b\\ a-b& -c\end{array}\right],W_2=\left[\begin{array}{cc}e& f+g\\ f-g& -c\end{array}\right],$$

we obtain

$$\begin{array}{cc}\hfill & ⟨W_1,\frac{\partial U_2}{\partial p}⟩+⟨W_2,\frac{\partial U_1}{\partial p}⟩=2e,⟨W_1,\frac{\partial U_2}{\partial q}⟩+⟨W_2,\frac{\partial U_1}{\partial q}⟩=2f,\hfill \\ \hfill & ⟨W_1,\frac{\partial U_2}{\partial r}⟩+⟨W_2,\frac{\partial U_1}{\partial r}⟩=2c,⟨W_1,\frac{\partial U_2}{\partial s}⟩+⟨W_2,\frac{\partial U_1}{\partial s}⟩=2a,\hfill \\ \hfill & ⟨W_1,\frac{\partial U_2}{\partial \lambda }⟩+⟨W_2,\frac{\partial U_1}{\partial \lambda }⟩=-2b-2g,⟨W_1,\frac{\partial U_1}{\partial p}⟩+ϵ⟨W_2,\frac{\partial U_2}{\partial p}⟩=2c,\hfill \\ \hfill & ⟨W_1,\frac{\partial U_1}{\partial q}⟩+ϵ⟨W_2,\frac{\partial U_2}{\partial q}⟩=2a,⟨W_1,\frac{\partial U_1}{\partial r}⟩+ϵ⟨W_2,\frac{\partial U_2}{\partial r}⟩=2ϵe,\hfill \\ \hfill & ⟨W_1,\frac{\partial U_1}{\partial s}⟩+ϵ⟨W_2,\frac{\partial U_2}{\partial s}⟩=2ϵf,⟨W_1,\frac{\partial U_1}{\partial \lambda }⟩+ϵ⟨W_2,\frac{\partial U_2}{\partial \lambda }⟩=-2b-2ϵg,\hfill \end{array}$$

which can be substituted into the following two sets of component-trace identity

$$\frac{\delta }{\delta u}\int \left(⟨W_1,\frac{\partial U_2}{\partial \lambda }⟩+⟨W_2,\frac{\partial U_1}{\partial \lambda }⟩\right)dx={\lambda }^{-\gamma }\frac{\partial }{\partial \lambda }{\lambda }^{\gamma }\left(⟨W_1,\frac{\partial U_2}{\partial u}⟩+⟨W_2,\frac{\partial U_1}{\partial u}⟩\right),$$

(25)

$$\frac{\delta }{\delta u}\int \left(⟨W_1,\frac{\partial U_1}{\partial \lambda }⟩+ϵ⟨W_2,\frac{\partial U_2}{\partial \lambda }⟩\right)dx={\lambda }^{-\gamma }\frac{\partial }{\partial \lambda }{\lambda }^{\gamma }\left(⟨W_1,\frac{\partial U_1}{\partial u}⟩+ϵ⟨W_2,\frac{\partial U_2}{\partial u}⟩\right).$$

(26)

Then, we substitute the Laurent series into the above identity (25), (26), and we compare the powers of $\lambda$ to yield

$$\frac{\delta }{\delta u}\int (b_{n+1}+g_{n+1})dx=(n-\gamma )\left[\begin{array}{c}{e}_n\\ f_n\\ c_n\\ a_n\end{array}\right],\frac{\delta }{\delta u}\int (b_{n+1}+ϵg_{n+1})dx=(n-\gamma )\left[\begin{array}{c}{c}_n\\ a_n\\ ϵe_n\\ ϵf_n\end{array}\right].$$

(27)

We find that $\gamma =0$ via substituting $m=1$ into (27). Hence,

$$\frac{\delta }{\delta u}\int \frac{b_{n+2}+g_{n+2}}{n+1}dx=\left[\begin{array}{c}{e}_{n+1}\\ f_{n+1}\\ c_{n+1}\\ a_{n+1}\end{array}\right]=\frac{\delta H_{1,n}}{\delta u},\frac{\delta }{\delta u}\int \frac{b_{n+2}+ϵg_{n+2}}{n+1}dx=\left[\begin{array}{c}{c}_{n+1}\\ a_{n+1}\\ ϵe_{n+1}\\ ϵf_{n+1}\end{array}\right]=\frac{\delta H_{2,n}}{\delta u}.$$

(28)

Consequently, we obtain the Hamilitonian structure of (22)

$${\overline{u}}_{t_n}=K_{2_n}=2\left[\begin{array}{c}{a}_{n+1}+ϵf_{n+1}\\ -c_{n+1}-ϵe_{n+1}\\ a_{n+1}+f_{n+1}\\ -c_{n+1}-e_{n+1}\end{array}\right]=J_1\frac{\delta H_{1,n}}{\delta u}=J_2\frac{\delta H_{2,n}}{\delta u},$$

(29)

with the Hamiltonian operators

$$J_1=\left[\begin{array}{cccc}0& 2ϵ& 0& 2\\ -2ϵ& 0& -2& 0\\ 0& 2& 0& 2\\ -2& 0& -2& 0\end{array}\right],J_2=\left[\begin{array}{cccc}0& 2& 0& 2\\ -2& 0& -2& 0\\ 0& 2& 0& \frac{2}{ϵ}\\ -2& 0& -\frac{2}{ϵ}& 0\end{array}\right],$$

and the Hamiltonian functionals

$$H_{1,n}=\int \frac{b_{n+2}+g_{n+2}}{n+1}dx,H_{2,n}=\int \frac{b_{n+2}+ϵg_{n+2}}{n+1}dx.$$

For the first component, one has the Hamiltonian structure for the integrable coupling hierarchy (22) as follows:

$${\overline{u}}_{t_n}=K_{2_n}=2\left[\begin{array}{c}{a}_{n+1}+ϵf_{n+1}\\ -c_{n+1}-ϵe_{n+1}\\ a_{n+1}+f_{n+1}\\ -c_{n+1}-e_{n+1}\end{array}\right]=J_1\left[\begin{array}{c}{e}_{n+1}\\ f_{n+1}\\ c_{n+1}\\ a_{n+1}\end{array}\right]=J_1\frac{\delta H_{1,n}}{\delta u}.$$

(30)

Now, using the recurrence relationships (17), we obtain the recursion operator $\overline{N}$ of the hierarchy (22) as follows:

$$\left[\begin{array}{c}{e}_{n+1}\\ f_{n+1}\\ c_{n+1}\\ a_{n+1}\end{array}\right]=\overline{N}\left[\begin{array}{c}{e}_n\\ f_n\\ c_n\\ a_n\end{array}\right]+\tilde{L}{k}_n\left(t\right)=\left[\begin{array}{cc}{N}_1& N_2\\ ϵN_2& N_1\end{array}\right]\left[\begin{array}{c}{e}_n\\ f_n\\ c_n\\ a_n\end{array}\right]+\left[\begin{array}{c}rx\\ sx\\ px\\ qx\end{array}\right]k_n\left(t\right),$$

(31)

where

$$N_1=\frac{1}{ϵ-1}\left[\begin{array}{cc}-2ϵp{\partial }^{-1}s-2ϵr{\partial }^{-1}q+2ϵr{\partial }^{-1}s+2p{\partial }^{-1}q& \frac{1}{2}\partial +2ϵp{\partial }^{-1}r+2ϵr{\partial }^{-1}p-2ϵr{\partial }^{-1}r-2p{\partial }^{-1}p\\ -\frac{1}{2}\partial -2ϵq{\partial }^{-1}s-2ϵs{\partial }^{-1}q+2ϵs{\partial }^{-1}s+2q{\partial }^{-1}q& 2ϵq{\partial }^{-1}r+2ϵs{\partial }^{-1}p-2ϵs{\partial }^{-1}r-2q{\partial }^{-1}p\end{array}\right],$$

$$N_2=\frac{1}{ϵ-1}\left[\begin{array}{cc}-2p{\partial }^{-1}q-2ϵr{\partial }^{-1}s+2r{\partial }^{-1}q+2p{\partial }^{-1}s& -\frac{1}{2}\partial +2p{\partial }^{-1}p+2ϵr{\partial }^{-1}r-2r{\partial }^{-1}p-2p{\partial }^{-1}r\\ \frac{1}{2}\partial -2q{\partial }^{-1}q-2ϵs{\partial }^{-1}s+2s{\partial }^{-1}q+2q{\partial }^{-1}s& 2q{\partial }^{-1}p+2ϵs{\partial }^{-1}r-2s{\partial }^{-1}p-2q{\partial }^{-1}r\end{array}\right].$$

Therefore, we obtain the first component of the Hamiltonian structure of the soliton hierarchy (22) as follows:

$${\overline{u}}_{t_n}={\left[\begin{array}{c}p\\ q\\ r\\ s\end{array}\right]}_{t_n}=K_{2_n}=\left[\begin{array}{c}{\Phi }_1^m+\sum _{i=0}^{n-1}{\Phi }_1^i{k}_{n-i}\left(t\right)x\end{array}\right]\left[\begin{array}{c}q+ϵs\\ -p-ϵr\\ q+s\\ -p-r\end{array}\right],$$

(32)

where the second pair of Hamiltonian operators

$$M_1=J_1\overline{N},$$

and the recursion operator

$${\Phi }_1=J_1\overline{N}{J}_1^{-1}=\left[\begin{array}{cc}{\Phi }_{11}& ϵ{\Phi }_{12}\\ {\Phi }_{12}& {\Phi }_{11}\end{array}\right].$$

(33)

Simliarily, we can obtain the following relationships

$$\left[\begin{array}{c}{c}_{n+1}\\ a_{n+1}\\ ϵe_{n+1}\\ ϵf_{n+1}\end{array}\right]=\overline{N}\left[\begin{array}{c}{c}_n\\ a_n\\ ϵe_n\\ ϵf_n\end{array}\right]+\widehat{L}{k}_n\left(t\right),\widehat{L}=\left[\begin{array}{c}px\\ qx\\ ϵrx\\ ϵsx\end{array}\right],$$

(34)

and for the second component, one has the Hamiltonian structure for the integrable coupling hierarchy (22) as follows:

$${\overline{u}}_{t_n}={\left[\begin{array}{c}p\\ q\\ r\\ s\end{array}\right]}_{t_n}=K_{2_n}=\left[\begin{array}{c}{\Phi }_2^m+\sum _{i=0}^{n-1}{\Phi }_2^i{k}_{n-i}\left(t\right)x\end{array}\right]\left[\begin{array}{c}q+ϵs\\ -p-ϵr\\ q+s\\ -p-r\end{array}\right],$$

(35)

where the second pair of Hammiltonian operators

$$M_2=J_2\overline{N},$$

and the recursion operator

$${\Phi }_2=J_2\overline{N}{J}_2^{-1}=\left[\begin{array}{cc}{\Phi }_{21}& ϵ{\Phi }_{22}\\ {\Phi }_{22}& {\Phi }_{21}\end{array}\right].$$

(36)

After calculation, we find

$$\begin{array}{cc}\hfill & {\Phi }_{11}={\Phi }_{21}=\hfill \\ \hfill & \frac{1}{ϵ-1}\left[\begin{array}{cc}2ϵq{\partial }^{-1}r+2ϵs{\partial }^{-1}p-2ϵs{\partial }^{-1}r-2q{\partial }^{-1}p& \frac{1}{2}\partial +2ϵq{\partial }^{-1}s+2ϵs{\partial }^{-1}q-2ϵs{\partial }^{-1}s-2q{\partial }^{-1}q\\ -\frac{1}{2}\partial -2ϵp{\partial }^{-1}r-2ϵr{\partial }^{-1}p+2ϵr{\partial }^{-1}r+2p{\partial }^{-1}p& -2ϵp{\partial }^{-1}s-2ϵr{\partial }^{-1}q+2ϵr{\partial }^{-1}s+2p{\partial }^{-1}q\end{array}\right].\hfill \end{array}$$

$$\begin{array}{cc}\hfill & {\Phi }_{12}={\Phi }_{22}=\hfill \\ \hfill & \frac{1}{ϵ-1}\left[\begin{array}{cc}2q{\partial }^{-1}p+2ϵs{\partial }^{-1}r-2s{\partial }^{-1}p-2q{\partial }^{-1}r& -\frac{1}{2}\partial +2q{\partial }^{-1}q+2ϵs{\partial }^{-1}s-2s{\partial }^{-1}q-2q{\partial }^{-1}s\\ \frac{1}{2}\partial -2p{\partial }^{-1}p-2ϵr{\partial }^{-1}r+2r{\partial }^{-1}p+2p{\partial }^{-1}r& -2p{\partial }^{-1}q-2ϵr{\partial }^{-1}s+2r{\partial }^{-1}q+2p{\partial }^{-1}s\end{array}\right].\hfill \end{array}$$

5. Self-Adjointness and Conservation Laws

In this section, we consider the strictly self-adjointness and conservation laws of Equation (12) by the method proposed by Ibragimov [26].

First, let us start with the following notation and basic definition

$$\begin{array}{cc}\hfill & x=(x^1,\dots ,x^n),\hfill \\ \hfill & u_i^{\alpha }=D_i\left(u^{\alpha }\right),u_{ij}=D_i{D}_j\left(u^{\alpha }\right),\dots ,v_i^{\alpha }=D_i\left(v^{\alpha }\right),v_{ij}=D_i{D}_j\left(v^{\alpha }\right),\dots ,\hfill \end{array}$$

where $x^k(k=1,2,\cdots ,n)$ are independent variables, and $D_i$ denotes the total differentiations operator with four dependent variables, u, v, $\overline{u},$ and $\overline{v}$, i.e.,

$$D_i=\frac{\partial }{\partial x^i}+u_i^{\alpha }\frac{\partial }{\partial u^{\alpha }}+v_i^{\alpha }\frac{\partial }{\partial v^{\alpha }}+u_{ij}^{\alpha }\frac{\partial }{\partial u_j^{\alpha }}+v_{ij}^{\alpha }\frac{\partial }{\partial v_j^{\alpha }}+\cdots .$$

The systems of m differential equations can be written as

$$F_{\alpha }(x,u,u_{\left(1\right)},\dots ,u_{\left(s\right)})=0,\alpha =1,\cdots ,m,$$

(37)

which admits the adjoint equations

$$F_{\alpha }^{*}(x,u,u_{\left(1\right)},v_{\left(1\right)},\dots ,u_{\left(s\right)},v_{\left(s\right)})=0,\alpha =1,\cdots ,m,$$

(38)

where

$$\begin{array}{cc}\hfill & F_{\alpha }^{*}(x,u,u_{\left(1\right)},v_{\left(1\right)},\dots ,u_{\left(s\right)},v_{\left(s\right)})=\frac{\delta \mathcal{L}}{\delta u^{\alpha }},\hfill \\ \hfill & u_{\left(1\right)}=\left\{u_i^{\alpha }\right\},u_{\left(2\right)}=\left\{u_{ij}^{\alpha }\right\},\dots ,u_{\left(s\right)}=\left\{u_{i_1\dots i_s}^{\alpha }\right\},\hfill \\ \hfill & v_{\left(1\right)}=\left\{v_i^{\alpha }\right\},v_{\left(2\right)}=\left\{v_{ij}^{\alpha }\right\},v_{\left(s\right)}=\left\{v_{i_1\dots i_s}^{\alpha }\right\},\hfill \end{array}$$

(39)

with $\mathcal{L}$ as the formal Lagrangian for Equation (37) given by

$$\mathcal{L}=\sum _{\alpha =1}^m{v}^{\alpha }{F}_{\alpha }(x,u,u_{\left(1\right)},\dots ,u_{\left(s\right)}),$$

(40)

and $\frac{\delta }{\delta u^{\alpha }}$ is the variational derivative that reads

$$\frac{\delta }{\delta u^{\alpha }}=\frac{\partial }{\partial u^{\alpha }}+\sum _{s=1}^{\infty }{(-1)}^s{D}_{i_1}\dots D_{i_s}\frac{\partial }{\partial u_{i_1\cdots i_s}^{\alpha }}.$$

(41)

Definition 1.

Equation (37) is said to be strictly self-adjoint, if the adjoint Equation (38) becomes equivalent to the original Equation (37) upon the substitution (see Ref. [26])

$$v^{\alpha }=u^{\alpha },\alpha =1,\dots ,m.$$

It means that the equation

$$F^{*}(x,u,\dots ,u_{\left(s\right)})=\lambda F(x,u,\dots ,u_{\left(s\right)}),$$

holds with a certain (in general, variable) coefficient λ.

Proposition 1.

Equation (12) is strictly self-adjoint.

Proof. 

Set

$$\left\{\begin{array}{c}{F}_1(x,t,u)=u_t+\frac{1}{2}{v}_{xx}-u^{2}v-v^3,\hfill \\ F_2(x,t,u)=v_t-\frac{1}{2}{u}_{xx}+u{v}^2+u^3;\hfill \end{array}\right.$$

(42)

then, the formal Lagrangian for (40) can be written as

$$\begin{array}{cc}\hfill \mathcal{L}& ={\omega }^1{F}_1(x,t,u)+{\omega }^2{F}_2(x,t,u)\hfill \\ \hfill & ={\omega }^1(u_t+\frac{1}{2}{v}_{xx}-u^{2}v-v^3)+{\omega }^2(v_t-\frac{1}{2}{u}_{xx}+u{v}^2+u^3),\hfill \end{array}$$

(43)

which admits the adjoint

$$\left\{\begin{array}{c}\frac{\delta \mathcal{L}}{\delta u}=-{\omega }_t^1-2uv{\omega }^1-\frac{1}{2}{\omega }_{xx}^2+3u^2{\omega }^2+v^2{\omega }^2,\hfill \\ \frac{\delta \mathcal{L}}{\delta v}=-{\omega }_t^2+2uv{\omega }^2+\frac{1}{2}{\omega }_{xx}^1-3v^2{\omega }^1-u^2{\omega }^1.\hfill \end{array}\right.$$

(44)

Substituting ${\omega }^1=u,{\omega }^2=v$ into (44), we have

$$\left\{\begin{array}{c}\frac{\delta \mathcal{L}}{\delta u}=-u_t-\frac{1}{2}{v}_{xx}+u^{2}v+v^3=-F_1,\hfill \\ \frac{\delta \mathcal{L}}{\delta v}=-v_t+\frac{1}{2}{u}_{xx}-u{v}^2-u^3=-F_2.\hfill \end{array}\right.$$

(45)

Thus, Equation (42) is strictly self-adjoint.

Next, we consider the conservation laws of Equation (12).

Let $X={\xi }^i\frac{\partial }{\partial x^i}+{\eta }^{\alpha }\frac{\partial }{\partial u^{\alpha }}$ be any Lie–B$\ddot{a}$cklund operator

$$X={\xi }^i\frac{\partial }{\partial x^i}+{\eta }^{\alpha }\frac{\partial }{\partial u^{\alpha }}+{\zeta }_i^{\alpha }\frac{\partial }{\partial u_i^{\alpha }}+{\zeta }_{i_1{i}_2}^{\alpha }\frac{\partial }{\partial u_{i_1{i}_2}^{\alpha }}+\cdots ,$$

(46)

where

$$\begin{array}{cc}\hfill & {\xi }_i^{\alpha }=D_i({\eta }^{\alpha }-{\xi }^j{u}_j^{\alpha })+{\xi }^j{u}_{ij}^{\alpha },\hfill \\ \hfill & {\xi }_{i_1{i}_2}^{\alpha }=D_{i_1}{D}_{i_2}({\eta }^{\alpha }-{\xi }^j{u}_j^{\alpha })+{\xi }^j{u}_{i_1{i}_{2}j}^{\alpha },\cdots .\hfill \end{array}$$

(47)

We associate with X the following n operators ${\mathcal{N}}^i(i=1,\dots ,n)$ by the formal sums:

$${\mathcal{N}}^i={\xi }^i+W^{\alpha }\frac{\delta }{\delta u_i^{\alpha }}+\sum _{s=1}^{\infty }{D}_{i_1}\cdots D_{i_s}\frac{\delta }{\delta u_{i{i}_1\cdots i_s}^{\alpha }},$$

(48)

where

$$W^{\alpha }={\eta }^{\alpha }-{\xi }^j{u}_j^{\alpha },\frac{\delta }{\delta u_i^{\alpha }}=\frac{\partial }{\partial u_i^{\alpha }}+\sum _{s=1}^{\infty }{(-1)}^s{D}_{i_1}\dots D_{i_s}\frac{\partial }{\partial u_{i{i}_1\cdots i_s}^{\alpha }},\alpha =1,\dots ,m,$$

(49)

The Euler–Lagrange (41), Lie–B$\ddot{a}$cklund (46), and the associated operators (49) are connected by the following fundamental identity (see [31]):

$$X+D_i\left({\xi }^i\right)=W^{\alpha }\frac{\delta }{\delta u^{\alpha }}+D_i{\mathcal{N}}^i.$$

(50)

□

Lemma 1.

A function $f(x,u,\dots ,u_{\left(s\right)})\in \mathcal{A}$ with several independent variables $x=(x^1,\dots ,x^n)$ and several dependent variables $u=(u^1,\dots ,u^m)$ is the divergence of a vector field $H=(h^1,\dots ,h^n),h_i\in \mathcal{A}$, where $\mathcal{A}$ represents the set of all finite order differential functions, i.e.,

$$f=divH=D_i\left(h^i\right),$$

(51)

if and only if the following equations hold identically in $x,u,u_{\left(1\right)},\dots :$

$$\frac{\delta f}{\delta u^{\alpha }}=0,\alpha =1,\dots ,m.$$

(52)

Theorem 1.

Any Lie point, Lie–B$\ddot{a}$cklund, and nonlocal symmetry (see Refs. [26,32])

$$X={\xi }^i(x,u,u_{\left(1\right)},\dots )\frac{\partial }{\partial x^i}+{\eta }^{\alpha }(x,u,u_{\left(1\right)},\dots )\frac{\partial }{\partial u^{\alpha }},$$

of the Frobenius Equation (37) leads to the conservation law $D_i(C^i)=0$ constructed by the formula

$$\begin{array}{cc}\hfill C^i=& {\xi }^i\mathcal{L}+W^{\alpha }\left[\begin{array}{c}\frac{\partial \mathcal{L}}{\partial u_i^{\alpha }}-D_j(\frac{\partial \mathcal{L}}{\partial u_{ij}^{\alpha }})+D_j{D}_k(\frac{\partial \mathcal{L}}{\partial u_{ijk}^{\alpha }})-\cdots \end{array}\right]\hfill \\ \hfill & +D_j(W^{\alpha })\left[\begin{array}{c}\frac{\partial \mathcal{L}}{\partial u_{ij}^{\alpha }}-D_k(\frac{\partial \mathcal{L}}{\partial u_{ijk}^{\alpha }})+\cdots \end{array}\right]\hfill \\ \hfill & +D_j{D}_k(W^{\alpha })\left[\begin{array}{c}\frac{\partial \mathcal{L}}{\partial u_{ijjk}^{\alpha }}-\cdots \end{array}\right]+\cdots ,\hfill \end{array}$$

(53)

with $W^{\alpha }={\eta }^{\alpha }-{\xi }^j{u}_j^{\alpha },\alpha =1,\dots ,m$.

Proof. 

Let us begin with the Euler–Lagrange equations

$$\frac{\delta \mathcal{L}}{\delta u^{\alpha }}\equiv \frac{\partial \mathcal{L}}{\partial u^{\alpha }}-D_i\left(\frac{\partial \mathcal{L}}{\partial u_i^{\alpha }}\right)=0,\alpha =1,\dots ,m,$$

(54)

where $\mathcal{L}(x,u,u_{\left(1\right)})$ is a first-order Lagrangian, i.e., it involves, along with the independent variables $x=(x^1,\dots ,x^n)$ and the dependent variables $u=(u,\dots ,u^m)$, the first-order derivatives $u_{\left(1\right)}=\left\{u_i^{\alpha }\right\}$ only.

Noether’s theorem states that if the variational integral with Lagrangian $\mathcal{L}(x,u,u_{\left(1\right)})$ is invariant under a group G with a generator

$$X={\xi }^i(x,u,u_{\left(1\right)},\dots )\frac{\partial }{\partial x^i}+{\eta }^{\alpha }(x,u,u_{\left(1\right)},\dots )\frac{\partial }{\partial u^{\alpha }},$$

(55)

then the vector field $C=(C^1,\dots ,C^n)$, defined by

$$C^i={\xi }^i\mathcal{L}+({\eta }^{\alpha }-{\xi }^j{u}_j^{\alpha })\frac{\partial \mathcal{L}}{\partial u_i^{\alpha }},i=1,\dots ,n,$$

(56)

provides a conservation law for the Euler–Lagrange Equation (54), i.e., obeys the equation $divC\equiv D_i\left(C^i\right)=0$ for all solutions of (54), i.e.,

$$D_i\left(C^i\right){|}_{\left(54\right)}=0.$$

(57)

Any vector field $C^i$, satisfying (57), is called a conserved vector for Equation (54). □

In order to apply Noether’s theorem, one has first of all to find the symmetries of Equation (54). Then, one should single out the symmetries leaving invariant the variational integral (54). This can be done by means of the following infinitesimal test for the invariance of the variational integral (see [31]):

$$X\left(\mathcal{L}\right)+\mathcal{L}{D}_i\left({\xi }^i\right)=0,$$

(58)

where the generator X is prolonged to the first derivatives $u_{\left(1\right)}$ by the formula

$$X={\xi }^i\frac{\partial }{\partial x^i}+{\eta }^{\alpha }\frac{\partial }{\partial u^{\alpha }}+[D_i\left({\eta }^{\alpha }\right)-u_j^{\alpha }{D}_i\left({\xi }^j\right)]\frac{\partial }{\partial u_i^{\alpha }}.$$

(59)

If Equation (58) is satisfied, then the vector (56) provides a conservation law.

From Lemma 1, we can obtain that if one adds to a Lagrangian the divergence of any vector field, the Euler–Lagrange equations remain invariant. Therefore, one can add to the Lagrangian $\mathcal{L}$ the divergence of an arbitrary vector field depending on the group parameter and replace the invariance condition (58) by the divergence condition

$$X\left(\mathcal{L}\right)+\mathcal{L}{D}_i\left({\xi }^i\right)=D_i\left(B^i\right).$$

(60)

Then, Equation (54) is again invariant and has a conservation law $D_i\left(C^i\right)=0$, where (56) is replaced by

$$C^i={\xi }^i\mathcal{L}+({\eta }^{\alpha }-{\xi }_j{u}_j^{\alpha })\frac{\partial \mathcal{L}}{\partial u_i^{\alpha }}-B^i.$$

(61)

It follows from Equations (50) and (58) that if a variational integral $\int \mathcal{L}dx$ with a higher-order Lagrangian $\mathcal{L}(x,u,u_{\left(1\right)},u_{\left(2\right)},\dots )$ is invariant under a group with a generator (59), then the vector

$$C^i={\mathcal{N}}^i\left(\mathcal{L}\right),$$

(62)

provides a conservation law for the corresponding Euler–Lagrange equations. Dropping the differentiations of $\mathcal{L}$ with respect to higher-order derivative $u_{\left(4\right)},\dots$ and changing the summation indices, we obtain from (62) and (48):

$$\begin{array}{cc}\hfill C^i=& {\xi }^i\mathcal{L}+W^{\alpha }\left[\begin{array}{c}\frac{\partial \mathcal{L}}{\partial u_i^{\alpha }}-D_j(\frac{\partial \mathcal{L}}{\partial u_{ij}^{\alpha }})+D_j{D}_k(\frac{\partial \mathcal{L}}{\partial u_{ijk}^{\alpha }})-\cdots \end{array}\right]\hfill \\ \hfill & +D_j(W^{\alpha })\left[\frac{\partial \mathcal{L}}{\partial u_{ij}^{\alpha }}-D_k(\frac{\partial \mathcal{L}}{\partial u_{ijk}^{\alpha }})+\cdots \right]+D_j{D}_k(W^{\alpha })\left[\frac{\partial \mathcal{L}}{\partial u_{ijjk}^{\alpha }}-\cdots \right]+\cdots ,\hfill \end{array}$$

(63)

where ${\mathcal{N}}^i$ is the operator (48), and $W^{\alpha }={\eta }^{\alpha }-{\xi }^j{u}_j^{\alpha }$ is given by (49).

With the aid of Maple, Equation (42) has five symmetries as follows:

$$\begin{array}{cc}\hfill & X_1=\frac{\partial }{\partial x},X_2=\frac{\partial }{\partial t},X_3=v\frac{\partial }{\partial u}-u\frac{\partial }{\partial v},\hfill \\ \hfill & X_4=t\frac{\partial }{\partial x}-vx\frac{\partial }{\partial u}+xu\frac{\partial }{\partial v},X_5=\frac{x}{2}\frac{\partial }{\partial x}+t\frac{\partial }{\partial t}-\frac{u}{2}\frac{\partial }{\partial u}-\frac{v}{2}\frac{\partial }{\partial v}.\hfill \end{array}$$

(64)

For the generator $X_3$, we have $W^1=v,$ and $W^2=-u$. Thus, formulas (53) yield the following conserved vector

$$\begin{array}{cc}\hfill C^1& =W^1\left[-D_x(\frac{\partial \mathcal{L}}{\partial u_{xx}})\right]+W^2\left[-D_x(\frac{\partial \mathcal{L}}{\partial v_{xx}})\right]+D_x(W^1)\left[\frac{\partial \mathcal{L}}{\partial u_{xx}}\right]+D_x(W^2)\left[\frac{\partial \mathcal{L}}{\partial v_{xx}}\right],\hfill \\ \hfill & =\frac{1}{2}v{\omega }_x^2+\frac{1}{2}u{\omega }_x^1-\frac{1}{2}{v}_x{\omega }^2-\frac{1}{2}{u}_x{\omega }^1,\hfill \\ \hfill C^2& =W^1\left[\frac{\partial \mathcal{L}}{\partial u_t}\right]+W^2\left[\frac{\partial \mathcal{L}}{\partial v_t}\right]=v{\omega }^1-u{\omega }^2.\hfill \end{array}$$

For the generator $X_1$, we have $W^1=-u_x,$ and $W^2=-v_x$. Thus, formulas (53) yield the following conserved vector

$$\begin{array}{cc}\hfill C^1=& {\omega }^1(u_t-u^{2}v-v^3)+{\omega }^2(v_t+u{v}^2+u^3)-\frac{1}{2}{u}_x{\omega }_x^2+\frac{1}{2}{v}_x{\omega }_x^1,\hfill \\ \hfill C^2=& -u_x{\omega }^1-v_x{\omega }^2.\hfill \end{array}$$

For the generator $X_2$, we have $W^1=-u_t,$ and $W^2=-v_t$. Thus, formulas (53) yield the following conserved vector

$$\begin{array}{cc}\hfill C^1=& -\frac{1}{2}{u}_x{\omega }_x^2+\frac{1}{2}{v}_x{\omega }_x^1+\frac{1}{2}{u}_{xt}{\omega }^2-\frac{1}{2}{v}_{xt}{\omega }^1,\hfill \\ \hfill C^2=& {\omega }^1(\frac{1}{2}{v}_{xx}-u^{2}v-v^3)+{\omega }^2(-\frac{1}{2}{u}_{xx}+u^3+u{v}^2).\hfill \end{array}$$

For the generator $X_4$, we have $W^1=-vx-t{u}_x,$ and $W^2=xu-t{v}_x$. Thus, formulas (53) yield the following conserved vector

$$\begin{array}{cc}\hfill C^1=& t[{\omega }^1(u_t-u^{2}v-v^3)+{\omega }^2(v_t+u{v}^2+u^3)]\hfill \\ \hfill & -\frac{1}{2}{\omega }_x^2(vx-t{u}_x)-\frac{1}{2}{\omega }_x^1(xu-t{v}_x)+\frac{1}{2}{\omega }^2(v+x{v}_x)+\frac{1}{2}{\omega }^1(u+x{u}_x),\hfill \\ \hfill C^2=& -{\omega }^1(vx+t{u}_x)+{\omega }^2(xu-t{v}_x).\hfill \end{array}$$

For the generator $X_5$, we have $W^1=-\frac{u}{2}-\frac{x}{2}{u}_x-t{u}_t,$ and $W^2=-\frac{v}{2}-\frac{x}{2}{v}_x-t{v}_t$. Thus, formulas (53) yield the following conserved vector

$$\begin{array}{cc}\hfill C^1=& \frac{x}{2}[{\omega }^1(u_t-u^{2}v-v^3)+{\omega }^2(v_t+u{v}^2+u^3)]\hfill \\ \hfill & -\frac{1}{2}{\omega }_x^2(\frac{u}{2}+\frac{x}{2}{u}_x+t{u}_t)+\frac{1}{2}{\omega }_x^1(\frac{v}{2}+\frac{x}{2}{v}_x+t{v}_t)+\frac{1}{2}{\omega }^2(u_x+t{u}_{xt})-\frac{1}{2}{\omega }^1(v_x+t{v}_{xt}),\hfill \\ \hfill C^2=& t[{\omega }^1(u_t-u^{2}v-v^3)+{\omega }^2(v_t+u{v}^2+u^3)]-\frac{{\omega }^1}{2}(u+x{u}_x)-\frac{{\omega }^2}{2}(v+x{v}_x).\hfill \end{array}$$

6. Exact Solutions of Equation (12)

Let us take a nonlinear partial differential equation (NLPDE) of the form

$$F(x,u_t,u_x,u_{tt},u_{xx},\dots )=0.$$

(65)

We assume that the solutions of Equation (65) can be expressed in the form

$$\begin{array}{c}\hfill u(x,t)=A_0+\sum _{K=1}^N\sum _{i+j=K}{A}_{ij}{\varphi }^i\left(\xi \right){\psi }^j\left(\eta \right)+\sum _{K=1}^N{B}_k{\psi }^{-K}\left(\eta \right)+\sum _{j=1}^N{C}_j{\varphi }^{-j}\left(\xi \right),\end{array}$$

(66)

where $A_0,A_{ij}(i,j=0,1,2,\dots ,N)$, and $B_k$ are constants to be determined, and the functions $\varphi \left(\xi \right)$ and $\psi \left(\eta \right)$ satisfy the Beronoulli and the Riccati equations, respectively,

$$\frac{d\varphi }{d\xi }=R_2{\varphi }^2\left(\xi \right)-R_1\varphi \left(\xi \right),R_2\ne 0,$$

(67)

$$\frac{d\psi }{d\eta }=S_2{\psi }^2\left(\eta \right)+S_1\psi \left(\eta \right)+S_0,S_2\ne 0,$$

(68)

where $R_2,R_1,S_2,S_1$, and $S_0$ are constants.The parameters $\xi$ and $\eta$ are given by $\xi ={\kappa }_{1}x+{\omega }_{1}t$ and $\eta ={\kappa }_{2}x+{\omega }_{2}t$, where ${\kappa }_1,{\kappa }_2,{\omega }_1,$ and ${\omega }_2$ are constants to be determined later. The solutions of the Bernoulli Equation (67) are

$$\varphi =\left\{\begin{array}{ccc}\hfill & \frac{R_1}{R_2+R_{1}exp(R_1\xi +{\xi }_0)},\hfill & \hfill R_1\ne 0,\\ \hfill & \frac{-1}{R_2\xi +{\xi }_0},\hfill & \hfill R_1=0,\end{array}\right.$$

(69)

where ${\xi }_0$ is a constant of integration.

It is well known that the Riccati Equation (68) admits several types of solutions

$$\begin{array}{cc}\hfill & \psi =\left\{\begin{array}{ccc}\hfill & \frac{-S_1}{2S_2}-\frac{\sqrt{\mu }}{2S_2}tanh(\frac{\sqrt{\mu }}{2}\eta +{\eta }_0),\hfill & \hfill \mu >0,\\ \hfill & \frac{-S_1}{2S_2}-\frac{\sqrt{\mu }}{2S_2}coth(\frac{\sqrt{\mu }}{2}\eta +{\eta }_0),\hfill & \hfill \mu >0,\end{array}\right.\hfill \end{array}$$

(70)

$$\begin{array}{cc}\hfill & \psi =\frac{-1}{S_2\eta +{\eta }_0},S_0=S_1=0,\hfill \end{array}$$

(71)

$$\begin{array}{cc}\hfill & \psi =\left\{\begin{array}{ccc}\hfill & \frac{-S_1}{2S_2}+\frac{\sqrt{-\mu }}{2S_2}tan(\frac{\sqrt{-\mu }}{2}\eta +{\eta }_0),\hfill & \hfill \mu <0,\\ \hfill & \frac{-S_1}{2S_2}-\frac{\sqrt{-\mu }}{2S_2}cot(\frac{\sqrt{-\mu }}{2}\eta +{\eta }_0),\hfill & \hfill \mu <0,\end{array}\right.\hfill \end{array}$$

(72)

where $\mu =S_1^2-4S_0{S}_2$, and ${\eta }_0$ is a constant of integration.

Now, we rewrite (12) as the following form

$$\left\{\begin{array}{cc}\hfill & u_t=-\frac{1}{2}{v}_{xx}+v{u}^2+v^3,\hfill \\ \hfill & v_t=\frac{1}{2}{u}_{xx}-u{v}^2-u^3.\hfill \end{array}\right.$$

(73)

We consider the exact solutions of Equation (73). To do that, let

$$\begin{array}{cc}\hfill & u(x,t)=A_0+\sum _{K=1}^N\sum _{i+j=K}{A}_{ij}{\varphi }^i\left(\xi \right){\psi }^j\left(\eta \right)+\sum _{K=1}^N{B}_k{\psi }^{-K}\left(\eta \right)+\sum _{j=1}^N{C}_j{\varphi }^{-j}\left(\xi \right),\hfill \\ \hfill & v(x,t)=a_0+\sum _{K=1}^N\sum _{i+j=K}{a}_{ij}{\varphi }^i\left(\xi \right){\psi }^j\left(\eta \right)+\sum _{K=1}^N{b}_k{\psi }^{-K}\left(\eta \right)+\sum _{j=1}^N{c}_j{\varphi }^{-j}\left(\xi \right).\hfill \end{array}$$

(74)

Next, by balancing the nonlinear term and the highest derivative term in Equation (12), we can obtain $N=1$ and $M=1$. Therefore, we have the following ansatz solution of Equation (12):

$$\begin{array}{cc}\hfill & u(x,t)=A_0+A_{10}\varphi \left(\xi \right)+A_{01}\psi \left(\eta \right)+\frac{B_1}{\psi \left(\eta \right)}+\frac{C_1}{\varphi \left(\xi \right)},\hfill \\ \hfill & v(x,t)=a_0+a_{10}\varphi \left(\xi \right)+a_{01}\psi \left(\eta \right)+\frac{b_1}{\psi \left(\eta \right)}+\frac{c_1}{\varphi \left(\xi \right)},\hfill \end{array}$$

(75)

where ${\kappa }_1,{\kappa }_2,{\omega }_1,{\omega }_2,A_0,A_{10},A_{01},B_1,C_1,a_0,a_{10},a_{01},b_1,$ and $c_1$ are constants to be determined, and the functions $\varphi \left(\xi \right)$ and $\psi \left(\eta \right)$ satisfy Equations (67) and (68). Substituting (75) into (73), we obtain a system of algebraic equations for ${\kappa }_1,{\kappa }_2,{\omega }_1,{\omega }_2,A_0,A_{10},A_{01},B_1,C_1,a_0,$$a_{10},a_{01},b_1.$ and $c_1$. We solve these algebraic equations with the aid of Maple. Therefore, we obtain the following formulae of the traveling wave solutions of Equation (73):

$$\begin{array}{cc}\hfill & u_1(x,t)=-\frac{R_2{\kappa }_1}{R_2\xi +{\xi }_0},\hfill \\ \hfill & v_1(x,t)=-\frac{a_{10}}{R_2\xi +{\xi }_0},\hfill \end{array}$$

(76)

where $\xi ={\kappa }_{1}x$,

$$\begin{array}{cc}\hfill & u_2(x,t)=\frac{2a_0^2}{k_2[\sqrt{-\mu }tan(\frac{\sqrt{-\mu }}{2}\eta +{\eta }_0)]},\hfill \\ \hfill & v_2(x,t)=a_0,\hfill \end{array}$$

(77)

where $\eta ={\kappa }_{2}x-a_0{\kappa }_{2}t,\mu =-4\frac{a_0^2}{{\kappa }_2^2}$,

Figure 1 and Figure 2 display the kind of solution structure of $u(x,t)$ and $v(x,t)$ determined by (76) and (77), respectively.

$$\begin{array}{cc}\hfill & u_3(x,t)=\pm i{a}_0\pm \frac{i{a}_{10}{R}_1}{R_2+R_{1}exp\left({\xi }_0\right)},\hfill \\ \hfill & v_3(x,t)=\frac{a_{10}{R}_1}{R_2+R_{1}exp\left({\xi }_0\right)},\hfill \end{array}$$

(78)

$$\begin{array}{cc}\hfill & u_4(x,t)=\pm i{a}_0\pm \frac{i{a}_{10}{R}_1}{R_2+R_{1}exp(R_1\xi +{\xi }_0)},\hfill \\ \hfill & v_4(x,t)=\frac{a_{10}{R}_1}{R_2+R_{1}exp(R_1\xi +{\xi }_0)},\hfill \end{array}$$

(79)

where $\xi ={\kappa }_{1}x\pm \frac{i{R}_1{\kappa }_1^2}{2}t$,

$$\begin{array}{cc}\hfill & u_5(x,t)=\pm i{a}_0\pm \frac{3i{a}_{10}{R}_1}{R_2+R_{1}exp(R_1\xi +{\xi }_0)},\hfill \\ \hfill & v_5(x,t)=a_0+\frac{a_{10}{R}_1}{R_2+R_{1}exp(R_1\xi +{\xi }_0)},\hfill \end{array}$$

(80)

where $\xi ={\kappa }_{1}x+\sqrt{2}i{a}_0{\kappa }_1,R_1=\pm \frac{2\sqrt{2}i{a}_0}{{\kappa }_1},R_2=\pm \frac{2\sqrt{2}i{a}_{10}}{{\kappa }_1}$,

$$\begin{array}{cc}\hfill & u_6(x,t)=\pm i{a}_0\pm \frac{i{R}_1{a}_{10}}{R_2+R_{1}exp\left({\xi }_0\right)}\pm \frac{2i{S}_2{a}_0}{S_1+\sqrt{\mu }tanh\left({\eta }_0\right)},\hfill \\ \hfill & v_6(x,t)=a_0+\frac{a_{10}{R}_1}{R_2+R_{1}exp\left({\xi }_0\right)}-\frac{2S_2{a}_0}{S_1+\sqrt{\mu }tanh\left({\eta }_0\right)},\hfill \end{array}$$

(81)

$$\begin{array}{cc}\hfill & u_7(x,t)=\pm i{a}_0\pm \frac{i{R}_1{a}_{10}}{R_2+R_{1}exp({\xi }_0)}\pm \frac{2i{S}_2{b}_1}{S_1+\sqrt{\mu }tanh(\frac{\sqrt{\mu }}{2}\eta +{\eta }_0)},\hfill \\ \hfill & v_7(x,t)=a_0+\frac{R_1{a}_{10}}{R_2+R_{1}exp({\xi }_0)}-\frac{2S_2{b}_1}{S_1+\sqrt{\mu }tanh(\frac{\sqrt{\mu }}{2}\eta +{\eta }_0)},\hfill \end{array}$$

(82)

where $\eta ={\kappa }_{2}x\mp \frac{i{\kappa }_2^2{S}_1}{2}t$,

$$\begin{array}{cc}\hfill & u_9(x,t)=\pm i{a}_0\pm \frac{2i{S}_2{b}_1}{S_1+\sqrt{\mu }tanh(\frac{\sqrt{\mu }}{2}\eta +{\eta }_0)},\hfill \\ \hfill & v_9(x,t)=a_0-\frac{2S_2{b}_1}{S_1+\sqrt{\mu }tanh(\frac{\sqrt{\mu }}{2}\eta +{\eta }_0)},\hfill \end{array}$$

(83)

where $\eta ={\kappa }_{2}x\mp \frac{i{\kappa }_2^2{S}_1}{2}t,\mu =S_1^2$,

$$\begin{array}{cc}\hfill u_{10}(x,t)& =\pm i{a}_0\pm \frac{2i{S}_2{b}_1}{-S_1-\frac{\sqrt{\mu }}{2}tanh({\eta }_0)}\pm \frac{i{c}_1(R_2+R_{1}exp(R_1\xi +{\xi }_0))}{R_1},\hfill \\ \hfill v_{10}(x,t)& =a_0-\frac{2S_2{b}_1}{S_1+\frac{\sqrt{\mu }}{2}tanh({\eta }_0)}+\frac{c_1(R_2+R_{1}exp(R_1\xi +{\xi }_0))}{R_1},\hfill \end{array}$$

(84)

where $\xi ={\kappa }_{1}x$,

$$\begin{array}{cc}\hfill u_{11}(x,t)& =\pm i{a}_0-\frac{2S_2{B}_1}{S_1+\frac{\sqrt{\mu }}{2}tanh(\frac{\sqrt{\mu }}{2}\eta +{\eta }_0)}\pm \frac{i{c}_1(R_2+R_{1}exp(R_1\xi +{\xi }_0))}{R_1},\hfill \\ \hfill v_{11}(x,t)& =a_0\pm \frac{2i{S}_2{B}_1}{S_1+\frac{\sqrt{\mu }}{2}tanh(\frac{\sqrt{\mu }}{2}\eta +{\eta }_0)}+\frac{c_1(R_2+R_{1}exp(R_1\xi +{\xi }_0))}{R_1}\hfill \end{array}$$

(85)

where $\xi ={\kappa }_{1}x\pm \frac{i{R}_1{k}_1^2}{2}t,\eta =k_{2}x\pm \frac{i{\kappa }_2^2{S}_1}{2}t$,

$$\begin{array}{cc}\hfill & u_{12}(x,t)=\pm \frac{2i{S}_2{b}_1}{S_1+\frac{\sqrt{\mu }}{2}tanh({\eta }_0)}\pm \frac{i{c}_1(R_2+R-1exp(R_1\xi +{\xi }_0))}{R_1},\hfill \\ \hfill & v_{12}(x,t)=-\frac{2S_2{b}_1}{S_1+\frac{\sqrt{\mu }}{2}tanh({\eta }_0)}+\frac{c_1(R_2+R-1exp(R_1\xi +{\xi }_0))}{R_1},\hfill \end{array}$$

(86)

where $\xi =k_{1}x\pm \frac{i{R}_1{k}_1}{2}t$.

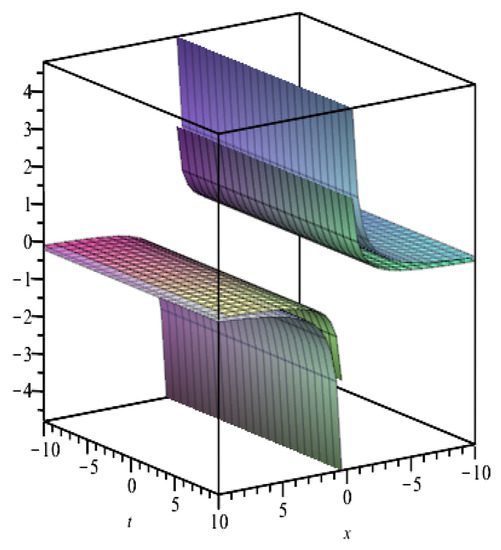
Figure 1. Plot of the $u(x,t)$ and $v(x,t)$ given by Equation (76) for parameters ${\kappa }_1=R_2=1,a_{10}=2,$ and ${\xi }_0=0$.

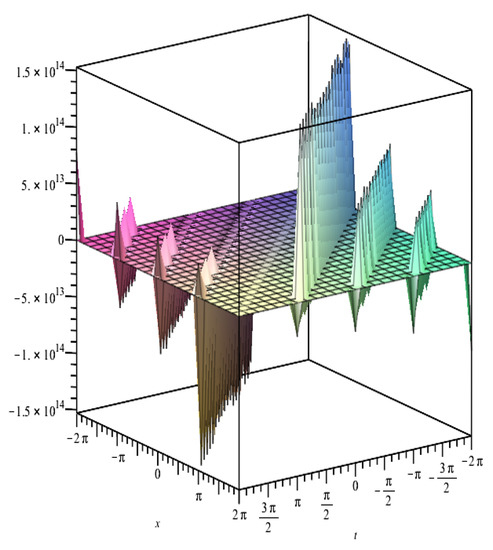
Figure 2. Plot of the $u(x,t)$ and $v(x,t)$ given by Equation (77) for parameters $a_0={\kappa }_2=1,$ and ${\eta }_0=0$.

7. Conclusions and Discussion

In this paper, the Lax pairs of Dirac spectral problems were studied by the improved Tu-scheme of Zhang et al., and the isospectral–non-isospectral integrable hierarchies were derived from their compatibility. The integrable hierarchy can be reduced to Equation (12). Subsequently, the self-adjointness and conservation laws of this system of equations were discussed using the method proposed by Ibragimov, and the exact solution of the equation system was obtained by using the solutions of the Bernoulli and Riccati equations. In Section 3 and Section 4, based on the non-semisimple Lie algebra $\tilde{g}$, we obtained the nonisospectral coupling hierarchies of the soliton hierarchy (22) and the Hamiltonian structure of its coupling hierarchy. We hope to apply the Tu scheme to find new nonisospectral integrable systems and their properties.