Abstract
We analyse the motions of a axisymmetric drop expanding between two rotating discs. We restrict to the case of a highly viscous fluid and a rapid rate of rotation. Therefore, we make modelling assumptions following from both a low Reynolds number and a low Rossby number. We investigate both the squeezing problem, where the top disc is pushed down on the drop; and the contraction problem, where the top plate is pulled away from the drop. Both problems have similar solutions to the non-rotating case but we find that the rotation term in the contraction problem allows a critical rotation rate that prevents the plates from moving apart. This exists because pressure in the fluid layer is lowered by the rotation and thus there is a suction effect between the two plates which promotes adhesion. We also complete the linear instability analysis of the squeezing problem and determine the critical values where the system shifts from symmetrical to asymmetrical.
1. Introduction
The study of expanding viscous drops has seen a lot of development in the last few decades. A good outline of this field can be found in Huppert (2006) [1], beginning with analysis from von Kármán (1940) [2]. Recent developments from Ward (2006) [3] and Moffatt et al. (2021) [4] have focused on the case of a drop expanding in the thin layer between two horizontal plates (a Hele-Shaw cell). These papers have fully described the motion and shown that the squeezing problem is stable under linear perturbations. Investigation by Gay (2002) [5] has demonstrated that the contraction problem is unstable: air is drawn in as the radius of the viscous drop decreases and, as the two interact, a viscous fingering instability develops and thus the symmetry breaks down. This is an example of a Saffman-Taylor instability (Saffman and Taylor, 1958 [6]). The rotating contraction problem is also expected to dominated by a Saffman-Taylor instability, despite the additional complexities caused by rotation but this has not previously been investigated; this paper is original in its inclusion of rotation in both the squeezing and contraction problems. Both of these rotating problems have great relevance to the adhesion industry which, in turn, has applications to the construction, transportation and machinery manufacture industries, among others, as detailed in Dinte and Sylvester (2017) [7]. The viscous fluid we consider throughout this paper can be used to model an adhesive, which Dinte and Sylvester (2017) [7] define “as a mixture in a liquid or semi-liquid state, capable to join permanently to surfaces, by an adhesive process”. In particular, the theory of this paper is most relevant to adhesively-bonded lap joints which were analytically investigated by Her (1999) [8]. It was demonstrated by de Bruyne and Houwink (1952) [9] that such a joint between the ends of two coaxial cylinders will break at high loads when subjected to torsion (by applying torque in opposite directions of rotation to the two cylinders). We can investigate an identical joint, but in the case that the cylinders rotate in the same direction, using the theory of this paper. In industry, such joints are used for torque transmission and have applications in aircraft, space structures and robot arms as outlined by Choi and Lee (1994) [10]. It is demonstrated in this paper that, by rotating such cylinders at a sufficiently fast rate, the adhesive layer between them can pull them closer together, even when the external forces are pulling them apart. We explicitly identify the minimum rotation rate required to achieve this effect.
2. Background
The system we are analysing consists of two plates which are a vertical distance h apart. Between the two plates is a volume of fluid V with surface tension , uniform density and uniform dynamic viscosity . The two plates are rotated about a vertical axis through the centre of the fluid drop at a rate of rotation and a force acts vertically and uniformly on the top plate. The fluid begins in a cylindrical drop of radius and the initial vertical distance between the plates is . We make the modelling assumptions that the height of the fluid drop does not vary radially and that the front of the fluid drop remains vertical at all times. We choose to work in a coordinate system with origin on the bottom plate directly below initial centre of the fluid drop. The pressure field in the fluid is denoted by p and the velocity field by .
We investigate this system by following a similar mathematical analysis to Moffatt et al. (2021) [4]. In contrast, we work in a rapidly rotating frame, more specifically at low Rossby number. The axis of rotation is vertical and passes through the centre of the drop.
We consider a reference frame rotating with the plates at constant angular frequency . This gives the same no-slip boundary conditions as the initial problem investigated by Moffatt et al. (2021) [4]; as well as adding Coriolis and centrifugal terms to the Navier-Stokes equations. We consider low Rossby number, so the centrifugal force dominates over both the Coriolis and advective effects, leaving us with the governing equation
3. The Pseudo-Pressure Field
We now observe the following identity from vector calculus, as in Tritton (1988) [11]
Hence, we can rewrite the governing equation as
Since we are working in the case where the axis of rotation passes vertically through the centre of the drop, and . Hence
We can also use the pseudo-pressure field to rewrite another of the key equations from Moffatt et al. (2021) [4]. Standard lubrication theory indicates that the pressure is independent of z, i.e., , and the radial component of velocity, , satisfies and obeys:
which we can rewrite as
It is also worth noting that
Hence, the problem now closely resembles that investigated by Moffatt et al. (2021) [4] but with this pseudo-pressure field, , in the place of . The only difference being that, on the boundary , we have the condition , where is the surface tension. This result can be recovered from Ungarish and Huppert (1998) [12] by directly considering the pressure field and neglecting the gravitational term due to both the thin layer approximation and low Rossby number.
4. Analysis of Basic State
Using the no slip boundary conditions, , we can solve for in terms of the pressure field
Thus, averaging over the depth, we find that:
Proceeding with the analysis, we find a corresponding result to the Reynolds equation
with boundary condition . We determine the solution as
We balance forces on the upper plate to obtain:
and arrive at the nonlinear ODE
5. The Squeezing Problem
In this section, we focus on the case . We use a change of variables to rewrite (16) as:
This is very similar to the ODE found by Moffatt et al. (2021) [4] for the corresponding problem in the non-rotating case; however, the parameter has now been increased by a quantity proportional to . We can solve the equation to determine the implicit solution
6. The Contraction Problem
We find a more interesting difference when we investigate the contraction problem, . We can, again, use a change of variables to rewrite the ODE as
But we now note that the system can be forced to remain at (i.e., ) if we choose such that . The critical value of which achieves this is
This indicates that, by spinning the plates at , we can prevent the contraction force from pulling the plates apart. If , then the plates pull apart; if , then the plates are pushed together. We note that does not necessarily exist: if , then and hence the plates are always pushed together.
7. Stability of Squeezing Problem
Other differences from the non-rotating case arise when we carry out a linear stability analysis. As noted in the introduction, the contraction problem, , is expected to develop complicated Saffman-Taylor instabilities at the interface between the air and the fluid. Therefore, we will focus on the squeezing problem, . We consider perturbing the boundary by:
and we consider a perturbed pressure field given by
As in the paper by Moffatt et al. (2021) [4], we find and hence . Thus, we have
We now find , using the condition ,
Hence:
and
We recall (11) and observe that . Hence, evaluating at , we obtain
Therefore, as in Moffatt et al. (2021) [4], at leading order we simply see a statement of the conservation of . At order , we find
This equation governs the stability of the basic state. It is different to the corresponding equation in Moffatt et al. (2021) [4] due to the term. Hence:
We can rewrite this condition using X and T as
Equation tells us that , where . We also recall that and, hence, we can rewrite the stability condition as
Therefore, we can see that the system is always stable if ; equivalently, the system is always stable if . Otherwise, we can rewrite (34) in terms of the radius of the drop as:
which we can rearrange as
Hence, if we let , then the mode is stable until the drop’s radius reaches the critical value .
These values are increasing as n increases so we observe that if , then the drop is symmetrical and stable under any perturbation. Therefore, is the critical radius of the drop at which the system becomes unstable, which we can explicitly write as
The above results are consistent with the results found by Moffatt et al. (2021) [4] because in their analysis so the condition is satisfied and hence the motion is always stable. These results also incorporate surface tension which is crucial for calculating but is less relevant in the non-rotating case.
We also observe that is decreasing as a function of so the system becomes unstable at a smaller critical radius when it is rotated at a faster rate.
8. Instability of Contraction Problem
If we use the same linear perturbation model as in the investigation of the squeezing problem, then again we arrive at (32). There is a difference when we rewrite this equation in terms of X and T (because ) so we find that
Equation tells us that , where . We also recall that and, hence, we can rewrite the stability condition as
Therefore, we can see that the system is always unstable if ; equivalently, the system is always unstable if: . Otherwise, we can rewrite (39) in terms of the radius of the drop as:
which we can rearrange as
We recall ; thus the n mode is unstable if but it is stable if .
As before, is increasing in n and we can calculate thus, if and , then the system is stable. At first glance, this may appear to be inconsistent with Saffman and Taylor (1958) [6]. However, we recall that, if , then the plates are not pulled apart, hence no Saffman-Taylor instabilities develop. Indeed, there is an equivalence between the statements and because (as the plates are pushed together).
In the case of non-rotating plates, the necessary and sufficient condition for stability simply reduces to which is equivalent to the plates not pulling apart.
9. Numerical Values
In this section we will use the following parameters to calculate the predicted critical values [these were the experimental values used by Moffatt et al. (2021) [4]].
Therefore, we can calculate the critical values identified earlier in the paper.
These values give a useful insight into how plausible it would be to stabilise the motion of an expanding drop and to force two contracting plates together. Using these values we can also calculate for a range of values of and accordingly construct phase diagram showing the different regions where the system is either stable (and will remain axisymmetric) or unstable (and will not) for the squeezing problem. The result of this is shown in Figure 1.
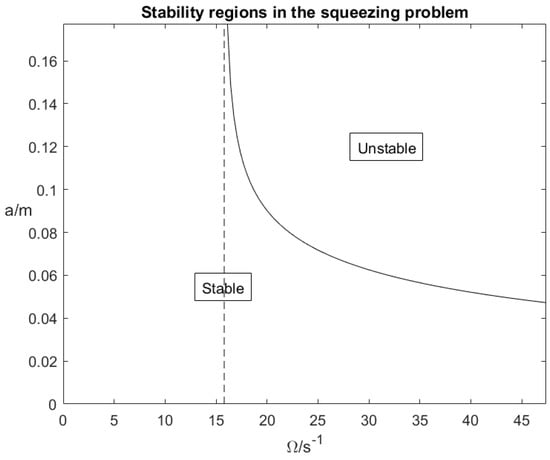
Figure 1.
Regions of stability in the phase plane under a squeezing force.
We can also plot the corresponding regions for the contraction problem, which is shown in Figure 2.
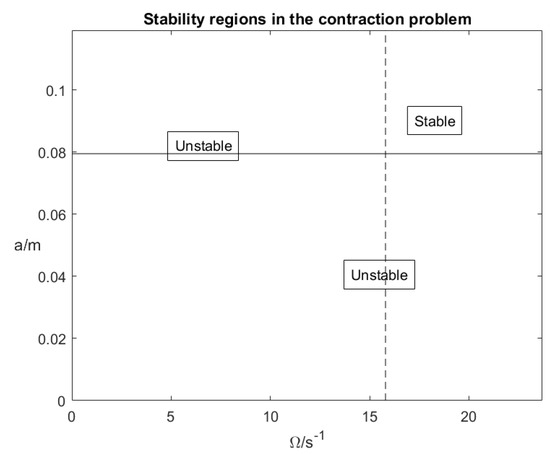
Figure 2.
Regions of stability in the phase plane under a contraction force.
10. Conclusions
We have identified the key equations for an axisymmetric viscous drop under compressing and contracting forces in a rotating system and the critical values at which the symmetry breaks down. In particular, we have shown that, under a squeezing force, the rotating viscous drop maintains its axisymmetry unless and the radius grows to be larger than , where:
and:
whereas, under a contraction force, symmetry breaks down if or if the drop starts at an initial radius less than
We have also found that the critical rotation rate which prevents a contracting force from pulling apart two plates joined by a viscous drop is:
which exists given that . Further research may be done in a laboratory to experimentally confirm these results.
Author Contributions
Formal analysis, writing—original draft preparation: M.G.E.R.; Conceptualization, supervision, writing—review and editing, correspondence: H.E.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used in the Numerical Values section can be found in Moffatt et al. (2021) [4]. DOI:10.1017/jfm.2021.668.
Acknowledgments
Let us firstly extend our thanks to a very talented group of summer undergraduate students: A. Cox, M. Liu, M. Loncar, J. Saville and O. Wilson. It was a pleasure to work alongside them. We must also thank H.K. Moffatt for taking the time to read an earlier draft of this article and helping us to progress. Lastly, we would like to give our dearest thanks to King’s College, Cambridge for providing us with a workspace and the Braithwaite Batty Fund for providing an accommodation subsidy.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Huppert, H.E. Gravity Currents: A personal perspective. J. Fluid Mech. 2006, 554, 299–322. [Google Scholar] [CrossRef]
- von Kármán, T. The engineer grapples with nonlinear problems. Bull. Am. Math. Soc. 1940, 46, 615–683. [Google Scholar] [CrossRef]
- Ward, T. Radial spreading of a viscous drop between parallel-plane surfaces. Phys. Fluids 2006, 354, 816–824. [Google Scholar] [CrossRef]
- Moffatt, H.K.; Guest, H.; Huppert, H.E. Spreading or contraction of viscous drops between plates: Single, multiple or annular drops. J. Fluid Mech. 2021, 925, A26. [Google Scholar] [CrossRef]
- Gay, C. Stickiness—Some fundamentals of adhesion. Integr. Comp. Biol. 2002, 42, 1123–1126. [Google Scholar] [CrossRef]
- Saffman, P.G.; Taylor, G.I. The penetration of a fluid into a porous medium or Hele–Shaw cell containing a more viscous liquid. Proc. R. Soc. Lond. 1958, A245, 312–329. [Google Scholar]
- Dinte, E.; Sylvester, B. Adhesives: Applications and Recent Advances. In Applied Adhesive Bonding in Science and Technology; InTech Rijeka: Rijeka, Croatia, 2017. [Google Scholar]
- Her, S.-C. Stress analysis of adhesively-bonded lap joints. Compos. Struct. 1999, 47, 673–678. [Google Scholar] [CrossRef]
- de Bruyne, N.A.; Houwink, R. Adhesion and Adhesives; Elsevier Publishing Co. Ltd.: Amsterdam, The Netherlands; Cleaver-Hume Press: London, UK, 1952. [Google Scholar]
- Choi, J.H.; Lee, D.G. The Torque Transmission Capabilities of the Adhesively-Bonded Tubular Single Lap Joint and the Double Lap Joint. J. Adhes. 1994, 44, 197–212. [Google Scholar] [CrossRef]
- Tritton, D.J. Physical Fluid Dynamics, 2nd ed.; Oxford Science Publications: Oxford, UK, 1988. [Google Scholar]
- Ungarish, M.; Huppert, H.E. The effects of rotation on axisymmetric gravity currents. J. Fluid Mech. 1998, 362, 17–51. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).