A Variety of New Explicit Analytical Soliton Solutions of q-Deformed Sinh-Gordon in (2+1) Dimensions

Abstract

In this paper, the (2+1)-dimensional q-deformed Sinh-Gordon model has been investigated via $(\frac{G^{{}^{\prime }}}{G},\frac{1}{G})$-expansion and Sine-Gordon-expansion methods. These techniques successfully retrieve trigonometric as well as hyperbolic solutions, along necessary restricted conditions applied on parameters. In addition to these solutions, dark solitons and complexiton solutions have also been obtained. The proposed equation expands the possibilities for modeling physical systems in which symmetry is broken. The obtained solutions are graphically illustrated. A Painlevé analysis for the proposed model has also been discussed in this paper.

1. Introduction

In the past few decades, the exploration of nonlinear wave propagation on the surface of the ocean has piqued the interest of scientists. Nonlinear wave processes have been experienced in numerous domains, such as chemical physics, plasma physics, control theory, tsunami waves, etc. [1,2,3,4,5,6,7,8]. Analytical and computational soliton solutions can explicitly define these phenomena. Solitons are particularly fascinating because of their true capacity for new applications in a wide range of scientific fields [9,10,11,12,13,14,15,16,17]. A balance of dispersion and nonlinearity can be used to describe them and are produced by various notable nonlinear partial differential equations such as the Kadomtsev–Petviashvili model [18], the nonlinear Schrodinger model [19], the Sine-Gordon, Korteweg–de Vries, and the Sinh-Gordon equations [20,21]. Indeed, solitons are one of the most distinct solutions of nonlinear dynamics. The Sinh-Gordon equation is useful in many contexts, including surface theory, crystal lattice creation, and the dynamics of strings in curved space. When the q-deformed hyperbolic function, developed by Arai in the nineteenth century, is added in the dynamical system, the symmetry of the system and, as a result, the symmetry of the solution are lost. Recent developments have resulted in the generation of several solutions for the Schrödinger equation and the Dirac equation with q-deformed hyperbolic potential. q-deformed functions are interesting for simulating atom-trapping potentials, statistical distributions in Bose–Einstein condensates, and diatomic molecule vibrational spectra [22,23,24].

Using soliton solutions, mathematicians have collaborated to develop many techniques for direct examining nonlinear evolution equations (NLEEs). Representing diverse physical phenomena, they have performed a key role in wide range of applications over the last several decades, including water waves, fluid mechanics, elastic media, nonlinear optics, solid-state physics, and acoustic waves within crystals. Over the last two decades, a huge amount of work has been devoted to developing solid and reliable analytical methods for solving these equations. Numerous plans for extracting exact and numerical solutions for these models have been concocted to give adequate data for understanding actual events happening in various science and technology fields. Examples include the unified technique [25] in order to find the exact wave solution, the Painlevé technique [26], linear superposition principle [27], Wronskian formulation [28], Hirota bilinear technique [29], inverse scattering [30], invariant subspaces [31], novel auxiliary equation technique, and symmetry reduction strategy [32,33]. The extraction of lump solutions [34,35,36,37] has become a popular topic of research among researchers. Huge headway has been made recently as various efficient and proficient techniques for acquiring exact solutions to NLEEs have been laid out [38,39,40,41,42].

The solutions of Klein–Gordon and Sine-Gordon equations were investigated in [43,44]. The generalized q-deformed Sinh-Gordon equation (Eleuch Equation) [22,23,24] is the subject of this paper in (2 + 1) dimensions. It describes

$$\begin{array}{ccc}\hfill \frac{{\partial }^{2}m}{\partial x^2}+\frac{{\partial }^{2}m}{\partial y^2}-\frac{{\partial }^{2}m}{\partial t^2}& =& {\left[{sinh}_q\left(m^{\gamma }\right)\right]}^p-\delta ,\hfill \end{array}$$

(1)

where $m=m(z,y,t)$ and ${sinh}_q$ is a function of the Arai q-deformed expression described by

$$\begin{array}{c}\hfill {sinh}_q\left(x\right)=\frac{e^x-q{e}^{-x}}{2},0<q\le 1.\end{array}$$

(2)

Taking $q=1$ provided standard functions of $\sinh$. ${cosh}_q\left(x\right)$ and ${tanh}_q\left(x\right)$ with their own reciprocals as well as their useful characteristics are discussed in detail in [45]. To examine the solution of Equation (1), we want to apply the proposed techniques. Contrarily, unique optical solitons and many other types of solution to the discussed model have been proposed in this article. This piece of paper discussed a noticeable achievement and moderate enhancements to previous work.

The article has been arranged as follows. Section 2 contains an explanation of the applicable methods. Section 3 discusses the mathematical analysis. Section 4 explains soliton solutions using the proposed method and the visual depiction is also discussed in this section. Section 5 contains a Painlevé analysis for the proposed model. At last, in Section 6, the conclusions of work are discussed.

The main motivation of writing this article is to solve the generalized q-deformed Sinh-Gordon equation in (2 + 1) dimension using $(\frac{G^{{}^{\prime }}}{G},\frac{1}{G})$-expansion and Sine-Gordon-expansion methods. A Painlevé analysis for the proposed model is also discussed in this paper. By introducing the generalized q-deformed Sinh-Gordon equation, we may begin to imagine models of physical systems in which the symmetry is either missing or broken.

2. Descriptions of Suggested Expansion Methods

The detailed overview of the suggested expansion methods $(\frac{G^{{}^{\prime }}}{G},\frac{1}{G})$-expansion and the Sine-Gordon expansion methods are presented as follows.

2.1. Description of $(\frac{G^{{}^{\prime }}}{G},\frac{1}{G})$-Expansion Method [46,47]

Consider the following ODE

$$\begin{array}{c}\hfill G^{{}^{″}}({\rm Y})+\epsilon G({\rm Y})=\rho ,\end{array}$$

(3)

and take $\Phi =\frac{G^{{}^{\prime }}}{G}$, $\Psi =\frac{1}{G}$, then we have

$${\Phi }^{{}^{\prime }}={\Phi }^2+\rho \Psi -\epsilon ,{\Psi }^{{}^{\prime }}=-\Phi \Psi ,$$

(4)

where $\epsilon$ and $\rho$ are constants.

Consider $\epsilon <0$ and

$${\Psi }^2=\frac{-\epsilon }{{\epsilon }^2{\sigma }_1+{\rho }^2}({\Phi }^2-2\rho \Psi +\epsilon ),$$

(5)

where ${\sigma }_1=A_1^2-A_2^2$; so, a general solution of Equation (3) becomes

$$G({\rm Y})=A_{1}sinh({\rm Y}\sqrt{-\epsilon })+A_{2}cosh({\rm Y}\sqrt{-\epsilon })+\frac{\rho }{\epsilon },$$

(6)

where $A_1$ and $A_2$ are arbitrary constants. Now, let $\epsilon >0$ and

$${\Psi }^2=\frac{\epsilon }{{\epsilon }^2{\sigma }_2-{\rho }^2}({\Phi }^2-2\rho \Psi +\epsilon ),$$

(7)

where ${\sigma }_2=A_1^2+A_2^2$, Equation (3) has a solution of the form

$$G({\rm Y})=A_{1}sin({\rm Y}\sqrt{(}\epsilon ))+A_{2}cos({\rm Y}\sqrt{(}\epsilon ))+\frac{\rho }{\epsilon },$$

(8)

where $A_1$ and $A_2$ are arbitrary constants.

Assume the following NLEE

$$S(u,u_t,u_x,u_y,u_{xx},u_{yy},u_{xy},u_{xt}\dots )=0.$$

(9)

Fundamental steps of the ($\frac{G^{{}^{\prime }}}{G},\frac{1}{G}$)-expansion method [46,47] are illustrated below.

The following wave transformation

$$u(x,y,t)=U({\rm Y}){\rm Y}=x+y-Ct,$$

(10)

is used for converting Equation (9) into an ordinary differential equation

$$Q(U,U^{{}^{\prime }},U^{{}^{″}},\dots )=0,$$

(11)

where x and y are space coordinates and t is the time coordinate, whereas C denotes the velocity of the wave.

Assume the solution of Equation (11) is

$$U({\rm Y})=\sum _{i=0}^N{a}_i{\Phi }^i+\sum _{i=1}^n{b}_i{\Phi }^{i-1}\Psi ,$$

(12)

where $\Phi =\frac{G^{{}^{\prime }}}{G}$ and $\Psi =\frac{1}{G}$. The solution can be obtained by finding the values of $a_i$ and $b_i$. For achieving this task, we substitute Equation (12) along Equation (4) and Equation (5) into Equation (11). This substitution converts Equation (11) into an expansion containing $\Phi$ and $\Psi$. Now, by comparing the coefficients of $\Psi$ and $\Phi$ to zero gives set of nonlinear equations. The values of $a_i$, $b_i,C,\rho ,A_1,A_2$ are to be extracted upon simultaneously solving the equations.

Next, we substitute Equation (12) with Equations (4) and (7) into Equation (11) for $\epsilon <0$. This substitution converts Equation (11) into an expansion containing $\Phi$ and $\Psi$. Now, by equating the coefficients of $\Phi$ and $\Psi$ to zero gives a set of nonlinear equations. The values of $a_i$, $b_i,C,\rho ,A_1,A_2$ are to be extracted upon simultaneously solving the equations.

2.2. Overview of Sine-Gordon Method [48,49,50]

Assume that the sine-Gordon equation has the following form

$$\begin{array}{c}\hfill u_{xx}-u_{tt}=a^{2}sinu,\end{array}$$

(13)

where $u(x,t)=U({\rm Y})$ and $a\ne 0$.

By the wave transformation $u(x,t)=U({\rm Y})$, ${\rm Y}=x-ct$, Equation (13) assumes the form:

$$\begin{array}{c}\hfill U^{″}=\frac{a^2}{1-c^2}sinU,\end{array}$$

(14)

where c represents the speed of the traveling wave. Integrating Equation (14) gives

$$\begin{array}{c}\hfill {\left[{\left(\frac{U}{2}\right)}^{\prime }\right]}^2=\frac{a^2}{1-c^2}{sin}^2\left(\frac{U}{2}\right).\end{array}$$

(15)

Here, the constant of integration is zero. Taking $ϵ({\rm Y})=\frac{U}{2}$ and $\frac{a^2}{1-c^2}=f^2$. Equation (15), becomes

$$\begin{array}{c}\hfill {ϵ}^{\prime }=fsinϵ.\end{array}$$

(16)

Choosing $f=1$ in Equation (16) and applying some trigonometric identities, we find

$$\begin{array}{c}\hfill sinϵ=\frac{2rexp({\rm Y})}{r^{2}exp(2{\rm Y})+1}{|}_{r=1}=sech({\rm Y}),\end{array}$$

(17)

$$\begin{array}{c}\hfill cosϵ=\frac{rexp(2{\rm Y})-1}{r^{2}exp(2{\rm Y})+1}{|}_{r=1}=tanh({\rm Y}),\end{array}$$

(18)

where $r\ne 0$ is a constant of integration.

According to Sine-Gordon expansion method, the predicted solution to Equation (11) assumes the form

$$\begin{array}{c}\hfill U({\rm Y})=A_0+\sum _{i=1}^N{tanh}^{i-1}\left(Y\right)\left(B_{i}sech({\rm Y})+A_{i}tanh({\rm Y})\right).\end{array}$$

(19)

Using Equations (17) and (18) into Equation (19), Equation (19) attains the form

$$\begin{array}{c}\hfill U\left(ϵ\right)=A_0+\sum _{i=1}^N{cos}^{i-1}\left(ϵ\right)\left(B_{i}sin\left(ϵ\right)+A_{i}cos\left(ϵ\right)\right).\end{array}$$

(20)

Substituting Equation (20) along with Equation (16) into Equation (11), an expression involving powers of $sin\left(ϵ\right)$ and $cos\left(ϵ\right)$ is attained. Now, by comparing the constants of $sin\left(ϵ\right)$ and $cos\left(ϵ\right)$ to zero gives a set of equations. The values of $A_i$, $B_i$, and $A_0$ are to be extracted upon simultaneously solving the equations.

3. Mathematical Examination

To find the traveling wave solution of Equation (1), we utilize the transformation

$$\begin{array}{c}\hfill {\rm Y}=\frac{1}{\sqrt{1-{\alpha }^2}}(x+y-\alpha t),\end{array}$$

(21)

where $\alpha$ represents the velocity of the wave. Utilizing Equation (21), Equation (1) can be transformed into an ODE,

$$\left(\frac{2-{\alpha }^2}{1-{\alpha }^2}\right)\frac{d^{2}m({\rm Y})}{d{{\rm Y}}^2}={\left[{sinh}_q\left(m^{\gamma }({\rm Y})\right)\right]}^p-\delta .$$

(22)

In this article, Equation (22) is studied for $p=1$, $\gamma =1$, and $\delta =0$. The solutions of Equation (22) have been extracted in the following portions using the suggested analytical techniques by using the following transformation

$$n({\rm Y})=e^{m({\rm Y})}.$$

(23)

After utilizing Equation (23), Equation (22) becomes

$$\left(\frac{2-{\alpha }^2}{1-{\alpha }^2}\right)\left(-2n^{\prime 2}+2n{n}^{″}\right)-n^3+qn=0.$$

(24)

4. Extraction of Solutions via $(\frac{G^{\prime }}{G},\frac{1}{G})$-Expansion Method

Before we start applying the proposed technique, the balancing law helps us in determining N. Balancing the highest-order derivative and nonlinear term in Equation (24) gives $N=2$.

The assumed solution of Equation (24), for this proposed method, has been obtained by putting $N=2$ in Equation (12):

$$n({\rm Y})=a_0+a_1\Phi ({\rm Y})+a_2{(\Phi ({\rm Y}))}^2+b_1\Psi ({\rm Y})+b_2\Phi ({\rm Y})\Psi ({\rm Y}),$$

(25)

where $\Phi =\frac{G^{{}^{\prime }}}{G}$, $\Psi =\frac{1}{G}$ and $a_0,a_1,a_2,b_1$, and $b_2$ are constants. Applying the $(\frac{G^{\prime }}{G},\frac{1}{G})$-expansion method as explained in Section 2, the solutions for $\epsilon <0$ and $\epsilon >0$ have been obtained as follows:

CASE 1

For $\epsilon <0$, the values of constants $a_0,a_1,a_2,b_1$, and $b_2$ have been obtained as

Family 1

$$\begin{array}{ccc}\hfill & & a_0=\frac{(-2+{\alpha }^2)\epsilon }{{\alpha }^2-1},a_1=0,a_2=\frac{2(-2+{\alpha }^2)}{{\alpha }^2-1},b_1=-\frac{2(-2+{\alpha }^2)\rho }{{\alpha }^2-1},\hfill \\ \hfill & & b_2=\pm \frac{2(-2+{\alpha }^2)\sqrt{{\rho }^2+{\epsilon }^2{\sigma }_1}}{({\alpha }^2-1)\sqrt{-\epsilon }},q=\frac{{(-2+{\alpha }^2)}^2{\epsilon }^2}{{({\alpha }^2-1)}^2}.\hfill \end{array}$$

The extracted hyperbolic solutions to Family 1 are

$$\begin{array}{ccc}\hfill m(x,y,t)& =& ln\left[\frac{(-2+{\alpha }^2)}{{\alpha }^2-1}\epsilon -\frac{2\epsilon (-2+{\alpha }^2)}{{\alpha }^2-1}{\left(\frac{A_{1}cosh({\rm Y}\sqrt{-\epsilon })+A_{2}sinh({\rm Y}\sqrt{-\epsilon })}{A_{1}sinh({\rm Y}\sqrt{-\epsilon })+A_{2}cosh({\rm Y}\sqrt{-\epsilon })+\frac{\rho }{\epsilon }}\right)}^2\right.\hfill \\ \hfill & & -\frac{2\rho (-2+{\alpha }^2)}{{\alpha }^2-1}\left(\frac{1}{A_{1}sinh({\rm Y}\sqrt{-\epsilon })+A_{2}cosh({\rm Y}\sqrt{-\epsilon })+\frac{\rho }{\epsilon }}\right)\hfill \\ & & \left.\pm \frac{2(-2+{\alpha }^2)\sqrt{{\rho }^2+{\epsilon }^2{\sigma }_1}}{({\alpha }^2-1)}\left(\frac{A_{1}cosh({\rm Y}\sqrt{-\epsilon })+A_{2}sinh({\rm Y}\sqrt{-\epsilon })}{{(A_{1}sinh({\rm Y}\sqrt{-\epsilon })+A_{2}cosh({\rm Y}\sqrt{-\epsilon })+\frac{\rho }{\epsilon })}^2}\right)\right].\hfill \end{array}$$

(26)

The solution corresponding to Family 1 has been expressed graphically in Figure 1 using the values of arbitrary parameters $\alpha =0.7$, $\rho =0.1$, ${\sigma }_1=0.1$, $\epsilon =-0.3$, $A_1=0.5$, and $A_2=0.1$.

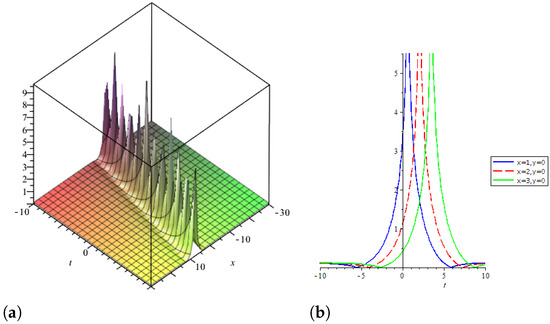
Figure 1. 3D graph of $\left|m\right(x,0,t\left)\right|$ is shown in (a), 2D line graph with the variation in x is shown in (b).

The solution corresponding to Family 1 has been expressed graphically in Figure 2 using the values of arbitrary parameters $\alpha =0.7$, $\rho =0.1$, ${\sigma }_1=0.1$, $\epsilon =-0.3$, $A_1=0.5$, and $A_2=0.1$.

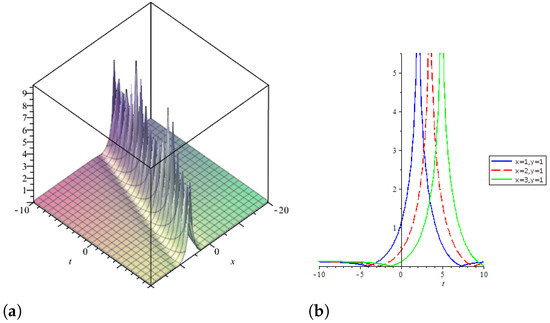
Figure 2. 3D graph of $\left|m\right(x,1,t\left)\right|$ is shown in (a), 2D line graph with the variation in x is shown in (b).

CASE 2

For $\epsilon >0$, the values of constants $a_0,a_1,a_2,b_1$, and $b_2$ have been obtained as

Family 2

$$\begin{array}{ccc}\hfill & & a_0=\frac{(-2+{\alpha }^2)\epsilon }{{\alpha }^2-1},a_1=0,a_2=\frac{2(-2+{\alpha }^2)}{{\alpha }^2-1},b_1=-\frac{2(-2+{\alpha }^2)\rho }{{\alpha }^2-1},\hfill \\ \hfill & & b_2=\pm \frac{2(-2+{\alpha }^2)\sqrt{-{\rho }^2+{\epsilon }^2{\sigma }_2}}{({\alpha }^2-1)\sqrt{\epsilon }},q=\frac{{(-2+{\alpha }^2)}^2{\epsilon }^2}{{({\alpha }^2-1)}^2}.\hfill \end{array}$$

The extracted trigonometric solutions corresponding to Family 2 are

$$\begin{array}{ccc}\hfill m(x,y,t)& =& ln\left[\frac{(-2+{\alpha }^2)\epsilon }{{\alpha }^2-1}+\frac{2\epsilon (-2+{\alpha }^2)}{{\alpha }^2-1}{\left(\frac{A_{1}cos({\rm Y}\sqrt{\epsilon })-A_{2}sin({\rm Y}\sqrt{\epsilon })}{A_{1}sin({\rm Y}\sqrt{\epsilon })+A_{2}cos({\rm Y}\sqrt{\epsilon })+\frac{\rho }{\epsilon }}\right)}^2\right.\hfill \\ \hfill & & -\frac{2(-2+{\alpha }^2)\rho }{{\alpha }^2-1}\left(\frac{1}{A_{1}sin({\rm Y}\sqrt{\epsilon })+A_{2}cos({\rm Y}\sqrt{\epsilon })+\frac{\rho }{\epsilon }}\right)\hfill \\ & & \left.\pm \frac{2(-2+{\alpha }^2)\sqrt{-{\rho }^2+{\epsilon }^2{\sigma }_2}}{({\alpha }^2-1)}\left(\frac{A_{1}cos({\rm Y}\sqrt{\epsilon })-A_{2}sin({\rm Y}\sqrt{\epsilon })}{{(A_{1}sin({\rm Y}\sqrt{\epsilon })+A_{2}cos({\rm Y}\sqrt{\epsilon })+\frac{\rho }{\epsilon })}^2}\right)\right],\hfill \end{array}$$

(27)

where the traveling wave variable ${\rm Y}$ used in Equations (26) and (27) is defined in Equation (21).

5. Extraction of Solutions via Sine-Gordon Expansion Method

Before we start applying the proposed technique, the balancing law helps us in determining N. Balancing the highest-order derivative and nonlinear term in Equation (24) gives $N=2$. For $N=2$, the assumed solution for Equation (24), for this proposed method, has been obtained by putting $N=2$ in Equation (20):

$$n\left(ϵ\right)=A_0+A_{1}cos\left(ϵ\right)+A_2{cos}^2\left(ϵ\right)+B_{1}sin\left(ϵ\right)+B_{2}sin\left(ϵ\right)cos\left(ϵ\right),$$

(28)

where $A_0,A_1,A_2,B_1$, and $B_2$ are arbitrary constants. Applying the Sine-Gordon expansion method as explained in Section 2, the following two families of solutions have been obtained.

Family 3

$$\begin{array}{cc}\hfill & A_0=0,B_1=0,A_1=0,B_2=0,\hfill \end{array}$$

$$\begin{array}{c}\hfill A_2=\frac{4\left({\alpha }^2-2\right)}{{\alpha }^2-1},q=\frac{16{\left({\alpha }^2-2\right)}^2}{{\left({\alpha }^2-1\right)}^2}.\end{array}$$

(29)

Family 4:

$$\begin{array}{cc}\hfill & A_0=\frac{2-{\alpha }^2}{{\alpha }^2-1},B_1=0,A_1=0,B_2=\pm \frac{2\iota ({\alpha }^2-2)}{{\alpha }^2-1},\hfill \end{array}$$

$$\begin{array}{c}\hfill A_2=\frac{2({\alpha }^2-2)}{{\alpha }^2-1},q=\frac{{\left({\alpha }^2-2\right)}^2}{{\left({\alpha }^2-1\right)}^2}.\end{array}$$

(30)

The dark solitons extracted from Family 3 are

$$\begin{array}{c}\hfill m(x,y,t)=ln\left[\frac{4\left({\alpha }^2-2\right)}{{\alpha }^2-1}{tanh}^2({\rm Y})\right].\end{array}$$

(31)

The solution corresponding to Family 3 has been expressed graphically in Figure 3 taking $\alpha =3$.

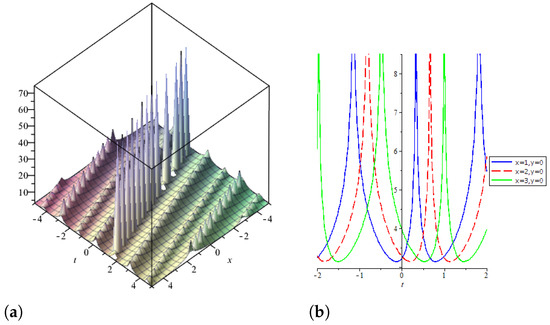
Figure 3. 3D graph of $\left|m\right(x,0,t\left)\right|$ is shown in (a), 2D line graph with the variation in x is shown in (b).

The solution corresponding to Family 3 has been expressed graphically in Figure 4 taking $\alpha =3$.

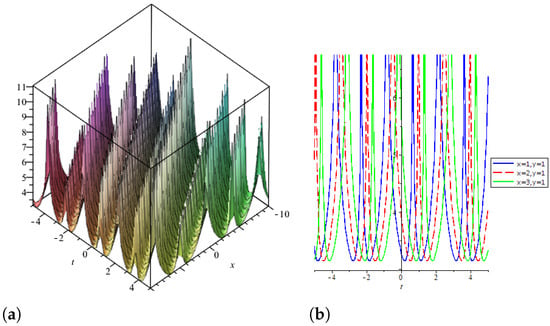
Figure 4. 3D graph of $\left|m\right(x,1,t\left)\right|$ is shown in (a), 2D line graph with the variation in x is shown in (b).

The complexiton solutions have been constructed from Family 4 as

$$\begin{array}{c}\hfill m(x,y,t)=ln\left[\frac{2-{\alpha }^2}{{\alpha }^2-1}\pm \frac{2\iota ({\alpha }^2-2)}{{\alpha }^2-1}tanh({\rm Y})sech({\rm Y})+\frac{2({\alpha }^2-2)}{{\alpha }^2-1}{tanh}^2({\rm Y})\right],\end{array}$$

(32)

where ${\rm Y}=\frac{1}{\sqrt{1-{\alpha }^2}}(x+y-\alpha t)$.

6. Painlevé Analysis

The Painlevé analysis is one of the most efficient approach for examining integrability of any PDEs [51,52,53]. The integrability of Equation (1) in case of $P=1$ and $\gamma =1$ and $\delta =0$ is tested assuming a solution in form of a Laurent series about the singular manifold $W(x,y,t)$ as

$$\begin{array}{c}\hfill m(x,y,t)=\sum _{v=0}^{\infty }{\lambda }_v(x,y,t)W^{v+\rho }(x,y,t),\end{array}$$

where ${\lambda }_v(x,y,t)$, $(v=0,1,2,\dots )$ are arbitrary functions of x, y, and t.

The leading order of the solution of Equation (1) is assumed as

$$\begin{array}{c}\hfill m(x,y,t)={\lambda }_0(x,y,t)W^{\rho }(x,y,t),\end{array}$$

(33)

where ${\lambda }_0(x,y,t)$ is the initial constant of integration and $\rho$ represents the dominant behavior which is to be evaluated initially.

Putting Equation (33) into Equation (1) and comparing the most significant terms, gives $\rho =-2$ and

$$\begin{array}{c}\hfill {\lambda }_0(x,y,t)=4W_x^2(x,y,t)+4W_y^2(x,y,t)-4W_t^2(x,y,t).\end{array}$$

Resonance v is computed for the dominant behavior $\rho =-2$ by putting

$$m(x,y,t)=\frac{4W_x^2(x,y,t)+4W_y^2(x,y,t)-4W_t^2(x,y,y,t)}{W^2(x,y,t)}+{\lambda }_v(x,y,t)W^{v-2}(x,y,t)$$

in Equation (1) and equating the least power of $W(x,y,t)$ (i.e., $W^{-6}(x,y,t)$) to zero. The following expression is the characteristic equation of the resonances

$$\begin{array}{c}\hfill v^2-v-2=0.\end{array}$$

Solving the above equation for v, we find

$$v_1=-1,v_2=2.$$

The resonance at $v=-1$ is compared to the arbitrariness of the singular manifold $W(x,y,t)=0$. The constant of integration is to be found by checking the compatibility conditions. Let us suppose

$$m(x,y,t)=W^{-2}(x,y,t)\sum _{v=0}^2{\lambda }_v(x,y,t)W^v(x,y,t).$$

(34)

Let us substitute Equation (34) in Equation (1) and equate the coefficients of different powers of $W(x,y,t)$ to zero at different levels of v, for the evaluation of ${\lambda }_v(x,y,t)$, $v=1,2$. After some computational work at level $v=1$, we obtain the explicit expression for ${\lambda }_1$ as

$$\begin{array}{c}\hfill {\lambda }_1(x,y,t)=4W_{tt}(x,y,t)-4W_{xx}(x,y,t)-4W_{yy}(x,y,t).\end{array}$$

(35)

It is observed that at level $v=2$, ${\lambda }_2(x,y,t)$ comes out to be an arbitrary function, which implies that the compatibility condition is satisfied identically. Hence, Equation (1) is Painlevé integrable. Throughout this work, we have made the following observations:

First, Maple was used to check the validity of all solutions to Equation (1) found here. Second, our solution functions are novel and have not been published previously, as shown by a comparison with the work given in [23,24].

7. Conclusions

In this paper, we studied the periodic and hyperbolic solutions of the (2+1)-dimensional q-deformed Sinh-Gordon equation. The $(\frac{G^{{}^{\prime }}}{G},\frac{1}{G})$-expansion and the Sine-Gordon-expansion methods have been effectively employed to obtain the model solutions. The proposed methods extract singular solitons, dark solitons, periodic solutions, and complexiton solutions. Bright solitons are not obtained by the applications of the proposed methods. The graphical illustration of the obtained results was presented. Moreover, a Painlevé analysis was applied for investigating integrability. The novel results showed that the proposed strategies were successful in identifying novel solutions of the (2+1)-dimensional q-deformed Sinh-Gordon equation.