A Variety of New Explicit Analytical Soliton Solutions of q-Deformed Sinh-Gordon in (2+1) Dimensions
Abstract
1. Introduction
2. Descriptions of Suggested Expansion Methods
2.1. Description of -Expansion Method [46,47]
2.2. Overview of Sine-Gordon Method [48,49,50]
3. Mathematical Examination
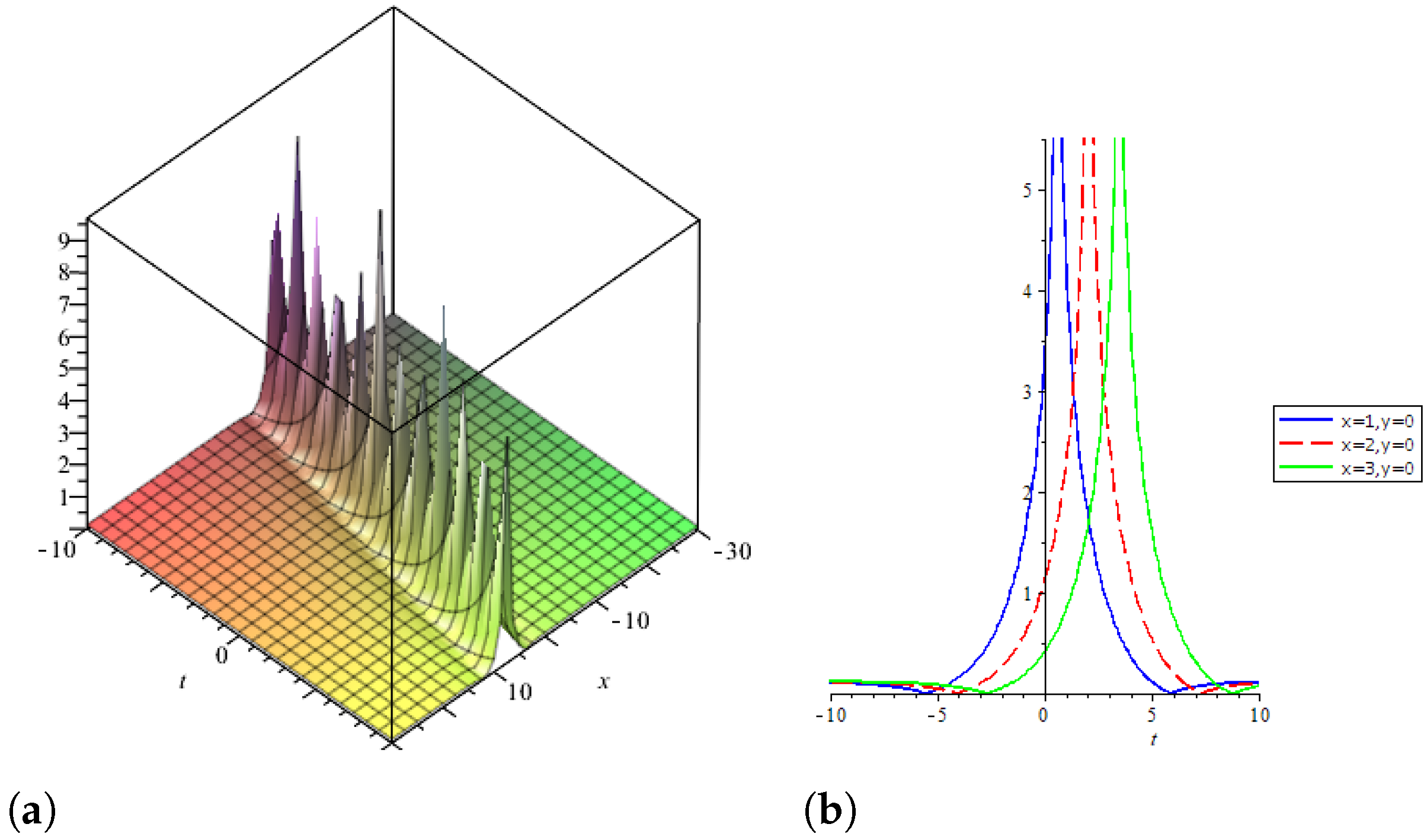
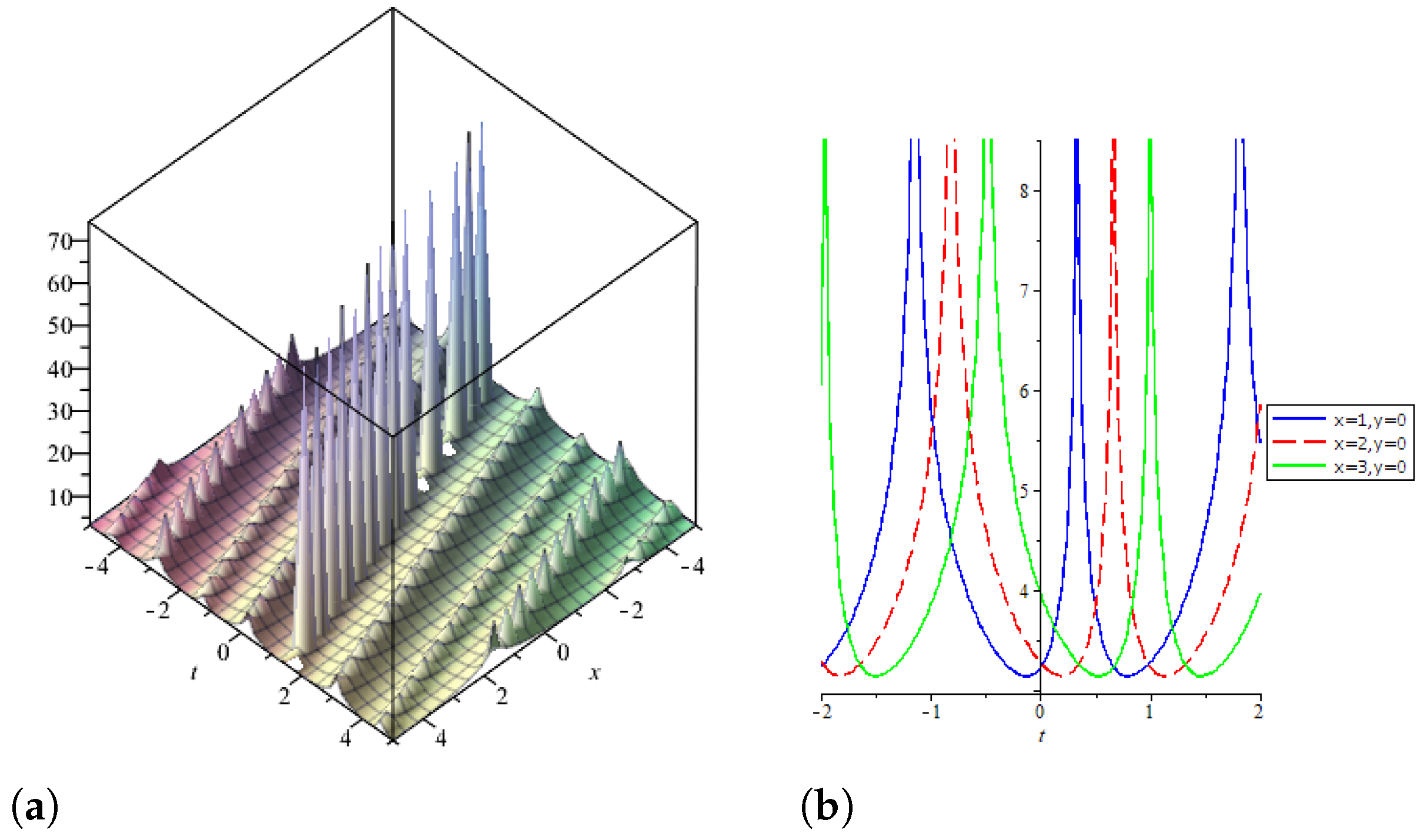
4. Extraction of Solutions via -Expansion Method
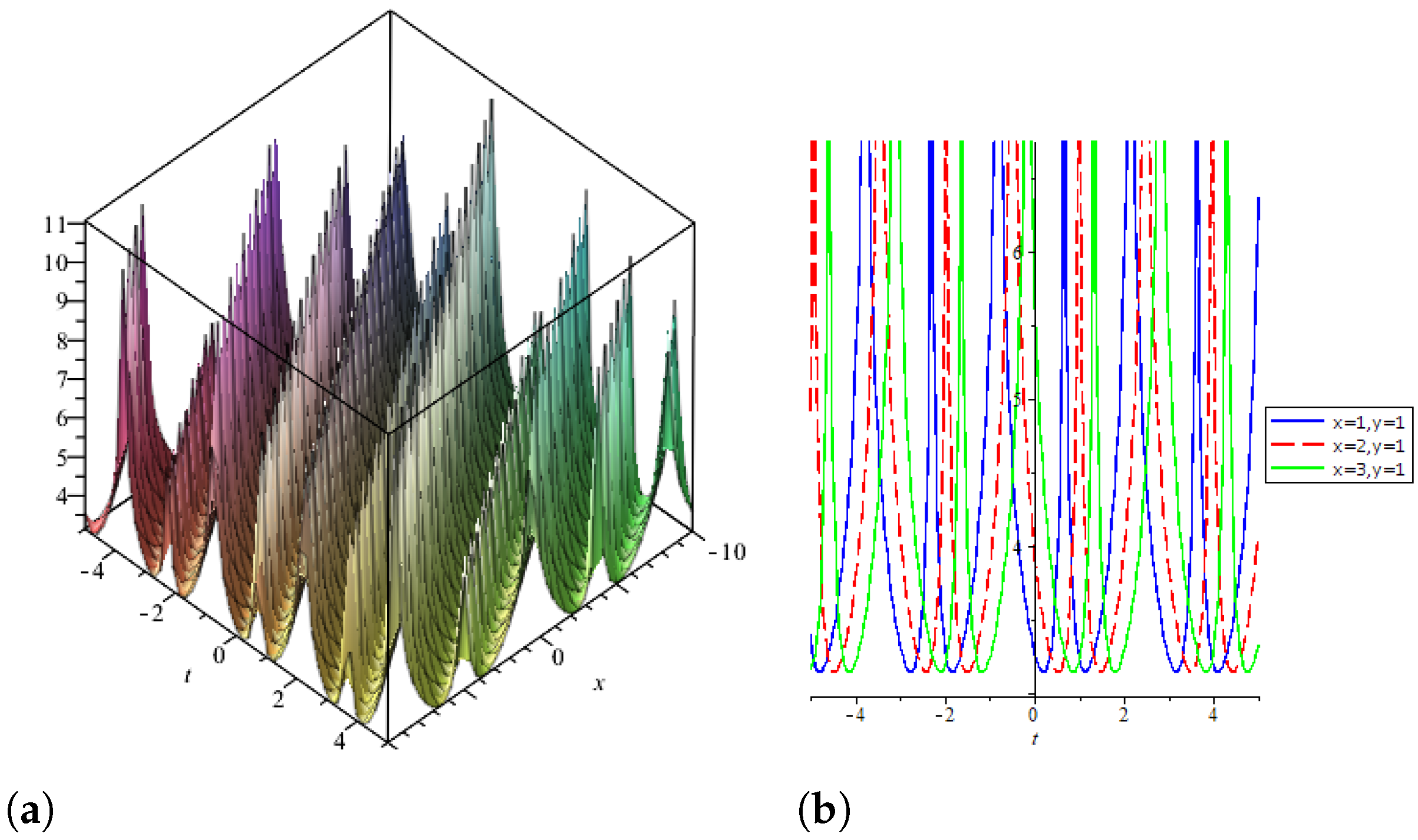
5. Extraction of Solutions via Sine-Gordon Expansion Method
6. Painlevé Analysis
7. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hashemi, M. A novel approach to find exact solutions of fractional evolution equations with non-singular kernel derivative. Chaos Solitons Fractals 2021, 152, 111367. [Google Scholar] [CrossRef]
- Zillur Rahman, M. Zulfikar Ali and Harun-Or Roshid. Chinese Phys. B 2021, 30, 050202. [Google Scholar]
- Kaplan, M.; Bekir, A.; Akbulut, A. A generalized Kudryashov method to some nonlinear evolution equations in mathematical physics. Nonlinear Dyn. 2016, 85, 2843–2850. [Google Scholar] [CrossRef]
- Zhang, S. Application of Exp-function method to high-dimensional nonlinear evolution equation. Chaos Solitons Fractals 2008, 38, 270–276. [Google Scholar] [CrossRef]
- Mesloub, S. On a singular two dimensional nonlinear evolution equation with nonlocal conditions. Nonlinear Anal. Theory Methods Appl. 2008, 68, 2594–2607. [Google Scholar] [CrossRef]
- Akbar, M.A.; Ali, N.H.M.; Islam, M.T. Multiple closed form solutions to some fractional order nonlinear evolution equations in physics and plasma physics. AIMS Math. 2019, 4, 397–411. [Google Scholar] [CrossRef]
- Abdel-Aty, A.H.; Khater, M.M.A.; Attia, R.A.M.; Abdel-Aty, M.; Eleuch, H. On the new explicit solutions of the fractional nonlinear space-time nuclear model. Fractals 2020, 28, 2040035. [Google Scholar] [CrossRef]
- Abdalla, M.S.; Eleuch, H. Exact analytic solutions of the Schr?dinger equations for some modified q-deformed potentials. J. Appl. Phys. 2014, 115, 234906. [Google Scholar] [CrossRef]
- Buckel, W.; Thauer, R.K. Flavin-Based Electron Bifurcation, A New Mechanism of Biological Energy Coupling. Chem. Rev. 2018, 118, 3862–3886. [Google Scholar] [CrossRef]
- Jabin, P.E.; Wang, Z. Quantitative estimates of propagation of chaos for stochastic systems with W−1,∞ kernels. Invent. Math. 2018, 214, 523591. [Google Scholar] [CrossRef]
- Lan, C.Z.Z.; Su, J.J. Solitary and rogue waves with controllable backgrounds for the nonautonomous generalized AB system. Nonlinear Dyn. 2019, 96, 25352546. [Google Scholar] [CrossRef]
- Zafar, A.; Shakeel, M.; Ali, A.; Akinyemi, L.; Rezazadeh, H. Optical solitons of nonlinear complex Ginzburg–Landau equation via two modified expansion schemes. Opt. Quantum Electron. 2022, 54, 5. [Google Scholar] [CrossRef]
- Darvishi, M.T.; Naja, M.; Wazwaz, A.M. Conformable space-time fractional nonlinear (1+1)- dimensional Schrodinger-type models and their traveling wave solutions. Chaos Solitons Fractals 2021, 150, 111187. [Google Scholar] [CrossRef]
- Fink, T.; Schade, A.; Höfling, S.; Schneider, C.; Imamoglu, A. Signatures of a dissipative phase transition in photon correlation measurements. Nat. Phys. 2018, 14, 365–369. [Google Scholar] [CrossRef]
- Arshed, S.; Rahman, R.U.; Raza, N.; Khan, A.K.; Inc, M. A variety of fractional soliton solutions for three important coupled models arising in mathematical physics. Int. J. Mod. Phys. B 2021, 36, 2250002. [Google Scholar] [CrossRef]
- Hao, R. Dark soliton in the exponentially decaying optical lattice with spatially inhomogeneous Gaussian nonlinearities. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrometers Detect. Assoc. Equip. 2011, 637, S145–S148. [Google Scholar] [CrossRef]
- Boutabba, N.; Eleuch, H.; Bouchriha, H. Thermal bath effect on soliton propagation in three-level atomic system. Synth. Met. 2009, 159, 1239–1243. [Google Scholar] [CrossRef]
- Osman, M.S.; Ghanbari, B.; Machado, J.A.T. New complex waves in nonlinear optics based on the complex Ginzburg-Landau equation with Kerr law nonlinearity. Eur. Phys. J. Plus 2019, 134, 20. [Google Scholar] [CrossRef]
- Ding, C.C.; Gao, Y.T.; Deng, G.F.; Wang, D. Lax pair, conservation laws, Darboux transformation, breathers and rogue waves for the coupled nonautonomous nonlinear SchrÖdinger system in an inhomogeneous plasma. Chaos Soliton Fract 2020, 133, 109580. [Google Scholar] [CrossRef]
- Wazwaz, A.-M. Travelling wave solutions for combined and double combined sine–cosine-Gordon equations by the variable separated ODE method. Appl. Math. Comput. 2006, 177, 755–760. [Google Scholar] [CrossRef]
- Akram, G.; Arshed, S.; Imran, Z. Soliton solutions for fractional DNA Peyrard-Bishop equation via the extended (G0/G2)-expansion method. Phys. Scr. 2021, 96, 094009. [Google Scholar] [CrossRef]
- Eleuch, H. Some Analytical Solitary Wave Solutions for the Generalized q-Deformed Sinh-Gordon Equation , Hindawi. Adv. Math. Phys. 2018, 2018, 5242757. [Google Scholar] [CrossRef]
- Raza, N.; Salman, F.; Butt, A.R.; Gandarias, M.L. Lie symmetry analysis, soliton solutions and qualitative analysis concerning to the generalized q-deformed Sinh-Gordon equation. Commun. Nonlinear Sci. Numer. Simul. 2023, 116, 106824. [Google Scholar] [CrossRef]
- Raza, N.; Arshed, S.; Alrebdi, H.; Abdel-Aty, A.-H.; Eleuch, H. Abundant new optical soliton solutions related to q-deformed Sinh–Gordon model using two innovative integration architectures. Results Phys. 2022, 35, 105358. [Google Scholar] [CrossRef]
- Kivshara, Y.S.; Davies, B.L. Dark optical solitons: Physics and applications. Phys. Rep. 1998, 298, 81–197. [Google Scholar] [CrossRef]
- Hao, R. Optical soliton control in inhomogeneous nonlinear media with the parity-time symmetric potentials. Opt. Commun. 2015, 338, 265–268. [Google Scholar] [CrossRef]
- Raza, N.; Hassan, Z.; Butt, A.R.; Rahman, R.U.; Abdel-Aty, A.; Mahmoud, M. New and more dual-mode solitary wave solutions for the Kraenkel–Manna–Merle system incorporating fractal effects. Math. Methods Appl. Sci. 2021, 45, 2964–2983. [Google Scholar] [CrossRef]
- Riaz, M.B.; Wojciechowski, A.; Oros, G.I.; Rahman, R.U. Soliton Solutions and Sensitive Analysis of Modified Equal-Width Equation Using Fractional Operators. Symmetry 2022, 14, 1731. [Google Scholar] [CrossRef]
- Bagheri, M.; Khani, A. Analytical Method for Solving the Fractional Order Generalized KdV Equation by a Beta-Fractional Derivative. Adv. Math. Phys. 2020, 2020, 8819183. [Google Scholar] [CrossRef]
- Sousa, J.V.D.C.; De Oliveira, E.C. A New Truncated M-Fractional Derivative Type Unifying Some Fractional Derivative Types with Classical Properties. Int. J. Anal. Appl. 2018, 16, 83–96. [Google Scholar]
- Abdalla, M.S.; Eleuch, H.; Barakat, T. Exact Analytical Solutions of the Wave Function for Some q-Deformed Potentials. Rep. Math. Phys. 2013, 71, 217–229. [Google Scholar] [CrossRef]
- Fabian, A.L.; Kohl, R.; Biswas, A. Perturbation of topological solitons due to sine-Gordon equation and its type. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1227–1244. [Google Scholar] [CrossRef]
- Biswas, A.; Rezazadeh, H.; Mirzazadeh, M.; Eslami, M.; Zhou, Q.; Moshokoa, S.P.; Belic, M. Optical solitons having weak non-local nonlinearity by two integration schemes. Optik 2018, 164, 380–384. [Google Scholar] [CrossRef]
- Kaur, L.; Wazwaz, A.-M. Lump, breather and solitary wave solutions to new reduced form of the generalized BKP equation. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 569–579. [Google Scholar] [CrossRef]
- Kaur, L.; Wazwaz, A.-M. Bright-dark lump wave solutions for a new form of the (3+1)-dimensional BKP-Boussinesq equation. Rom. Rep. Phys. 2019, 71, 102. [Google Scholar]
- Kaur, L.; Wazwaz, A.-M. Dynamical analysis of lump solutions for (3+ 1) dimensional generalized KP-Boussinesq equation and259its dimensionally reduced equation. Phys. Scr. 2018, 93, 075203. [Google Scholar] [CrossRef]
- Kaur, L.; Wazwaz, A.-M. Bright-dark optical solitons for Schrödinger-Hirota equation with variable coefficients. Commun. Phys. Scr. 2019, 179, 479–484. [Google Scholar] [CrossRef]
- Seadawy, A.; El-Rashidy, K. Dispersive solitary wave solutions of Kadomtsev-Petviashvili and modified Kadomtsev-Petviashvili dynamical equations in unmagnetized dust plasma. Results Phys. 2018, 8, 1216–1222. [Google Scholar] [CrossRef]
- Liu, J.-G.; Zhu, W.-H. Multiple rogue wave, breather wave and interaction solutions of a generalized (3+1)-dimensional variable-coefficient nonlinear wave equation. Nonlinear Dyn. 2021, 103, 1841–1850. [Google Scholar] [CrossRef]
- Kumar, D.; Park, C.; Tamanna, N.; Paul, G.C.; Osman, M. Dynamics of two-mode Sawada-Kotera equation: Mathematical and graphical analysis of its dual-wave solutions. Results Phys. 2020, 19, 103581. [Google Scholar] [CrossRef]
- Rezazadeh, H.; Kurt, A.; Tozar, A.; Tasbozan, O.; Mirhosseini-Alizamini, S.M. Wave behaviors of Kundu–Mukherjee–Naskar model arising in optical fiber communication systems with complex structure. Opt. Quantum Electron. 2021, 53, 317. [Google Scholar] [CrossRef]
- Tozar, A.; Tasbozan, O.; Kurt, A. Optical soliton solutions for the (1+1)-dimensional resonant nonlinear Schröndinger’s equation arising in optical fibers. Opt. Quantum Electron. 2021, 53, 316. [Google Scholar] [CrossRef]
- Abdeljabbar, A.; Roshid, H.-O.; Aldurayhim, A. Bright, Dark, and Rogue Wave Soliton Solutions of the Quadratic Nonlinear Klein–Gordon Equation. Symmetry 2022, 14, 1223. [Google Scholar] [CrossRef]
- Batiha, B. New Solution of the Sine-Gordon Equation by the Daftardar-Gejji and Jafari Method. Symmetry 2022, 14, 57. [Google Scholar] [CrossRef]
- Arshed, S.; Biswas, A.; Mallawi, F.; Belic, M.R. Optical solitons with complex Ginzburg–Landau equation having three nonlinear forms. Phys. Lett. A 2019, 383, 126026. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Abdelaziz, M.A.M. The two-variable (G’/G,1/G)-expansion method for solving the nonlinear KdV-mKdV equation. Math. Probl. Eng. 2012, 2012, 725061. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Hoda Ibrahim, S.A.; Abdelaziz, M.A.M. Traveling wave solutions of the nonlinear (3 + 1)- dimensional Kadomtsev-Petviashvili equation using the two variables (G’/G,1/G)-expansion method. J. Appl. Math. 2012, 2012, 560531. [Google Scholar] [CrossRef]
- Azzouzi, F.; Triki, H.; Mezghiche, K.; El Akrmi, A. Solitary wave solutions for high dispersive cubic-quintic nonlinear Schrödinger equation. Chaos Solitons Fractals 2009, 39, 1304–1307. [Google Scholar] [CrossRef]
- Kumar, D.; Hosseini, K.; Samadani, F. The sine-Gordon expansion method to look for the traveling wave solutions of the Tzitéica type equations in nonlinear optics. Optik 2017, 149, 439–446. [Google Scholar] [CrossRef]
- Korkmaz, A.; Hepson, O.E.; Hosseini, K.; Rezazadeh, H.; Eslami, M. Sine-Gordon expansion method for exact solutions to conformable time fractional equations in RLW-class. J. King Saud Univ. -Sci. 2018, 32, 567–574. [Google Scholar] [CrossRef]
- Raza, N.; Arshed, S.; Javid, A. Optical solitons and stability analysis for the generalized second-order nonlinear Schrödinger equation in an optical fiber. Int. J. Nonlinear Sci. Numer. Simul. 2020, 21, 855–863. [Google Scholar] [CrossRef]
- Weiss, J.; Tabor, M.; Carnevale, G. The Painlevé property for partial differential equations. J. Math. Phys. 1983, 24, 522–526. [Google Scholar] [CrossRef]
- Malik, S.; Almusawa, H.; Kumar, S.; Wazwaz, A.M.; Osman, M.S. A (2+1)-dimensional Kadomtsev–Petviashvili equation with competing dispersion effect: Painlevé analysis, dynamical behavior and invariant solutions. Results Phys. 2021, 23, 104043. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alrebdi, H.I.; Raza, N.; Arshed, S.; Butt, A.R.; Abdel-Aty, A.-H.; Cesarano, C.; Eleuch, H. A Variety of New Explicit Analytical Soliton Solutions of q-Deformed Sinh-Gordon in (2+1) Dimensions. Symmetry 2022, 14, 2425. https://doi.org/10.3390/sym14112425
Alrebdi HI, Raza N, Arshed S, Butt AR, Abdel-Aty A-H, Cesarano C, Eleuch H. A Variety of New Explicit Analytical Soliton Solutions of q-Deformed Sinh-Gordon in (2+1) Dimensions. Symmetry. 2022; 14(11):2425. https://doi.org/10.3390/sym14112425
Chicago/Turabian StyleAlrebdi, Haifa I., Nauman Raza, Saima Arshed, Asma Rashid Butt, Abdel-Haleem Abdel-Aty, Clemente Cesarano, and Hichem Eleuch. 2022. "A Variety of New Explicit Analytical Soliton Solutions of q-Deformed Sinh-Gordon in (2+1) Dimensions" Symmetry 14, no. 11: 2425. https://doi.org/10.3390/sym14112425
APA StyleAlrebdi, H. I., Raza, N., Arshed, S., Butt, A. R., Abdel-Aty, A.-H., Cesarano, C., & Eleuch, H. (2022). A Variety of New Explicit Analytical Soliton Solutions of q-Deformed Sinh-Gordon in (2+1) Dimensions. Symmetry, 14(11), 2425. https://doi.org/10.3390/sym14112425







