(I, JP) = (1, 1/2+)ΣNN Quasibound State

Humberto Garcilazo; Alfredo Valcarce

doi:10.3390/sym14112381

and

¹

Escuela Superior de Física y Matemáticas, Instituto Politécnico Nacional, Edificio 9, México D. F. 07738, Mexico

²

Departamento de Física Fundamental, Universidad de Salamanca, E-37008 Salamanca, Spain

^*

Author to whom correspondence should be addressed.

^†

These authors contributed equally to this work.

Symmetry2022, 14(11), 2381;https://doi.org/10.3390/sym14112381

This article belongs to the Section Physics

Version Notes

Order Reprints

Abstract

JLab has recently found indications of the possible existence of a

Σ N N

resonance at

(3.14 \pm 0.84) - i (2.28 \pm 1.2)

MeV. In the past, using models that exploit symmetries between the two-baryon sector with and without strangeness, hyperon–nucleon interactions that reproduce the experimental data of the strangeness

- 1

sector have been derived. We make use of these interactions to review the existing Faddeev studies of the

Λ N N - Σ N N

system that show theoretical evidence of a

(I, J^{P}) = (1, 1 / 2^{+})

Σ N N

quasibound state near the threshold. The calculated position of the pole is at 2.92

- i

2.17 MeV, which is in reasonable agreement with the experimental findings.

Keywords:

multiquarks; quark models; few-body systems

The Hall A Collaboration at Jefferson Lab made use of the

(e, e^{'} K^{+})

reaction to study the possible existence of neutral three-body

Λ

and

Σ

hypernuclei [1]. They reported an excess of events around the

Σ

thresholds. The most significant enhancement appeared

3.14 \pm 0.84

MeV below the

Σ^{0} n n

threshold and had a width of

σ \approx 2.28 \pm 1.2

MeV. This possibly hints at a bound

Σ^{0} n n

(I = 1) state.

The existing experimental data and the expected forthcoming optimized data call for theoretical studies that could help with their interpretation. In this letter, it is our purpose to emphasize the relevant findings of the existing Faddeev studies of the

Λ N N - Σ N N

system. The theoretical results obtained are a valuable tool for analyzing the Hall A Collaboration data.

We carried out a detailed study of the

Λ N N - Σ N N

three-body system at the threshold to look for bound states or resonances [2]. The strangeness

- 1

two-body interactions were derived from the chiral quark cluster model (CQCM) [3] by exploiting the symmetries with the two-nucleon sector. In the CQCM, hadrons are clusters of massive (constituent) quarks. As color carriers, massive quarks are confined through a confining potential. They interact through a one-gluon exchange potential arising from the perturbative effects of quantum chromodynamics (QCD). The non-perturbative effects generate one-boson exchange potentials between quarks [3,4].

The nucleon–nucleon (

N N

) and hyperon–nucleon (

Y N

) interactions describe the

N N

and

Y N

two-body observables reasonably well [4]. In particular, the low-energy parameters,

N N

S

-wave phase shifts, and triton binding energy in a two-nucleon system were described correctly [3]. In addition, there was a reasonable agreement with the hyperon–nucleon elastic and inelastic scattering cross-sections and the hypertriton binding energy. Finally, the isospin one-

Λ n n

system was found to be unbound [2,4,5].

At the two-body level, the

N Λ - N Σ

coupling and the tensor force, which is responsible for the coupling between S and D waves, have been considered. The

Λ \leftrightarrow Σ

conversion is crucial in order to have a correct description of the

Λ N N

system [2]. The

N N

and

Y N

interactions contain sizable non-central terms that are responsible for, among other things, the deuteron binding energy. The relevance of the

Y N

tensor force becomes apparent when studying the

Σ^{-} p \to Λ n

reaction. This process is controlled by the

Σ N (ℓ = 0) \to Λ N (ℓ = 2)

transition, so if only the central interaction

Σ N (ℓ = 0) \to Λ N (ℓ = 0)

is considered, the cross-section cannot be correctly described [6]. The non-central

N Λ - N Σ

interaction induces a three-body force through the coupling between the

Y N N

channels with

(ℓ, λ) = (0, 0)

and

(ℓ, λ) = (2, 2)

, where the relative orbital angular momentum of the

Y N

is denoted by ℓ, and

λ

stands for that of the spectator nucleon in the

Y N

system.

For this study, different models were designed by choosing sets of spin-singlet and spin-triplet

Λ N

scattering lengths that correctly described the available experimental data. In particular, in addition to its reasonable description of the

Y N

cross-sections, the hypertriton binding energy corresponded to its experimental value within the error bars of

B_{0, 1 / 2} = 0.130 \pm 0.050

MeV [7]. The upper limit of the

Λ N

spin-triplet scattering length,

a_{1 / 2, 1}^{Λ N}

, was established by requiring that the

(I, J^{P}) = (0, 3 / 2^{+})

Λ N N

state does not become bound [2]. The lower limit was set by requiring a correct description of the

Y N

cross-sections, which deteriorated markedly as the

Λ N

spin-triplet scattering length decreased. Thus, it was found that

1.41 \leq a_{1 / 2, 1}^{Λ N} \leq 1.58

fm. Once the

Λ N

spin-triplet scattering length was defined, the

Λ N

spin-singlet scattering length,

a_{1 / 2, 0}^{Λ N}

, was constrained by demanding for the hypertriton binding energy to be in the experimental interval of

B = 0.130 \pm 0.050

MeV, leading to

2.33 \leq a_{1 / 2, 0}^{Λ N} \leq 2.48

fm. Without loss of generality, we take the model with

a_{1 / 2, 1}^{Λ N} = 1.41

and

a_{1 / 2, 0}^{Λ N} = 2.48

as the reference model. All calculations were performed for several models within the scattering length intervals, and the conclusions remained unchanged. For the reference model, the hypertriton binding energy obtained was 129 keV. To illustrate the relevant role played by the D waves of the three-body system, it is worth noting that when considering only S-wave three-body channels, the hypertriton binding energy is 89 keV, which is out of the experimental range.

The solutions of the three-body problem have been described elsewhere [2] and are out of the scope of this letter. We focus on the results concerning the possible existence of a

Σ N N

(I, J^{P}) = (1, 1 / 2^{+})

resonance [1].

Let us first discuss the attractive or repulsive character of the different

J^{P} = 1 / 2^{+}

Σ N N

channels. Figure 1 shows the Fredholm determinant of the

J^{P} = 1 / 2^{+}

Σ N N

channels below the

Σ d

threshold, where the continuum starts. The Fredholm determinant of the

I = 0

and 1 channels is complex because the

Λ N N

channels are open. The imaginary part is small and uninteresting. It can be seen that the channel showing the most attractive character is

(I, J^{P}) = (1, 1 / 2^{+})

. For an attractive channel, the Fredholm determinant,

D_{F}

, is smaller than 1, and it becomes negative if a bound state exists [5]. Thus, the fact that the Fredholm determinant is very close to zero at the

Σ d

threshold is a clear indication of a quasibound state. The

(I, J^{P}) = (0, 1 / 2^{+})

channel is also attractive, but far less so than the

I = 1

one. This can be easily understood as follows. We show in Table 1 the two-body channels that contribute to a given

J^{P} = 1 / 2^{+}

Λ N N - Σ N N

state with isospin I. The most attractive two-body channels, in particular, the

Σ N

^{3} S_{1} (I = 1 / 2)

and

^{1} S_{0} (I = 3 / 2)

and the

N N

^{3} S_{1} (I = 0)

channels, contribute to the

(I, J^{P}) = (1, 1 / 2^{+})

Σ N N

state. However, the last two are forbidden for the

(I, J^{P}) = (0, 1 / 2^{+})

Σ N N

state, with one of them being the deuteron channel.

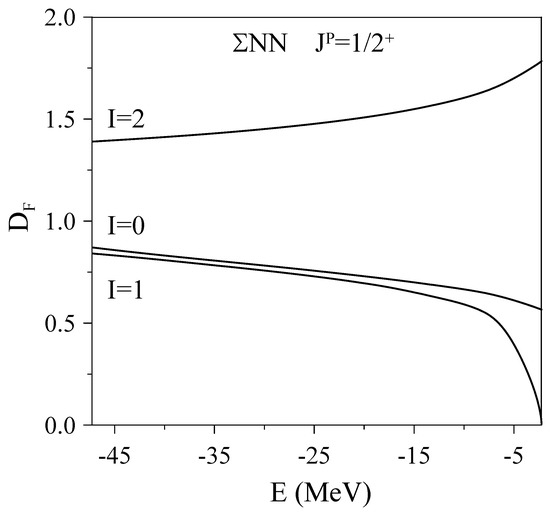
Figure 1. The Fredholm determinant,

D_{F}

, for the

J^{P} = 1 / 2^{+}

Σ N N

channels when utilizing the reference model, in which the deuteron binding energy is

E = - 2.225

MeV [2].

Table 1. Two-body

Σ N

channels

(i_{Σ}, s_{Σ})

,

Λ N

channels

(i_{Λ}, s_{Λ})

,

N N

channels with a

Σ

spectator

(i_{N (Σ)}, s_{N (Σ)})

, and

N N

channels with a

Λ

spectator

(i_{N (Λ)}, s_{N (Λ)})

that contribute to a given

J^{P} = 1 / 2^{+}

Λ N N - Σ N N

state with total isospin I.

The most interesting result in connection with the results reported in [1] is the prediction of a

Σ N N

(I, J^{P}) = (1, 1 / 2^{+})

quasibound state in the region near the threshold. We show in Figure 2 the real, Re

(A_{1, 1 / 2})

, and imaginary, Im

(A_{1, 1 / 2})

, parts of the

Σ d

scattering length as a function of the attraction in the three-body channel. The real part becomes negative, while the imaginary part has a maximum, which are the typical signals of a quasibound state [8]. The position of the pole almost does not change for the different models, and it is at 2.92

- i

2.17 MeV for the reference model. The width of this state comes mainly from the coupling to a D-wave

Λ N N

channel. It is worth emphasizing that the enhancement suggested as a possible

Σ N N

resonance by the Hall A Collaboration at Jefferson Lab appeared at about

(3.14 \pm 0.84) - i (2.28 \pm 1.2)

MeV [1], which is in very good agreement with the theoretical results reported in this study.

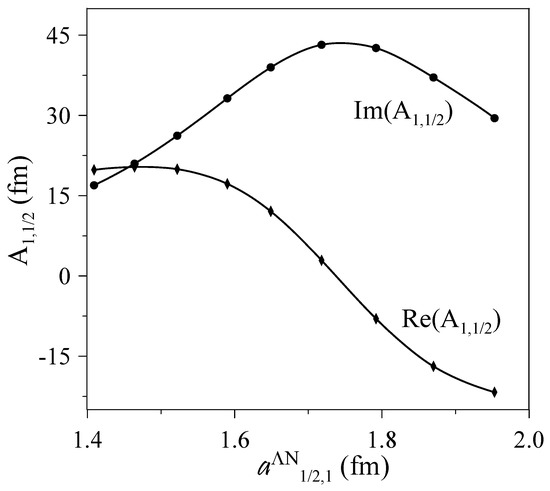
Figure 2. Real and imaginary parts of the

Σ d

scattering length,

A_{1, 1 / 2}

.

The existence of a

(I, J^{P}) = (1, 1 / 2^{+})

Σ N N

quasibound state was suggested in a variational calculation for the investigation of the structure of

A = 3

Σ

-hypernuclei [9]. Similar results were obtained by Harada and Hirabayashi [10] by using a distorted-wave impulse approximation within a coupled

(2 N - Λ) + (2 N - Σ)

model with a spreading potential. Afnan and Gibson found a near-threshold

I = 0

resonance while exploring

Λ d

elastic scattering with a continuum Faddeev calculation [11]. Recent preliminary calculations [12] suggested that the pole for the

I = 1

resonance is also located near the

Σ N N

threshold, but the two resonances are unlikely to be distinguished experimentally.

To conclude, the Hall A Collaboration at Jefferson Lab [1] has found indications of the possible existence of a

Σ N N

resonance at

(3.14 \pm 0.84) - i (2.28 \pm 1.2)

MeV. The state is likely a

Σ^{0} n n

state, although this has to be confirmed in future experiments. We have presented a detailed study of the

Λ N N - Σ N N

system by using the hyperon–nucleon and nucleon–nucleon interactions derived from a chiral constituent quark model with full inclusion of the

Λ \leftrightarrow Σ

conversion and by taking all three-body configurations with S- and D-wave components into account. In the case of the

Σ N N

system, there exists a narrow quasibound state near the threshold in the

(I, J^{P}) = (1, 1 / 2^{+})

channel. The position of the pole is at 2.92

- i

2.17 MeV. There is a reasonable agreement with the enhancement suggested as a possible

Σ N N

resonance by the Hall A Collaboration at Jefferson Lab, appearing at about

(3.14 \pm 0.84) - i (2.28 \pm 1.2)

MeV, and our result is inside the error bar of the experimental data.

Author Contributions

Conceptualization, H.G. and A.V.; Methodology, H.G. and A.V.; Formal analysis, H.G. and A.V.; Investigation, H.G. and A.V.; Writing—original draft preparation, H.G. and A.V.; Writing—review and editing, H.G. and A.V. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by COFAA-IPN (México) and by Ministerio de Economía, Industria y Competitividad, and EU FEDER under Contract Nos. PID2019-105439GB-C22 and RED2018-102572-T.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

Pandey, B.; Tang, L.; Gogami, T.; Suzuki, K.N.; Itabashi, K.; Nagao, S.; Okuyama, K.; Nakamura, S.N.; Abrams, D.; Afnan, I.R.; et al. Spectroscopic study of a possible Λnn resonance and a pair of ΣNN states using the (e, e′K⁺) reaction with a tritium target. Phys. Rev. C 2022, 105, L051001. [Google Scholar] [CrossRef]
Garcilazo, H.; Valcarce, A.; Fernández-Caramés, T. ΛNN and ΣNN systems at threshold. II. The effect of D waves. Phys. Rev. C 2007, 76, 034001. [Google Scholar] [CrossRef]
Valcarce, A.; Garcilazo, H.; Fernández, F.; González, P. Quark-model study of few-baryon systems. Rep. Prog. Phys. 2005, 68, 965–1042. [Google Scholar] [CrossRef]
Garcilazo, H.; Fernández-Caramés, T.; Valcarce, A. ΛNN and ΣNN systems at threshold. Phys. Rev. C 2007, 75, 034002. [Google Scholar] [CrossRef]
Garcilazo, H. Non-existence of ΛNN or Σ⁻nn bound states. J. Phys. G 1987, 13, L63–L67. [Google Scholar] [CrossRef]
Straub, U.; Zhang, Z.; Bräuer, K.; Faessler, A.; Khadkikar, S.B. Hyperon-nucleon interaction in the quark cluster model. Nucl. Phys. A 1988, 483, 686–710. [Google Scholar] [CrossRef]
Jurič, M.; Bohm, G.; Klabuhn, J.; Krecker, U.; Wysotzki, F.; Coremans-Bertr, G.; Sacton, J.; Wilquet, G.; Cantwell, T.; Esmael, F.; et al. A new determination of the binding-energy values of the light hypernuclei (A ≤ 15). Nucl. Phys. B 1973, 52, 1–30. [Google Scholar] [CrossRef]
Deloff, A. η − d and K⁻ − d zero-energy scattering: A Faddeev approach. Phys. Rev. C 2000, 61, 024004. [Google Scholar] [CrossRef]
Koike, Y.H.; Harada, T. Structure of the A = 3 Σ-hypernuclei. Nucl. Phys. A 1996, 611, 461–483. [Google Scholar] [CrossRef]
Harada, T.; Hirabayashi, Y. ΣNN quasibound states in ³He(K⁻, π^∓) reactions at 600 MeV/c. Phys. Rev. C 2014, 89, 054603. [Google Scholar] [CrossRef]
Afnan, I.R.; Gibson, B.F. Hypertriton: Λ ↔ Σ conversion and tensor forces. Phys. Rev. C 1990, 41, 2787–2799. [Google Scholar] [CrossRef] [PubMed]
Gibson, B.F. Possible ΣNN resonant states. In Proceedings of the 14th International Conference on Hypernuclear and Strange Particle Physics-HYP2022, Prague, Czech Republic, 27 June–1 July 2022. [Google Scholar]

Figure 1. The Fredholm determinant,

D_{F}

, for the

J^{P} = 1 / 2^{+}

Σ N N

channels when utilizing the reference model, in which the deuteron binding energy is

E = - 2.225

MeV [2].

Figure 2. Real and imaginary parts of the

Σ d

scattering length,

A_{1, 1 / 2}

.

Table 1. Two-body

Σ N

channels

(i_{Σ}, s_{Σ})

,

Λ N

channels

(i_{Λ}, s_{Λ})

,

N N

channels with a

Σ

spectator

(i_{N (Σ)}, s_{N (Σ)})

, and

N N

channels with a

Λ

spectator

(i_{N (Λ)}, s_{N (Λ)})

that contribute to a given

J^{P} = 1 / 2^{+}

Λ N N - Σ N N

state with total isospin I.

Table 1. Two-body

Σ N

channels

(i_{Σ}, s_{Σ})

,

Λ N

channels

(i_{Λ}, s_{Λ})

,

N N

channels with a

Σ

spectator

(i_{N (Σ)}, s_{N (Σ)})

, and

N N

channels with a

Λ

spectator

(i_{N (Λ)}, s_{N (Λ)})

that contribute to a given

J^{P} = 1 / 2^{+}

Λ N N - Σ N N

state with total isospin I.

I	$(i_{Σ}, s_{Σ})$	$(i_{Λ}, s_{Λ})$	$(i_{N (Σ)}, s_{N (Σ)})$	$(i_{N (Λ)}, s_{N (Λ)})$
0	(1/2,0),(1/2,1)	(1/2,0),(1/2,1)	(1,0)	(0,1)
1	(1/2,0),(3/2,0),(1/2,1),(3/2,1)	(1/2,0),(1/2,1)	(0,1),(1,0)	(1,0)
2	(3/2,0),(3/2,1)		(1,0)

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

(I, J^P) = (1, 1/2⁺)ΣNN Quasibound State

Abstract

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

Article Metrics

Citations

Article Access Statistics