Abstract
The timeliness of order deliveries seriously impacts customers’ evaluation of logistics services and, hence, has increasingly received attention. Due to the diverse and large quantities of orders under the background of electronic commerce, how to pick orders efficiently while also adapting these features has become one of the most challenging problems for distribution centers. However, previous studies have not accounted for the differences in the stochastic characteristics of order generation, which may lead to asymmetric optimization problems. With this in mind, a new asymmetric polling-based model that assumes the varying stochastic characteristics to analyze such order picking systems is put forward. In addition, two important indicators of the system, mean queue length (MQL) and mean waiting time (MWT), are derived by using probability-generating functions and the embedded Markov chain. Then, simulation experiments and a comparison of the numerical and theoretical results are conducted, showing the usefulness and practicalities of the proposed model. Finally, the paper discusses the characteristics of the novel order picking system and the influence of the MQL and MWT on it.
1. Introduction
Currently, as the development of electronic commerce drives the growth of consumer demand, reducing the order-to-delivery time has become the primary challenge for distribution centers under the conditions of smaller order sizes and more varieties of orders [1]. Due to the length of time and financial costs, order picking is considered an important activity of storage and distribution centers. Some studies have shown that the cost of order picking can account for more than 60% of the total warehouse operating costs [2].
Order picking has been an important research topic in logistics studies for the last several decades, and scholars have used a variety of methods in their attempts to improve order picking activities including order batching, order storage assignment strategies, order picking sequencing, and stock-to-picker systems [3,4,5,6]. (i) Order batching: The goal of order batching is to minimize the travel distance between the picker and orders to obtain an optimal order batching strategy by picking the orders synchronously in one tour [4,7,8,9,10]. For example, Lu et al. (2016) [6] used an interference algorithm to realize dynamic picking path optimization, which is better than the static path algorithm and heuristic dynamic order picking path algorithm. Hong and Kim (2017) [11] proposed a batching model of path selection order based on the S-type path, which has better performance in large-scale order processing environments. To reduce the running distance of freight cars, Wu et al. (2022) [12] proposed an approach that used symmetry/asymmetry traffic context data for multicriteria decision. (ii) Storage assignment strategies: Storage assignment strategies can be divided into random storage, class-based storage, and closest open location storage [13,14,15]. Karasawa et al. (1980) [16] designed an automated warehouse system-based on nonlinear mixed integer programming to minimize the storage costs. Quader and Castillo-Villar (2018) [17] proposed a new algorithm based on normative order picking, which can reduce the cycle time and increase the throughput of the system. Torre et al. (2022) [18] weighed storage risk and service level and determined the best storage location of e-commerce products through the multicriteria decision-making method. Boru et al. (2022) [19] used nondominated sorting genetic algorithm to solve inventory routing problems under different demand patterns. (iii) Order picking sequencing: The study of order picking sequencing focuses on optimizing the distribution of the order-picking areas. It has two main aspects: the sequence of order picking and the layout of picking locations [20,21,22]. Boysen et al. (2017) [23] presented a type of accurate heuristic algorithm to improve the space utilization of the warehouse with mobile racks. Ning et al. (2022) [24] designed a hand–eye collaborative service system based on depth vision for sorting robot. (iv) Stock-to-picker systems: According to the relative motion state between orders and picking workers, these systems can be divided into stock-to-picker and picker-to-stock [25,26]. In addition, the research on exact optimization methods also contributed the field of logistics supply chain. For deep reviews of the methods, consider the works by Amjadian and Abolfazl (2022) [27], Gharaei et al. (2022) [28], Gharaei et al. (2021) [29], and Rezaei et al. (2022) [30].
Motivated by the literature review, this paper focused on a significant order-picking problem: how to improve the picking efficiency and reduce the order picking time at a system level. In response, researchers began to use polling theory. A polling system is usually described as a system that consists of a server and a plurality of queues and includes three processes: queue arrival, serving queue, and switching service object [31]. Polling systems generally have three types of service disciplines: gated, exhaustive, and k-limited. Under gated service disciplines, the server only serves the orders that arrive at the service point before the set time [32]. Under exhaustive service disciplines, the server will not stop serving the order until the current order queue is exhausted. Under k-limited service disciplines, the server serves up to k queues at a service time. Now, polling theory has been widely used in the field of network and communication such as in wireless network random accessing applications [33] and in the antijamming ability of wireless networks to power grid systems [34]. However, we have found few studies based on limited polling theory in the field of order picking. References [35,36,37] first used polling theory to study the dynamic picking systems of online retailers under e-commerce considering the stochastic variables of the orders and obtained the approximate explicit expressions of the order line waiting time in the systems. Reference [4] showed that compared with traditional batch-picking methods, the proposed polling-based dynamic order-picking system can improve the order-picking efficiency.
However, the feature of the e-commerce businesses that generates an order with variable stochastic characteristics suggests that it is essentially an asymmetric optimizations problem. The diversity of order demands will lead to variations in the stochastic characteristics of the orders, which may lower the efficiency of the order picking and bring potential errors, and traditional picking systems have failed to address this issue. Most of the literature has focused on the traditional way of organizing the picking process through pick batches and releasing orders to the shop floor so that items can be picked and sorted by workers or robots. As a result, they failed to address this gap. The studies in [35,36,37] attempted to construct a dynamic order picking model based on asymmetric queue assumptions; however, they failed to solve the average queue length of orders. To our knowledge, the existing studies still cannot fully examine the performance of an asymmetric polling order picking system to adapt the multi-stochastic characteristics of orders.
To reveal the difference between symmetric and asymmetric polling-based order picking systems, there is a specific example. Consider that polling systems usually include three processes, queue arrival, serving queue, and switching service object [31], which are determined by three stochastic properties, the queue arrival rate (λ), queue service time (β), and queue service switch time (γ). In the case of N queues, symmetric polling theory assumes that λ1 = λ2 = … = λn, β1 = β2 = … = βn, and γ1 = γ2 = … = γn. For example, due to the different sizes and sales, retailers choose different order intervals to maintain their inventory levels, and the order interval directly affects the order queue arrival rate, λ. Therefore, the assumption that λ1 = λ2 = … = λn is invalid, and in a real situation, the stochastic characteristics of all order queues are variable. At the very least, not every order queue is the same, which is the assumption of asymmetric polling theory [38,39]. The difference between symmetric and asymmetric polling systems is the stochastic properties constraint of order queues. The asymmetric polling system loosens the constraints on the stochastic properties compared to the symmetric polling system, which is closer to the practical production requirements.
Therefore, to resolve the research gap, this paper designed a novel asymmetric polling-based dynamic order picking system that allows orders with diversiform stochastic characteristics to exist in different picking lines. Under gated service discipline, we combined the probability generating function and the embedded Markov chain to gain the explicit solutions of mean queue length (MQL) and mean waiting time (MWT) in the model. Finally, we verified its performance by numerical examples. The rest of the paper is structured as follows. Section 2 introduces the proposed new model. Section 3 presents our numerical example. The conclusions and discussion are presented in Section 4.
2. Model
2.1. Problem Statement
Currently, most Chinese cigarette logistics distribution centers are automating their business processes; therefore, the model in this paper was put forward based on a highly automated picking system. Taking the Qujing tobacco distribution center of the Hongyunhonghe Group in Yunnan Province, China, as an example, the cigarette brands of the distribution center are diverse, and the packaging of each type of cigarette is standardized such that the goods picked are cartons of cigarettes. If cigarette retailers send order requests to the distribution center through a unified ordering system, the distribution center can pick and deliver the order within 24 h of receiving the request.
The order-picking system considered here is similar to that of Gong and De Koster (2008) [35], which they describe as a “dynamic picking system”. To help understand and implement such a complex system, the picking problem can be described as follows. The system consists of a sorter and N order queues and includes three processes: queue arrival, serving queue (picking order), and switching service object. (i) The arrival of an order starts from generation to the picking operation after a customer orders in the system. The arrival order line stream at position i is a Poisson process with expectation arrival rate λi. (ii) The performance of the picking service depends on the speed and efficiency of the picking machine. This process is measured by the expectation βi of the picking time. (iii) Switching the service objects is where the picking machine switches to pick order queue i + 1 after serving order queue i. This process is measured by the expectation γi of switching times in the picking service. The length of switching time reflects the flexibility of the picking machine and the interval between different orders.
To help understand and implement such a complex system to gain explicit solutions of mean queue length and mean waiting time, the picking problem can be described as shown in Figure 1. The model divides N queues into sub-queue i (containing only queue i) and parent queue set (containing N − 1 queues except queue i). Queue i + 1 is the first queue of parent queue set . At time tn, when the sorter machine starts picking the queue in sub-queue. ξi(n) is the number of orders that accept the picking service in sub-queue i. Only the orders of parent queue set that arrive before tn+1, except queue i + 1, can obtain the picking service at time tn. ξi(n + 1) is the number of orders that accept the picking service in the parent queue set at the time tn+1. Due to the fact that i + 1 ∈ , . Once ξi(n + 1) orders finish the picking services, the next round of polling starts. In addition, as a reference, we provide an example with the MATLAB program of the asymmetric polling-based dynamic order picking system in Appendix A.
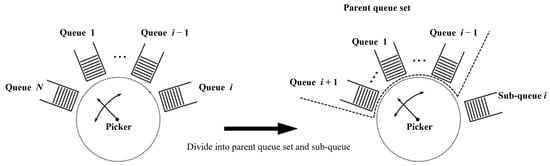
Figure 1.
A model of the dynamic order picking system.
In addition, there are several basic conditions for the polling model-based picking system:
(1) The picking machines combine the unit materials into different orders according to the priority and requirements of the orders. The arrival rate, picking time, and service switching time of the orders on the same order queue have certain distributions, and the service switching time determines the distance between the adjacent orders. Each order has only one layer, and we thus only consider its area. The area is determined by the number of standardized smallest unit materials, which can be seen as the order requirements, as shown in Figure 2.
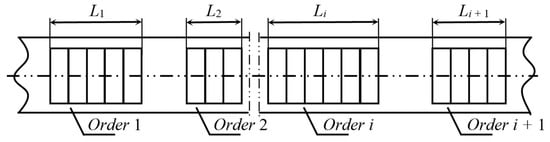
Figure 2.
Order queue plan.
(2) The time of the model is divided into N unit time slots, which is a discrete time system model. (a) The arrival process of the orders was that orders form and reach the picking operation point after they are generated by the system. This process is measured by the probability distribution expectation, λ. (b) The picking service process determines the speed and efficiency of the picking machine. This process is measured by the probability distribution expectation, β. (c) The process of switching the service objects involves the picking machine switching to pick order queue i + 1 after serving order queue i. This process is measured by the probability distribution expectation, λ. The switching time reflects the flexibility of the picking machine and the interval between different orders.
(3) Every queue buffer (i.e., the area where an order waits to be picked) is sufficiently large, and no order will be lost. It is easy to understand that this assumption guarantees that orders can be generated continuously, i.e., the case of unlimited orders.
(4) The order queue accepts the picking service according to (a) first-come, first-served (FCFS) rules and (b) the gated service discipline, as shown in Figure 3: the discipline requires that the picking machine only sort the orders that enter the queue before starting the service; therefore, the other orders are delayed until the next processing.
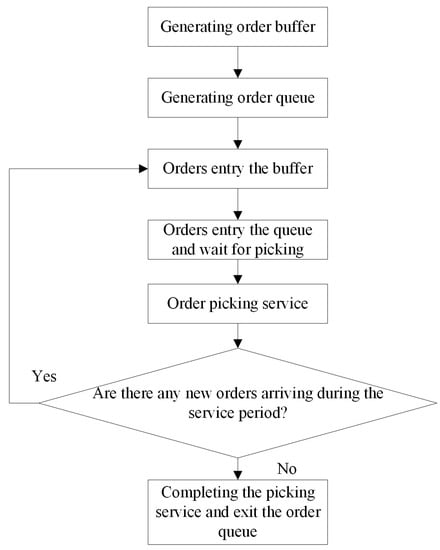
Figure 3.
A flow chart of the order queue under a gated service discipline.
2.2. Notation and Definitions
(1) Ai(zi): The probability distribution function of a queue’s arrival rate. Ai′(zi) is its first derivative, and Ai″(zi) is its second derivative;
(2) The arrival rates are independent of each other. The expectation λi and variance σ2λi of the probability distribution all satisfy the following conditions: and ;
(3) Bi(zi): The probability distribution function of a queue’s picking time. Bi′(zi) is its first derivative, and Bii″((zi) is its second derivative;
(4) The times of accepting the picking service are independent of each other. The expectation βi and variance σ2βi of the probability distribution all satisfy the following conditions: and ;
(5) Ri(zi): The probability distribution function of the adjacent queue’s picking service switching time. Ri′(zi) is its first derivative, and Ri″(zi) is its second derivative;
(6) The switching times of the picking service are independent of each other. The expectation γi and variance σ2γi of the probability distribution all satisfy the following conditions: and . After processing, we obtain and ;
(7) ξi(n): The number of orders that arrived before moment tn in the order queue i; [ξ1(n), ξ2(n), …, ξi(n), …, ξN(n)] is the state of the whole picking system at moment tn; πi(x1, x2, …, xi, …, xN) is the probability distribution of the picking system state at moment tn; Gi(z1, z2, …, zi, …, zN) is the generating function of πi(x1, x2, …, xi, …, xN); gi (k) is the first order characteristic of Gi(z1, z2, …, zi, …, zN), and it indicates the number of orders that are waiting to be picked in queue k when queue i starts to obtain the picking service; gi (j, k) and are its second characteristic quantity;
(8) ui(n): The time of the picking service switching from sub-queue i to order parent queue set ; represents the time of picking service switching from parent queue set to sub-queue i; vi(n) is the time when order queue i has picking service; μj(ui) is the number of orders that arrive at order queue j within ui(n), j∈; is the number of orders that arrive at order queue j within ; ηj(vi) is the number of orders that arrive at order queue j within vi(n);
2.3. System Generating Function
The model starts to pick the parent queue set at moment tn+1, and the gated control polling system theory requires that the stability of the system must meet the condition [40]. When the polling system is stable, it has the following relationships:
According to Equations (1) and (2), the state generating function of the parent queue set and sub-queue will be obtained:
2.4. The Characteristic Parameters of the System Generating Function
2.4.1. Mean Queue Length
When the queue i starts to accept the picking service, the number of orders that wait for picking in queue j is gi(j). Supposing i = j, gi(i) represents the number of orders that wait for the next picking in queue i buffer; it can also be called the mean queue length of the picking system. gi(j) is obtained by seeking the partial derivative of Gi(z1, z2, …, zi, …, zN) as follows:
Equations (3) and (4) can be substituted into Equation (5) to obtain Equations (6) and (7):
According to Equations (5)–(7), the mean queue length of the sub-queue and the parent queue set can be obtained as follows (the relevant proofs will be given in the Appendix B):
2.4.2. Mean Waiting Time
Another characteristic parameter to measure the performance of the asymmetric polling system is the mean waiting time of the system. It refers to the time from the order entering the buffer of the order queue to finishing the picking service and leaving the picking machine. The mean waiting time of the symmetric polling system considers the waiting time of the order on the arrival time slot. The mean waiting time can be expressed as follows (the relevant proofs are given in the Appendix C):
According to the properties of the probability-generating functions in random process and gi(j, k) are obtained by seeking the second partial derivative of Gi(z1, z 2, …, zi, …, zN) as follows:
By combining Equations (3), (4) and (10), Equation (11) is obtained, and the relevant proofs are given in the Appendix D.
The mean waiting time of the asymmetric gated polling control system can be obtained by bringing Equations (8) and (11) into Equation (9).
3. Numerical Example and Discussion
In this section, we use several numerical examples to validate the performance of the new model using the MATLAB (R2012b version) software platform. First, we examined the impact of variable stochastic characteristics (i.e., λiβi and γi) on the proposed model, and then, we compared the performance of the new picking system in the cases of different amounts of the picking station. The results of the MQL and MWT illustrate the major results of the paper.
3.1. Numerical Example
To facilitate numerical analysis, we assumed that the picked goods are all the same kind and that the number of materials contained in each order is the same. The distribution center is responsible for the picking operation of the variety order. We suppose the outer package of the unit material width was 100 mm, the order conveyor speed was 60 m/min, the picking speed per of unit material was 2 s, and the order switch time was 1 min. Each group of the parameters was analyzed 5000 times, and the theoretical calculations used normalized parameters. Each order consisted of a combination of unit materials, and the speed of the conveyor was uniform. Furthermore, the system met the stable conditions of and i = 1, 2, …, N.
Figure 4 and Figure 5, respectively, show how λβ impacted the order picking system’s two important performance indexes, mean queue length (MQL) and mean waiting time (MWT), with a different number of picking station (P.S.n, n = 1, 2, 3, 4, and 5, meaning there were n picking stations), and we assumed that λ1:λ2:λ3:λ4:λ5 = 1:2:4:6:8 and γi = 10 (i = 1, 2, …, 5). represents the overall load level of the picking system. The larger λβ means the higher system load. With the increasing system load λβ, MQL and MWT also grow nonlinearly. When λβ is small (λβ < 0.1), the difference in the MWT was not obvious and far less than that of the MQL. As the system’s load increased, the divergence of the MWT became apparent. If the other parameters were the same, the size of λ was positively related to the increase in the MQL and MWT.
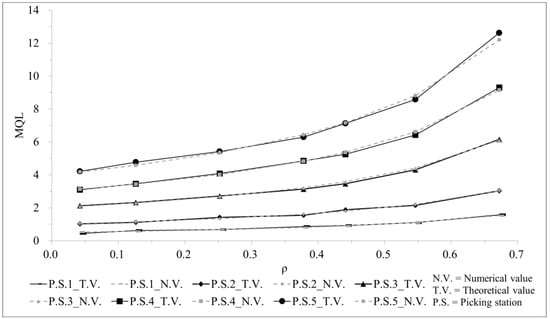
Figure 4.
Range of the MQL with λβ’s change.
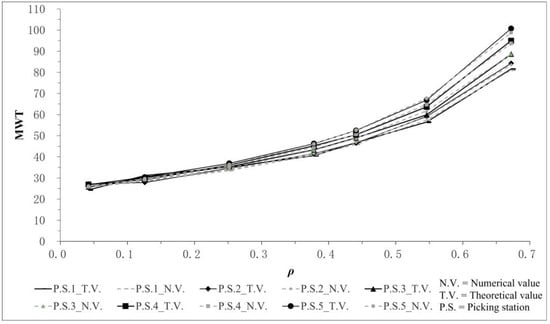
Figure 5.
Range of the MWT with λβ’s change.
Figure 6 and Figure 7, respectively, show how γ impacted the order picking system’s mean queue length (MQL) and mean waiting time (MWT) under a low system load, and we assumed that λ1λ2:λ3:λ4:λ5 = 1:2:4:6:8, βi = 0.6 (i = 1, 2, …, 5), and . Figure 8 and Figure 9, respectively, show how γ impacted the mean queue length (MQL) and the mean waiting time (MWT) under a high system load, we assume that λ1:λ2:λ3:λ4:λ5 = 1:2:4:6:8, βi = 3.6 (i = 1, 2, …, 5) and . P.S.n (n = 1, 2, 3, 4, and 5) means there are n picking stations. Figure 6, Figure 7, Figure 8 and Figure 9 show the theoretical values of the MQL and MWT at different system load levels. At any system load level, the MQL and MWT will grow with the increasing in γ. When γ is determined, the higher system load expands the MQL and MWT. As shown in Figure 7, the differences in the picking stations’ MWT were very small under a low system load.
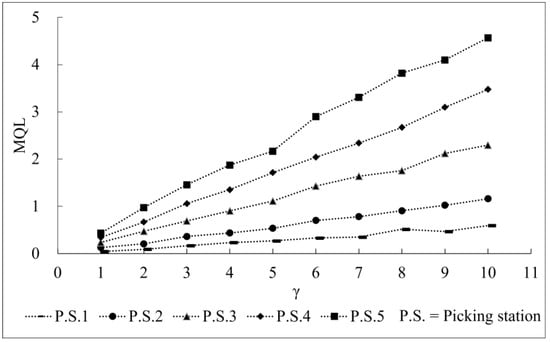
Figure 6.
Range of the MQL with γ’s change under a low system load.
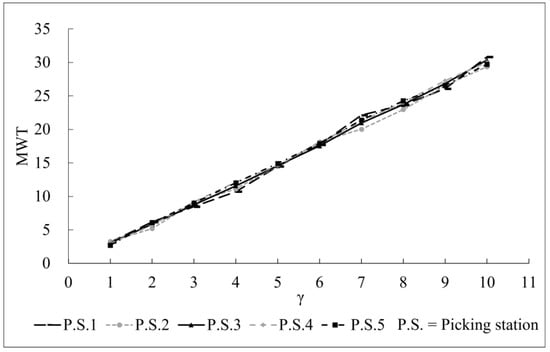
Figure 7.
Range of the MWT with γ’s change under a low system load.
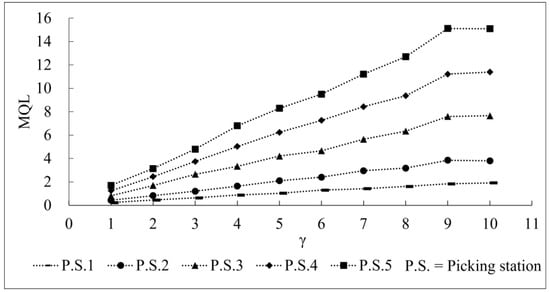
Figure 8.
Range of the MQL with γ’s change under a high system load.
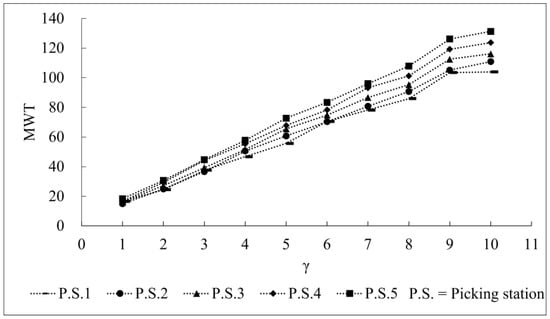
Figure 9.
Range of the MWT with γ’s change under a high system load.
Table 1 show that the numerical results of the system’s performance under different amounts of the picking station. The second set of data had more than one picking station in the first set of data, and they had the same stochastic characteristic parameters as the three picking stations. The third set of data had five picking stations, but its system load (λβ = 0.078) was close to the second set of data (λβ = 0.0777).

Table 1.
The numerical results of the different picking stations.
3.2. Discussion
(1) The numerical values were very close to the theoretical values; this means that the proposed model of an asymmetric polling-based dynamic order picking system is valid.
(2) With the increase in the λβ and γ, the MQL and MWT also grew correspondingly. This shows that these stochastic characteristics (λiβi and γi) have an important impact on the performance of the picking system. The higher system load and longer switching times of a picking service can increase the queue length and waiting time of a picking system. In addition, the differences in the picking stations’ MQL were larger than that of the picking stations’ MWT with the increase in the system load, which could be due to the order arrival rate’s greater impact on the length of the order queue.
(3) Under a low system load, the differences in the picking stations’ MWT were too small and not obvious. This means that the arrival rate hardly affected the waiting time of the picking system in the case of a low system load. However, with the growth in the system load, the differences in the picking stations’ MWT also increased and the effect of the differences in the picking stations’ arrival rates on the MWT gradually became apparent. This indicates that the picking system could better identify the stochastic characteristics of the order queues under a high load and is more flexible in actual situations.
(4) An increasing number of picking stations will enlarge the MQL and MWT, even if the system load remains the same. This means that the number of picking stations is also an important factor affecting the system’s performance as well as the stochastic characteristic parameters. The diversity of the order queue characteristics complicates the picking system, and a longer queue length and waiting time of the order picking are unavoidable.
4. Conclusions
In this paper, we established a new model for an asymmetric polling-based dynamic order picking system. First, the arrival rate, service time, and service switching time of each order queue were assumed to have different probability distributions, and the picking machine was required to serve different queues according to the gated service discipline for polling. Furthermore, we used the probability generating function and embedded Markov chain to accurately solve the model and to obtain the MQL and MWT of the model.
This paper extended the theory and application of asymmetric polling in automated order picking systems and contributed to existing research. Considering the existing research [35,36,38,39,41,42], which did not take into account the influence of the diversity of the order demand on the probability distribution of the different order queues, we established an asymmetric polling-based order picking system under gated service disciplines, and our model assumed that different queues have different arrival rates, service times, and service switching times. The proposed model can more closely reflect the actual changes in the orders in e-commerce and make the order picking system more efficient and stable. The numerical examples results indicate the usefulness and practicality of the new model. It is conducive for logistics enterprises to complete efficient order assignments and provide timely and satisfactory logistics services.
Finally, our study has some limitations. For example, it has lots of necessary conditions for the new model, such as the conditions of the system stability, the order queue arrival, the picking process, and the picking service switch process. The condition change of random characteristics will directly affect the probability generating function. This may make the problem-solving methods more complex, and they may not even obtain accurate solutions. Therefore, future research should focus on reducing these constraints and making the model more flexible to adapt to the actual situations of distribution centers.
Author Contributions
Conceptualization, D.Y. and Z.Z.; methodology, D.Y. and Z.Z.; formal analysis, D.Y.; data curation, Z.Z.; writing—original draft preparation, D.Y.; writing—review and editing, Z.Z. and S.L.; supervision, S.L.; funding acquisition, S.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation Council of China under Project No. 71862035 and by The 21st Yunnan Young and Middle-Aged Academic and Technical Leaders Reserve Personnel Training Program under Grant No. 2019HB030.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All the relevant data are within the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Example Program
| Algorithm A1: An example program of the asymmetric polling-based dynamic order picking system with n = 5 picking stations |
| for i = 1:N seg = [exprnd(1/a(1,1),1,M1);exprnd(1/a(1,2),1,M1);exprnd(1/a(1,3),1,M1);exprnd(1/a(1,4),1,M1);exprnd(1/a(1,5),1,M1)]; T(i,:) = seg(i,:); end for i = 1:M start_time = t; for j = 1:N while temp(1,j) < t if temp(1,j) + T(j,m(1,j)) < = t temp(1,j) = temp(1,j) + T(j,m(1,j)); n(1,j) = n(1,j) + 1; m(1,j) = m(1,j) + 1; each_time1(1,j) = each_time1(1,j) + (t-temp(1,j)); else break; end end res(j) = n(1,j)-stemp(1,j);% if res(j) = = 0; t = t+r(1,j); else t = t + res(j)*b(1,j) + r(1,j); end stemp(1,j) = stemp(1,j) + res(j); que_length(j) = que_length(j) + res(j); if res(j) > 0 for q = 1:res(j) each_time2(1,j) = each_time2(1,j) + ((res(j)-q)*b(1,j)); end end end time1(i) = t-start_time; end time_sum = sum(sum(time1)); for k = 1:N g1(1,k) = que_length(k)/M; w1(1,k) = (each_time1(1,k) + each_time2(1,k))./stemp(1,k); end |
Appendix B. Proof of Equation (8)
According to Equation (7), Equation (A1) can be obtained:
Both sides of Equation (A1) are multiplied by :
According to Equation (6), Equation (A3) can be obtained:
Then, Equation (A2) can be taken into Equation (A3):
Bringing Equation (A4) into Equation (A2) provides the following:
By combining Equations (7) and (A5), Equation (A6) can be obtained:
Taking Equations (A6) and (A4) into Equation (7) gives the following:
Appendix C. Proof of Equation (9)
According to gated service discipline, the order queue i arrives at the service counter during τm(τm = tm+1 − tm) and accepts the picking service at tn time. The order k in queue i ends the picking service at t*m(tm< tm+1 < tn < t*m). We assume that θi(n) represents the time interval of the picking machine serving the same order queue i and there are yia(n) and yib(n) that satisfy the following conditions:
From the gated service strategy, the waiting time Wi of the order can be represented by the following formula:
The expectations of Wia and Wib can be obtained as follows:
Therefore, the mean waiting time E[Wi]G can be obtained:
Appendix D. Proof of Equation (11)
Seeking the two-order partial derivative of Equations (10), (A12) and (A13) can be obtained:
Accordingly, Equations (A12) and (A14) can be obtained:
Accordingly, Equations (A13) and (A15) can be obtained:
By combining Equations (11), (A14) and (A15) can be obtained.
References
- Yang, J.Q.; Zhang, X.M.; Fu, H.Y.; Liu, C. Inventory competition in a dual-channel supply chain with delivery lead time consideration. Appl. Math. Model. 2017, 42, 675–692. [Google Scholar] [CrossRef]
- Rubrico, J.I.U.; Higashi, T.; Tamura, H.; Ota, J. Online rescheduling of multiple picking agents for warehouse management. Robot. Comput.-Integr. Manuf. 2011, 27, 62–71. [Google Scholar] [CrossRef]
- Malmborg, C.J.; Al-Tassan, K. An integrated performance model for orderpicking systems with randomized storage. Appl. Math. Model. 2000, 24, 95–111. [Google Scholar] [CrossRef]
- de Koster, R.; Le-Duc, T.; Roodbergen, K.J. Design and control of warehouse order picking: A literature review. Eur. J. Oper. Res. 2007, 182, 481–501. [Google Scholar] [CrossRef]
- Manzini, R.; Accorsi, R.; Gamberi, M.; Penazzi, S. Modeling class-based storage assignment over life cycle picking patterns. Int. J. Prod. Econ. 2015, 170 Pt C, 790–800. [Google Scholar] [CrossRef]
- Lu, W.; McFarlane, D.; Giannikas, V.; Zhang, Q. An algorithm for dynamic order-picking in warehouse operations. Eur. J. Oper. Res. 2016, 248, 107–122. [Google Scholar] [CrossRef]
- Won, J.; Olafsson, S. Joint order batching and order picking in warehouse operations. Int. J. Prod. Res. 2005, 43, 1427–1442. [Google Scholar] [CrossRef]
- Tang, L.; Gong, H. A hybrid two-stage transportation and batch scheduling problem. Appl. Math. Model. 2008, 32, 2467–2479. [Google Scholar] [CrossRef]
- Grubbström, R.W. Dynamic lotsizing with a finite production rate. Int. J. Prod. Econ. 2014, 149, 68–79. [Google Scholar] [CrossRef][Green Version]
- Lam, C.H.Y.; Choy, K.L.; Ho, G.T.S.; Lee, C.K.M. An order-picking operations system for managing the batching activities in a warehouse. Int. J. Syst. Sci. 2014, 45, 1283–1295. [Google Scholar] [CrossRef]
- Hong, S.; Kim, Y. A route-selecting order batching model with the S-shape routes in a parallel-aisle order picking system. Eur. J. Oper. Res. 2017, 257, 185–196. [Google Scholar] [CrossRef]
- Wu, M.-Y.; Ke, C.-K.; Lai, S.-C. Optimizing the Routing of Urban Logistics by Context-Based Social Network and Multi-Criteria Decision Analysis. Symmetry 2022, 14, 1811. [Google Scholar] [CrossRef]
- Rouwenhorst, B.; Reuter, B.; Stockrahm, V.; van Houtum, G.J.; Mantel, R.J.; Zijm, W.H.M. Warehouse design and control: Framework and literature review. Eur. J. Oper. Res. 2000, 122, 515–533. [Google Scholar] [CrossRef]
- Atmaca, E.; Ozturk, A. Defining order picking policy: A storage assignment model and a simulated annealing solution in AS/RS systems. Appl. Math. Model. 2013, 37, 5069–5079. [Google Scholar] [CrossRef]
- Guerriero, F.; Pisacane, O.; Rende, F. Comparing heuristics for the product allocation problem in multi-level warehouses under compatibility constraints. Appl. Math. Model. 2015, 39, 7375–7389. [Google Scholar] [CrossRef]
- Karasawa, Y.; Nakayama, H.; Dohi, S. Trade-off analysis for optimal design of automated warehouses. Int. J. Syst. Sci. 1980, 11, 567–576. [Google Scholar] [CrossRef]
- Quader, S.; Castillo-Villar, K.K. Design of an enhanced multi-aisle order-picking system considering storage assignments and routing heuristics. Robot. Comput.-Integr. Manuf. 2018, 50, 13–29. [Google Scholar] [CrossRef]
- Torre, N.M.M.; Salomon, V.A.P.; Loche, E.; Gazale, S.A.; Palermo, V.M. Warehouse Location for Product Distribution by E-Commerce in Brazil: Comparing Symmetrical MCDM Applications. Symmetry 2022, 14, 1987. [Google Scholar] [CrossRef]
- Boru, A.; Dosdoğru, A.T.; Göçken, M.; Erol, R. A Novel Hybrid Artificial Intelligence Based Methodology for the Inventory Routing Problem. Symmetry 2019, 11, 717. [Google Scholar] [CrossRef]
- Van Nieuwenhuyse, I.; de Koster, R.B.M. Evaluating order throughput time in 2-block warehouses with time window batching. Int. J. Prod. Econ. 2009, 121, 654–664. [Google Scholar] [CrossRef]
- Theys, C.; Bräysy, O.; Dullaert, W.; Raa, B. Using a TSP heuristic for routing order pickers in warehouses. Eur. J. Oper. Res. 2010, 200, 755–763. [Google Scholar] [CrossRef]
- Rath, S.; Gutjahr, W.J. A math-heuristic for the warehouse location-routing problem in disaster relief. Comput. Oper. Res. 2014, 42, 25–39. [Google Scholar] [CrossRef]
- Boysen, N.; Briskorn, D.; Emde, S. Sequencing of picking orders in mobile rack warehouses. Eur. J. Oper. Res. 2017, 259, 293–307. [Google Scholar] [CrossRef]
- Ning, T.; Wang, C.; Han, Y. Deep Vision Servo Hand-Eye Coordination Planning Study for Sorting Robots. Symmetry 2022, 14, 152. [Google Scholar] [CrossRef]
- de Koster, R. Performance approximation of pick-to-belt orderpicking systems. Eur. J. Oper. Res. 1994, 72, 558–573. [Google Scholar] [CrossRef]
- Pan, J.C.-H.; Wu, M.-H. A study of storage assignment problem for an order picking line in a pick-and-pass warehousing system. Comput. Ind. Eng. 2009, 57, 261–268. [Google Scholar] [CrossRef]
- Amjadian, A.; Gharaei, A. An integrated reliable five-level closed-loop supply chain with multi-stage products under quality control and green policies: Generalised outer approximation with exact penalty. Int. J. Syst. Sci. Oper. Logist. 2022, 9, 429–449. [Google Scholar] [CrossRef]
- Gharaei, A.; Amjadian, A.; Amjadian, A.; Shavandi, A.; Hashemi, A.; Taher, M.; Mohamadi, N. An integrated lot-sizing policy for the inventory management of constrained multi-level supply chains: Null-space method. Int. J. Syst. Sci. Oper. Logist. 2022, 1–14. [Google Scholar] [CrossRef]
- Gharaei, A.; Amjadian, A.; Shavandi, A. An integrated reliable four-level supply chain with multi-stage products under shortage and stochastic constraints. Int. J. Syst. Sci. Oper. Logist. 2021, 1–22. [Google Scholar] [CrossRef]
- Baradaran Rezaei, H.; Amjadian, A.; Sebt, M.V.; Askari, R.; Gharaei, A. An ensemble method of the machine learning to prognosticate the gastric cancer. Ann. Oper. Res. 2022, 1–42. [Google Scholar] [CrossRef]
- Levy, H.; Sidi, M. Polling systems: Applications, modeling, and optimization. IEEE Trans. Commun. 1990, 38, 1750–1760. [Google Scholar] [CrossRef]
- Eliazar, I. Gated Polling Systems with Lévy Inflow and Inter-Dependent Switchover Times: A Dynamical-Systems Approach. Queueing Syst. 2005, 49, 49–72. [Google Scholar] [CrossRef]
- Dorsman, J.-P.L.; Borst, S.C.; Boxma, O.J.; Vlasiou, M. Markovian polling systems with an application to wireless random-access networks. Perform. Eval. 2015, 85–86, 33–51. [Google Scholar] [CrossRef][Green Version]
- Abdrabou, A.; Gaouda, A.M. Considerations for packet delivery reliability over polling-based wireless networks in smart grids. Comput. Electr. Eng. 2015, 41, 368–382. [Google Scholar] [CrossRef]
- Gong, Y.; De Koster, R. A polling-based dynamic order picking system for online retailers. IIE Trans. 2008, 40, 1070–1082. [Google Scholar] [CrossRef]
- Gong, Y.; Winands, E.M.M.; de Koster, R.e.B.M. A Real-Time Picking and Sorting System in E-Commerce Distribution Centers. 2010. Available online: http://www.mhi.org/downloads/learning/cicmhe/colloquium/2010/gong.pdf (accessed on 30 October 2022).
- Ran, W.; Liu, S.; Zhang, Z. A Polling-Based Dynamic Order-Picking System considering Priority Orders. Complexity 2020, 2020, 4595316. [Google Scholar] [CrossRef]
- Takine, T.; Takagi, H.; Takahashi, Y.; Hasegawa, T. Analysis of asymmetric single-buffer polling and priority systems without switchover times. Perform. Eval. 1990, 11, 253–264. [Google Scholar] [CrossRef]
- Levy, H. Delay computation and dynamic behavior of non-symmetric polling systems. Perform. Eval. 1989, 10, 35–51. [Google Scholar] [CrossRef]
- Konheim, A.G.; Meister, B. Waiting Lines and Times in a System with Polling. J. ACM 1974, 21, 470–490. [Google Scholar] [CrossRef]
- Gianini, J.; Manfield, D.R. An analysis of symmetric polling systems with two priority classes. Perform. Eval. 1988, 8, 93–115. [Google Scholar] [CrossRef]
- Takagi, H. On the analysis of a symmetric polling system with single-message buffers. Perform. Eval. 1985, 5, 149–157. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).