LARO: Opposition-Based Learning Boosted Artificial Rabbits-Inspired Optimization Algorithm with Lévy Flight

Abstract

The artificial rabbits optimization (ARO) algorithm is a recently developed metaheuristic (MH) method motivated by the survival strategies of rabbits with bilateral symmetry in nature. Although the ARO algorithm shows competitive performance compared with popular MH algorithms, it still has poor convergence accuracy and the problem of getting stuck in local solutions. In order to eliminate the effects of these deficiencies, this paper develops an enhanced variant of ARO, called Lévy flight, and the selective opposition version of the artificial rabbit algorithm (LARO) by combining the Lévy flight and selective opposition strategies. First, a Lévy flight strategy is introduced in the random hiding phase to improve the diversity and dynamics of the population. The diverse populations deepen the global exploration process and thus improve the convergence accuracy of the algorithm. Then, ARO is improved by introducing the selective opposition strategy to enhance the tracking efficiency and prevent ARO from getting stuck in current local solutions. LARO is compared with various algorithms using 23 classical functions, IEEE CEC2017, and IEEE CEC2019 functions. When faced with three different test sets, LARO was able to perform best in 15 (65%), 11 (39%), and 6 (38%) of these functions, respectively. The practicality of LARO is also emphasized by addressing six mechanical optimization problems. The experimental results demonstrate that LARO is a competitive MH algorithm that deals with complicated optimization problems through different performance metrics.

1. Introduction

Most practical applications of problem processing often go to the appropriate solution of an optimization problem by their very nature [1]. Therefore, the optimization problem has been a problem that has received much attention from the beginning, and the exploration of various efficient methods for complicated optimization problems (COPs) has captured the attention of scholars in many fields. Among them, the traditional mathematical optimization method as an optimization strategy requires that the associated objective function needs meet convexity and separability. This property requirement guarantees that it approximates the optimal solution theoretically. However, traditional mathematical strategies are complicated in dealing with highly complex and demanding optimization problems [2]. Newton’s method and the branch-and-bound method are typical deterministic algorithms. Although such algorithms are superior to metaheuristic nature-inspired algorithms in solving some single-parameter tests in terms of functional tests, deterministic algorithms tend to fall into local optimal solutions when faced with more demanding objective functions and constraint functions. Deterministic methods may not be effective when facing multimodal, discrete, non-differentiable, or non-convex problems, or with a comprehensive search space. In addition, deterministic algorithms sometimes require a derivative. Therefore, deterministic algorithms often do not work in solving engineering problems [3].

MH techniques have recently attracted more scholarly attention because of their unique idea of providing a suitable candidate to handle various complex and realistic optimization problems. In general, MH methods have some available advantages over traditional mathematical optimization methods: MH algorithms are an efficient search, low-complexity global optimization method, and different solutions can be searched for in each iteration, making these other solutions highly competitive in obtaining optimal solutions [4].

Depending on the object of construction, experts tend to classify MH algorithms into four parts: evolution-based algorithms, group-intelligence-based algorithms, physical- or chemical-based algorithms, and human-behavior-based algorithms (HBAs) [5]. Evolution-based algorithms imitate the natural evolutionary laws of the biological world; examples of this category include genetic algorithms [6], evolutionary strategies [7], differential evolution [8] which is a variation, crossover, and selection-based garlic algorithm, and evolutionary planning (EP) [9].

Group-intelligence-based (GIB) algorithms are often motivated by the cooperative conduct of various plants and animals in natural environments that live in groups and work together to find food/prey. This GIB category includes aphid–ant mutualism (AAM) [10], bottlenose dolphin optimizer (BDO) [11], beluga whale optimization (BWO) [12], capuchin search algorithm (CapSA) [13], sand cat swarm optimization (SCSO) [14], manta ray foraging optimization algorithm (MRFO) [15], black widow optimization algorithm (BWOA) [16], and chimp optimization algorithm (CHOA) [17].

A physical- or chemical-based algorithm simulates the physical laws and chemical phenomena of biological nature, usually following a generic set of rules to discriminate the influence of interactions between candidate solutions. The type includes the gravitational search algorithm [18], a popular physical- or chemical-based algorithm motivated by Newton’s law of gravity. According to some gravitational force, subjects are attracted to each other according to the law of gravitation. Examples include atom search optimization [19], ion motion algorithm [20], equilibrium optimizer [21], and water cycle algorithm (WCA) [22].

In the last case of the four types, HBAs are exploited by taking advantage of various characteristics associated with humans. The main types of this category include human mental search [23], poor and rich optimization algorithm [24], and teaching learning-based optimization [25].

Dealing with COPs usually consists of two steps: exploration and exploitation. Exploration and exploitation are two opposite strategies. The algorithm searches for a better solution in the global discovery domain in the exploration step. In the development step, the algorithm tends to locate the best solution found so far by exploring the vicinity of the candidate solutions. The trade-off between exploration and exploitation is considered one of the most common problems in current metaheuristic algorithms [26]. This general problem forces the optimization search process to utilize one of the search mechanisms at the expense of the other strategy. In this context, many scholars have proposed algorithms to balance such mechanisms. For example, Zamani proposed a quantum-based avian navigation optimizer algorithm inspired by the navigation behavior of migratory birds [27]. In addition, Nadimi-Shahraki introduced the proposed multi-trial vector approach and archiving mechanism to the differential evolution algorithm, thus proposing a diversity-maintained differential evolution algorithm [28]. ARO was suggested as a newly developed metaheuristic technique with steps inspired by the laws of rabbit survival in the natural world [29].

Regarding the no-free-lunch theory [30], no nature-inspired method can optimally handle every realistic COP [31]. The above facts imply that optimization methods are applied to solve specific COPs but may not be valid for solving other COPs, and experimental results tend to reveal that artificial rabbits optimization has poor convergence accuracy and tends to get stuck in local solutions when handling complicated or high-latitude issues. Therefore, based on the importance of the above two reasons, this paper suggests a hybrid artificial rabbit optimization with Lévy flight and selective opposition strategy, called enhanced ARO algorithm (LARO). LARO is a variant of the ARO algorithm. First, to enhance the worldwide finding capability of ARO, the Lévy flight strategy is fully utilized [32]. The Lévy flight strategy helps LARO to design local solution avoidance and international exploration. Secondly, local exploitation of LARO is achieved by using a selective opposition strategy with improved convergence accuracy [33]. The innovative points and the major contributions of this paper are given below:

(i)

The Lévy flight strategy is introduced in the random hiding phase to improve the diversity and dynamics of the population, which further improves the convergence accuracy of ARO.

(ii)

The introduced selection opposition strategy extends the basic opposition strategy and adaptively re-updates the algorithm to improve the ability to jump out of the local optimum.

(iii)

Numerical experiments are tested on 23 standard test functions, the CEC2017 test set, and the CEC2019 test set.

(iv)

LARO is implemented and tested on six engineering design cases.

The remainder of this study is organized as given below. Section 2 describes the ARO mathematical model. The Lévy flight strategy, selective opposition strategy, and LARO algorithm are introduced in Section 3. Section 4 presents the numerical results and discussion of the proposed algorithm, mainly applied to 23 benchmark functions and the CEC2019 test set. An application of LARO to six real engineering problems is described in Section 5. Section 6 concludes this research work and discusses future prospects.

2. Artificial Rabbits Optimization (ARO)

The ARO algorithm is proposed mainly by referring to two laws of rabbit survival in the natural world: detour foraging and random hiding [29]. Among them, detour foraging is an exploration strategy to prevent detection by natural predators by having rabbits eat the grass near the nest. Random hiding is a strategy in which rabbits move to other burrows, mainly to hide further. The beginning of any search algorithm relies on the initialization process. Considering that the size of the design variable has dimension d, the size of the artificial rabbit colony is N, and the upper and lower limits are ub and lb. Then the initialization is done as follows.

$${\overrightarrow{z}}_{i,k}=r\cdot (u{b}_k-l{b}_k)+l{b}_k,k=1,2,\cdots ,d$$

(1)

where ${\overrightarrow{z}}_{i,k}$ denotes the position of the jth dimension of the ith rabbit and r is a random number that we are given along with it.

The metaheuristic algorithm mainly considers the two processes of exploration and exploitation, while detour foraging mainly considers the exploration phase. Detour foraging is the tendency of each rabbit to stir around the food source and explore another rabbit location randomly chosen in the group to obtain enough food. The updated formula for detour foraging is given below.

$${\overrightarrow{v}}_i(t+1)={\overrightarrow{z}}_j(t)+R\cdot ({\overrightarrow{z}}_i(t)-{\overrightarrow{z}}_j(t))+round(0.5\cdot (0.05+r_1))\cdot n_1,$$

(2)

$$R=l\cdot C$$

(3)

$$l=(e-e^{{(\frac{t-1}{T_{\max }})}^2})\cdot \sin (2\pi r_2)$$

(4)

$$C(k)=\{\begin{array}{c}1\hspace{1em}if\hspace{0.17em}k==G(l)\\ 0\hspace{1em}\hspace{1em}else\hspace{1em}\hspace{1em}\hspace{0.17em}\end{array}k=1,\dots ,d\hspace{0.17em}and\hspace{0.17em}l=1,\dots ,[r_3\cdot d]$$

(5)

$$G=\mathit{randp}\left(d\right)$$

(6)

$$n_1~N(0,1)$$

(7)

where ${\overrightarrow{v}}_{i,k}(t+1)$ denotes the new position of the artificial rabbit, i,j = 1, …, N. ${\overrightarrow{z}}_i$ denotes the position of the ith artificial rabbit, and ${\overrightarrow{z}}_j$ represents artificial rabbits at other random positions. T_max is the maximum number of iterations. [·] symbolizes the ceiling function, which represents rounding to the nearest integer, and randp represents a stochastic arrangement from 1 to d random permutation of integers. r₁, r₂, and r₃ are stochastic numbers from 0 to 1. L represents the running length, which is movement speed when detour foraging. n₁ obeys the standard normal distribution. The perturbation is mainly reflected by the normal distribution random number of n₁. The perturbation of the last term of Equation (2) can help ARO avoid local extremum and perform a global search.

Random hiding is mainly modeled after the exploration stage of the algorithm, where rabbits usually dig several burrows around their nests and randomly choose one to hide in to reduce the probability of being predated. We first define the process by which rabbits randomly generate burrows. The ith rabbit produces the jth burrow by:

$${\overrightarrow{b}}_{i,j}(t)={\overrightarrow{z}}_i(t)+H\cdot g\cdot {\overrightarrow{z}}_i(t),$$

(8)

$$H=\frac{T_{\max }-t+1}{T_{\max }}\cdot n_2$$

(9)

$$n_2~N(0,1)$$

(10)

$$g(k)=\{\begin{array}{c}1\hspace{1em}if\hspace{1em}k==j\\ 0\hspace{1em}\hspace{1em}else\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\end{array}\hspace{1em}k=1,\dots d$$

(11)

where i = 1, …, N and j = 1, …, d, and n₂ follows the standard normal distribution. H denotes the hidden parameter that decreases linearly from 1 to 1/T_max with stochastic perturbations. Figure 1 shows the change in the value of an over the course of 1000 iterations. In the figure, the H value trend generally decreases, thus maintaining a balanced transition from exploration to exploitation throughout the iterations.

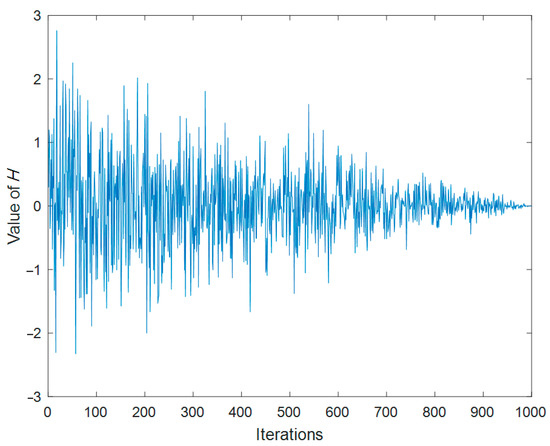
Figure 1. The change of H over the course of 1000 iterations.

The update formula for the random hiding method is shown below.

$${\overrightarrow{v}}_i(t+1)={\overrightarrow{z}}_i(t)+R\cdot (r_4\cdot {\overrightarrow{b}}_{i,r}(t)-{\overrightarrow{z}}_i(t)),$$

(12)

$$g_r(k)=\{\begin{array}{c}1\hspace{1em}if\hspace{1em}k==[r_5\cdot d]\\ 0\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{1em}else\hspace{1em}\hspace{1em}\end{array}\hspace{1em}k=1,\dots ,d$$

(13)

$${\overrightarrow{b}}_{i,r}(t)={\overrightarrow{z}}_i(t)+H\cdot g_r\cdot {\overrightarrow{z}}_i(t)$$

(14)

where ${\overrightarrow{v}}_{i,k}(t+1)$ is the new position of the artificial rabbit,${\overrightarrow{b}}_{i,r}(t)$ represents a randomly selected burrow among the d burrows generated by the rabbit for hiding, and r₄ and r₅ represent the random number given by us in the interval 0 to 1. R is given by Equations (3)–(6).

After the two update strategies are implemented, we renew the position of the ith artificial rabbit by Equation (15).

$${\overrightarrow{z}}_i(t+1)=\{\begin{array}{c}{\overrightarrow{z}}_i(t)\hspace{1em}if\hspace{0.17em}f({\overrightarrow{z}}_i(t))\le f({\overrightarrow{v}}_i(t+1))\\ {\overrightarrow{v}}_i(t+1)\hspace{0.17em}else\hspace{0.17em}f({\overrightarrow{z}}_i(t))>f({\overrightarrow{v}}_i(t+1))\end{array}$$

(15)

This equation represents an adaptive update. The rabbit automatically chooses whether to stay in its current position or move to a new one based on the adaptation value.

For an optimization algorithm, populations prefer to perform the exploration phase in the early stages and an exploitation phase in the middle and late stages. ARO relies on the energy of the rabbits to design a finding scheme: the rabbits’ energy decreases over time, thus simulating the exploration to exploitation transition. The definition of the energy factor in the artificial rabbits algorithm we give is:

$$A(t)=4\cdot (1-\frac{t}{T_{\max }})\cdot \ln \frac{1}{r}$$

(16)

where r is a given random number and r is the random number in (0, 1). Figure 2 shows the change in the value of an over the course of 1000 iterations. Analysis of the information in the figure shows that the trend in the value of A’s is that the overall situation is decreasing, thus maintaining a balanced transition from exploration to exploitation throughout the iterations. Algorithm 1 gives the pseudo-code of the fundamental artificial rabbits optimization. Figure 3 provides the flow chart of ARO.

Algorithm 1: The framework of artificial rabbits optimization

1: The parameters of artificial rabbits optimization including the size of artificial rabbits N, and TMax.

2: Random initializing a set of rabbits zi and calculate fi.

3: Find the best rabbits.

4: While t ≤ TMax do

5:  For i = 1 to N do

6:   Calculate the energy factor A by Equation (16).

7:   If A > 1 then

8:    Random choose a rabbits from all individuals.

9:    Compute the R using Equations (3)–(6).

10:     Perform detour foraging strategy by Equation (2).

11:     Calculate the fitness value of the rabbit’s position fi.

12:     Updated the position of rabbit by Equation (15).

13:    Else

14:     Generate d burrows and select one randomly according to Equation (14).

15:     Perform random hiding strategy by Equation (12).

16:     Calculate the fitness value of the rabbit’s position fi.

17:     Updated the position of rabbit by Equation (15).

18:    End if

19:   End for

20:   Search for the best artificial rabbit.

21:   t = t + 1.

22: End while

23: Output the most suitable artificial rabbit.

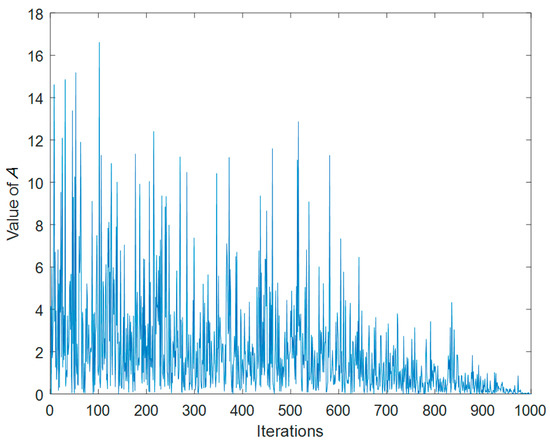
Figure 2. The change of A over the course of 1000 iterations.

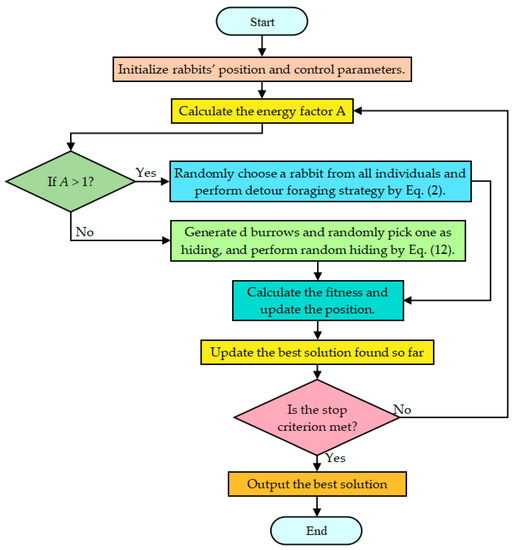
Figure 3. Flow chart of ARO.

3. Hybrid Artificial Rabbits Optimization

Hybrid optimization algorithms are widely used in practical engineering due to targeted improvements to the original algorithm that enhance the different performances of the algorithm. For example, Liu proposed a new hybrid algorithm that combines particle swarm optimization and single layer neural network to achieve the complementary advantages of both and successfully implemented in wavefront shaping [34]. Islam effectively solves the clustered vehicle routing problem by combining particle swarm optimization (PSO) and variable neighborhood search (VNS), fusing the diversity of solutions in PSO and bringing solutions to local optima in VNS [35]. Devarapalli proposed a hybrid modified grey wolf optimization–sine cosine algorithm that effectively solves the power system stabilizer parameter tuning in a multimachine power system [36]. To mitigate the poor accuracy and ease of falling into local solutions of the original ARO algorithm, we propose a hybrid, improved LARO algorithm by introducing a Lévy flight strategy and selective opposition in the ARO algorithm and applying the proposed algorithm to engineering optimization problems. Among them, Lévy flight is employed to boost the algorithm’s accuracy. The selective opposition strategy helps the algorithm jump out of local solutions.

3.1. Lévy Flight Method

The Lévy flight method is often introduced in improved algorithms and proposed algorithms, mainly to provide dynamism to the algorithm updates, where the Lévy flight operator is mentioned primarily for generating a regular random number, which is characterized as a small number in most cases and a large random number in few cases. This arbitrary number generation law can help various update strategies to provide dynamics and jump out of local solutions. Lévy distribution is defined by the following equation. Figure 4 provides Levy’s flight path in two-dimensional space [32].

$$\mathrm{Levy}(t)~u=t^{-1-\gamma },\hspace{1em}0<\gamma \le 2,$$

(17)

where t is the step length, which can be calculated by Equation (18). The formulas for solving the step size of the Lévy flight are given in Equations (18)–(21).

$$t=\frac{u}{|v{|}^{1/\gamma }},$$

(18)

$$u~N(0,{\sigma }_u^2), v~N(0,{\sigma }_v^2)$$

(19)

$${\sigma }_u={\left(\frac{\Gamma (1+\beta )\cdot \sin (\pi \cdot \beta /2)}{\Gamma ((1+\beta /2)\cdot \beta \cdot 2^{(\beta -1)/2})}\right)}^{1/\beta },$$

(20)

$${\sigma }_v=1,$$

(21)

where σ_u and σ_v are defined as given in Equations (20) and (21). Both u and v obey Gaussian distributions with mean 0 and variance σ_u² and σ_v², as shown in Equation (19). Γ denotes a standard Gamma function, while β denotes a correlation parameter, which is usually set to 1.5.

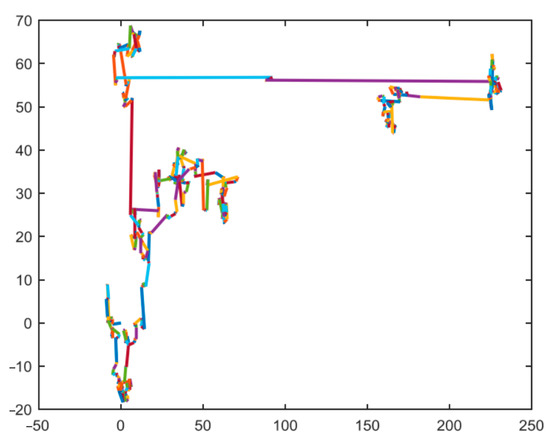
Figure 4. Lévy flight path of 500 times movements in a two-dimensional space.

In the random hiding phase, we replace the r₄ random numbers with the random numbers generated by the Lévy flight strategy. Since the random hiding stage is an exploitation stage, we introduce Lévy flight in this strategy to avoid ARO from falling into local candidate solutions in the exploitation phase. Additionally, it helps the algorithm improve the convergence accuracy and the flexibility of the random hiding stage. The following equation provides the random hidden phase based on the Lévy flight, where α is a parameter fixed to 0.1.

$${\overrightarrow{v}}_i(t+1)={\overrightarrow{z}}_i(t)+R\cdot (\alpha \cdot levy(\beta )\cdot {\overrightarrow{b}}_{i,r}(t)-{\overrightarrow{z}}_i(t)),i=1,\dots ,N$$

(22)

3.2. Selective Opposition (SO) Strategy

SO is a modified idea of opposition-based learning (OBL) [33]. The idea of SO is to modify the size of the rabbits far from the optimal solution by using new opposition-based learning to bring it closer to the rabbit in the optimal position. In addition, the selective opposition strategy tends to be affected by a linearly decreasing threshold. When the rabbits deploy SO, selective opposition assists the rabbits in achieving a better situation in the development phase by changing the proximity dimension of different rabbits [37]. The updates are as follows.

First, we define a threshold value. The threshold value will be decreased until the limit case is reached. As shown in the following equation, SO checks the distance of each candidate rabbit location from the current rabbit dimension to the best rabbit location for all candidate rabbit locations.

$$d{d}_i=\left|z_{ibest,j}-z_{i,j}\right|$$

(23)

where dd_j is the difference distance of all dimensions of each rabbit. When dd_j is greater than the Threshold (TS) value we define, the far and near rabbit positions are calculated. Then, all difference distances for all rabbit positions are listed.

$$src=1-\frac{6\cdot {\displaystyle {\sum }_{j=1}{(d{d}_j)}^2}}{d{d}_j\cdot (d{d}_j^2-1)}$$

(24)

The src is proposed mainly to measure the correlation between the current rabbit and the optimal rabbit position. Assuming that src < 0 and the far dimension (d_f) is larger than the close dimensions (d_c), the rabbit’s position will be updated by Equation (25).

$$Z_{df}^{\prime }=l{b}_{df}+u{b}_{df}-Z_{df}$$

(25)

Algorithm 2 gives the pseudo-code for selective opposition (SO).

Algorithm 2: Selective Opposition (SO)

1: The parameters of selective opposition including: initial generation (t), rabbit size (N), the maximum generation (TMax), dimension (d), dc = [], and df = [].

2: TS = 2 − [t·(2/TMax)].

3: For i = 1 to N do

4:  If Zi ≠ Zibest then

5:   For j = 1 to d do

6:    ddj = |zibest,j-zi,j|{ddj = the discrepancy distance of the jth dimension}

7:    If ddj < TS then

8:     Determine the far dimensions (df).

9:     Calculate far distance dimensions (df).

10:     Else

11:      Determine the close dimensions (dc).

12:      Calculate close distance dimensions (dc).

13:     End if

14:    End for

15:    Summing over all ddj.

16:    $src=1-\frac{6\cdot {\displaystyle {\sum }_{j=1}{(d{d}_j)}^2}}{d{d}_j\cdot (d{d}_j^2-1)}$.

17:    If src ≤ 0 and size(df) > size(dc) then

18:     Perform Z′df = LBdf + UBdf − Zdf.

19:    End if

20:   End if

21: End for

3.3. Detailed Implementation of LARO

Two modifications, namely Lévy flight and selective opposition, are included in ARO. These modifications suitably help the ARO algorithm to increase the convergence and population variety while obtaining more qualitative candidate solutions. The detailed procedures of LARO are shown below.

Step1: Suitable parameters for LARO are supplied: the size of artificial rabbit N, the dimensionality of the variables d, the upper and lower bounds ub and lb of the problem variables, and all iterations T_Max;

Step2: Randomly select a series of rabbit locations and calculate their fitness values. Find the rabbit with the best position;

Step3: Calculate the value of the energy factor A by Equation (16). If A > 1, select an arbitrary rabbit from all groups of rabbits;

Step4: Calculate the value of R by using Equations (3)–(6). Perform detour foraging strategy by means of Equation (2). Then calculate the adaptation value of the updated rabbit position and update the rabbit position by means of Equation (15);

Step5: If A ≤ 1, randomly generate burrows and randomly select one according to Equation (14). The new position of the rabbit is updated by a random hiding strategy based on the improved Lévy flight strategy of Equation (22). The corresponding fitness is calculated and then the rabbit’s position is updated by Equation (15);

Step6: The distance of each candidate rabbit position from the current rabbit dimension to the best rabbit position is calculated by Equation (23);

Step7: If dd_j > Threshold, determine the near size d_f and count the number of d_f. If dd_j ≤ Threshold, determine the far dimension d_c and count the number of d_c. Then calculate src from the calculated dd_j by Equation (24);

Step8: If src <= 0 and d_f > d_c, execute Equation (25) and re-update the rabbit’s position;

Step9: If the iterations exceed the maximum case, the optimal result is exported.

To better introduce the proposed LARO algorithm in this study, the pseudo-code of LARO is offered in Algorithm 3. Among them, line 15 is the Lévy flight strategy improved with the random hiding strategy. Lines 20–40 are the selective opposition strategy. Figure 5 illustrates the flowchart of the LARO algorithm.

Algorithm 3: The algorithm composition of LARO

1: The parameters of artificial rabbits optimization: the size of artificial rabbits N, TMax, the sensitive parameter α, β, dc = [], and df = [].

2: Random initializing a set of rabbits zi and calculate fi.

3: Find the best rabbits.

4: While t ≤ TMax do

5:  For i =1 to N do

6:   Compute the energy factor A using Equation (16).

7:   If A > 1 then

8:    Random choose a rabbits from all individuals.

9:    Compute the R using Equations (3)–(6).

10:     Perform detour foraging strategy by Equation (2).

11:     Calculate the fitness value of the rabbit’s position fi.

12:     Updated the position of rabbit by Equation (15).

13:    Else

14:     Generate d burrows and select one randomly according to Equation (14).

15:     Perform random hiding strategy by Equation (22).

16:     Calculate the fitness value of the rabbit’s position fi.

17:     Updated the position of rabbit by Equation (15).

18:    End if

19:   End for

20:   TS = 2 − [t·(2/TMax)].

21:   For i = 1 to N do

22:    If Zi ≠ Zibest then

23:     For j = 1 to d do

24:      ddj = |zibest,j-zi,j|{ddj = the discrepancy distance of the jth dimension}

25:      If ddj < TS then

26:       Determine the far dimensions (df).

27:       Calculate far distance dimensions (df).

28:      Else

29:       Determine the close dimensions (dc).

30:       Calculate close distance dimensions (dc).

31:      End if

32:     End for

33:     Summing over all ddj.

34:     $src=1-\frac{6\cdot {\displaystyle {\sum }_{j=1}{(d{d}_j)}^2}}{d{d}_j\cdot (d{d}_j^2-1)}$.

35:     If src ≤ 0 and size(df) > size(dc) then

36:      Perform Z′df = LBdf + UBdf − Zdf.

37:     End if

38:    End if

39:   End for

40:   Updated the position of rabbit by Equation (15).

41:   Search for the best rabbits bestj.

42:   t = t + 1.

43: End while

44: Output the most suitable artificial rabbit.

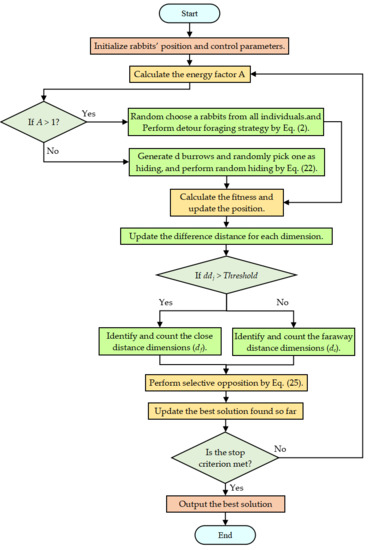
Figure 5. Flowchart for the LARO algorithm.

3.4. In-Depth Discussion of LARO Complexity

The estimation of LARO complexity is mainly done by adding the selective opposition part to the ARO base algorithm. At the same time, the Lévy strategy only improves how ARO is updated without increasing the complexity. Calculating the complexity is an effective method when assessing the complexity of solving real problems. The complexity is associated with the size of artificial rabbits N, d, and T_Max. The total complexity of the artificial rabbits algorithm is as follows [29].

$$\begin{array}{cc}\hfill O(ARO)& =O(1+N+T_{Max}N+0.5T_{Max}Nd+0.5T_{Max}Nd)\hfill \\ & =O(T_{Max}Nd+T_{Max}N+N)\hfill \end{array}$$

(26)

The selective opposition strategy focuses on the consideration of all dimensions of all rabbit locations. Therefore, the complication of the LARO algorithm is:

$$O(LARO)=O(2T_{Max}Nd+T_{Max}N+N)$$

(27)

4. Numerical Experiments

To numerically experimentally validate the capabilities of the LARO algorithm, two basic suites were selected: 23 benchmark test functions [26] and ten benchmark functions from the standard CEC2019 test suite [26]. We selected some optimized metaheuristic algorithms to compare with our proposed LARO, including arithmetic optimization algorithm (AOA) [38], grey wolf optimization (GWO) [39], coot optimization algorithm (COOT) [40], golden jackal optimization (GJO) [41], weighted mean of vectors (INFO) [42], moth–flame optimization (MFO) [43], multi-verse optimization (MVO) [44], sine cosine optimization algorithm (SCA) [45], salp swarm optimization algorithm (SSA) [46], and whale optimization algorithm (WOA) [47]. The LARO algorithm was compared with all the different search algorithms subjected to Wilcoxon rank sum and Friedman’s mean rank test. The full algorithm was run 20 times separately. In addition, to better demonstrate the experiments, we tested the best, worst, mean, and standard deviation (STD) values for this period. The main parameters of the other relevant algorithms we provide are in Table 1.

Table 1. Suitable parameters for different algorithms.

Methods	Parameters	Value Situation
AOA [38]	µ	0.499
	a	a5
GWO [39]	Convergence parameter (a)	Linear decrease from 2 to 0
WOA [47]	A	Drop from 2 to 0
	b	2
SSA [46]	Leader position update probability	c3 = 0.5
INFO [42]	c	2
	d	4
MVO [43]	Wormhole Existence Probability WEPMax	1
	Wormhole Existence Probability WEPMin	0.2
SCA [44]	A	2

4.1. Experimental Analysis of Exploration and Exploitation

Differences between candidate solutions in different dimensions and the overall direction tend to influence whether the group tends to diverge or aggregate. When growing to separate, the differences among all candidate individuals in all dimensions will come to the fore. This situation means that all candidate individuals will explore the domain in a particular manner. This approach will allow the optimization method to analyze the candidate solution space more extensively through the transient features. Alternatively, when a trend toward aggregation is generated, the candidate solutions explore the room based on a broad synergistic situation, reducing the variability of all candidate individuals and exploiting the exploration region of candidate solutions in a detailed manner. Maintaining the right synergy between this divergent discovery pattern and the aggregated development pattern is necessary to ensure optimization capability.

For the experimental part, we draw on the dimensional diversity metric suggested by Hussain et al. in [48] and calculate corresponding exploration and exploitation ratios. We selected the CEC2019 test set and provided the exploration and exploitation analysis graphs for some of the CEC2019 test functions in Figure 6.

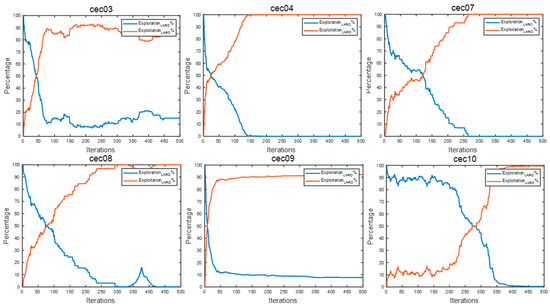
Figure 6. The exploration and exploitation diagrams of LARO.

From the figure, we can find that LARO starts from exploration in all the test functions and then gradually transitions to the exploitation stage. In the test functions of cec03 and cec09, we find that LARO can still maintain an efficient investigation rate in the middle and late iterations, and in the face of cec04, cec07, and cec08, LARO will quickly shift to an efficient discovery rate in the mid-term, ending the iteration with an efficient exploration situation. This discovery process shows that the more efficient exploration rate early in LARO guarantees a reasonable full-range finding capability to prevent getting stuck in current local solutions. In contrast, the middle step is smooth over the low, and the more efficient development rate in the later period guarantees that it can be exploited with higher accuracy after high exploration.

4.2. Comparative Analysis of Populations and Maximum Iterations

The population size and the maximum iterations affect the performance of the population-based metaheuristic algorithm. Therefore, in this section, we perform a sensitivity analysis of LARO involving the size of the initial population as well as the maximum iterations. This study considers the two most commonly used combinations of population and maximum iterations: (1) the size of artificial rabbit colonies is 50, and T_max = 1000, (2) the size of artificial rabbit colonies is 100, and T_max = 500, and LARO for the experiments conducted in case (1) is defined as LARO1, and LARO in case (2) is LARO2. The performance and running time of LARO1 and LARO2 are compared in the experiments with 23 test functions.

Table 2 provides a comparison of LARO with two different parameters in 23 benchmark functions. From the numerical results, it can be found that both parameters of ARO used almost similar running times. However, the convergence accuracy of LARO1 is better than that of LARO2, which indicates that LARO, with the case 1 parameter, can provide better convergence accuracy with the same guaranteed running cost. Therefore, the results show that the performance of LARO is affected by the population size and the number of iterations. The best performance was returned when the population size was set to 50, and the maximum number of iterations was 1000.

Table 2. Comparison of LARO with two different parameters in 23 benchmark functions.

Functions	Algorithms	Mean	STD	Time	Functions	Algorithms	Mean	STD	Time
F01	LARO1	2.17E-181	0	7.22299	F13	LARO1	0.00110	0.00338	22.00742
	LARO2	4.78E-91	1.39E-90	7.38622		LARO2	0.00059	0.00247	19.16593
F02	LARO1	1.45E-96	6.15E-96	6.97114	F14	LARO1	0.99800	0	31.32199
	LARO2	1.90E-49	3.98E-49	6.97564		LARO2	0.99800	0	29.23997
F03	LARO1	5.18E-146	1.97E-145	16.08589	F15	LARO1	0.00031	2.97E-16	5.84512
	LARO2	5.48E-73	2.11E-72	14.75086		LARO2	0.00031	2.37E-08	6.53547
F04	LARO1	8.57E-75	3.61E-74	7.35237	F16	LARO1	−1.03163	2.16E-16	5.51881
	LARO2	1.10E-37	2.49E-37	6.88073		LARO2	−1.03163	2.10E-16	6.22799
F05	LARO1	0.00470	0.00436	7.95983	F17	LARO1	0.39789	0	5.33003
	LARO2	0.03234	0.03371	7.86360		LARO2	0.39789	0	6.17085
F06	LARO1	5.06E-06	6.23E-06	6.85314	F18	LARO1	3	5.94E-16	5.36706
	LARO2	0.00014	0.00012	6.81894		LARO2	3	6.28E-16	5.99102
F07	LARO1	0.00021	0.00014	10.94454	F19	LARO1	−3.86278	2.28E-15	6.59347
	LARO2	0.00032	0.00021	10.75831		LARO2	−3.86278	2.28E-15	6.07269
F08	LARO1	−1.15E+04	334.44374	8.30804	F20	LARO1	−3.29227	0.05282	6.68436
	LARO2	−1.15E+04	299.32023	8.43271		LARO2	−3.32200	4.44E-16	7.05183
F09	LARO1	0	0	7.25003	F21	LARO1	−10.15320	3.36E-15	11.62110
	LARO2	0	0	7.61304		LARO2	−10.15320	2.79E-15	7.59196
F10	LARO1	8.88E-16	0	8.25929	F22	LARO1	−10.06901	1.49339	9.18435
	LARO2	8.88E-16	0	7.80431		LARO2	−10.40294	3.58E-15	8.20396
F11	LARO1	0	0	8.49955	F23	LARO1	−10.53636	0.00024	8.69545
	LARO2	0	0	8.82418		LARO2	−10.53641	1.58E-15	9.09290
F12	LARO1	2.43E-07	2.89E-07	20.03895
	LARO2	6.01E-06	2.89E-06	20.26232

4.3. Analysis of Lévy Flight the Jump Parameter α

According to the mechanism of the Lévy flight strategy, we replace the r₄ random numbers with the random numbers generated by the Lévy flight strategy. Thus, ARO is prevented from falling into local candidate solutions in the utilization phase. Additionally, the jump parameter α will affect the change of the updated position. In general, a larger jump parameter α, which increases the step size of the Lévy flight strategy, can ensure that the algorithm jumps out of the local solution, but it may also cause the optimal solution information not to be preserved. If the value is too small, it will affect the sensitivity of the Lévy flight strategy and, thus, the accuracy of the algorithm. Therefore, the jump parameter α has a great impact on the performance of LARO.

This section discusses the impact of the jump parameter α on the performance of the algorithm, and 10 test functions of CEC2019 are used to explore the impact of the jump parameter. The relevant jump parameters take four different values of 0.1, 0.01, 0.5, and 0.5, and three value intervals [0.01, 0.05], [0.05, 0.1], and [0.1, 0.5], respectively. The numerical intervals indicate the random number within each provided interval. The mean values of the solutions obtained by LARO for the CEC2019 test function over 20 independent trials are provided in Table 3. For a clearer view of the effect of the jump parameter α on LARO performance, Figure 7 provides the convergence curves for the ten test functions.

Table 3. Performance analysis of jump parameter α in CEC2019.

Function	Index	Algorithms
		α = 0.1	α = 0.01	α = 0.05	α = 0.5	α = [0.01, 0.05]	α = [0.05, 0.1]	α = [0.1, 0.5]
cec01	Mean	1	1	1	1	1	1	1
	Rank	1	1	1	1	1	1	1
cec02	Mean	4.2462	4.2195	4.2553	4.2226	4.1176	4.2233	4.2304
	Rank	6	2	7	3	1	4	5
cec03	Mean	1.7488	1.5887	1.5539	1.5272	1.6122	1.7864	1.6667
	Rank	6	3	2	1	4	7	5
cec04	Mean	12.8513	11.0993	12.6871	16.1851	13.7460	13.8487	13.8736
	Rank	3	1	2	7	4	5	6
cec05	Mean	1.0747	1.1089	1.1029	1.0880	1.0876	1.0790	1.0776
	Rank	1	7	6	5	4	3	2
cec06	Mean	1.5055	1.5995	1.6011	1.4881	1.4857	1.4156	1.4059
	Rank	5	6	7	4	3	2	1
cec07	Mean	386.6686	437.5734	464.3752	450.1384	467.1603	489.9973	465.0378
	Rank	1	2	4	3	6	7	5
cec08	Mean	3.0415	3.3443	3.0979	3.2720	3.2620	3.4022	3.5178
	Rank	1	5	2	4	3	6	7
cec09	Mean	1.1386	1.1156	1.1255	1.1151	1.1143	1.1186	1.1130
	Rank	7	4	6	3	2	5	1
cec10	Mean	18.0553	20.0059	19.9964	20.0029	20.0859	21.0005	20.0014
	Rank	1	5	2	4	6	7	3
Mean rank		3.2	3.6	3.9	3.5	3.4	4.7	3.6
Final ranking		1	4	6	3	2	7	4

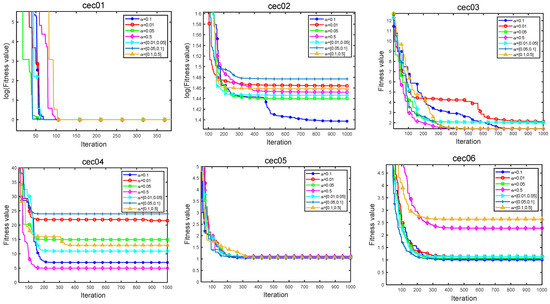
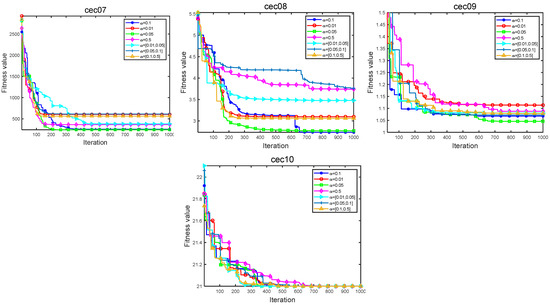
Figure 7. Iteration plot of seven parameters in CEC2019.

By analyzing Table 3, it can be observed that the average rank is the smallest when the jump parameter α = 0.1 at 3.2. and the best average values are obtained for five test functions (cec01, cec05, cec07, cec08, cec10). The value of the jump parameter α is a more in-between suitable value, indicating that the value balances the information of retaining the optimal solution and jumping out of the local solution. Figure 7 provides an iterative plot of the seven jump parameters. From the graph, it can be found that the LARO algorithm has a faster convergence rate, as well as a higher iteration accuracy for the jump parameter α = 0.1. Therefore, LARO can show the best performance when the jump parameter α is taken at 0.1.

4.4. Experiments on the 23 Classical Functions

To evaluate the strength of LARO in traversing the solution space, finding the optimal candidate solution, and getting rid of local solutions, we used 23 benchmark functions, where the unimodal test benchmarks (F1–F7) were used to examine the ability of LARO to develop accuracy. The multimodal benchmark set (F8–F13) was used to test the capability of LCAHA for spatial exploration. The fixed-dimensional multimodal test benchmarks (F14–F23) are mainly used to verify LARO’s excellent ability to handle low-dimensional spatial investigation. The dimensions of F01–F11 are 30, while the dimensions of F14–F23 are all different because they are fixed-dimensional multimodal test functions (the dimensions of F14–F23 functions are 2, 4, 2, 2, 2, 3, 6, 4, 4, 4, 4).

Table 4 shows LARO’s experimental and statistical results, the original ARO, and ten other search algorithms. Five relevant evaluation metrics (best, worst, average, standard, and ranking) were selected for this experiment. Additionally, we used Friedman ranking test results for all algorithms based on the mean value. In addition, the statistical presentation of the Wilcoxon test for LARO and other selected MH algorithms is shown in Table 4. When calculating the significance level, we let the default value of the significance level be set to 0.05. In addition, “+” denotes that a particular MH algorithm converges better than LARO. “−” denotes the opposite effect. “=” suggests that the impact of convergence in a given test problem is the same as the convergence of a particular MH algorithm.

Table 4. Statistical outcomes of the different MH methods on the 23 test functions.

Function	Index	Algorithms
		ARO	AOA	GWO	COOT	GJO	INFO	MFO	MVO	SCA	SSA	WOA	LARO
F1	Best	1.21E-138	9.28E-10	5.04E-73	1.68E-93	7.76E-132	9.34E-56	1.60E-06	0.0009	2.20E-07	5.37E-09	1.09E-186	6.69E-199
	Worst	2.30E-127	9.90E-07	2.39E-69	2.23E-18	9.04E-127	4.43E-55	1.00E+04	0.0049	0.0073	1.10E-08	6.38E-173	2.12E-177
	Mean	1.74E-128	4.73E-07	3.70E-70	1.12E-19	9.55E-128	3.11E-55	1.00E+03	0.0023	0.0010	8.60E-09	4.09E-174	1.08E-178
	STD	5.61E-128	2.34E-07	7.22E-70	4.99E-19	2.29E-127	9.13E-56	3.08E+03	0.0009	0.0019	1.60E-09	0	0
	Rank	3	9	5	7	4	6	12	11	10	8	2	1
F2	Best	1.06E-74	2.49E-13	4.85E-42	1.57E-47	1.47E-143	7.02E-29	2.94E-20	0.0054	2.91E-24	4.52E-06	7.23E-118	4.88E-105
	Worst	2.80E-67	0.0006	1.55E-40	7.37E-18	8.09E-137	2.40E-28	1.43E-18	0.0216	3.94E-20	8.69E-06	4.13E-105	1.84E-95
	Mean	2.19E-68	0.0001	3.81E-41	3.68E-19	6.36E-138	1.58E-28	2.79E-19	0.0130	3.20E-21	6.09E-06	2.10E-106	9.20E-97
	STD	6.66E-68	0.0002	4.24E-41	1.65E-18	1.82E-137	3.66E-29	3.93E-19	0.0039	9.22E-21	1.28E-06	9.22E-106	4.11E-96
	Rank	4	11	5	9	1	6	8	12	7	10	2	3
F3	Best	2.19E-115	7.27E-08	9.95E-24	1.69E-108	5.66E-150	1.41E-55	7.16E-12	0.0024	2.53E-20	4.86E-10	1.02E+03	9.25E-160
	Worst	4.64E-98	0.0005	1.70E-18	3.75E-17	3.30E-136	3.43E-54	7.83E-08	0.0274	4.50E-09	2.26E-09	2.52E+04	8.97E-145
	Mean	2.99E-99	0.0001	1.35E-19	1.87E-18	2.21E-137	7.44E-55	6.93E-09	0.0152	2.35E-10	1.31E-09	9.94E+03	6.05E-146
	STD	1.06E-98	0.0001	4.11E-19	8.38E-18	7.66E-137	7.17E-55	1.99E-08	0.0085	1.00E-09	5.18E-10	7.06E+03	2.09E-145
	Rank	3	10	5	6	2	4	9	11	7	8	12	1
F4	Best	2.49E-59	0.0012	8.10E-19	1.00E-50	3.15E-102	3.80E-29	2.24E-10	0.0149	8.01E-14	9.04E-06	2.09E-05	6.58E-83
	Worst	1.51E-51	0.0386	8.67E-17	1.10E-18	2.48E-94	9.71E-29	4.81E-06	0.0558	3.26E-09	1.97E-05	83.8975	1.08E-74
	Mean	8.18E-53	0.0082	9.98E-18	5.69E-20	1.34E-95	7.06E-29	3.41E-07	0.0289	5.72E-10	1.49E-05	26.7587	5.69E-76
	STD	3.36E-52	0.0095	1.86E-17	2.46E-19	5.54E-95	1.69E-29	1.09E-06	0.0109	1.01E-09	2.60E-06	27.7544	2.40E-75
	Rank	3	10	6	5	1	4	8	11	7	9	12	2
F5	Best	0.0006	26.3419	25.1729	12.7342	5.9635	1.00E-15	0.5337	0.3466	6.3912	1.0423	25.9605	0.0002
	Worst	0.0090	27.8627	27.9110	164.4579	8.7006	3.82E-08	9.00E+04	420.5066	8.0566	326.6321	26.9912	0.0259
	Mean	0.0029	26.9276	26.6522	33.4068	6.8759	4.47E-09	4.68E+03	43.9598	7.0330	48.0257	26.5465	0.0057
	STD	0.0023	0.3875	0.6903	31.0189	0.7159	1.08E-08	2.01E+04	100.2646	0.3919	81.8641	0.3124	0.0069
	Rank	2	8	7	9	4	1	12	10	5	11	6	3
F6	Best	2.65E-07	0.3379	8.71E-06	3.83E-05	1.56E-06	0	0	0.0011	0.1184	2.99E-10	0.0017	8.78E-07
	Worst	2.57E-06	0.8442	0.9951	0.0009	0.4997	4.93E-32	4.50E-31	0.0039	0.5995	9.36E-10	0.0073	1.50E-05
	Mean	1.09E-06	0.5939	0.2872	0.0003	0.1376	6.16E-33	6.39E-32	0.0023	0.2553	6.36E-10	0.0041	4.77E-06
	STD	6.58E-07	0.1378	0.2839	0.0002	0.1512	1.16E-32	1.13E-31	0.0008	0.1261	1.80E-10	0.0015	4.17E-06
	Rank	4	12	11	6	9	1	2	7	10	3	8	5
F7	Best	2.92E-05	3.42E-08	0.0001	0.0001	6.24E-06	7.13E-05	0.0005	0.0002	0.0001	0.0005	2.56E-05	1.02E-05
	Worst	0.0006	6.65E-05	0.0013	0.0090	0.0002	0.0013	0.0066	0.0035	0.0024	0.0118	0.0025	0.0004
	Mean	0.0002	2.38E-05	0.0005	0.0021	6.19E-05	0.0003	0.0026	0.0012	0.0006	0.0045	0.0006	0.0002
	STD	0.0002	2.11E-05	0.0003	0.0023	5.14E-05	0.0003	0.0014	0.0008	0.0006	0.0031	0.0006	0.0001
	Rank	4	1	6	10	2	5	11	9	8	12	7	3
F8	Best	−1.18E+04	−6.15E+03	−7.74E+03	−8.96E+03	−2.77E+03	−4.19E+03	−4.19E+03	−3.83E+03	−2.64E+03	−3.30E+03	−1.26E+04	−1.21E+04
	Worst	−1.02E+04	−4.95E+03	−4.93E+03	−7.04E+03	−1.84E+03	−3.36E+03	−2.52E+03	−2.43E+03	−2.05E+03	−2.23E+03	−8.37E+03	−1.08E+04
	Mean	−1.09E+04	−5.49E+03	−6.35E+03	−7.90E+03	−2.32E+03	−3.63E+03	−3.38E+03	−3.16E+03	−2.30E+03	−2.80E+03	−1.20E+04	−1.16E+04
	STD	4.52E+02	3.84E+02	7.00E+02	5.59E+02	2.58E+02	2.08E+02	3.78E+02	3.27E+02	1.55E+02	2.95E+02	1.18E+03	3.94E+02
	Rank	3	6	5	4	11	7	8	9	12	10	1	2
F9	Best	0	0	0	0	0	0	3.9798	3.9804	0	6.9647	0	0
	Worst	0	4.39E-07	11.5726	1.71E-13	0	0	44.8440	22.8853	0.3257	41.7882	5.68E-14	0
	Mean	0	1.10E-07	1.0975	8.53E-15	0	0	17.9128	12.0401	0.0163	15.0239	2.84E-15	0
	STD	0	1.55E-07	2.9474	3.81E-14	0	0	10.3395	5.8096	0.0728	7.9590	1.27E-14	0
	Rank	1	7	9	6	1	1	12	10	8	11	5	1
F10	Best	8.88E-16	7.48E-08	7.99E-15	8.88E-16	8.88E-16	8.88E-16	4.44E-15	0.0088	8.88E-16	5.88E-06	8.88E-16	8.88E-16
	Worst	8.88E-16	0.0003	1.87E-14	1.54E-11	4.44E-15	8.88E-16	7.99E-15	0.0228	7.99E-15	2.0133	7.99E-15	8.88E-16
	Mean	8.88E-16	0.0001	1.40E-14	8.04E-13	3.91E-15	8.88E-16	4.62E-15	0.0178	4.80E-15	0.5489	4.09E-15	8.88E-16
	STD	0	8.13E-05	2.33E-15	3.43E-12	1.30E-15	0	7.94E-16	0.0035	1.59E-15	0.8664	2.28E-15	0
	Rank	1	10	8	9	4	1	6	11	7	12	5	1
F11	Best	0	1.15E-06	0	0	0	0	0.0271	0.1110	0	0.0836	0	0
	Worst	0	0.0123	0.0404	2.22E-16	0	0	0.3173	0.5909	0.7448	0.7018	0.0372	0
	Mean	0	0.0006	0.0027	1.11E-17	0	0	0.1347	0.3030	0.0381	0.2650	0.0034	0
	STD	0	0.0028	0.0094	4.97E-17	0	0	0.0818	0.1209	0.1664	0.1495	0.0104	0
	Rank	1	6	7	5	1	1	10	12	9	11	8	1
F12	Best	1.11E-08	0.4017	0.0054	7.28E-07	8.14E-07	4.71E-32	4.71E-32	2.93E-05	0.0300	3.35E-12	0.0001	3.24E-08
	Worst	2.49E-07	0.5290	0.0581	0.1037	0.0593	4.93E-32	0.9329	0.3122	0.1082	0.3712	0.0201	1.16E-06
	Mean	6.05E-08	0.4541	0.0253	0.0052	0.0298	4.79E-32	0.1088	0.0313	0.0655	0.0688	0.0016	3.27E-07
	STD	5.65E-08	0.0331	0.0158	0.0232	0.0218	8.02E-34	0.2527	0.0960	0.0205	0.1336	0.0044	3.40E-07
	Rank	2	12	6	5	7	1	11	8	9	10	4	3
F13	Best	7.63E-08	2.8252	1.91E-05	7.71E-05	3.30E-06	1.35E-32	1.35E-32	0.0001	0.0798	1.39E-11	0.0027	1.95E-07
	Worst	0.0439	2.9661	0.4064	0.0364	0.3992	0.0439	0.0110	0.0118	0.3257	0.0110	0.1943	7.23E-06
	Mean	0.0039	2.9528	0.2462	0.0091	0.1081	0.0033	0.0016	0.0015	0.2240	0.0016	0.0522	1.81E-06
	STD	0.0102	0.0408	0.1180	0.0092	0.1023	0.0101	0.0040	0.0034	0.0648	0.0040	0.0605	1.90E-06
	Rank	6	12	11	7	9	5	3	2	10	4	8	1
F14	Best	0.9980	0.9980	0.9980	0.9980	0.9980	0.9980	0.9980	0.9980	0.9980	0.9980	0.9980	0.9980
	Worst	0.9980	12.6705	12.6705	0.9980	12.6705	2.9821	1.9920	0.9980	2.9821	0.9980	10.7632	0.9980
	Mean	0.9980	8.4157	5.2933	0.9980	4.9158	1.1469	1.0974	0.9980	1.4941	0.9980	2.6117	0.9980
	STD	0	4.4965	5.0354	2.88E-16	4.2395	0.4857	0.3060	5.24E-12	0.8814	1.02E-16	3.5461	0
	Rank	1	12	11	1	10	7	6	5	8	1	9	1
F15	Best	0.0003	0.0003	0.0003	0.0003	0.0003	0.0003	0.0006	0.0003	0.0004	0.0003	0.0003	0.0003
	Worst	0.0003	0.0207	0.0204	0.0012	0.0012	0.0012	0.0023	0.0204	0.0015	0.0012	0.0014	0.0003
	Mean	0.0003	0.0031	0.0024	0.0004	0.0004	0.0004	0.0010	0.0066	0.0009	0.0007	0.0006	0.0003
	STD	2.47E-19	0.0051	0.0062	0.0002	0.0003	0.0002	0.0004	0.0093	0.0004	0.0003	0.0003	1.29E-16
	Rank	1	11	10	4	5	3	9	12	8	7	6	2
F16	Best	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316
	Worst	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316
	Mean	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316	−1.0316
	STD	2.22E-16	7.42E-12	3.08E-09	4.04E-14	1.70E-08	2.28E-16	2.28E-16	6.22E-08	1.79E-05	6.02E-15	1.97E-11	2.28E-16
	Rank	1	8	9	5	10	1	1	11	12	5	7	1
F17	Best	0.3979	0.4960	0.3979	0.3979	0.3979	0.3979	0.3979	0.3979	0.3979	0.3979	0.3979	0.3979
	Worst	0.3979	2.5958	0.3979	0.3979	0.3981	0.3979	0.3979	0.3979	0.3994	0.3979	0.3979	0.3979
	Mean	0.3979	1.3108	0.3979	0.3979	0.3979	0.3979	0.3979	0.3979	0.3984	0.3979	0.3979	0.3979
	STD	0	0.6557	4.30E-07	7.30E-08	3.92E-05	0	0	7.31E-08	0.0004	4.68E-15	8.28E-08	0
	Rank	1	12	9	6	10	1	1	8	11	5	7	1
F18	Best	3	3	3.0000	3	3.0000	3	3	3.0000	3.0000	3	3.0000	3
	Worst	3	30	3.0000	3	3.0000	3	3	3.0000	3.0000	3	3.0000	3
	Mean	3	11.1	3.0000	3	3.0000	3	3	3.0000	3.0000	3	3.0000	3
	STD	6.28E-16	12.6944	4.15E-06	2.78E-14	4.45E-07	2.88E-16	1.45E-15	3.93E-07	9.62E-06	4.37E-14	4.46E-06	9.56E-16
	Rank	1	12	10	5	7	1	1	8	11	6	9	1
F19	Best	−3.8628	−3.8628	−3.8628	−3.8628	−3.8628	−3.8628	−3.8628	−3.8628	−3.8623	−3.8628	−3.8628	−3.8628
	Worst	−3.8628	−3.8628	−3.8549	−3.8628	−3.8549	−3.8628	−3.8628	−3.8628	−3.8535	−3.8628	−3.8549	−3.8628
	Mean	−3.8628	−3.8628	−3.8615	−3.8628	−3.8592	−3.8628	−3.8628	−3.8628	−3.8569	−3.8628	−3.8614	−3.8628
	STD	2.28E-15	6.30E-07	0.0028	2.03E-15	0.0040	2.28E-15	2.28E-15	1.34E-07	0.0034	1.51E-14	0.0028	2.28E-15
	Rank	1	8	9	1	11	1	1	7	12	6	10	1
F20	Best	−3.3220	−3.3220	−3.3220	−3.3220	−3.3220	−3.3220	−3.3220	−3.3220	−3.1559	−3.3220	−3.3220	−3.3220
	Worst	−3.2031	−3.2031	−3.1981	−3.2031	−2.8404	−3.2031	−3.1376	−3.2024	−2.6213	−3.1989	−3.0867	−3.2031
	Mean	−3.2982	−3.2804	−3.2739	−3.2982	−3.1169	−3.2625	−3.2322	−3.2565	−3.0157	−3.2261	−3.2356	−3.3101
	STD	0.0488	0.0582	0.0605	0.0488	0.1234	0.0610	0.0634	0.0608	0.1298	0.0492	0.0768	0.0366
	Rank	2	4	5	3	11	6	9	7	12	10	8	1
F21	Best	−10.1532	−10.1532	−10.1531	−10.1532	−10.1524	−10.1532	−10.1532	−10.1532	−6.1684	−10.1532	−10.1532	−10.1532
	Worst	−2.6305	−5.1007	−5.0552	−10.1532	−5.0551	−2.6305	−2.6305	−5.1007	−0.8798	−2.6305	−2.6303	−10.1532
	Mean	−9.7771	−7.8795	−9.3905	−10.1532	−9.3888	−9.7771	−7.3843	−8.8900	−3.9983	−8.7666	−8.6480	−10.1532
	STD	1.6821	2.5788	1.8621	3.40E-13	1.8613	1.6821	3.2457	2.2446	1.7187	2.5157	3.0870	3.51E-15
	Rank	3	10	5	2	6	3	11	7	12	8	9	1
F22	Best	−10.4029	−10.4029	−10.4029	−10.4029	−10.4025	−10.4029	−10.4029	−10.4029	−7.6292	−10.4029	−10.4029	−10.4029
	Worst	−3.7243	−3.7243	−10.4021	−10.4029	−4.4596	−2.7659	−2.7659	−2.7659	−0.9097	−2.7519	−5.0877	−10.4017
	Mean	−10.0690	−9.2076	−10.4026	−10.4029	−10.1033	−8.9235	−7.5987	−9.3755	−4.2828	−10.0204	−9.8710	−10.4029
	STD	1.4934	2.4737	0.0002	3.97E-13	1.3284	3.0418	3.2662	2.5480	2.0099	1.7108	1.6359	0.0003
	Rank	5	9	3	1	4	10	11	8	12	6	7	2
F23	Best	−10.5364	−10.5364	−10.5363	−10.5364	−10.5363	−10.5364	−10.5364	−10.5364	−10.2588	−10.5364	−10.5364	−10.5364
	Worst	−10.5364	−2.4217	−10.5355	−10.5364	−10.5304	−2.4217	−2.4217	−5.1756	−0.9487	−2.8711	−2.4217	−10.5364
	Mean	−10.5364	−8.7521	−10.5360	−10.5364	−10.5337	−8.6684	−8.9409	−9.4642	−5.0736	−9.8851	−8.1094	−10.5364
	STD	1.82E-15	3.2104	0.0002	2.30E-13	0.0014	3.3361	2.9057	2.2000	1.6543	2.0392	3.4234	3.43E-15
	Rank	1	9	4	3	5	10	8	7	12	6	11	1
Mean rank		2.3478	9.0870	7.2174	5.1739	5.8696	3.7391	7.3913	8.8261	9.5217	7.7826	7.0870	1.6957
Final ranking		2	11	7	4	5	3	8	10	12	9	6	1
+/=/−		2/16/5	1/1/21	0/1/22	0/11/12	3/2/18	3/12/8	1/5/17	0/1/22	0/1/22	1/7/15	2/3/18	−/−/−

Analysis of the table shows that the proposed LARO has a Friedman rank of 1.6957 and is in the first place. Next is ARO, with 2.3478 ranked seconds. Figure 8 provides the average rank of the 12 comparison algorithms. LARO provides the best case among all algorithms on the 16 tested functions. In more detail, LARO ranked first in two unimodal functions (F1 and F3) and obtained the best results in four multimodal functions (F9, F10, F11, F13), respectively. Additionally, the best case was obtained in eight fixed-dimensional functions (F14, F16, F17, F18, F19, F20, F21, and F23). In addition to this, LARO shows strong competitiveness in some functions (F4, F8, F15, F22). Moreover, LARO and some other algorithms offer the best case when facing some of the tested functions. For example, ARO, GJO, INFO, and LARO obtain the best average solution when facing the F9 and F11 functions. In addition, ARO shows a notable ability to successfully solve three and seven problems in the face of unimodal and multimodal functions. Thus, it can be seen that LARO mainly improves the ability of the original algorithm to deal with unimodal problems while somewhat enhancing the ability to deal with multimodal and fixed-dimensional problems.

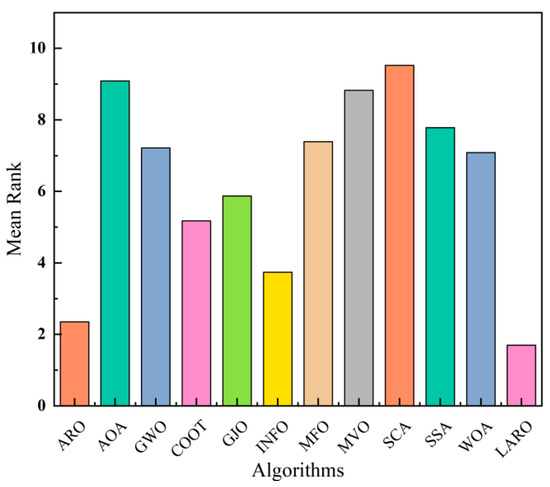
Figure 8. The average rank of the twelve algorithms.

By analyzing the experimental results and tests, it can be seen that LARO improves the convergence ability of the algorithm by introducing a Lévy flight strategy in the random hiding phase, which leads to a good convergence effect and accuracy of LARO when facing unimodal problems without multiple solutions. In addition, due to the introduction of the selective opposition strategy in ARO, LARO can effectively filter the optimal solution among multiple local solutions when dealing with multimodal problems and fixed-dimensional problems. This result is because the selective opposition strategy helps the algorithm to jump out of the local solutions adaptively. Experimental results also demonstrate that LARO has better convergence than other algorithms and ARO when dealing with multimodal and fixed-dimension problems. Therefore, it can be shown that LARO is a reliable optimization method in terms of performance. However, it is also found that LARO tends to break the balance between exploration and exploration in the overall iterative process, affecting the algorithm’s performance.

In Table 5, we give the p-values of 11 MH algorithms, LARO algorithm, and the Wilcoxon test to check whether LARO outperforms other MH algorithms. The Wilcoxon test results for ARO, AOA, GWO, COOT, GJO, and INFO algorithms are 2/16/5, 1/1/21, 0/1/22, 0/11/12, 3/2/18, and 3/12/8. The Wilcoxon test results for MFO, MVO, SCA, SSA, and WOA were 1/5/17, 0/1/22, 0/1/22, 1/7/15, and 2/3/18, respectively.

Table 5. Statistical output and associated p-values on 23 test functions.

p-Value	ARO	AOA	GWO	COOT	GJO	INFO	MFO	MVO	SCA	SSA	WOA
F1	6.80E-08/−	6.80E-08/−	6.80E-08/−	6.80E-08/−	6.80E-08/−	6.80E-08/−	6.80E-08/−	6.80E-08/−	6.80E-08/−	6.80E-08/−	1.25E-05/−
F2	6.80E-08/−	6.80E-08/−	6.80E-08/−	6.80E-08/−	6.80E-08/+	6.79E-08/−	6.80E-08/−	6.80E-08/−	6.80E-08/−	6.80E-08/−	6.80E-08/+
F3	6.80E-08/−	6.79E-08/−	6.79E-08/−	6.80E-08/−	2.06E-06/−	6.80E-08/−	6.80E-08/−	6.80E-08/−	6.80E-08/−	6.80E-08/−	6.80E-08/−
F4	6.80E-08/−	6.80E-08/−	6.80E-08/−	6.80E-08/−	6.80E-08/+	6.80E-08/−	6.80E-08/−	6.80E-08/−	6.80E-08/−	6.79E-08/−	6.80E-08/−
F5	0.3507/=	6.80E-08/−	6.80E-08/−	6.80E-08/−	6.80E-08/−	6.80E-08/+	6.79E-08/−	6.80E-08/−	6.80E-08/−	6.80E-08/−	6.80E-08/−
F6	0.0001/+	6.80E-08/−	4.87E-07/−	6.80E-08/−	0.0020/−	4.85E-08/+	6.68E-08/+	6.80E-08/−	6.80E-08/−	6.80E-08/+	6.80E-08/−
F7	0.9676/=	4.54E-07/+	0.0001/−	6.67E-06/−	1.92E-05/+	0.2733/=	6.80E-08/−	6.01E-07/−	0.0013/−	6.80E-08/−	0.0256/−
F8	0.0003/−	6.80E-08/−	6.80E-08/−	6.80E-08/−	6.80E-08/−	6.74E-08/−	6.72E-08/−	6.80E-08/−	6.80E-08/−	6.79E-08/−	0.0002/+
F9	NaN/=	9.42E-06/−	0.0198/−	0.3421/=	NaN/=	NaN/=	7.98E-09/−	8.01E-09/−	0.3421/=	7.95E-09/−	0.3421/+
F10	NaN/=	8.01E-09/−	3.84E-09/−	9.90E-08/−	8.64E-08/−	NaN/=	7.43E-10/−	8.01E-09/−	8.30E-09/−	7.98E-09/−	2.17E-06/−
F11	NaN/=	8.01E-09/−	0.1626/=	0.3421/=	NaN/=	NaN/=	8.01E-09/−	8.01E-09/−	0.0009/−	8.01E-09/−	0.1626/=
F12	1.81E-05/+	6.80E-08/−	6.80E-08/−	1.06E-07/−	1.23E-07/−	6.13E-08/+	0.0012/−	6.80E-08/−	6.80E-08/−	0.0071/−	6.80E-08/−
F13	0.8604/=	6.80E-08/−	6.80E-08/−	6.80E-08/−	2.56E-07/−	0.0001/−	0.0002/−	6.80E-08/−	6.80E-08/−	0.0002/−	6.80E-08/−
F14	NaN/=	9.32E-08/−	6.41E-05/−	NaN/=	2.71E-06/−	0.1626/=	0.1624/=	NaN/=	7.72E-09/−	NaN/=	0.0045/−
F15	NaN/=	8.01E-09/−	7.79E-09/−	0.0004/−	7.98E-09/−	0.3421/=	6.80E-09/−	7.95E-09/−	8.01E-09/−	2.97E-08/−	8.01E-09/−
F16	NaN/=	NaN/=	2.53E-05/−	NaN/=	7.93E-09/−	NaN/=	NaN/=	2.99E-08/−	8.01E-09/−	NaN/=	NaN/=
F17	NaN/=	8.01E-09/−	8.01E-09/−	0.1626/=	8.01E-09/−	NaN/=	NaN/=	7.99E-09/−	8.01E-09/−	NaN/=	0.0002/−
F18	NaN/=	0.0093/−	8.01E-09/−	NaN/=	8.01E-09/−	NaN/=	NaN/=	8.01E-09/−	7.99E-09/−	NaN/=	8.01E-09/−
F19	NaN/=	8.01E-09/−	8.01E-09/−	NaN/=	8.01E-09/−	NaN/=	NaN/=	8.01E-09/−	8.01E-09/−	NaN/=	8.01E-09/−
F20	0.3939/=	8.54E-07/−	6.38E-07/−	0.3939/=	2.91E-08/−	0.0068/−	0.0001/−	2.61E-07/−	1.51E-08/−	4.09E-06/−	1.93E-07/−
F21	0.3421/=	8.01E-09/−	8.01E-09/−	NaN/=	8.01E-09/−	0.3421/=	0.0009/−	8.01E-09/−	8.01E-09/−	0.0196/−	8.01E-09/−
F22	1/=	1.50E-07/−	2.78E-07/−	0.3421/=	1.86E-08/−	0.1379/=	0.0028/−	1.75E-07/−	1.13E-08/−	1/=	1.75E-07/−
F23	NaN/=	8.01E-09/−	8.01E-09/−	NaN/=	8.01E-09/−	0.0198/−	0.0198/−	8.01E-09/−	8.01E-09/−	0.1626/=	8.01E-09/−
+/=/−	2/16/5	1/1/21	0/1/22	0/11/12	3/2/18	3/12/8	1/5/17	0/1/22	0/1/22	1/7/15	2/3/18

Figure 9 offers the convergence plots of the twelve different methods on the 23 benchmark functions, where the X-axis of the plot represents the iterations, and the Y-axis represents the degree of adaptation (some test functions (F1, F2, F3, F4, F5, F6, F7, F10, F11, F12, F13, F14, F15) are represented as logarithms of 10). The results in the figure demonstrate that LARO has a high-speed convergence rate and convergence accuracy when dealing with a part of the functions (F1, F2, F3, F4, F5) in the face of F1–F7 unimodal functions. Additionally, LARO continues to improve accuracy near the optimal solution later in the iteration. This analysis shows its reliable performance in getting rid of the local key. For the F8–F23 functions, we can see that LARO exhibits a characteristic that transitions rapidly between the early search and late development phases and converges near the optimal position at the beginning of the iteration. Then, LARO progressively determines the best marquee position and updates the answer to confirm the previous search results. Figure 10 illustrates box plots of 12 different MH algorithms for showing the distribution of means in various problems. In most of the issues tested, the distribution of LARO is more concentrated and downward than the other algorithms. This finding also illustrates the consistency and stability of LARO. Overall, LARO can handle the 23 basic test sets very well.

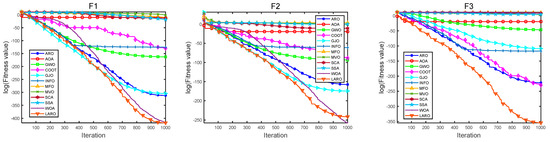
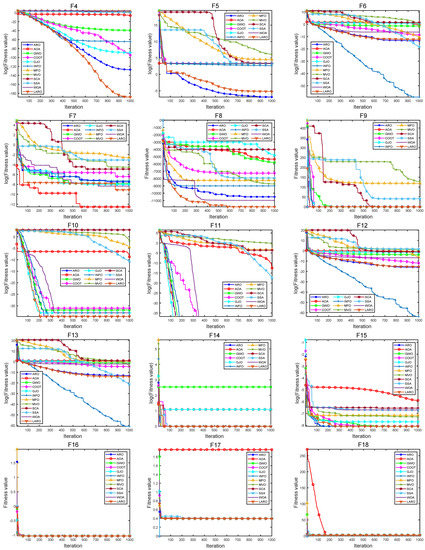
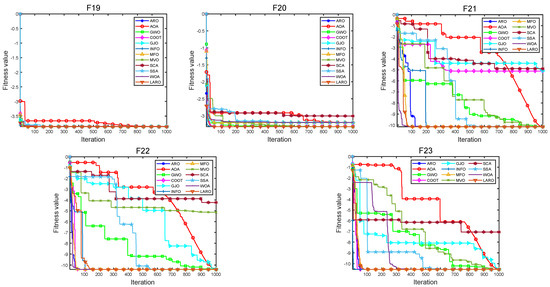
Figure 9. Convergence plots of LARO and different MH methods on 23 test functions.

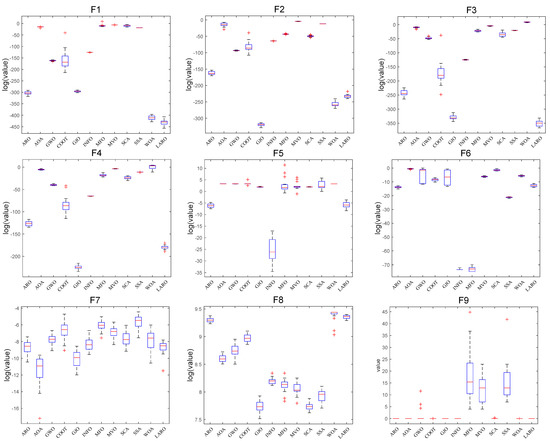
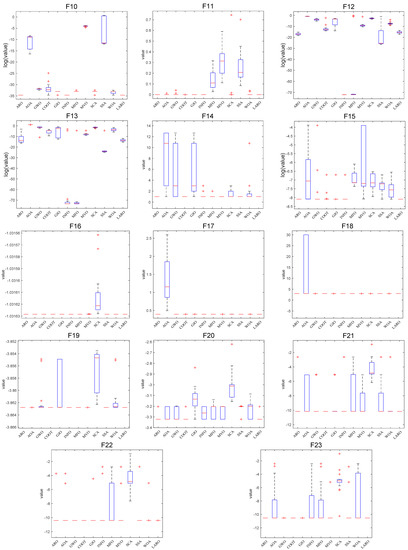
Figure 10. Box plot of LARO and ARO, AOA, GWO, COOT, GJO, INFO, MFO, MVO, SCA, SSA, WOA on 23 test functions.

4.5. Experiments on the CEC2017 Classical Functions

In this section, the proposed LARO is simulated in CEC2017 for 29 of these test functions. LARO and the other comparison methods are executed 20 times individually, with the same relevant parameters set in Section 4.4. Cec01 and cec03–cec30 have a problem dimension of 10. Numerical results include the output of ARO [29], BWO [12], CapSA [13], GA [49], PSO [50], RSA [51], WSO [52], GJO [41], E-WOA [53], WMFO [54], and CSOAOA [26] outputs. As shown in Table 6, the evaluation methods of all 29 tested functions are compared by the proposed LARO algorithm. In addition, the results of Friedman’s statistical test are given in the last part of the table. In this case, Friedman’s statistical test ranking is given based on the mean value.

Table 6. Statistical outcomes of the different search methods on the CEC2017 test functions.

Function	Algorithms
	Index	LARO	ARO	BWO	CapSA	RSA	WSO	GJO	PSO	GA	E-WOA	WMFO	CSOAOA
cec01	AVE	822.7731	1155.6589	9.20E+07	1987.7279	1.03E+10	343.4283	2.48E+08	1.39E+08	4.41E+07	5.21E+09	2.43E+10	4.78E+05
	STD	868.5412	1306.0545	3.87E+07	1757.9178	3.66E+09	893.9934	3.17E+08	3.43E+08	5.58E+07	4.34E+09	7.66E+09	1.05E+06
	Rank	2	3	7	4	11	1	9	8	6	10	12	5
cec03	AVE	300.0046	300.0177	1290.6426	300.0000	9725.5951	300.0103	2256.8681	300.0786	1.82E+05	1.67E+04	6.20E+06	397.3366
	STD	0.0134	0.0492	325.1198	1.24E-07	3043.9470	0.0280	2505.1808	0.1975	5.92E+05	6.62E+03	1.17E+07	151.6787
	Rank	2	4	7	1	9	3	8	5	11	10	12	6
cec04	AVE	402.5610	404.3365	410.8631	400.0000	1059.8248	401.5091	441.9227	447.2097	477.4278	694.0931	3366.0150	404.4857
	STD	1.8729	1.4857	2.4854	1.10E-05	506.3864	1.5468	25.7778	89.9889	50.4126	131.8941	1568.4437	1.3019
	Rank	3	4	6	1	11	2	7	8	9	10	12	5
cec05	AVE	507.3202	510.4546	525.6527	518.5186	585.3797	509.0703	531.3297	528.7659	543.3536	577.9511	663.3490	515.2876
	STD	2.6297	5.3525	4.2007	7.8720	13.2798	5.4537	11.0190	10.3710	15.8263	21.9652	36.9435	7.4489
	Rank	1	3	6	5	11	2	8	7	9	10	12	4
cec06	AVE	600.0014	600.0012	604.9375	601.1525	645.8434	600.3361	605.6297	605.8022	635.5544	647.6467	705.6071	600.2195
	STD	0.0021	0.0027	1.2290	2.8209	7.8591	0.8400	4.5783	4.8637	11.3938	13.8161	15.7671	0.2002
	Rank	2	1	6	5	10	4	7	8	9	11	12	3
cec07	AVE	724.8801	725.0783	737.1078	731.7659	806.3894	729.3690	745.4072	731.0701	776.8818	815.2582	1203.7555	741.0450
	STD	5.6162	5.6710	6.2551	8.5109	10.9819	7.8112	13.2441	8.8893	31.9986	23.8207	109.3032	9.4407
	Rank	1	2	6	5	10	3	8	4	9	11	12	7
cec08	AVE	808.7147	813.8299	818.0646	820.1136	856.2384	804.3845	828.7147	823.3905	837.1595	854.5212	950.9072	819.7897
	STD	2.4744	4.7212	4.3031	7.4712	7.4357	2.1384	7.7656	12.3620	11.1249	15.4288	21.5027	4.3114
	Rank	2	3	4	6	11	1	8	7	9	10	12	5
cec09	AVE	900.1293	900.6541	915.7054	911.2544	1477.5334	900.3249	962.9553	924.0709	1091.0698	1712.3349	5670.2241	917.3586
	STD	0.2419	1.8939	7.5101	17.7217	167.3821	0.6134	63.1277	54.7140	191.0585	381.5732	1788.9473	32.5949
	Rank	1	3	5	4	10	2	8	7	9	11	12	6
cec10	AVE	1333.2841	1425.8487	1517.7474	1582.2125	2508.4268	1222.8987	1920.4328	2035.3573	1976.5992	2401.3452	3808.6357	1415.7327
	STD	153.5287	150.0427	132.9630	218.1276	295.4488	211.1734	357.3134	404.6299	281.2993	383.0208	367.5857	195.5798
	Rank	2	4	5	6	11	1	7	9	8	10	12	3
cec11	AVE	1103.9241	1106.2944	1128.9591	1132.8656	2919.6980	1108.4846	1397.4074	1250.7483	4878.9851	4082.6925	4.12E+04	1113.7413
	STD	2.0568	4.0116	8.4656	28.0784	1220.3271	5.0667	977.4104	206.6429	4671.9494	5143.4045	7.72E+04	5.8604
	Rank	1	2	5	6	9	3	8	7	11	10	12	4
cec12	AVE	7362.3077	8907.6028	6.51E+05	5967.1769	2.84E+08	1637.4174	8.96E+05	2.50E+07	4.22E+06	4.15E+07	3.39E+09	1.59E+05
	STD	5635.1644	7205.5933	4.36E+05	5347.1860	2.75E+08	216.8342	9.71E+05	9.45E+07	5.90E+06	4.88E+07	1.81E+09	2.90E+05
	Rank	3	4	6	2	11	1	7	9	8	10	12	5
cec13	AVE	1495.1186	1318.4492	1.49E+04	1433.9709	1.56E+07	1315.1106	1.23E+04	1.01E+04	6.08E+04	1.72E+04	3.90E+08	2546.0110
	STD	733.9714	15.5138	7.51E+03	182.3506	1.98E+07	9.1354	7.88E+03	1.60E+04	1.38E+05	1.19E+04	3.71E+08	2019.8441
	Rank	4	2	8	3	11	1	7	6	10	9	12	5
cec14	AVE	1407.2627	1406.0305	1722.5713	1455.1041	4655.9859	1417.4027	2591.5071	2864.1741	1.02E+04	2.81E+03	5.97E+06	1410.5210
	STD	4.3140	3.7572	311.9721	24.1156	1706.5656	9.6436	1687.2328	6123.7598	1.03E+04	1.55E+03	5.96E+06	4.9376
	Rank	2	1	6	5	10	4	7	9	11	8	12	3
cec15	AVE	1502.8435	1503.8847	2474.5922	1536.5028	7655.4446	1511.7791	3297.2031	1985.8665	8896.4395	1.38E+04	6.44E+07	1584.7036
	STD	1.9719	3.0724	1015.2813	45.9443	4511.8019	9.7082	1864.2684	1260.1608	7789.9250	7.26E+03	1.04E+08	286.2738
	Rank	1	2	7	4	9	3	8	6	10	11	12	5
cec16	AVE	1681.0383	1700.5540	1645.5941	1791.1364	2065.9143	1653.2314	1829.6800	1752.6860	1853.5242	1990.3877	2912.3284	1815.4437
	STD	89.8554	73.8873	36.3768	155.7101	148.5882	64.2038	138.0245	138.4040	109.7768	123.0833	325.0862	132.8314
	Rank	3	4	1	6	11	2	8	5	9	10	12	7
cec17	AVE	1710.4204	1715.6868	1740.5664	1754.9179	1830.7302	1739.6489	1762.4890	1798.3087	1783.9662	1874.9130	2392.9067	1736.2611
	STD	8.5866	11.3720	6.7098	48.1189	29.9292	10.3976	15.9251	49.1671	54.1561	105.8992	249.2424	11.0306
	Rank	1	2	5	6	10	4	7	9	8	11	12	3
cec18	AVE	1802.0153	1803.5385	2.09E+04	1886.8073	7.14E+07	1819.7303	3.87E+04	2.07E+04	1.44E+04	1.58E+04	1.11E+09	3106.6477
	STD	1.7139	3.3011	1.58E+04	114.1450	2.16E+08	14.9707	1.09E+04	1.94E+04	9.04E+03	1.21E+04	8.18E+08	2504.4269
	Rank	1	2	9	4	11	3	10	8	6	7	12	5
cec19	AVE	1900.9929	1900.6600	3234.2361	1918.0008	8.96E+05	1902.7298	2.19E+04	7.53E+03	9507.9076	7.25E+05	1.23E+08	1930.8991
	STD	0.8475	0.5529	1852.0372	28.2498	4.92E+05	2.4025	5.32E+04	1.84E+04	7146.5548	1.73E+06	2.25E+08	83.0316
	Rank	2	1	6	4	11	3	9	7	8	10	12	5
cec20	AVE	2007.9923	2009.4715	2035.4837	2045.3706	2273.1132	2022.3897	2105.1502	2087.8262	2104.4795	2226.8165	2561.8671	2016.8935
	STD	8.6332	7.8729	3.7348	27.1370	55.3155	8.7340	57.6261	50.9035	58.3071	68.3003	179.7417	27.6321
	Rank	1	2	5	6	11	4	9	7	8	10	12	3
cec21	AVE	2252.4061	2256.7777	2217.0089	2294.8833	2319.9113	2274.5655	2328.4265	2309.4987	2343.7029	2365.4102	2464.8377	2283.5269
	STD	58.2520	57.8941	37.4034	56.7617	55.9856	49.7005	7.8421	56.6547	60.0185	35.9432	27.5057	51.9989
	Rank	2	3	1	6	8	4	9	7	10	11	12	5
cec22	AVE	2297.0035	2297.7619	2315.3592	2306.1043	3002.0119	2300.9966	2339.0118	2311.5027	2378.5713	2842.3513	4529.4903	2319.1097
	STD	19.1834	16.1737	2.0610	2.8618	250.7253	0.7424	33.7433	32.3536	41.4632	516.2846	584.2641	7.3529
	Rank	1	2	6	4	11	3	8	5	9	10	12	7
cec23	AVE	2611.9041	2616.1971	2622.2634	2622.9895	2694.3460	2617.0344	2635.1356	2662.0241	2678.9789	2692.2280	2907.2304	2616.0528
	STD	5.1923	7.2004	3.8793	9.2004	19.1961	9.3109	15.2658	51.9838	19.9896	40.7824	97.3616	5.2518
	Rank	1	3	5	6	11	4	7	8	9	10	12	2
cec24	AVE	2669.8595	2694.3331	2700.0746	2747.9803	2858.8428	2644.1129	2761.8726	2791.8194	2782.8764	2811.5630	3037.4102	2500.5324
	STD	114.1729	99.9286	100.6219	60.7637	52.1016	120.9738	17.2575	32.3088	76.7190	60.6137	104.3361	0.4202
	Rank	3	4	5	6	11	2	7	9	8	10	12	1
cec25	AVE	2919.7572	2917.1473	2933.7838	2932.0474	3337.8921	2923.8388	2938.7048	2927.6247	3008.3435	3250.4673	4727.9793	2915.9381
	STD	23.9114	23.4579	18.8070	22.7472	120.5463	22.9220	47.4083	83.6443	39.4223	181.1080	880.7767	22.8398
	Rank	3	2	7	6	11	4	8	5	9	10	12	1
cec26	AVE	2912.3350	2902.9671	2934.0831	2980.5261	4079.5676	2915.7621	3061.9770	3223.6248	3503.1009	4221.5281	5222.1585	2907.7708
	STD	39.4393	13.2691	78.6913	126.0442	281.2591	46.8308	208.2813	407.6659	346.3298	393.2302	426.7847	120.3242
	Rank	3	1	5	6	10	4	7	8	9	11	12	2
cec27	AVE	3094.4428	3096.3048	3095.1574	3101.5396	3177.9799	3097.3961	3100.0783	3133.9845	3209.3003	3226.3975	3482.9544	3093.0179
	STD	2.2491	4.1114	2.3241	16.9910	50.4451	3.9855	14.0880	30.7557	38.7323	68.9513	208.3466	2.6834
	Rank	2	4	3	7	9	5	6	8	10	11	12	1
cec28	AVE	3126.9366	3161.7143	3298.2474	3271.5503	3788.6401	3150.7065	3398.1036	3437.7179	3603.9845	3526.9242	4076.7351	3254.7122
	STD	67.5801	114.0390	129.1247	145.5009	136.6237	106.4742	87.7514	154.4405	162.5968	165.7635	407.5146	139.0270
	Rank	1	3	6	5	11	2	7	8	10	9	12	4
cec29	AVE	3156.8756	3164.7344	3177.3593	3225.5586	3422.4252	3152.0410	3193.7297	3264.3518	3307.7829	3447.6726	4124.6753	3182.2187
	STD	13.9195	15.6979	11.3675	59.3761	147.8922	13.1740	38.3279	82.4457	70.9418	143.8086	317.0168	27.7701
	Rank	2	3	4	7	10	1	6	8	9	11	12	5
cec30	AVE	8279.3916	1.48E+05	1.79E+05	1.26E+05	1.14E+07	6.55E+04	7.48E+05	1.72E+06	4.54E+06	5.39E+06	2.16E+08	9.22E+04
	STD	5677.8504	3.47E+05	2.77E+05	2.99E+05	3.73E+07	2.77E+05	9.13E+05	2.16E+06	3.31E+06	6.60E+06	1.51E+08	2.00E+05
	Rank	1	5	6	4	11	2	7	8	9	10	12	3
Mean rank		1.8621	2.7241	5.4483	4.8276	10.3793	2.6897	7.6552	7.2414	8.9655	10.0690	12.0000	4.1379
Final ranking		1	3	6	5	11	2	8	7	9	10	12	4

As shown in Table 6, the average rank of Friedman for LARO is 1.8621, while the average rank of WOS and ARO are 2.6897 and 2.7241, respectively. Therefore, LARO’s final ranking is the first. The results show that LARO provides a good output profile on 29 tested functions. LARO can succeed on 11 functions (cec05, cec07, cec09, cec11, cec15, cec17, cec18, cec20, cec22, cec23, cec28, cec30). In addition, LARO was able to obtain better optimization results and average values for the ten tested functions (cec01, cec03, cec06, cec08, cec10, cec14, cec19, cec21, cec27, cec29). The numerical results show that the proposed LARO exhibits excellent performance in the unimodal problem, indicating that the LARO algorithm again converges quickly. The performance of LARO for multimodal functions also illustrates that the introduced selective opposition effectively helps the algorithm to jump out of local solutions. In the face of composition and hybrid functions, LARO demonstrates excellent optimization ability, indicating the effectiveness of the Lévy flight strategy in improving the accuracy of the algorithm, while WSO and ARO can successfully solve six (cec01, cec08, cec10, cec12, cec13, cec29) and four functions (cec06, cec14, cec19, cec26), respectively.

4.6. Experiments on CEC2019 Test Functions

In this section, the proposed LARO has experimented with ten functions in CEC2019 [26]. The LARO algorithm is executed 20 times individually, and the parameters given are consistent with those of the numerical experiments in Section 4.3. Among them, the dimensionality of the functions cec01–cec03 is different from the others, with 9, 16, and 18 for cec01–cec03, respectively, while the problem dimensionality of cec04–cec10 is 10 [55]. The numerical results in agreement with AOA [38], GWO [39], COOT [40], GJO [41], INFO [42], MFO [43], MVO [44], SCA [45], SSA [46], WOA [47] are compared. As shown in Table 7, the four relevant evaluation methods are compared by the proposed LARO algorithm in all ten tested functions. In addition, the Wilcoxon and the Friedman statistical test results are given in the last part of the table. The experimental results conclude that LARO is superior in handling these challenging optimization function problems. LARO ranks first with an average ranking of 1.3636. In addition, LARO performs as the optimal case in seven of the ten CEC2019 functions (cec01, cec04, cec05, cec06, cec07, cec08, cec10), and ARO shows the best results in the other three functions (cec02, cec03, cec09). Numerical experimental results demonstrate that the LARO algorithm can accurately approach the optimal solution and is highly competitive with other MH methods for various types of problems. Moreover, experimental results likewise demonstrate that the LARO algorithm enhances the variety of the population and the accuracy of solving the problem due to the addition of the Lévy flight and the selective opposition, which effectively avoids local optimal solutions.

Table 7. Statistical outcomes of the different search methods on the CEC2019 test functions.

Function	Index	Algorithms
		ARO	AOA	GWO	COOT	GJO	INFO	MFO	MVO	SCA	SSA	WOA	LARO
F1	Best	1	5.12E+07	1	1	1	1	1.10E+05	8.03E+04	1.1597	5.62E+04	1.71E+03	1
	Worst	1	2.53E+08	1.97E+05	3.48E+04	1.22E+03	1	2.02E+07	1.36E+06	8.30E+06	2.99E+06	2.27E+07	1
	Mean	1	1.50E+08	1.45E+04	4.77E+03	73.8930	1	7.36E+06	5.78E+05	1.20E+06	7.12E+05	5.09E+06	1
	STD	0	4.89E+07	4.41E+04	9.90E+03	270.3287	0	7.51E+06	3.72E+05	2.43E+06	6.81E+05	7.25E+06	0
	Rank	1	12	6	5	4	1	11	7	9	8	10	1
F2	Best	3.6956	7.07E+03	31.2720	4.4266	4.1176	4.1009	220.3923	170.7931	470.2927	181.5879	3610.0945	4.0581
	Worst	4.3289	2.28E+04	557.6110	5.1682	511.4838	4.4573	8.76E+03	651.5037	5186.1495	2492.1742	9352.6034	4.3569
	Mean	4.2012	1.34E+04	282.4243	4.8954	75.4032	4.2881	1.95E+03	426.7448	3063.8568	763.7683	6258.6962	4.2462
	STD	0.1354	4.23E+03	161.7419	0.2301	155.6277	0.0735	2.69E+03	122.9275	1529.9521	707.5083	1510.3098	0.0656
	Rank	1	12	6	4	5	3	9	7	10	8	11	2
F3	Best	1.0002	1.0000	1.4095	1.0001	1.4738	1.4091	1.4091	1.0004	6.0194	1.0000	2.4098	1.4096
	Worst	2.2963	7.4860	7.7112	3.0803	7.9002	7.7120	9.7120	11.7116	10.7667	7.6856	6.3092	2.7905
	Mean	1.5027	5.9894	2.9010	1.7676	4.2363	2.0046	6.0528	7.0826	8.5244	3.1456	4.7440	1.7488
	STD	0.2936	1.4624	2.1050	0.5700	2.1100	1.7895	2.4467	2.4192	1.2749	2.0016	1.0459	0.4476
	Rank	1	9	5	3	7	4	10	11	12	6	8	2
F4	Best	5.9748	17.9783	4.3685	9.9571	12.4412	9.9546	11.8842	8.9610	32.1676	10.9496	23.3010	5.9748
	Worst	25.8739	98.5047	29.1872	25.8762	38.2053	55.7224	67.0167	34.8318	63.4652	60.6973	109.5274	25.8739
	Mean	13.1948	51.7232	13.6604	17.1728	23.6225	23.9248	28.6234	17.9337	44.8955	30.6497	52.8681	12.8513
	STD	5.3627	22.4378	5.7726	4.5372	7.9510	11.5911	14.0432	7.2782	7.9633	14.0322	21.9166	5.6119
	Rank	2	11	3	4	6	7	8	5	10	9	12	1
F5	Best	1.0295	63.4709	1.1014	1.0197	1.2417	1.0393	1.0394	1.1584	4.2734	1.1255	1.6358	1.0172
	Worst	1.1796	162.4614	3.7402	1.2462	12.2916	1.3124	1.5710	1.6776	10.2743	1.4698	3.2060	1.1451
	Mean	1.0834	99.5302	1.6601	1.1215	3.3635	1.1568	1.1840	1.3015	6.8768	1.2416	1.9146	1.0747
	STD	0.0444	25.3320	0.5639	0.0631	2.4720	0.0860	0.1387	0.1315	1.6355	0.0980	0.3590	0.0295
	Rank	2	12	8	3	10	4	5	7	11	6	9	1
F6	Best	1.0002	9.9422	1.1943	1.2148	1.5455	1.2230	1.3329	1.1446	4.6953	1.1324	5.1549	1.0000
	Worst	3.6226	13.6628	6.7684	6.0470	6.9893	6.1077	8.3903	4.8063	8.1101	8.1578	11.3601	3.7205
	Mean	1.5631	11.5779	2.6487	2.7564	4.0616	2.9446	4.0108	2.4997	6.7221	3.6808	7.8918	1.5055
	STD	0.8595	1.0823	1.6038	1.3475	1.2616	1.4091	1.8679	1.0611	1.0922	1.7390	1.8031	0.7416
	Rank	2	12	4	5	9	6	8	3	10	7	11	1
F7	Best	126.4556	783.7085	55.0048	500.4912	515.5437	365.0528	355.7205	298.1040	1205.5680	527.5808	281.0483	16.3069
	Worst	825.4110	1551.2995	1300.9418	1427.8328	1744.2935	1461.9015	1587.9233	1192.0592	1696.1676	1690.0135	1936.0646	916.3734
	Mean	449.8192	1130.5116	693.0267	869.9624	995.5096	871.7417	1076.1407	753.1381	1386.4741	1002.0974	1116.1865	386.6686
	STD	186.7004	240.2304	310.3256	229.9777	315.9565	283.0647	305.6328	212.0728	133.1321	351.7500	402.5621	231.7633
	Rank	2	11	3	5	7	6	9	4	12	8	10	1
F8	Best	2.4227	4.1448	2.6217	3.1559	3.2444	3.1557	3.6285	2.8028	3.9434	3.7487	3.7071	2.3788
	Worst	3.7115	5.4639	4.0229	4.5897	4.5352	4.5020	4.8170	4.9911	4.6740	5.0188	5.0633	3.7337
	Mean	3.2039	4.9734	3.3252	3.9339	3.9005	3.7804	4.3742	3.9554	4.3846	4.3860	4.6611	3.0415
	STD	0.3518	0.3363	0.3717	0.3625	0.3488	0.3550	0.3658	0.5442	0.2045	0.3809	0.3024	0.3829
	Rank	2	12	3	6	5	4	8	7	9	10	11	1
F9	Best	1.0196	1.4159	1.0978	1.1280	1.0971	1.0692	1.1023	1.0814	1.3574	1.0377	1.1542	1.0504
	Worst	1.1224	4.4516	1.2875	1.5646	1.4555	1.2857	1.6253	1.2568	1.7237	1.8722	1.9729	1.2603
	Mean	1.0818	3.2542	1.1693	1.2653	1.2327	1.1556	1.3485	1.1604	1.5082	1.3141	1.3701	1.1386
	STD	0.0296	0.6902	0.0638	0.1173	0.0808	0.0658	0.1414	0.0527	0.1161	0.1880	0.1972	0.0474
	Rank	1	12	5	7	6	3	9	4	11	8	10	2
F10	Best	20.9808	20.9450	7.4256	1.0001	11.7255	21.0000	21.0000	21.0061	21.2087	20.9985	21.0235	1.0000
	Worst	21.0054	20.9995	21.5092	21.6509	21.5793	21.1073	21.2712	21.3117	21.5232	21.0000	21.4009	21.0076
	Mean	20.9985	20.9828	20.7075	18.4406	20.5348	21.0471	21.0929	21.0338	21.3816	20.9999	21.1489	18.0553
	STD	0.0056	0.0102	3.1269	6.8324	2.6525	0.0412	0.0898	0.0669	0.0818	0.0003	0.0969	7.1881
	Rank	6	5	4	2	3	9	10	8	12	7	11	1
Mean rank		1.9091	10.9091	5.0000	4.2727	6.5455	4.6364	8.3636	6.3636	10.6364	7.5455	10.1818	1.3636
Final ranking		2	12	5	3	7	4	9	6	11	8	10	1
+/=/−		2/7/1	0/0/10	0/2/8	0/1/9	0/0/10	0/3/7	0/0/10	0/1/9	0/0/10	0/1/9	0/0/10	−/−/−

The convergence plots of the MH method in Figure 11 show the high quality and high accuracy of the LARO solutions and the significant convergence speed, such as cec01, cec02, cec03, cec04, cec05, cec06, cec7, cec08, cec10. Box plots and radar plots of the test function runs in CEC2019 are provided in Figure 12 and Figure 13, respectively, where these box-line plots provide very small widths, indicating the stability and superiority of LARO. In comparison, the radar plot demonstrates that LARO has the smallest ranking among all the tested functions. In Table 8, we give the p-values of 11 MH methods, the LARO algorithm, and the Wilcoxon test to check whether LARO outperforms other MH algorithms. The Wilcoxon test results for AROO, AOA, GWO, COOT, GJO, and INFO algorithms are 2/7/1, 0/0/10, 0/2/8, 0/1/9, 0/0/ The Wilcox test results for MFO, MVO, SCA, SSA, and WOA are 0/0/10, 0/1/9, 0/0/10, 0/1/9, and 0/0/10, respectively.

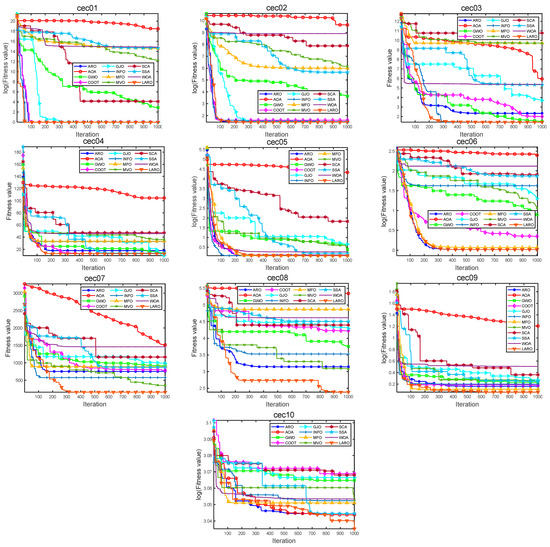
Figure 11. Convergence plots of LARO and other search methods on the CEC2019 test functions.

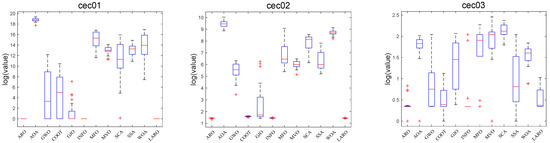
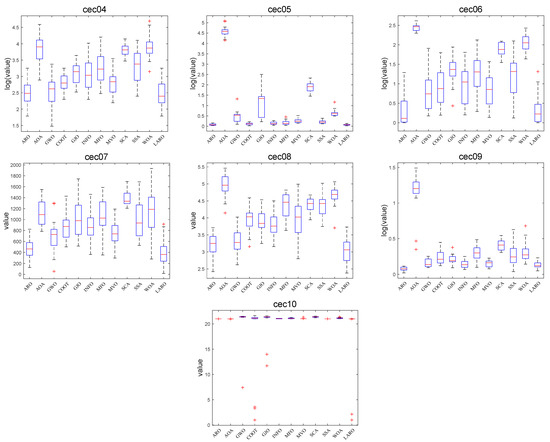
Figure 12. Box plot of LARO and ARO, AOA, GWO, COOT, GJO, INFO, MFO, MVO, SCA, SSA, WOA on CEC2019 test functions.

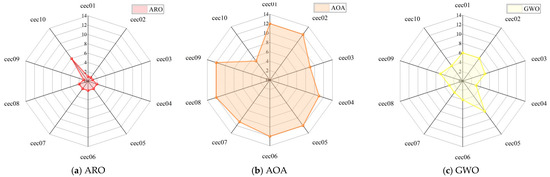
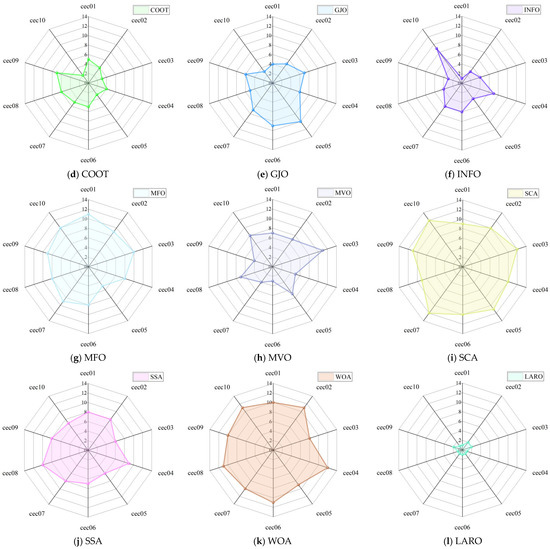
Figure 13. Radar chart of ARO, AOA, GWO, COOT, GJO, INFO, MFO, MVO, SCA, SSA, WOA, and LARPO on CEC2019.

Table 8. Statistical output and associated p-values on the CEC2019 test functions.

p-Value	ARO	AOA	GWO	COOT	GJO	INFO	MFO	MVO	SCA	SSA	WOA
F1	NaN/=	8.01E-09/−	2.99E-08/−	2.57E-05/−	0.0002/−	NaN/=	7.99E-09/−	8.01E-09/−	8.01E-09/−	8.01E-09/−	8.01E-09/−
F2	0.0531/=	6.80E-08/−	6.80E-08/−	6.80E-08/−	5.87E-06/−	0.0810/=	6.80E-08/−	6.80E-08/−	6.80E-08/−	6.80E-08/−	6.80E-08/−
F3	0.0167/+	1.20E-06/−	0.0499/−	0.4903/=	2.04E-05/−	3.73E-05/−	2.92E-05/−	1.20E-06/−	6.80E-08/−	0.0908/=	9.17E-08/−
F4	0.8285/=	1.22E-07/−	0.4092/=	0.0036/−	2.58E-05/−	0.0002/−	2.58E-05/−	0.0077/−	6.73E-08/−	1.40E-05/−	7.82E-08/−
F5	0.8181/=	6.80E-08/−	1.66E-07/−	0.0114/−	6.80E-08/−	0.0006/−	0.0011/−	6.80E-08/−	6.80E-08/−	1.43E-07/−	6.80E-08/−
F6	0.6949/=	6.80E-08/−	0.0007/−	0.0002/−	6.92E-07/−	0.0001/−	3.99E-06/−	0.0005/−	6.80E-08/−	1.81E-05/−	6.80E-08/−
F7	0.0208/−	1.92E-07/−	0.0016/−	2.36E-06/−	1.20E-06/−	1.25E-05/−	1.20E-06/−	4.68E-05/−	6.80E-08/−	1.20E-06/−	2.06E-06/−
F8	0.1806/=	6.80E-08/−	0.0385/−	1.05E-06/−	6.92E-07/−	7.58E-06/−	1.06E-07/−	1.10E-05/−	6.80E-08/−	6.80E-08/−	7.90E-08/−
F9	7.41E-05/+	6.80E-08/−	0.2977/=	6.61E-05/−	7.41E-05/−	0.5428/=	7.58E-06/−	0.1988/=	6.80E-08/−	0.0003/−	7.95E-07/−
F10	0.3648/=	0.0015/−	7.95E-07/−	7.41E-05/−	7.58E-06/−	1.20E-06/−	7.95E-07/−	7.90E-08/−	6.80E-08/−	0.0009/−	6.80E-08/−
+/−/=	2/7/1	0/0/10	0/2/8	0/1/9	0/0/10	0/3/7	0/0/10	0/1/9	0/0/10	0/1/9	0/0/10

4.7. Impact Analysis of Each Improvement

The experiments in this section focus on numerical experiments of LARO with the compared algorithms on three standard test sets (23 benchmark test functions, CEC2017, CEC2019). This section summarizes the impact of different improvement strategies on the algorithm performance.

The introduction of the Lévy flight strategy in ARO is mainly used to solve the problem of low convergence accuracy of the original ARO. In contrast, single-peaked functions (e.g., F01–F07) are often used to test the convergence accuracy of the algorithm due to characteristics such as the absence of multiple solutions and the ease of exploration to the vicinity of the optimal solution. In the numerical experiments of 23 benchmark test functions, LARO ranks 1, 3, 1, 2, 3, 5, and 3 among the F01–F07 single-peaked functions, respectively. Except for F05–F06, the convergence accuracy of LARO is higher than that of the original ARO. In addition, in the numerical experiments of CEC2017, LARO ranks better than the original in both cec01 and cec03 ARO. Therefore, the Lévy flight strategy helps ARO to improve convergence accuracy successfully.

The selective backward learning strategy is introduced mainly to help ARO to jump out of the local solution in time. The multi-peaked functions (e.g., F08–F13, cec04–cec10 of CEC2017, and cec01–cec10 of CEC2019) are prone to fall into the vicinity of local solutions during the search process due to the existence of multiple solutions, which affects the convergence performance of the algorithm. Therefore, the algorithm’s ability to iterate over the multi-peaked functions reflects its ability to jump out of local solutions. In the numerical experiments with 23 benchmark test functions, LARO ranks 2, 1, 1, 1, 1, 3, and 1 for functions F08–F13, respectively. Except for F12, LARO’s optimization average is higher than the original ARO. In addition, LARO ranks 3, 1, 2, 1, 2, 1, 1, and 2 against cec04–cec10 of CEC2017, respectively. Except for cec06, the optimized average value of LARO is higher than that of the original ARO, and when facing the test set of CEC2019, the average ranking of LARO is 1.3636, which is higher than ARO at 1.9091. Therefore, LARO converges better than the original ARO when dealing with multi-peaked functions, which indicates that the selective backward learning strategy helps LARO to better jump out of the local solution.

5. Application of LARO in Semi-Real Mechanical Engineering

This subsection uses six practical mechanical engineering applications. There are many constraint treatments for optimization problems, such as penalty functions, co-evolutionary, adaptive, and annealing penalties [56]. Among them, penalty functions are the most used treatment strategy because they are simple to construct and easy to operate. Therefore, this paper uses the penalty function strategy to handle the optimization constraints of these six mechanical engineering optimization models, for the engineering optimization problem with minimization constraints defined as:

Minimize:

$$f(\overline{x}),\overline{x}=[x_1,x_2,\dots ,x_n]$$

(28)

Subject to:

$$\{\begin{array}{c}{g}_i(\overline{x})\le 0,i=1,2,\dots ,m\\ h_j(\overline{x})=0,j=1,2,\dots ,k\end{array}$$

(29)

where m is the number of inequality constraints and k is the number of equation constraints. $\overline{x}$ is the design variable of the engineering problem with dimension n. For the case with boundary constraints, a boundary requirement exists for all dimensional variables:

$$l{b}_i\le x_i\le u{b}_i,i=1,2,\dots n$$

(30)

where lb and ub are the lower and upper bounds of the n-dimensional variable and n is the number of dimensions of the variable.

Therefore, the mathematical description of the engineering optimization problem after constraint weighting is

$$f(\overline{x})=f(\overline{x})+\alpha {\displaystyle \sum _{i=1}^m\max \{g_i(\overline{x}),0\}}+\beta {\displaystyle \sum _{j=1}^k\max \{h_j(\overline{x}),0\}}$$

(31)

where α is the weight of the inequality constraint and β is the weight of the equation constraint. Considering the optimization process to satisfy the inequality and equation constraints, we require α and β to be large values. This paper sets them to 1 × 10⁵ [38]. Therefore, the objective function is severely penalized (the value of the objective function increases) when the optimization solution exceeds any constraint. This mechanism will allow the algorithm to avoid illegal solutions inadvertently computed during the iterative process.

LARO and all the comparison algorithms were executed 30 times. The relevant parameters were a maximum iteration of 1000 and a population size of 50. In addition, for the solution of the practical engineering applications, we used the same comparison algorithms as in the numerical experiments, including AOA [38], GWO [39], COOT [40], GJO [41], INFO [42], MFO [43], MVO [44], SCA [45], SSA [46], WOA [47].

5.1. Welded Beam Design Problem (WBD)

The WBD requires that the design cost of the WBD be guaranteed to be minimal under various restraints. The schematic structural diagram of the WBD is provided in Figure 14. Four main relevant independent variables are obtained for the WBD: the welding thickness (h), rod attachment length (l), rod height (t), and rod thickness (b) [38]. The given variables are required to satisfy seven constraints. The model of the WBD is given below.

$$\overrightarrow{z}=[z_1,z_2,z_3,z_4]=[h,l,t,b]$$

(32)

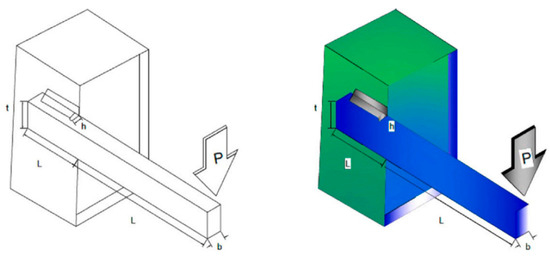
Figure 14. WBD structure.

Minimize:

$$f(z)=1.10471z_1^2{z}_2+0.04811z_3{z}_4(14.0+z_2),$$

(33)

Variable:

$$0.1\le z_1\le 2,0.1\le z_2\le 10,$$

(34)

$$0.1\le z_3\le 10,0.1\le z_4\le 2,$$

(35)

Subject to:

$$g_1(z)=\tau (z)-{\tau }_{\max }\le 0,$$

(36)

$$g_2(z)=\sigma (z)-{\sigma }_{\max }\le 0,$$

(37)

$$g_3(z)=\delta (z)-{\delta }_{\max }\le 0,$$

(38)

$$g_4(z)=z_1-z_4\le 0,$$

(39)

$${\mathrm{g}}_5(z)=P-P_C(z)\le 0,$$

(40)

$$g_6(z)=0.125-z_1\le 0,$$

(41)

$$g_7(z)=1.10471z_1^2+0.04811z_3{z}_4(14.0+z_2)-5.0\le 0,$$

(42)

where,

$$\tau (z)=\sqrt{{({\tau }^{\prime })}^2+2{\tau }^{\prime }{\tau }^{″}\frac{z_2}{R}+{({\tau }^{″})}^2},$$

(43)

$${\tau }^{\prime }=\frac{P}{\sqrt{2}{x}_1{x}_2},{\tau }^{″}=\frac{MR}{J},$$

(44)

$$M=P(L+\frac{z_2}{2}),$$

(45)

$$R=\sqrt{\frac{z_2^2}{4}+{(\frac{z_1+z_3}{2})}^2},$$

(46)

$$J=2\left\{\sqrt{2z_1{z}_2}\left[\frac{z_2^2}{4}+{\left(\frac{z_1+z_3}{2}\right)}^2\right]\right\},$$

(47)

$$\sigma (z)=\frac{6PL}{z_4{z}_3^2},\delta (z)=\frac{6P{L}^3}{E{z}_3^2{z}_4},$$

(48)

$$P_c(z)=\frac{\sqrt[4.013E]{\frac{z_3^2{z}_4^6}{36}}}{L^2}\left(1-\frac{z_3}{2L}\sqrt{\frac{E}{4G}}\right)\hspace{0.17em},$$

(49)

$$P=6000\hspace{0.17em}lb,L=14\hspace{0.17em}in,{\delta }_{\max }=0.25\hspace{0.17em}in,E=30\times 1^6 psi,$$

(50)

$$G=12\times {10}^6 psi,{\tau }_{\max }=13600 psi,{\sigma }_{\max }=30000 psi$$

(51)

Table 9 provides the output results and best-fit cases for the search methods, and Table 10 documents the statistical output of the search methods. The combined evaluation of these two tables indicates that LARO obtained: the best outcomes for LARO with the same conditioning parameters. LARO has the best optimal value of the average. LARO obtains better results under the same conditioning parameters for the average and STD metrics, and, regarding the worst score metric, LARO performs well compared to different methods. The output results suggest that the LARO algorithm has good applicability for solving the WBD problem. Figure 15 provides the convergence iterations of LARO and the compared algorithms for the WBD problem. The figure shows that the proposed LARO has the best convergence and converges to the vicinity of the optimal solution in the early iterations. In comparison, the AOA has the worst convergence effect and convergence accuracy.

Table 9. The output results of search methods and the best average solution for solving the WBD problem.

Methods	Variables				Average Value
	z1	z2	z3	z4
AOA	0.458604565	5.343890233	7.07733473	0.582699182	4.580028691
WOA	0.213580688	3.755905076	8.582703553	0.275485632	2.030078497
SCA	0.195946114	3.347664206	9.347897424	0.210332519	1.779589725
SSA	0.163373335	4.29728193	9.060682709	0.206031604	1.762193145
MVO	0.193848845	3.212754588	9.065064873	0.205658775	1.676674633
MFO	0.206309461	3.005386467	8.998268989	0.207726916	1.66898036
GJO	0.200505501	3.091330062	9.041439917	0.205824498	1.667357263
GWO	0.204598361	3.017498369	9.038280088	0.205769906	1.662180603
COOT	0.204717093	3.013102973	9.039712907	0.205733798	1.661704081
INFO	0.205729646	2.996844583	9.036623765	0.205729646	1.660343027
LARO	0.20572964	2.996844651	9.03662391	0.20572964	1.660343003

Table 10. The statistical output results of the search methods in solving the WBD problem.

Methods	Best	Worst	Average	STD
AOA	2.794423948	6.845549744	4.580028691	0.91504286
WOA	1.679641671	3.086559568	2.030078497	0.434995141
SCA	1.697528285	1.854267461	1.779589725	0.037930287
SSA	1.662402066	2.101924119	1.762193145	0.118760299
MVO	1.663463164	1.704297699	1.676674633	0.011127428
MFO	1.660343003	1.803084286	1.66898036	0.032089776
GJO	1.661661498	1.681240824	1.667357263	0.005566875
GWO	1.660983594	1.664569661	1.662180603	0.000980854
COOT	1.660411733	1.667097175	1.661704081	0.001993273
INFO	1.660343003	1.660343483	1.660343027	1.08E-07
LARO	1.660343003	1.660343003	1.660343003	1.61E-12

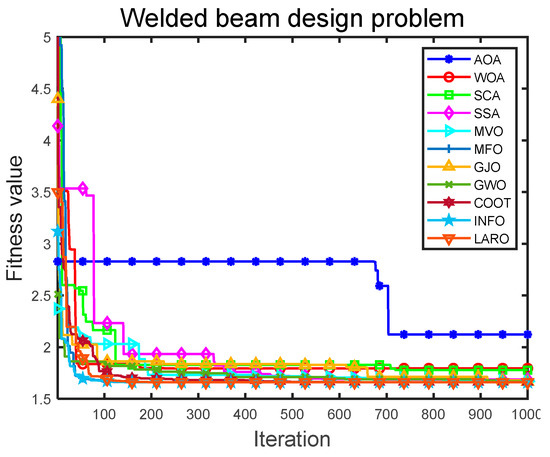
Figure 15. Convergence iteration plot of LARO and comparison algorithms in WBD problem.

5.2. Pressure Vessel Design Problem (PVD)

The structure of the PVD is illustrated in Figure 16. The ultimate aim of the PVD is to keep the total cost of the three aspects of the cylindrical vessel to a minimum. Both edges of the vessel are capped while the top is hemispherical. The PVD has four relevant design variables, including the shell (Ts), the thickness of the head (Th), the radius of entry (R), and the length of the cylindrical section (L) [38]. The mathematical model (four constraints) of the PVD is presented as follows.

$$\overrightarrow{z}=[z_1,z_2,z_3,z_4]=[T_s,T_h,R,L]$$

(52)

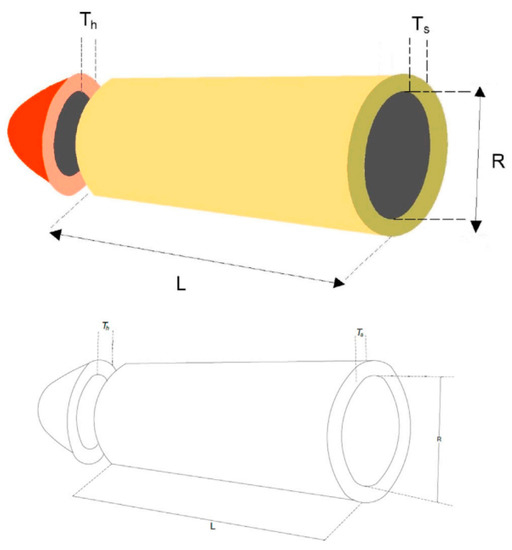
Figure 16. PVD structure.

Minimize:

$$f(\overrightarrow{x})=0.6224z_1{z}_3{z}_4+1.7781z_2{z}_3^2+3.1661z_1^2{z}_4+19.84z_1^2{z}_3,$$

(53)

Variable range:

$$0\le z_1,z_2\le 99,$$

(54)

$$10\le z_3,z_4\le 200.$$

(55)

Subject to:

$$g_1(z)=-z_1+0.0193z_3\le 0,$$

(56)

$$g_2(z)=-z_2+0.00954z_3\le 0,$$

(57)

$$g_3(z)=-\pi z_3^2{z}_4-\frac{4}{3}\pi z_3^3+1,296,000\le 0,$$

(58)

$$g_4(z)=z_4-240\le 0,$$

(59)

Table 11 provides the output results of the different search methods and the suitable average solution for solving the PVD problem. Table 12 documents the statistical outputs of the different methods of solving the PVD problem. By analyzing and evaluating two data, we find that LARO obtains suitable results for LARO with the same conditioning parameters. LARO has the suitable optimal value for the average value. LARO obtains the best case for the average and STD metrics compared to different search methods. The experimental output suggests that the LARO algorithm performs well in completing the PVD problem. Figure 17 provides the convergence iterations of LARO and the comparison algorithms in the PVD problem. From the results, it can be seen that LARO converges to the optimal solution. Compared to the other algorithms, LARO has the fastest convergence rate. SCA and SSA have poor convergence in the early stages, while AOA has poor convergence throughout. The results show that LARO has an advantage over the other algorithms in solving the PVD problem.

Table 11. The output results of the different search methods and suitable average for solving the PVD problem.

Methods	Variables				Average Value
	z1	z2	z3	z4
AOA	23.36588368	22.25433926	61.53559125	107.6810327	19175.76962
MVO	15.24826219	7.671749955	49.48975553	107.3562022	6308.314027
INFO	14.57872411	7.36326842	47.58766135	126.8355535	6220.150067
SSA	14.8454006	7.375997301	48.36652284	118.851193	6207.171299
WOA	15.46867282	7.297109316	49.96403036	112.8166863	6183.161843
COOT	14.53850536	7.378281368	46.86702321	129.8317982	6174.664451
SCA	12.80061756	6.934700092	41.84828537	187.0166496	6066.462829
GJO	12.93626745	6.44471116	42.86942058	179.8874482	5841.359167
MFO	12.66209378	6.561732656	42.01439281	180.7348524	5836.539712
GWO	12.0299589	5.957082715	40.32001823	200	5654.433575
LARO	11.79284485	5.927148417	40.31961872	200	5654.370337

Table 12. The statistical output of the different search methods in completing the PVD problem.

Methods	Best	Worst	Average	STD
AOA	4187.053145	39246.47427	19175.76962	11415.14805
MVO	5902.478907	6989.797802	6308.314027	276.6784548
INFO	5654.370337	7332.841508	6220.150067	372.4182866
SSA	5593.159652	6820.410118	6207.171299	323.7892186
WOA	3239.204029	7896.968613	6183.161843	1062.960652
COOT	5654.370337	6410.086761	6174.664451	201.1646918
SCA	5400.311322	6480.192013	6066.462829	325.5644391
GJO	5654.371874	7348.583394	5841.359167	516.7116594
MFO	5654.370337	6406.492768	5836.539712	241.0245654
GWO	5654.37137	5654.727705	5654.433575	0.078883037
LARO	5654.370337	5654.370337	5654.370337	0

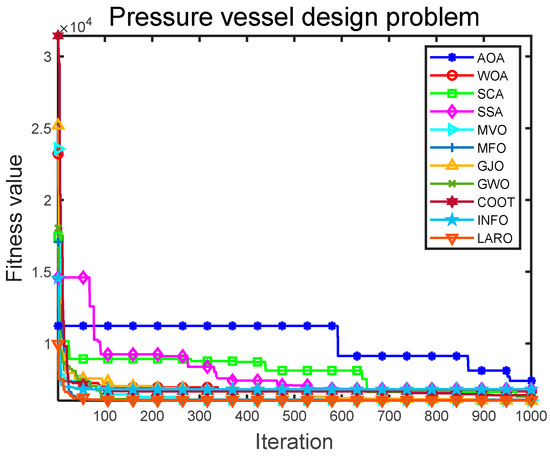
Figure 17. Convergence iteration plot of LARO and comparison algorithms in PVD problem.

5.3. Tension/Compression String Design (TCS)

The most crucial objective of the TCS is to fit the mass optimally. The TCS includes three relevant design variables: wire diameter (d), number of active coils (N), and average coil diameter (D) [38]. A schematic representation of the TCS problem is displayed in Figure 18. The design model of the TCS is given below.

$$\overrightarrow{z}=[z_1,z_2,z_3]=[d,D,N]$$

(60)

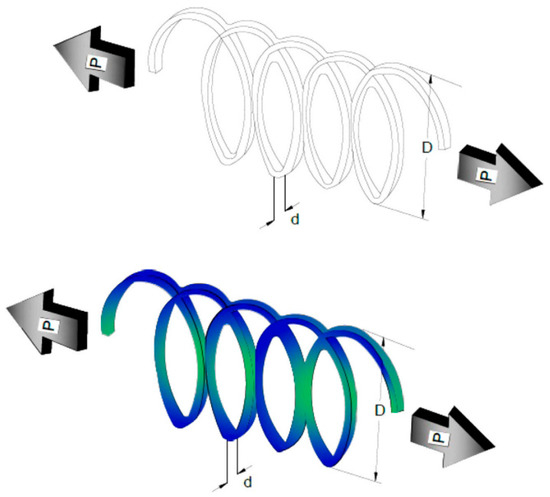
Figure 18. TCS structure.

Minimize:

$$f(z)=(z_3+2)z_2{z}_1^2$$

(61)

Variable range:

$$0.05\le z_1\le 2,\hspace{0.17em}0.25\le z_2\le 1.3,\hspace{0.17em}2\le z_3\le 15,$$

(62)

Subject to:

$$g_1(z)=1-\frac{z_3{z}_2^3}{71785z_1^4}\le 0,$$

(63)

$$g_2(z)=\frac{4z_2^2-z_1{z}_2}{12566(z_2{z}_1^3-z_1^4)}+\frac{1}{5108z_1^2}-1\le 0,$$

(64)

$$g_3(z)=1-\frac{140.45z_1}{z_2^2{z}_3}\le 0,$$

(65)

$$g_4(\overrightarrow{x})=\frac{z_1+z_2}{1.5}-1\le 0.$$

(66)

Table 13 provides the experimental results of all search methods and the best decision variables and the best average objective function values for solving the TCS problem, and provides the four constraint values for all algorithms, and Table 14 gives the statistical results for all search algorithms in solving the TCS problem. By analyzing and evaluating both data, we can find that LARO obtains better experimental results than other comparative algorithms. LARO has the best optimal, average, worst, and STD values. The numerical experimental results suggest that the LARO algorithm is a superior performance method for dealing with TCS. Figure 19 provides the convergence iterations of LARO and the comparison algorithms in the TCS problem. The vertical coordinates in the figure are the log values of the fitness values. From the results, it can be seen that LARO converges to the optimal solution. Compared to other algorithms, LARO has faster convergence. SSA has poor convergence in the early stage, while MVO has poor convergence throughout the process compared to different algorithms. The results show that LARO has an advantage over the other algorithms in solving the TCS problem.

Table 13. The output results of the different search methods and suitable average for solving the TCS problem.

Methods	Variables			Constraints				Average Value
	z1	z2	z3	g1	g2	g3	g4
AOA	0.104108762	0.895747796	9.974698398	−0.727734476	−0.483278426	−2.066153786	−0.333428961	0.159056177
MVO	0.068310124	0.905983841	2.190034779	−0.009015503	−0.000527276	−4.493836611	−0.35047069	0.017530118
WOA	0.058645235	0.561075504	5.965217771	−6.03E-06	−3.83E-09	−4.298337604	−0.58685284	0.013873948
MFO	0.053398387	0.406129633	10.28537326	−7.77E-17	−0.001737508	−4.100612643	−0.693647987	0.013015725
SSA	0.051633058	0.360068897	12.6417731	−5.15E-07	−0.004482237	−4.005031941	−0.72553203	0.013008419
SCA	0.05080346	0.334825245	13.19661988	−0.009149089	−0.004520311	−3.933453135	−0.742914197	0.012934593
COOT	0.053201979	0.397112193	9.864478444	−2.33E-05	−1.59E-05	−4.113557864	−0.699790552	0.012806575
GJO	0.050609914	0.331631961	13.10680319	−0.000992211	−0.000352761	−3.991490705	−0.745172084	0.012725811
INFO	0.05262987	0.380756851	10.2445935	−2.64E-07	−1.50E-06	−4.093957217	−0.711075519	0.012716498
GWO	0.050541414	0.329996477	13.17162459	−0.000408023	−0.000169331	−3.992540736	−0.746308073	0.01271224
LARO	0.051804915	0.359516418	11.12900459	−2.02E-05	−1.50E-05	−4.063715705	−0.724095628	0.012665939

Table 14. The statistical output of the different search methods in completing the TCS problem.

Methods	Best	Worst	Average	STD
AOA	0.013150163	0.622991013	0.159056177	0.173444481
MVO	0.013867314	0.018384424	0.017530118	0.00099031
WOA	0.012666252	0.017773302	0.013873948	0.001345825
MFO	0.012665268	0.015266478	0.013015725	0.000614519
SSA	0.012704122	0.01460674	0.013008419	0.000441887
SCA	0.012802077	0.013207983	0.012934593	0.00012683
COOT	0.012665665	0.013373361	0.012806575	0.000194775
GJO	0.012683357	0.012740967	0.012725811	1.61E-05
INFO	0.012665233	0.012945697	0.012716498	6.46E-05
GWO	0.012681434	0.012731782	0.01271224	1.55E-05
LARO	0.012665275	0.012669109	0.012665939	9.49E-07

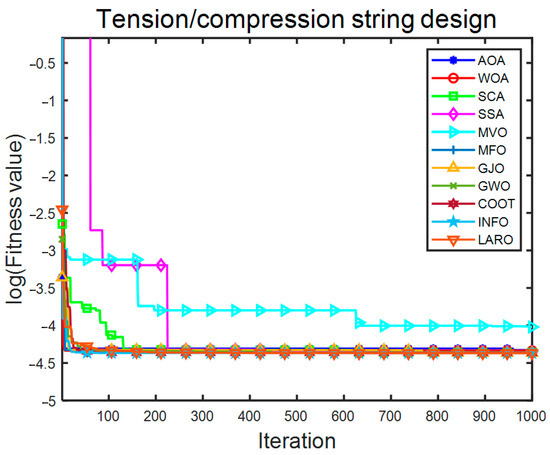
Figure 19. Convergence iteration plot of LARO and comparison algorithms in TCS problem.

5.4. Gear Train Design (GTD)

The ultimate requirement of the GTD problem is to make the gear set with the most appropriate gear ratio cost to prepare the composite gear train. Figure 20 illustrates a schematic diagram of the GTD problem. There are four relevant integer variables for the GTD, where the four variables stand for the size of the teeth of four other gears [26]. These design variables represent the number of teeth on the gears and are denoted as T_a, T_b, T_c, and T_d. The mathematical model of the GTD is given below.

$$\overrightarrow{z}=[z_1,z_2,z_3,z_4]=[T_a,T_b,T_c,T_d]$$

(67)

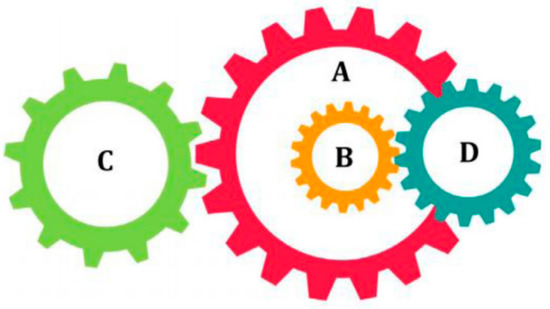
Figure 20. GTD structure.

Minimize:

$$f(\overrightarrow{x})={(\frac{1}{6.931}-\frac{z_1{z}_2}{z_3{z}_4})}^2$$

(68)

Variable range:

$$12\le z_1,z_2,z_3,z_4\le 60,$$

(69)

Table 15 provides the experimental results for all search algorithms and the best average solution for the GTD problem. Table 16 presents the statistical output for the different search methods in solving the GTD. The analysis shows that LARO gives better experimental results compared to other search algorithms. LARO provides the best optimal, average, worst, and STD value. Numerical experiments show that the LARO algorithm can obtain good accuracy in solving the GTD problem. Figure 21 provides the convergence iteration results of LARO and the comparison algorithm on the GTD problem. The vertical coordinates in the figure are the log values of the adaptation values. From the results, it can be seen that LARO converges to the optimal solution. LARO’s convergence speed and accuracy are reasonable compared to other algorithms. SSA, GWO, INFO, and LARO all have good convergence, while AOA has poor convergence throughout the process compared to different algorithms. The results show that LARO has an advantage over other algorithms in solving the GTD problem.

Table 15. The output results of the different search methods and suitable average for solving the GTD problem.

Methods	Variables				Average Value
	z1	z2	z3	z4
AOA	27	19	49	47	0.00587623
MFO	19	21	47	52	5.37E-09
SCA	22	20	52	50	1.17E-09
WOA	17	18	45	45	8.45E-10
MVO	22	16	49	47	6.45E-10
SSA	18	17	42	50	6.15E-10
COOT	18	19	47	48	2.98E-10
INFO	18	22	49	50	2.95E-10
GJO	20	20	50	50	1.76E-10
GWO	18	19	49	47	1.66E-10
LARO	19	19	47	49	1.19E-11

Table 16. The statistical output of the different search methods in completing the GTD problem.

Methods	Best	Worst	Average	STD
AOA	1.09E-07	0.030969704	0.00587623	0.007816411
WOA	2.31E-11	2.18E-08	5.37E-09	5.89E-09
MFO	2.31E-11	2.36E-09	1.17E-09	6.59E-10
SCA	2.70E-12	2.36E-09	8.45E-10	8.19E-10
MVO	2.70E-12	1.36E-09	6.45E-10	4.78E-10
GJO	2.70E-12	2.36E-09	6.15E-10	6.58E-10
INFO	2.70E-12	2.36E-09	2.98E-10	5.83E-10
SSA	2.31E-11	1.36E-09	2.95E-10	4.25E-10
GWO	2.70E-12	1.36E-09	1.76E-10	3.42E-10
COOT	2.70E-12	9.92E-10	1.66E-10	3.43E-10
LARO	2.70E-12	2.31E-11	1.19E-11	1.04E-11

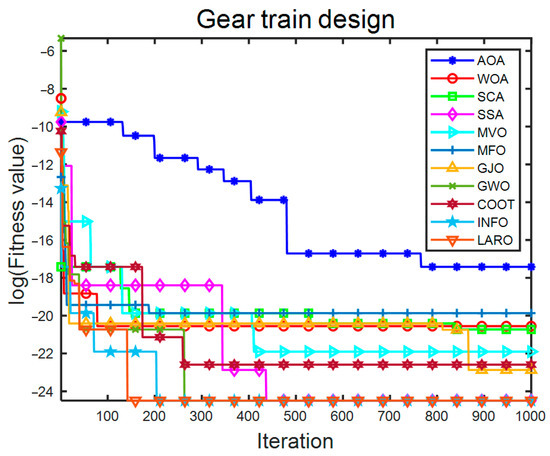
Figure 21. Convergence iteration plot of LARO and comparison algorithms in GTD problem.

5.5. Speed Reducer Design (SRD)

The ultimate aim of the SRD is to ensure that the weight of the mechanical equipment is minimized while satisfying the 11 constraints. The schematic design diagram of the SRD is shown in Figure 22. The SRD has seven relevant variables, including the bending stress of the gear teeth, the covering stress, the transverse deflection of the shaft, and the stress in the shaft, used to control the facilities of the SRD problem [38]. Here, z₁ is the tooth width, z₂ is the tooth mode, and z₃ is the discrete design variable representing the teeth in the pinion. Similarly, z₄ is the length of the first axis between the bearings and z₅ is the length of the second axis between the bearings. The sixth and seventh design variables (z₆ and z₇) are the diameters of the first and second shafts, respectively. The design model of the SRD (11 constraints and objective functions) is given below.

$$\overrightarrow{z}=[z_1,z_2,z_3,z_4,z_5,z_6,z_7]=[b,m,p,l_1,l_2,d_1,d_2]$$

(70)

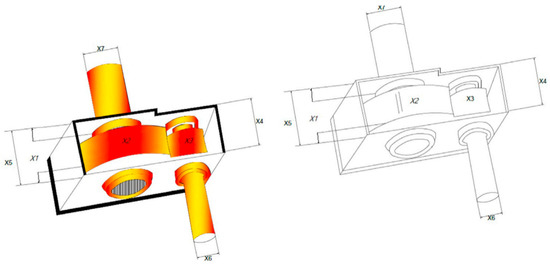
Figure 22. SRD structure.

Minimize:

$$\begin{array}{l}f(\overrightarrow{x})=0.7854z_1{z}_2^2(3.3333z_3^2+14.9334z_3-43.0934)\\ \hspace{1em}\hspace{1em}\hspace{1em}-1.508z_1(z_6^2+z_7^2)+7.4777(z_6^3+z_7^3),\end{array}$$

(71)

Variable range:

$$2.6\le z_1\le 3.6,0.7\le z_2\le 0.8,$$

(72)

$$17\le z_3\le 28,7.3\le z_4\le 8.3,$$

(73)

$$7.8\le z_5\le 8.3,2.9\le z_6\le 3.9,5\le z_7\le 5.5.$$

(74)

Subject to:

$$g_1(z)=\frac{27}{z_1{z}_2^2{z}_3}-1\le 0,$$

(75)

$$g_2(z)=\frac{397.5}{z_1{z}_2^2{z}_3^2}-1\le 0,$$

(76)

$$g_3(z)=\frac{1.93z_4^3}{z_2{z}_3{z}_6^4}-1\le 0,$$

(77)

$$g_4(\overrightarrow{x})=\frac{1.93z_5^3}{z_2{z}_3{z}_7^4}-1\le 0,$$

(78)

$$g_5(z)=\frac{\sqrt{{(\frac{745z_4}{z_2{z}_3})}^2+16.9\times {10}^6}}{110.0z_6^3}-1\le 0,$$

(79)

$$g_6(z)=\frac{\sqrt{{(\frac{745z_4}{z_2{z}_3})}^2+157.5\times {10}^6}}{85.0z_6^3}-1\le 0,$$

(80)

$$g_7(z)=\frac{z_2{z}_3}{40}-1\le 0,$$

(81)

$$g_8(z)=\frac{5z_2}{z_1}-1\le 0,$$

(82)

$$g_9(z)=\frac{z_1}{12z_2}-1\le 0,$$

(83)

$$g_{10}(z)=\frac{1.5z_6+1.9}{z_4}-1\le 0,$$

(84)

$$g_{11}(z)=\frac{1.1z_7+1.9}{z_5}-1\le 0,$$

(85)

Table 17 shows the most suitable outputs from LARO and the different selection comparison methods in dealing with the SRD problem. Table 18 gives the statistics of all search algorithms. It can be found that LARO outperforms the different search algorithms in terms of optimal performance. LARO has the best optimal, worst, average, and STD values for the same maximum iterations, while the smaller STD also indicates that LARO has good robustness. Therefore, LARO is effective in optimizing SRD solutions. Figure 23 provides the results of the convergence iterations of the LARO and comparison algorithms on the SRD problem. The vertical coordinates in the figure are the log values of the adaptation values. From the results, it can be seen that LARO converges to the optimal solution. The convergence speed and convergence accuracy of LARO are good compared to other algorithms. All the algorithms converge to near the optimal solution in the early iteration. The results show that LARO is an excellent algorithm for solving the SRD problem.

Table 17. The output results of the different search methods and suitable average for solving the SRD problem.

Methods	Variables							Average Value
	z1	z2	z3	z4	z5	z6	z7
AOA	3.467971409	0.723513271	21.74751447	7.880516747	8.061914543	3.576430883	5.404132188	4264.527578
WOA	3.523843197	0.7	17.1345532	7.702300289	7.976748724	3.443370435	5.319866042	3085.450381
SCA	3.593050846	0.700150831	17.0002346	7.633189151	8.058133822	3.428687329	5.319457954	3084.05852
MVO	3.519000807	0.7	17	7.496881857	7.969722319	3.428863386	5.287122464	3030.335706
SSA	3.515761593	0.700000002	17	7.788164831	8.039769946	3.413625503	5.286767009	3029.139433
GJO	3.505489383	0.700118821	17.00158842	7.6603505	7.906273576	3.364100739	5.288853105	3009.67407
GWO	3.502240237	0.700011154	17.00068413	7.593587258	7.889626	3.354667829	5.287834784	3003.700073
MFO	3.505	0.7	17	7.35	7.825	3.350640526	5.286692041	2999.286604
COOT	3.500000039	0.700000001	17	7.300000174	7.8	3.350541026	5.28668327	2996.301629
INFO	3.5	0.7	17	7.3	7.8	3.350540949	5.28668323	2996.301563
LARO	3.5	0.7	17.00002328	7.300000374	7.8	3.350540931	5.286683226	2996.301563
AOA	3.467971409	0.723513271	21.74751447	7.880516747	8.061914543	3.576430883	5.404132188	4264.527578

Table 18. The statistical output of the different search methods in completing the SRD problem.

Methods	Best	Worst	Average	STD
AOA	3227.920049	6010.091558	4264.527578	742.9424323
WOA	3012.692509	3392.408954	3085.450381	90.75866975
SCA	3047.198643	3133.520817	3084.05852	23.93469942
MVO	3003.777974	3072.80323	3030.335706	18.55650452
SSA	3002.149409	3094.789692	3029.139433	23.381985
GJO	3000.131855	3029.622228	3009.67407	6.744875293
GWO	2999.778235	3009.290864	3003.700073	2.904547932
MFO	2996.301563	3035.578647	2999.286604	9.103443233
COOT	2996.301564	2996.301848	2996.301629	9.34E-05
INFO	2996.301563	2996.301563	2996.301563	4.00E-08
LARO	2996.301563	2996.301563	2996.301563	9.54E-10

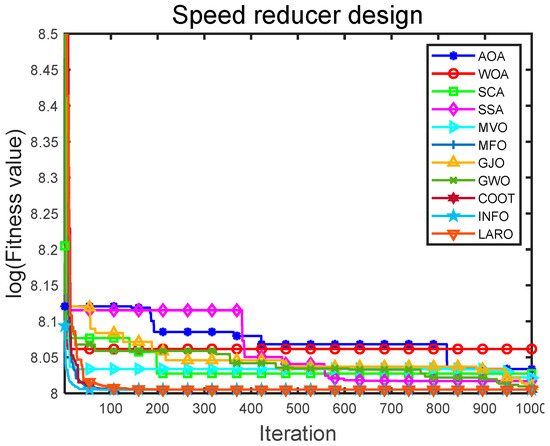
Figure 23. Convergence iteration plot of LARO and comparison algorithms in SRD problem.

5.6. Tubular Column Design (TCD)

The TCD problem is to ensure that the cost of designing a homogeneous column with a tubular cross-section is minimized under the condition that six constraints are satisfied with suitable compressive loads [4]. The schematic design diagram of the TCD is illustrated in Figure 24. Two material-related conditions to be established for the TCD problem include yield stress σ_y = 500 kgf/cm² and modulus of elasticity E = 0.85 × 10⁶ kgf/cm². The mathematical model of the TCD problem is given below.

$$\overrightarrow{z}=[z_1,z_2]=[d,t]$$

(86)

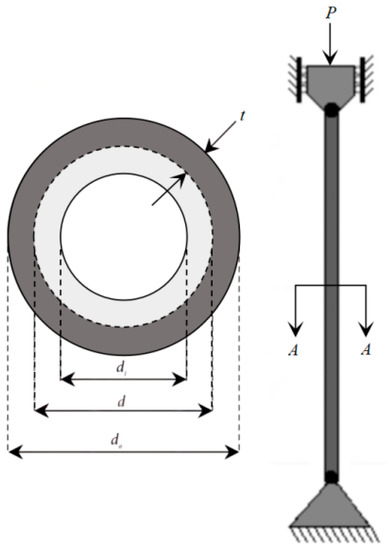
Figure 24. TCD structure.

Minimize:

$$f(z)=9.8z_1{z}_2+2z_1$$

(87)

Variable range:

$$2\le z_1\le 14,0.2\le z_2\le 0.8,$$

(88)

Subject to:

$$g_1(z)=\frac{P}{\pi \hspace{0.17em}{z}_1{z}_2{\sigma }_y}-1\le 0,$$

(89)

$$g_2(z)=\frac{8P{L}^2}{{\pi }^{3}E\hspace{0.17em}{z}_1{z}_2(z_1^2+z_2^2)}-1\le 0,$$

(90)

$$g_3(z)=\frac{2.0}{z_1}-1\le 0,$$

(91)

$$g_4(z)=\frac{z_1}{14}-1\le 0,$$

(92)

$$g_5(z)=\frac{0.2}{z_2}-1\le 0,$$

(93)

$$g_6(z)=\frac{z_2}{8}-1\le 0.$$

(94)

Table 19 presents the most suitable outputs obtained by the LARO and other selection comparison algorithms for the TCD problem. Table 20 gives the statistics of all search algorithms dealing with the TCD. It can be noticed that LARO outperforms the different search methods in terms of optimal performance. LARO has the best optimal, worst, average, and STD values for the same maximum iterations, while the smaller STD also indicates that LARO has good robustness. Therefore, LARO is effective in optimizing the solution of TCD problems. Figure 25 provides the results of the convergence iterations of the LARO and comparison algorithms on the TCD problem. From the results, it can be seen that LARO converges to the optimal solution. LARO converges faster compared to the other algorithms. MVO converges poorly in the early stages, while AOA and WOA converge poorly throughout the process compared to the different algorithms. The results show that LARO has an advantage over the other algorithms in solving the TCD problem.

Table 19. The output results of the different search methods and suitable average for solving the TCD problem.

Methods	Variables		Average Value
	z1	z2
AOA	6.012282217	0.315448278	30.15798064
WOA	5.489385602	0.292558846	26.70565649
SCA	5.470272666	0.292197171	26.60424231
GJO	5.453519738	0.291625884	26.49283541
GWO	5.452340993	0.291660602	26.4889654
MVO	5.452234536	0.29165614	26.4882102
COOT	5.452180789	0.291626468	26.48636379
INFO	5.452181458	0.291626391	26.48636292
SSA	5.45218082	0.29162643	26.48636194
MFO	5.452180736	0.291626429	26.48636147
LARO	5.452180736	0.291626429	26.48636147
AOA	6.012282217	0.315448278	30.15798064

Table 20. The statistical output of the different search methods in completing the TCD problem.

Methods	Best	Worst	Average	STD
AOA	26.81127923	34.46559721	30.15798064	2.258475608
WOA	26.49962106	27.5573071	26.70565649	0.23330885
SCA	26.52613096	26.69821662	26.60424231	0.050054727
GJO	26.48802612	26.49798174	26.49283541	0.002808313
GWO	26.48685573	26.49234446	26.4889654	0.001724975
MVO	26.48681494	26.49219586	26.4882102	0.001225866
COOT	26.48636148	26.4863693	26.48636379	2.65E-06
INFO	26.48636147	26.48639027	26.48636292	6.44E-06
SSA	26.48636153	26.48636257	26.48636194	3.10E-07
MFO	26.48636147	26.48636147	26.48636147	3.09E-10
LARO	26.48636147	26.48636147	26.48636147	3.65E-15

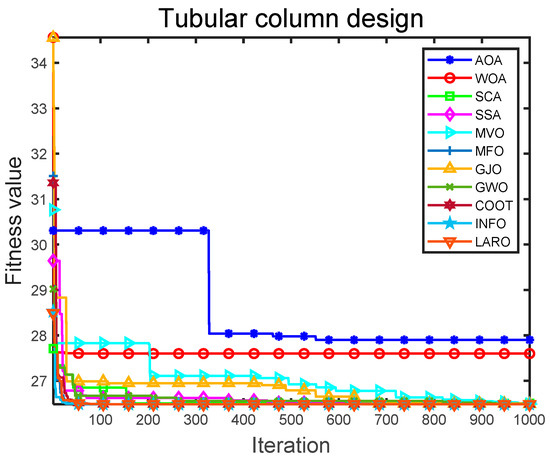
Figure 25. Convergence iteration plot of LARO and comparison algorithms in TCD problem.

6. Conclusions

In this study, an effective metaheuristic method called the enhanced ARO algorithm (LARO) is proposed. LARO is a variant of the ARO algorithm. To boost the global finding ability of ARO, the avoidance of local solutions and international exploration of LARO are designed by making full use of the Lévy flight strategy. In addition, local exploitation of LARO is achieved by using the selective opposition strategy. The most remarkable feature of LARO is that it has a straightforward structure and high computational accuracy, often requiring only the basic parameters (i.e., population size and termination conditions) for solving optimization problems. We tested the performance of LARO with 23 test functions, the CEC2019 test suite, and six mechanical engineering design problems. The experimental results show that LARO can obtain the optimal average solution in 16 of the 23 classical test functions and obtain the smallest average rank (2.3478). Additionally, LARO obtains the best solutions for five and seven functions in CEC2017 and CEC2019, respectively. The conclusion shows that the strategies for improved ARO are very effective in improving the optimization performance. However, there is still room for further improvement in the exploration ability of LARO when facing the CEC2017 test functions. In the mechanical optimization problem, all six practical problems are complex problems with multiple nonlinear constraints and multiple local solutions, and the output results show that LARO can obtain the best decision variables and objective function values. Because of its excellent convergence, exceptional exploration ability, and lack of need to fine-tune the initial parameters, LARO has excellent potential to handle optimization problems with various characteristics.

In future work, this study will expand the versions of the ARO algorithm to include the ARO algorithm for opposing learning initialization, the multi-objective ARO algorithm, the binary ARO algorithm, and the discrete version of the ARO algorithm [57,58,59,60,61,62]. In addition, we will focus on applying LARO to various complex real-world engineering optimization problems, such as hyperparametric optimization of machine learning algorithms, urban travel recommendations in intelligent cities, job-shop scheduling problems, image segmentation, developable surface modeling [63], and smooth path planning for mobile robots.