Abstract
In this paper, we focus on a developable surface tangent to a timelike surface along a curve in Minkowski 3-space, which is called the osculating developable surface of the timelike surface along the curve. The ruling of the osculating developable surface is parallel to the osculating Darboux vector field. The main goal of this paper is to classify the singularities of the osculating developable surface. To this end, two new invariants of curves are defined to characterize these singularities. Meanwhile, we also research the singular properties of osculating developable surfaces near their lightlike points. Moreover, we give a relation between osculating Darboux vector fields and normal vector fields of timelike surfaces along curves from the viewpoint of Legendrian dualities. Finally, some examples with symmetrical structures are presented to illustrate the main results.
Keywords:
osculating developable surfaces; Lorentzian support functions; singularities; Legendrian dualities MSC:
57R45; 58K05
1. Introduction
Minkowski space, which is regarded as the mathematical setting for the theory of relativity, has been studied by both physicists and differential geometers in large amounts; see, for example, [,,,,,,]. As is known to all, there exist spacelike surfaces, timelike surfaces and lightlike surfaces in Minkowski 3-space. Timelike surfaces have a vital role in theoretical physics, which is usually called world sheets. In string theory, the world sheet is generated by a string, which moves through space–time. Recently, some new results concerning world sheets were obtained by physicists. For instance, Rojas introduced a covariant framework to research the stability of small perturbations on the gonihedric string model by variational techniques. A general expression of the world sheet perturbations is displayed in []. Singularity theory, on the other hand, which is a direct descendant of differential calculus, appeals to the research about geometry, equations and other disciplines (see [,,,,,,,,,,,,,,,,,,,,,,,,,,,,]). A singularity is a point such that a function reaches a maximum/minimum or a submanifold is no longer smooth and regular. In this paper, we focus on a non-lightlike curve on a timelike surface and a developable surface tangent to the timelike surface along the curve in Minkowski 3-space. We focus on the investigation of the singularities of such a developable surface here.
Darboux frames along curves on surfaces in Euclidean 3-space are classical and famous. By using Darboux frames, Hananoi and Izumiya introduced a normal developable surface of a surface along a curve in []. At this point, the developable surface is orthogonal to the surface along the curve. Moreover, there exists a Lorentzian version of Darboux frames along curves on surfaces []. Inspired by the above work, we define a special direction in the Darboux frame at each point of the non-lightlike curve, which is directed by a vector in the tangent plane to the timelike surface. In this case, the vector field is called an osculating Darboux vector field along the non-lightlike curve. There exist three invariants with respect to the Darboux frame. Under a certain condition of these invariants, we define a ruled surface along the non-lightlike curve, which is called an osculating developable surface. The rulings of the osculating developable surface are directed by the osculating Darboux vector field. We show the relation between normalized osculating Darboux vector fields and normal vector fields of timelike surfaces along curves from the viewpoint of Legendrian dualities in Section 3. Moreover, the osculating developable surface is also shown as the envelope of the tangent planes of the timelike surface along the curve. By using the three invariants above, we introduce two new invariants, which are closely related to the singularities of osculating developable surfaces. In fact, one of these invariants equals zero constantly if and only if the osculating developable surface is a cylindrical surface. At this time, the non-lightlike curve is a contour generator associated with an orthogonal projection (Theorem 2, (A)). In the case that the first invariant never vanished, the other invariant equals zero constantly if and only if the osculating developable surface is a conical surface. Meanwhile, the non-lightlike curve is a contour generator associated with a central projection (Theorem 2, (B)). The concept of contour generators plays a significant role in computer vision theory []. By using these two invariants, we also show the classification of the singularities of the osculating developable surface (Theorem 3). Lightlike submanifolds are degenerate submanifolds and they were systematically studied in []. Here, we consider the singularities of the osculating developable surface near its lightlike rulings (Corollary 2). In Section 6, the geometric meaning of the second invariant is further discussed.
In Section 7, we consider curves on special timelike surfaces. Since de Sitter space is a classical model for studying Lorentzian spherical geometry and de Sitter 2-space is a timelike surface in Minkowski 3-space, we consider osculating developable surfaces of de Sitter 2-space along curves. If we consider the small spacelike circle or the great timelike hyperbolic curve, the osculating developable surface along the curve is a cylindrical surface. If we consider the great spacelike circle or the small timelike hyperbolic curve, the osculating developable surface along the curve is a conical surface (Propositions 5 and 6). In order to illustrate Theorem 6, we also display an example of a timelike curve on de Sitter 2-space so that the osculating developable surface along the curve has swallowtail singularities. At last, we consider non-lightlike curves on timelike surfaces of revolution. We show that the osculating developable surface along a timelike meridian curve is a cylinder, while the osculating developable surface along a spacelike circle is a cylinder or a cone.
We assume that all manifolds and maps are throughout the paper, unless contrary statements are given.
2. Basic Notions
We introduce some basic notions in this section. Let be a 3-dimensional vector space. For any two vectors
and , the pseudo-scalar product of them is defined by
We call the pair , a Minkowski 3-space and denote it as
For any two vectors we obtain a vector that is defined by
where is the canonical basis of . We say that a non-zero vector is timelike, spacelike or lightlike if , or , respectively. The norm of is defined by , in which sign() denotes the signature of , which is given by , or 1 when is timelike, lightlike or spacelike, respectively. Moreover, for a vector and a real number we define a plane whose normal vector is as Then, we call a spacelike plane, a timelike plane or a lightlike plane if is timelike, spacelike or lightlike, respectively.
Let be a regular curve (i.e., ), where I is an open interval. For any , the curve is called timelike, lightlike or spacelike if , or , respectively. We say that is a non-lightlike curve if is a spacelike curve or a timelike curve. On the other hand, the arc-length of a non-lightlike curve measured from is . It is obvious that the parameter s is determined such that =1 for a non-lightlike curve. Then, is called the unit tangent vector of at s. We now define the hyperbolic space by
the de Sitter 2-space by
and the close lightcone by
We set a timelike embedding from an open subset We denote and identify M and U according to the embedding Then, we say that X is a timelike embedding if its tangent space is a timelike plane at any point Moreover, let be a regular curve. Then, another curve is defined by At this time, we say that is a curve on the timelike surface
In this paper, we consider as a non-lightlike curve; then, we can reparametrize it by the arc-length s. Therefore, we can obtain the unit tangent vector of Taking into consideration that X is a timelike embeding, then we can acquire a spacelike normal vector field along Therefore, we construct a vector . Thus, we have a pseudo-orthonormal frame along Moreover, we also have the following Frenet–Serret-type formulae:
where , and . We say that is the normal curvature, is the geodesic curvature and is the geodesic torsion of , respectively. Meanwhile, we say that
- (1)
- is an asymptotic curve of M if and only if
- (2)
- is a geodesic curve of M if and only if
- (3)
- is a principal curve of M if and only if
In addition, a vector field along , which is defined by
is called an osculating Darboux vector along . If and , we have the following expressions of normalized osculating Darboux vector fields:
On the other hand, we list some basic notions and important properties of ruled surfaces and developable surfaces here. Let and be -mappings. Then, we define a mapping by
which is called a ruled surface in At the same time, we call a base curve and a director curve. Moreover, the straight line defined for a fixed is called a ruling. Moreover, we know that the ruled surface is developable if and only if
If the director curve satisfies , then we say that is a cylinder. If the singularity of the developable surface is a constant, then we say is a cone.
Finally, we recall relevant notions of contour generators, briefly. Let be a surface and be the unit normal vector field. Then, for a fixed vector , the contour generator of the orthogonal projection with respect to the direction is defined by
Actually, the set above is the singular set of the orthogonal projection with respect to the direction . Furthermore, for a fixed point , the definition of the contour generator of the central projection with the center is given by
It can be found that the set is the singular set of the central projection with the center . The concept of contour generators plays a significant role in computer vision theory [].
3. Legendrian Dualities
In this section, we recall some properties of Legendrian submanifolds and contact manifolds [].
Let M be a -dimensional smooth manifold and W be a tangent hyperplane field on Such a field is defined as the field of zeros of a 1-form ℘ locally. We say that the tangent hyperplane field W is non-degenerate if at any point of Then, we say that the pair is a contact manifold if W is a non-degenerate hyperplane field. In this case, ℘ and W are called the contact form and the contact structure, respectively. Suppose: is a diffeomorphism between contact manifolds and Then, is called a contact diffeomorphism if Meanwhile, contact manifolds and are contact diffeomorphic if there exists the contact diffeomorphism: Moreover, a submanifold of a contact manifold is Legendrian if and hold at any In addition, the mapping i is called an isotropic mapping if at any A smooth fiber bundle is a Legendrian fibration if its total space E is provided with a contact structure and its fibers are Legendrian submanifolds. Suppose to be a Legendrian fibration. Then, for a Legendrian submanifold the map is called a Legendrian map. Meanwhile, the image of a Legendrian map is called a wavefront set of i. For any as is known to all, there exists a local coordinate system near y such that
Simultaneously, the contact structure is given by the 1-form
In [], the Legendrian dualities between pseudo-spheres in Minkowski space are introduced, which become basic tools for studying submanifolds in pseudo-spheres. Firstly, we define 1-forms in . Then, we consider the following:
- (1)
- (a)(b)(c)
- (2)
- (a)(b)(c)
Here, Moreover, we remark that and define the same tangent hyperplane field over , which are denoted by It has been shown that is a contact manifold and are Legendrian fibrations. Then, if we say that is - to Details of Legendrian fibrations can be found in []. Then, we have the following duality theorem.
Theorem 1.
Let be a non-lightlike curve with and .
- (1)
- If then is a -dual of
- (2)
- If then is a -dual of
Proof.
We define a mapping by Then, we have and . Thus, is an isotropic mapping, so that is a -dual of We define another mapping
Then, we can also show that is an isotropic mapping. This means that (2) holds. □
4. Osculating Developable Surfaces
We investigate a special surface of a given timelike surface M along a non-lightlike curve in this section.
For a non-lightlike curve with , we define a mapping as
This is a ruled surface. Then, we have
Thus, we obtain
This means that is a developable surface. In this case, we call an osculating developable surface of M along . Moreover, we show two invariants , of as follows:
On the other hand, by calculation, we obtain if and only if
which is equivalent to . We also calculate that
Therefore, is a singular point of if and only if and If is a regular point (namely, ), then the normal vector of at has the same direction of the normal vector of M at . Therefore, it is reasonable that we call the osculating developable surface of M along . On the other hand, we use these two invariants to characterize the contour generators of M as the following.
Theorem 2.
Let be a non-lightlike curve with . Then, we have the following:
- (A)
- The following are equivalent:
- (1)
- is a cylinder,
- (2)
- ,
- (3)
- is a non-lightlike contour generator with respect to an orthogonal projection.
- (B)
- If , then the following are equivalent:
- (1)
- is a cone,
- (2)
- (3)
- is a non-lightlike contour generator with respect to a central projection.
Proof.
(A) By definition, is a cylinder if and only if . Because if and only if , it means that (1) is equivalent to (2). Suppose that (3) holds; there exists a vector such that Then, for some real numbers . Since we have , so that is parallel to . Condition (1) holds. It is obvious that (1) implies (3).
(B) If the condition (1) is satisfied, then the singular value set of is a point. We consider the following vector-valued function defined by
Therefore, if the condition (1) holds, it is equivalent to saying that the condition holds. By a straightforward calculation, we obtain
This means that the conditions (1) and (2) are equivalent. According to the definition of the contour generator with respect to a central projection, condition (3) implies that there exists such that If condition (1) holds, then we know that is constant. Therefore, for the constant vector , we have
This means that condition (3) is satisfied. Conversely, by condition (3), there exists a constant vector such that By taking the derivative at both sides, we have
Then, there exists such that . By taking the derivative again, we obtain
Then, we obtain
Hence, is constant; namely, condition (1) holds. □
Corollary 1.
The osculating developable surface is non-cylindrical if and only if .
According to the conclusions in Theorem 2, the invariants and might be closely related to the singularities of osculating developable surfaces. In fact, by using these two invariants, we can obtain the classification for the singularities of osculating developable surfaces of M along non-lightlike curves. The main result of this paper is as follows.
Theorem 3.


Let be a non-lightlike curve with . Then, we have the following.
- (A)
- The osculating developable surface of M along non-lightlike curve is not singular at if and only if .
- (B)
- The osculating developable surface of M along non-lightlike curve is locally diffeomorphic to the cuspidal edge at if(i) , and , or(ii) , andor(iii) and .
- (C)
- The osculating developable surface of M along non-lightlike curve is locally diffeomorphic to the swallowtail at if , , and .

Figure 1.
Cuspidal edge.

Figure 2.
Swallowtail.
Let be a non-lightlike curve. If , then is a lightlike vector, and we call a lightlike point of . If is a non-lightlike curve with , then along are lightlike vectors. In this case, we say that is a lightlike osculating developable surface of M along . Then, we have the following corollary.
Corollary 2.
Let be a non-lightlike curve with . Then, we have the following:
- (1)
- If , the lightlike osculating developable surface of M along has no singular points.
- (2)
- If is not a lightlike osculating developable surface of M along and is a lightlike point of , then the osculating developable surface is locally diffeomorphic to the cuspidal edge at if , and . The osculating developable surface of M along non-lightlike curve is locally diffeomorphic to the swallowtail at if , , and .
5. Lorentzian Support Functions
5.1. Unfoldings of Lorentzian Support Functions
We show a family of functions on a non-lightlike curve, which will be useful for studying invariants of curves on timelike surfaces in this section. Let be a non-lightlike curve. Then, we define a function by . Here, G is called a Lorentzian support function on with respect to . We denote for any . Then, we have the following proposition.
Proposition 1.
Let be a non-lightlike curve with . Then, we have
- (1)
- if and only if there exist such that .
- (2)
- if and only if there exists such that .
Suppose . Then, we have the following:
- (3)
- if and only if .
- (4)
- if and only if and .
- (5)
- if and only if , and .
Suppose . Then, we have
- (6)
- if and only if (namely, ) and there exists such that .
- (7)
- if and only if one of the following equations holds:(a) , , namely,and(b) (namely, ), and there exists such that .
Proof.
Since , we have the following:
We know that is a pseudo-orthonormal frame for the formula , so the assertion (1) holds.
By the formula , if and only if there exist such that and . Thus, there exists such that and . The assertion (2) holds.
Moreover, by the formula , if and only if
and
Since , then . It follows that and , or and This means that the proof of the assertions (3) and (6) is complete.
Suppose that . Then, by the formula (iv), if and only if
at . Since
then the above equation is equivalent to . It follows that The assertion also holds in reverse.
Suppose that . Then, by the formulae (iv), if and only if , and there exists such that and
It follows that
and
or
Moreover, is equivalent to Then, we have (6) and (7).
By a similar discussion to the above, we have the assertion (5). This completes the proof. □
For the sake of proving Theorem 3, we need some general results on the singularity theory for the germs of functions. For detailed descriptions, please refer to the book []. Let be a function germ and . We say F is an r-parameter unfolding of f. If for all and , then we say f has -singularity at . We also say f has -singularity at if for all . Meanwhile, let F be an r-parameter unfolding of f and f has -singularity at ; we define the -jet of the partial derivative at as
If the rank of the matrix is k, where , then F is called an R-versal unfolding of The discriminant set of F is defined by
Then, there exists the following famous result (see []).
Theorem 4.
Let be an r-parameter unfolding of that has -singularity at . Supposing that F is an R-versal unfolding of if then the germ of at is diffeomorphic to if then the germ of at is diffeomorphic to
For the sake of proving Theorem 3, we have the following.
Proposition 2.
Let be a non-lightlike curve with and be the Lorentzian support function on with respect to . If has an -singularity at , then G is an R-versal unfolding of Here, we suppose for
Proof.
We denote that , and . Then,
so that
Therefore, the 2-jet is
We denote the following matrix:
According to the Frenet–Serret-type formulae, we obtain
Therefore, rank . Moreover, the rank of
is always 2. Then, the rank of
is also always 2.
If has an -singularity at , then G is an R-versal unfolding of This completes the proof. □
5.2. Proof of Theorem 3
Proof Theorem 3.
Now, we prove the main result of Theorem 3. By straightforward calculations, we obtain
We know that is non-singular if and only if
It is equivalent to . Thus, we finish the proof of the assertion (1).
According to Proposition 1, the discriminant set of the Lorentzian support functions G of with respect to is the osculating developable surface of M along
Suppose By assertions (3), (4) and (5) in Proposition 1, has the -singularity (respectively, the -singularity) at if and only if
and (respectively, and ). Then, by Theorem 4 and Proposition 2, we know assertions (2), (i) and (3) hold.
Suppose By assertions (6) and (7) of Proposition 1, has the -singularity at if and only if , and
It means that
and
or
Since is equivalent to By Theorem 4 and Proposition 2, we obtain the assertions (2), (ii) and (iii). Therefore, we finish the proof. □
6. Invariants of Non-Lightlike Curves on Timelike Surfaces
In this section, we will consider geometric meanings of the invariant .
Let be a curve and be a submersion. We say that and have the contact of at least order k at if the function satisfies . Moreover, if and have the contact of at least order k at and satisfy the condition , then we say that and have the contact of order k at . Meanwhile, for any , we define the function as . Then, we have
For a fixed , is a timelike plane that is defined by where . For the reason that this plane is pseudo-orthogonal to , it is parallel to the tangent plane at . On the other hand, we can represent the tangent bundle of as follows:
Let be the canonical projection, where . Then, is a bundle over . Moreover, a map is defined by ; then, is a bundle isomorphism. Here, we denote . Meanwhile, we call it an affine tangent bundle over through .
Let be a non-lightlike curve with . Assume that . According to the proof of Theorem 2 (B), we have the derivative of the vector-valued function , which is . Thus, if we suppose that then is a constant vector . We have
Therefore, we obtain
On the other hand, if there exists such that then we can obtain
and We consider such a curve . Then, we have
Proposition 3.
Let be a non-lightlike curve with and Then, there exists such that if and only if
The result of the proposition above states that the geometric meaning of the singularities of is related to both the curve and the shape of the timelike surface along the non-lightlike curve. Let be a non-lightlike curve with . Meanwhile, we consider the support function . According to Proposition 1 (2), one can find that is tangent to at if and only if for some . In addition, we have the following.
Proposition 4.
Let with be a non-lightlike curve and For , we have the following:
- (1)
- and have contact of order 2 at if and only if and .
- (2)
- and have contact of order 3 at if and only if , and .
Proof.
By Proposition 1, (3) and (4), one can obtain and if and only if and . Since , the conditions above imply that and have contact of order 2 at . By using Proposition 1, (4) and (5), we can obtain the assertion (2) similar to the case above. □
Moreover, for the classification results of Theorem 3, we show the geometric meaning as follows.
Theorem 5.
Let be a non-lightlike curve with and
- (1)
- and have contact of order 2 at if and only if and . In this case, the image of the osculating developable surface of M along is locally diffeomorphic to the cuspidal edge at .
- (2)
- and have contact of order 3 at if and only if , and . In this case, the image of the osculating developable surface of M along is locally diffeomorphic to the swallowtail at .
7. Curves on Special Timelike Surfaces
7.1. Curves on the de Sitter 2-Space
De Sitter 2-space is a special timelike surface in . We consider the non-lightlike curves on . Let be a non-lightlike curve. In this case, the Darboux frame along is . We have and The Frenet–Serret-type formula is as follows:
It follows that and Therefore, we have
Then, as a corollary of Theorem 3, we have the following theorem.
Theorem 6.
Let be a non-lightlike curve. Then,
- (1)
- is regular if and only if
- (2)
- The image of is locally diffeomorphic to the cuspidal edge if and .
- (3)
- The image of is locally diffeomorphic to the swallowtail if , and .
Now, we consider some special curves on , such as the spacelike circle, which is the intersection of the plane with . It is defined by
We call it a small circle if and call it a great circle if . is a spacelike curve on .
Proposition 5.
Let be a non-lightlike curve and be the osculating developable surface of along . Then, we have the assertions below.
- (1)
- If is a small circle, then is a circular cylinder.
- (2)
- If is a great circle, then is a circular cone.
Proof.
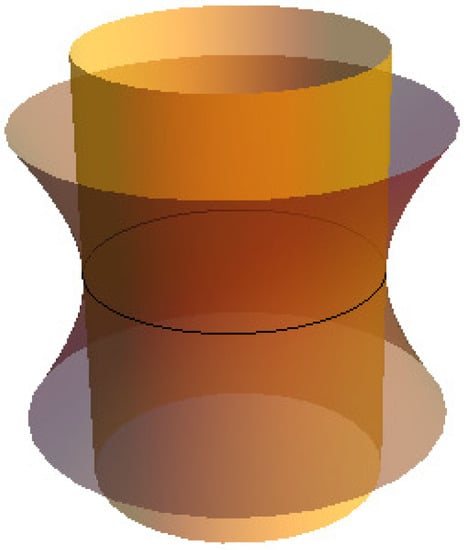

If is a small circle, then and is constant. Thus, is a circular cylinder that is tangential to along (see Figure 3). If is a great circle, then and , so that and . It means that is a cone tangent that is tangential to along (see Figure 4). □

Figure 3.
along the small circle.

Figure 4.
along the great circle.
On the other hand, we consider the timelike hyperbolic curve, which is the intersection of the plane with . It is defined by
We call it a great hyperbolic curve if and call it a small hyperbolic curve if . is a timelike curve on , and we have the proposition below.
Proposition 6.
Let be a non-lightlike curve and the osculating developable surface of along . Then, we have the assertions below.
- (1)
- If is a great hyperbolic curve, then is a cylinder.
- (2)
- If is a small hyperbolic curve, then is a cone.
Proof.


Let be a timelike hyperbolic curve ; then, one can define by
Then, we have
and . If is a great hyperbolic curve, then and is constant. Hence, is a cylinder that is tangential to along (see Figure 5). If is a small hyperbolic curve, then and . It follows that is a cone that is tangential to along (see Figure 6). □

Figure 5.
along the great hyperbolic curve.

Figure 6.
along the small hyperbolic curve.
The following example of a timelike curve on shown below serves to illustrate Theorem 6.
Example 1.

Let be a timelike curve defined by
The Darboux frame along is . Then, by a straightforward calculation, we obtain
The derivative of is given by
By the Frenet-type formulae, one can obtain . It follows that
We have if and only if at this moment, and . By Theorem 6, if the osculating developable surface along has the swallowtail singularities (see Figure 7).

Figure 7.
along the timelike curve with swallowtail singularities.
7.2. Curves on a Timelike Surface of Revolution
We focus on non-lightlike curves on a timelike surface of revolution in this subsection. A timelike surface of revolution is defined by
for , where and . It is easy to show that
Then, the unit spacelike normal vector field along is
Then, for a non-lightlike curve
on we obtain the Darboux frame as follows.
where
We can calculate that
Moreover, one can obtain
For a timelike meridian curve , we have . Then,
In this case the osculating developable surface along is a cylinder (see Figure 8).

Figure 8.
along the timelike meridian curve.
For a spacelike circle , we have . Then,
Since if , we have . At this time, the osculating developable surface along is a cylinder (see Figure 9). If , then is a nonzero constant and . At this time, the osculating developable surface along is a cone (see Figure 10).
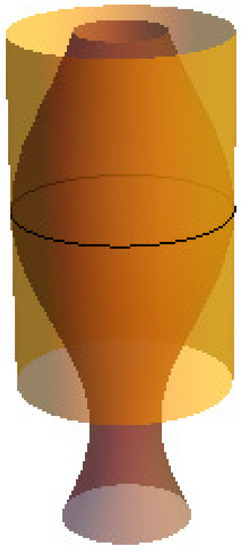
Figure 9.
If , along the spacelike circle.
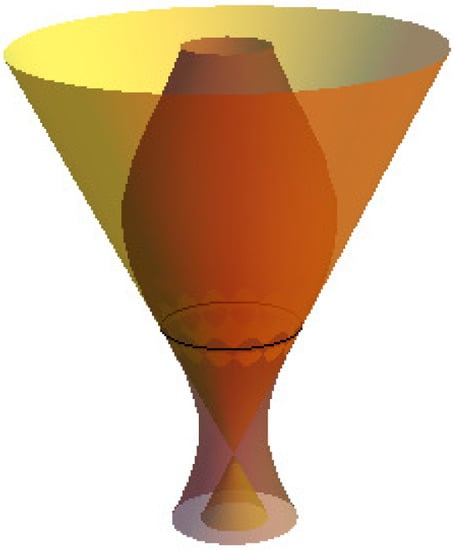
Figure 10.
If , along the spacelike circle.
8. Conclusions
By choosing the three-dimensional Minkowski space as a background in space–time, we define the osculating developable surface of a timelike surface along a curve, whose ruling is parallel to the osculating Darboux vector field. Our main purpose is to study the singularities of such a surface. For this, by using the singularity theory, we classify the generic singularities of osculating developable surfaces that are cuspidal edges and swallowtails. In particular, these types of singularities are characterized by the invariants and . In fact, the osculating developable surface is a cylinder if and only if ; the osculating developable surface is a cone if and only if and . We also show some special geometric properties of the singularities of osculating developable surfaces from the viewpoint of contact geometry. Moreover, we obtain the dual relationship between the rulings and the normals of osculating developable surfaces.
Author Contributions
Formal analysis, Y.W. and L.Y.; Funding acquisition, Y.W. and Y.C.; Resources, Y.W.; Software, P.L.; Supervision, Y.C.; Writing—original draft, L.Y.; Writing—review and editing, P.L. and Y.C. All authors have read and agreed to the published version of the manuscript.
Funding
The first author is supported by the National Natural Science Foundation of China (Grant No. 12001079 and 11801053), Fundamental Research Funds for the Central Universities (Grant No. 3132022205) and Scientific Research Foundation of Liaoning Education Department (Grant No. LJKZ0053). The corresponding author is supported by the Liaoning Province Doctor Startup Fund (Grant No. 2022-BS-118).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank the reviewers for their comments and suggestions, which were very helpful in improving the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cheng, S.Y.; Yau, S.T. Maximal space-like hypersurfaces in the Lorentz-Minkowski spaces. Ann. Math. 1976, 104, 407–419. [Google Scholar] [CrossRef]
- Cui, X.P.; Pei, D.H. Singularities of Null Hypersurfaces of Pseudonull Curves. J. Funct. Spaces 2015, 1, 1–9. [Google Scholar] [CrossRef]
- Li, M.X.; Yao, X.K.; Li, P.C.; Pei, D.H. Pedal Curves of Non-Lightlike Curves in Minkowski 3-Space. Symmetry 2022, 14, 59. [Google Scholar] [CrossRef]
- Li, P.C.; Pei, D.H. Nullcone Fronts of Spacelike Framed Curves in Minkowski 3-Space. Mathematics 2021, 9, 2939. [Google Scholar] [CrossRef]
- Liu, T.C.; Pei, D.H. Null helices and Cartan slant helices in Lorentz-Minkowski 3-space. Int. J. Geom. Methods Mod. Phys. 2019, 16, 1950179. [Google Scholar] [CrossRef]
- Palomo, F.J.; Romero, A. On spacelike surfaces in four-dimensional Lorentz-Minkowski spacetime through a light cone. Proc. Roy. Soc. Edinb. Sect. A 2013, 143, 881–892. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Pei, D.H.; Cui, X.P. Pseudo-spherical normal Darboux images of curves on a lightlike surface. Math. Methods Appl. Sci. 2017, 40, 7151–7161. [Google Scholar] [CrossRef]
- Rojas, E. Covariant perturbations in the gonihedric string model. Int. J. Mod. Phys. A 2017, 32, 1750192. [Google Scholar] [CrossRef]
- Yang, Z.C.; Li, Y.; Erdoǧdub, M.; Zhu, Y.S. Evolving evolutoids and pedaloids from viewpoints of envelope and singularity theory in Minkowski plane. J. Geom. Phys. 2022, 104513, 1–23. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Z.G. Lightlike tangent developables in de Sitter 3-space. J. Geom. Phys. 2021, 164, 1–11. [Google Scholar] [CrossRef]
- Li, Y.; Liu, S.Y.; Wang, Z.G. Tangent developables and Darboux developables of framed curves. Topol. Appl. 2021, 301, 107526. [Google Scholar] [CrossRef]
- Li, Y.; Ganguly, D.; Dey, S.; Bhattacharyya, A. Conformal η-Ricci solitons within the framework of indefinite Kenmotsu manifolds. AIMS Math. 2022, 7, 5408–5430. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Z.G.; Zhao, T.H. Geometric Algebra of Singular Ruled Surfaces. Adv. Appl. Clifford Algebr. 2021, 31, 1–19. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, Y.S.; Sun, Q.Y. Singularities and dualities of pedal curves in pseudo-hyperbolic and de Sitter space. Int. J. Geom. Methods Mod. Phys. 2021, 18, 1–31. [Google Scholar] [CrossRef]
- Li, Y.; Lone, M.A.; Wani, U.A. Biharmonic submanifolds of Kähler product manifolds. AIMS Math. 2021, 6, 9309–9321. [Google Scholar] [CrossRef]
- Li, Y.; Alkhaldi, A.H.; Ali, A.; Laurian-Ioan, P. On the Topology of Warped Product Pointwise Semi-Slant Submanifolds with Positive Curvature. Mathematics 2021, 9, 3156. [Google Scholar] [CrossRef]
- Li, Y.; Ali, A.; Mofarreh, F.; Alluhaibi, N. Homology groups in warped product submanifolds in hyperbolic spaces. J. Math. 2021, 2021, 8554738. [Google Scholar] [CrossRef]
- Li, Y.; Ali, A.; Ali, R. A general inequality for CR-warped products in generalized Sasakian space form and its applications. Adv. Math. Phys. 2021, 2021, 5777554. [Google Scholar] [CrossRef]
- Li, Y.; Ali, A.; Mofarreh, F.; Abolarinwa, A.; Ali, R. Some eigenvalues estimate for the ϕ-Laplace operator on slant submanifolds of Sasakian space forms. J. Funct. Spaces 2021, 2021, 6195939. [Google Scholar]
- Li, Y.; Dey, S.; Pahan, S.; Ali, A. Geometry of conformal η-Ricci solitons and conformal η-Ricci almost solitons on Paracontact geometry. Open Math. 2022, 20, 1–20. [Google Scholar] [CrossRef]
- Li, Y.; Abolarinwa, A.; Azami, S.; Ali, A. Yamabe constant evolution and monotonicity along the conformal Ricci flow. AIMS Math. 2022, 7, 12077–12090. [Google Scholar] [CrossRef]
- Li, Y.; Khatri, M.; Singh, J.P.; Chaubey, S.K. Improved Chen’s Inequalities for Submanifolds of Generalized Sasakian-Space-Forms. Axioms 2022, 11, 324. [Google Scholar] [CrossRef]
- Li, Y.; Mofarreh, F.; Agrawal, R.P.; Ali, A. Reilly-type inequality for the ϕ-Laplace operator on semislant submanifolds of Sasakian space forms. J. Inequal. Appl. 2022, 1, 102. [Google Scholar]
- Li, Y.; Mofarreh, F.; Dey, S.; Roy, S.; Ali, A. General Relativistic Space-Time with η1-Einstein Metrics. Mathematics 2022, 10, 2530. [Google Scholar] [CrossRef]
- Li, Y.; Uçum, A.; İlarslan, K.; Camcı, Ç. A New Class of Bertrand Curves in Euclidean 4-Space. Symmetry 2022, 14, 1191. [Google Scholar] [CrossRef]
- Li, Y.; Şenyurt, S.; Özduran, A.; Canlı, D. The Characterizations of Parallel q-Equidistant Ruled Surfaces. Symmetry 2022, 14, 1879. [Google Scholar] [CrossRef]
- Li, Y.; Haseeb, A.; Ali, M. LP-Kenmotsu manifolds admitting η-Ricci solitons and spacetime. J. Math. 2022, 2022, 6605127. [Google Scholar] [CrossRef]
- Li, Y.; Mofarreh, F.; Abdel-Baky, R.A. Timelike Circular Surfaces and Singularities in Minkowski 3-Space. Symmetry 2022, 14, 1914. [Google Scholar] [CrossRef]
- Li, Y.; Alluhaibi, N.; Abdel-Baky, R.A. One-Parameter Lorentzian Dual Spherical Movements and Invariants of the Axodes. Symmetry 2022, 14, 1930. [Google Scholar] [CrossRef]
- Li, Y.; Prasad, R.; Haseeb, A.; Kumar, S.; Kumar, S. A Study of Clairaut Semi-Invariant Riemannian Maps from Cosymplectic Manifolds. Axioms 2022, 11, 503. [Google Scholar] [CrossRef]
- Li, Y.; Nazra, S.H.; Abdel-Baky, R.A. Singularity Properties of Timelike Sweeping Surface in Minkowski 3-Space. Symmetry 2022, 14, 1996. [Google Scholar] [CrossRef]
- Li, Y.; Eren, K.; Ayvacı, K.H.; Ersoy, S. Simultaneous characterizations of partner ruled surfaces using Flc frame. AIMS Math. 2022, 7, 20213–20229. [Google Scholar]
- Li, Y.; Gur Mazlum, S.; Senyurt, S. The Darboux trihedrons of timelike surfaces in the Lorentzian 3-space. Int. J. Geom. Methods Mod. Phys. 2022, 1–35. [Google Scholar] [CrossRef]
- Pei, D.H.; Kong, L.L.; Sun, J.G.; Wang, Q. Singularities of lightlike hypersurface in semi-Euclidean 4-space with index 2. Sci. China Math. 2010, 53, 3243–3254. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Chang, Y.; Liu, H.M. Singularities of helix surfaces in Euclidean 3-space. J. Geom. Phys. 2020, 156, 103781. [Google Scholar] [CrossRef]
- Bruce, J.W.; Giblin, P.J. Curves and Singularities; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Zhou, K.A.; Wang, Z.G. Pseudo-spherical Darboux images and lightcone images of principal-directional curves of nonlightlike curves in Minkowski 3-space. Math. Methods Appl. Sci. 2018, 43, 35–77. [Google Scholar] [CrossRef]
- Hananoi, S.; Izumiya, S. Normal developable surfaces of surfaces along curves. Proc. Roy. Soc. Edinb. Sect. A 2017, 147, 177–203. [Google Scholar] [CrossRef]
- Sato, T. Pseudo-spherical evolutes of curves on a spacelike surface in three dimensional Lorentz-Minkowski space. J. Geom. 2012, 103, 319–331. [Google Scholar] [CrossRef]
- Cipolla, R.; Giblin, P.J. Visual Motion of Curves and Surfaces; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Duggal, K.L.; Sahin, B. Differential Geometry of Lightlike Submanifolds; Birkhäuser: Basel, Switzerland, 2010. [Google Scholar]
- Chen, L.; Izumiya, S. A mandala of Legendrian dualities for pseudo-spheres in semi-Euclidean space. Proc. Japan Acad. Ser. A Math. Sci. 2009, 85, 49–54. [Google Scholar] [CrossRef]
- Arnold, V.I.; Gusein-Zade, S.M.; Varchenko, A.N. Singularities of Differentiable Maps; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1986; Volume 1. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).