Generalized Cyclic p-Contractions and p-Contraction Pairs Some Properties of Asymptotic Regularity Best Proximity Points, Fixed Points

Abstract

This paper studies a general $p$-contractive condition of a self-mapping $T$ on $X$, where $\left(X ,d\right)$ is either a metric space or a dislocated metric space, which combines the contribution to the upper-bound of $d\left(Tx\hspace{0.33em},\hspace{0.33em}Ty\right)$, where $x$ and $y$ are arbitrary elements in $X$ of a weighted combination of the distances $d\left(x,y\right) ,\hspace{0.33em}d\left(x,Tx\right),d\left(y,Ty\right),d\left(x,Ty\right),d\left(y,Tx\right)$$, \left|d\left(x,Tx\right)-d\left(y,Ty\right)\right|$ and $\left|d\left(x,Ty\right)-d\left(y,Tx\right)\right|$. The asymptotic regularity of the self-mapping $T$ on $X$ and the convergence of Cauchy sequences to a unique fixed point are also discussed if $\left(X,d\right)$ is complete. Subsequently, $\left(T, S\right)$ generalized cyclic $p$-contraction pairs are discussed on a pair of non-empty, in general, disjoint subsets of $X$. The proposed contraction involves a combination of several distances associated with the $\left(T, S\right)$-pair. Some properties demonstrated are: (a) the asymptotic convergence of the relevant sequences to best proximity points of both sets is proved; (b) the best proximity points are unique if the involved subsets are closed and convex, the metric is norm induced, or the metric space is a uniformly convex Banach space. It can be pointed out that both metric and a metric-like (or dislocated metric) possess the symmetry property since their respective distance values for any given pair of elements of the corresponding space are identical after exchanging the roles of both elements.

1. Introduction

Popescu [1] has proposed a type of contraction (so-called $p$-contraction) that extends Banach’s contraction principle for mapping $T:X\to X$, where $\left(X,d\right)$ is a metric space, which is defined by:

$$d\left(Tx,\hspace{0.33em}Ty\right)\le k\left\{d\left(x,y\right)+\left|d\left(x,Tx\right)-d\left(y,Ty\right)\right|\right\}; \forall x,y\in X$$

for some $k\in \left[0,1\right)$. The precise formal definition is recalled later on in the next section. Basically, the well-known Banach’s contraction principle is weakened by incorporating the absolute value of the difference between the distances of any involved points $x,y\in X$ to their images through $T$. It is well-known that an important support as an “a priori” property for the Cauchyness of sequences and their convergence to fixed points is that the mappings be asymptotically regular; basically, the sequences of distances between points and their images through the involved mapping converge asymptotically to zero [2]. On the other hand, in the rich existing background literature on fixedpoint theory and its applications, special attention is paid to $q$-cyclic contractions on the union of $q\left(\ge 2\right)$ subsets in metric spaces. The cyclic contractions take account of the distances between adjacent sets and important results to be dealt with are the convergence of the sequences of orbital distances between neighboring points (i.e., distances between sequences of points and their images) to the distances between adjacent subsets in the cyclic disposal. Under certain conditions in the metric space, such as uniform convexity, and on the sets, basically, non-emptiness, closeness, and convexity (of at least one of them), the distances are those between the best proximity points of the adjacent subsets and the orbits converge to an orbit of the $q$ unique best proximity points. The best proximity points are confluent to a unique fixed point if the subsets of the cyclic disposal intersect. There are many results available in the literature since the pioneering work in [3] on the convergence of distances to distances between adjacent subsets and the convergence of sequences of the iterations through the contractive cyclic mapping to an orbit of unique cyclic best proximity points. New results were derived in [4,5] related to Meir–Keeler cyclic contractions. More general contractive cyclic contractions of a rational type were proposed in [6,7]. In [8], a class of cyclic contractions for multivalued self-mappings was investigated. In [9], cyclic $p$-contractions for pairs of, in general, non-self-mappings between adjacent subsets were proposed and dealt with. The results obtained in that paper were partially inspired by the previous work of [1] for the non-cyclic case of $p$-contractions. On the other hand, some best proximity results for multivalued mappings were provided in [10] by generalizing Feng and Liu’s previous results on fixed points proved in [11]. In particular, in [11], some fixed point theorems for multi-valued contractive mappings and multi-valued Caristi-type mappings were obtained by considering multivalued mappings on non-empty closed and non-necessarily bounded sets of a metric space. Moreover, a previous Nadler’s type result was generalized by their approach. Some convergence and best proximity theorems were proved in [12] concerned with relatively quasi-asymptotic cyclic and non-cyclic contractions in cone uniform spaces of set-valued dynamic systems. The existing background literature on the convergence of sequences to best proximity points under different types of contractions is very exhaustive and is concerned, in particular, with partial metric spaces, partially ordered metric spaces, metric-like spaces, and quasi-partial metric and $b$-metric spaces as well as the more general $b_v\left(s\right)$-metric spaces and some extensions to cyclic mappings. See, for instance, [13,14,15,16,17,18,19] and also some of the related references therein.

The first main contribution of this paper is the study of a more general $p$-contraction of a self-mapping $T$ on $X$, where $\left(X ,d\right)$ is either a metric space or a dislocated metric space. Such a generalized $p$-contraction involves the contribution to the upper-bound of $d\left(Tx\hspace{0.33em},\hspace{0.33em}Ty\right)$ of a weighted combination of the distances $d\left(x,y\right) ,\hspace{0.33em}d\left(x,Tx\right),d\left(y,Ty\right),d\left(x,Ty\right),d\left(y,Tx\right)$$, \left|d\left(x,Tx\right)-d\left(y,Ty\right)\right|$ and $\left|d\left(x,Ty\right)-d\left(y,Tx\right)\right|$, where $x,y$ are arbitrary elements in $X$. The asymptotic regularity of $T$ and the convergence of Cauchy sequences to a unique fixed point are proved if $\left(X,d\right)$ is complete. The second main contribution is concerned with a generalized contraction referred to $\left(T, S\right)$ cyclic $p$-contraction pairs on a pair of non-empty, in general, disjoint subsets, $A$ and $B$ of $X$. The proposed generalized contraction rule also involves a combination of several terms for contribution of distances involving the images of the points through the, in general, two non-self-mappings $T:A\to B$ and $S:B\to A$ which define the $\left(T, S\right)$ cyclic $p$-contraction pair. The asymptotic convergence of the relevant sequences to best proximity points of both sets is proved. The best proximity points are proved to be unique if the distance is norm induced and the metric space is a uniformly convex Banach space while the involved subsets in the $\left(T, S\right)$ cyclic $p$-contraction pair are closed and convex. An application example is given concerning a discrete control problem, subject to feedback and disturbances, which is discussed. Moreover, numerical illustrative examples are given concerned with the generalized $p$-contraction and the generalized $\left(T, S\right)$ cyclic $p$-contraction pairs.

Notation

$Z_{0+}=\left\{z\in Z:z\ge 0\right\}$, $Z_{+}=\left\{z\in Z:z>0\right\}$, $\overline{n}=\left\{1,2, \dots ,n\right\}$;

$R_{0+}=\left\{r\in R:r\ge 0\right\}$, $R_{+}=\left\{r\in R:r>0\right\}$;

$D=d\left(A,B\right)=\underset{x\in A,y\in B}{inf}d\left(x,y\right)$ is the distance between the sets $A$ and $B$ (for an interesting geometric interpretation, see [20]).

2. Main Asymptotic Regularity and Fixed Point Results for a Class of Generalized $\mathit{p}$-Contractions in Metric Spaces and in Dislocated Metric Spaces

The following two definitions from the background literature are used in this paper as basic support ideas for the results stated and proved:

Definition 1 

([1,9]).Let$\left(X,d\right)$be a metric space. Then,$T:X\to X$is a$p$-contraction if there exists$k\in \left[0,1\right)$such that

$$d\left(Tx,\hspace{0.33em}Ty\right)\le k\left\{d\left(x,y\right)+\left|d\left(x,Tx\right)-d\left(y,Ty\right)\right|\right\}; \forall x,y\in X.$$

Definition 2 

([9]).Let$\left(X,d\right)$be a metric space and$A$and$B$be non-empty subsets of$X$. Let$T:A\to B$and$S:B\to A$be two mappings. Then,$\left(T,S\right)$is called a cyclic $p$-contraction pair if there exists$k\in \left[0,1\right)$such that

$$d\left(Tx,\hspace{0.33em}Sy\right)\le k\left\{d\left(x,y\right)+\left|d\left(x,Tx\right)-d\left(y,Sy\right)\right|\right\}+\left(1-k\right)d\left(A,B\right)$$

for all $x\in A$,$\hspace{0.33em}y\in B$. Note that if$\left(T, S\right)$ is a cyclic $p$-contraction pair, then $\left(T, S\right)$ is also a cyclic $p$-contraction pair.

It has been proved in [1] that, if $\left(X,d\right)$ is complete and $T:X\to X$ is a $p$-contraction, then $T:X\to X$ has a unique fixed point. It can be noticed that if $\left(T,S\right)$ is a cyclic $p$-contraction pair, then $\left(S,T\right)$ is also a cyclic $p$-contraction pair. In [9], a study of best proximity results of cyclic $p$-contraction pairs was performed. The following results refer to a proposed kind of generalized $p$-contractions in a metric space $\left(X,d\right)$. The asymptotic regularity of the orbits generated for any initial condition of the iteration as well as the existence and uniqueness of a fixed point and the boundedness and Cauchyness of the iterated sequences are proved if $\left(X,d\right)$ is complete. It can be pointed out that the study of the behavior of orbital contraction conditions has been proved to be informative to obtain results and conclusions on fixed points, coupled fixed points, and best proximity issues. See, for instance, [21].

Concerning distances between sets, it is convenient to point out that the distances between sets built via unbounded sequences can be zero even if they are closed and disjoint. The subsequent example addresses such an issue:

Example 1.

Consider the following sets$Y={\left\{{\alpha }_n\right\}}_{n=0}^{\infty }\left(\subset Z_{+}\right)$and$Z={\left\{{\alpha }_n+{\beta }_n\right\}}_{n=0}^{\infty }\left(\subset R_{+}\right)$with${\left\{ {\alpha }_n\right\}}_{n=0}^{\infty }\to \infty$and$\Delta ={\left\{{\beta }_n\right\}}_{n=0}^{\infty }\left(\subset \left(0,1\right)\right)\to 0$. Thus, one has under the Euclidean metric that:

$$d\left(Y,Z\right)=d\left(Z,Y\right)=inf \left(d\left(y,z\right):y\in Y\hspace{0.33em},\hspace{0.33em}z\in Z\right)=\underset{n\to \infty }{lim}d\left({\alpha }_n\hspace{0.33em},\hspace{0.33em}{\alpha }_n+{\beta }_n\right)=\underset{n\to \infty }{lim}\left|{\beta }_n\right|=0,$$

while $Y$and $Z$ are unbounded, closed and disjoint.

If we now consider the truncated bounded and closed sequences $Y_N={\left\{{\alpha }_n\right\}}_{n=0}^N\left(\subset Y\right)$, $Z_N={\left\{{\alpha }_n+{\beta }_n\right\}}_{n=0}^N\left(\subset R_{+}\right)$, and ${\Delta }_N={\left\{{\beta }_n\right\}}_{n=0}^N\left(\subset \left(0,1\right)\right)$ for any arbitrary finite $N\subset Z_{0+}$, it follows that the sets $Y_N$ and $Z_N$ are still closed and disjoint (although bounded), and

$$d\left(Y,Z\right)=inf \left(d\left(y,z\right):y\in Y\hspace{0.33em},\hspace{0.33em}z\in Z\right)=min\left(d\left({\alpha }_n\hspace{0.33em},\hspace{0.33em}{\alpha }_n+{\beta }_n\right):0\le n\le N\right)>0.$$

Theorem 1.

Consider a self-mapping$T$on$X$, where $\left(X,d\right)$is a metric space subject to the following generalized $p$-contraction:

$$\begin{array}{c}d\left(Tx\hspace{0.33em},\hspace{0.33em}Ty\right)\le k_{1}d\left(x,y\right)+k_{2}d\left(x,Tx\right)+k_{3}d\left(y,Ty\right)+k_{4}d\left(x,Ty\right)+k_{5}d\left(y,Tx\right)\\ +k_6\left|d\left(x,Tx\right)-d\left(y,Ty\right)\right|+k_7\left|d\left(x,Ty\right)-d\left(y,Tx\right)\right|; \forall x,y\in X,\end{array}$$

(1)

where $k_i\in R_{0+}$; $\forall i\in \overline{7}$. Then, the following properties hold:

(i)

$T:X\to X$is asymptotically regular at all$x$in$X$if$k_6\le k_1+k_2+k_4+k_7<1-k_3-k_4-k_7$. Any orbit $O\left(x\right)=\left(x , Tx ,T^{2}x,\dots \right)$for$x\in X$is subject to the contraction rule$d\left(T^{2}x\hspace{0.33em},\hspace{0.33em}Tx\right)\le kd\left(x,Tx\right)$under the contraction constant$k=max \left(\frac{k_1+k_2+k_4-k_6+k_7}{1-k_3-k_6-k_4-k_7}\hspace{0.33em},\hspace{0.33em}\hspace{0.33em}\frac{k_1+k_2+k_4+k_6+k_7}{1-k_3+k_6-k_4-k_7}\right)\in \left[0 ,\hspace{0.33em}1\right)$.

(ii)

If, furthermore, $\left(X,d\right)$ is complete and the contractivity constraint of property (i) is modified to the stronger subsequent form $k_6\le k_1+k_2+k_4+k_7<1-k_3-k_4-k_7-k_5$, then there is a unique fixed point $z\left(=Tz\right)\in X$and ${\left\{T^{n}x\right\}}_{n=0}^{\infty }\to z$so that ${\left\{T^{n}x\right\}}_{n=0}^{\infty }$ is bounded; $\forall x\in X$and ${\left\{T^{n}x\right\}}_{n=0}^{\infty }$ is a Cauchy sequence.

Proof. 

Construct the orbit $O\left(x\right)=\left(x , Tx ,T^{2}x,\dots \right)$ for any given $x\in X$ with $y=Tx$ in Equation (1), and $d\left(x,x\right)=0$ for any $x\in X$ since $d:X\times X\to R_{0+}$ is a metric. Thus, the following constraint follows as a particular case of (1):

$$\begin{array}{l}d\left(Tx\hspace{0.33em},\hspace{0.33em}{T}^{2}x\right)\le k_{1}d\left(x,Tx\right)+k_{2}d\left(x,Tx\right)+k_{3}d\left(Tx,T^{2}x\right)+k_{4}d\left(x,T^{2}x\right)+k_{5}d\left(Tx,Tx\right)\\ \hspace{1em}\hspace{1em}+k_6\left|d\left(x,Tx\right)-d\left(Tx,T^{2}x\right)\right|+k_7\left|d\left(x,T^{2}x\right)-d\left(Tx,Tx\right)\right|\\ \hspace{1em}\hspace{1em}=k_{1}d\left(x,Tx\right)+k_{2}d\left(x,Tx\right)+k_{3}d\left(Tx,T^{2}x\right)+k_{4}d\left(x,T^{2}x\right)+k_{5}d\left(Tx,Tx\right)\\ \hspace{1em}\hspace{1em}+k_6\alpha \left(x,Tx, T^{2}x\right) \left(d\left(x,Tx\right)-d\left(Tx,T^{2}x\right)\right)+k_7\left|d\left(x,T^{2}x\right)-d\left(Tx,Tx\right)\right|\\ \hspace{1em}\hspace{1em}=k_{1}d\left(x,Tx\right)+k_{2}d\left(x,Tx\right)+k_{3}d\left(Tx,T^{2}x\right)+k_{4}d\left(x,T^{2}x\right)\\ \hspace{1em}\hspace{1em}+k_6\alpha \left(x,Tx, T^{2}x\right) \left(d\left(x,Tx\right)-d\left(Tx,T^{2}x\right)\right)+k_{7}d\left(x,T^{2}x\right)\end{array}$$

(2)

where:

$$\alpha \left(x,Tx , T^{2}x\right)=\left\{\begin{array}{c}1\hspace{1em}if\hspace{1em}d\left(x,Tx\right)>d\left(Tx,T^{2}x\right)\\ 0\hspace{1em}if\hspace{1em}d\left(x,Tx\right)=d\left(Tx,T^{2}x\right)\\ -1\hspace{1em}if\hspace{1em}d\left(x,Tx\right)<d\left(Tx,T^{2}x\right)\end{array}\right.$$

(3)

The following cases can arise:

Case 1: $d\left(x,Tx\right)>d\left(Tx,T^{2}x\right)$, equivalently, $\alpha \left(x,Tx , T^{2}x\right)=1$. Then, from Equation (2) it can be determined that:

$$\begin{array}{ll}d\left(Tx\hspace{0.33em},\hspace{0.33em}{T}^{2}x\right)& \le \frac{k_1+k_2+k_6}{1-k_3+k_6}d\left(x,Tx\right)+\frac{k_4+k_7}{1-k_3+k_6}d\left(x,T^{2}x\right)\\ & \le \frac{k_1+k_2+k_6}{1-k_3+k_6}d\left(x,Tx\right)+\frac{k_4+k_7}{1-k_3+k_6}d\left(x,Tx\right)+\frac{k_4+k_7}{1-k_3+k_6}d\left(Tx,T^{2}x\right)\end{array}$$

(4)

Note that $1-k_3+k_6>0$ in the above expression since, otherwise, $k_3\ge 1+k_6$ would contradict the contractivity condition given as the hypothesis for the combination of constants. Now, Equation (4) is identical to

$$\left(1-\frac{k_4+k_7}{1-k_3+k_6}\right)d\left(Tx,T^{2}x\right)\le \frac{k_1+k_2+k_4+k_6+k_7}{1-k_3+k_6}d\left(x,Tx\right)$$

(5)

and, equivalently,

$$d\left(Tx,T^{2}x\right)\le \frac{k_1+k_2+k_4+k_6+k_7}{1-k_3+k_6-k_4-k_7}d\left(x,Tx\right)$$

(6)

so that the contraction constant $K=\frac{k_1+k_2+k_4+k_6+k_7}{1-k_3+k_6-k_4-k_7}<1$ if and only if $k_1+k_2+k_3+2\left(k_4+k_7\right)<1$ which is independent of $k_5$ and $k_6$ and which is guaranteed by the given constraint $k_1+k_2+k_3+2\left(k_4+k_7\right)+k_5<1$. Furthermore, for coherency of Equation (5) leading to Equation (6), the coefficients of constants of the left and right-hand-sides of (5) have to be non-negative, so as to guarantee that $K\ge 0$, which leads to the denominator of $K$ to be positive under the constraint $k_6>k_3+k_4+k_7-1=-\alpha <0$, which holds directly under the above constraint $k_1+k_2+k_3+2\left(k_4+k_7\right)<1$. As a result, $K\in \left[0,\hspace{0.33em}1\right)$ if $k_1+k_2+k_3+2\left(k_4+k_7\right)<1$.

Case 2: $d\left(x,Tx\right)=d\left(Tx,T^{2}x\right)$, equivalently, $\alpha \left(x,Tx , T^{2}x\right)=0$ and $k_6\alpha \left(x,Tx, T^{2}x\right)=0$ in (2). Then, one can determine from (2) that (6) holds again under the associated constraint $k_1+k_2+k_3+2\left(k_4+k_7\right)<1$ with the same contraction constant $K$ as in Case 1.

Case 3: $d\left(x,Tx\right)<d\left(Tx,T^{2}x\right)$, equivalently, $\alpha \left(x,Tx , T^{2}x\right)=-1$. Then, from (2) it can be determined that:

$$\begin{array}{ll}d\left(x,Tx\right)<d\left(Tx\hspace{0.33em},\hspace{0.33em}{T}^{2}x\right)& \le \frac{k_1+k_2-k_6}{1-k_3-k_6}d\left(x,Tx\right)+\frac{k_4+k_7}{1-k_3-k_6}d\left(x,T^{2}x\right)\\ & \le \left(\frac{k_1+k_2-k_6}{1-k_3-k_6}+\frac{k_4+k_7}{1-k_3-k_6}\right)d\left(x,Tx\right)+\frac{k_4+k_7}{1-k_3-k_6}d\left(Tx,T^{2}x\right)\\ & =\frac{k_1+k_2+k_4+k_7-k_6}{1-k_3-k_6}d\left(x,Tx\right)+\frac{k_4+k_7}{1-k_3-k_6}d\left(Tx,T^{2}x\right)\end{array}$$

(7)

which implies that

$$d\left(Tx,T^{2}x\right)\le \frac{k_1+k_2+k_4-k_6+k_7}{1-k_3-k_4-k_6-k_7}d\left(x,Tx\right)$$

(8)

and the contraction constant $K^{\prime }=\frac{k_1+k_2+k_4-k_6+k_7}{1-k_3-k_6-k_4-k_7}<1$ if and only if $k_1+k_2+k_3+2\left(k_4+k_7\right)<1$ which is the same condition as that given for Cases 1 and 2. It has to be also guaranteed that $K^{\prime }\ge 0$ with a non-negative numerator and a positive denominator. This gives the sufficiency-type a new additional constraint $k_6\le k_1+k_2+k_4+k_7<1-k_3-k_4-k_7$.

Since $k=max\left(K , K^{\prime }\right)\in \left[0\hspace{0.33em},\hspace{0.33em}1\right)$, then $d\left(T^{n}x,T^{n+1}x\right)\le k^{n}d\left(x,Tx\right)$ and $\underset{n\to \infty }{lim}d\left(T^{n}x,T^{n+1}x\right)=0$; $\forall x\in X$. Then, $T:X\to X$ is asymptotically regular at all $x$ in $X$ if $k_6\le k_1+k_2+k_4+k_7<1-k_3-k_4-k_7$. Property (i) has been proved.

Moreover, one can determine from the triangle inequality that:

$$d\left(T^{n+1}x, x\right)\le d\left(T^{n+1}x,\hspace{0.33em}{T}^{n}x\right)+d\left(T^{n}x\hspace{0.33em},\hspace{0.33em}x\right); d\left(T^{n}x, x\right)\le d\left(T^{n+1}x,\hspace{0.33em}{T}^{n}x\right)+d\left(T^{n+1}x\hspace{0.33em},\hspace{0.33em}x\right)$$

(9)

Then,

$$\left|d\left(T^{n+1}x\hspace{0.33em},\hspace{0.33em}x\right)-d\left(T^{n}x\hspace{0.33em},x\right)\right|\le d\left(T^{n+1}x,T^{n}x\right)$$

which leads to $\underset{n\to \infty }{lim} \left(d\left(T^{n+1}x, x\right)-d\left(T^{n}x\hspace{0.33em},\hspace{0.33em}x\right)\right)=0$; $\forall x\in X$ since $\underset{n\to \infty }{lim}d\left(T^{n}x,T^{n+1}x\right)=0$. Thus,

$$\begin{array}{l}\underset{n\to \infty }{lim} \left(d\left(T^{n+1}x, x\right)-d\left(T^{n}x\hspace{0.33em},\hspace{0.33em}x\right)\right)=0\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\Rightarrow d\left(\underset{n\to \infty }{lim}{T}^{n+1}x, x\right)=d\left(T\left(\underset{n\to \infty }{lim}{T}^{n}x\right)\hspace{0.33em},\hspace{0.33em}x\right)=d\left(\underset{n\to \infty }{lim}{T}^{n}x\hspace{0.33em},\hspace{0.33em}x\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\Rightarrow {\left\{T^{n}x\right\}}_{n=0}^{\infty }\to z=Tz \mathrm{for} \mathrm{some} z\in X\end{array}$$

(10)

The limit of the distance is moved to the limit of the sequence in the above Equation (10) since $T$ is Lipschitz-continuous because it is contractive at points in any sequence $T^{n}x$ for $n\ge 2$ belonging to any orbit ${\left\{T^{n}x\right\}}_{n=0}^{\infty }$. As a result of (10), $z=Tz$ is a fixed point of $T:X\to X$ since $\underset{n\to \infty }{lim}d\left(T^{n}x,T\left(T^{n}x\right)\right)=d\left(\underset{n\to \infty }{lim}{T}^{n}x,T\left(\underset{n\to \infty }{lim}{T}^{n}x\right)\right)=d\left(z,Tz\right)=0$ due to ${\left\{T^{n}x\right\}}_{n=0}^{\infty }\to z$.

Since $d\left(T^{2}x,\hspace{0.33em}Tx\right)\le kd\left(x,Tx\right)$ with $k=max\left(K , K^{\prime }\right)<1$ then one can determine that:

$$d\left(T^{n+m+1}x,\hspace{0.33em}{T}^{m+n}x\right)\le k^{n}d\left(T^{m+1}x,T^{m}x\right) \mathrm{and} d\left(T^{n+m+1}x,\hspace{0.33em}{T}^{n}x\right)\le k^{n}d\left(T^{m+1}x,Tx\right)$$

(11)

for any $m\in Z_{0+}$ and also $d\left(T^{n+m+1}x,\hspace{0.33em}{T}^{n}x\right)\to 0$ as $n\to \infty$ for any $m\in Z_{0+}$. Furthermore

$$\begin{array}{c}d\left(T^{m}x, T^{n}x\right)={\displaystyle {\sum }_{i=n}^{m-1}d\left(T^{i+1}x,T^{i}x\right)}\le k^n\left({\displaystyle {\sum }_{j=0}^{m-n-1}{k}^j}\right)d\left(Tx,x\right)\\ \le \frac{k^n\left(1-k^{m-n}\right)}{1-k}d\left(x, Tx\right)\le \frac{k^n}{1-k}d\left(x, Tx\right)<\epsilon \end{array}$$

(12)

for any $n,\hspace{0.33em}m\left(>n\right)\in Z_{0+}$ with $n\left(\ge N\right)\in Z_{0+}$ and any given real constant $\epsilon >0$ provided that $N=N\left(\epsilon ,x\right)\in Z_{0+}$ satisfies that $k^N<\frac{1-k}{d\left(x,Tx\right)}\epsilon$. Thus, ${\left\{T^{n}x\right\}}_{n=0}^{\infty }$ is a Cauchy sequence for any given $x\in X$ which converges to the fixed point $z$.

Theorem 1 has used the obvious constraint $d\left(x,x\right)=0$ if $d$ is a metric. However, this does not necessarily hold for any $x\in X$ if $\left(X,d\right)$ is a metric-like (or “dislocated metric”) space. Note that dislocated metric spaces also keep the symmetry property of distances as in the case of metric spaces.

Moreover, since ${\left\{T^{n}x\right\}}_{n=0}^{\infty }$ is convergent and then bounded, and since any convergent sequence is a Cauchy sequence then ${\left\{T^{n}x\right\}}_{n=0}^{\infty }$ is a Cauchy sequence for any $x\in X$ and, in addition, its limit is $z\in X$ since $\left(X,d\right)$ is complete. To prove that the fixed point $z$ is unique, assume that there are two distinct fixed points $z , \omega \in X$ of $T:X\to X$. Then, one concludes from (1) with $z=Tz$ and $\omega =T\omega$ that:

$$\begin{array}{ll}d\left(z,\omega \right)& =d\left(Tz ,\hspace{0.33em}T\omega \right)\le k_{1}d\left(z,\omega \right)+\left(k_4+k_7\right)d\left(z, T\omega \right)+k_{5}d\left(\omega , Tz\right)+\left(k_2+k_3+k_6\right)\times 0\\ & =\left(k_1+k_4+k_5+k_7\right)d\left(z, \omega \right)\end{array}$$

(13)

so that $\left(1-k_1-k_4-k_5-k_7\right)d\left(z,\omega \right)\le 0$, and since $d\left(z,\omega \right)>0$, one gets the contradiction $k_1+k_4+k_5+k_7\ge 1$ to the stronger contractivity constraint $k_6<k_1+k_2+k_4+k_7<1-k_3-k_4-k_7-k_5$ since then $1+k_2+k_3+k_4+k_7\le k_1+k_2+k_3+k_5+2\left(k_4+k_7\right)<1$ would imply that $k_2+k_3+k_4+k_7<0$. Therefore, $\omega =z$ and the fixed point is unique. Property (ii) has been proved. □

Remark 1. 

Note that if$k_6=k_1$and$k_2=k_3=k_4=k_5=k_7=0$in (1) then Theorem 1 holds with$k=\frac{2k_1}{1+k_1}\in \left[0\hspace{0.33em},\hspace{0.33em}1\right)$which holds if and only if$k_1\in \left[0,\hspace{0.33em}1\right)$, which is the$p$-contraction condition of (1). Thus, the generalized$p$-contraction condition of Theorem 1 includes, in particular, the original$p$-contraction concept. In this case,$T:X\to X$^{is a so-called}$p$-contraction that was proposed and discussed in [1] as an expansion of Banach’s contraction principle. See also [2] for the conceptual extensions to the proposed$p$-contraction pairs as well as for the discussion of their properties. Other typical contractive mappings are also included as particular cases of (1) satisfying the general given constraints. For instance, if$k_1\in \left[0,1\right)$and$k_i=0$; $\forall i\in \overline{7\hspace{0.33em}}\backslash \left\{1\right\}$, one has Banach’s contraction. If$k_2=k_3\in \left[0,\hspace{0.33em}1/2\right)$and$k_i=0$;$\forall i\in \overline{7\hspace{0.33em}}\backslash \left\{2 , 3\right\}$, one has Kannan’s contraction, [6,9]. If$k_6=k_7=0$, one gets a Hardy–Roger’s contraction. If$k_i=0$,$\forall i\in \overline{7\hspace{0.33em}}\backslash \left\{1 ,2,3\right\}$, one gets a Reich’s contraction [19].

Remark 2.

Note that Cauchyness referred to in Theorem 1(ii) does not require for the metric space$\left(X,d\right)$to be complete although completeness is assumed for the sequence limit to belong to$X$. It is a well-known property that any convergent sequence is a Cauchy sequence. However, there is a direct route to prove the property for this particular case with an “ad hoc” simple proof as follows. Note that since$d\left(T^{2}x,\hspace{0.33em}Tx\right)\le kd\left(x,Tx\right)$with$k=max\left(K , K^{\prime }\right)<1$then$d\left(T^{m}x, T^{n}x\right)<\epsilon$for any$\epsilon >0$and$n,\hspace{0.33em}m\left(>n\right)\in Z_{0+}$with$n\left(\ge N\right)\in Z_{0+}$provided that$N=N\left(\epsilon ,x\right)\in Z_{0+}$is large enough to fulfil$k^N<\frac{1-k}{d\left(x,Tx\right)}\epsilon$. Thus,${\left\{T^{n}x\right\}}_{n=0}^{\infty }$is a Cauchy sequence for any given$x\in X$.

Theorem 1 has used the obvious constraint $d\left(x,x\right)=0$ if $d$ is a metric. However, this does not necessarily hold for any $x\in X$ if $\left(X,d\right)$ is a metric-like (or “dislocated metric”) space. Note that dislocated metric spaces also keep the symmetry property of distances as in the case of metric spaces. A reformulation of Theorem 1 for the case of metric-like spaces is now given:

Theorem 2.

Consider a self-mapping$T$on$X$, where$\left(X,d\right)$is a metric-like space, subject to the generalized $p$-contraction constraint (1). Then, the following properties hold:

(i)

$T:X\to X$is asymptotically regular at all$x$in$X$if$k_6+k_7\le k_1+k_2+k_4+2k_5<1-k_3-k_4$. Any orbit $O\left(x\right)=\left(x , Tx ,T^{2}x,\dots \right)$for$x\in X$is subject to the contraction rule$d\left(T^{2}x\hspace{0.33em},\hspace{0.33em}Tx\right)\le k\left(\alpha \left(x,Tx ,T^{2}x\right)\hspace{0.33em},\hspace{0.33em}\beta \left(x,Tx ,T^{2}x\right)\right)d\left(x,Tx\right)$under the contraction constant:

$$k\left(\alpha \left(x,Tx ,T^{2}x\right)\hspace{0.33em},\hspace{0.33em}\beta \left(x,Tx ,T^{2}x\right)\right)=\frac{k_1+k_2+k_4+2k_5+k_6\alpha \left(x ,Tx , T^{2}x\right)-k_7\beta \left(x ,Tx , T^{2}x\right)}{1-k_3-k_4+k_6\alpha \left(x ,Tx , T^{2}x\right)-k_7\beta \left(x ,Tx , T^{2}x\right)}\in \left[0\hspace{0.33em},\hspace{0.33em}1\right).$$

(ii)

If, in addition, $\left(X,d\right)$ is complete then there is a unique fixed point $z\left(=Tz\right)\in X$ and ${\left\{T^{n}x\right\}}_{n=0}^{\infty }\to z$;$\forall x\in X$ and ${\left\{T^{n}x\right\}}_{n=0}^{\infty }$ is a Cauchy sequence.

Proof. 

The first inequality of (2) in Theorem 1, subject to (3), still holds, that is

$$\begin{array}{c}d\left(Tx\hspace{0.33em},\hspace{0.33em}{T}^{2}x\right)\le k_{1}d\left(x,Tx\right)+k_{2}d\left(x,Tx\right)+k_{3}d\left(Tx,T^{2}x\right)+k_{4}d\left(x,T^{2}x\right)+k_{5}d\left(Tx,Tx\right)\\ +k_6\left|d\left(x,Tx\right)-d\left(Tx,T^{2}x\right)\right|+k_7\left|d\left(x,T^{2}x\right)-d\left(Tx,Tx\right)\right|\end{array}$$

(14)

Since $d\left(Tx,Tx\right)$ can be non-zero, the last right-hand-side absolute value of (14) has to be monitored by defining:

$$\beta \left(x ,Tx , T^{2}x\right)=\left\{\begin{array}{c}1 \hspace{1em}if\hspace{1em}d\left(x ,T^{2}x\right)>d\left(Tx\hspace{0.33em},\hspace{0.33em}Tx\right)\\ 0\hspace{1em}if\hspace{1em}d\left(x ,T^{2}x\right)=d\left(Tx\hspace{0.33em},\hspace{0.33em}Tx\right)\\ -1\hspace{1em}if\hspace{1em}d\left(x ,T^{2}x\right)<d\left(Tx\hspace{0.33em},\hspace{0.33em}Tx\right)\end{array}\right.$$

(15)

Using $\alpha \left(x ,Tx , T^{2}x\right)$ defined in (3) and $\beta \left(x ,Tx , T^{2}x\right)$ defined in (15) as well as $d\left(Tx,Tx\right)\le 2d\left(x ,Tx\right)$ from the triangle inequality, one gets from (14) that

$$\begin{array}{l}\left(1-k_3+k_6\alpha \left(x ,Tx , T^{2}x\right)\right)d\left(Tx ,\hspace{0.33em}{T}^{2}x\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\le \left(k_1+k_2+k_6\alpha \left(x ,Tx , T^{2}x\right)\right)d\left(x,Tx\right)+\left(k_4+k_7\beta \left(x ,Tx , T^{2}x\right)\right)d\left(x ,T^{2}x\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\left(k_5-k_7\beta \left(x ,Tx , T^{2}x\right)\right)d\left(Tx ,Tx\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\le \left(k_1+k_2+k_6\alpha \left(x ,Tx , T^{2}x\right)+2\left(k_5-k_7\beta \left(x ,Tx , T^{2}x\right)\right)\right)d\left(x,Tx\right)+\left(k_4+k_7\beta \left(x ,Tx , T^{2}x\right)\right)d\left(x ,T^{2}x\right)\end{array}$$

(16)

which is obtained after modifying the right-hand-side upper-bound by adding the non-negative term $k_{5}d\left(Tx,Tx\right)$. Then, after using $d\left(x ,T^{2}x\right)\le d\left(Tx ,T^{2}x\right)+d\left(x,Tx\right)$, leads to

$$\begin{array}{l}\left(1-k_3+k_6\alpha \left(x ,Tx , T^{2}x\right)-k_4-k_7\beta \left(x ,Tx , T^{2}x\right)\right)d\left(Tx ,\hspace{0.33em}{T}^{2}x\right)\\ \le \left(k_1+k_2+k_6\alpha \left(x ,Tx , T^{2}x\right)+2\left(k_5-k_7\beta \left(x ,Tx , T^{2}x\right)\right)\right)d\left(x,Tx\right)+\left(k_4+k_7\beta \left(x ,Tx , T^{2}x\right)\right)d\left(x ,Tx\right),\end{array}$$

(17)

equivalently,

$$d\left(T^{2}x\hspace{0.33em},\hspace{0.33em}Tx\right)\le k\left(\alpha \left(x,Tx ,T^{2}x\right)\hspace{0.33em},\hspace{0.33em}\beta \left(x,Tx ,T^{2}x\right)\right)d\left(x,\hspace{0.33em}Tx\right)$$

(18)

where

$$k\left(\alpha \left(x,Tx ,T^{2}x\right)\hspace{0.33em},\hspace{0.33em}\beta \left(x,Tx ,T^{2}x\right)\right)=\frac{k_1+k_2+k_4+2k_5+k_6\alpha \left(x ,Tx , T^{2}x\right)-k_7\beta \left(x ,Tx , T^{2}x\right)}{1-k_3-k_4+k_6\alpha \left(x ,Tx , T^{2}x\right)-k_7\beta \left(x ,Tx , T^{2}x\right)}<1$$

(19)

if $k_1+k_2+k_3+2\left(k_4+k_5\right)<1$. Furthermore the coefficients of the left and right-hand-sides of (18) have to be positive for the coherency of the manipulation of (17) to obtain (18). Equivalently the numerator of $k\left(\alpha \left(x,Tx ,T^{2}x\right)\hspace{0.33em},\hspace{0.33em}\beta \left(x,Tx ,T^{2}x\right)\right)$ in (19) has to be non-negative and its denominator has to be positive in order that $k\left(\alpha \left(x,Tx ,T^{2}x\right)\hspace{0.33em},\hspace{0.33em}\beta \left(x,Tx ,T^{2}x\right)\right)\ge 0$ for the four possible combinations of $\left(\alpha ,\beta \right)=\left(\pm 1,\pm 1\right)$ since the zero values are already guaranteed by the above constraint $k_1+k_2+k_3+2\left(k_4+k_5\right)<1$. This required new constraints combined with $k_1+k_2+k_3+2\left(k_4+k_5\right)<1$, which is identical to $k_1+k_2+k_4+2k_5<1-k_3-k_4$, leads to:

$$k_6+k_7<1-k_3-k_4\Rightarrow k_6+k_7<min\left(1-k_3-k_4\hspace{0.33em},\hspace{0.33em}{k}_1+k_2+k_4+2k_5\right)=k_1+k_2+k_4+2k_5$$

(20)

which guarantees that the numerator of $k\left(\alpha \left(x,Tx ,T^{2}x\right)\hspace{0.33em},\hspace{0.33em}\beta \left(x,Tx ,T^{2}x\right)\right)$ is non-negative and its denominator is positive and, together with $k_1+k_2+k_3+2\left(k_4+k_5\right)<1$, that $k\left(\alpha \left(x,Tx ,T^{2}x\right)\hspace{0.33em},\hspace{0.33em}\beta \left(x,Tx ,T^{2}x\right)\right)\in \left[0\hspace{0.33em},\hspace{0.33em}1\right)$. The joint constraints $k_1+k_2+k_3+2\left(k_4+k_5\right)<1$ and $k_6+k_7<k_1+k_2+k_4+2k_5$ are expressed by $k_6+k_7\le k_1+k_2+k_4+2k_5<1-k_3-k_4$. Then, one gets under the above constraint that $d\left(T^{n}x,T^{n+1}x\right)\le {\overline{k}}^{n}d\left(x,Tx\right)$, with $\overline{k}=\underset{\mu ,\nu \in \left\{-1\hspace{0.33em},\hspace{0.33em}1\right\}}{max}k\left(\mu \hspace{0.33em},\hspace{0.33em}\nu \right)\in \left[0\hspace{0.33em},\hspace{0.33em}1\right)$ and $T^0$ being the identity mapping, that is, $T^{0}x=x$; $\forall x\in X$. As a result, $\underset{n\to \infty }{lim}d\left(T^{n}x,T^{n+1}x\right)=0$. Property (i) has been proved. The proof of the first part of Property (ii) is similar to that of Theorem 1 (ii) to conclude that ${\left\{T^{n}x\right\}}_{n=0}^{\infty }$ is convergent to a fixed point $z=Tz$ of $X$, since $\left(X,d\right)$ is complete, and a Cauchy sequence for any given $x\in X$ through a close proof to that of its counterpart in Theorem 1. It remains to be proven that the fixed point is unique. Assume that this is not the case so that there are two distinct fixed points $\omega$ and $z$ of $T$ in $X$. Thus, one can determine from (1) that

$$\begin{array}{l}0<d\left(z\hspace{0.33em},\hspace{0.33em}\omega \right)=d\left(Tz\hspace{0.33em},\hspace{0.33em}T\omega \right)\le k_{1}d\left(z,\omega \right)+k_{2}d\left(z,Tz\right)+k_{3}d\left(\omega ,T\omega \right)+k_{4}d\left(z,T\omega \right)+k_{5}d\left(\omega ,Tz\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+k_6\left|d\left(z\hspace{0.33em},\hspace{0.33em}Tz\right)-d\left(\omega ,T\omega \right)\right|+k_7\left|d\left(z,T\omega \right)-d\left(\omega ,Tz\right)\right|\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=k_{1}d\left(z,\omega \right)+k_{4}d\left(z,\omega \right)+k_{5}d\left(\omega ,z\right)+k_6\left|d\left(z,\hspace{0.33em}z\right)-d\left(\omega ,\omega \right)\right|+k_7\left|d\left(z,\omega \right)-d\left(\omega ,z\right)\right|\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\left(k_1+k_4+k_5\right)d\left(z,\omega \right)\end{array}$$

(21)

which holds, since $d\left(z,\omega \right)>0$, if and only if $1\le k_1+k_4+k_5$, which holds, since $d\left(z,\omega \right)>0$, if and only if $1\le k_1+k_4+k_5$. It has been used in the derivation of (21) that $d\left(z,z\right)=d\left(\omega ,\omega \right)=0$ for $z$ and $\omega$ being fixed points of $T$, despite that $\left(X,d\right)$ is a metric-like space, since $d\left(z,Tz\right)=d(z,z)=d\left(T^{n}z,T^{n+1}z\right)>0$ for any $n\in Z_{0+}$ and $z$ being any fixed point of $T$ would contradict $d\left(T^{n}z,T^{n+1}z\right)\to 0$ as $n\to \infty$. Comparing this constraint with the contractivity constraint $k_6+k_7<k_1+k_2+k_4+2k_5<1-k_3-k_4$, one concludes that $k_2+k_4+k_5+k_3<0$, a contradiction. Thus, $z=\omega$ so that the fixed point is unique. Property (ii) has been proved. □

Remark 3. 

Note that the constant$k_5$is irrelevant in Theorem 1(i) for proving asymptotic regularity, that is, if$\left(X,d\right)$is a metric space. However, it is relevant in Theorem 1(ii), together with the metric space completeness, for proving the uniqueness of the fixed point and it is also relevant in Theorem 2[(i)–(ii)], that is, in the case when$\left(X,d\right)$is a metric-like space.

3. Some Convergence and Best Proximity Results for a Class of Generalized $\left(T,S\right)$ Cyclic p-Contraction Pairs in Metric Spaces

The following result relies on a generalized contraction related to $\left(T, S\right)$ cyclic $p$-contraction pairs [9] and some of its properties. It is proved that, for given arbitrary initial points $x\in A$ with $y\left(=Tx\right)\in B$, the sequences generated through $\left(T,S\right)$ or dually, if $y\in B$ with $x\left(=Sy\right)\in A$, the sequences generated through $\left(S,T\right)$ have the following asymptotic properties $d\left({\left(ST\right)}^{n}x,T{\left(ST\right)}^{n}x\right)\to d\left(A, B\right)$, $n\to \infty$ $d\left(S{\left(TS\right)}^{n}y,{\left(TS\right)}^{n+1}Sy\right)\to d\left(A, B\right)$ as $n\to \infty$. In particular, if $A$ and $B$ intersect then $d\left({\left(ST\right)}^{n}x,T{\left(ST\right)}^{n}x\right)\to 0$, $n\to \infty$ $d\left(S{\left(TS\right)}^{n}y,{\left(TS\right)}^{n+1}Sy\right)\to 0$ as $n\to \infty$.

Theorem 3.

Consider two mappings$T:A\to B$and$S:B\to A$, where $A, B\subset X$are non-empty and $\left(X,d\right)$is a metric space, subject to the subsequent generalized$\left(T, S\right)$cyclic$p$-contraction constraint:

$$\begin{array}{l}d\left(Tx\hspace{0.33em},\hspace{0.33em}Sy\right)\le k_{1}d\left(x,y\right)+k_{2}d\left(x,Tx\right)+k_{3}d\left(y,Sy\right)+k_{4}d\left(x,Sy\right)+k_{5}d\left(y,Tx\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+k_6\left|d\left(x,Tx\right)-d\left(y,Sy\right)\right|+k_7\left|d\left(x,Sy\right)-d\left(y,Tx\right)\right|+kD; \forall x\in A,\forall y\in B,\end{array}$$

(22)

where $k\in R_{+}$,$k_i\in R_{0+}$; $\forall i\in \overline{7}$, with, and $D=d\left(A, B\right)$. Assume that:

$$k_1+k_2+k_3+2\left(max\left(k_4 ,k_5\right)+k_7\right)<1;k_6<1-k_3-max\left(k_4 ,k_5\right)-k_7$$

(23)

and define $\zeta =max\left(\rho ,\hspace{0.33em} \sigma \right)\in \left[0,\hspace{0.33em}1\right)$ and $k=max\left(k_{\rho } ,k_{\sigma }\right)>0$, where:

$$\begin{array}{l}\rho =\frac{k_1+k_2+k_6+k_4+k_7}{1-k_3+k_6-k_4-k_7;} \sigma =\frac{k_1+k_2+k_6+k_5+k_7}{1-k_3+k_6-k_5-k_7}\\ k_{\rho }=1-k_1-k_2-k_3-2\left(k_4+k_7\right); k_{\sigma }=1-k_1-k_2-k_3-2\left(k_5+k_7\right).\end{array}$$

(24)

Then, the following properties hold:

$$D\le d\left({\left(ST\right)}^{n}x,T{\left(ST\right)}^{n}x\right)\le {\rho }^{2n}d\left(x,Tx\right)+\left(1-{\rho }^{2n}\right)D\le {\xi }^{2n}d\left(x,Tx\right)+\left(1-{\xi }^{2n}\right)D; \forall x\in A, \forall n\in Z_{0+}$$

(25)

$$D\le d\left({\left(TS\right)}^{n}y,{\left(TS\right)}^{n}Sy\right)\le {\sigma }^{2n}d\left(y,Sy\right)+\left(1-{\sigma }^{2n}\right)D\le {\xi }^{2n}d\left(y,Sy\right)+\left(1-{\xi }^{2n}\right)D; \forall y\in B, \forall n\in Z_{0+}$$

(26)

$$\begin{array}{l}\underset{n\to \infty }{lim}d\left({\left(ST\right)}^{n}x,T{\left(ST\right)}^{n}x\right)=\underset{n\to \infty }{lim}d\left({\left(ST\right)}^{n}x,{\left(TS\right)}^{n}Tx\right)=\underset{n\to \infty }{lim}d\left(T{\left(ST\right)}^{n}x,{\left(ST\right)}^{n+1}x\right)\\ =\underset{n\to \infty }{lim}d\left({\left(TS\right)}^{n}y,{\left(ST\right)}^{n}Sy\right)=\underset{n\to \infty }{lim}d\left({\left(ST\right)}^{n}Sy,{\left(TS\right)}^{n+1}y\right)=\underset{n\to \infty }{lim}d\left(S{\left(TS\right)}^{n}y,{\left(TS\right)}^{n+1}y\right)=D \end{array}$$

(27)

for either$x\in A$and$y=Tx$or$y\in B$and$x=Sy$.

If$A\cap B\ne Ø$ then the limits in (27) are zero.

Proof. 

Consider the following cases:

Case A: For $y=Tx$ and any $x\in A$:

$$\begin{array}{l}d\left(Tx\hspace{0.33em},\hspace{0.33em}STx\right)\le k_{1}d\left(x,Tx\right)+k_{2}d\left(x,Tx\right)+k_{3}d\left(Tx,STx\right)+k_{4}d\left(x,STx\right)+k_{5}d\left(Tx,Tx\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+k_6\left|d\left(x,Tx\right)-d\left(Tx,STx\right)\right|+k_7\left|d\left(x,STx\right)-d\left(Tx,Tx\right)\right|+k_{\rho }D\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\left(k_1+k_2\right)d\left(x,Tx\right)+k_{3}d\left(Tx,STx\right)+\left(k_4+k_7\right)d\left(x,STx\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+k_6\left|d\left(x,Tx\right)-d\left(Tx,STx\right)\right|+k_{\rho }D\end{array}$$

(28)

for some $k_{\rho }\in R_{+}$ to be fixed which yields:

$$\left(1-k_3+k_6\alpha \left(x,Tx ,STx\right)\right)d\left(Tx\hspace{0.33em},\hspace{0.33em}STx\right)\le \left(k_1+k_2+k_6\alpha \left(x,Tx ,STx\right)\right)d\left(x,Tx\right)+\left(k_4+k_7\right)d\left(x,STx\right)+k_{\rho }D$$

(29)

by defining for any $x\in A$:

$$\alpha \left(x,Tx , STx\right)=\left\{\begin{array}{c}1\hspace{1em}if\hspace{1em}d\left(x,Tx\right)>d\left(Tx,STx\right)\\ 0\hspace{1em}if\hspace{1em}d\left(x,Tx\right)=d\left(Tx,STx\right)\\ -1\hspace{1em}if\hspace{1em}d\left(x,Tx\right)<d\left(Tx,STx\right)\end{array}\right..$$

(30)

Then,

$$d\left(Tx\hspace{0.33em},\hspace{0.33em}STx\right)\le \frac{k_1+k_2+k_6\alpha \left(x,Tx , STx\right)}{1-k_3+k_6\alpha \left(x,Tx , STx\right)}d\left(x,Tx\right)+\frac{k_4+k_7}{1-k_3+k_6\alpha \left(x,Tx , STx\right)}d\left(x,STx\right)+\frac{k_{\rho }}{1-k_3+k_6\alpha \left(x,Tx , STx\right)}D$$

(31)

Using $d\left(x,STx\right)\le d\left(x,Tx\right)+d\left(Tx,STx\right)$ yields:

$$\begin{array}{l}\left(1-\frac{k_4+k_7}{1-k_3+k_6\alpha \left(x,Tx , STx\right)}\right)d\left(Tx,STx\right)\le \left(\frac{k_1+k_2+k_6\alpha \left(x,Tx , STx\right)}{1-k_3+k_6\alpha \left(x,Tx , STx\right)}+\frac{k_4+k_7}{1-k_3+k_6\alpha \left(x,Tx , STx\right)}\right)d\left(x,Tx\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{k_{\rho }}{1-k_3+k_6\alpha \left(x,Tx , STx\right)}D\end{array}$$

(32)

so that

$$\left(1-k_3+k_6\alpha \left(x,Tx , STx\right)-k_4-k_7\right)d\left(Tx,STx\right)\le \left(k_1+k_2+k_6\alpha \left(x,Tx , STx\right)+k_4+k_7\right)d\left(x,Tx\right)+k_{\rho }D$$

(33)

leading to

$$\begin{array}{c}d\left(Tx,STx\right)\le \frac{k_1+k_2+k_6\alpha \left(x,Tx , STx\right)+k_4+k_7}{1-k_3+k_6\alpha \left(x,Tx , STx\right)-k_4-k_7}d\left(x,Tx\right)+\frac{k_{\rho }}{1-k_3+k_6\alpha \left(x,Tx , STx\right)-k_4-k_7}D\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\le \frac{k_1+k_2+k_6\alpha \left(x,Tx , STx\right)+k_4+k_7}{1-k_3+k_6\alpha \left(x,Tx , STx\right)-k_4-k_7}d\left(x,Tx\right)+\frac{k_{\rho }}{1-k_3-k_6-k_4-k_7}D\end{array}$$

(34)

Define $\rho =\underset{\theta \in \left\{-1, ,1 , 0\right\}}{max}\frac{k_1+k_2+k_6\theta +k_4+k_7}{1-k_3+k_6\theta -k_4-k_7}$ which is independent of $\theta$ and then independent of the sequence $\left\{\alpha \left(T^{n}x,T^{n+1}x , S{T}^{n+1}x\right)\right\}{ }_{n=0}^{\infty }$ and note that $\rho \in \left[0\hspace{0.33em}, 1\right)$ if and only if $k_1+k_2+k_3+2\left(k_4+k_7\right)<1$. This last constraint implies that $\rho =\frac{k_1+k_2+k_6+k_4+k_7}{1-k_3+k_6-k_4-k_7}\ge \underset{\theta \in \left\{-1, 0\right\}}{max}\frac{k_1+k_2+k_6\theta +k_4+k_7}{1-k_3+k_6\theta -k_4-k_7}$ if $k_6<1-k_3-k_4-k_7$. Now fix $k_{\rho }=\left(1-\rho \right) \left(1-k_3-k_4-k_6-k_7\right)=1-k_1-k_2-k_3-2\left(k_4+k_7\right)$. Thus, one has:

$$\begin{array}{l}d\left(Tx,STx\right)\le \rho d\left(x,Tx\right)+\left(1-\rho \right)D\\ d\left(STx,TSTx\right)=d\left(\left(ST\right)x,T\left(ST\right)x\right)\le \rho \left(\rho d\left(x,Tx\right)+\left(1-\rho \right)D\right)+\left(1-\rho \right)D\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\le {\rho }^{2}d\left(x,Tx\right)+\left(1-{\rho }^2\right)D={\rho }^{2}d\left({\left(ST\right)}^{0}x,{\left(ST\right)}^{0}Tx\right)+\left(1-{\rho }^2\right)D\\ d\left(TSTx,STSTx\right)\le {\rho }^{3}d\left(x,Tx\right)+\left(1-{\rho }^3\right)D\\ d\left(STSTx,TSTSTx\right)=d\left({\left(ST\right)}^{2}x,T{\left(ST\right)}^{2}x\right)\le {\rho }^{4}d\left(x,Tx\right)+\left(1-{\rho }^4\right)D={\rho }^{4}d\left({\left(ST\right)}^{0}x,{\left(ST\right)}^{0}Tx\right)+\left(1-{\rho }^4\right)D\\ d\left({\left(ST\right)}^{n}x,T{\left(ST\right)}^{n}x\right)\le {\rho }^{2n}d\left(x,Tx\right)+\left(1-{\rho }^{2n}\right)D; \forall n\in Z_{0+}\end{array}$$

(35)

Since $x\in A$, $Tx\in B$, ${\left(ST\right)}^{n}x\in A$, and $T{\left(ST\right)}^{n}x\in B$; $\forall n\in Z_{0+}$ and $d\left(A,B\right)=D$, one can determine that

$$D\le d\left({\left(ST\right)}^{n}x,T{\left(ST\right)}^{n}x\right)\le {\rho }^{2n}d\left(x,Tx\right)+\left(1-{\rho }^{2n}\right)D; \forall x\in A, \forall n\in Z_{0+}$$

(36)

so that there exists $\underset{n\to \infty }{lim}d\left({\left(ST\right)}^{n}x,T{\left(ST\right)}^{n}x\right)=D$; $\forall x\in A$.

(Case B): For $x=Sy$ and any $y\in B$, one proceeds in a similar way as in A:

$$\begin{array}{l}d\left(TSy\hspace{0.33em},\hspace{0.33em}Sy\right)\le \left(k_1+k_3\right)d\left(Sy,y\right)+k_{2}d\left(Sy,TSy\right)+\left(k_5+k_7\right)d\left(y,TSy\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+k_6\left|d\left(Sy,TSy\right)-d\left(y,Sy\right)\right|+k_{\sigma }D\end{array}$$

(37)

for some $k_{\sigma }\in R_{+}$ to be fixed. Use the inequality $d\left(y,TSy\right)\le d\left(y,Sy\right)+d\left(Sy,TSy\right)$ and define for any $y\in B$:

$$\beta \left(y,Sy , TSy\right)=\left\{\begin{array}{c}1\hspace{1em}if\hspace{1em}d\left(y,Sy\right)>d\left(Sy,TSy\right)\\ 0\hspace{1em}if\hspace{1em}d\left(y,Sy\right)=d\left(Sy,TSy\right)\\ -1\hspace{1em}if\hspace{1em}d\left(y,Sy\right)<d\left(Sy,TSy\right)\end{array}\right.$$

(38)

to yield under a similar procedure as that used in Case A:

$$\left(1-k_2-k_5-k_7+k_6\beta \left(y,Sy , TSy\right)\right)d\left(TSy\hspace{0.33em},\hspace{0.33em}Sy\right)\le \left(k_1+k_3+k_5+k_7+k_6\beta \left(y,Sy , TSy\right)\right)d\left(Sy,y\right)+k_{\sigma }D$$

(39)

that is

$$d\left(TSy,Sy\right)\le \frac{k_1+k_3+k_6\beta \left(y,Sy , STy\right)+k_5+k_7}{1-k_3+k_6\beta \left(y,Sy , STy\right)-k_5-k_7}d\left(x,Tx\right)+\frac{k_{\sigma }}{1-k_3+k_6\beta \left(y,Sy , STy\right)-k_5-k_7}D$$

(40)

Define $\sigma =\underset{\theta \in \left\{-1, ,1 , 0\right\}}{max}\frac{k_1+k_3+k_6\theta +k_5+k_7}{1-k_3+k_6\theta -k_5-k_7}$ which is independent of $\theta$ and then independent of the sequence $\left\{\beta \left(S^{n}y,S^{n+1}y , S^{n+1}Tx\right)\right\}{ }_{n=0}^{\infty }$ and note that $\sigma \in \left[0\hspace{0.33em}, 1\right)$ if and only if $k_1+k_2+k_3+2\left(k_5+k_7\right)<1$. This last constraint implies that $\sigma =\frac{k_1+k_2+k_6+k_5+k_7}{1-k_3+k_6-k_5-k_7}\ge \underset{\theta \in \left\{-1, 0\right\}}{max}\frac{k_1+k_2+k_6\theta +k_5+k_7}{1-k_3+k_6\theta -k_5-k_7}$ if $k_6<1-k_3-k_5-k_7$. Now fix $k_{\sigma }=\left(1-\sigma \right) \left(1-k_3-k_5-k_6-k_7\right)=1-k_1-k_2-k_3-2\left(k_5+k_7\right)$. Thus, one has:

$$d\left(Sy\hspace{0.33em},\hspace{0.33em}TSy\right)\le \sigma d\left(y,Sy\right)+\left(1-\sigma \right)D$$

(41)

and proceeding recursively as in Case A, one obtains:

$$D\le d\left({\left(TS\right)}^{n}y,{\left(TS\right)}^{n}Sy\right)\le {\sigma }^{2n}d\left(y,Sy\right)+\left(1-{\sigma }^{2n}\right)D; \forall y\in B,\forall n\in Z_{0+}$$

(42)

so that there exists $\underset{n\to \infty }{lim}d\left({\left(TS\right)}^{n}y,{\left(TS\right)}^{n}Sy\right)=D$; $\forall y\in B$ and $x=Sy$. Thus, from the combined constraints (23)–(24) and the conclusions of Cases A and B, one directly obtains (25)–(27) by also using $T{\left(ST\right)}^{n}x={\left(TS\right)}^{n}Tx$ for $x\in A$. Then, put $x^{\prime }={\left(ST\right)}^{n}x$, $y^{\prime }=T{\left(ST\right)}^{n}x$ so that $d\left(x^{\prime },y^{\prime }\right)=d\left({\left(ST\right)}^{n}x,T{\left(ST\right)}^{n}x\right)$, $d\left(T{x}^{\prime },T{y}^{\prime }\right)=d\left(T{\left(ST\right)}^{n}x,{\left(ST\right)}^{n+1}x\right)$ and use also ${\left(ST\right)}^{n}Sy=S{\left(TS\right)}^{n}y$ for $y\in B$. The first inequality of the recursion (35) leads to

$$d\left(T{x}^{\prime },T{y}^{\prime }\right)=d\left(T{\left(ST\right)}^{n}x,{\left(ST\right)}^{n+1}x\right)\le \rho d\left({\left(ST\right)}^{n}x,T{\left(ST\right)}^{n}x\right)+\left(1-\rho \right)D$$

and then, for $x\in A$,

$$\underset{n\to \infty }{lim}d\left(T{\left(ST\right)}^{n}x,{\left(ST\right)}^{n+1}x\right)=D\le \rho \underset{n\to \infty }{lim}d\left({\left(ST\right)}^{n}x,T{\left(ST\right)}^{n}x\right)+\left(1-\rho \right)D=\rho D+\left(1-\rho \right)D=D$$

In the same way, one can prove from (41) that $\underset{n\to \infty }{lim}d\left(S{\left(TS\right)}^{n}y,{\left(TS\right)}^{n+1}Sy\right)=D$ for $y\in B$. If $A$ and $B$ intersect, $D=0$ so that the limits in (27) are equal to zero. Thus, the proof is complete. □

Remark 4.

If one takes$k_6=k_1\in \left[0 ,\hspace{0.33em}1\right)$,$k_2=k_4=k_5=k_7=0$, and$k=k_{\rho }=k_{\sigma }=1-k_1$in (22), then such a constraint becomes that proposed in ([2], Definition 2) for the so-called cyclic$p$-contraction pair$\left(T,S\right)$.

Note that Theorem 3 describes some best proximity properties of the mappings $T:A\to B$ and $\mathrm{S}:B\to A$ for particular related initial points $x\in A$ and $y=Tx\in B$, respectively, and $y\in B$ and $x=Sy\in A$ of the involved sequences since the constraint (22) becomes simplified for initial points in $B$ which are the images through $T$ of initial points in $A$ or initial points in $A$ which are the images through $S$ of initial points in $B$. Further results include arbitrary initial points without such constraints for the initial points in $A$ and $B$ and their corresponding images. The results also include the existence of unique fixed points in $A$ and $B$ of the composite self-mappings $ST$ and $TS$ and unique best proximity points of the non-self-mappings $T:A\to B$ and $S:B\to A$ provided that $A$ and $B$ are non-empty, closed, and convex subsets of a uniformly convex Banach space $\left(X ,‖‖\right)$. The price to be paid is the use of stronger contraction conditions based on the general form (22) without using the simplifying particular constraints $y=Tx\in B$ for $x\in A$ used in Theorem 3.

The subsequent result revisits Theorem 3 when the iterated sequences are generated with the initial points in $B$ are not necessarily the images through $T:A\to B$ of the initial points in $A$ or the initial points in $A$ are not necessarily the images through $S:B\to A$ of the initial points in $B$. This allows to prove the existence and the uniqueness of fixed points in each of both sets which are also best proximity points with respect to the other set if $\left(X ,‖‖\right)$ is a uniformly convex Banach space and the two subsets $A$ and $B$ of $X$ are non-empty, closed, and convex. In addition to the convergence of distances to the distance $D$ between the subsets $A$ and $B$ of $X$ proved in Theorem 3, the asymptotic regularity within each of the subsets is also proved, that is, $\underset{n\to \infty }{lim}d\left({\left(ST\right)}^{n+1}x, \hspace{0.33em}{\left(ST\right)}^{n}x\right)=\underset{n\to \infty }{lim}d\left({\left(TS\right)}^{n+1}y, \hspace{0.33em}{\left(TS\right)}^{n}y\right)=0$, for any given $x\in A$ and $y\in B$ even if $D\ne 0$. The results are derived under stronger conditions on the now controlled, in general, point-dependent functions $k_i=k_i\left(x,y\right)$; $\forall i\in \overline{7}$, which define the generalized $\left(T, S\right)$ cyclic $p$-contraction.

Theorem 4.

Consider two mappings$T:A\to B$and$S:B\to A$, where$A, B\subset X$are non-empty and$\left(X,d\right)$is a metric space, subject to the generalized$\left(T, S\right)$cyclic$p$-contraction constraint (22) of Theorem 3. Then, the following properties hold:

(i)

$$d\left(Tx,Sy\right)\le \sigma d\left(x,Tx\right)+\left(1-\sigma \right)D ; \forall x\in A, \forall y\in B$$

(43)

where

$$\sigma =\sigma \left(x,y\right)=\frac{k_1\left(1+\lambda \right)+k_2+k_3\lambda +k_4+k_6\left|1-\lambda \right|+k_7+\left(k_5\lambda +k_7\right)\lambda }{k_1+k_4+k_5+2k_7+k_5\lambda }$$

(44)

with $\lambda :R^2\to R_{0+}$ and $k_i=k_i\left(x,y\right)$ being given by $\lambda =\lambda \left(x,y\right)=d\left(y,Sy\right)/d\left(x,Tx\right)$ and $k_i:R^2\to R_{0+}$, $\forall i\in \overline{7}$. Thus, $\lambda \in \left[0\hspace{0.33em},\hspace{0.33em}1\right]$ and $\sigma \in \left[0\hspace{0.33em},\hspace{0.33em}1\right)$ if any of the two subsequent sets of constraints holds:

$$k_1+k_4<1; k_2+k_6<min\left(k_1+k_2+k_3+k_7\hspace{0.33em},\hspace{0.33em}\frac{1-k_1-k_4}{2}\right)$$

(45)

$$k_2+k_6-k_7<k_5<min\left(k_1+k_2+k_3\hspace{0.33em},\hspace{0.33em}\frac{1-k_1-k_4}{2}-k_7\right)$$

(46)

or

$$k_5=0; k_2<k_7; k_6<min\left(k_7-k_2 ,\hspace{0.33em}{k}_1+k_3+k_7\right)$$

(47)

$$k_1+k_4+2k_7<1$$

(48)

(ii)

Equation (43), subject to (44), holds with $\lambda \left(x,y\right)=d\left(y,Sy\right)/d\left(x,Tx\right)>1$, $k_i\in R_{0+}$,$\forall i\in \overline{7}$ and $\sigma \in \left[0\hspace{0.33em},\hspace{0.33em}1\right)$ if any of the two subsequent sets of constraints holds:

$$k_7<\frac{1-k_1-k_4}{2}; k_1+k_3+k_2<k_5<min\left(k_1+k_3+k_6+k_7,\frac{1-k_1-k_4}{2}-k_7 \right)$$

(49)

or

$$k_7<\frac{1-k_1-k_4}{2}; \frac{1-k_1-k_4}{2}-k_7>k_5>k_1+k_3+max\left(k_2, k_6+k_7\right)$$

(50)

$$k_1+k_4+2\left[k_1+k_3+k_7+max\left(k_2 ,k_6+k_7\right)\right]<1$$

(51)

(iii)

Assume that $D\ne 0$ and that $A$ and $B$ are bounded. Then,

$$1-\frac{diam A+diam B}{D+diam A+diam B}\le \lambda \left(x,y\right)\le 1+\frac{diam A+diam B}{D}; \forall x\in A, \forall y\in B.$$

(iv)

If either Property (i) or Property (ii) holds for each iteration then one obtains

$$D\le d\left({\left(ST\right)}^{n}x,T{\left(ST\right)}^{n}y\right)\le \left({\displaystyle {\prod }_{i=0}^{2n}\left[\sigma \left(T^{i}x,\hspace{0.33em}{T}^{i+1}x\right)\right]}\right)d\left(x,Tx\right)+\left(1-\left({\displaystyle {\prod }_{i=0}^{2n}\left[\sigma \left(T^{i}x,\hspace{0.33em}{T}^{i+1}x\right)\right]}\right)\right)D; \forall x\in A, \forall y\in B,\forall n\in Z_{0+}$$

(52)

and

$$\begin{array}{l}\underset{n\to \infty }{lim}d\left({\left(ST\right)}^{n}x,{\left(ST\right)}^{n}Sy\right)=\underset{n\to \infty }{lim}d\left({\left(ST\right)}^{n+1}x,T{\left(ST\right)}^{n}y\right)\\ =\underset{n\to \infty }{lim}d\left({\left(ST\right)}^{n+1}x,{\left(ST\right)}^{n}Sy\right)=\underset{n\to \infty }{lim}d\left(T{\left(ST\right)}^{n}x,{\left(TS\right)}^{n+1}y\right)=\underset{n\to \infty }{lim}d\left({\left(TS\right)}^{n}Tx,{\left(TS\right)}^{n+1}y\right)=D; \forall x\in A, \forall y\in B, \forall n\in Z_{0+}. \end{array}$$

(53)

(v)

In addition, let $\left(X ,‖‖\right)$ be a uniformly convex Banach space, with $d:X\times X\to R_{0+}$ being a $\Vert \Vert$-norm-induced metric, and let $A\subset X$ be closed and convex and let $B\subset X$ be closed. If either Property (i) or Property (ii) holds, then the composite mappings $ST:A\to A$ and $TS:B\to B$ are asymptotically regular, that is,

$$\underset{n\to \infty }{lim}d\left({\left(ST\right)}^{n+1}x, \hspace{0.33em}{\left(ST\right)}^{n}x\right)=\underset{n\to \infty }{lim}d\left({\left(TS\right)}^{n+1}y, \hspace{0.33em}{\left(TS\right)}^{n}y\right)=0; \forall x\in A, \forall y\in B.$$

(54)

If, furthermore, $B$ is also convex, then for any given $x\in A$, ${\left\{{\left(ST\right)}^{n}x\right\}}_{n=0}^{\infty }$ is bounded, convergent to some $z\in A$, and it is a Cauchy sequence; and, for any given $y\in B$, ${\left\{{\left(TS\right)}^{n}y\right\}}_{n=0}^{\infty }$ is bounded, convergent to some $\omega \in B$, and it is a Cauchy sequence. Furthermore, $z$ and $\omega$ are unique best proximity points so that $d\left(\omega ,z\right)=D$.

If $A$ and $B$ intersect then there is a unique common fixed point, allocated in $A\cap B$, of $T:A\to B$, $S:B\to A$, $ST:A\to A$ and $TS:B\to B$.

Proof. 

Note that if $d\left(x,Tx\right)\ne 0$ then there is some $\lambda =\lambda \left(x,y\right)\in R_{0+}$ $d\left(y,Sy\right)=\lambda d\left(x,Tx\right)$:

$$d\left(x,y\right)\le \left(1+\lambda \right)d\left(x,Tx\right)+d\left(Tx, Sy\right)$$

(55)

$$d\left(x,Sy\right)\le d\left(x,Tx\right)+d\left(Tx,Sy\right)$$

(56)

$$d\left(y,Tx\right)\le \lambda d\left(x,Tx\right)+d\left(Tx,Sy\right).$$

(57)

Thus, one can determine from (22) that

$$\begin{array}{r}d\left(Tx,Sy\right)\le \left[k_1\left(1+\lambda \right)+k_2+k_3\lambda +k_4+k_6\alpha \left(1-\lambda \right)+k_7\beta \right]d\left(x,Tx\right)\\ +\left[k_1+k_4+k_5+k_7\beta \right]d\left(Tx,Sy\right)+\left[k_5\lambda -k_7\beta \right]d\left(y,Tx\right)+kD\end{array}$$

(58)

with $\alpha$ and $\beta$ being defined in (30) and (38) and, note that

(a)

if $\lambda =d\left(y,Sy\right)/d\left(x,Tx\right)>\underset{\beta \in \left\{-1,0,1\right\}}{max}{k}_7\beta /k_5=k_7/k_5$ then one can determine from (55)–(57) in (58) that:

$$\begin{array}{c}d\left(Tx,Sy\right)\le \left[k_1\left(1+\lambda \right)+k_2+k_3\lambda +k_4+k_6\alpha \left(1-\lambda \right)+k_7\beta +\left(k_5\lambda -k_7\beta \right)\lambda \right]d\left(x,Tx\right)\\ +\left[k_1+k_4+k_5+k_7\beta \right]d\left(Tx,Sy\right)+\left[k_5\lambda -k_7\beta \right]d\left(Sy,Tx\right)+kD\end{array}$$

(59)

(b)

if $\lambda \le k_7/k_5$ then one can determine from (59) that:

$$\begin{array}{c}d\left(Tx,Sy\right)\le \left[k_1\left(1+\lambda \right)+k_2+k_3\lambda +k_4+k_6\alpha \left(1-\lambda \right)+k_7\beta \right]d\left(x,Tx\right)\\ +\left[k_1+k_4+k_5+k_7\beta \right]d\left(Tx,Sy\right)+kD\end{array}$$

(60)

and (59)–(60) jointly hold for any $\lambda \in R_{0+}$ and $\alpha ,\beta \in \left\{-1,0,1\right\}$ if

$$\begin{array}{l}d\left(Tx,Sy\right)\le \left[k_1\left(1+\lambda \right)+k_2+k_3\lambda +k_4+k_6\alpha \left(1-\lambda \right)+k_7\beta +\left|k_5\lambda -k_7\beta \right|\lambda \right]d\left(x,Tx\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\left[k_1+k_4+k_5+k_7\beta +\left|k_5\lambda -k_7\beta \right|\right]d\left(Tx,Sy\right)+kD\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\le \left[k_1\left(1+\lambda \right)+k_2+k_3\lambda +k_4+k_6\left|1-\lambda \right|+k_7+\left(k_5\lambda +k_7\right)\lambda \right]d\left(x,Tx\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\left[k_1+k_4+k_5+k_7+\left(k_5\lambda +k_7\right)\right]d\left(Tx,Sy\right)+kD\end{array}$$

(61)

If $\lambda <\left(1/2-k_1-k_4-k_5-2k_7\right)/k_5$ then $2\left(k_1+k_4+k_5+k_7+\left(k_5\lambda +2k_7\right)\right)<1$ so that

$$d\left(Tx,Sy\right)\le \frac{k_1\left(1+\lambda \right)+k_2+k_3\lambda +k_4+k_6\left|1-\lambda \right|+k_7+\left(k_5\lambda +k_7\right)\lambda }{k_1+k_4+k_5+2k_7+k_5\lambda }d\left(x,Tx\right)+\frac{k}{k_1+k_4+k_5+2k_7+k_5\lambda }D$$

(62)

which can be compacted as $d\left(Tx,Sy\right)\le \sigma d\left(x,Tx\right)+\left(1-\sigma \right)D$ by defining

$$\sigma =\frac{b}{a}=\frac{k_1\left(1+\lambda \right)+k_2+k_3\lambda +k_4+k_6\left|1-\lambda \right|+k_7+\left(k_5\lambda +k_7\right)\lambda }{k_1+k_4+k_5+2k_7+k_5\lambda }$$

(63)

and

$$\frac{k}{k_1+k_4+k_5+2k_7+k_5\lambda }D=\frac{k}{a}D=\left(1-\sigma \right)D=\left(1-\frac{b}{a}\right)D$$

(64)

$$\iff k=a-b=k_5-k_2+k_7-\left(k_1+k_3-k_5+k_7\right)\lambda -k_6\left|1-\lambda \right|-k_5{\lambda }^2$$

(65)

and note that $k=a-b>0$ if and only if $\sigma =b/a<1$. The following cases can arise:

Case A: Assume that $\lambda \in \left[0\hspace{0.33em},\hspace{0.33em}1\right]$. Then, $\sigma \in \left[0\hspace{0.33em},\hspace{0.33em}1\right)$ and $k>0$ from (65) if and only if

$$k_5+k_7-k_2-k_6+\left(k_5+k_6-k_1-k_3-k_7\right)\lambda -k_5{\lambda }^2>0$$

(66)

Consider the convex parabola:

$$p\left(\lambda \right)=k_5{\lambda }^2+\left(k_1+k_3+k_7-k_5-k_6\right)\lambda +k_2+k_6-k_5-k_7$$

Define $a=k_5$, $b=k_1+k_3+k_7-k_5-k_6$ and $c=k_2+k_6-k_5-k_7$. It is clear that $p\left(\lambda \right)<0$ with $\lambda \ge 0$ if ${\lambda }_1=\frac{-b+\sqrt{b^2-4ac}}{2a}\in \left(0 ,\hspace{0.33em}1\right]$ with one of the subcases below:

Subcase A1:$a=k_5>0$ and $k_5+k_7>k_2+k_6$, i.e., $c<0$ with $\lambda \in \left[0,{\lambda }_1\right)$. Since $a>0$, then ${\lambda }_1=\frac{\sqrt{b^2+4a\left|c\right|}-b}{2a}\in \left(0 ,\hspace{0.33em}1\right]$ if, equivalently, if and only if $4a\left(a+b-\left|c\right|\right)\ge 0$, that is if and only if $\left|c\right|=k_5+k_7-k_2-k_6\le a+b=k_1+k_3+k_7-k_6$. Both constraints together lead to $k_2+k_6-k_7<k_5\le k_1+k_2+k_3$. Since we also have $0\le \lambda \le 1<\left(1/2-k_1-k_4-k_5-2k_7\right)/k_5$ before the constraint, one obtains $1>2\left(k_1+k_4+2\left(k_5+k_7\right)\right)$ which leads to the total constraint

$k_2+k_6-k_7<k_5<min\left(k_1+k_2+k_3\hspace{0.33em},\hspace{0.33em}\frac{1-k_1-k_4}{2}-k_7\right)$ under the necessary constraints $k_1+k_4<1$, $k_2+k_6<min\left(k_1+k_2+k_3+k_7\hspace{0.33em},\hspace{0.33em}\frac{1-k_1-k_4}{2}\right)$. Subcase A1 leads to (53) subject to (64)–(66).

Subcase A2: $a=k_5=0$, $\lambda \in \left[0\hspace{0.33em},\hspace{0.33em}\frac{k_7-k_2-k_6}{k_1+k_3+k_7-k_6}\right)\subset \left[0,1\right]$ with $k_6<min\left(k_7-k_2, \hspace{0.33em}{k}_1+k_3+k_7\right)$ and $k_2<k_7$. The constraint $\lambda \in \left[0,1\right)$ follows directly if $k_1+k_3>0$ since, equivalently, $-k_2\le 0<k_1+k_3$ since $k_1+k_3\ge 0$. Subcase A2 leads to (53) subject to (64)–(66). Then, Property (i) is proved from Subcases A1–A2.

Case B: Assume that $\lambda >1$. Then, $\sigma \in \left[0\hspace{0.33em},\hspace{0.33em}1\right)$ and, equivalently, $k>0$ from (53) if and only if for $\lambda \in \left(1\hspace{0.33em},\hspace{0.33em}\overline{\lambda }\right]$ and some real $\overline{\lambda }>1$, one has:

$$p_1\left(\lambda \right)=k_5{\lambda }^2+\left(k_1+k_3-k_5+k_6+k_7\right)\lambda +k_2-k_5-k_6-k_7<0.$$

Define $b_1=k_1+k_3+k_7-k_5+k_6$ and $c_1=k_2-k_6-k_5-k_7$. It is clear that $p\left(\lambda \right)<0$ with $\lambda >1$ if ${\lambda }_2=\frac{-b_1+\sqrt{b_1^2-4a{c}_1}}{2a}>1$ with one of the Subcases B1 and B2 below:

Subcase B1: $a=k_5>0$ and $k_5+k_6+k_7>k_2$, i.e., $c_1<0$ with $\lambda >1$ irrespective of the value of $b_1$. Since $a>0$, ${\lambda }_2=\frac{\sqrt{b_1^2+4a\left|c_1\right|}-b_1}{2a}>1$. Equivalently, $b_1^2+4a\left|c_1\right|>{\left(2a+b_1\right)}^2$ and, equivalently, $\left|c_1\right|=-c_1=k_6+k_5+k_7-k_2>k_5+b_1=k_5+k_1+k_3+k_7-k_5+k_6$ which is identical to $k_5>k_1+k_3+k_2$. Consider the two subsequent sub-subcases of Subcase B1 for $c_1<0$, together with the above last constraint, specifying either sign or null value constraints on $b_1$:

Sub-Subcase B11: $c_1<0$ and $b_1\ge 0$ so that $k_1+k_2+k_3<k_5\le k_1+k_3+k_6+k_7$ under the induced necessary condition $k_2<k_6+k_7$. The former constraint $1<\lambda <\left(1/2-k_1-k_4-k_5-2k_7\right)/k_5$ induces the necessary condition $k_5<\frac{1}{2}\left(1-k_1-k_4\right)-k_7$, with $k_7<\frac{1}{2}\left(1-k_1-k_4\right)$, so that $k_1+k_2+k_3<k_5<min\left(k_1+k_3+k_6+k_7,\frac{1}{2}\left(1-k_1-k_4\right)-k_7 \right)$.

Sub-Subcase B12: $c_1<0$ and $b_1<0$ so that

$$\frac{1-k_1-k_4}{2}-k_7>k_5>k_1+k_3+max\left(k_2, k_6+k_7\right)$$

subject to $1>k_1+k_4+2\left[k_1+k_3+k_7+max\left(k_2 ,k_6+k_7\right)\right]$ from the above upper-bound of $k_5$ to be greater than its lower- bound and $k_7<\frac{1-k_1-k_4}{2}$.

Subcase B2: Now, suppose that $b_1<0$, equivalently, $k_5>k_1+k_3+k_6+k_7$ jointly with $0<c_1<\frac{b_1^2}{4a}$. Then, ${\lambda }_2>1$ if and only if $+\sqrt{{\left|b_1\right|}^2-4a{c}_1}>2a+b_1=2a-\left|b_1\right|$ which leads to the equivalent constraint $0<c_1<\left|b_1\right|-a$, subject to $\left|b_1\right|=-b_1=k_5-k_1-k_3-k_6-k_7>a=k_5$, a contradiction. Thus, Subcase B2 is unfeasible.

Subcase B3: $a=k_5=0$, $\lambda \in \left[0\hspace{0.33em},\hspace{0.33em}\frac{k_7-k_2+k_6}{k_1+k_3+k_7+k_6}\right)$ with $k_2<k_6+k_7$. The constraint $\lambda >1$ fails since the necessary condition $-k_2>k_1+k_3$ fails. Thus, the condition (4) is unfeasible for $\lambda >1$. Thus, Subcase B3 is unfeasible. Then, Property (ii) follows from Subcases B11 and B12.

Property (iii) follows directly from the subsequent inequalities:

$$\frac{D}{D+diam A\hspace{0.33em}+diam B}\le \frac{{inf}_{x\in A}d\left(x,Tx\right)}{{sup}_{y\in B}d\left(y,Sy\right)}\le \lambda \left(x,y\right)\le \frac{{sup}_{x\in A}d\left(x,Tx\right)}{{inf}_{y\in B}d\left(y,Sy\right)}\le \frac{D+diam A\hspace{0.33em}+diam B}{D}$$

Property (iv) follows from the combined Properties [(i)–(ii)] in the same way as the proof of Property (i) of Theorem 3 is addressed by taking into account that now $\sigma \left(x,y\right)$ is iteration-dependent as a result of the point dependence of $\lambda ,k_i:R^2\to R_{0+}$.

To prove Property (v), note from (53) that $d\left({\left(ST\right)}^{n}x,{\left(ST\right)}^{n}Sy\right)\to D$ as $n\to \infty$ and $d\left({\left(ST\right)}^{n+1}x,{\left(ST\right)}^{n}Sy\right)\to D$ as $n\to \infty$ for any $x\in A$ and any $y\in B$. Since $\left(X ,d\right)$ is a uniformly convex Banach space, with $A\subset X$ being closed and convex and $B\subset X$ being closed, then $d\left({\left(ST\right)}^{n}x\hspace{0.33em},{\left(ST\right)}^{n+1}x\hspace{0.33em}\right)\to 0$ as $n\to \infty$ (see [3], Lemma 3.8) for any $x\in A$, with $\left\{{\left(ST\right)}^{n}x\right\}{ }_{n=0}^{\infty }\subset A$ and then $ST:A\to A$ is asymptotically regular. In the same way, it can be proved that $TS:B\to B$ is asymptotically regular by proving that $d\left({\left(TS\right)}^{n+1}y\hspace{0.33em},{\left(TS\right)}^{n}y\hspace{0.33em}\right)\to 0$ as $n\to \infty$ for any $y\in B$. Now, note that $d\left({\left(ST\right)}^{n}x\hspace{0.33em},{\left(ST\right)}^{n+1}x\hspace{0.33em}\right)\to 0$ as $n\to \infty$ for any given $x\in A$, and since the metric is norm induced, then it is also translation invariant. Therefore, for any given $x\in A$, $d\left({\left(ST\right)}^{n}x\hspace{0.33em},{\left(ST\right)}^{n+1}x\hspace{0.33em}\right)=d\left({\left(ST\right)}^{n}x\hspace{0.33em}-{\left(ST\right)}^{n+1}x ,\hspace{0.33em}0\hspace{0.33em}\right)\to 0$ as $n\to \infty$ so that $‖{\left(ST\right)}^{n+1}x\hspace{0.33em}-{\left(ST\right)}^{n}x‖\to 0$ as $n\to \infty$ so that the sequence $\left\{{\left(ST\right)}^{n}x\right\}{ }_{n=0}^{\infty }$ is convergent in $A$, then bounded and a Cauchy sequence, since convergent, for any given $x\in A$. In the same way, one might easily prove that the sequence $\left\{{\left(TS\right)}^{n}y\right\}{ }_{n=0}^{\infty }$ has the same properties as those of $\left\{{\left(ST\right)}^{n}x\right\}{ }_{n=0}^{\infty }$ for any given $y\in B$.

Now, take the same $x\in A$ and $y\in B$ as above and also some arbitrary $x^{\prime }\left(\ne x\right)\in A$ and one can again determine from (53) that $d\left({\left(ST\right)}^n{x}^{\prime },{\left(ST\right)}^{n}Sy\right)\to D$ as $n\to \infty$ together with $d\left({\left(ST\right)}^{n+1}x,{\left(ST\right)}^{n}Sy\right)\to D$ as $n\to \infty$. Again from [3] (Lemma 3.8), one has $d\left({\left(ST\right)}^{n}x,{\left(ST\right)}^n{x}^{\prime }\right)\to 0$ as $n\to \infty$ and $\left\{{\left(ST\right)}^n{x}^{\prime }\right\}{ }_{n=0}^{\infty }\to z^{\prime }\left(\in A\right)$ and $\left\{{\left(ST\right)}^{n}x\right\}{ }_{n=0}^{\infty }\to z\left(\in A\right)$ with both sequences being bounded and Cauchy sequences as a result. Since $d\left({\left(ST\right)}^{n}x,{\left(ST\right)}^n{x}^{\prime }\right)\to 0$ as $n\to \infty$, $\left\{{\left(ST\right)}^n{x}^{\prime }\right\}{ }_{n=0}^{\infty }\to z^{\prime }\left(\in A\right)$ and $\left\{{\left(ST\right)}^{n}x\right\}{ }_{n=0}^{\infty }\to z\left(\in A\right)$ then $d\left(z,z^{\prime }\right)=0$, since otherwise, $d\left({\left(ST\right)}^{n}x,{\left(ST\right)}^n{x}^{\prime }\right)\to 0$ as $n\to \infty$ would be untrue. Therefore, $z^{\prime }=z$, although $x^{\prime }\ne x$, so that the fixed and the limit $z\in A$ of any sequence $\left\{{\left(ST\right)}^{n}x\right\}{\hspace{0.33em}}_{n=0}^{\infty }$ is unique irrespective of $x\in A$. Moreover, such a unique limit is the unique fixed point of $ST:A\to A$. Otherwise $\left\{{\left(ST\right)}^{n+1}x\right\}{\hspace{0.33em}}_{n=0}^{\infty }\to z$ would fail for some $x\in A$. In the same way, if $B$ is both closed and convex, it can be proved that all sequences $\left\{{\left(TS\right)}^{n}y\right\}{\hspace{0.33em}}_{n=0}^{\infty }\to \omega \left(\in B\right)$ for any given $y\in B$ are Cauchy sequences and their limit $\omega$ is unique (irrespective of $y$) which is also the unique fixed point of $T\mathrm{S}:B\to B$. From Property (iv), $\left\{d\left(S{\left(TS\right)}^{n}y, TS{\left(TS\right)}^n{y}^{\prime }\right)\right\}{ }_{n=0}^{\infty }\to D=d\left(z,\omega \right)=\underset{x\in A ,\hspace{0.33em}y\in B}{inf}d\left(x,y\right)$ so that $z$ and $\omega$ are best proximity points of $A$ and $B$, then $\omega =Tz$ which are unique since $z$ and $\omega$ are unique best proximity points of the subsets $A$ and $B$. In the same way, it can be proved that $z=S\omega$.

Now, if $A\cap B\ne Ø$ then $D=0$ and $d\left(z,Tz\right)=d\left(\omega ,S\omega \right)=0$ so that $z=Tz$, $\omega =Sz=STz=z=S\omega =TS\omega$ since $z$ is the unique fixed point of $ST:A\to A$ and $\omega$ is the unique fixed point of $T\mathrm{S}:B\to B$. Therefore, $z=\omega \left(\in A\cap B\right)$ is the unique fixed point of the self-mappings $ST:A\to A$, $T\mathrm{S}:B\to B$ and of the non-self-mappings $T:A\to B$ and $S:B\to A$. Property (v) has been fully proved. □

Remark 5. 

The isolated proof of boundedness of the sequences if Theorem 4(ii) does not require that the sets be closed and convex nor that the metric be norm induced. From the convergence of the distances to that between the subsets, we know that$d\left(W^{2n+1}x,W^{2n}Tz\right)\to D$as$n\to \infty$, where$W=ST$and$y\in B$and$x,z=Sy\in A$. If the metric is the discrete one then the whole metric space is totally bounded so that there is no need for any specific proof of the boundedness of the sequences${\left\{W^{2n}x\right\}}_{n=0}^{\infty }$. For other metrics, assume that${\left\{W^{2n}x\right\}}_{n=0}^{\infty }$is unbounded to proceed by contradiction. Then, there is a strictly increasing subsequence of distances${\left\{d\left(W^{2n_k}x,Tz\right)\right\}}_{k=0}^{\infty }\subset {\left\{ d\left(W^{2n}x,Tz\right)\right\}}_{n=0}^{\infty }$for any given$z\in A$. Since${\left\{d\left(W^{2n_k}x,Tz\right)\right\}}_{k=0}^{\infty }$is strictly increasing, direct calculations lead to:

$$d\left(x_{m_k},T{z}_{m_k}\right)<d\left(W^{2n_k+2}{x}_{m_k} ,\hspace{0.33em}{W}^{2n_k}T{z}_{m_k}\right)\le {\sigma }^{2n_k}d\left(x_{m_k},T{z}_{m_k}\right)+\left(1-{\sigma }^{2n_k}\right)D$$

where ${\left\{x_{m_k}\right\}}_{k=0}^{\infty }$ and ${\left\{z_{m_k}\right\}}_{k=0}^{\infty }$ are in $A$ so that $\underset{k\to \infty }{lim\hspace{0.33em}sup}d\left(x_{m_k},T{z}_{m_k}\right)<D$, a contradiction.

Remark 6. 

The asymptotic regularity property (54), typically known as UC-property [9,22], is formulated for$2$-cyclic contractions in the former work [3] with$A$being a non-empty convex and closed and$B$being closed subsets of the uniformly convex Banach space$\left(X ,d\right)$. The subsequent convergence to unique best proximity points of the sequences generated through the cyclic self-mapping which are also respective unique fixed points of the composite cyclic self-mapping with itself within each of the subsets is addressed in [3] if$B$is, in addition, convex. In [22], the UC property only requires for one of the involved subsets, say$A$, to be non-empty and convex (non-necessarily closed) while the other one is assumed simply non-empty. If$\left(X ,d\right)$is a uniformly convex Banach space in each direction, which is a weaker condition than uniform convexity (see [22]), then$A$is assumed both convex and relatively compact, that is, with bounded closure.

Remark 7.

It can be pointed out that certain hybrid algorithms for non-self-mappings on real Hilbert spaces have been proposed in [23]. Under those mentioned algorithms, the iterated sequences converge strongly to the proximity point of any non-expansive mapping whose proximity point set is non-empty. On the other hand, F-contractions in the framework of b-metric spaces are discussed in [24] together with applications to integral equations of the Fredholm type.

Example 2.

Model tracking in a linear discrete control theory problem. Consider the following single-input coupled time-varying discrete time$n$-th order linear systems which are the reference model and the controlled system:

Reference model

$$x_{k+1}^m=A_k^m{x}_k^m+b_k^m{r}_k;\forall k\in Z_{0+}$$

(67)

where ${\left\{x_k^m\right\}}_{k=0}^{\infty }\left(\subset R^n\right)$, with arbitrary finite initial condition$x_0^m=x_{0m}$, and${\left\{r_k^m\right\}}_{k=0}^{\infty }\left(\subset R\right)$are, respectively, the reference model state sequence and the reference input sequence.${\left\{A_k^m\right\}}_{k=0}^{\infty }\left(\subset R^{n\times n}\right)$and${\left\{b_k^m\right\}}_{k=0}^{\infty }\left(\subset R^n\right)$are, respectively, the bounded matrix of dynamics of the model and its control vector. The reference model state sequence defines the suitable behavior to be performed either exactly or approximately, and either for all time or asymptotically as time tends to infinity, by the controlled system depending on the application. The controllability and stability of the reference model is suitable as well as the boundedness of all its parameters. This translates in the time-invariant case to the matrix$A^m$to be convergent, that is its spectral radius is less than one, and the pair$\left(A^m , b^m\right)$to be controllable, that is,$rank\left(b^m , A^m{b}^m ,\dots ,{\left(A^m\right)}^{n-1}{b}^m\right)=n$.

Controlled system

$$x_{k+1}^p=A_k^p{x}_k^p+b_k^p{u}_k+{\delta }_k; \forall k\in Z_{0+}$$

(68)

where ${\left\{x_k^p\right\}}_{k=0}^{\infty }\left(\subset R^n\right)$, with arbitrary finite initial condition $x_0^p$, and ${\left\{u_k\right\}}_{k=0}^{\infty }\left(\subset R\right)$ are, respectively, the controlled system state sequence and the control input sequence, and ${\left\{{\delta }_k\right\}}_{k=0}^{\infty }\left(\subset R^n\right)$ describes disturbances which can be noise, deterministic perturbations, or an unmodeled dynamics contribution or combinations of them. ${\left\{A_k^p\right\}}_{k=0}^{\infty }\left(\subset R^{n\times n}\right)$ and ${\left\{b_k^p\right\}}_{k=0}^{\infty }\left(\subset R^n\right)$ are, respectively, the matrix of dynamics of the controlled system and its control vector. The control input sequence is generated through the subsequent feedback law:

$$u_k=c_k{r}_k-m_k^T{x}_k^p$$

(69)

where ${\left\{c_k\right\}}_{k=0}^{\infty }\left(\subset R\right)$ is the feed-forward compensation scalar gain sequence and ${\left\{m_k\right\}}_{k=0}^{\infty }\left(\subset R^n\right)$ is the feedback compensation vector gain sequence. The replacement of (69) into the system (68) defined the closed-loop description of the system as follows:

$$x_{k+1}^p=\left(A_k^p-b_k^p{m}_k^T\right)x_k^p+b_k^p{c}_k{r}_k+{\delta }_k; \forall k\in Z_{0+}.$$

Suitable conditions depending on the application are that the reference sequence be bounded and that the closed-loop matrix of dynamics ${\left\{\left(A_k^p-b_k^p{m}_k^T\right)\right\}}_{k=0}^{\infty }$ be a convergent matrix sequence, and that ${\left\{b_k^p\right\}}_{k=0}^{\infty }$ and ${\left\{c_k\right\}}_{k=0}^{\infty }$ be bounded, that is, a stable matrix in the discrete constant so that the spectral radius of its elements is less than one. In this case, the state vector sequence is bounded provided that the disturbance sequence is bounded.

The error sequence ${\left\{e_k\right\}}_{k=0}^{\infty }$ between both states satisfies the subsequent identical relations:

$$\begin{array}{ll}{e}_{k+1}& =x_{k+1}^p-x_{k+1}^m\\ & =\left(A_k^p-b_k^p{m}_k^T\right)x_k^p-A_k^m{x}_k^m+\left(b_k^p{c}_k-b_k^m\right)r_k+{\delta }_k\\ & =\left(A_k^p-b_k^p{m}_k^T\right)\left(e_k+x_k^m\right)-A_k^m{x}_k^m+\left(b_k^p{c}_k-b_k^m\right)r_k+{\delta }_k\\ & =\left(A_k^p-b_k^p{m}_k^T\right)e_k-\left(x_{k+1}^m-\left(A_k^p-b_k^p{m}_k^T\right)x_k^m\right)+b_k^p{c}_k{r}_k+{\delta }_k\\ & =\left(A_k^p-b_k^p{m}_k^T\right)e_k+\left(A_k^p-A_k^m-b_k^p{m}_k^T\right)x_k^m+\left(b_k^p{c}_k-b_k^m\right)r_k+{\delta }_k, \forall k\in Z_{0+}\end{array}$$

(70)

Some properties if ${\left\{{\delta }_k\right\}}_{k=0}^{\infty }\equiv 0$ are:

1.

If $A_k-A_k^m=b_k^p{m}_k^T$ and $b_k^p=c_k^{-1}{b}_k^m\left(c_k\ne 0\right)$ for some $k\in Z_{0+}$, then $e_k=0\Rightarrow e_{k+1}=0$ (exact tracking in finite time).

2.

If $b_k^p=c_k^{-1}{b}_k^m\left(c_k\ne 0\right)$, or if ${\left\{r_k\right\}}_{k=0}^{\infty }\equiv 0$, and $A_k^p-A_k^m=b_k^p{m}_k^T$, or if ${\left\{x_k^m\right\}}_{k=0}^{\infty }\equiv 0$, then ${\left\{e_k\right\}}_{k=0}^{\infty }\to 0$ (asymptotic tracking) if $A_k^p-b_k^p{m}_k^T$ is convergent for all $k\left(\ge k_0\right)\in Z_{0+}$ and some finite $k_0\in Z_{0+}$.

3.

If ${\left\{r_k\right\}}_{k=0}^{\infty }\to 0$ and ${\left\{A_k^m\right\}}_{k=0}^{\infty }$ is convergent then ${\left\{x_k^m\right\}}_{k=0}^{\infty }\to 0$, ${\left\{x_k^p\right\}}_{k=0}^{\infty }\to 0$, and ${\left\{e_k\right\}}_{k=0}^{\infty }\to 0$ (asymptotic tracking) if, in addition, $A_k^p-b_k^p{m}_k^T$ is a convergent matrix for all $k\left(\ge k_0\right)\in Z_{0+}$ and some finite $k_0\in Z_{0+}$.

Now, consider an extended Equation (70) under the following “a priori” and “a posteriori” equation error forms:

$$e_{k+1}^{\left(0\right)}+\left(b_k^p{m}_k^T-A_k^p\right)e_k^{\left(0\right)}=\left(A_k^p-A_k^m-b_k^p{m}_k^T\right)x_k^m+\left(b_k^p{c}_k-b_k^m\right)r_k+{\delta }_k^{\left(0\right)}, \forall k\in Z_{0+}$$

(71)

$$\begin{array}{ll}{e}_{k+1}^{\left(p\right)}+& \left(b_k^p{m}_k^T-A_k^p\right)e_k^{\left(p\right)}=e_{k+1}^{\left(0\right)}+\left(b_k^p{m}_k^T-A_k^p\right)e_k^{\left(0\right)}+{\delta }_k^{\left(p\right)}-{\delta }_k^{\left(0\right)}\\ & =\left(A_k^p-A_k^m-b_k^p{m}_k^T\right)x_k^m+\left(b_k^p{c}_k-b_k^m\right)r_k+{\delta }_k^{\left(p\right)}, \forall k\in Z_{0+}\end{array}$$

(72)

where $e_{k+1}^{\left(0\right)}=x_{k+1}^{p\left(0\right)}-x_{k+1}^m$ and $e_{k+1}^{\left(p\right)}=x_{k+1}^{p\left(p\right)}-x_{k+1}^m$, are “a priori” and refined “a posteriori” estimated tracking errors, and ${\left\{{\delta }_k^{\left(0\right)}\right\}}_{k=0}^{\infty }$ and ${\left\{{\delta }_k^{\left(p\right)}\right\}}_{k=0}^{\infty }$ are “a priori” and refined “a posteriori” estimations of the disturbance sequence. In the most elementary case, the “a priori” estimation could be taken as identically zero reflecting the evolution of the estimated error in the absence of noise. Define the following non-empty closed, in general non-convex, and eventually bounded under weak assumptions subsets of $R^n$ which are also real sequences:

$$B^0={\left\{e_{k+1}^{\left(0\right)}+\left(b_k^p{m}_k^T-A_k^p\right)e_k^{\left(0\right)}\right\}}_{k=0}^{\infty }=A+{\left\{{\delta }_k^{\left(0\right)}\right\}}_{k=0}^{\infty }; A={\left\{\left(A_k^p-A_k^m-b_k^p{m}_k^T\right)x_k^m+\left(b_k^p{c}_k-b_k^m\right)r_k\right\}}_{k=0}^{\infty }$$

(73)

$$B^p={\left\{e_{k+1}^{\left(p\right)}+\left(b_k^p{m}_k^T-A_k^p\right)e_k^{\left(p\right)}\right\}}_{k=0}^{\infty }=A+{\left\{{\delta }_k^{\left(p\right)}\right\}}_{k=0}^{\infty }=B^0+{\left\{{\delta }_k^{\left(p\right)}\right\}}_{k=0}^{\infty }-{\left\{{\delta }_k^{\left(0\right)}\right\}}_{k=0}^{\infty }$$

(74)

Take points $x^{\left(0\right)}\in A$, $y^{\left(0\right)}\in B^0$, and $y^{\left(p\right)}\in B^p$. Taking a metric $d$ on $R^n\times R^n$, we can define the mappings, $S^0:A\to B^0$, $U_s:B^0\to B^p$, and $T:B^p\to A$ as well as the composite one $S=U_S{S}^0:A\to B^p$, defined according to (73)–(74) for any $x_k^{\left(0\right)}\in A$ as $S^0{x}_k^{\left(0\right)}=y_k^{\left(0\right)}=x_k^{\left(0\right)}+{\delta }_k^{\left(0\right)}\left(\in B^0\right)$, $U_S{y}_k^{\left(0\right)}=S{x}_k^{\left(0\right)}=S^0{U}_S{x}_k^{\left(0\right)}=x_k^{\left(p\right)}=x_k^{\left(0\right)}+\left({\delta }_k^{\left(p\right)}-{\delta }_k^{\left(0\right)}\right)\left(\in B^p\right)$ and, in the same way, for $y_k^{\left(p\right)}\in B^p$, $T{y}_k^{\left(p\right)}=y_k^{\left(p\right)}-{\delta }_k^{\left(p\right)}\left(\in A\right)$. Similar descriptions can be developed with the appropriate modifications in the definitions of the sets (73)–(74) if the “a priori” and “a posteriori” changes affect, for instance, the reference input sequence or to a joint “a priori” and “a posteriori” combination of the estimation of the additive disturbance and reference modification.

4. Numerical Examples

This section provides some numerical examples concerning the theoretical results introduced in the previous sections. In particular, two examples will be presented. The first one is related to Theorem 1 concerning the existence of a unique fixed point for generalized p-contractive self-mappings. The second numerical example is related to Theorem 3 concerning generalized cyclic $\left(T ,S\right)$$p$-contractions. Both examples will show the applicability of the introduced results to analyze the stability of discrete-time dynamical systems.

4.1. Fixed Points for Generalized p-Contractive Mappings

Consider the discrete-time dynamical system in one dimension given by:

$$x_{k+1}=T(x_k)=\frac{\mu x_k^2}{0.1+\lambda x_k^5}$$

(75)

with arbitrary initial condition $x_0\ge 0$. With this restriction on the initial condition, the trajectory is confined to $R_{0+}$. The values of $\mu =2$ and $\lambda =3$ are considered in this example with the usual metric in $R\times R$. The question we want to answer is whether this system has a (asymptotically) stable equilibrium point or not. Notice that this problem is related to the existence of a fixed point for the system (75) and the issue that the orbit converge to this fixed point or not, since the solution to this discrete-time dynamical system, for N steps ahead, is given by:

$$x_N=\underset{N}{\underbrace{T\circ T\circ \dots \circ T}}(x_0)=T^N(x_0).$$

Moreover, the self-mapping $T(x)=\frac{\mu x_{}^2}{0.1+\lambda x_{}^5}$ does not satisfy the classical Banach’s contraction principle since:

$$d(Tx,Ty)=\left|T(x)-T(y)\right|=\left|\frac{\mu x_{}^2}{0.1+\lambda x_{}^5}-\frac{\mu y_{}^2}{0.1+\lambda y_{}^5}\right|=\left(\frac{0.1\lambda \mu \left|x+y\right|+\left|x^2+xy+y^2\right|}{\left(0.1+\lambda x_{}^5\right)\left(0.1+\lambda y_{}^5\right)}\right)\left|x-y\right|$$

The value of $\left(\frac{0.1\lambda \mu \left|x+y\right|+\left|x^2+xy+y^2\right|}{\left(0.1+\lambda x_{}^5\right)\left(0.1+\lambda y_{}^5\right)}\right)$ depends on x and y and when $x=y=1$, for instance, it equals to 3.65 > 1. It is equally possible to test the contractivity from the derivative $T^{\prime }\left(x\right)$, since $T\left(x\right)$ is differentiable with respect to $x$ and we get that for $x$ in an open ball centered at $x_0=0$, one has $T\left(x\right)=T^{\prime }\left(x\right)x+o\left(x\right)$. The direct calculation yields:

$$\begin{array}{c}d\left(x,Tx\right)=\left|Tx-x\right|\le \left|\left(T^{\prime }\left(x\right)-1\right)x\right|+\left|o\left(x\right)\right|=\left|T^{\prime }\left(x\right)-1\right|\left|x\right|+\left|o\left(x\right)\right|=\left|\left(\frac{3\lambda \mu x^6}{{\left(0.1+\lambda x^5\right)}^2}-1\right)\right|d\left(x,0\right)+\left|o\left(x\right)\right|\\ \le \left|\left(\frac{3\mu }{\lambda x^4}-1\right)\right|d\left(x,0\right)+\left|o\left(x\right)\right|=\left|\frac{2}{x^4}-1\right|d\left(x,0\right)+\left|o\left(x\right)\right|\end{array}$$

It turns out that the absolute value of the first summand of the last term in the above formula either equalizes or exceeds unity infinitely for many positive real numbers $x$ being arbitrarily close to $x_0=0$, so that $\left|o\left(x\right)\right|\to 0$ as $x\to 0$ and $d\left(x,Tx\right)\ge d\left(x,0\right)$ for such numbers. Thus, $T:R_{0+}\to R_{0+}$ is not contractive.

Consequently, the Banach’s theorem cannot be applied to conclude the existence of a fixed point and, hence, discuss the stability of the dynamical system (75). The fact that this self-mapping does not satisfy the classical Banach’s theorem condition can also be assessed by using a numerical/graphical approach. In this way, Figure 1 displays the surfaces corresponding to the values of $d\left(x,y\right)$ and $d\left(Tx,Ty\right)$ for different non-negative values of x and y. The three-dimensional surfaces depicted in Figure 1a show that both surfaces intersect at some values, pointing out the fact that there is not a constant $k\in \left[0,1\right)$ satisfying $d(Tx,Ty)\le kd(x,y)$ for all $x,y\ge 0$. This situation is confirmed by Figure 1b, showing the surface projection onto the plane XY. The projection changes the displayed color depending on which surface is on top of the other. Since both surfaces intersect, Figure 1b shows different colors and shows that there is no constant k. This numerical/graphical procedure of depicting surfaces is of interest to quickly check the contraction and $p$-contraction conditions in order to apply the introduced results in practical applications.

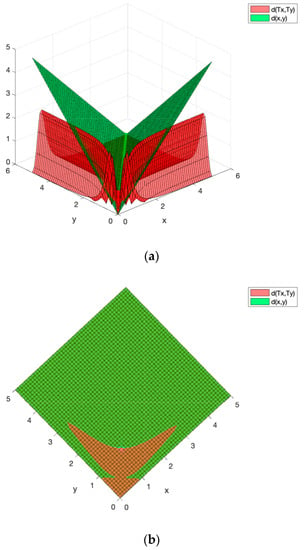
Figure 1. (a) Three dimensional surfaces representing the values of d(x,y) and d(Tx,Ty) in terms of non-negative x and y values. (b) Projection of both surfaces onto the XY plane. The change in color represents the fact that one surface is on top of the other depending on the values of x and y.

Furthermore, the self-mapping T does not even satisfy the Popescu’s condition given in Section 1 [9], as Figure 2 shows.

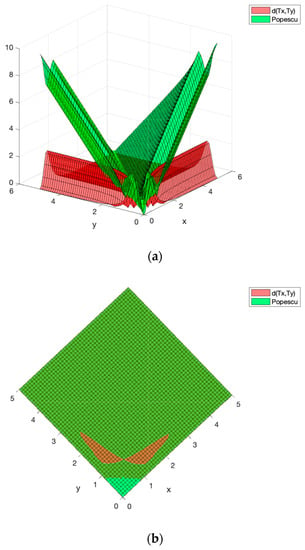
Figure 2. (a) Three dimensional surfaces representing the values of d(Tx, Ty) and the right-hand side of the Popescu condition considered in Section 1 [9], in terms of non-negative x and y values. (b) Projection of both surfaces onto the XY plane. The change in color represents the fact that one surface is on top of the other depending on the values of x and y.

Thus, we cannot conclude the existence of a (unique) fixed point with the previous results. However, we can apply the Theorem 1 concerned with the generalized p-contractive self-mappings defined in this work. Hence, Figure 3 displays the value of d(Tx,Ty) and the right-hand side of Equation (1) in terms of non-negative x and y with constants k₁ = 0.7, k₂ = k₃ = 0.05, k₄ = 0.04, k₅ = 50, k₆ = 0.08, and k₇ = 0.05. Figure 3 shows that the right-hand side of (1) is always greater than or equal to the value of d(Tx,Ty) for all non-negative values of x and y. In fact, Figure 4 shows that condition (1) is also fulfilled for negative values for x and y. Notice also from Figure 3 that for larger values of x and y, the condition (1) is fulfilled. The constants are determined through a trial and error procedure by performing numerical simulations in an easy way, since they only involve direct calculations in a computer program. Moreover, the constant k₅ can be used as a wild parameter to fulfill the condition of (1) since it does not appear in the conditions of Theorem 1.

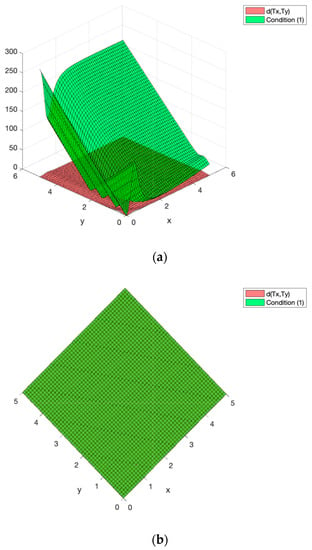
Figure 3. (a) Three dimensional surfaces representing the values of $d\left(Tx,Ty\right)$ and the right-hand side of Equation (1) (generalized p-contraction) in terms of non-negative x and y values. (b) Projection of both surfaces onto the XY plane. The uniform green color represents the fact that one surface is always on top of the other regardless of the values of x and y.

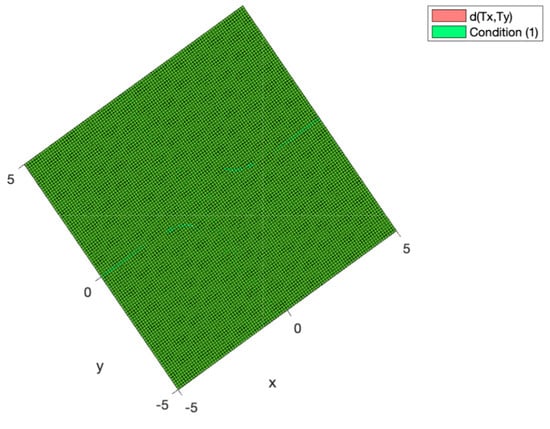
Figure 4. Projection of d(Tx,Ty) and the right-hand side of Equation (1) surfaces onto the XY plane. The uniform green color represents the fact that the right-hand side of the Equation (1) surface is always on top of the other regardless of the values of x and y being either positive or negative.

In addition, since $0.08=k_6\le k_1+k_2+k_4+k_7=0.84<1-k_3-k_4-k_7=0.86$, we can apply Theorem 1 and, consequently, T is asymptotically regular, the contraction constant k is 0.9787, and there is a unique fixed point. Thus, Theorem 1 has allowed us to prove the existence of a unique fixed-point associated to a unique asymptotically stable equilibrium point for the discrete-time dynamical system (75). This fact can be observed in Figure 5, where the solution to the dynamical system is displayed for different initial conditions.

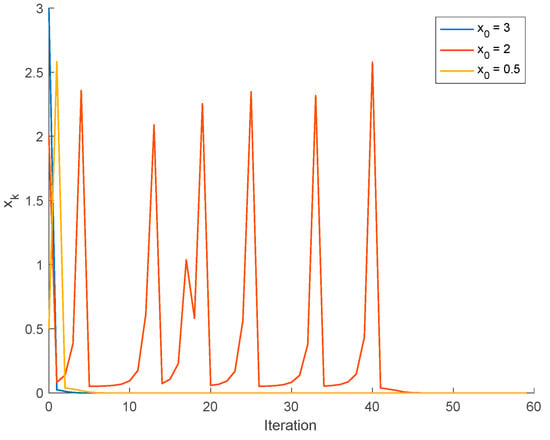
Figure 5. Solution of the discrete-time dynamical system (75) for different initial conditions.

It is observed in Figure 5 that the system converges to the unique asymptotically stable fixed point x = 0, as predicted by Theorem 1. Notice that the fixed points of the dynamical system are calculated as the solution of:

$$x=T(x)=\frac{\mu x_{}^2}{0.1+\lambda x_{}^5}$$

This equation has six roots, $x=0,x=0.89,x=0.05,x=-0.9157,x=-0.0125\pm i0.904$. Two of them are complex and one is negative, being thus non-reachable. Out of the three positive solutions, Theorem 1 allows us to conclude that only one is asymptotically stable. This fact is observed in Figure 6 where the solution of the discrete-time system with initial conditions close to the fixed points $x=0.89,x=0.05$ is depicted. It is observed that the system trajectories leave the neighborhood of the fixed points and converges to $x=0$, the unique stable fixed point. In conclusion, Theorem 1 generalizes previous contraction results (since they would not be applicable in this situation) and is useful to discuss the stability of discrete-time dynamical systems.

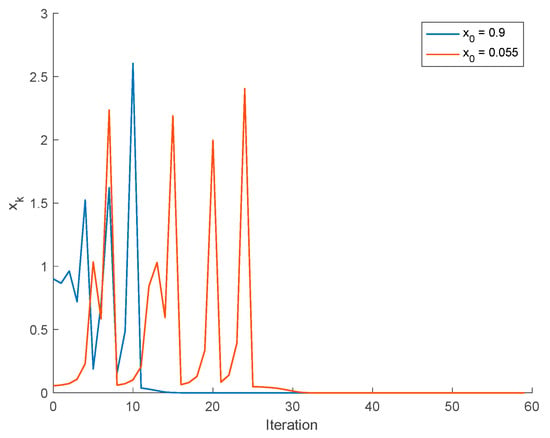
Figure 6. Solution of the discrete-time dynamical system for different initial conditions close to the unstable fixed points x = 0.89 and x = 0.05.

Note that the above equation could be associated, for instance, to a discrete time-varying generalized Beverton–Holt equation [25] of interest for the description of the evolution sequence of species which reproduce by eggs of the form:

$$x_{n+1}=\frac{f_n\left(x_n\right)a_n\left(x_n\right)}{1+\left(a_n\left(x_n\right)-1\right)x_n/K}{x}_n; \forall n\in Z_{+}, x_0>0$$

where $K$ is the carrying capacity of the environment, ${\left\{a_n\right\}}_{n=0}^{\infty }$ is the sequence of population-dependent intrinsic growth rates given by $a_n=a_n\left(x_n\right)=1+10\lambda x_n^4$; $\forall n\in Z_{0+}$, and ${\left\{f_n\right\}}_{n=0}^{\infty }$ is the correction sequence which takes account the, in general, sample-dependent population level, which is given by $f_n=f_n\left(x_n\right)=\frac{10\mu x_n}{1+10\lambda K{x}_n^4}$; $\forall n\in Z_{0+}$. Note that $f_n\left(x_n\right)$ being small for small levels of population, with $f_n\left(0\right)=0$, describes the so-called Allee effect, that is, the low reproductive capacity associated with the difficulty of individuals to meet because of the small population levels. Moreover, $f_n\left(x_n\right)$, large levels of population, including an infinity limit of $x_n\to +\infty$, describes the inter-individual competence within a habitat for seeking food, seeking refuge, etc., associated with the existence of large levels of population.

4.2. Fixed Points for Generalized $\left(T,S\right)$ Cyclic p-Contractive Mappings

This subsection contains a numerical example regarding the Theorem 3 concerned with generalized $\left(T,S\right)$ cyclic p-contractive mappings. To this end, consider the switched discrete-time dynamical system (extended from the previous example) given by:

$$x_{k+1}=\left\{\begin{array}{cc}\frac{-{\mu }_1{x}_k^2}{0.1+{\lambda }_1{x}_k^5}=T(x_k)& x_k\ge 0\\ \left|\frac{{\mu }_2{x}_k^2}{0.1+{\lambda }_2{x}_k^5}\right|=S(x_k)& x_k<0\end{array}\right.$$

(76)

with ${\mu }_1=0.45$, ${\mu }_2=2$, and ${\lambda }_1={\lambda }_2=3$. The question we want to answer is, as before, whether the fixed point $x=0$ is an asymptotically stable equilibrium point or not. Theorem 3 will be used for such a purpose. Notice that switched systems appear frequently in engineering as a natural description for many phenomena, [26], and the discussion of its stability is a current field of research. Hence, we consider the sets defined by:

$$\begin{array}{l}A=\left\{x\in R|x\ge 0\right\}\\ B=\left\{x\in R|x\le 0\right\}\end{array}$$

The switched system is described by two cyclic operators T and S satisfying $T:A\to B$ and $S:B\to A$, as it can be readily observed from (76). Moreover, $A\cap B=\left\{0\right\}$, which is the fixed point of interest and $d\left(A,B\right)=0$. The next step is to check that both operators satisfy the Equation (22) for some constants k fulfilling the constraints (23) and (24). The numerical/graphical approach introduced in the previous Section 4.1 will be used to this end. Thus, the surface corresponding to $d\left(Tx,Sy\right)$ and the one corresponding to the right-hand side of (22) are depicted simultaneously. If the surface of (22) is on top of the one corresponding to $d\left(Tx,Sy\right)$, then the condition (22) is satisfied. This condition is shown in Figure 7. The constants can be obtained by means of a trial and error procedure, which is easy to perform using a computer numerical suite. Figure 7 displays the condition (22) for $k_1=0.8$, $k_2=0.199,k_3=0.0002$, $k_4=k_5=0.0001$, $k_6=0.999$, and $k_7=0$. As it is observed in Figure 7, condition (22) is fulfilled while (23) and (24) are also achieved with:

$$k_{\rho }=k_{\sigma }=k=6\times {10}^{-4}>0, \rho =\sigma =\zeta =0.9997\in \left[0,1\right)$$

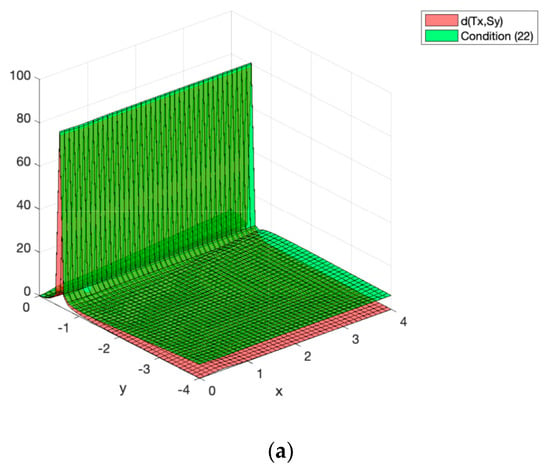
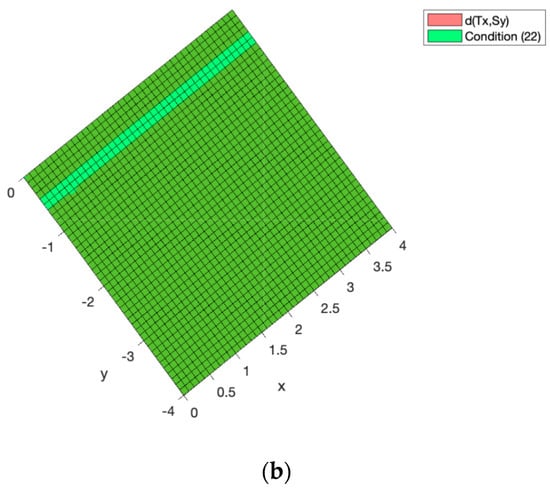
Figure 7. (a) Three dimensional surfaces representing the values of $d\left(Tx,Sy\right)$ and the right-hand side of Equation (22) (generalized ($\left(T,S\right)$ cyclic p-contraction) in terms of $x\in A$ and $y\in B$. (b) Projection of both surfaces onto the XY plane. The green color represents the fact that one surface is always on top of the other regardless of the values of x and y.

Consequently, we can apply Theorem 3 and the generalized $\left(T,S\right)$ cyclic p-contraction pair has a fixed point, or equivalently, the switched discrete-time dynamical system has an asymptotically stable equilibrium point. In fact, Figure 8 shows that the trajectories of the system (76) for different initial conditions converge to $x=0$ as predicted by Theorem 3.

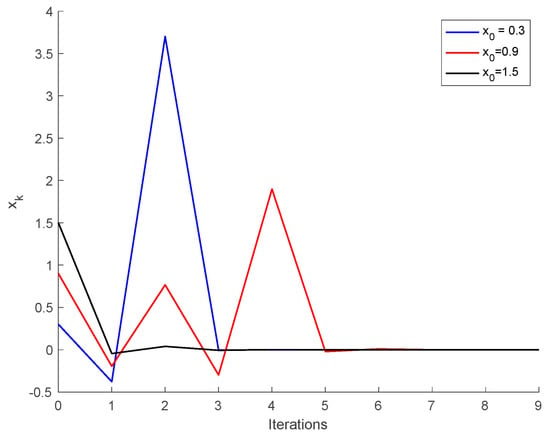
Figure 8. Solution of the switched discrete-time dynamical system for different initial conditions.

Moreover, Figure 9 depicts the right-hand side of the $\left(T,S\right)$ cyclic pair contraction condition (Definition 2) of [9] with k = 0.95, k = 0.98, and k = 0.99. As it is observed in Figure 9, the achievement of the condition is highly dependent on the values for k while the proposed generalized condition (22) from Theorem 3 allows the satisfaction of the constraint in an easier way with a larger variety of values for the constants. Overall, the results introduced in this work generalize the previously presented results and offer a less conservative approach that might be of interest in different applications, such as the ones shown in the numerical examples concerning dynamical systems.

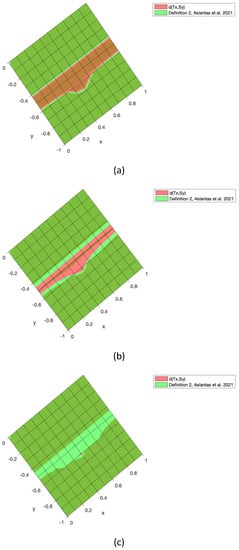
Figure 9. Projection of the three dimensional surfaces representing the values of $d\left(Tx,Sy\right)$ and the right-hand side of Definition 2 in [9] with k = 0.95 (a), k = 0.98 (b), and k = 0.99 (c).

5. Concluding Remarks

This paper has studied a generalization of $p$-contractive self-mappings $T$ in metric and metric-like spaces $\left(X,d\right)$. Such a contractive condition for the pairs $\left(x,y\right)\in X\times X$ considers, in general, a sum of distances involving the various pairs including the quadruple $\left\{x ,y ,Tx , Ty\right\}$ plus the additive contributions of the absolute values $\left|d\left(x,Tx\right)-d\left(y,Ty\right)\right|$ and $\left|d\left(x,Ty\right)-d\left(y,Tx\right)\right|$. The asymptotic regularity of $T$ as well as the convergence of Cauchy sequences to a unique fixed point in $X$ are proved if $\left(X,d\right)$ is complete. The second part of the paper body is devoted to a $\left(T, S\right)$ generalized cyclic $p$-contraction pair defined on a pair of non-empty, in general, disjoint subsets of $X$. The contraction rule involves, in general, a combination of several terms for contribution of distances involving the images of the points through the two non-self-mappings of the $\left(T, S\right)$ cyclic $p$-contraction pair. The asymptotic convergence of the relevant sequences to best proximity points of both sets is proved. Moreover, the best proximity points are proved to be unique if the involved subsets are closed and convex, the metric is norm induced, and the metric space is a uniformly convex Banach space. Numerical examples were discussed a well as an application example of $\left(T,\hspace{0.33em}S\right)$ contraction pairs for a discrete control problem.