Singularity Properties of Timelike Sweeping Surface in Minkowski 3-Space

Abstract

In this paper, we give the parametric equation of the Bishop frame for a timelike sweeping surface with a unit speed timelike curve in Minkowski 3-space. We introduce a new geometric invariant to explain the geometric properties and local singularities of this timelike surface. We derive the sufficient and necessary conditions for this timelike surface to be a timelike developable ruled surface. Afterwards, we take advantage of singularity theory to give the classification of singularities of this timelike developable surface. Furthermore, we give some representative examples to show the applications of the theoretical results.

1. Introduction

Singularity theory of curves and surfaces is an efficient area of research in various branches of mathematics and physics. In the view of differential geometry, curves and surfaces are performed by functions with one variable and two variables, respectively. In recent years, singularity theory for curves and surfaces has become a paramount tool for different interesting fields such as medical imaging and computer vision (see, e.g., [1,2,3,4] ).

As we know, a sweeping surface is the surface traced by the movement of a plane curve (the profile curve or generatrix) whilst the plane is moved through space in such a way that the movement of the plane is always in the direction of the normal to the plane. Sweeping is a very important, powerful, and widespread method in geometric modelling. The basic concept is to select some geometrical object (generator) that is then swept along a spine curve (trajectory) in the space. The result of such evolution, consisting of movement through space and intrinsic shape deformation, is a sweep object. The sweep object kind is determined by the choice of the generator and the trajectory. Thus, sweeping a curve over another curve generates a sweeping surface. There are several names of sweeping surfaces that we are familiar with, such as tubular surface, pipe surface, string, and canal surface. In [5], J. Suk and D.W Yoon initiated the study of a tube in Euclidean 3-space, satisfying some equation in terms of the Gaussian curvature, the mean curvature, and the second Gaussian curvature. The kinematic geometry of circular surfaces with a fixed radius based on Euclidean invariants was defined by L. Cui et al. in [6]. RA. Abdel-Baky in [7] considered the study of developable surfaces through sweeping surfaces in Euclidean 3-space. S. Izumiya et al. in [8] examined some corresponding properties of circular surfaces with classical ruled surfaces. A survey of the principle geometric features of canal surfaces has been defined by Xu et al. in [9]. Furthermore, the authors presented sufficient conditions for canal surfaces without local self-intersection. Moreover, they derived a simple expression for the area and Gaussian curvature of canal surfaces.

One of the most suitable methods to analyzing curves and surfaces in differential geometry is the Serret–Frenet frame, but it is not unique; there are also other frame fields such as the rotation minimizing frame (RMF) or the Bishop frame [10]. Some applications of the Bishop frame can be found in [11,12,13,14]. Corresponding to the Bishop frame in Euclidean space, there exists a Minkowski version frame that is called a Minkowski–Bishop frame as applied to Minkowski geometry. When we investigate a space curve, it is more convenient for us to use the Minkowski–Bishop frame along the curve as the basic tool than the Serret–Frenet frame in Lorentzian space. There are several papers about the Minkowski–Bishop frame; for example, [1,7,15].

In this paper, we present the notion of timelike sweeping surfaces with rotation minimizing frames in Minkowski 3-space. Thus, by applying singularity theory, we classify the generic properties and present q new invariant connected to the singularity of this timelike sweeping surface. The main generic singularities of this sweeping surface are the well-known cuspidal edge and swallowtail, and they are characterized by this new invariant. Furthermore, from the viewpoint of singularity theory, we present the singularity properties of timelike sweeping surfaces in Minkowski 3-space. In this way, we take advantage of some classical and well-known results in singularity theory as evidence to prove our main results in this paper. Moreover, this paper gives the necessary and sufficient conditions to characterize when the timelike sweeping surface is a timelike developable ruled surface and discusses further conclusions. Regarding the timelike developable surfaces, we studied the uniqueness properties. Furthermore, this paper also focuses on the singularity properties of the timelike developable surfaces. Finally, to illustrate the main results, two examples are given and investigated in detail. Our plans for the future research are to conduct interdisciplinary research because it can provide valuable new insights, but synthesizing articles across disciplines with highly varied standards, formats, terminology, and methods requires an adapted approach. Therefore, we find some of the latest related studies in [16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66]. One possible way to achieve the interdisciplinary research goal of obtaining more singularity and symmetry properties of timelike sweeping surfaces is to apply a mix or a blend of the techniques in [16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66] combine them the methods of this paper.

2. Preliminaries

We introduce in this section some basic notions on Minkowski 3-space. For basic concepts and properties, see [67,68].

Let ${\mathbb{R}}^3=\{\left(a_1,a_2,a_3\right)\mid$, $a_i\in \mathbb{R}$ (i=1, 2, 3)} be a 3-dimensional Cartesian space. For any $\mathbf{a}=\left(a_1,a_2,a_3\right)$, and $\mathbf{b}=\left(b_1,b_2,b_3\right)\in {\mathbb{R}}^3$, the pseudo-scalar product of $\mathbf{a}$ and $\mathbf{b}$ is defined by

$$<\mathbf{a},\mathbf{b}>=-a_1{b}_1+a_2{b}_2+a_3{b}_3.$$

(1)

We call $({\mathbb{R}}^3,<,>)$ Minkowski 3-space. We write ${\mathbb{E}}_1^3$ instead of (${\mathbb{R}}^3,<,>)$. We say that a non-zero vector $\mathbf{a}\in {\mathbb{E}}_1^3$ is spacelike, lightlike, or timelike if $<\mathbf{a},\mathbf{a}>>0$, $<\mathbf{a},\mathbf{a}>=0$ or $<\mathbf{a},\mathbf{a}><0$. The norm of the vector $\mathbf{a}\in {\mathbb{E}}_1^3$ is defined to be $∥\mathbf{a}∥=\sqrt{\left|<\mathbf{a},\mathbf{a}>\right|}$. For any two vectors $\mathbf{a}$, $\mathbf{c}\in {\mathbb{E}}_1^3$, we define a vector $\mathbf{a}\times \mathbf{c}$ by

$$\mathbf{a}\times \mathbf{c}=\left|\begin{array}{ccc}-{\mathbf{e}}_1& {\mathbf{e}}_2& {\mathbf{e}}_3\\ a_1& a_2& a_3\\ c_1& c_2& c_3\end{array}\right|=\left(-(a_2{c}_3-a_3{c}_2),(a_3{c}_1-a_1{c}_3),(a_1{c}_2-a_2{c}_1)\right),$$

(2)

where ${\mathbf{e}}_1$, ${\mathbf{e}}_2$, ${\mathbf{e}}_3$ is the canonical basis of ${\mathbb{E}}_1^3$. We can easily check that

$$det(\mathbf{a},\mathbf{c},\mathbf{b})=<\mathbf{a}\times \mathbf{c},\mathbf{b}>,$$

(3)

so that $\mathbf{a}\times \mathbf{c}$ is pseudo-orthogonal to any $\mathbf{b}=\left(b_1,b_2,b_3\right)\in {\mathbb{E}}_1^3$. The Lorentzian unit sphere with center in the origin of ${\mathbb{E}}_1^3$ is defined by

$${\mathbb{S}}_1^2=\{\mathbf{x}\in {\mathbb{E}}_1^3\mid <\mathbf{x},\mathbf{x}>=1\}.$$

(4)

Let $\mathbf{\beta }=\mathbf{\beta }\left(s\right)$ be a unit speed timelike curve; by $\kappa \left(s\right)$ and $\tau \left(s\right)$, we denote the natural curvature and torsion of $\mathbf{\beta }\left(s\right)$, respectively. Let $\left\{\mathbf{T}\right(s),$$\mathbf{N}\left(s\right)$, $\mathbf{B}\left(s\right)\}$ be the Serret–Frenet frame associated with $\mathbf{\beta }\left(s\right)$. For each point of $\mathbf{\beta }\left(s\right)$, the corresponding Serret–Frenet formulae read:

$$\left(\begin{array}{c}{\mathbf{T}}^{{}^{\prime }}\hfill \\ {\mathbf{N}}^{{}^{\prime }}\hfill \\ {\mathbf{B}}^{{}^{\prime }}\hfill \end{array}\right)=\left(\begin{array}{ccc}0\hfill & \kappa \left(s\right)\hfill & 0\hfill \\ \kappa \left(s\right)\hfill & 0\hfill & \tau \left(s\right)\hfill \\ 0\hfill & -\tau \left(s\right)\hfill & 0\hfill \end{array}\right)\left(\begin{array}{c}\mathbf{T}\hfill \\ \mathbf{N}\hfill \\ \mathbf{B}\hfill \end{array}\right)=\omega \times \left(\begin{array}{c}\mathbf{T}\hfill \\ \mathbf{N}\hfill \\ \mathbf{B}\hfill \end{array}\right),$$

(5)

where $\omega \left(s\right)=\tau \mathbf{T}+\kappa \mathbf{B}$ is the Darboux vector of the Serret–Frenet frame. In this paper, dashes denote the derivatives with respect to the arc-length parameter s. It is easy to see that

$$\mathbf{T}\times \mathbf{N}=\mathbf{B},\mathbf{T}\times \mathbf{B}=-\mathbf{N},\mathbf{N}\times \mathbf{B}=-\mathbf{T}.$$

(6)

Definition 1.

A pseudo -orthogonal moving frame $\{{\xi }_1,$${\xi }_3$, ${\xi }_3\}$ along a non-null space curve $\alpha \left(s\right)$ is a rotation minimizing frame (RMF) with respect to ${\xi }_1$ if the derivatives of ${\xi }_2$ and ${\xi }_3$ are both parallel to ${\xi }_1$, or its angular velocity ω satisfies $<\omega ,{\xi }_1>=0$. An analogous characterization holds when ${\xi }_2$ or ${\xi }_3$ is chosen as the reference direction [11].

According to Definition 1, we observe that the Serret–Frenet frame is an RMF with respect to the principal normal $\mathbf{N}$, but not with respect to the tangent $\mathbf{T}$ and the binormal $\mathbf{B}$. Although the Serret–Frenet frame is not an RMF with respect to $\mathbf{T}$, one can easily derive such an RMF from it. New normal plane vectors (${\mathbf{N}}_1$,${\mathbf{N}}_2$) are specified through a rotation of ($\mathbf{N}$,$\mathbf{B}$) according to

$$\left(\begin{array}{c}{\mathbf{T}}_1\hfill \\ {\mathbf{N}}_1\hfill \\ {\mathbf{N}}_2\hfill \end{array}\right)=\left(\begin{array}{ccc}1\hfill & 0\hfill & 0\hfill \\ 0\hfill & cos\vartheta \hfill & sin\vartheta \hfill \\ 0\hfill & -sin\vartheta \hfill & cos\vartheta \hfill \end{array}\right)\left(\begin{array}{c}\mathbf{T}\hfill \\ \mathbf{N}\hfill \\ \mathbf{B}\hfill \end{array}\right),$$

(7)

with a certain spacelike angle $\vartheta \left(s\right)\ge 0$. Here, we call the set $\{{\mathbf{T}}_1$, ${\mathbf{N}}_1$, ${\mathbf{N}}_2\}$ an RMF or Bishop frame. The RMF vector satisfies the relations

$${\mathbf{T}}_1\times {\mathbf{N}}_1={\mathbf{N}}_2,{\mathbf{T}}_1\times {\mathbf{N}}_2=-{\mathbf{N}}_1,{\mathbf{N}}_1\times {\mathbf{N}}_2=-{\mathbf{T}}_1.$$

(8)

Therefore, we have the alternative frame equations

$$\left(\begin{array}{c}{\mathbf{T}}_1^{{}^{\prime }}\hfill \\ {\mathbf{N}}_1^{{}^{\prime }}\hfill \\ {\mathbf{N}}_2^{{}^{\prime }}\hfill \end{array}\right)=\left(\begin{array}{ccc}0\hfill & {\kappa }_1\left(s\right)\hfill & -{\kappa }_2\left(s\right)\hfill \\ {\kappa }_1\left(s\right)\hfill & 0\hfill & 0\hfill \\ -{\kappa }_2\left(s\right)\hfill & 0\hfill & 0\hfill \end{array}\right)\left(\begin{array}{c}{\mathbf{T}}_1\hfill \\ {\mathbf{N}}_1\hfill \\ {\mathbf{N}}_2\hfill \end{array}\right)=\tilde{\omega }\times \left(\begin{array}{c}{\mathbf{T}}_1\hfill \\ {\mathbf{N}}_1\hfill \\ {\mathbf{N}}_2\hfill \end{array}\right),$$

(9)

where $\tilde{\omega }\left(s\right)={\kappa }_2{\mathbf{N}}_1+{\kappa }_1{\mathbf{N}}_2$ is the RMF Darboux vector. Here, the Bishop curvatures are defined by ${\kappa }_1\left(s\right)=\kappa cos\vartheta$ and ${\kappa }_2\left(s\right)=\kappa sin\vartheta$. One can show that

$$\left.\begin{array}{c}\kappa \left(s\right)=\sqrt{{\kappa }_1^2+{\kappa }_2^2},\mathrm{and}\vartheta ={tan}^{-1}\left(\frac{{\kappa }_2}{{\kappa }_1}\right);{\kappa }_1\ne 0,\hfill \\ \vartheta \left(s\right)=-\underset{s_0}{\stackrel{s}{\int }}\tau \left(s\right)ds+{\vartheta }_0,{\vartheta }_0=\vartheta \left(0\right).\hfill \end{array}\right\}$$

(10)

Comparing Equation (4) with Equation (8) we observe that the relative velocity is

$$\tilde{\omega }\left(s\right)-\omega \left(s\right)=\tau \left(s\right)\mathbf{T}.$$

(11)

Consequently, the Serre–Frenet frame and the RMF are identical if and only if $\mathbf{\beta }\left(s\right)$ is a planar, i.e., $\tau \left(s\right)=0$. Now we define the spacelike Bishop spherical Darboux image $\mathbf{e}:I\to {\mathbb{S}}_1^2$, by

$$\mathbf{e}\left(s\right)=\frac{\tilde{\omega }\left(s\right)}{∥\tilde{\omega }\left(s\right)∥}=\frac{{\kappa }_1}{\sqrt{{\kappa }_1^2+{\kappa }_2^2}}\left(\frac{{\kappa }_2}{{\kappa }_1}{\mathbf{N}}_1+{\mathbf{N}}_2\right).$$

(12)

Therefore, we consider a new geometric invariant $\rho \left(s\right)={\kappa }_1{\kappa }_2^{{}^{\prime }}-{\kappa }_2{\kappa }_1^{{}^{\prime }}$.

We denote a surface M in ${\mathbb{E}}_1^3$ by

$$M:\mathbf{R}(s,u)=\left(x_1(\left(s,u\right),x_2(\left(s,u\right),\left(x_3\right(\left(s,u\right)\right),(s,u)\in D\subseteq {\mathbb{R}}^2.$$

(13)

Let $\mathbf{U}$ be the standard unit normal vector field on a surface M defined by $\mathbf{U}=\frac{{\mathbf{R}}_s\times {\mathbf{R}}_u}{∥{\mathbf{R}}_s\times {\mathbf{R}}_u∥}$ where ${\mathbf{R}}_i=\frac{\partial \mathbf{R}}{\partial i}$. Then, the metric (first fundamental form) I of a surface M is defined by

$$I=g_{11}d{s}^2+2g_{12}dsdu+g_{22}d{u}^2,$$

where $g_{11}=<{\mathbf{R}}_s,{\mathbf{R}}_s>$, $g_{12}=<{\mathbf{R}}_s,{\mathbf{R}}_u>,g_{22}=<{\mathbf{R}}_u,{\mathbf{R}}_u>$. We define the second fundamental form $II$ of M by

$$II=h_{11}d{s}^2+2h_{12}dsdu+h_{22}d{u}^2,$$

where $h_{11}=<{\mathbf{R}}_{ss},\mathbf{N}>$, $h_{12}=<{\mathbf{R}}_{su},\mathbf{U}>,h_{22}=<{\mathbf{R}}_{uu},\mathbf{U}>$.

3. Timelike Sweeping Surface

The concept of a sweeping surface is obtained kinematically by a planar curve moving such that the motion of any point on the surface is constantly orthogonal to the plane. Then, the sweeping surface along $\mathbf{\beta }\left(s\right)$ is [13,14]:

$$M:\mathbf{R}(s,u)=\mathbf{\beta }\left(s\right)+T\left(s\right)\mathbf{r}\left(u\right)=\mathbf{\beta }\left(s\right)+r_1\left(u\right){\mathbf{N}}_1\left(s\right)+r_2\left(u\right){\mathbf{N}}_2\left(s\right),$$

(14)

where $\mathbf{\beta }\left(s\right)$ is called the $C^1$-continuous. $\mathbf{r}\left(u\right)$ is the planar profile (cross-section) curve given by parametric representation $\mathbf{r}\left(u\right)=(0,$$r_1\left(u\right),r_2{\left(u\right))}^t$. The symbol ’t’ represents transposition, with another parameter $u\in I\subseteq \mathbb{R}$. The semi orthogonal matrix $A\left(s\right)=\{{\mathbf{T}}_1,$${\mathbf{N}}_1$, ${\mathbf{N}}_2\}$ specifies the RMF along $\mathbf{\beta }\left(s\right)$. Geometrically, the sweeping surface $\mathbf{R}(s,u)$ is generated by moving the profile curve $\mathbf{r}\left(u\right)$ along the spine curve $\mathbf{\beta }\left(s\right)$ with the orientation as specified by $A\left(s\right)$.

Without loss of generality, we can suppose the profile curve $\mathbf{r}\left(u\right)$ is a unit speed spacelike curve, that is, ${\stackrel{.}{r}}_1^2+{\stackrel{.}{r}}_2^2=1$. In the following, “dot” denotes the derivative with respect to the parameter u of the profile curve $\mathbf{r}\left(u\right)$. From now on, we shall often not write the parameters s and t explicitly in our formulae. Therefore, from the derivative formulas of RMF, partial differentiation with respect to s and u is as follows:

$$\left.\begin{array}{c}{\mathbf{R}}_s(s,u)=\left(1+r_1{\kappa }_1-r_2{\kappa }_2\right){\mathbf{T}}_1,\hfill \\ {\mathbf{R}}_u(s,u)={\stackrel{.}{r}}_1{\mathbf{N}}_1+{\stackrel{.}{r}}_2{\mathbf{N}}_2.\hfill \end{array}\right\}$$

(15)

By simple calculations, we have the following:

$$g_{11}=-{\left(1+r_1{\kappa }_1\left(s\right)-r_2{\kappa }_2\right)}^2,g_{12}=0,g_{22}=1,$$

(16)

and

$$\mathbf{U}(s,u)=-{\stackrel{.}{r}}_2{\mathbf{N}}_1+{\stackrel{.}{r}}_1{\mathbf{N}}_2.$$

(17)

Note that ${∥\mathbf{U}(s,u)∥}^2=1$ means that M is a timelike surface. Furthermore, we have:

$$\left.\begin{array}{c}{\mathbf{R}}_{ss}=(r_1{\kappa }_1^{{}^{\prime }}-r_2{\kappa }_2^{{}^{\prime }}){\mathbf{T}}_1+\left(1+r_1{\kappa }_1-r_2{\kappa }_2\right)\left({\kappa }_1{\mathbf{N}}_1-{\kappa }_2{\mathbf{N}}_2\right),\hfill \\ {\mathbf{R}}_{su}=({\stackrel{.}{r}}_1{\kappa }_1+{\stackrel{.}{r}}_2{\kappa }_2){\mathbf{T}}_1,\hfill \\ {\mathbf{R}}_{\mathrm{uu}}={\stackrel{..}{r}}_1{\mathbf{N}}_1+{\stackrel{..}{r}}_2{\mathbf{N}}_2.\hfill \end{array}\right\}$$

(18)

Then, we can compute

$$\left.\begin{array}{c}{h}_{11}=-(1+r_1{\kappa }_1-r_2{\kappa }_2)({\stackrel{.}{r}}_2{\kappa }_1+{\stackrel{.}{r}}_1{\kappa }_2),\hfill \\ h_{12}=0,\hfill \\ h_{22}=-{\stackrel{.}{r}}_2{\stackrel{..}{r}}_1+{\stackrel{.}{r}}_1{\stackrel{..}{r}}_2.\hfill \end{array}\right\}$$

(19)

Hence, the u-and s curves of M are curvature lines; that is, $g_{12}=h_{12}=0$.

Corollary 1.

Let M be the sweeping surface defined by Equation (14). Then:

(1) 

The s-parameter curve is also a geodesic on M if

$${\stackrel{.}{r}}_1{\kappa }_1-{\stackrel{.}{r}}_2{\kappa }_2=0,and{\kappa }_1^{{}^{\prime }}{r}_1-{\kappa }_2^{{}^{\prime }}{r}_2=0;$$

(2) 

The s-parameter curve is also an asymptotic curve on M if

$${\stackrel{.}{r}}_2{\kappa }_1+{\stackrel{.}{r}}_1{\kappa }_2=0.$$

Proof. 

Since the u-and s curves of M are curvature lines, from Equations (17) and (18), we have:

(1)

The s-parameter curve is a also geodesic if ${\mathbf{R}}_{ss}\times \mathbf{U}(s,t)=\mathbf{0}$; that is,

$$\left.\begin{array}{c}\left(1+r_1{\kappa }_1-r_2{\kappa }_2\right)({\stackrel{.}{r}}_2{\kappa }_2-{\stackrel{.}{r}}_1{\kappa }_1){\mathbf{T}}_1+\hfill \\ -(r_1{\kappa }_1^{{}^{\prime }}-r_2{\kappa }_2^{{}^{\prime }})({\stackrel{.}{r}}_1{\mathbf{N}}_1+{\stackrel{.}{r}}_2{\mathbf{N}}_2)=\mathbf{0}.\hfill \end{array}\right\}$$

Since ${\mathbf{T}}_1$, ${\mathbf{N}}_1$ and ${\mathbf{N}}_2$ are linearly independent unit vectors, we have the desired equation system;

(2)

The s-parameter curve is also an asymptotic curve on M if $<\mathbf{U},{\mathbf{R}}_{ss}>=0$; that is,

$$\left({\stackrel{.}{r}}_2{\kappa }_1+{\stackrel{.}{r}}_1{\kappa }_2\right)(1+r_1{\kappa }_1-r_2{\kappa }_2)=0.$$

Since $1+r_2\kappa -r_3\tau \ne 0$ (See Equation (15)), it follows that ${\stackrel{.}{r}}_2{\kappa }_1+{\stackrel{.}{r}}_1{\kappa }_2=0=0$ as claimed. □

Corollary 2.

Let M be the sweeping surface represented by Equation (14). Then:

(1) 

The $u-$parameter curve cannot be also a geodesic on M;

(2) 

The $u-$ parameter curve is also an asymptotic curve on M if

$${\stackrel{.}{r}}_1{\stackrel{..}{r}}_2-{\stackrel{.}{r}}_2{\stackrel{..}{r}}_1=0.$$

Proof. 

Since the u and s curves of M are curvature lines, from Equations (17) and (18), we have:

(1)

Since ${\stackrel{.}{r}}_1^2+{\stackrel{.}{r}}_2^2=1$ and ${\mathbf{R}}_{uu}\times \mathbf{U}(s,t)=\left(-{\stackrel{.}{r}}_1{\stackrel{..}{r}}_1+{\stackrel{.}{r}}_2{\stackrel{..}{r}}_2\right){\mathbf{T}}_1$, the $u-$parameter curve cannot be also a geodesic on M;

(2)

The $u-$parameter curve is also an asymptotic curve on M if $<\mathbf{U},{\mathbf{R}}_{uu}>=0$; that is,

$${\stackrel{.}{r}}_1{\stackrel{..}{r}}_2-{\stackrel{.}{r}}_2{\stackrel{..}{r}}_1=0$$

as claimed. In this case, $h_{22}=0$, so M is a developable ruled surface, that is, its Gaussian curvature is identically zero.

□

The aim of this work is the following theorem:

Theorem 1.

Let β: $I\to {\mathbb{E}}_1^3$ be a unit speed timelike curve with ${\kappa }_1>0$. Then, for any fixed $\mathbf{x}\in {\mathbb{S}}_1^2$, one has the following:

A—(1) $\mathbf{e}\left(s\right)$ is locally diffeomorphic to a line {$\mathbf{0}$}$\times \mathbb{R}$ at $s_0$ if and only if $\rho \left(s_0\right)\ne 0$;

(2) $\mathbf{e}\left(s\right)$ is locally diffeomorphic to the cusp $C\times \mathbb{R}$ at $s_0$ if and only if $\rho \left(s_0\right)=0$, and ${\rho }^{{}^{\prime }}\left(s_0\right)\ne 0$.

B—(1) M is locally diffeomorphic to cuspidal edge $CE$ at ($s_0,u_0)$ if and only if $\mathbf{x}=\pm \mathbf{e}\left(s_0\right)$ and $\rho \left(s_0\right)\ne 0$;

(2) M is locally diffeomorphic to swallowtail SW at ($s_0,u_0)$ if and only if $\mathbf{x}=\pm \mathbf{e}\left(s_0\right)$, $\rho \left(s_0\right)=0$ and ${\rho }^{{}^{\prime }}\left(s_0\right)=0$.

The proof will appear later. Here,

$$\begin{array}{ccc}\hfill C\times \mathbb{R}& =& \left\{(x_1,x_2)\mid x_1^2=x_2^3\right\}\times \mathbb{R},\hfill \\ \hfill CE& =& \left\{(x_1,x_2,x_3)\mid x_1{=u,x}_2{=v}^2{,x}_3{=v}^3\right\},\hfill \\ \hfill W& =& \left\{(x_1,x_2,x_3)\mid x_1=u,x_2=3v^2+u{v}^2,x_3=4v^3+2uv\right\}.\hfill \end{array}$$

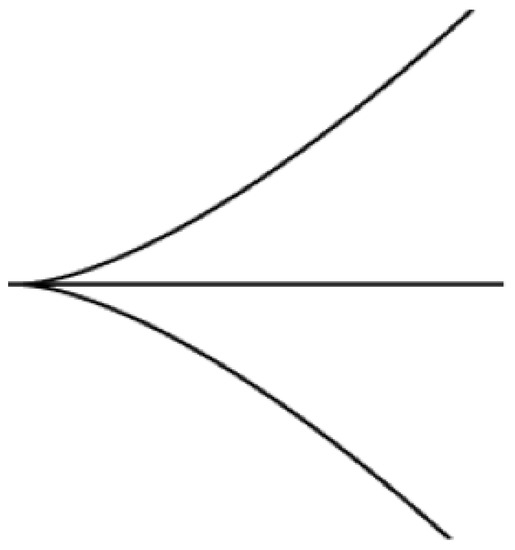
The pictures of $C\times \mathbb{R}$, $CE$, and $SW$ are presented in Figure 1, Figure 2 and Figure 3.

Figure 1. $C\times \mathbb{R}.$.

Figure 2. CE.

Figure 3. SW.

3.1. Lorentzian Height Functions

Next, let us introduce two different families of Lorentzian height functions that will be useful to study the singularities of M as follows [1,11,67]: $H:I\times {\mathbb{S}}_1^2\to \mathbb{R},$ by $H(s,\mathbf{x})=<\mathbf{\beta }\left(\mathbf{s}\right),\mathbf{x}>$. We call this the Lorentzian height function. We use the notation $h_{\mathbf{x}}\left(s\right)=H(s,\mathbf{x})$ for any fixed $\mathbf{x}\in {\mathbb{S}}_1^2$. We also define $\tilde{H}:I\times {\mathbb{S}}_1^2\times \mathbb{R}\to \mathbb{R}$ as $\tilde{H}(s,\mathbf{x},w)=<\mathbf{\beta },\mathbf{x}>-w$. We call it the extended Lorentzian height function of $\mathbf{\beta }\left(\mathbf{s}\right)$. We denote that ${\tilde{h}}_{\mathbf{x}}\left(s\right)=\tilde{H}(s,\mathbf{x})$. From now on, we shall often not write the parameter s. Then, we give the following proposition:

Proposition 1.

Let β: $I\to {\mathbb{E}}_1^3$ be a unit speed timelike curve with ${\kappa }_1\ne 0$. Then, the following holds:

(A).

(1) $h_{\mathbf{x}}^{{}^{\prime }}\left(s\right)=0$ if and only if $\mathbf{x}=a_1{\mathbf{N}}_1+a_2{\mathbf{N}}_2$ and $a_1^2+a_2^2=1$;

(2) $h_{\mathbf{x}}^{{}^{\prime }}\left(s\right)=h_x^{{}^{″}}\left(s\right)=0$ if and only if $\mathbf{x}=\pm \mathbf{e}\left(s\right)$;

(3) $h_{\mathbf{x}}^{{}^{\prime }}\left(s\right)=h_x^{{}^{″}}\left(s\right)=h_{\mathbf{x}}^{{}^{‴}}\left(s\right)=0$ if and only if $\mathbf{x}=\pm \mathbf{e}\left(s\right)$ and $\rho \left(s\right)=0;$

(4) $h_{\mathbf{x}}^{{}^{\prime }}\left(s\right)=h_x^{{}^{″}}\left(s\right)=h_{\mathbf{x}}^{{}^{‴}}\left(s\right)=h_{\mathbf{x}}^{\left(4\right)}\left(s\right)=0$ if and only if $\mathbf{x}=\pm \mathbf{e}\left(s\right)$ and $\rho \left(s\right)={\rho }^{{}^{\prime }}\left(s\right)=0;$

(5) $h_{\mathbf{x}}^{{}^{\prime }}\left(s\right)=h_x^{{}^{″}}\left(s\right)=h_{\mathbf{x}}^{{}^{‴}}\left(s\right)=h_{\mathbf{x}}^{\left(4\right)}\left(s\right)=h_{\mathbf{x}}^{\left(5\right)}\left(s\right)=0$ if and only if $\mathbf{x}=\pm \mathbf{e}\left(s\right)$ and $\rho \left(s\right)={\rho }^{{}^{\prime }}\left(s\right)={\rho }^{{}^{{}^{″}}}\left(s\right)=0.$

(B).

(1) ${\tilde{h}}_{\mathbf{x}}\left(s\right)=0$ if and only if there exist $<\mathbf{\beta },\mathbf{x}>=w$;

(2) ${\tilde{h}}_{\mathbf{x}}\left(s\right)={\tilde{h}}_x^{{}^{\prime }}\left(s\right)=0$ if and only if there exist $a_1$, $a_2\in \mathbb{R}$ such that $\mathbf{x}=cosu{\mathbf{N}}_1+sinu{\mathbf{N}}_2$ and $<\mathbf{\beta },\mathbf{x}>=w$;

(3) ${\tilde{h}}_{\mathbf{x}}\left(s\right)={\tilde{h}}_{\mathbf{x}}^{{}^{\prime }}\left(s\right)={\tilde{h}}_x^{{}^{″}}\left(s\right)={\tilde{h}}_x^{{}^{″}}\left(s\right)=0$ if and only if $\mathbf{x}=\pm \mathbf{e}\left(s\right)$, $<\mathbf{\beta },\mathbf{x}>=w$, and $\rho \left(s\right)=0$;

(4) ${\tilde{h}}_{\mathbf{x}}\left(s\right)={\tilde{h}}_{\mathbf{x}}^{{}^{\prime }}\left(s\right)={\tilde{h}}_x^{{}^{″}}\left(s\right)={\tilde{h}}_x^{{}^{″}}\left(s\right)={\tilde{h}}_x^{{}^{{}^{‴}}}\left(s\right)=0$ if and only if $\mathbf{x}=\pm \mathbf{e}\left(s\right)$, $<\mathbf{\beta },\mathbf{x}>=w$, and $\rho \left(s\right)={\rho }^{{}^{\prime }}\left(s\right)=0$;

(5) ${\tilde{h}}_{\mathbf{x}}\left(s\right)={\tilde{h}}_{\mathbf{x}}^{{}^{\prime }}\left(s\right)={\tilde{h}}_x^{{}^{″}}\left(s\right)={\tilde{h}}_x^{{}^{″}}\left(s\right)={\tilde{h}}_x^{{}^{{}^{‴}}}\left(s\right)={\tilde{h}}_x^{{}^{{}^{\left(4\right)}}}\left(s\right)=0$ if and only if $\mathbf{x}=\pm \mathbf{e}\left(s\right)$, $<\mathbf{\beta },\mathbf{x}>=w$, and $\rho \left(s\right)={\rho }^{{}^{\prime }}\left(s\right)={\rho }^{{}^{{}^{″}}}\left(s\right)=0.$

Proof. 

(A). (1) Since $h_{\mathbf{x}}^{{}^{\prime }}\left(s\right)=<{\mathbf{T}}_1,\mathbf{x}>$, and $\{{\mathbf{T}}_1,$${\mathbf{N}}_1$, ${\mathbf{N}}_2\}$ is RMF along $\mathbf{\beta }\left(s\right)$, then there exists $a_1$, $a_2\in \mathbb{R}$ such that $\mathbf{x}=a_1{\mathbf{N}}_1+a_2{\mathbf{N}}_2$. Moreover, in combination with $\mathbf{x}\in {\mathbb{S}}_1^2$, we obtain $a_1^2+a_2^2=1$; it follows that $h_{\mathbf{x}}^{{}^{\prime }}\left(s\right)=0$ if and only if $\mathbf{x}=a_1{\mathbf{N}}_1+a_2{\mathbf{N}}_2$ and $a_1^2+a_2^2=1$.

(2) When $h_{\mathbf{x}}^{{}^{\prime }}\left(s\right)=0$, the assertion (2) follows from the fact that $h_{\mathbf{x}}^{{}^{″}}\left(s\right)=<{\mathbf{T}}_1^{{}^{\prime }},\mathbf{x}>=<{\kappa }_1{\mathbf{N}}_1-{\kappa }_2{\mathbf{N}}_2,\mathbf{x}>=0$. Thus, we have $a_1{\kappa }_1-a_2{\kappa }_2=0$. It follows from the fact $a_1^2+a_2^2=1$ that $a_1=\pm {\kappa }_2/\sqrt{{\kappa }_1^2+{\kappa }_2^2}$ and $a_2=\pm {\kappa }_1/\sqrt{{\kappa }_1^2+{\kappa }_2^2}$. Thereby, we have

$$\mathbf{x}=\left(\mp \frac{{\kappa }_1}{\sqrt{{\kappa }_1^2+{\kappa }_2^2}}\left(\frac{{\kappa }_2}{{\kappa }_1}{\mathbf{N}}_1+{\mathbf{N}}_2\right)\right)\left(s\right)=\pm \mathbf{e}\left(s\right).$$

(20)

Thus, we obtain $h_{\mathbf{x}}^{{}^{\prime }}\left(s\right)=h_x^{{}^{″}}\left(s\right)=0$ if and only if $\mathbf{x}=\pm \mathbf{e}\left(s\right)$.

(3) Under the condition that $h_{\mathbf{x}}^{{}^{\prime }}\left(s\right)=h_x^{{}^{″}}\left(s\right)=0$, $h_{\mathbf{x}}^{{}^{{}^{‴}}}\left(s\right)=<{\mathbf{T}}_1^{{}^{{}^{″}}},\mathbf{x}>=<\left({\kappa }_1^2+{\kappa }_2^2\right){\mathbf{T}}_1+{\kappa }_1^{{}^{\prime }}{\mathbf{N}}_1-{\kappa }_2^{{}^{\prime }}{\mathbf{N}}_2,\mathbf{x}>=0$, and by Equation (20), we have

$$\pm \frac{{\kappa }_1}{\sqrt{{\kappa }_1^2+{\kappa }_2^2}}\left(\frac{{\kappa }_2{\kappa }_1^{{}^{\prime }}-{\kappa }_1{\kappa }_2^{{}^{\prime }}}{{\kappa }_1}\right)\left(s\right)=\pm \frac{{\kappa }_1}{\sqrt{{\kappa }_1^2+{\kappa }_2^2}}\left(\frac{\rho }{{\kappa }_1}\right)\left(s\right)=0.$$

Since ${\kappa }_1\ne 0$, we obtain $h_{\mathbf{x}}^{{}^{{}^{‴}}}\left(s\right)=0$ if and only if $\mathbf{x}=\pm \mathbf{e}\left(s\right)$ and $\rho \left(s\right)=0$.

(4) Since

$$\left.\begin{array}{c}{h}_{\mathbf{x}}^{{}^{{}^{\left(4\right)}}}\left(s\right)=<{\mathbf{T}}_1^{{}^{{}^{{}^{‴}}}},\mathbf{x}>=<3({\kappa }_1{\kappa }_1^{{}^{\prime }}+{\kappa }_2{\kappa }_2^{{}^{\prime }}){\mathbf{T}}_1+\left({\kappa }_1^{{}^{{}^{″}}}+{\kappa }_1\left({\kappa }_1^2+{\kappa }_2^2\right)\right){\mathbf{N}}_1\hfill \\ -\left({\kappa }_2^{{}^{{}^{″}}}+{\kappa }_2\left({\kappa }_1^2+{\kappa }_2^2\right)\right){\mathbf{N}}_2,\mathbf{x}>=0.\hfill \end{array}\right\}$$

Thus, making use of Equation (20) in the above, we have that

$$\pm \frac{{\kappa }_1}{\sqrt{{\kappa }_1^2+{\kappa }_2^2}}\left(\frac{{\left({\kappa }_2{\kappa }_1^{{}^{\prime }}-{\kappa }_1{\kappa }_2^{{}^{\prime }}\right)}^{{}^{\prime }}}{{\kappa }_1}\right)\left(s\right)=0.$$

This is equivalent to the condition $\rho \left(s\right)={\rho }^{{}^{\prime }}\left(s\right)=0$.

(5) Since $h_{\mathbf{x}}^{{}^{{}^{\left(5\right)}}}\left(s\right)=<{\mathbf{T}}_1^{{}^{{}^{{}^{\left(4\right)}}}},\mathbf{x}>=0$, we have

$$\left.\begin{array}{c}<\left({\left({\kappa }_1^2+{\kappa }_2^2\right)}^2+4\left({\kappa }_2{\kappa }_2^{{}^{{}^{″}}}+{\kappa }_1{\kappa }_1^{{}^{{}^{″}}}\right)+3\left({\kappa }_1^{{}^{\prime }2}+{\kappa }_2^{{}^{\prime }2}\right)\right){\mathbf{T}}_1+\hfill \\ \left({\kappa }_1^{{}^{{}^{‴}}}+5{\kappa }_1\left({\kappa }_1^{{}^{\prime }}{\kappa }_1+{\kappa }_2^{{}^{\prime }}{\kappa }_2\right)+{\kappa }_1^{{}^{\prime }}\left({\kappa }_1^2+{\kappa }_2^2\right)\right){\mathbf{N}}_1-\hfill \\ \left({\kappa }_2^{{}^{{}^{‴}}}+5{\kappa }_2\left({\kappa }_2^{{}^{\prime }}{\kappa }_2+{\kappa }_1^{{}^{\prime }}{\kappa }_1\right)+{\kappa }_2^{{}^{\prime }}\left({\kappa }_1^2+{\kappa }_2^2\right)\right){\mathbf{N}}_2,\mathbf{x}>=0.\hfill \end{array}\right\}$$

Similarly, by Equation (20) in the above, we have

$$\pm \frac{1}{\sqrt{{\kappa }_1^2+{\kappa }_2^2}}\left(\frac{{\kappa }_2{\kappa }_1^{{}^{{}^{‴}}}-{\kappa }_1{\kappa }_2^{{}^{{}^{‴}}}+\left({\kappa }_2{\kappa }_1^{{}^{\prime }}-{\kappa }_1{\kappa }_2^{{}^{\prime }}\right)\left({\kappa }_1^2+{\kappa }_2^2\right)}{{\kappa }_1}\right)=0.$$

This is equivalent to the condition $\rho \left(s\right)={\rho }^{{}^{\prime }}\left(s\right)={\rho }^{{}^{{}^{″}}}\left(s\right)=0$. (B). Using the same computation as the proof of (A), we can obtain (B). □

Proposition 2.

Let β: $I\to {\mathbb{E}}_1^3$ be a unit speed timelike curve with ${\kappa }_1\ne 0$. Then, we have $\rho \left(s\right)=0$ if and only if

$$\mathbf{e}\left(s\right)=\frac{{\kappa }_1}{\sqrt{{\kappa }_1^2+{\kappa }_2^2}}\left(\frac{{\kappa }_2}{{\kappa }_1}{\mathbf{N}}_1+{\mathbf{N}}_2\right)$$

is a constant vector.

Proof. 

Suppose that ${\kappa }_1\ne 0$. By simple calculations, we have

$${\mathbf{e}}^{{}^{\prime }}\left(s\right)=\frac{\rho \left(s\right)}{{\left(\sqrt{{\kappa }_1^2+{\kappa }_2^2}\right)}^3}\left({\kappa }_1{\mathbf{N}}_1+{\kappa }_2{\mathbf{N}}_2\right).$$

Thus, ${\mathbf{e}}^{{}^{\prime }}\left(s\right)=\mathbf{0}$ if and only if $\rho \left(s\right)={\kappa }_2{\kappa }_1^{{}^{\prime }}-{\kappa }_1{\kappa }_2^{{}^{\prime }}=0.$ □

Proposition 3.

Let β: $I\to {\mathbb{E}}_1^3$ be a unit speed timelike curve with ${\kappa }_1\ne 0$. Then, we state the following:

(a) 

β is a slant helix if and only if ${\kappa }_2/{\kappa }_1$ is constant;

(b) 

${\mathbf{N}}_2$ is a part of a circle on ${\mathbb{S}}_1^2$ whose center is the spacelike constant vector ${\mathbf{e}}_0.$

Proof. 

(a)

Suppose that $\rho \left(s\right)={\kappa }_2{\kappa }_1^{{}^{\prime }}-{\kappa }_1{\kappa }_2^{{}^{\prime }}=0$. Hence, we can write

$${\left(\frac{{\kappa }_2}{{\kappa }_1}\right)}^{{}^{\prime }}=\frac{{\kappa }_1{\kappa }_2^{{}^{\prime }}-{\kappa }_2{\kappa }_1^{{}^{\prime }}}{{\kappa }_1^2}=\frac{-\rho \left(s\right)}{{\kappa }_1^2}=0.$$

This means that $\frac{{\kappa }_2}{{\kappa }_1}$=constant; that is, $\mathbf{\beta }$ is a slant helix;

(b)

Suppose that ${\kappa }_1\ne 0$. Since

$$<\mathbf{e},{\mathbf{N}}_2>=\frac{{\kappa }_1}{\sqrt{{\kappa }_1^2+{\kappa }_2^2}}<\left(\frac{{\kappa }_2}{{\kappa }_1}{\mathbf{N}}_1+{\mathbf{N}}_2\right),{\mathbf{N}}_2>=\frac{1}{\sqrt{1+{\kappa }_2^2/{\kappa }_1^2}}=const.$$

${\mathbf{N}}_2$ is a part of a circle on ${\mathbb{S}}_1^2$ whose center is the constant spacelike vector ${\mathbf{e}}_0\left(s\right)$. □

3.2. Unfolding of Functions by One-Variable

Now, we use some general results on the singularity theory for families of function germs [1,2,3]. Let F:$\left(\mathbb{R}\times {\mathbb{R}}^r,(s_0,{\mathbf{x}}_0)\right)\to \mathbb{R}$ be a smooth function and $f\left(s\right)=F_{x_0}(s,{\mathbf{x}}_0)$. Then, F is called an r-parameter unfolding of $f\left(s\right)$. We say that $f\left(s\right)$ has A${}_k$-singularity at $s_0$ if $f^{\left(p\right)}\left(s_0\right)=0$ for all $1\le p\le k$, and $f^{(k+1)}\left(s_0\right)\ne 0$. We also say that f has A${}_{⩾k}$-singularity ($k⩾1$) at s${}_0$. Let the $\left(k-1\right)$-jet of the partial derivative $\frac{\partial F}{\partial x_i}$ at $s_0$ be $j^{\left(k-1\right)}\left(\frac{\partial F}{\partial x_i}\left(s,{\mathbf{x}}_0\right)\right)\left(s_0\right)={\Sigma }_{j=0}^{k-1}{L}_{ji}{\left(s-s_0\right)}^j$ (without the constant term), for $i=1,...,r$. Then, $F\left(s\right)$ is called a p-versal unfolding if the $k\times r$ matrix of coefficients $\left(L_{ji}\right)$ has rank k$\left(k\le r\right)$. Therefore, we write an important set about the unfolding relative to the above notations. The discriminant set of F is the set

$${\mathfrak{D}}_F=\left\{\mathbf{x}\in {\mathbb{R}}^r\mid \mathrm{there}\mathrm{exists}s\mathrm{with}F\left(s,\mathbf{x}\right)=\frac{\partial F}{\partial s}\left(s,\mathbf{x}\right)=0\mathrm{at}(s,\mathbf{x})\right\}.$$

(21)

The bifurcation set of F is the set

$${\mathfrak{B}}_F=\left\{\mathbf{x}\in {\mathbb{R}}^r\mid \mathrm{there}\mathrm{exists}s\mathrm{with}\frac{\partial F}{\partial s}\left(s,\mathbf{x}\right)=\frac{{\partial }^{2}F}{\partial s^2}\left(s,\mathbf{x}\right)=0\mathrm{at}(s,\mathbf{x})\right\}.$$

(22)

Then, similar to [1,11,67], we state the following theorem:

Theorem 2.

Let F:$\left(\mathbb{R}\times {\mathbb{R}}^r,(s_0,{\mathbf{x}}_0)\right)\to \mathbb{R}$ be an r-parameter unfolding of $f\left(s\right)$, which has the $A_k$ singularity at $s_0$.

Suppose that F is a p-versal unfolding;

(a) 

If $k=1$, then ${\mathfrak{D}}_F$ is locally diffeomorphic to $\left\{\mathbf{0}\right\}\times {\mathbb{R}}^{r-1}$, and ${\mathfrak{B}}_F=⌀$;

(b) 

If $k=2$, then ${\mathfrak{D}}_F$ is locally diffeomorphic to $\mathbf{C}\times {\mathbb{R}}^{r-2}$ and ${\mathfrak{B}}_F$ is locally diffeomorphic to $\left\{\mathbf{0}\right\}\times {\mathbb{R}}^{r-1}$;

(c) 

If $k=3$, then ${\mathfrak{D}}_F$ is locally diffeomorphic to $\mathbf{SW}\times {\mathbb{R}}^{r-3}$ and ${\mathfrak{B}}_F$ is locally diffeomorphic to $\mathbf{C}\times {\mathbb{R}}^{r-2}$.

Hence, we have the following fundamental proposition:

Proposition 4.

Let β: $I\to {\mathbb{E}}_1^3$ be a unit speed timelike curve ${\kappa }_1\ne 0$. (1). If $h_{\mathbf{x}}\left(s\right)=H(s,\mathbf{x})$ has an $A_k$-singularity ($k=$$2,3)$ at $s_0\in \mathbb{R}$, then H is a $p-$versal unfolding of $h_{{\mathbf{x}}_0}\left(s_0\right)$. (2). If ${\tilde{h}}_{\mathbf{x}}\left(s\right)=\tilde{H}(s,\mathbf{x},w)$ has an $A_k$-singularity ($k=2,$$3)$ at $s_0\in \mathbb{R}$, then $\tilde{H}$ is a $p-$versal unfolding of ${\tilde{h}}_{{\mathbf{x}}_0}\left(s_0\right)$

Proof. 

(1) Since $\mathbf{x}=\left(x_0,x_1,x_2\right)\in {\mathbb{S}}_1^2$ and $\mathbf{\beta }\left(s\right)=\left({\beta }_0\left(s\right),{\beta }_1\left(s\right),{\beta }_2\left(s\right)\right)\in {\mathbb{E}}_1^3$. Without loss of generality, suppose $x_2\ne 0$. Then, by $x_2=\sqrt{1+x_0^2-x_1^2}$, we have

$$H(s,\mathbf{x})=-x_0{\beta }_0\left(s\right)+x_1{\beta }_1\left(s\right)+\sqrt{1+x_0^2-x_1^2}{\beta }_2\left(s\right).$$

(23)

Thus, we have that

$$\left.\begin{array}{c}\frac{\partial H}{\partial x_0}=-{\beta }_0\left(s\right)+\frac{x_0{\beta }_2\left(s\right)}{\sqrt{1+x_0^2-x_1^2}},\frac{\partial H}{\partial x_1}={\beta }_1\left(s\right)-\frac{x_1{\beta }_2\left(s\right)}{\sqrt{1+x_1^2-x_2^2}},\hfill \\ \frac{{\partial }^{2}H}{\partial s\partial x_0}=-{\beta }_0^{{}^{\prime }}\left(s\right)+\frac{x_0{\beta }_2^{{}^{\prime }}\left(s\right)}{\sqrt{1+x_0^2-x_1^2}},\frac{{\partial }^{2}H}{\partial s\partial x_1}={\beta }_1^{{}^{\prime }}\left(s\right)-\frac{x_1{\beta }_2^{{}^{\prime }}\left(s\right)}{\sqrt{1+x_1^2-x_2^2}}.\hfill \end{array}\right\}$$

Therefore, the 2-jets of $\frac{\partial H}{\partial x_i}$ at $s_0$ (i = 0, 1) are as follows. Let ${\mathbf{x}}_0=\left(x_{00},x_{10},x_{20}\right)\in {\mathbb{S}}_1^2$ and assume $x_{20}\ne 0$; then

$$\left.\begin{array}{c}{j}^1\left(\frac{\partial H}{\partial x_0}(s,{\mathbf{x}}_0)\right)=\left(-{\beta }_0^{{}^{\prime }}\left(s\right)+\frac{x_{00}{\beta }_2^{{}^{\prime }}\left(s\right)}{x_{20}}\right)(s-s_0),\hfill \\ j^1\left(\frac{\partial H}{\partial x_1}(s,{\mathbf{x}}_0)\right)=\left({\beta }_1^{{}^{\prime }}\left(s\right)-\frac{x_{10}{\beta }_2^{{}^{\prime }}\left(s\right)}{x_{20}}\right)(s-s_0),\hfill \end{array}\right\}$$

(24)

and

$$\left.\begin{array}{c}{j}^2\left(\frac{\partial H}{\partial x_0}(s,{\mathbf{x}}_0)\right)=\left(-{\beta }_0^{{}^{\prime }}\left(s\right)+\frac{x_{00}{\beta }_2\left(s\right)}{x_{20}}\right)(s-s_0)\\ +\frac{1}{2}\left(-{\beta }_0^{{}^{{}^{″}}}+\frac{x_{00}{\beta }_2^{{}^{{}^{″}}}\left(s\right)}{x_{20}}\right){\left(s-s_0\right)}^2,\\ j^2\left(\frac{\partial H}{\partial x_1}(s,{\mathbf{x}}_0)\right)=\left({\beta }_1^{{}^{\prime }}\left(s\right)-\frac{x_{10}{\beta }_2^{{}^{\prime }}\left(s\right)}{x_{20}}\right)\left(s-s_0\right)\\ +\frac{1}{2}\left({\beta }_1^{{}^{{}^{″}}}\left(s\right)-\frac{x_{10}{\beta }_2^{{}^{{}^{″}}}\left(s\right)}{x_{20}}\right){\left(s-s_0\right)}^2\end{array}\right\}$$

(25)

(i)

If $h_{{\mathbf{x}}_0}\left(s_0\right)$ has the $A_2$-singularity at $s_0$, then $h_{{\mathbf{x}}_0}^{{}^{\prime }}\left(s_0\right)=0$. Therefore, the $(2-1)\times 2$ matrix of coefficients $\left(L_{ji}\right)$ is:

$$A=\left(\begin{array}{cc}-{\beta }_0^{{}^{\prime }}\left(s\right)+\frac{x_{00}{\beta }_2^{{}^{\prime }}\left(s\right)}{x_{20}}& {\beta }_1^{{}^{\prime }}\left(s\right)-\frac{x_{10}{\beta }_2^{{}^{\prime }}\left(s\right)}{x_{20}}\end{array}\right).$$

(26)

Suppose that the rank of the matrix A is zero; then, we have:

$${\beta }_0^{{}^{\prime }}\left(s\right)=\frac{x_{00}{\beta }_2^{{}^{\prime }}\left(s\right)}{x_{20}},{\beta }_1^{{}^{\prime }}\left(s\right)=\frac{x_{10}{\beta }_2^{{}^{\prime }}\left(s\right)}{x_{20}}.$$

(27)

Since $∥{\mathbf{\beta }}^{{}^{\prime }}\left(s_0\right)∥=∥{\mathbf{T}}_1\left(s_0\right)∥=1$, we have ${\beta }_2^{{}^{\prime }}\left(s_0\right)\ne 0$ and the contradiction as follows:

$$\begin{array}{ccc}\hfill 0& =& <\left({\beta }_0^{{}^{\prime }}\left(s_0\right),{\beta }_1^{{}^{\prime }}\left(s_0\right),{\beta }_2^{{}^{\prime }}\left(s_0\right)\right),\left(x_{00},x_{10},x_{20}\right)>\hfill \\ & =& -{\beta }_0^{{}^{\prime }}\left(s_0\right)x_{00}+{\beta }_1^{{}^{\prime }}\left(s_0\right)x_{10}+{\beta }_2^{{}^{\prime }}\left(s_0\right)x_{20}\hfill \end{array}$$

(28)

$$\begin{array}{ccc}& =& -\frac{x_{00}^2{\beta }_2^{{}^{\prime }}\left(s_0\right)}{x_{20}}+\frac{x_{10}^2{\beta }_2^{{}^{\prime }}\left(s_0\right)}{x_{20}}+{\beta }_2^{{}^{\prime }}\left(s_0\right)x_{20}\hfill \\ & =& \frac{{\beta }_2^{{}^{\prime }}\left(s_0\right)}{x_{20}}\left(-x_{00}^2+x_{10}^2+x_{20}^2\right)\hfill \\ & =& \frac{{\beta }_2^{{}^{\prime }}\left(s_0\right)}{x_{20}}\ne 0.\hfill \end{array}$$

(29)

Therefore, rank($A)=1$, and H is the (p) versal unfolding of $h_{{\mathbf{x}}_0}$ at $s_0$.

(ii)

If $h_{{\mathbf{x}}_0}\left(s_0\right)$ has the $A_3$-singularity at $s_0\in \mathbb{R}$, then $h_{{\mathbf{x}}_0}^{{}^{\prime }}\left(s_0\right)=h_{{\mathbf{x}}_0}^{{}^{″}}\left(s_0\right)=0$ and by Proposition 1:

$$\mathbf{e}\left(s_0\right)=\frac{{\kappa }_1}{\sqrt{{\kappa }_1^2+{\kappa }_2^2}}\left(\frac{{\kappa }_2}{{\kappa }_1}{\mathbf{N}}_1+{\mathbf{N}}_2\right),$$

(30)

where ${\rho }^{{}^{\prime }}\left(s_0\right)=0$, and ${\rho }^{{}^{″}}\left(s_0\right)\ne 0$. Therefore, the $(3-1)\times 2$ matrix of the coefficients $\left(L_{ji}\right)$ is

$$B=\left(\begin{array}{cc}{L}_{11}& L_{12}\\ L_{21}& L_{22}\end{array}\right)=\left(\begin{array}{cc}-{\beta }_0^{{}^{\prime }}\left(s\right)+\frac{x_{00}{\beta }_2\left(s\right)}{x_{20}}& {\beta }_1^{{}^{\prime }}\left(s\right)-\frac{x_{10}{\beta }_2^{{}^{\prime }}\left(s\right)}{x_{20}}\\ -{\beta }_0^{{}^{{}^{″}}}+\frac{x_{00}{\beta }_2^{{}^{{}^{″}}}\left(s\right)}{x_{20}}& {\beta }_1^{{}^{{}^{″}}}\left(s\right)-\frac{x_{10}{\beta }_2^{{}^{{}^{″}}}\left(s\right)}{x_{20}}\end{array}\right).$$

(31)

For the purpose, we also require the $2\times 2$ matrix B to be non-singular, which always holds true. In fact, the determinate of this matrix at $s_0$ is

$$\begin{array}{ccc}\hfill det\left(B\right)& =& \frac{1}{x_{20}}\left|\begin{array}{ccc}-{\beta }_0^{{}^{\prime }}& {\beta }_1^{{}^{\prime }}& {\beta }_2^{{}^{\prime }}\\ -{\beta }_0^{{}^{{}^{″}}}& {\beta }_1^{{}^{{}^{″}}}& {\beta }_2^{{}^{{}^{″}}}\\ x_{00}& x_{10}& x_{20}\end{array}\right|\hfill \\ & =& \frac{1}{x_{20}}<{\mathbf{\beta }}^{{}^{\prime }}\times {\mathbf{\beta }}^{{}^{″}},{\mathbf{x}}_{\mathbf{0}}>\hfill \end{array}$$

(32)

$$\begin{array}{ccc}& =& \mp \frac{{\kappa }_1}{x_{20}\sqrt{{\kappa }_1^2+{\kappa }_2^2}}<{\mathbf{\beta }}^{{}^{\prime }}\times {\mathbf{\beta }}^{{}^{″}},\left(\frac{{\kappa }_2}{{\kappa }_1}{\mathbf{N}}_1+{\mathbf{N}}_2\right)>.\hfill \end{array}$$

(33)

Since ${\mathbf{\beta }}^{{}^{\prime }}={\mathbf{T}}_1$, we have ${\mathbf{\beta }}^{{}^{″}}={\kappa }_1{\mathbf{N}}_1-{\kappa }_2{\mathbf{N}}_2$. Substituting these relations for the above equality, we have

$$det\left(B\right)=\mp \frac{\sqrt{{\kappa }_1^2+{\kappa }_2^2}}{x_{20}}\ne 0.$$

(34)

This means that rank $\left(B\right)=2$.

(2) Under the same notation as in (1), we have

$$\tilde{H}(s,\mathbf{x},x_2)=-x_0{\beta }_0\left(s\right)+x_1{\beta }_1\left(s\right)+\sqrt{1+x_0^2-x_1^2}{\beta }_2\left(s\right)-x_2.$$

(35)

We require the $2\times 3$ matrix

$$G=\left(\begin{array}{ccc}-{\beta }_0^{{}^{\prime }}\left(s\right)+\frac{x_{00}{\beta }_2\left(s\right)}{x_{20}}& {\beta }_1^{{}^{\prime }}\left(s\right)-\frac{x_{10}{\beta }_2^{{}^{\prime }}\left(s\right)}{x_{20}}& -1\\ -{\beta }_0^{{}^{{}^{″}}}+\frac{x_{00}{\beta }_2^{{}^{{}^{″}}}\left(s\right)}{x_{20}}& {\beta }_1^{{}^{{}^{″}}}\left(s\right)-\frac{x_{10}{\beta }_2^{{}^{{}^{″}}}\left(s\right)}{x_{20}}& 0\end{array}\right),$$

to have the maximal rank. By case (1) in Equation (30), the second raw of G does not vanish, so rank $\left(G\right)=2$. □

Proof 

(Proof of Theorem 1). (1) By Proposition 1, the bifurcation set of $H(s,\mathbf{x})$ is

$${\mathfrak{B}}_H=\left\{\frac{{\kappa }_1}{\sqrt{{\kappa }_1^2+{\kappa }_2^2}}\left(\frac{{\kappa }_2}{{\kappa }_1}{\mathbf{N}}_1+{\mathbf{N}}_2\right)\mid s\in \mathbb{R}\mid s\in \mathbb{R}\right\}.$$

(36)

The assertion (1) of Theorem 1 follows from Proposition 1, Proposition 4, and Theorem 2. The discriminant set of $\tilde{H}(s,\mathbf{x})$ is given as follows:

$${\mathfrak{D}}_{\tilde{H}}=\left\{{\mathbf{x}}_0=\mathbf{\beta }+cosu{\mathbf{N}}_1+sinu{\mathbf{N}}_2\mid s\in \mathbb{R}\right\}.$$

(37)

The assertion (1) of Theorem 1 follows from Proposition 1, Proposition 4, and Theorem 2.

□

Example 1.

Given the timelike helix:

$$\mathbf{\beta }\left(s\right)=(\sqrt{3}sinhs,\sqrt{2}s,\sqrt{3}coshs),-1\le s\le 1,$$

It is easy to show that

$$\left.\begin{array}{c}\mathbf{T}\left(s\right)=(\sqrt{3}coshs,\sqrt{2},\sqrt{3}sinhs),\\ \mathbf{N}\left(s\right)=(sinhs,0,coshs),\\ \mathbf{B}\left(s\right)=(-\sqrt{2}coshs,-\sqrt{3},-\sqrt{2}sinhs),\\ \kappa \left(s\right)=\sqrt{3},\mathrm{and}\tau \left(s\right)=-\sqrt{2}.\end{array}\right\}$$

Taking ${\theta }_0=0$, we have $\theta \left(s\right)=\sqrt{2}s$. Using the Equation (9), we obtain

$${\kappa }_1\left(s\right)=\sqrt{3}cos\sqrt{2}s,\mathrm{and}{\kappa }_2\left(s\right)=\sqrt{3}sin\sqrt{2}s.$$

Hence, the geometric invariant is

$$\rho \left(s\right)=\sqrt{6}.$$

The transformation matrix can be expressed as

$$\left(\begin{array}{c}{\mathbf{T}}_1\hfill \\ {\mathbf{N}}_1\hfill \\ {\mathbf{N}}_2\hfill \end{array}\right)=\left(\begin{array}{ccc}1\hfill & 0\hfill & 0\hfill \\ 0\hfill & cos\sqrt{2}s\hfill & sin\sqrt{2}s\hfill \\ 0\hfill & -sin\sqrt{2}s\hfill & cos\sqrt{2}s\hfill \end{array}\right)\left(\begin{array}{c}\mathbf{T}\hfill \\ \mathbf{N}\hfill \\ \mathbf{B}\hfill \end{array}\right).$$

From this, we have

$$\begin{array}{ccc}\hfill {\mathbf{N}}_1& =& \left(\begin{array}{c}{N}_{11}\hfill \\ N_{12}\hfill \\ N_{13}\hfill \end{array}\right)=\left(\begin{array}{c}sinhscos\sqrt{2}s-\sqrt{2}coshssin\sqrt{2}s\hfill \\ -\sqrt{3}sin\sqrt{2}s\hfill \\ coshscos\sqrt{2}s-\sqrt{2}sinhssin\sqrt{2}s\hfill \end{array}\right),\hfill \\ \hfill {\mathbf{N}}_2& =& \left(\begin{array}{c}{N}_{21}\hfill \\ N_{22}\hfill \\ N_{23}\hfill \end{array}\right)=\left(\begin{array}{c}-sinhssin\sqrt{2}s-\sqrt{2}coshscos\sqrt{2}s\hfill \\ -\sqrt{3}cos\sqrt{2}s\hfill \\ -coshssin\sqrt{2}s-\sqrt{2}sinhscos\sqrt{2}s\hfill \end{array}\right).\hfill \end{array}$$

Hence, the timelike sweeping surface is (Figure 4)

$$M:\mathbf{R}(s,u)=\left(\sqrt{3}sinhs,\sqrt{2}s,\sqrt{3}coshs\right)+cosu\left(\begin{array}{c}{N}_{11}\hfill \\ N_{12}\hfill \\ N_{13}\hfill \end{array}\right)+sinu\left(\begin{array}{c}{N}_{21}\hfill \\ N_{22}\hfill \\ N_{23}\hfill \end{array}\right).$$

Figure 4. Timelike sweeping surface.

The Bishop spherical Darboux image is

$$\mathbf{e}\left(s\right)=sin\sqrt{2}s\left(\begin{array}{c}{N}_{11}\hfill \\ N_{12}\hfill \\ N_{13}\hfill \end{array}\right)+cos\sqrt{2}s\left(\begin{array}{c}{N}_{21}\hfill \\ N_{22}\hfill \\ N_{23}\hfill \end{array}\right).$$

3.3. Timelike Developable Surfaces and Singularities

In this subsection, we analyze the case that the profile curve $\mathbf{r}\left(u\right)=(0,$$r_1\left(u\right),r_2{\left(u\right))}^t$ degenerates to a spacelike straight line; that is, $\mathbf{r}\left(u\right)=(0,$${u,0)}^t$. Then, we can give the following timelike developable surface

$$M:\mathfrak{D}(s,u)=\mathbf{\beta }\left(s\right)+u{\mathbf{N}}_1\left(s\right),u\in \mathbb{R}.$$

(38)

Similarly, we have the following timelike developable surface

$$M^{\perp }:{\mathfrak{D}}^{\perp }(s,u)=\mathbf{\beta }\left(s\right)+u{\mathbf{N}}_2\left(s\right),u\in \mathbb{R}.$$

(39)

It is easy to show that $\mathfrak{D}(s,0)=\gamma \left(s\right)$ (resp. ${\mathfrak{D}}^{\perp }(s,0)=\mathbf{\beta }\left(s\right)$), $0\le s\le L$; that is, the surface ${\mathfrak{D}}^{\perp }$ (resp. $\mathfrak{D}$) interpolates the curve $\mathbf{\beta }\left(s\right)$. Furthermore, we have

$$\frac{\partial \mathfrak{D}}{\partial s}\times \frac{\partial \mathfrak{D}}{\partial u}=\left(1-u{\kappa }_1\right){\mathbf{N}}_2\left(s\right),$$

(40)

and

$$\frac{\partial {\mathfrak{D}}^{\perp }}{\partial s}\times \frac{\partial {\mathfrak{D}}^{\perp }}{\partial u}=-\left(1-u{\kappa }_2\right){\mathbf{N}}_1\left(s\right).$$

(41)

Hence, we have that M (resp. $M^{\perp }$) is non-singular at $(s_0,u_0)$ if and only if $1-u_0{\kappa }_1\left(s_0\right)\ne 0$ (resp. $\left(1-u_0{\kappa }_2\left(s_0\right)\ne 0\right)$. We designate $\mu \left(s\right)$ to represent ${\kappa }_i\left(s\right)$ (i = 1, 2); based on the Theorem 3 in [69], we can give the following corollary:

Corollary 3.

For the timelike developable ruled surfaces $\mathfrak{D}(s,u)$ and ${\mathfrak{D}}^{\perp }(s,u)$, we have the following:

(1) 

$\mathfrak{D}$(resp. ${\mathfrak{D}}^{\perp }$) is locally diffeomorphic to the cuspidal edge CE at $(s_0,u_0)$ if $\mu \left(s_0\right)=0$, and ${\mu }^{{}^{\prime }}\left(s_0\right)\ne 0$;

(2) 

$\mathfrak{D}$(resp. ${\mathfrak{D}}^{\perp }$) is locally diffeomorphic to the swallowtail SW at $(s_0,u_0)$ if $\mu \left(s_0\right)\ne 0$ and $\frac{{\mu }^{{}^{\prime }}\left(s_0\right)}{{\mu }^2\left(s_0\right)}\ne 0$.

Example 2.

By using Example 1, the timelike developable surfaces, respectively, are

$$M:\mathfrak{D}(s,u)=\left(\sqrt{3}sinhs,\sqrt{2}s,\sqrt{3}coshs\right)+u\left(\begin{array}{c}sinhscos\sqrt{2}s-\sqrt{2}coshssin\sqrt{2}s\hfill \\ -\sqrt{3}sin\sqrt{2}s\hfill \\ coshscos\sqrt{2}s-\sqrt{2}sinhssin\sqrt{2}s\hfill \end{array}\right),$$

and

$$M^{\perp }:{\mathfrak{D}}^{\perp }(s,u)=\left(\sqrt{3}sinhs,\sqrt{2}s,\sqrt{3}coshs\right)+u\left(\begin{array}{c}sinhssin\sqrt{2}s-\sqrt{2}coshscos\sqrt{2}s\hfill \\ -\sqrt{3}cos\sqrt{2}s\hfill \\ coshscos\sqrt{2}s-\sqrt{2}sinhscos\sqrt{2}s\hfill \end{array}\right).$$

The singular loci of M, and $M^{\perp }$, respectively, are

$$\mathfrak{D}\left(s\right)=\left(\sqrt{3}sinhs,\sqrt{2}s,\sqrt{3}coshs\right)+\frac{1}{\sqrt{3}}\left(\begin{array}{c}sinhs-\sqrt{2}coshstan\sqrt{2}s\hfill \\ -\sqrt{3}tan\sqrt{2}s\hfill \\ coshs-\sqrt{2}sinhstan\sqrt{2}s\hfill \end{array}\right),$$

and

$${\mathfrak{D}}^{\perp }\left(s\right)=\left(\sqrt{3}sinhs,\sqrt{2}s,\sqrt{3}coshs\right)+\frac{1}{\sqrt{3}}\left(\begin{array}{c}sinhs-\sqrt{2}coshscot\sqrt{2}s\hfill \\ -\sqrt{3}cot\sqrt{2}s\hfill \\ coshs-\sqrt{2}sinhscot\sqrt{2}s\hfill \end{array}\right).$$

We consider a local part of this curve when $\frac{\pi }{6\sqrt{2}}\le s\le \frac{\pi }{3\sqrt{2}}$. We see that ${\kappa }_1^{-1}\left(s\right)=\frac{1}{\sqrt{3}cos\sqrt{2}s}\ne 0$ and ${\kappa }_1^{{}^{\prime }}\left(s\right)=-\sqrt{6}sin\left(\sqrt{2}s\right)\ne 0$ for $\frac{\pi }{6\sqrt{2}}\le s\le \frac{\pi }{3\sqrt{2}}$. This means that M is locally diffeomorphic to a CE and its singular locus is locally diffeomorphic to a line (the green line); see Figure 5. For $M^{\perp }$, when $\frac{\pi }{6\sqrt{2}}\le s\le \frac{5\pi }{6\sqrt{2}}$, we see that ${\kappa }_2^{-1}\left(s\right)=\frac{1}{\sqrt{3}sin\sqrt{2}s}\ne 0$, ${\kappa }_2^{{}^{\prime }}\left(s\right)=\sqrt{6}cos\left(\sqrt{2}s\right)=0$ gives one real root $s=\frac{\pi }{2\sqrt{2}}$. This means that $M^{\perp }$ is locally diffeomorphic to SW and the singular locus is locally diffeomorphic to a line (the green line) at $s=\frac{\pi }{2\sqrt{2}}$; see Figure 6.

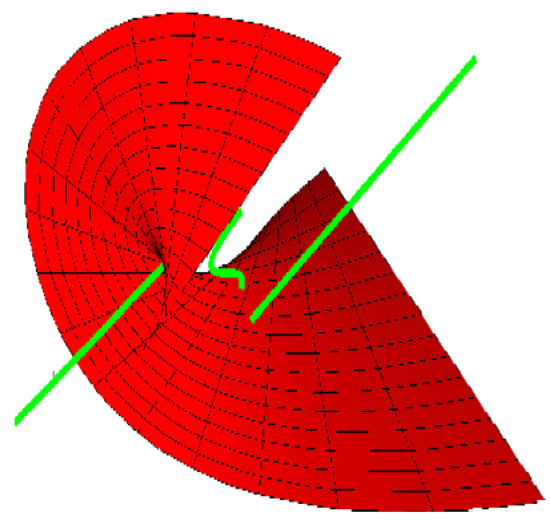
Figure 5. CE timelike developable surface.

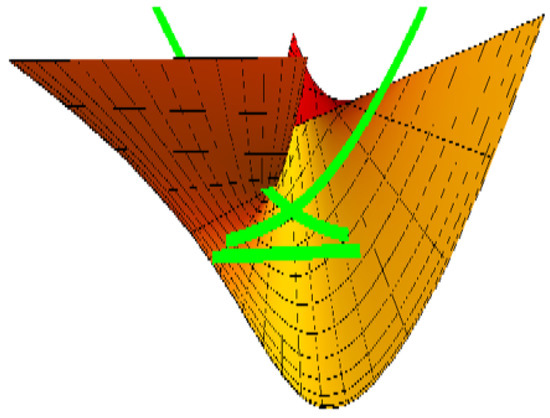
Figure 6. SW timelike developable surface.

4. Conclusions

This paper is concerned with the study of a special kind of timelike tube surface, called the named timelike sweeping surface in Minkowski 3-space. It is traced by a spacelike plane curve moving through a timelike curve such that the movement of any point on the surface is constantly orthogonal to the plane. Then, the problems of singularity and convexity of such a timelike sweeping surface are discussed. In particular, we derived the sufficient and necessary conditions for this timelike sweeping surface to be a timelike developable ruled surface. Afterwards, the problem of singularity of a timelike developable ruled surface is investigated. We also illustrated our main results by giving some representative examples. Hopefully, these results will be useful to physicists and those studying the general relativity theory. There are several opportunities for further work. An analogue of the problem addressed in this paper may be consider for 3-surfaces in 4-space. We will study this problem in the future.