Inscribed Triangles in the Unit Sphere and a New Class of Geometric Constants

Abstract

In this paper, we firstly investigate the constant $H\left(X\right)$ proposed by Gao further by discussing several properties of it that have not yet been discovered. Secondly, we focus on a new constant $G_L\left(X\right)$ closely related to $H\left(X\right)$, along with a variety of geometric properties. In addition, we show several relations among it and the several basic geometric constants via a few inequalities. Finally, we manage to characterize the geometric properties of its generalized forms $G_L(X,p)$ and $C_L\left(X\right)$ explicitly.

1. Introduction

The geometric constant has received widespread attention, for the reason that it not only essentially reflects the geometric properties of a space X, but also enables us to study the space quantitatively. As a research tool, geometric constants are also of great significance for their exclusive research, such as the estimations of them on some specific space, the relationships among them via several inequalities, and the relationships between one of them and its dual.

The most classic constants are the Jordan–von Neumann constant $C_{\mathrm{NJ}}\left(X\right)$ and James constant $J\left(X\right)$. The James constant $J\left(X\right)$ was proposed by Gao et al. in 1990, and the concept of it was derived from James’ characterization of uniformly non-square space. Further research concerning $J\left(X\right)$ has been conducted on the issue of whether the space has a normal structure or not. For the result and application of this constant, please refer to the article [1,2,3,4,5].

The constant $H\left(X\right)$ was proposed by Gao in 2000. Distinct from the existing geometric constants, this one combines the unit sphere inscribed with an equilateral triangle, innovatively taking the quantity $2x-y$ into consideration. It is worth mentioning that the introduction of the quantity $2x-y$ here has actually increased the difficulty of its study to a large extent. Some classical geometric properties and the connection of constants might be invalid. On the one hand, the constant $H\left(X\right)$ is no longer symmetrical, although most of the geometric constants we know all have a symmetrical structure. On the other hand, there are also differences in a few techniques for inequalities scaling when tackling the issues brought by the asymmetric geometric constants.

Motivated by Gao’s constant $H\left(X\right)$, we continue to study the geometric property of it in the subsequent section. In addition, we will introduce a brand new geometric constant $G_L\left(X\right)$ by giving an explanation at the very beginning of Section 3 of this paper in a geometric sense. In particular, some characterizations of geometric properties such as the value of inner product space and uniform non-squareness are given by utilizing certain equalities and inequalities on Banach spaces. Furthermore, we will provide the relationships among it and some other geometric constants via several inequalities.

2. Preliminaries

Throughout the paper, we will assume that X represents a non-trivial Banach space, that is, $dimX\ge 2$, and use $S_X$ and $B_X$ to represent the unit sphere and unit ball of X, respectively.

Definition 1

([6]). A Banach space X is called uniformly convex if, for any $\epsilon >0$, there exists $\delta >0$, such that for any $x,y\in S\left(X\right)$ with $\parallel x-y\parallel >\epsilon ,\parallel (x+y)/2\parallel <1-\delta$.

The Clarkson modulus of convexity of a Banach space X is defined as follows [7]:

$${\delta }_X\left(ϵ\right)=inf\left\{1-\frac{\parallel x+y\parallel }{2}:x,y\in S_X,\parallel x-y\parallel \ge ϵ\right\}.$$

The constant $J\left(X\right)$

$$J\left(X\right)=sup\left\{min(\parallel x+y\parallel ,\parallel x-y\parallel ):x,y\in S_X\right\}$$

is called the James constant [8], and the constant $C_{\mathrm{NJ}}\left(X\right)$ [9] is introduced by Clarkson to describe the inner product space. In a sense, it can be understood as the following formula, for which

$$C_{\mathrm{NJ}}\left(X\right)=sup\left\{\frac{{\parallel x+y\parallel }^2+{\parallel x-y\parallel }^2}{2\left({\parallel x\parallel }^2+{\parallel y\parallel }^2\right)}:(x,y)\ne (0,0)\right\}.$$

The constant $C_Z\left(X\right)$ was introduced by Zbăganu [10]:

$$C_{\mathrm{Z}}\left(X\right)=sup\left\{\frac{\parallel x+y\parallel \parallel x-y\parallel }{{\parallel x\parallel }^2+{\parallel y\parallel }^2}:x,y\in X,(x,y)\ne (0,0)\right\}.$$

$C_Z\left(X\right)$ and $C_{\mathrm{NJ}}\left(X\right)$ seem to be compatible. It is worth mentioning that Alonso and Martin [11] gave a counterexample that $C_Z\left(X\right)\ne C_{\mathrm{NJ}}\left(X\right)$.

The next constant, which is closely related to the new constant we studied, was defined by Gao. The constant $H\left(X\right)$ is defined as [12]

$$H\left(X\right)=sup\{min\{\parallel x+y\parallel ,\parallel 2x-y\parallel \}:x,y,x-y\in S(X\left)\right\}.$$

Listed below are some of the results of the constant $H\left(X\right)$ given in [12]:

(i)

For a Banach space, $H\left(X\right)\le 2$.

(ii)

If X is a Hilbert space, then $H\left(X\right)=\sqrt{3}$.

(iii)

If $H\left(X\right)<2$, then X is uniformly non-square.

Next, we give more properties of the $H\left(X\right)$ constant, because some of the techniques used in it only appeared after the $H\left(X\right)$ constant was introduced. The proof of Theorem 2 is based on the method published in 2001 by Kato et al.

Theorem 1.

Let Banach space X be finite-dimensional, if $H\left(X\right)=2$, then X is not strictly convex.

Proof. 

Assume that $H\left(X\right)=2$. Since the unit sphere of finite-dimensional Banach space is compact, so there exist $x_0,y_0,x_0-y_0\in S\left(X\right)$, such that $\parallel x_0+y_0\parallel =2$, which implies that point $\frac{x_0+y_0}{2}$ is not an extreme point of a closed unit sphere of X, so X is not strictly convex. □

Theorem 2.

Let X be a Banach space, then

$$2H\left(X\right)-2\le H\left(X^{*}\right)\le \frac{1}{2}H\left(X\right)+1.$$

Proof. 

For any $x,y,x-y\in S\left(X\right)$, we have $\parallel x+y\parallel \le \parallel x\parallel +\parallel y\parallel =2$, $\parallel 2x-y\parallel \le 2$, thus

$$\parallel x+y\parallel +\parallel 2x-y\parallel \le sup\{min\{\parallel x+y\parallel ,\parallel 2x-y\parallel \left\}\right\}+2.$$

For any $\epsilon >0$, there exist $x,y,x-y\in S\left(X\right)$, such that

$$min\{\parallel x+y\parallel ,\parallel 2x-y\parallel \}\ge H\left(X\right)-\epsilon .$$

Additionally, by Hahn–Banach Theorem, there exist functionals $u^{*},v^{*}\in S\left(X^{*}\right)$, such that

$$u^{*}(x+y)=\parallel x+y\parallel ,v^{*}(y-2x)=\parallel y-2x\parallel =\parallel 2x-y\parallel .$$

Thus,

$$\begin{array}{cc}\hfill H\left(X^{*}\right)& =sup\{\parallel u^{*}+v^{*}\parallel ,\parallel 2u^{*}-v^{*}\parallel \}\hfill \\ & \ge \parallel u^{*}+v^{*}\parallel +\parallel 2u^{*}-v^{*}\parallel -2\hfill \\ & \ge (u^{*}+v^{*})(y-x)+(2u^{*}-v^{*})\left(x\right)-2\hfill \\ & =u^{*}(x+y)+v^{*}(y-2x)-2\hfill \\ & =\parallel x+y\parallel +\parallel 2x-y\parallel -2\hfill \\ & \ge 2(min\{\parallel x+y\parallel ,\parallel 2x-y\parallel \left\}\right)-2\hfill \\ & \ge 2\left(H\right(X)-\epsilon )-2.\hfill \end{array}$$

Since $\epsilon$ can be arbitrarily small,

$$H\left(X^{*}\right)\ge 2H\left(X\right)-2.$$

To prove the right side of inequality, assume that $u^{*},v^{*}\in S\left(X^{*}\right)$, there exist $x,y,x-y\in S\left(X\right)$, such that

$$(u^{*}+v^{*})(y-x)>\parallel u^{*}+v^{*}\parallel -\epsilon ,(2u^{*}-v^{*})\left(x\right)>\parallel 2u^{*}-v^{*}\parallel -\epsilon .$$

Therefore,

$$\begin{array}{cc}\hfill sup\{min\{\parallel u^{*}+v^{*}\parallel ,\parallel 2u^{*}-v^{*}\parallel \left\}\right\}& \le \frac{1}{2}(\parallel u^{*}+v^{*}\parallel +\parallel 2u^{*}-v^{*}\parallel )\hfill \\ & \le \frac{1}{2}((u^{*}+v^{*})(y-x)+(2u^{*}-v^{*})\left(x\right)+2\epsilon )\hfill \\ & =\frac{1}{2}(u^{*}(x+y)+v^{*}(y-2x)+2\epsilon )\hfill \\ & \le \frac{1}{2}(\parallel u^{*}\parallel ·\parallel x+y\parallel +\parallel v^{*}\parallel ·\parallel 2x-y\parallel )+\epsilon \hfill \\ & =\frac{1}{2}(\parallel x+y\parallel +\parallel 2x-y\parallel )+\epsilon \hfill \\ & \le \frac{1}{2}sup\{min\{\parallel x+y\parallel ,\parallel 2x-y\parallel \left\}\right\}+1+\epsilon \hfill \\ & \le \frac{1}{2}H\left(X\right)+1+\epsilon .\hfill \end{array}$$

Since $\epsilon$ can be arbitrarily small, we prove the result as desired. □

3. The Constant ${\mathit{G}}_{\mathit{L}}\left(\mathit{X}\right)$

As was mentioned in the Introduction, the issues brought by the asymmetric structure are too tricky to tackle because many geometric properties of asymmetric geometric constants remain uncertain. In this section, we will introduce a new constant based on the constant $H\left(X\right)$ with an asymmetric structure. We begin by introducing the following key definition:

$$G_L\left(X\right)={sup\{\parallel x+y\parallel }^2{+\parallel 2x-y\parallel }^2:\parallel x\parallel =\parallel y\parallel =\parallel x-y\parallel =1\}.$$

The geometric background of $G_L\left(X\right)$ is shown in Figure 1: consider the unit sphere on the Euclidean plane with $\parallel x\parallel =\parallel y\parallel =\parallel y-x\parallel =1$. Assume that $\overrightarrow{AC}=x$, $\overrightarrow{AB}=y$, then $\overrightarrow{AE}=x+y$. Assume that $\overrightarrow{CB}=y-x$, then $\overrightarrow{DC}=2x-y$. Apparently, triangle $▵ABC$ is equilateral. Then, the hexagon with vertices $\pm x,\pm y,\pm (x-y)$ is an affine regular hexagon inscribed to the unit sphere of the 2-dimensional normed space. Moreover, $\overrightarrow{AD}=x-y$, $\overrightarrow{CE}=y$, $\overrightarrow{DE}=2x$. Since

$$\begin{array}{cc}\hfill 2(\parallel x{\parallel }^2+\parallel x-y{\parallel }^2)& =2\left(\Vert \frac{(2x-y)+y}{2}{\Vert }^2+\Vert \frac{(2x-y)-y}{2}{\Vert }^2\right)\hfill \\ & =2\left(2{∥\frac{2x-y}{2}∥}^2+2{∥\frac{y}{2}∥}^2\right)\hfill \\ & ={\parallel 2x-y\parallel }^2+{\parallel y\parallel }^2,\hfill \end{array}$$

therefore,

$${\overrightarrow{CD}}^2+{\overrightarrow{AB}}^2=2({\overrightarrow{AC}}^2+{\overrightarrow{BC}}^2)$$

holds, and then the quadrilateral $\square ACBD$ satisfies the parallelogram law. Similarly, we can deduce that the quadrilateral $\square ABEC$ satisfies the parallelogram law as well. In general, the quadrilateral $\square ACED$ can be described as half a regular hexagon.

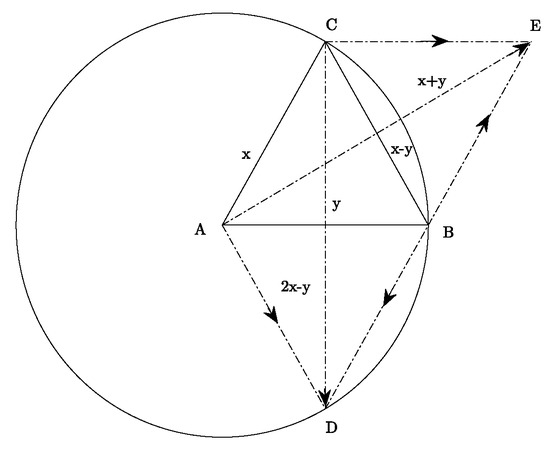
Figure 1. Geometric explanation on the unit sphere.

Corollary 1.

Let Banach space X be finite dimensional, if $G_L\left(X\right)=8$, then X is not strictly convex.

Example 1.

Let X be ${\ell }_{\infty }$ endowed with the norm ${\parallel x\parallel }_{\infty }={sup}_n\left|x_n\right|$ for $\left(x_n\right)\in {\ell }_{\infty }$. Then, $G_L\left({\ell }_{\infty }\right)=8$.

Assume that $x_0=(1,1,0,\dots ),y_0=(1,0,0,\cdots )\in S\left({\ell }_{\infty }\right)$, then $x_0-y_0=(0,1,0,\dots )\in S\left({\ell }_{\infty }\right)$. We can get

$$\begin{array}{cc}\hfill G_L\left({\ell }_{\infty }\right)& \ge \parallel x_0+y_0{\parallel }^2+{\parallel 2x_0-y_0\parallel }^2\hfill \\ & =2^2+2^2=8,\hfill \end{array}$$

which implies that $G_L\left({\ell }_{\infty }\right)=8$.

Example 2.

Let X be ${\mathbb{R}}^2$ endowed with the ${\ell }_{\infty }-{\ell }_1$ norm

$$\parallel x\parallel =\left\{\begin{array}{cc}\hfill {\parallel x\parallel }_{\infty }& if{x}_1{x}_2\ge 0,\\ \hfill {\parallel x\parallel }_1& if{x}_1{x}_2\le 0.\end{array}\right.$$

Let $x=(1,\frac{1}{2})$, $y=(\frac{1}{2},1)$, then $x-y=(\frac{1}{2},-\frac{1}{2})$.

Example 3.

Let X be ${\ell }_p,1<p<\infty$, then $G_L\left(X\right)\le 2{(2^p-1)}^{\frac{2}{p}}$ for $p\ge 2$ and $G_L\left(X\right)\le 2·3^{\frac{2}{p}}$ for $1\le p<2$.

Applying the Clarkson inequality that when $p\ge 2,x,y\in X$, we have

$$\begin{array}{cc}\hfill 2(\parallel x{\parallel }^p+\parallel y{\parallel }^p)& \le {\parallel x+y\parallel }^p+{\parallel x-y\parallel }^p\hfill \\ & \le (\parallel x\parallel +{\parallel y\parallel )}^p+|\parallel x\parallel -{\parallel y\parallel |}^p,\hfill \end{array}$$

when $1\le p<2,x,y\in X$, we have

$$\begin{array}{cc}\hfill 2(\parallel x{\parallel }^p+\parallel y{\parallel }^p)& \ge {\parallel x+y\parallel }^p+{\parallel x-y\parallel }^p\hfill \\ & \ge (\parallel x\parallel +{\parallel y\parallel )}^p+|\parallel x\parallel -{\parallel y\parallel |}^p.\hfill \end{array}$$

Then, we can deduce that when $p\ge 2,x,y,x-y\in S_X$,

$$\begin{array}{cc}\hfill {\parallel x+y\parallel }^p& \le (\parallel x\parallel +{\parallel y\parallel )}^p+|\parallel x\parallel -{\parallel y\parallel |}^p-{\parallel x-y\parallel }^p\hfill \\ & =2^p-1,\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\parallel 2x-y\parallel }^p& \le {(\parallel x\parallel +\parallel x-y\parallel )}^p{+|\parallel x\parallel -\parallel x-y\parallel |}^p-{\parallel x-(x-y)\parallel }^p\hfill \\ & =2^p-1,\hfill \end{array}$$

when $1\le p<2,x,y,x-y\in S_X$,

$$\begin{array}{cc}\hfill {\parallel x+y\parallel }^p& \le {2(\parallel x\parallel }^p+{\parallel y\parallel }^p{)-\parallel x-y\parallel }^p\hfill \\ & \le {2(\parallel x\parallel }^2+{\parallel y\parallel }^2{)-\parallel x-y\parallel }^2\hfill \\ & =3,\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\parallel 2x-y\parallel }^p& \le {2(\parallel x\parallel }^p{+\parallel x-y\parallel }^p{)-\parallel x-(x-y)\parallel }^p\hfill \\ & \le {2(\parallel x\parallel }^2{+\parallel x-y\parallel }^2{)-\parallel x-(x-y)\parallel }^2\hfill \\ & =3,\hfill \end{array}$$

as desired.

Proposition 1.

If X is an inner product space, then $G_L\left(X\right)=6$.

Proof. 

For any $x,y,x-y\in S\left(X\right)$, we have

$${\parallel x+y\parallel }^2={2(\parallel x\parallel }^2+{\parallel y\parallel }^2{)-\parallel x-y\parallel }^2=3,$$

$${\parallel 2x-y\parallel }^2={2(\parallel x\parallel }^2{+\parallel x-y\parallel }^2{)-\parallel x-(x-y)\parallel }^2=3,$$

which implies that $G_L\left(X\right)=6$. □

Theorem 3.

For any Banach space X, we have $\frac{9}{2}\le G_L\left(X\right)\le 8$.

Proof. 

Since

$$\begin{array}{cc}\hfill \parallel x+y\parallel +\parallel 2x-y\parallel & \ge \parallel x+y+2x-y\parallel \hfill \\ & =\parallel 3x\parallel \hfill \\ & =3,\hfill \end{array}$$

hence

$$\parallel 2x-y\parallel \ge 3-\parallel x+y\parallel .$$

Then, we can deduce that

$$\begin{array}{cc}\hfill {\parallel x+y\parallel }^2+{\parallel 2x-y\parallel }^2& \ge {\parallel x+y\parallel }^2+{(3-\parallel x+y\parallel )}^2\hfill \\ & ={2\parallel x+y\parallel }^2+9-6\parallel x+y\parallel \hfill \\ & =2\left[{\left(\parallel x+y\parallel -\frac{3}{2}\right)}^2+\frac{9}{4}\right]\hfill \\ & \ge \frac{9}{2}.\hfill \end{array}$$

On the other hand, by $\parallel 2x-y\parallel \le \parallel x\parallel +\parallel x-y\parallel =2$, it is implied that $G_L\left(X\right)\le 8$, as desired. □

Proposition 2.

For any Banach space X, we have

$$4{(1-{\delta }_X\left(1\right))}^2\ge G_L\left(X\right)-4.$$

Proof. 

First, note that

$$\begin{array}{cc}\hfill {\delta }_X\left(t\right)& =inf\left\{1-\frac{1}{2}\parallel x+y\parallel :\parallel x\parallel =\parallel y\parallel =1,\parallel x-y\parallel \ge \epsilon \right\}\hfill \\ & =inf\left\{1-\frac{1}{2}\parallel x+y\parallel :\parallel x\parallel =\parallel y\parallel =1,\parallel x-y\parallel =\epsilon \right\}.\hfill \end{array}$$

Then, we can deduce that

$${\delta }_X(\parallel x-y\parallel )\le 1-\frac{\parallel x+y\parallel }{2}$$

for any $\parallel x\parallel =\parallel y\parallel =\parallel x-y\parallel =1$.

Applying the triangle inequality, we have the following inequality estimate:

$$\begin{array}{cc}\hfill (1-{\delta }_X(\parallel x-{y\parallel \left)\right)}^2+4& \ge \frac{{\parallel x+y\parallel }^2}{4}+1+3\hfill \\ & =\frac{1}{4}{(\parallel x+y\parallel }^2+{\parallel x\parallel }^2{+\parallel x-y\parallel }^2+2\parallel x\parallel \parallel x-y\parallel )+3\hfill \\ & \ge \frac{1}{4}{(\parallel x+y\parallel }^2{+\parallel 2x-y\parallel }^2)+3\hfill \end{array}$$

for any $\parallel x\parallel =\parallel y\parallel =\parallel x-y\parallel =1$, and hence

$$(1-{\delta }_X(\parallel x-{y\parallel \left)\right)}^2+4\ge \frac{1}{4}{(\parallel x+y\parallel }^2{+\parallel 2x-y\parallel }^2)+3$$

for any $\parallel x\parallel =\parallel y\parallel =\parallel x-y\parallel =1$. This means that

$$4{(1-{\delta }_X\left(1\right))}^2\ge G_L\left(X\right)-4,$$

as desired. □

Proposition 3.

For any Banach space X, we have

$$H{\left(X\right)}^2\le \frac{1}{2}{G}_L\left(X\right).$$

Proof. 

Consider points x and y in space X, we have the following estimates

$$\begin{array}{cc}\hfill min\{\parallel x+y{\parallel }^2,\parallel 2x-y{\parallel }^2\}& \le \frac{{(\parallel x+y\parallel +\parallel 2x-y\parallel )}^2}{4}\hfill \\ & \le \frac{{\parallel x+y\parallel }^2+{\parallel 2x-y\parallel }^2}{2},\hfill \end{array}$$

as desired. □

Theorem 4.

Let X be a Banach space, we have (i)⇒(ii) ⇒(iii).

(i) 

$G_L\left(X\right)<8$.

(ii) 

$H\left(X\right)<2$.

(iii) 

X is uniformly non-square.

Proof. 

(i)⇒ (ii). Applying Proposition 3.

(ii)⇒ (iii). Using the result in ([12], p. 243, Theorem 2.10), if $H\left(X\right)<2$, then X is uniformly non-square. □

Corollary 2.

If X is not super-reflexive, then $G_L\left(X\right)=8$.

4. The Constant ${\mathit{G}}_{\mathit{L}}(\mathit{X},\mathit{p})$ and ${\mathit{C}}_{\mathit{L}}\left(\mathit{X}\right)$

Next, we will introduce two generalizations of constants and consider their related properties.

Given any Banach space X and a number $p\in [1,\infty )$, another geometric constant $G_L(X,p)$ is defined by

$$G_L(X,p)={sup\{\parallel x+y\parallel }^p{+\parallel 2x-y\parallel }^p:\parallel x\parallel =\parallel y\parallel =\parallel x-y\parallel =1\}.$$

Proposition 4.

For any Banach space X, we have $2^{1-p}·3^p\le G_L(X,p)\le 2^{p+1}$.

Proof. 

By the convexity of the function $f\left(u\right)=u^p$ on $[0,\infty )$, we have the following inequality:

$$\frac{{\parallel x+y\parallel }^p+{\parallel 2x-y\parallel }^p}{2}\ge {\left(\frac{\parallel x+y\parallel +\parallel 2x-y\parallel }{2}\right)}^p.$$

Then, we can deduce that

$$\begin{array}{cc}\hfill \frac{{\parallel x+y\parallel }^p+{\parallel 2x-y\parallel }^p}{2}& \ge {\left(\frac{\parallel x+y\parallel +\parallel 2x-y\parallel }{2}\right)}^p\hfill \\ & \ge {\left(\frac{\parallel x+y+2x-y\parallel }{2}\right)}^p\hfill \\ & =2^{-p}·3^p,\hfill \end{array}$$

hence

$${\parallel x+y\parallel }^p+{\parallel 2x-y\parallel }^p\ge 2^{1-p}·3^p.$$

On the other hand, according to the triangle inequality, we can have the following estimates

$$\begin{array}{cc}\hfill {\parallel x+y\parallel }^p+{\parallel 2x-y\parallel }^p& \le (\parallel x\parallel +{\parallel y\parallel )}^p+{(\parallel x\parallel +\parallel x-y\parallel )}^p\hfill \\ & =2^{p+1}.\hfill \end{array}$$

This completes the proof. □

Theorem 5.

For any $1<p<\infty$ and any Banach space X, the following inequality holds:

$$H\left(X\right)\le 2^{-\frac{1}{p}}\sqrt[p]{G_L(X,p)}.$$

Proof. 

Indeed, if $1<p<\infty$, then for any $x,y,x-y\in S\left(X\right)$, we have

$$2(min\{\parallel x+y\parallel ,\parallel 2x-{y\parallel \left\}\right)}^p\le {\parallel x+y\parallel }^p+{\parallel 2x-y\parallel }^p,$$

which implies that

$$min\{\parallel x+y\parallel ,\parallel 2x-y\parallel \}\le 2^{-\frac{1}{p}}\sqrt[p]{G_L(X,p)},$$

and the proof is completed. □

Combining our new constant $G_L\left(X\right)$ with the constant $C_{\mathrm{Z}}\left(X\right)$, we define the $C_L\left(X\right)$ constant as follows:

$$C_L\left(X\right)=sup\{\parallel x+y\parallel ·\parallel 2x-y\parallel :\parallel x\parallel =\parallel y\parallel =\parallel x-y\parallel =1\}.$$

Proposition 5.

Let X be a Banach space, then

$$C_L\left(X\right)\le \frac{1}{2}{G}_L\left(X\right).$$

Proof. 

Consider points x and y in space X, we have the following estimates

$$2\parallel x+y\parallel ·\parallel 2x-y\parallel \le {\parallel x+y\parallel }^2+{\parallel 2x-y\parallel }^2,$$

as desired. □

Example 4.

Let X be ${\ell }_{\infty }$ endowed with the norm ${\parallel x\parallel }_{\infty }={sup}_n\left|x_n\right|$ for $\left(x_n\right)\in {\ell }_{\infty }$. Then, $C_L\left({\ell }_{\infty }\right)=4$.

Assume that $x=(1,1,0,\dots ),y=(1,0,0,\cdots )\in S\left({\ell }_{\infty }\right)$, then $x-y=(0,1,0,\dots )\in S\left({\ell }_{\infty }\right)$. Then, $C_L\left({\ell }_{\infty }\right)\ge \parallel x+y\parallel ·\parallel 2x-y\parallel =2·2=4$. Since $C_L\left({\ell }_{\infty }\right)\le \frac{1}{2}{G}_L\left({\ell }_{\infty }\right)=4$, so $C_L\left({\ell }_{\infty }\right)=4$.

Proposition 6.

For any Banach space X, we have

$$C_L\left(X\right)\ge \frac{1}{2}(9-G_L\left(X\right)).$$

Proof. 

Since

$$\begin{array}{cc}\hfill \parallel x+y\parallel +\parallel 2x-y\parallel & \ge \parallel x+y+2x-y\parallel \hfill \\ & =\parallel 3x\parallel \hfill \\ & =3,\hfill \end{array}$$

hence

$${\parallel 2x-y\parallel }^2{+\parallel x+y\parallel }^2+2\parallel 2x-y\parallel \parallel x+y\parallel \ge 9.$$

Then, we can deduce that

$$\parallel x+y\parallel \parallel 2x-y\parallel \ge \frac{1}{2}(9-G_L\left(X\right)),$$

which implies that $C_L\left(X\right)\ge \frac{1}{2}(9-G_L\left(X\right))$, as desired. □

5. Conclusions

In light of the geometric constant $H\left(X\right)$ proposed by Gao, we explore the geometric properties of it in depth by discussing the strict convexity of it, together with representing the relationship between it and its dual. Meanwhile, we introduce a new geometric constant $G_L\left(X\right)$, which is based on the equilateral triangle in the unit sphere. With the relationships among $G_L\left(X\right)$ and some other basic geometric constants through some inequalities, we manage to describe several geometric properties, such as strict convexity, uniformly non-square properties, etc. Furthermore, we continue to study the generalized forms of it, $G_L(X,p)$ and $C_L\left(X\right)$ explicitly, via exploration of their relations with the aforementioned geometric constants, such as $H\left(X\right)$ and $G_L\left(X\right)$. Nevertheless, there are still plenty of problems that remain to be discovered. How can $H\left(X\right)$ and $G_L\left(X\right)$ be employed to characterize more geometric properties? Are there any more relationships among $G_L\left(X\right)$ and some other geometric constants awaiting more discussion? In the future, we will continue to explore the geometric properties of these two constants, and hopefully obtain better results.