Symmetries and Covariant Poisson Brackets on Presymplectic Manifolds ^†

Abstract

As the space of solutions of the first-order Hamiltonian field theory has a presymplectic structure, we describe a class of conserved charges associated with the momentum map, determined by a symmetry group of transformations. A gauge theory is dealt with by using a symplectic regularization based on an application of Gotay’s coisotropic embedding theorem. An analysis of electrodynamics and of the Klein–Gordon theory illustrate the main results of the theory as well as the emergence of the energy–momentum tensor algebra of conserved currents.

1. Introduction

Symmetries play a crucial role in the development and analysis of physical theories. Beyond the paradigmatic examples in the classical field theory of Einstein’s equations of general relativity, or the Yang–Mills equation for gauge fields, symmetries are used, for instance, to determine the form of the Lagrangian (or respectively of the Hamiltonian) function within the Lagrangian (respectively, Hamiltonian) formulation theory (an interesting example, in this perspective, is given by Utiyama’s theorem). Symmetries are also used to uncover significant global properties of a theory itself, such as the existence of different phases or sectors, or even as an effective tool to analyze its quantum aspects (ranging from the study of the properties of quantum states, to the study of the renormalizability or to obtain definite predictions when anomalies arise).

In most cases, these symmetries of interest can be termed “geometrical”, as they emerge from underlying geometrical structures (consider, for instance, geometrical symmetries of the space–time of the theory). This is the case of the relativistic covariance of a field theory associated with the action of Poincaré group on the (vector) bundle used to formulate the theory itself (see, Section 4), or of the invariance under the action of a gauge group, described in terms of identity-based automorphisms of a suitable (principal) bundle (see Section 4.3). Other examples of geometrical symmetries include conformal invariance, which is instrumental in the analysis of quantum field theories in two dimensions, or the group of causal diffeomorphisms of a space–time, in the case of theories of gravitation.

There is another use of symmetries that runs parallel to the development of the previous physical motivations. They are instrumental, from a mathematical point of view, to analyze the problem of the integrability of differential equations. Indeed, they emerge from the discovery of integrable hierarchies of non-linear partial differential equations, such as the KdV equation or the KP hierarchy. In such cases, the integrability properties of the model are associated with rich geometrical data, such as a bi-Hamiltonian structure or a Lax representation of the equation, which often can be interpreted as the existence of families of transformations on the space of solutions of the equations. Examples of such symmetries are related to the Miura transform in the KdV case, to the Backlünd transformations, or to Darboux transformations, for integrable systems obtained from a factorization property.

These aspects, and many more, have been extensively analyzed in the last two centuries, both within the mathematical and theoretical physics literature: a (far from exhaustive) list of contributions where the previous ideas have been developed include [1,2,3,4,5,6,7,8,9,10,11,12,13,14], where Noether’s theorems (that is the relation between symmetries and the so called conservation laws) are also elucidated. In particular, in recent references where classical field theories were analyzed within the setting of jet bundles and their duals, conserved currents associated with symmetries of an action functional are modeled as $(m-1)$-forms on a fiber bundle underlying the theory (with m the dimension of the space–time in which the theory is developed, see, for instance, [8,15,16,17]).

In the present paper, we show how the above-mentioned conserved currents emerge from the momentum map associated with a symmetry group action on the space of solutions of the theory. In particular, we focus on the first-order Hamiltonian field theories, whose setting is developed in [16,18].

The space of solutions of first-order Hamiltonian field theories is a presymplectic manifold, which is locally diffeomorphic (within the multisymplectic formalism) to the space of integral curves of a presymplectic system constructed on a space of fields on an arbitrary slice of the space–time of the theory (see Section 3, Proposition 2, and [15,18,19,20]). It turns out that a class of conserved charges, defined directly on the space of solutions of the theory, is defined in terms of the momentum map associated to a suitable symmetry group, extending the well-known Hamiltonian version of Noether’s theorem (see, for instance, [21] for a comprehensive review) to a global presymplectic covariant description of field theories.

Gauge theories are identified with theories such that the space of solutions have a presymplectic structure with non-trivial characteristic distribution. The conserved charges associated with a symmetry groups of the theory are studied within a symplectic formalism, i.e., restoring its natural algebraic structure by using the symplectic regularization of the theory provided by the coisotropic embedding theorem (see, for instance, [22]). We find it relevant that one of the advantages of this approach is that it allows considering, within the same formalism, Noether’s first and second theorems, the difference determined by the intersection of the orbits of the group, and the characteristic distribution of the presymplectic structure.

The paper is organized as follows. The first section of the paper (Section 2) is devoted to reviewing the basic structures of the theory of canonical symmetry groups on symplectic and presymplectic manifolds, respectively, and, in the second case, their symplectic realizations, by using the equivariant extension of the coisotropic embedding theorem. Section 3 is devoted to succinctly reviewing the geometry of the space of solutions of a first-order Hamiltonian field theory and, in particular, its natural presymplectic structure, which is the arena where we construct a theory of symmetries. In Section 4, we apply the abstract ideas developed in Section 2 to the Euler–Lagrange space of a Hamiltonian field theory, described in Section 3, by considering three significant examples: a finite-dimensional system, the free-relativistic particle (Section 4.1), a symplectic system, the Klein–Gordon theory (Section 4.2), and a gauge theory, free electrodynamics (Section 4.3).

2. Symmetries for Presymplectic Dynamics

In this section, we review the geometrical theory of symmetries that can be constructed for dynamical systems, admitting a symplectic or presymplectic formulation. We refer to [6,7,21], and references therein, for a more detailed exposition.

2.1. Presymplectic Manifolds

A presymplectic manifold $(\mathcal{M},\omega )$ is a smooth manifold $\mathcal{M}$, equipped with a closed two-form $\omega$, i.e., such that $\mathrm{d}\omega =0$. By “manifold”, we mean a smooth (not necessarily finite) dimensional manifold. In the infinite dimensional case, $\mathcal{M}$ is assumed to be a paracompact, second countable, Hausdorff Banach manifold (see, for instance, [23,24], where both cases are analyzed) so that a rigorous definition of the tangent $\mathbf{T}\mathcal{M}$ and the cotangent ${\mathbf{T}}^{\star }\mathcal{M}$ bundles over $\mathcal{M}$ exist, as well as the standard Cartan differential calculus. Associated to the two-form $\omega$, it is immediate to define its characteristic set:

$${\ker }_m\omega =\left\{X_m\in {\mathbf{T}}_m\mathcal{M}:{\omega }_m(X_m,V_m)=0\forall V_m\in {\mathbf{T}}_m\mathcal{M}\right\},$$

(1)

at any point $m\in \mathcal{M}$. When this set is zero, $(\mathcal{M},\omega )$ is said to be weakly symplectic; when $\omega$ induces an isomorphism between ${\mathbf{T}}_m\mathcal{M}$ and ${\mathbf{T}}_m^{\star }\mathcal{M}$, then $(\mathcal{M},\omega )$ is said strongly symplectic. It is easy to see that such notions coincide when $\mathcal{M}$ is finite dimensional, or more generally when the Banach space modeling $\mathcal{M}$ is isomorphic to its Banach dual. When the characteristic set ${ker}_m\omega$ is not zero and defines a vector subbundle of $\mathbf{T}\mathcal{M}$, it will be called the characteristic bundle. We denote it by $\mathbf{K}\to \mathcal{M}$, whereas we denote by $K_m$ the distribution ${\ker }_m\omega$ on $\mathcal{M}$, which we call the characteristic distribution. Defined as the kernel of a closed two-form, such characteristic distribution turns to be involutive, i.e., if X and $X^{\prime }$ are vector fields in K, its Lie bracket $[X,X^{\prime }]$ is again in K. Thus, the space of smooth sections of $\mathbf{K}$, say $\Gamma (\mathbf{K})$, is a Lie algebra (possibly infinite dimensional). The space of leaves of the distribution K gives rise to a foliation of $\mathcal{M}$. A leaf $\mathcal{N}$ is a maximal connected integral submanifold of the distribution K. The space of leaves, denoted by $\mathcal{M}/K$, carries a natural topological structure defined as the coarsest topology that makes the canonical projection:

$$\mathrm{pr}:\mathcal{M}\to \mathcal{M}/K:m\mapsto {\mathcal{N}}_m,$$

(2)

continuous, where ${\mathcal{N}}_m$ is the leaf of K passing through m. In general, $\mathcal{M}/K=:{\mathcal{M}}_{\omega }$ is not a smooth manifold, not even Hausdorff. When this is the case, and when the map $\mathrm{pr}$ is a submersion, then ${\mathcal{M}}_{\omega }$ inherits a canonical symplectic structure, ${\omega }_K$, defined as

$${\omega }_K(\tilde{X},\tilde{Y})=\omega (X,Y)$$

where $\tilde{X},\tilde{Y}\in {\mathbf{T}}_{\mathcal{N}}{\mathcal{M}}_{\omega }$ and $X,Y\in {\mathbf{T}}_m\mathcal{M}$, with $\mathrm{pr}(m)=\mathcal{N}$ and $X,Y$ two arbitrary lifts of $\tilde{X},\tilde{Y}$ to $\mathcal{M}$.

2.2. Hamiltonian Systems

A Hamiltonian system on a presymplectic manifold $(\mathcal{M},\omega )$ is defined as a triple $(\mathcal{M},\omega ,H),$ where H is a smooth real valued function on $\mathcal{M}$ called a Hamiltonian, with a corresponding Hamiltonian vector field $\Gamma$ on $\mathcal{M}$ satisfying:

$$i_{\Gamma }\omega =\mathrm{d}H.$$

(3)

When $\omega$ is not weakly symplectic, the vector field $\Gamma$ (if it exists) is undetermined as $\Gamma +Z$ satisfies (3) for any $Z\in K$. A sufficient condition for the existence of a Hamiltonian vector field $X_H=\Gamma$ is clearly that $Z(H)=0$, for all $Z\in K$. When such a condition is fulfilled, we say that the dynamics is global on $\mathcal{M}$. When this is not the case, the relation

$$Z(H)=0,$$

for any $Z\in K$ selects a subset of $\mathcal{M}$ on which a vector field $\Gamma$ can be obtained. The further condition that $\Gamma$ is tangent to such a subset may provide a further constraint. This is the first step of the so-called presymplectic constraint algorithm (PCA) [25]. The subset (which is assumed to be a submanifold) ${\mathcal{M}}_1=\left\{m\in \mathcal{M}:Z_m(H)=0\forall Z\in K\right\}$ is called the primary constraint submanifold of the presymplectic Hamiltonian system $(\mathcal{M},\omega ,H)$. The restriction of $\omega$ and H to ${\mathcal{M}}_1$ determines a new presymplectic system provided that ${\mathcal{M}}_1$ is a smooth submanifold of $\mathcal{M}$, which we denote by $({\mathcal{M}}_1,{\omega }_1,H_1)$. Denoting by $K_1$, the characteristic distribution of ${\omega }_1$, we define recursively:

$$\begin{array}{cc}\hfill {\mathcal{M}}_{k+1}& =\left\{m\in {\mathcal{M}}_k:Z_m(H_k)=0\forall Z\in K_k\right\}k=1,2,\dots \hfill \\ \hfill {\omega }_{k+1}& ={\omega }_k{|}_{{\mathcal{M}}_{k+1}};\hfill \\ \hfill H_{k+1}& =H_k{|}_{{\mathcal{M}}_{k+1}};\hfill \\ \hfill K_{k+1}& =\ker {\omega }_{k+1}.\hfill \end{array}$$

(4)

At each step of the previous process, it will be assumed that ${\mathcal{M}}_k$ is a manifold, so that $({\mathcal{M}}_k,{\omega }_k)$ is a (presymplectic) manifold. Often it is assumed that the PCA stops after a finite number of steps, i.e., ${\mathcal{M}}_r={\mathcal{M}}_{r+1}$ for some r, implying that ${\omega }_r={\omega }_{r+1}$. The manifold $({\mathcal{M}}_r,{\omega }_r)$ will be called the final constraints manifold. It follows that the system $({\mathcal{M}}_r,{\omega }_r,H_r)$ is consistent; that is, there is a solution to (3) all over ${\mathcal{M}}_r$. In the subsequent analysis, it will be assumed that our presymplectic system is a consistent Hamiltonian system obtained after a PCA analysis if needed.

2.3. Action of Lie Groups on Presymplectic Manifolds and the Momentum Map

Consider a Lie group acting on $\mathcal{M}$, namely, consider a Lie group $\mathcal{G}$ together with a representation of it on $\mathcal{M}$:

$$\Phi :\mathcal{G}\to \mathcal{T}(\mathcal{M}):g\mapsto {\Phi }_g,$$

(5)

where $\mathcal{T}(\mathcal{M})$ is the set of maps from $\mathcal{M}$ to itself. Such a map is a representation if it is a homomorphism, i.e., if:

$${\Phi }_{g·h}={\Phi }_g\circ {\Phi }_h,$$

(6)

where · is the composition law of $\mathcal{G}$ and ∘ is the composition of two maps in $\mathcal{T}(\mathcal{M})$. We will refer to ${\Phi }_g$ as the action of $\mathcal{G}$ on $\mathcal{M}$. It will be assumed that the action is smooth; that is that the map ${\Phi }_m:\mathcal{G}\to \mathcal{M}$, given by ${\Phi }_m(g)={\Phi }_g(m)$ is smooth for all $m\in \mathcal{M}$. The action of a Lie group on $(\mathcal{M},\omega )$ is said to be canonical if ${\Phi }_g^{\star }\omega =\omega \forall g\in \mathcal{G}$. Equivalently, the action is canonical if ${\mathfrak{L}}_{X_{\xi }}\omega =0\forall \xi \in \mathfrak{g}$ where $X_{\xi }$ is the Killing vector field on $\mathcal{M}$ corresponding to the element $\xi$ in the Lie algebra $\mathfrak{g}$ of $\mathcal{G}$. The action is said to be Hamiltonian if a function $J_{\xi }$ on $\mathcal{M}$ exists, such that:

$$i_{X_{\xi }}\omega =\mathrm{d}{J}_{\xi }.$$

(7)

It is easy to see that if the action of $\mathcal{G}$ is Hamiltonian, then it is canonical. The converse is not true: there exist canonical actions that are not Hamiltonians (the form $i_{X_{\xi }}\omega$ is closed, not necessarily exact). In this case, the action is also said to be weakly Hamiltonian.

When the action of $\mathcal{G}$ on $\mathcal{M}$ is Hamiltonian, the map $\mathbb{J}$ defined by:

$$\mathbb{J}:\mathcal{M}\to {\mathfrak{g}}^{\star }:\langle \mathbb{J}(m),\xi \rangle =J_{\xi }(m)m\in \mathcal{M},\xi \in \mathfrak{g},$$

(8)

is well defined, and is called the momentum map of the action of $\mathcal{G}$ on $(\mathcal{M},\omega )$. Here, ${\mathfrak{g}}^{\star }$ denotes the dual of the Lie algebra of $\mathcal{G}$. If the Lie algebra is infinite-dimensional, ${\mathfrak{g}}^{\star }$ is the topological dual.

The functions $J_{\xi }$ can be determined up to constants. Even more, the identity $[X_{\xi },X_{\zeta }]=X_{[\xi ,\zeta ]}$ for $\xi ,\zeta \in \mathfrak{g}$ implies that the map $\mathbb{J}$ is equivariant up to a ${\mathfrak{g}}^{\star }$-valued 1-cocycle on $\mathcal{G}$, with respect to the co-adjoint action of $\mathcal{G}$ on ${\mathfrak{g}}^{\star }$ (see [21] (Proposition 4.5.21)). If the momentum map $\mathbb{J}$ is equivariant, i.e., if:

$$\mathbb{J}({\Phi }_g·m)={\mathrm{Ad}}_g^{\star }(\mathbb{J}(m))\forall g\in \mathcal{G},m\in \mathcal{M},$$

(9)

we say that the action of $\mathcal{G}$ on $(\mathcal{M},\omega )$ is strongly Hamiltonian.

The Lie group $\mathcal{G}$ is said to be a symmetry group for the Hamiltonian system $(\mathcal{M},\omega ,H)$ if the action of $\mathcal{G}$ on $(\mathcal{M},\omega )$ is canonical (or, a fortiori, Hamiltonian/strongly Hamiltonian), and if $\mathcal{G}$ is a symmetry for H, i.e., $H_{{\Phi }_g(m)}=H_m$, for all $g\in \mathcal{G},\forall m\in \mathcal{M}$. The latter condition is equivalent to say that H is invariant, with respect to the action of $\mathcal{G}$ on $\mathcal{M}$, i.e., $X_{\xi }(H)=0\forall \xi \in \mathfrak{g}$. The converse also holds, i.e., $X_{\xi }(H)=0\forall \xi \in \mathfrak{g}$ implies that $\mathcal{G}$ is a symmetry for H, provided that $\mathcal{G}$ is connected.

If $\mathcal{G}$ acts canonically on the presymplectic manifold $(\mathcal{M},\omega )$, it preserves the characteristic foliation, i.e.,

$${{\Phi }_g}_{\star }{K}_m\subseteq K_{{\Phi }_g(m)}\forall g\in \mathcal{G},\forall m\in \mathcal{M}.$$

(10)

Then, the $\mathcal{G}$-invariance of K implies that $[X_{\xi },K]\subseteq K$$\forall \xi \in \mathfrak{g}$.

Now, let F and G be two functions on $\mathcal{M}$, such that there exist vector fields $X_F$ and $X_G$, such that $i_{X_F}\omega =\mathrm{d}F$ and $i_{X_G}\omega =\mathrm{d}G$ (i.e., such that $Z(F)=Z(G)=0$$\forall Z\in K$). We define the (presymplectic) Poisson bracket between F and G as:

$$\{F,G\}=\omega (X_F,X_G)=X_G(F)=-X_F(G).$$

(11)

It turns out that this bracket is well-defined, bilinear, satisfies the Jacobi identity (because the map $\xi \mapsto X_{\xi }$ is a homomorphism of Lie algebras) and the Leibniz rule (because $\mathrm{d}(FG)=(\mathrm{d}F)G+F\mathrm{d}G$). Moreover, if the action of $\mathcal{G}$ on $(\mathcal{M},\omega )$ is strongly Hamiltonian, then it follows from (9) that:

$$\{J_{\xi },J_{\zeta }\}=J_{[\xi ,\zeta ]},$$

(12)

i.e., the components of the momentum map close a Lie algebra, called the algebra of currents of the symmetry.

If $\mathcal{G}$ is a strongly Hamiltonian symmetry group of the presymplectic Hamiltonian system $(\mathcal{M},\omega ,H)$, we get:

$$0=X_{\xi }(H)=i_{X_{\xi }}\mathrm{d}H=\omega (X_H,X_{\xi })=\{H,J_{\xi }\}=-\{J_{\xi },H\}=-i_{X_H}{i}_{X_{\xi }}\omega =-X_H(J_{\xi })=0,$$

(13)

i.e.,

$$X_{\xi }(H)=-X_H(J_{\xi })=0,$$

(14)

which is the particular form of Noether’s theorem in this setting (any strongly Hamiltonian infinitesimal symmetry, $X_{\xi }(H)=0$, defines a constant of the motion, $X_H(J_{\xi })=0$, and vice-versa).

The sections Z of the characteristic distribution K define a Lie algebra (possibly infinite-dimensional). If the Lie algebra $\Gamma (K)$ can be integrated, i.e., there is a group $\mathcal{K}$ (possibly infinite-dimensional) whose Lie algebra is $\Gamma (K)$, then it will be called the gauge group of transformations of the theory (that in some cases can be identified with the group of, geometric, gauge transformations of the theory, see Section 4).

Functions that are constant along the leaves of the characteristic distribution are called the (classical) observables of the theory, and if the quotient space $\mathcal{M}/K$ is a manifold, they are in one-to-one correspondence with smooth functions on $\mathcal{M}/K$, i.e., $K(F)=0$ iff $F=\mathrm{pr}f$ for some $f:\mathcal{M}/K\to \mathbb{R}$. Moreover, in such a situation

$$\{F,G\}={\mathrm{pr}}^{\star }\{f,g\},$$

where $F={\mathrm{pr}}^{\star }f$ and $G={\mathrm{pr}}^{\star }g$, while $\{f,g\}$ is the Poisson bracket on $\mathcal{M}/K$ with respect to the induced symplectic structure on $\mathcal{M}/K$.

Getting rid of the gauge degrees of freedom amounts to pass to the quotient space $\mathcal{M}/K$ (note that the canonical action of the group $\mathcal{G}$ passes to the quotient too because of (10), and the induced action on the quotient symplectic manifold is canonical/Hamiltonian/ strongly Hamiltonian, respectively). Since such a quotient is in general quite singular (one of the most interesting ways to deal with such singularity is to study it within a cohomological approach [26]), we prefer, here, to consider a suitable symplectic realization of the presymplectic manifold $(\mathcal{M},\omega )$. This is the content of the following section.

2.4. The Coisotropic Embedding Theorem

To this aim, we analyze an equivariant version of the coisotropic embedding theorem stated by M. Gotay [22,27]. The main idea is that, given a presymplectic manifold $(\mathcal{M},\omega )$, it is possible to construct, in a canonical way, a symplectic manifold $(\mathcal{P},{\omega }_{\mathcal{P}})$ and an embedding $\mathfrak{i}:\mathcal{M}\hookrightarrow \mathcal{P}$, such that $(\mathcal{M},\omega )$ is a coisotropic submanifold of $(\mathcal{P},{\omega }_{\mathcal{P}})$, i.e., ${\mathfrak{i}}^{\star }{\omega }_{\mathcal{P}}=\omega$. Such a manifold $\mathcal{P}$ can be constructed explicitly as a tubular neighborhood of the zero section of the dual of the characteristic bundle of $\mathcal{M}$, $\mathbf{K}$, i.e., of the bundle ${\mathbf{K}}^{\star }\to \mathcal{M}$. Note that the tangent bundle of ${\mathbf{K}}^{\star }\to \mathcal{M}$ along the zero section, we denote by ${\mathbf{T}}_{\mathcal{M}}{\mathbf{K}}^{\star }$, can be decomposed as:

$${\mathbf{T}}_{\mathcal{M}}{\mathbf{K}}^{\star }={\mathbf{K}}^{\star }\oplus \mathbf{T}\mathcal{M},$$

(15)

i.e., at each point $(m,0)=0_m$, we have:

$${\mathbf{T}}_{0_m}{\mathbf{K}}^{\star }\simeq K_m^{\star }\oplus {\mathbf{T}}_m\mathcal{M}=K_m^{\star }\oplus K_m\oplus W_m,$$

(16)

where $W_m$ is a complementary subspace to $K_m\subset {\mathbf{T}}_m\mathcal{M}$, i.e., ${\mathbf{T}}_m\mathcal{M}=K_m\oplus W_m$. Then $W_m$ is a symplectic subspace of $({\mathbf{T}}_m\mathcal{M},{\omega }_m)$ and we can define a (linear) symplectic form on ${\mathbf{T}}_{0_m}{\mathbf{K}}^{\star }=:{\mathbf{T}}_{0_m}\mathcal{P}$ as follows:

$$\begin{array}{cc}\hfill {\omega }_{\mathcal{P}}(W\oplus Z\oplus \mu ,W^{\prime }\oplus Z^{\prime }\oplus {\mu }^{\prime })& =\omega (W,W^{\prime })+\langle \mu ,Z^{\prime }\rangle -\langle {\mu }^{\prime },Z\rangle \hfill \\ & W,W^{\prime }\in W_m,Z,Z^{\prime }\in K_m,\mu ,{\mu }^{\prime }\in K_m^{\star }.\hfill \end{array}$$

(17)

Such a linear symplectic form along the subbundle ${\mathbf{T}}_{\mathcal{M}}{\mathbf{K}}^{\star }$ can be extended to a symplectic form on a tubular neighborhood of the zero section of ${\mathbf{K}}^{\star }\to \mathcal{M}$ and it gives the symplectic form we are looking for (note that $\mathcal{M}\hookrightarrow \mathcal{P}\subset {\mathbf{K}}^{\star }$ is canonically embedded in ${\mathbf{K}}^{\star }$, and ${\omega }_{\mathcal{P}}{|}_{\mathcal{M}}=\omega$). Local coordinates on $(\mathcal{P},{\omega }_{\mathcal{P}})$ can be chosen as follows. Let $\left\{E_a\right\}$ be a local frame on K, then $\mu \in K^{\star }$ can be written as $\mu ={\mu }_a{E}^a$, where $E^a$ is the dual frame of $E_a$. Around any point on a regular leaf of the foliation K we can find coordinates $(w^{\alpha },Z^a)$, such that $w^{\alpha }$ are transverse coordinates and $Z^a$ are such that $Z=Z^a{E}_a$ is a tangent vector in K. Then we get:

$${\omega }_{\mathcal{P}}={\omega }_{\alpha \beta }\mathrm{d}{w}^{\alpha }\wedge \mathrm{d}{w}^{\beta }+\mathrm{d}{Z}^a\wedge \mathrm{d}{\mu }_a.$$

(18)

Moreover, the embedding $\mathfrak{i}:\mathcal{M}\hookrightarrow \mathcal{P}$ is described by ${\mu }_a=0$.

If the action of $\mathcal{G}$ on $(\mathcal{M},\omega )$ is strongly Hamiltonian, then there is a lift of such action to ${\mathbf{K}}^{\star }$. The lift is explicitly described as follows. For each $g\in \mathcal{G}$, consider the map $T{g}_m:K_m\to K_{{\Phi }_g·m}$ given by

$$T{g}_m(Z)=\frac{d}{ds}{|}_{s=0}{\Phi }_g·\gamma (s),$$

with $\gamma$ a curve in K and $\dot{\gamma }(0)=Z_m$, i.e., as the distribution K is $\mathcal{G}$-invariant, the tangent map ${{\Phi }_g}_{\star }=Tg$ maps K into itself. The dual map $T{g}_m^{\star }:K_{{\Phi }_g·m}^{\star }\to K_m^{\star }$, is defined as:

$$\langle T{g}_m^{\star }{\mu }_{{\Phi }_g·m},Z_m\rangle =\langle {\mu }_{{\Phi }_g·m},T{g}_m{Z}_m\rangle \forall Z_m\in K_m.$$

(19)

Then we define the lift of the action of $\mathcal{G}$ to ${\mathbf{K}}^{\star }$ as:

$${\tilde{\Phi }}_g(m,\mu )=({\Phi }_g(m),{(T{g}^{-1})}^{\star }\mu )g\in \mathcal{G},(m,\mu )\in {\mathbf{K}}^{\star }.$$

(20)

If the tubular neighborhood $\mathcal{P}$ can be chosen to be $\mathcal{G}$-invariant (for instance, if there is a $\mathcal{G}$-invariant metric on $\mathcal{M}$), then the induced action of $\mathcal{G}$ on $(\mathcal{P},{\omega }_{\mathcal{P}})$ is strongly Hamiltonian if the action of $\mathcal{G}$ is. The best way to see that is by explicitly constructing an equivariant momentum map for such action. We do it upon introducing the technical requirement that the action of $\mathcal{G}$ on $\mathcal{M}$ is quasi-free, i.e., the isotropy group ${\mathcal{G}}_m$ is finite (or discrete). If this is the case, then the map ${\mathfrak{i}}_m:\mathfrak{g}\to {\mathbf{T}}_m\mathcal{M}$, that maps the element $\xi \in \mathfrak{g}$ into the tangent vector $X_{\xi }(m)\in {\mathbf{T}}_m\mathcal{M}$ is injective and we can identify $\mathfrak{g}$ with its image ${\mathfrak{i}}_m(\mathfrak{g})\subset {\mathbf{T}}_m\mathcal{M}$. Denoting by ${\mathfrak{g}}_m:={\mathfrak{i}}_m\mathfrak{g}$, we can construct the subbundle $\tilde{\mathfrak{g}}={\bigcup }_{m\in \mathcal{M}}{\mathfrak{g}}_m\subset \mathbf{T}\mathcal{M}$, where fibers are copies of the Lie algebra $\mathfrak{g}$. Then, we can consider the intersection $K\bigcap \tilde{\mathfrak{g}}$, i.e., at each point $m\in \mathcal{M}$, ${\left(K\bigcap \tilde{\mathfrak{g}}\right)}_m=K_m\bigcap {\mathfrak{g}}_m$. Assuming that $K\bigcap \tilde{\mathfrak{g}}\subset \mathbf{T}\mathcal{M}$ is again a subbundle, we can denote it by ${\tilde{\mathfrak{g}}}_{gauge}=K\bigcap \tilde{\mathfrak{g}}$. Then we have the short exact sequence of bundles:

$$\begin{array}{c}\hfill 0\to {\tilde{\mathfrak{g}}}_{gauge}\to \tilde{\mathfrak{g}}\to \tilde{\mathfrak{g}}/{\tilde{\mathfrak{g}}}_{gauge}\to 0.\end{array}$$

(21)

The space of sections of $\tilde{\mathfrak{g}}\to \mathcal{M}$ carries a Lie algebra structure as ${[\tilde{\xi },\tilde{\zeta }]}_m=[{\tilde{\xi }}_m,{\tilde{\zeta }}_m]$, where ${\tilde{\xi }}_m$ and ${\tilde{\zeta }}_m\in {\mathfrak{g}}_m$, are identified with the corresponding elements in $\mathfrak{g}$ (by means of ${\mathfrak{i}}_m$) and the bracket is the Lie algebra bracket in $\mathfrak{g}$. The space of sections of ${\tilde{\mathfrak{g}}}_{gauge}$ is a Lie algebra ideal of $\tilde{\mathfrak{g}}$ and the quotient $\tilde{\mathfrak{g}}/{\tilde{\mathfrak{g}}}_{gauge}$ becomes a Lie algebra again. We may denote the underlying bundle ${\tilde{\mathfrak{g}}}_{dyn}$, and, at each point $m\in \mathcal{M}$, it defines a Lie subalgebra of $\mathfrak{g}$ (that could vary with m). A $(\mathcal{G},K)$-connection on $(\mathcal{M},\omega )$ will be an equivariant bundle map $A:\tilde{\mathfrak{g}}\to {\tilde{\mathfrak{g}}}_{gauge}$, i.e., $A_m:{\tilde{\mathfrak{g}}}_m\to {\tilde{\mathfrak{g}}}_{gauge,m}$ and

$${({\mathrm{Ad}}_g)}_{\star }(A_m({\tilde{\xi }}_m))=A_{{\Phi }_g·m}({({\mathrm{Ad}}_g)}_{\star }{\tilde{\xi }}_m),$$

for any $g\in \mathcal{G}$, $m\in \mathcal{M}$, ${\tilde{\xi }}_m\in {\mathfrak{g}}_m$ (note that such a map always exists, it can be constructed using local trivializations and summing them using a partition of unity.). Then, we construct the map ${\mathbb{J}}_{\mathcal{P}}:\mathcal{P}\to {\mathfrak{g}}^{\star }$ as:

$$\langle {\mathbb{J}}_{\mathcal{P}}(m,\mu ),\xi \rangle =\langle \mathbb{J}(m),\xi \rangle +\langle \mu ,A_m({\alpha }_{\xi })\rangle \forall m\in \mathcal{M},\mu \in K^{\star },\xi \in \mathfrak{g}.$$

(22)

One can now show that ${\mathbb{J}}_{\mathcal{P}}$ is equivariant, i.e.:

$${\mathbb{J}}_{\mathcal{P}}({\tilde{\Phi }}_g·(m,\mu ))={\mathrm{Ad}}_{g^{-1}}^{\star }({\mathbb{J}}_{\mathcal{P}}(m,\mu )),$$

(23)

and the action of $\mathcal{G}$ on $\mathcal{P}$ is strongly Hamiltonian.

3. The Euler–Lagrange Space as Presymplectic Manifold

It is well known that the space of solutions of a first-order Hamiltonian field theory can be canonically equipped with a presymplectic structure [28,29,30,31,32,33,34,35,36,37]. In this section, we briefly explain the main steps of the construction in order to introduce the setting to which we will apply the abstract theory developed in Section 2, to fix the notations and the relevant geometrical structures, so that this contribution will be as self-consistent as possible. We refer to [15,18,19,20] and to a companion paper [38] for all of the technical details and for many proofs.

In the multisymplectic formalism, a first-order Hamiltonian field theory is specified by:

• A fiber bundle over an underlying (orientable) space–time $\mathcal{M}$ of dimension $1+d$ with smooth boundary $\partial \mathcal{M}$, say $\pi :\mathbb{E}\to \mathcal{M}$, whose sections $\varphi$ represent the configuration fields of the theory. The carrier space where the description of the field theory takes place is the so called covariant phase space (it is worth pointing out that this terminology is not standard and that many authors in the literature refer to covariant phase space as the space of the solutions of the equations of motion. Instead, we refer to it as the Euler–Lagrange space). It is defined as the reduced dual (in the standard terminology of affine bundles [18,39]) of the first order jet bundle of the fibration $\pi$ and it is denoted by $\mathcal{P}(\mathbb{E})$. Here, we only recall that given a chart on $\mathcal{M}$, $(U_{\mathcal{M}},{\psi }_{U_{\mathcal{M}}})$, ${\psi }_{U_{\mathcal{M}}}(m)=(x^0,\dots ,x^d)=:x$ (with $m\in U_{\mathcal{M}}\subset \mathcal{M}$) and a fibered chart on $\pi$, $(U_{\mathbb{E}},{\psi }_{U_{\mathbb{E}}})$, ${\psi }_{U_{\mathbb{E}}}(\mathfrak{e})=(x^0,\dots ,x^d,u^1,\dots ,u^r)=:(x,u)$ (with $\mathfrak{e}\in U_{\mathbb{E}}\subset \mathbb{E}$ and r being the dimension of the fiber of $\pi$), an adapted fibered chart can be given on the first order jet bundle of $\pi$, ${\mathbf{J}}^1\pi$, say $(U_{{\mathbf{J}}^1\pi },{\psi }_{U_{{\mathbf{J}}^1\pi }})$, ${\psi }_{U_{{\mathbf{J}}^1\pi }}({\mathfrak{e}}_x)=(x^0,\dots ,x^d,u^1,\dots ,u^r,z_0^1,\dots ,z_d^r)=:(x,u,z)$ (with ${\mathfrak{e}}_x\in U_{{\mathbf{J}}^1\pi }\subset {\mathbf{J}}^1\pi$). Moreover, $\mathcal{P}(\mathbb{E})$ is a fiber bundle, both over $\mathbb{E}$ and over $\mathcal{M}$ where an adapted fibered chart can be given as $(U_{\mathcal{P}(\mathbb{E})},{\psi }_{U_{\mathcal{P}(\mathbb{E})}})$, ${\psi }_{U_{\mathcal{P}(\mathbb{E})}}(\mathfrak{p})=(x^0,\dots ,x^d,u^1,\dots ,u^r,{\rho }_1^0,\dots ,{\rho }_r^d)=:(x,u,\rho )$ (with $\mathfrak{p}\in U_{\mathcal{P}(\mathbb{E})}\subset \mathcal{P}(\mathbb{E})$) where the coordinates ${\rho }_a^{\mu }$ represent the “dual coordinates” of the fibered coordinates $z_{\mu }^a$ on ${\mathbf{J}}^1\pi$.

  (24)
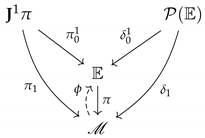
• A Hamiltonian function that, for all the purposes of the present paper, can be considered as a local function on $\mathcal{P}(\mathbb{E})$

  $$H:U_{\mathcal{P}(\mathbb{E})}\to \mathbb{R}:{\psi }_{U_{\mathcal{P}(\mathbb{E})}}^{-1}(x,u,\rho )\mapsto H({\psi }_{U_{\mathcal{P}(\mathbb{E})}}^{-1}(x,u,\rho )).$$

  (25)
  Throughout the paper, with the usual (slight) abuse of notation, we will use H to denote $H\circ {\psi }_{U_{\mathcal{P}(\mathbb{E})}}^{-1}$.

The space of fields used to describe the dynamical content of the theory within the Hamiltonian formalism is the space of sections of ${\delta }_1$, which factorizes into a section of $\pi$, say $\varphi$, and a section of ${\delta }_0^1$, say P. We denote elements of this space as ordered pairs $(\varphi ,P)$. Note that:

$$\chi =P\circ \varphi ,$$

(26)

is a section of ${\delta }_1$. Often we denote the pair $(\varphi ,P)$ by $\chi$ itself. In this space of sections, we define the action functional encoding the dynamical content of the theory. For technical reasons, it would be worth working on a space of fields, admitting at least a Banach manifold structure, but this is not the case for the space of smooth sections of a fiber bundle, which is a Fréchet space. For this reason, in all the examples considered, we complete the space of fields with respect to a suitable Banach norm (actually, in all the cases considered, it will be a Sobolev norm), in which the action functional is a continuous one. In this way, the action functional can be extended by continuity to such a completion which turns to be our new space of fields. We call this space the space of dynamical fields and we denote it by ${\mathcal{F}}_{\mathcal{P}(\mathbb{E})}$ (the corresponding subset of ${\Gamma }^{\infty }(\pi )$ of configuration fields is denoted by ${\mathcal{F}}_{\mathbb{E}}$). In developing the abstract theory, we consider the action functional to be well defined on the Banach manifold ${\mathcal{F}}_{\mathcal{P}(\mathbb{E})}$, and we construct the proper completion case-by-case in the examples.

The covariant phase space admits a canonical $(d+1)$-form whenever a Hamiltonian is fixed, which, in local adapted coordinates, takes the form:

$${\Theta }_H={\rho }_a^{\mu }\mathrm{d}{u}^a\wedge i_{\mu }vo{l}_{\mathcal{M}}-Hvo{l}_{\mathcal{M}},$$

(27)

where $vo{l}_{\mathcal{M}}$ is a volume form on $\mathcal{M}$ and $i_{\mu }$ denotes the contraction with the vector field $\frac{\partial }{\partial x^{\mu }}$. In terms of such a differential form, an action functional on the space of dynamical fields can be defined in the following way:

$${\mathcal{S}}_{\chi }={\int }_{\mathcal{M}}{\chi }^{\star }{\Theta }_H.$$

(28)

The first variation of $\mathcal{S}$ along the direction ${\mathbb{X}}_{\chi }\in {\mathbf{T}}_{\chi }{\mathcal{F}}_{\mathcal{P}(\mathbb{E})}$ reads:

$${\delta }_{{\mathbb{X}}_{\chi }}{\mathcal{S}}_{\chi }={\int }_{\mathcal{M}}{\chi }^{\star }\left[i_X\mathrm{d}{\Theta }_H\right]+{\int }_{\partial \mathcal{M}}{\chi }_{\partial \mathcal{M}}^{\star }\left[i_X{\Theta }_H\right],$$

(29)

where ${\chi }_{\partial \mathcal{M}}=\chi {|}_{\partial \mathcal{M}}={\mathfrak{i}}_{\partial \mathcal{M}}^{\star }\chi \in {\mathcal{F}}_{\mathcal{P}(\mathbb{E})}{|}_{\partial \mathcal{M}}=:{\mathcal{F}}_{\mathcal{P}(\mathbb{E})}^{\partial \mathcal{M}}$, ${\mathfrak{i}}_{\partial \mathcal{M}}$ denoting the canonical immersion of $\partial \mathcal{M}$ into $\mathcal{M}$, and X is a vector field over an open neighborhood of the image of $\chi$, which restricts to ${\mathbb{X}}_{\chi }$ when evaluated along $\chi$. Equation (29) is known as first variational formula.

The first variational formula can be given an interpretation in terms of differential forms on ${\mathcal{F}}_{\mathcal{P}(\mathbb{E})}$ in the following way. The term on the left hand side is the differential of the function (on ${\mathcal{F}}_{\mathcal{P}(\mathbb{E})}$) $\mathcal{S}$ contracted along the tangent vector ${\mathbb{X}}_{\chi }\in {\mathbf{T}}_{\chi }{\mathcal{F}}_{\mathcal{P}(\mathbb{E})}$, i.e., what we can write as $i_{{\mathbb{X}}_{\chi }}\mathrm{d}\mathcal{S}$. Regarding the right-hand side, the first term can be interpreted as the contraction of a differential 1-form on ${\mathcal{F}}_{\mathcal{P}(\mathbb{E})}$ (seen as an application from each ${\mathbf{T}}_{\chi }{\mathcal{F}}_{\mathcal{P}(\mathbb{E})}$ to $\mathbb{R}$) with the tangent vector ${\mathbb{X}}_{\chi }$. We call such a differential 1-form the Euler–Lagrange form and we denote it by $\mathbb{EL}$:

$$i_{{\mathbb{X}}_{\chi }}{\mathbb{EL}}_{\chi }={\int }_{\mathcal{M}}{\chi }^{\star }\left[i_X\mathrm{d}{\Theta }_H\right].$$

(30)

Regarding the last term on the right hand side, again it can be seen as the contraction of a differential form with a tangent vector. However, since it only depends on the restriction of $\chi$ to the boundary $\partial \mathcal{M}$, if we want to interpret it in terms of a differential form on ${\mathcal{F}}_{\mathcal{P}(\mathbb{E})}$, it must be a form which is the pull-back of a differential form on ${\mathcal{F}}_{\mathcal{P}(\mathbb{E})}^{\partial \mathcal{M}}$ via the restriction map:

$${\Pi }_{\partial \mathcal{M}}:{\mathcal{F}}_{\mathcal{P}(\mathbb{E})}\to {\mathcal{F}}_{\mathcal{P}(\mathbb{E})}^{\partial \mathcal{M}}:\chi \mapsto \chi {|}_{\partial \mathcal{M}}.$$

(31)

We denote such a differential form by ${\Pi }_{\partial \mathcal{M}}^{\star }{\alpha }^{\partial \mathcal{M}}$:

$$i_{{\mathbb{X}}_{\chi }}{\Pi }_{\partial \mathcal{M}}^{\star }{\alpha }^{\partial \mathcal{M}}={\int }_{\partial \mathcal{M}}{\chi }_{\partial \mathcal{M}}^{\star }\left[i_X\mathrm{d}{\Theta }_H\right].$$

(32)

We have a few more comments regarding the latter differential form. Indeed, it is exactly the differential form, which will make the space of solutions of the theory into a presymplectic manifold. First, let us note that, by virtue of the embedding theorem, we can always choose the coordinate system on $\mathcal{M}$ around $\partial \mathcal{M}$, such that $x^0$ is the coordinate transversal to $\partial \mathcal{M}$. Consequently, the space of fields restricted to $\partial \mathcal{M}$, say ${\mathcal{F}}_{\mathcal{P}(\mathbb{E})}^{\partial \mathcal{M}}$, splits as follows:

$${\mathcal{F}}_{\mathcal{P}(\mathbb{E})}^{\partial \mathcal{M}}=\left\{{\varphi }^a{|}_{\partial \mathcal{M}},P_a^{\mu }{|}_{\partial \mathcal{M}}\right\}={\left\{{\varphi }^a{|}_{\partial \mathcal{M}},P_a^0{|}_{\partial \mathcal{M}},P_a^j{|}_{\partial \mathcal{M}}\right\}}_{j=1,\dots ,d}=:\left\{{\phi }^a,p_a,{\beta }_a^j\right\}={\mathcal{F}}_{\mathcal{P}(\mathbb{E}),0}^{\partial \mathcal{M}}\times {\mathcal{B}}^{\partial \mathcal{M}},$$

(33)

where $({\phi }^a,p_a)\in {\mathcal{F}}_{\mathcal{P}(\mathbb{E}),0}^{\partial \mathcal{M}}$ and ${\beta }_a^j\in {\mathcal{B}}^{\partial \mathcal{M}}$.

Now, the space ${\mathcal{F}}_{\mathcal{P}(\mathbb{E}),0}^{\partial \mathcal{M}}$ is isomorphic with the cotangent bundle of the space of sections of the bundle $\mathbb{E}$ restricted to $\partial \mathcal{M}$, ${\mathcal{F}}_{\mathbb{E}}{\mid }_{\partial \mathcal{M}}$, denoted as ${\mathcal{F}}_{\partial \mathbb{E}}$ and, denoting by $\tau$ the projection from ${\mathcal{F}}_{\mathcal{P}(\mathbb{E})}^{\partial \mathcal{M}}$ to ${\mathbf{T}}^{\star }{\mathcal{F}}_{\mathbb{E}}$, it is a direct computation to show that:

$$-\mathrm{d}{\Pi }_{\partial \mathcal{M}}^{\star }{\alpha }^{\partial \mathcal{M}}=:{\Pi }_{\partial \mathcal{M}}^{\star }{\Omega }^{\partial \mathcal{M}}={\tau }^{\star }\omega ,$$

(34)

where $\omega =-\mathrm{d}{\alpha }^{\partial \mathcal{M}}$, is the canonical symplectic structure of ${\mathbf{T}}^{\star }{\mathcal{F}}_{\partial \mathbb{E}}$. Explicitly it reads:

$${\Pi }_{\partial \mathcal{M}}^{\star }{\Omega }^{\partial \mathcal{M}}(\mathbb{X},\mathbb{Y})={\int }_{\partial \mathcal{M}}\left[{\mathbb{X}}_{\phi }^a{{\mathbb{Y}}_p}_a-{{\mathbb{X}}_p}_a{\mathbb{Y}}_{\phi }^a\right]vo{l}_{\partial \mathcal{M}},$$

(35)

which, in the particular instance of particle dynamics, becomes the standard differential form $\mathrm{d}{q}^j\wedge \mathrm{d}{p}_j$ of the Hamiltonian formalism [20].

In terms of the differential forms on ${\mathcal{F}}_{\mathcal{P}(\mathbb{E})}$ defined above, the first variational formula reads:

$$\mathrm{d}{\mathcal{S}}_{\chi }={\mathbb{EL}}_{\chi }+{\Pi }_{\partial \mathcal{M}}^{\star }{\alpha }_{\chi }^{\partial \mathcal{M}}.$$

(36)

The dynamical content of the theory, i.e., the equations of motion, can be obtained via a variational principle á la Schwinger-Weiss [40,41]. It states that the solutions of the theory considered are those $\chi$ for which the first variation of the action functional only depends on boundary terms, i.e., on terms that only depends on the restrictions of the fields to the boundary $\partial \mathcal{M}$. Therefore, by looking at the first variational formula, the solutions of the theory are those for which:

$${\mathbb{EL}}_{\chi }=0.$$

(37)

In this perspective, the solutions of the equations of motion are the zeroes of a differential form (the Euler–Lagrange form) on an infinite-dimensional manifold. From now on, we look at the space of solutions of the equations of motion as the space of zeroes of $\mathbb{EL}$ and we denote it by $\mathcal{E}{\mathcal{L}}_{\mathcal{M}}$:

$$\begin{array}{cc}\hfill \mathcal{E}{\mathcal{L}}_{\mathcal{M}}& =\left\{\chi \in {\mathcal{F}}_{\mathcal{P}(\mathbb{E})}:{\mathbb{EL}}_{\chi }=0\right\}=\left\{\chi \in {\mathcal{F}}_{\mathcal{P}(\mathbb{E})}:{\chi }^{\star }\left[i_X\mathrm{d}{\Theta }_H\right]=0\forall X\in {\mathfrak{X}}^v(U^{(\chi )})\right\}=\hfill \\ \hfill & =\left\{\chi \in {\mathcal{F}}_{\mathcal{P}(\mathbb{E})}:\frac{\partial {\varphi }^a}{\partial x^{\mu }}=\frac{\partial H}{{\rho }_a^{\mu }}{|}_{\chi }\mathrm{and}\frac{\partial P_a^{\mu }}{\partial x^{\mu }}=-\frac{\partial H}{\partial u^a}{|}_{\chi }\right\}.\hfill \end{array}$$

(38)

Even if nothing is said about the differential structure of $\mathcal{E}{\mathcal{L}}_{\mathcal{M}}$ we will always assume, from now on, $\mathcal{E}{\mathcal{L}}_{\mathcal{M}}$ to be a smooth differential manifold that can be properly embedded into ${\mathcal{F}}_{\mathcal{P}(\mathbb{E})}$ via the embedding ${\mathfrak{i}}_{\mathcal{E}{\mathcal{L}}_{\mathcal{M}}}$. We take care of the validity of these assumptions case-by-case in the examples considered.

We proceed by recalling that the the differential form ${\Pi }_{\partial \mathcal{M}}^{\star }{\Omega }^{\partial \mathcal{M}}$ gives rise to a canonical structure on the space of solutions of the theory and that it is a presymplectic structure.

First, let us note that the differential form ${\Pi }_{\partial \mathcal{M}}^{\star }{\alpha }^{\partial \mathcal{M}}$ can be defined similarly for any codimension-1 hypersurface in $\mathcal{M}$, say $\Sigma$, in the following way:

$${\Pi }_{\Sigma }^{\star }{\alpha }_{\chi }^{\Sigma }({\mathbb{X}}_{\chi })={\int }_{\Sigma }{\chi }_{\Sigma }^{\star }\left[i_X\mathrm{d}{\Theta }_H\right],$$

(39)

where ${\Pi }_{\Sigma }$ is defined analogously to ${\Pi }_{\partial \mathcal{M}}$: ${\Pi }_{\Sigma }:{\mathcal{F}}_{\mathcal{P}(\mathbb{E})}\to {\mathcal{F}}_{\mathcal{P}(\mathbb{E})}^{\Sigma }$, $\chi \mapsto \chi {|}_{\Sigma }$. Its (minus) differential gives rise to the following 2-form:

$${\Pi }_{\Sigma }^{\star }{\Omega }_{\chi }^{\Sigma }({\mathbb{X}}_{\chi },{\mathbb{Y}}_{\chi })=-{\int }_{\Sigma }{\chi }_{\Sigma }^{\star }\left[i_Y{i}_X\mathrm{d}{\Theta }_H\right],$$

(40)

which is the analogue of ${\Pi }_{\partial \mathcal{M}}^{\star }{\Omega }^{\partial \mathcal{M}}$ for a generic co-dimension 1 hypersurface in $\mathcal{M}$. We will say that a smooth hypersurface $\Sigma$ of the spacetime $\mathcal{M}$ is a slice of $\mathcal{M}$ if $\mathcal{M}\setminus \Sigma$ is the disjoint union of two spacetimes ${\mathcal{M}}_{+}$ and ${\mathcal{M}}_{-}$. Now, the following, crucial, result holds [38].

Proposition 1.

The differential two-form ${\Pi }_{\Sigma }^{\star }{\Omega }^{\Sigma }$ does not depend on the particular slice Σ chosen if it is evaluated on the solutions of the equations of motion.

An immediate consequence of this result is that the differential form ${\mathfrak{i}}_{\mathcal{E}{\mathcal{L}}_{\mathcal{M}}}^{\star }{\Pi }_{\Sigma }^{\star }{\Omega }^{\Sigma }$ does not depend on the particular slice $\Sigma$ chosen and, consequently, it defines a presymplectic structure on the Euler–Lagrange space $\mathcal{E}{\mathcal{L}}_{\mathcal{M}}$ because it is closed by construction. In particular, when it has a non-empty kernel, we refer to the theory under investigation as a gauge theory. That this notion coincides with the usual one, in terms of principal fiber bundles, is discussed in [38].

We conclude the section by discussing the relation between the presymplectic structure ${\Pi }_{\Sigma }^{\star }{\Omega }^{\Sigma }$ and the presymplectic structure ${\Omega }_{\infty }^{\Sigma }$, which comes from the PCA analysis (4). Given a slice $\Sigma$, we will say that is defines a well-posed boundary problem if the restriction of the map ${\Pi }_{\Sigma }$ to $\mathcal{E}{\mathcal{L}}_{\mathcal{M}}$ is surjective, in other words, for any functions $({\phi }^a,p_a)$ on $\Sigma$ there is a solution $\chi \in \mathcal{E}{\mathcal{L}}_{\mathcal{M}}$ possessing them as boundary data. First, the following result holds (see [15,18]).

Proposition 2.

Given a slice Σ, suppose that there exist an $ϵ>0$ such that there exists a collar $C_{ϵ}^{\Sigma }=(-ϵ,ϵ)\times \Sigma$, such that Σ defines a well-posed boundary problem for the space of solutions $\mathcal{E}{\mathcal{L}}_{C_{ϵ}^{\Sigma }}$. Then the space of solutions in such a collar $\mathcal{E}{\mathcal{L}}_{C_{ϵ}^{\Sigma }}$ consist of the solutions of the presymplectic Hamiltonian system $({\mathcal{F}}_{\mathcal{P}(\mathbb{E})}^{\Sigma },{\Omega }^{\Sigma },\mathcal{H})$, where ${\Omega }^{\Sigma }$ is the differential form on ${\mathcal{F}}_{\mathcal{P}(\mathbb{E})}^{\Sigma }$ from which the structure ${\Pi }_{\Sigma }^{\star }{\Omega }^{\Sigma }$ comes (Equation (40)), and $\mathcal{H}$ is the Hamiltonian functional:

$$\mathcal{H}={\int }_{\Sigma }\left({\beta }_a^k{\partial }_k{\phi }^a-H(\phi ,p,\beta )\right)vo{l}_{\Sigma },$$

(41)

where $({\phi }^a,p_a,{\beta }_a^k)={\Pi }_{\Sigma }({\varphi }^a,P_a^0,P_a^k)=({\varphi }^a,P_a^0,P_a^k){|}_{\Sigma }$.

The form ${\Omega }^{\Sigma }$ is, in general, presymplectic and, thus, solutions of the presymplectic system above can be found via the presymplectic constraint algorithm (Equation (4)). Denote by ${\mathcal{M}}_{\infty }$ the final stable manifold resulting from the presymplectic constraint algorithm applied to $({\mathcal{F}}_{\mathcal{P}(\mathbb{E})}^{\Sigma },{\Omega }^{\Sigma },\mathcal{H})$. Denote by ${\mathfrak{i}}_{\infty }$, its immersion into ${\mathcal{F}}_{\mathcal{P}(\mathbb{E})}^{\Sigma }$, by ${\Omega }_{\infty }^{\Sigma }={\mathfrak{i}}_{\infty }^{\star }{\Omega }^{\Sigma }$, and by ${\mathcal{H}}_{\infty }={\mathfrak{i}}_{\infty }^{\star }\mathcal{H}$. In case ${\mathcal{M}}_{\infty }$ is (strongly) symplectic, it can be proved [38] that:

$${\Pi }_{\Sigma }^{\star }{\Omega }^{\Sigma }={\Psi }^{\star }{\Omega }_{\infty }^{\Sigma },$$

(42)

where $\Psi =F^{{\mathbb{X}}_{{\mathcal{H}}_{\infty }}}\circ {\mathfrak{i}}_{\infty }$, with $F^{{\mathbb{X}}_{{\mathcal{H}}_{\infty }}}:({\phi }^a,p_a)\mapsto ({\phi }_t^a,p_{a,t})$, being the flow of the Hamiltonian vector field associated to ${\mathcal{H}}_{\infty }$, which is a diffeomorphism under the conditions stated in the proposition.

When ${\mathcal{M}}_{\infty }$ is a presymplectic manifold as well, it can be proved [38] that a relation of the type (42) holds, but only along a cross-section on the bundle ${\mathcal{M}}_{\infty }\to {\mathcal{M}}_{\infty }/K$ (K denoting the characteristic distribution of ${\Omega }_{\infty }^{\Sigma }$), which represents the fixing of a particular gauge.

4. Symmetry Theory on the Euler–Lagrange Space

In this section, we apply the general theory developed in Section 2 and Section 3 to the study of symmetry groups on the bundle over the space–time underlying the field theory and investigate their properties. The corresponding momentum maps will be constructed for two instrumental examples, Klein–Gordon theory, Section 4.2, and electrodynamics, Section 4.3, using the the coisotropic embedding in the presymplectic case. We deal with them after discussing the case of a free relativistic particle (Section 4.1) seen as a field theory over a one-dimensional “space–time” representing the parametrization of the trajectories.

4.1. Free Relativistic Particle

In this section, we apply the theory developed in Section 2 to the space of solutions of a free relativistic particle. This section aims to apply the whole machinery introduced so far to a more manageable situation. Indeed, in this case, the space of Cauchy data and, thus, the space of solutions is a finite-dimensional presymplectic manifold.

We first show how to formulate the theory within the multisymplectic Hamiltonian formalism constructing the presymplectic structure on the space of solutions of the theory, then we show that the dynamics of the theory lies entirely in the kernel of a presymplectic manifold since the PCA leads to a final manifold in which the Hamiltonian identically vanishes. Then, we note that the group of reparametrizations represents a symmetry of the theory and we construct the associated conserved charge by the aid of the coisotropic embedding theorem as described in Section 2.

Here, the “space–time” $\mathcal{M}$ is an interval of the real line, say $\mathbb{I}\subset \mathbb{R}$ where we denote by $\left\{s\right\}$ a system of global Cartesian coordinates. The fiber bundle $\mathbb{E}$ is the trivial bundle $\pi :\mathbb{I}\times {\mathbb{R}}^4\to \mathbb{I}$ where we use the following (global) Cartesian coordinate system ${\{s,x^{\mu }\}}_{\mu =0,\dots ,3}$. We endow ${\mathbb{R}}^4$ with a Lorentzian metric tensor denoted by g. Therefore, the covariant phase space is $\mathcal{P}(\mathbb{E})=\mathbb{I}\times {\mathbf{T}}^{\star }{\mathbb{R}}^4\simeq \mathbb{I}\times {\mathbb{R}}^4\times {\mathbb{R}}^4$ where we chose the system of (global) Cartesian coordinates ${\{s,x^{\mu },p_{\mu }\}}_{\mu =0,\dots ,4}$. The Hamiltonian of the theory is:

$$H=\frac{1}{2m}{g}^{\mu \nu }(x)p_{\mu }{p}_{\nu },$$

(43)

where $g^{\mu \nu }$ denote the contravariant components of (the inverse of) the metric tensor $g=g_{\mu \nu }\mathrm{d}{x}^{\mu }\otimes \mathrm{d}{x}^{\nu }$ and m is a real positive number. The action functional associated with this Hamiltonian function is well-defined on the space of smooth sections of ${\delta }_1:\mathcal{P}(\mathbb{E})\to \mathbb{I}$. It can be extended by continuity to the space of sections $(x^{\mu },p_{\mu })$ where $x^{\mu }$ is a ${\left[{\mathcal{H}}^1(\mathbb{I},vo{l}_{\mathbb{I}})\right]}^4$ function and p is an ${\left[{\mathcal{L}}^2\right]}^4$ section of $x^{\star }\mathcal{P}(\mathbb{E})$. This space of sections is a Hilbert space and will represent our space of “dynamical fields” ${\mathcal{F}}_{\mathcal{P}(\mathbb{E})}$.

In this trivial example, a “Cauchy hypersurface” in $\mathbb{I}$ is represented by a single point, say the one with coordinate $\tilde{s}$. Therefore, the Hamiltonian functional (41) reads:

$$\mathcal{H}=\frac{1}{2m}{g}^{\mu \nu }(\gamma ){\varrho }_{\mu }{\varrho }_{\nu },$$

(44)

where $({\gamma }^{\mu },{\rho }_{\mu })={\left(x^{\mu }(s),p_{\mu }(s)\right)}_{s=\tilde{s}}$ represent the “fields” restricted to the “hypersurface” $\left\{\tilde{s}\right\}$, say ${\mathcal{F}}_{\mathcal{P}(\mathbb{E})}^{\tilde{s}}$. The canonical structure in this case is:

$${\Pi }_{\tilde{s}}^{\star }{\Omega }^{\tilde{s}}(\mathbb{X},\mathbb{Y})={\left({{\mathbb{X}}_x}^{\mu }{{\mathbb{Y}}_p}_{\mu }-{{\mathbb{X}}_p}_{\mu }{{\mathbb{Y}}_x}^{\mu }\right)}_{\tilde{s}},$$

(45)

where $\mathbb{X}$ and $\mathbb{Y}$ are vector fields over ${\mathcal{F}}_{\mathcal{P}(\mathbb{E})}$. The latter is actually the symplectic structure of ${\mathbf{T}}^{\star }{\mathbb{R}}^4$.

To correctly describe a physical system, a particle of a given mass, we have to restrict our coordinates by means of the mass-shell relation (note that we are setting the velocity of the light $c=1$):

$$g^{\mu \nu }{p}_{\mu }{p}_{\nu }=m^2,$$

(46)

thus, we need to restrict ourselves to the subbundle of $\mathcal{P}(\mathbb{E})$ defined by such a constraint and restrict all of our geometric objects to it. We denote such a subbundle by ${\Sigma }_m$, ${\Sigma }_m^{\tilde{s}}$ denotes its restriction to $s=\tilde{s}$, and, with a slight abuse of notation, we keep denoting the new space of dynamical fields by ${\mathcal{F}}_{\mathcal{P}(\mathbb{E})}$ and their restrictions by ${\mathcal{F}}_{\mathcal{P}(\mathbb{E})}^{\tilde{s}}$. On ${\Sigma }_m$, the Hamiltonian becomes:

$${\mathcal{H}}_m=\frac{m}{2},$$

(47)

and the tensor ${\Pi }_{\tilde{s}}^{\star }{\Omega }^{\tilde{s}}$ becomes presymplectic since at each point of ${\mathcal{F}}_{\mathcal{P}(\mathbb{E})}$ it contains in the kernel all the tangent vectors with ${{\mathbb{X}}_x}^{\mu }=\frac{1}{m}{g}^{\mu \nu }{p}_{\nu }$ and ${{\mathbb{X}}_p}_{\mu }=-\frac{1}{2m}{\partial }_{\mu }{g}^{\rho \sigma }{p}_{\rho }{p}_{\sigma }$. The equations of motion read:

$$\begin{array}{cc}\hfill {\dot{x}}^{\mu }& =\frac{1}{m}{g}^{\mu \nu }{p}_{\nu },\hfill \\ \hfill {\dot{p}}_{\mu }& =-\frac{1}{2m}{\partial }_{\mu }{g}^{\rho \sigma }{p}_{\rho }{p}_{\sigma },\hfill \end{array}$$

(48)

whose solutions are actually integral curves of the vector field in the kernel of the presymplectic structure being the geodesics of the metric g (see also [42,43]). They are in one-to-one correspondence with the solutions of the presymplectic Hamiltonian system $({\mathcal{F}}_{\mathcal{P}(\mathbb{E})}^{\tilde{s}},{\Omega }_m^{\tilde{s}},{\mathcal{H}}_m)$. Since ${\mathcal{H}}_m=\frac{m}{2}$, $\mathrm{d}{\mathcal{H}}_m=0$ and, thus, such solutions are the integral curves of a vector field $\Gamma$ in the kernel of ${\Omega }_m^{\tilde{s}}$. The vector field $\Gamma$ is the one satisfying:

$$i_{\Gamma }{\Omega }_m^{\tilde{s}}=0.$$

(49)

Note that ${\mathcal{F}}_{\mathcal{P}(\mathbb{E})}^{\tilde{s}}$ is actually a finite-dimensional manifold diffeomorphic with ${\Sigma }_m^{\tilde{s}}$ and $\Gamma$ is the vector field tangent to ${\Sigma }_m$:

$$\Gamma =\frac{1}{m}{g}^{\mu \nu }{p}_{\nu }\frac{\partial }{\partial x^{\mu }}-\frac{1}{2m}{\partial }_{\mu }{g}^{\rho \sigma }{p}_{\rho }{p}_{\sigma }\frac{\partial }{\partial p_{\mu }}.$$

(50)

Note that, in this case, the PCA stops at the zero step since ${\mathcal{F}}_{\mathcal{P}(\mathbb{E})}^{\tilde{s}}$ is already a stable presymplectic manifold. On the other hand, the fact that the dynamics lies in the kernel of the presymplectic structure, brings out an obvious symmetry of the theory, i.e., the reparametrizations of the solutions. Indeed, since $\Gamma$ is in the kernel of ${\Omega }_m^{\tilde{s}}$, it can be multiplied, for instance, by any non-vanishing constant $\alpha =e^{-\beta }$. The transformation $\Gamma \mapsto \alpha \Gamma$ amounts to “pass” from parametrizing the trajectories by the parameter s to parametrizing them by $e^{\beta }s$. The generator of such a transformation is actually $\Gamma$.

We stress that invariance under reparametrization of the free relativistic particle was recently analyzed in [44,45,46], where the authors deal with the implications of such invariance within the problem of quantization.

Here, we deal with this symmetry via the coisotropic embedding theorem which, in this case, works as follows. The kernel of ${\Omega }_m^{\tilde{s}}$ is, at each point, a one-dimensional vector space. Let us denote by $\left\{\mu \right\}$ the system of global Cartesian coordinates on it representing all the constant real values that the Hamiltonian of $\Gamma$ could take. The physical space is recovered for $\mu ={\mathcal{H}}_m=\frac{m}{2}$. Since the kernel is generated by the vector field $\Gamma$, its dual can be coordinatized by any time-function, i.e., any function on ${\Sigma }_m$, say $\tau$, such that $i_{\Gamma }\mathrm{d}\tau =1$; that is, any function whose differential gives rise to a one-form being dual to $\Gamma$ (see [47,48]). Therefore, the symplectic manifold obtained out of the coisotropic embedding theorem is isomorphic with $\mathcal{P}={\Sigma }_m\times K^{\star }$ with symplectic structure given by:

$${\Omega }^{\mathcal{P}}=\mathrm{d}{x}^{\mu }\wedge \mathrm{d}{p}_{\mu }{|}_{{\Sigma }_m}+\mathrm{d}\mu \wedge \mathrm{d}\tau .$$

(51)

The generator of the symmetry group, $\Gamma$, can be lifted to $\mathcal{P}$ as explained in Section 2 obtaining the vector field:

$${\Gamma }^{\uparrow }=\frac{1}{m}{g}^{\mu \nu }{p}_{\nu }\frac{\partial }{\partial x^{\mu }}-\frac{1}{2m}{\partial }_{\mu }{g}^{\rho \sigma }{p}_{\rho }{p}_{\sigma }\frac{\partial }{\partial p_{\mu }},$$

(52)

that is, no $\mu$ components appear. A straightforward calculation shows that ${\Gamma }^{\uparrow }$ is Hamiltonian for ${\Omega }^{\mathcal{P}}$ with Hamiltonian $\mu$. Any regular value of $\mu$ define a submanifold of $\mathcal{P}$ preserved by $\Gamma$. In particular, the physical space is the submanifold for which $\mu =\frac{m}{2}$. This means that the symmetry under reparametrization of the theory gives rise to the mass of the particle as a conserved charge.

4.2. The Symplectic Case: Klein–Gordon Theory

This section is devoted to applying the theory developed in Section 2 to the particular case in which the symplectic manifold is the space of solutions of a first-order Hamiltonian field theory, without gauge symmetries. We consider the group of symmetries of the underlying space–time of the Klein–Gordon theory, consider its action upon the space of solutions of the theory, and investigate whether it is canonical/Hamiltonian/strongly Hamiltonian. Moreover, we construct the related momentum map and the conserved currents.

We consider the real scalar Klein–Gordon theory, representing an uncharged spinless massive boson field, on the Minkowski space–time $(\mathbb{M},\eta )$ where $\eta$ is the Minkowski metric of signature $-+++$, and where we adopt the (global) chart $(U_{\mathbb{M}},{\psi }_{U_{\mathbb{M}}})$, ${\psi }_{U_{\mathbb{M}}}(m)=(x^0,\dots ,x^3)=:x$ where $m\in U_{\mathbb{M}}\subset \mathbb{M}$.

The fields of the theory in this case are real valued functions on $\mathcal{M}$ with appropriate boundary conditions at infinity, denoted by $\varphi (x)$. The dynamics of the theory are usually described by means of the following action functional of the fields and their first derivatives:

$$\mathcal{S}[\varphi ,{\partial }_{\mu }\varphi ]=\frac{1}{2}{\int }_{\mathcal{M}}\left[{\partial }_{\mu }\varphi (x){\partial }^{\mu }\varphi (x)-m^2{\varphi }^2(x)\right]d^{4}x,$$

(53)

whose field equations read:

$$({\partial }_{\mu }{\partial }^{\mu }+m^2)\varphi (x)=0.$$

(54)

The energy–momentum tensor of the theory associated to the action functional above is:

$${\mathcal{T}}^{\mu \nu }={\partial }^{\mu }\varphi {\partial }^{\nu }\varphi -{\eta }^{\mu \nu }\left(\frac{1}{2}{\partial }_{\lambda }\varphi {\eta }^{\lambda \eta }{\partial }_{\eta }\varphi -\frac{1}{2}{m}^2{\varphi }^2\right).$$

(55)

A multisymplectic Hamiltonian formulation of such a theory can be given by considering the bundle $\mathbb{E}\to \mathbb{M}$ with typical fiber $\mathcal{E}=\mathbb{R}$ and, thus, the covariant phase space $\mathcal{P}(\mathbb{E})=\mathbb{M}\times \mathbb{R}\times {\mathbb{R}}^4$ where we chose the following adapted fibered chart $(U_{\mathcal{P}(\mathbb{E})},{\psi }_{U_{\mathcal{P}(\mathbb{E})}})$, ${\psi }_{U_{\mathcal{P}(\mathbb{E})}}(\mathfrak{p})=(x^0,\dots ,x^3,u,{\rho }^0,\dots ,{\rho }^3)=:(x,u,\rho )$, where $\mathfrak{p}\in U_{\mathcal{P}(\mathbb{E})}\subset \mathcal{P}(\mathbb{E})$. The Hamiltonian of the theory reads:

$$H=\frac{1}{2}({\eta }_{\mu \nu }{\rho }^{\mu }{\rho }^{\nu }+m^2{u}^2),$$

(56)

with $\mu =0,1,2,3$. The space of dynamical fields ${\mathcal{F}}_{\mathcal{P}(\mathbb{E})}$ is the space of sections of the bundle ${\delta }_1:\mathcal{P}(\mathbb{E})\to \mathbb{M}$ of the type:

$$\chi :U_{\mathbb{M}}\to U_{\mathcal{P}(\mathbb{E})}:{\psi }_{U_{\mathbb{M}}}^{-1}(x)\mapsto \chi \left({\psi }_{U_{\mathbb{M}}}^{-1}(x)\right)=\left({\psi }_{U_{\mathbb{I}}}^{-1}(x),\varphi ({\psi }_{U_{\mathbb{I}}}^{-1}(x)),P^{\mu }({\psi }_{U_{\mathbb{I}}}^{-1}(x))\right),$$

(57)

where $\varphi$ is a section of the bundle $\mathbb{E}\to \mathbb{M}$ belonging to the Sobolev space ${\mathcal{H}}^1(\mathbb{M},vo{l}_{\mathbb{M}})$, i.e., the space of real-valued functions on $\mathbb{M}$ such that they are differentiable in the weak sense and their differentials are square integrable, and P is a square integrable section of the pull-back bundle ${\varphi }^{\star }\mathcal{P}(\mathbb{E})$. This is consistent because the action functional originally defined on ${\Gamma }^{\infty }({\delta }_1)$ can be extended by continuity to ${\mathcal{H}}^1(\mathbb{M},vo{l}_{\mathbb{M}})\times {\mathcal{L}}^2({\varphi }^{\star }\mathcal{P}(\mathbb{E}))$ as discussed in more detail in [38]. For the sake of simplicity, we will simply denote them by $\chi (x)=(x,\varphi (x),P^{\mu }(x))$.

The Hamiltonian functional (41) is ($i,j=1,2,3$):

$$\mathcal{H}={\int }_{\Sigma }\left[{\beta }^k{\partial }_k\phi -\frac{1}{2}\left({\delta }_{jk}{\beta }^j{\beta }^k-p^2-m^2{\phi }^2\right)\right]vo{l}_{\Sigma },$$

for any $\Sigma$ a slice of $\mathbb{M}$, $vo{l}_{\Sigma }$ the volume form defined by the Riemannian metric induced on $\Sigma$ by $\eta$ and $(\phi ,p,{\beta }^j)=(\varphi ,P^0,P^j){|}_{\Sigma }$. In particular, $\Sigma$ will be chosen to be a Cauchy hypersurface, i.e., a space-like codimension-1 smooth submanifold that intersects each light ray in $\mathbb{M}$ at exactly one point.

The equations of motion read:

$$\frac{\partial \varphi }{\partial x^{\mu }}={\eta }_{\mu \nu }{P}^{\nu },\frac{\partial P^{\mu }}{\partial x^{\mu }}=-m^2\varphi ,$$

(58)

whose solutions are parametrized by the Cauchy data at $\Sigma$, $x^0=x_{\Sigma }^0$, $({\phi }_{\Sigma }(\underline{x})=\varphi (x^0=x_{\Sigma }^0,\underline{x}),p_{\Sigma }(\underline{x})=P^0(x^0=x_{\Sigma }^0,\underline{x})$ (where $\underline{x}=(x^1,x^2,x^3)$) in the following way:

$$\begin{array}{cc}\hfill \mathcal{E}{\mathcal{L}}_{\mathbb{M}}=\{& \chi \in {\mathcal{F}}_{\mathcal{P}(\mathbb{E})}:\hfill \\ & \varphi (x^0,\underline{x})={\int }_{{\mathbb{R}}^3\times {\mathbb{R}}^3}\left({\varphi }_{\Sigma }({\underline{x}}^{\prime })\cos {\omega }_k(x^0-x_{\Sigma }^0)-p_{\Sigma }({\underline{x}}^{\prime })\frac{\sin {\omega }_k(x^0-x_{\Sigma }^0)}{{\omega }_k}\right)e^{i\underline{k}·(\underline{x}-{\underline{x}}^{\prime })}{\mathrm{d}}^{3}k{\mathrm{d}}^3{x}^{\prime }\hfill \\ & P^0(x^0,\underline{x})={\int }_{{\mathbb{R}}^3\times {\mathbb{R}}^3}\left({\omega }_k{\varphi }_{\Sigma }({\underline{x}}^{\prime })\sin {\omega }_k(x^0-x_{\Sigma }^0)+p_{\Sigma }({\underline{x}}^{\prime })\cos {\omega }_k(x^0-x_{\Sigma }^0)\right)e^{i\underline{k}·(\underline{x}-{\underline{x}}^{\prime })}{\mathrm{d}}^{3}k{\mathrm{d}}^3{x}^{\prime }\hfill \\ & P^k(x^0,\underline{x})={\delta }^{jk}\frac{\partial \varphi }{\partial x^j}\},\hfill \end{array}$$

(59)

where ${\omega }_k=\sqrt{k^2+m^2}$, $k^2=k_1^2+k_2^2+k_3^2$.

The canonical structure of $\mathcal{E}{\mathcal{L}}_{\mathbb{M}}$ reads:

$${\Pi }_{\Sigma }^{\star }{\Omega }^{\Sigma }(\mathbb{X},\mathbb{Y})={\int }_{\Sigma }{\left[{\mathbb{X}}_u{\mathbb{Y}}_{{\rho }^0}-{\mathbb{X}}_{{\rho }^0}{\mathbb{Y}}_u\right]}_{\Sigma }vo{l}_{\Sigma },$$

(60)

where $\mathbb{X},\mathbb{Y}\in \mathfrak{X}(\mathcal{E}{\mathcal{L}}_{\mathbb{M}})$ and ${\mathbb{X}}_u,{\mathbb{X}}_{{\rho }^0},{\mathbb{Y}}_u,{\mathbb{Y}}_{{\rho }^0}$ denote their components. This structure is nondegenerate and, since the space of dynamical fields considered is a Hilbert manifold, it is strongly symplectic.

We consider the group of symmetries of the space–time $\mathbb{M}$; that is, the Poincaré group $\mathcal{P}=\tau ⋊\mathcal{L}$, the semidirect product of the translations and the Lorentz group $\mathcal{L}$, contain the subgroup of translations, which we denote by $\tau$, the subgroup of spatial rotations, which we denote by $\mathcal{R}$, and the so called Lorentz boosts, which we denote by $\mathcal{B}$. The group we are dealing with is an affine group that can be represented via its natural action on $\mathbb{M}$ by means of $5\times 5$ matrices:

$${\Phi }_{\tau }^{\mathbb{M}}=\left[\begin{array}{ccccc}1& 0& 0& 0& a^0\\ 0& 1& 0& 0& a^1\\ 0& 0& 1& 0& a^2\\ 0& 0& 0& 1& a^3\\ 0& 0& 0& 0& 1\end{array}\right],$$

(61)

$${\Phi }_{\mathcal{R}}^{\mathbb{M}}=\left[\begin{array}{ccccc}1& 0& 0& 0& 0\\ 0& {\mathcal{R}}_{11}& {\mathcal{R}}_{12}& {\mathcal{R}}_{13}& 0\\ 0& {\mathcal{R}}_{21}& {\mathcal{R}}_{22}& {\mathcal{R}}_{23}& 0\\ 0& {\mathcal{R}}_{31}& {\mathcal{R}}_{32}& {\mathcal{R}}_{33}& 0\\ 0& 0& 0& 0& 1\end{array}\right],$$

(62)

$${\Phi }_{\mathcal{B}}^{\mathbb{M}}=\left[\begin{array}{ccccc}{\mathcal{B}}_{00}& {\mathcal{B}}_{01}& {\mathcal{B}}_{02}& {\mathcal{B}}_{03}& 0\\ {\mathcal{B}}_{10}& {\mathcal{B}}_{11}& {\mathcal{B}}_{12}& {\mathcal{B}}_{13}& 0\\ {\mathcal{B}}_{20}& {\mathcal{B}}_{21}& {\mathcal{B}}_{22}& {\mathcal{B}}_{23}& 0\\ {\mathcal{B}}_{30}& {\mathcal{B}}_{31}& {\mathcal{B}}_{32}& {\mathcal{B}}_{33}& 0\\ 0& 0& 0& 0& 1\end{array}\right],$$

(63)

obtained by taking the first 4 components of the result of the action of the corresponding elements in the Poincaré group on the point with components $(x^0,x^1,x^2,x^3,1)$:

$${\Phi }_{\tau }^{\mathbb{M}}·m=\left[\begin{array}{ccccc}1& 0& 0& 0& a^0\\ 0& 1& 0& 0& a^1\\ 0& 0& 1& 0& a^2\\ 0& 0& 0& 1& a^3\\ 0& 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}{x}^0\\ x^1\\ x^2\\ x^3\\ 1\end{array}\right]=\left[\begin{array}{c}{x}^0+a^0\\ x^1+a^1\\ x^2+a^2\\ x^3+a^3\\ 1\end{array}\right],$$

(64)

$${\Phi }_{\mathcal{R}}^{\mathbb{M}}·m=\left[\begin{array}{ccc}1& \mathbf{0}& 0\\ 0& {\mathcal{R}}_k^j& \mathbf{0}\\ 0& \mathbf{0}& 1\end{array}\right]\left[\begin{array}{c}{x}^0\\ x^k\\ 1\end{array}\right]=\left[\begin{array}{c}{x}^0\\ {\mathcal{R}}_k^j{x}^k\\ 1\end{array}\right],$$

(65)

where ${\mathcal{R}}_k^j$ are the components of a matrix in $O(3)$, and:

$${\Phi }_{\mathcal{B}}^{\mathbb{M}}·m=\left[\begin{array}{cc}{\mathcal{B}}_{\nu }^{\mu }& 0\\ \mathbf{0}& 1\end{array}\right]\left[\begin{array}{c}{x}^{\mu }\\ 1\end{array}\right]=\left[\begin{array}{c}{\mathcal{B}}_{\nu }^{\mu }{x}^{\nu }\\ 1\end{array}\right],$$

(66)

where ${\mathcal{B}}_{\nu }^{\mu }$ are the components of a matrix in $SO(1,3)$. These actions can be lifted to a diffeomorphism of the bundle $\mathbb{E}\to \mathbb{M}$, to $\mathcal{P}(\mathbb{E})$ (following the general theory of [15]), and to $\mathcal{E}{\mathcal{L}}_{\mathbb{M}}$ in the following way:

$${\Phi }_{\tau }^{\mathcal{P}(\mathbb{E})}:\mathcal{P}(\mathbb{E})\to \mathcal{P}(\mathbb{E}):(x^{\mu },u,{\rho }^{\mu })\mapsto {\Phi }_{\tau }^{\mathcal{P}(\mathbb{E})}(x^{\mu },u,{\rho }^{\mu })=(x^{\mu }+a^{\mu },u,{\rho }^{\mu }),$$

(67)

$${\Phi }_{\mathcal{R}}^{\mathcal{P}(\mathbb{E})}:\mathcal{P}(\mathbb{E})\to \mathcal{P}(\mathbb{E}):(x^{\mu },u,{\rho }^{\mu })\mapsto {\Phi }_{\mathcal{R}}^{\mathcal{P}(\mathbb{E})}(x^{\mu },u,{\rho }^{\mu })=\left(x^0,{\mathcal{R}}_k^j{x}^k,u,{\rho }^0,{\mathcal{R}}_k^j{\rho }^k\right),$$

(68)

$${\Phi }_{\mathcal{B}}^{\mathcal{P}(\mathbb{E})}:\mathcal{P}(\mathbb{E})\to \mathcal{P}(\mathbb{E}):(x^{\mu },u,{\rho }^{\mu })\mapsto {\Phi }_{\mathcal{B}}^{\mathcal{P}(\mathbb{E})}(x^{\mu },u,{\rho }^{\mu })=\left({\mathcal{B}}_{\nu }^{\mu }{x}^{\nu },u,{\mathcal{B}}_{\nu }^{\mu }{\rho }^{\nu }\right),$$

(69)

$$\begin{array}{cc}\hfill {\Phi }_{\tau }^{\mathcal{E}{\mathcal{L}}_{\mathbb{M}}}:\mathcal{E}{\mathcal{L}}_{\mathbb{M}}\to \mathcal{E}{\mathcal{L}}_{\mathbb{M}}:(x^{\mu },\varphi (x^{\mu }),P^{\mu }(x^{\mu }))& \mapsto {\Phi }_{\tau }^{\mathcal{E}{\mathcal{L}}_{\mathbb{M}}}(x^{\mu },\varphi (x^{\mu }),P^{\mu }(x^{\mu }))=\hfill \\ \hfill & =\left(x^{\mu }+a^{\mu },\varphi (x^{\mu }+a^{\mu }),P^{\mu }(x^{\mu }+a^{\mu })\right),\hfill \end{array}$$

(70)

$$\begin{array}{cc}\hfill {\Phi }_{\mathcal{R}}^{\mathcal{E}{\mathcal{L}}_{\mathbb{M}}}:\mathcal{E}{\mathcal{L}}_{\mathbb{M}}\to \mathcal{E}{\mathcal{L}}_{\mathbb{M}}& :(x^{\mu },\varphi (x^{\mu }),P^{\mu }(x^{\mu }))\mapsto {\Phi }_{\mathcal{R}}^{\mathcal{E}{\mathcal{L}}_{\mathbb{M}}}(x^{\mu },\varphi (x^{\mu }),P^{\mu }(x^{\mu }))=\hfill \\ \hfill & =\left(x^0,{\mathcal{R}}_k^j{x}^k,\varphi (x^0,{\mathcal{R}}_k^j{x}^k),P^0(x^0,{\mathcal{R}}_k^j{P}^k(x^0,{\mathcal{R}}_k^j{x}^k),{\mathcal{R}}_k^j{x}^k)\right),\hfill \end{array}$$

(71)

$$\begin{array}{cc}\hfill {\Phi }_{\mathcal{B}}^{\mathcal{E}{\mathcal{L}}_{\mathbb{M}}}:\mathcal{E}{\mathcal{L}}_{\mathbb{M}}\to \mathcal{E}{\mathcal{L}}_{\mathbb{M}}:(x^{\mu },\varphi (x^{\mu }),P^{\mu }(x^{\mu }))& \mapsto {\Phi }_{\mathcal{B}}^{\mathcal{E}{\mathcal{L}}_{\mathbb{M}}}(x^{\mu },\varphi (x^{\mu }),P^{\mu }(x^{\mu }))=\hfill \\ \hfill & =({\mathcal{B}}_{\nu }^{\mu }{x}^{\nu },\varphi ({\mathcal{B}}_{\nu }^{\mu }{x}^{\nu }),{\mathcal{B}}_{\nu }^{\mu }{P}^{\nu }({\mathcal{B}}_{\nu }^{\mu }{x}^{\nu })).\hfill \end{array}$$

(72)

The fact that this action sends solutions into solutions is readily proven by noting that $(\varphi (x^0,x^j+a^j),P^{\mu }(x^0,x^j+a^j))$ is the solution associated with the Cauchy datum $({\phi }_{\Sigma }(\underline{x}-\underline{a}),p_{\Sigma }(\underline{x}-\underline{a}))$ at $x^0=x_{\Sigma }^0$, $(\varphi (x^0+a^0,x^j),P^{\mu }(x^0+a^0,x^j))$ is the solution associated with the Cauchy datum $({\phi }_{\Sigma }(\underline{x}),p_{\Sigma }(\underline{x}))$ at $x^0=x_{\Sigma }^0+a^0$, $(\varphi (x^0,{\mathcal{R}}_k^j{x}^k),P^{\mu }(x^0,{\mathcal{R}}_k^j{x}^k))$ is the solution associated with the Cauchy datum $({\phi }_{\Sigma }(\underline{x}),p_{\Sigma }(\underline{x}))$ at $x^0=x_{\Sigma }^0$ and $(\varphi ({\mathcal{B}}_{\nu }^{\mu }{x}^{\nu }),{\mathcal{B}}_{\nu }^{\mu }{P}^{\nu }({\mathcal{B}}_{\nu }^{\mu }{x}^{\nu }))$ is the solution associated with the Cauchy datum $({\phi }_{\Sigma }({\mathcal{B}}_{\nu }^j{x}^{\nu }),{\mathcal{B}}_{\nu }^{\mu }{p}_{\Sigma }^{\nu }({\mathcal{B}}_{\nu }^j{x}^{\nu }))$ at ${\mathcal{B}}_{\nu }^0{x}^{\nu }=x_{\Sigma }^0$ where $p_{\Sigma }^{\mu }=(p_{\Sigma },{\delta }^{jk}{\partial }_j{\varphi }_{\Sigma })$.

The action of the Poincaré group onto $\mathcal{E}{\mathcal{L}}_{\mathbb{M}}$ written above is Hamiltonian for the symplectic structure ${\Pi }_{\Sigma }^{\star }{\Omega }^{\Sigma }$. Indeed, a function $J_{\xi }$ exists for all $\xi \in \mathfrak{g}$, such that:

$${\Pi }_{\Sigma }^{\star }{\Omega }^{\Sigma }({\mathbb{X}}_{\xi },·)=J_{\xi },$$

(73)

where ${\mathbb{X}}_{\xi }$ is the Killing vector field associated with $\xi$.

When $\xi ={\xi }_{{\tau }^0}$ is the element in the Lie algebra $\mathfrak{g}={\mathbb{R}}^4⋊\mathfrak{so}(1,3)$ of the Poincaré group $\mathcal{P}$, generating the translation $x^{\mu }\mapsto (x^0+a^0,x^j)$, the corresponding Killing vector field reads:

$$\begin{array}{cc}\hfill {\mathbb{X}}_{{\xi }_{{\tau }^0}}=\frac{d}{d{a}^0}{\left[{\Phi }_{e^{a^0{\xi }_{{\tau }^0}}}·\chi \right]}_{a^0=0}& =\left({\left({\mathbb{X}}_{{\xi }_{{\tau }^0}}\right)}_u=\frac{\partial \varphi }{\partial x^0},{\left({\mathbb{X}}_{{\xi }_{{\tau }^0}}\right)}_{{\rho }^0}=\frac{\partial P^0}{\partial x^0},{\left({\mathbb{X}}_{{\xi }_{{\tau }^0}}\right)}_{{\rho }^j}={\delta }^{jk}\frac{\partial }{\partial x^k}\frac{\partial \varphi }{\partial x^0}\right)=\hfill \\ \hfill & =\left(-P^0,-m^2\varphi -\Delta \varphi ,-{\delta }^{jk}\frac{\partial P^0}{\partial x^k}\right),\hfill \end{array}$$

(74)

and, thus:

$${\Pi }_{\Sigma }^{\star }{\Omega }^{\Sigma }({\mathbb{X}}_{{\xi }_{{\tau }^0}},\mathbb{Y})={\int }_{\Sigma }\left[-P^0{\mathbb{Y}}_{{\rho }^0}+(m^2\varphi +\Delta \varphi ){\mathbb{Y}}_u\right]vo{l}_{\Sigma }.$$

(75)

On the other hand:

$$\mathrm{d}{J}_{{\xi }_{{\tau }^0}}(\mathbb{Y})={\int }_{\mathbb{M}}\left[\frac{\delta J_{{\xi }_{{\tau }^0}}}{\delta \varphi }{\mathbb{Y}}_u+\frac{\delta J_{{\xi }_{{\tau }^0}}}{\delta P^0}{\mathbb{Y}}_{{\rho }^0}\right]vo{l}_{\mathbb{M}}.$$

(76)

Therefore, from the two latter equations, one determines the function $J_{{\xi }_{{\tau }^0}}$ as the function (determined up to constants) satisfying, in the sense of distributions:

$$\frac{\delta J_{{\xi }_{{\tau }^0}}}{\delta \varphi }\delta (x^0-x_{\Sigma }^0)=(m^2\varphi +\Delta \varphi ),\frac{\delta J_{{\xi }_{{\tau }^0}}}{\delta P^0}\delta (x^0-x_{\Sigma }^0)=-P^0,$$

(77)

i.e.,

$$J_{{\xi }_{{\tau }^0}}={\int }_{\Sigma }\frac{1}{2}{\left[m^2{\varphi }^2-{\delta }^{jk}\frac{\partial \varphi }{\partial x^j}\frac{\partial \varphi }{\partial x^k}-{P^0}^2\right]}_{\Sigma }vo{l}_{\Sigma }.$$

(78)

A similar computation can be performed for the elements ${\xi }_{{\tau }^k}\in \mathfrak{g}$ generating the translation $x^{\mu }\mapsto (x^0,x^j+{\delta }_k^j{a}^k)$, obtaining the function $J_{{\xi }_{{\tau }^k}}$ satisfying:

$$\frac{\delta J_{{\xi }_{{\tau }^0}}}{\delta \varphi }\delta (x^0-x_{\Sigma }^0)=-\frac{\partial P^0}{\partial x^k},\frac{\delta J_{{\xi }_{{\tau }^0}}}{\delta P^0}\delta (x^0-x_{\Sigma }^0)=\frac{\partial \varphi }{\partial x^k},$$

(79)

i.e.,

$$J_{{\xi }_{{\tau }^k}}={\int }_{\Sigma }{P}^0\frac{\partial \varphi }{\partial x^k}{|}_{\Sigma }vo{l}_{\Sigma }.$$

(80)

Note that $J_{{\xi }_{{\tau }^0}}$ and $J_{{\xi }_{{\tau }^k}}$ coincide with the charges associated with the energy–momentum tensor of the Klein–Gordon theory (55).

The momentum map is the map between $\mathcal{E}{\mathcal{L}}_{\mathbb{M}}$ and ${\mathfrak{g}}^{\star }$ satisfying:

$$\mathbb{J}:\mathcal{E}{\mathcal{L}}_{\mathbb{M}}\to {\mathfrak{g}}^{\star }:\langle \mathbb{J}(\chi ),\xi \rangle =J_{\xi }.$$

(81)

Let us compute it in the case $\xi ={\xi }_{{\tau }^0}$. The element ${\xi }_{{\tau }^0}\in \mathfrak{g}$ such that $e^{a^0{\xi }_{{\tau }^0}}={\Phi }_{{\tau }^0}^{\mathbb{M}}$ is represented as:

$${\Phi }_{{\xi }_{{\tau }^0}}=\left[\begin{array}{ccccc}0& 0& 0& 0& 1\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right].$$

(82)

Therefore, if we represent $\mathbb{J}(\chi )$ as:

$${\Phi }_{\mathbb{J}}=\left[\begin{array}{ccc}{\mathbb{J}}_{00}(\chi )& \cdots & {\mathbb{J}}_{04}(\chi )\\ ⋮& & ⋮\\ {\mathbb{J}}_{40}(\chi )& \cdots & {\mathbb{J}}_{44}(\chi )\end{array}\right],$$

(83)

we get:

$$\langle \mathbb{J}(\chi ),{\xi }_{{\tau }^0}\rangle =\mathrm{Tr}\left[{{\Phi }_{\mathbb{J}}}^{†}{\Phi }_{{\xi }_{{\tau }^0}}^{\mathbb{M}}\right]={\mathbb{J}}_{04}(\chi ),$$

(84)

and, consequently:

$${\mathbb{J}}_{04}(\chi )=J_{{\xi }_{{\tau }^0}}.$$

(85)

A similar computation for $\xi ={\xi }_{{\tau }^k}$ gives:

$${\mathbb{J}}_{0(4-k)}(\chi )=J_{{\xi }_{{\tau }^k}}.$$

(86)

A computation analogous to the one made in the previous section shows that the momentum maps associated with ${\xi }_{{\tau }^0}$ and ${\xi }_{{\tau }^k}$ are equivariant.

Now, let us compute the conserved current and the momentum map in the case of a rotation ${\mathcal{R}}^{x^3}$ around the $x^3$ axis. It is represented by the $5\times 5$ matrix:

$${\Phi }_{{\mathcal{R}}^3}^{\mathbb{M}}=\left[\begin{array}{ccccc}1& 0& 0& 0& 0\\ 0& \cos \theta & \sin \theta & 0& 0\\ 0& -\sin \theta & \cos \theta & 0& 0\\ 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 1\end{array}\right].$$

(87)

The Killing vector field associated with ${\xi }_{{\mathcal{R}}^3}$ reads:

$$\begin{array}{cc}\hfill {\mathbb{X}}_{{\xi }_{{\mathcal{R}}^3}}=\frac{d}{d\theta }{\left[{\Phi }_{e^{\theta {\xi }_{{\mathcal{R}}^3}}}^{\mathcal{E}{\mathcal{L}}_{\mathbb{M}}}·\chi \right]}_{\theta =0}=(& {\left({\mathbb{X}}_{{\xi }_{{\mathcal{R}}^3}}\right)}_u=x^2\frac{\partial \varphi }{\partial x^1}-x^1\frac{\partial \varphi }{\partial x^2},\hfill \\ & {\left({\mathbb{X}}_{{\xi }_{{\mathcal{R}}^3}}\right)}_{{\rho }^0}=x^2\frac{\partial P^0}{\partial x^1}-x^1\frac{\partial P^0}{\partial x^2},\hfill \\ & {\left({\mathbb{X}}_{{\xi }_{{\mathcal{R}}^3}}\right)}_{{\rho }^1}=x^2\frac{\partial P^1}{\partial x^1}-x^1\frac{\partial P^1}{\partial x^2}+P^2,\hfill \\ & {\left({\mathbb{X}}_{{\xi }_{{\mathcal{R}}^3}}\right)}_{{\rho }^2}=x^2\frac{\partial P^2}{\partial x^1}-x^1\frac{\partial P^2}{\partial x^2}-P^1,\hfill \\ & {\left({\mathbb{X}}_{{\xi }_{{\mathcal{R}}^3}}\right)}_{{\rho }^3}=x^2\frac{\partial P^3}{\partial x^1}-x^1\frac{\partial P^3}{\partial x^2}).\hfill \end{array}$$

(88)

Consequently:

$${\Pi }_{\Sigma }^{\star }{\Omega }^{\Sigma }({\mathbb{X}}_{{\xi }_{{\mathcal{R}}^3}},\mathbb{Y})={\int }_{\Sigma }\left[\left(x^2\frac{\partial \varphi }{\partial x^1}-x^1\frac{\partial \varphi }{\partial x^2}\right){\mathbb{Y}}_{{\rho }^0}-\left(x^2\frac{\partial P^0}{\partial x^1}-x^1\frac{\partial P^0}{\partial x^2}\right){\mathbb{Y}}_u\right]vo{l}_{\Sigma },$$

(89)

whereas:

$$\mathrm{d}{J}_{{\xi }_{{\mathcal{R}}^3}}(\mathbb{Y})={\int }_{\mathbb{M}}\left[\frac{\delta J_{{\xi }_{{\mathcal{R}}^3}}}{\delta \varphi }{\mathbb{Y}}_u+\frac{\delta J_{{\xi }_{{\mathcal{R}}^3}}}{\delta \varphi }{\mathbb{Y}}_{{\rho }^0}\right]vo{l}_{\mathbb{M}}.$$

(90)

Therefore, $J_{{\xi }_{{\mathcal{R}}^3}}$ is the function satisfying, as always, in the sense of distributions:

$$\begin{array}{c}\hfill \frac{\delta J_{{\xi }_{{\mathcal{R}}^3}}}{\delta \varphi }\delta (x^0-x_{\Sigma }^0)=-x^2\frac{\partial P^0}{\partial x^1}+x^1\frac{\partial P^0}{\partial x^2},\\ \hfill \frac{\delta J_{{\xi }_{{\mathcal{R}}^3}}}{\delta P^0}\delta (x^0-x_{\Sigma }^0)=x^2\frac{\partial \varphi }{\partial x^1}-x^1\frac{\partial \varphi }{\partial x^2},\end{array}$$

(91)

i.e.,

$$J_{{\xi }_{{\mathcal{R}}^3}}={\int }_{\Sigma }{\left[P^0\left(x^2\frac{\partial \varphi }{\partial x^1}-x^1\frac{\partial \varphi }{\partial x^2}\right)\right]}_{\Sigma }vo{l}_{\Sigma }.$$

(92)

An analogous calculation gives

$$\begin{array}{c}\hfill J_{{\xi }_{{\mathcal{R}}^{x^2}}}={\int }_{\Sigma }{\left[P^0\left(x^1\frac{\partial \varphi }{\partial x^3}-x^3\frac{\partial \varphi }{\partial x^1}\right)\right]}_{\Sigma }vo{l}_{\Sigma },\\ \hfill J_{{\xi }_{{\mathcal{R}}^{x^1}}}={\int }_{\Sigma }{\left[P^0\left(x^2\frac{\partial \varphi }{\partial x^3}-x^3\frac{\partial \varphi }{\partial x^2}\right)\right]}_{\Sigma }vo{l}_{\Sigma }.\end{array}$$

(93)

Note that $J_{{\xi }_{{\mathcal{R}}^{x^j}}}$ are the j-components (j going from 1 to 3) of the divergence of the generalized angular momentum of the Klein–Gordon field.

Now, to compute the momentum map associated with ${\xi }_{{\mathcal{R}}^{x^k}}$, one can recall that the group of spatial rotations is the subgroup $SO(3)$ of the Poincaré group and that its Lie algebra is isomorphic with ${\mathbb{R}}^3$. Consequently, the dual of $\mathfrak{so}(3)$ is isomorphic with ${\mathbb{R}}^3$ and, thus, if we consider ${\xi }_{{\mathcal{R}}^{x^j}}$ as a basis for $\mathfrak{so}(3)$, the components of the momentum map satisfying $\langle \mathbb{J}(\chi ),{\xi }_{{\mathcal{R}}^{x^j}}\rangle =J_{{\xi }_{{\mathcal{R}}^{x^j}}}$ read:

$$\mathbb{J}{(\chi )}_j=J_{{\xi }_{{\mathcal{R}}^{x^j}}}j=1,2,3.$$

(94)

The computations of the currents associated to the boosts of the Poincaré group are analogous to the ones we did for the rotation, if one recalls that the boosts along the three-axis can be represented as:

$$\begin{array}{cc}\hfill {\Phi }_{{\mathcal{B}}^{x^1}}^{\mathbb{M}}& =\left[\begin{array}{ccccc}\cosh w& -\sinh w& 0& 0& 0\\ -\sinh w& \cosh w& 0& 0& 0\\ 0& 0& 1& 0& 0\\ 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 1\end{array}\right]\hfill \\ \hfill {\Phi }_{{\mathcal{B}}^{x^2}}^{\mathbb{M}}& =\left[\begin{array}{ccccc}\cosh w& 0& -\sinh w& 0& 0\\ 0& 1& 0& 0& 0\\ -\sinh w& 0& \cosh w& 0& 0\\ 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 1\end{array}\right]\hfill \\ \hfill {\Phi }_{{\mathcal{B}}^{x^3}}^{\mathbb{M}}& =\left[\begin{array}{ccccc}\cosh w& 0& 0& -\sinh w& 0\\ 0& 1& 0& 0& 0\\ 0& 0& 1& 0& 0\\ -\sinh w& 0& 0& \cosh w& 0\\ 0& 0& 0& 0& 1\end{array}\right],\hfill \end{array}$$

(95)

where w represents the rapidity of the boost. The three currents obtained in this case are:

$$\begin{array}{cc}\hfill J_{{\xi }_{{\mathcal{B}}^{x^1}}}& =-{\int }_{\Sigma }{\left[P^0\left(x^1\frac{\partial \varphi }{\partial x^0}+x^0\frac{\partial \varphi }{\partial x^1}\right)+P^1\varphi \right]}_{\Sigma }vo{l}_{\Sigma }\hfill \\ \hfill J_{{\xi }_{{\mathcal{B}}^{x^2}}}& =-{\int }_{\Sigma }{\left[P^0\left(x^2\frac{\partial \varphi }{\partial x^0}+x^0\frac{\partial \varphi }{\partial x^2}\right)+P^2\varphi \right]}_{\Sigma }vo{l}_{\Sigma }\hfill \\ \hfill J_{{\xi }_{{\mathcal{B}}^{x^3}}}& =-{\int }_{\Sigma }{\left[P^0\left(x^3\frac{\partial \varphi }{\partial x^0}+x^0\frac{\partial \varphi }{\partial x^3}\right)+P^3\varphi \right]}_{\Sigma }vo{l}_{\Sigma },\hfill \end{array}$$

(96)

which are the remaining three independent components of the divergence of the generalized angular momentum usually found in field theory textbooks. The components of the momentum map in this case are:

$$\mathbb{J}{(\chi )}_j=J_{{\xi }_{{\mathcal{B}}^{x^j}}}j=1,2,3.$$

(97)

4.3. Gauge Theories: Free Electrodynamics

In this section, we apply the theory developed in Section 2 to the case in which the presymplectic manifold is the space of solutions of a gauge theory.

In the example considered, the underlying space–time is, as in the Klein–Gordon theory discussed in Section 4.2, the Minkowski space–time $(\mathbb{M},\eta )$, where we chose the (global) chart $(U_{\mathbb{M}},{\psi }_{U_{\mathbb{M}}})$, ${\psi }_{U_{\mathbb{M}}}(m)=x^{\mu }$ where $m\in U_{\mathbb{M}}\subset \mathbb{M}$. A covariant formulation of free classical electrodynamics is usually given in terms of the so called quadri-potential $A_{\mu }(x)$ and the associated field strength $F_{\mu \nu }={\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu }$. Indeed, in terms of these objects, an action functional is given as follows:

$$\mathcal{S}[A_{\mu },{\partial }_{\mu }{A}_{\nu }]=\frac{1}{4}{\int }_{\mathcal{M}}{F}^{\mu \nu }{F}_{\mu \nu }{d}^{4}x,$$

(98)

whose field equations:

$${\partial }_{\mu }{F}^{\mu \nu }=0,$$

(99)

coincide with the free Maxwell equations involving the electric and magnetic fields that are written in terms of $A_{\mu }$, as follows:

$$E_j=\frac{\partial }{\partial x^0}{A}_j-\frac{\partial }{\partial x^j}{A}_0{B}_j={ϵ}_{jkl}\frac{\partial }{\partial x^k}{A}^l.$$

(100)

The energy–momentum tensor of the theory reads:

$${\mathcal{T}}^{\mu \nu }=F^{\mu \sigma }{F_{\sigma }}^{\nu }+\frac{1}{4}{\eta }^{\mu \nu }{F}^{\sigma \eta }{F}_{\sigma \eta }.$$

(101)

A multisymplectic Hamiltonian formulation of the theory can be given by considering the bundle $\mathbb{E}\to \mathbb{M}$ to be the cotangent bundle over $\mathbb{M}$, i.e., the typical fiber is $\mathcal{E}={\mathbf{T}}_m^{\star }\mathbb{M}$ and the configuration fields $\varphi$ to be (Lie algebra-valued) one-forms over $\mathbb{M}$ (In this case, the Lie algebra is that of the abelian group $U(1)$, which is isomorphic with $\mathbb{R}$) that we will denote by $\varphi =A=A_{\mu }(x)\mathrm{d}{x}^{\mu }$.

The covariant phase space $\mathcal{P}(\mathbb{E})$ has typical fiber ${\mathbf{T}}_m^{\star }\mathbb{M}\otimes \left({\bigwedge }^2{\mathbf{T}}_m\mathbb{M}\right)$. We chose on it the following adapted fibered chart $(U_{\mathcal{P}(\mathbb{E})},{\psi }_{U_{\mathcal{P}(\mathbb{E})}})$, ${\psi }_{U_{\mathcal{P}(\mathbb{E})}}(\mathfrak{p})=(u_{\mu },{\rho }^{\mu \nu },x^{\mu })$ where $\mathfrak{p}\in U_{\mathcal{P}(\mathbb{E})}\subset \mathcal{P}(\mathbb{E})$. The space of dynamical fields ${\mathcal{F}}_{\mathcal{P}(\mathbb{E})}$ is the space of factorizable sections of the bundle ${\delta }_1:\mathcal{P}(\mathbb{E})\to \mathbb{M}$, (Equation (26)):

$$\chi :U_{\mathbb{M}}\to U_{\mathcal{P}(\mathbb{E})}:{\psi }_{\mathbb{M}}^{-1}(x^{\mu })\mapsto \chi \left({\psi }_{U_{\mathbb{M}}}^{-1}(x^{\mu })\right)=\left({\psi }_{U_{\mathbb{M}}}^{-1}(x^{\mu }),A_{\mu }({\psi }_{U_{\mathbb{M}}}^{-1}(x^{\mu })),P^{\mu \nu }({\psi }_{U_{\mathbb{M}}}^{-1}(x^{\mu }))\right),$$

(102)

where $A_{\mu }$ are sections of $\mathbb{E}\to \mathbb{M}$ belonging to the Sobolev space ${\mathcal{H}}^1(\mathbb{M},vo{l}_{\mathbb{M}})$ and $P^{\mu \nu }$ are square integrable sections of the pull-back bundle $A^{\star }\mathcal{P}(\mathbb{E})$. This is consistent for the same reasons as the previous example. For the sake of simplicity, we denote them by:

$$\chi (x^{\mu })=(x^{\mu },A_{\mu }(x^{\nu }),P^{\mu \nu }(x^{\sigma })).$$

The Hamiltonian of the theory is just the quadratic function:

$$H=\frac{1}{2}{\eta }_{\mu \alpha }{\eta }_{\nu \beta }{\rho }^{\mu \nu }{\rho }^{\alpha \beta },$$

and the Hamiltonian functional is:

$$\mathcal{H}={\int }_{\Sigma }\left[p^k{\partial }_k{a}_0+\frac{1}{2}{\beta }^{kj}\left({\partial }_k{a}_j-{\partial }_j{a}_k\right)+\frac{1}{4}{\delta }_{jl}{\delta }_{km}{\beta }^{jk}{\beta }^{lm}+\frac{1}{2}{\delta }_{jk}{p}^k{p}^j\right]{\mathrm{vol}}_{\Sigma },$$

(103)

where $\Sigma$ is any slice of $\mathbb{M}$, which, for definiteness, we take to be a Cauchy hypersurface diffeomorphic to ${\mathbb{R}}^3$ defined by $x^0=x_{\Sigma }^0$, and $a_{\mu }$, $p^k$ and ${\beta }^{jk}$ denote the restrictions of $A_{\mu }$, $P^{0k}$ and $P^{jk}$ respectively, to $\Sigma$. The equations of motion are:

$$\begin{array}{cc}\hfill F_{\mu \nu }+\frac{1}{2}{\eta }_{\mu \alpha }{\eta }_{\nu \beta }{P}^{\alpha \beta }& =0,\hfill \\ \hfill \frac{\partial P^{\mu \nu }}{\partial x^{\mu }}& =0,\hfill \end{array}$$

(104)

where $F_{\mu \nu }=\frac{1}{2}({\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu })$, and whose solutions are given by:

$$\begin{array}{cc}\hfill A_k(x^{\mu })=\frac{1}{4\pi }[& {\int }_{\Sigma }\left(a_k^{\Sigma }(\underline{y})+|x^0-x_{\Sigma }^0|{\delta }_{kj}{p}_{\Sigma }^j(\underline{y})\right){\tilde{G}}_{\underline{x},|x^0-x_{\Sigma }^0|}(\underline{y})vo{l}_{\Sigma }+\hfill \\ & {\int }_{\Sigma }|x^0-x_{\Sigma }^0|a_k^{\Sigma }(\underline{y})\frac{\partial }{\partial s}{\tilde{G}}_{\underline{x},(x^0-x_{\Sigma }^0)}(\underline{y})(\Theta (x^0-x_{\Sigma }^0)-\Theta (x_{\Sigma }^0-x^0))vo{l}_{\Sigma }],\hfill \end{array}$$

(105)

where the integration on $\Sigma$ is over the $\underline{y}$ variables and ${\tilde{G}}_{\underline{x},a}(\underline{y})$ is the characteristic function of the surface of the sphere with center $\underline{x}$ and radius a and $\Theta$ is the Heaviside function, i.e., the discontinuous function being 1 for its argument being positive and 0 for its argument being less then or equal to 0. On the other hand $A_0$ is completely undetermined by the equations of motion and the standard treatment is to fix it using a suitable gauge fixing (in [38] the Coulomb gauge is fixed) while the $P^{\mu \nu }$ are determined by the constraint equation:

$$F_{\mu \nu }+\frac{1}{2}{\eta }_{\mu \alpha }{\eta }_{\nu \beta }{P}^{\alpha \beta }=0.$$

(106)

As proven in [49] (see, for instance, [18] and references therein for the geometric treatment of the non-Abelian case), the final manifold of constraints obtained by using the PCA, ${\mathcal{M}}_{\infty }$, is:

$${\mathcal{M}}_{\infty }=\left\{(a_k,p^k):{\partial }_k{p}^k=0k=1,2,3\right\}={\mathcal{H}}^1(\Sigma )\times \mathcal{H}(\mathrm{div}0,\Sigma ),$$

(107)

where $\mathcal{H}(\mathrm{div}0,\Sigma )$ denotes the closed Hilbert subspace of ${\mathcal{L}}^2(\Sigma ,vo{l}_{\Sigma })$ such that ${\partial }_k{p}^k=0$ (see [50] (Equation (1.41), Equation (1.42))). The structure ${\Omega }_{\infty }^{\Sigma }$ reads:

$${\Omega }_{\infty }^{\Sigma }(\mathbb{X},\mathbb{Y})={\int }_{\Sigma }\left({\mathbb{X}}_{a_k}{\mathbb{Y}}_p^k-{\mathbb{X}}_p^k{\mathbb{Y}}_{a_k}\right)vo{l}_{\Sigma }.$$

(108)

The kernel of ${\Omega }_{\infty }^{\Sigma }$ consists of vector fields with ${\mathbb{X}}_{a_k}={\partial }_k\varphi$ for some $\varphi$. They generate (via their flow) the following action on ${\mathcal{M}}_{\infty }$:

$${\Phi }_{{\mathbb{X}}_{\partial \varphi }}:{\mathcal{M}}_{\infty }\to {\mathcal{M}}_{\infty }:m_{\infty }\mapsto {\Phi }_{{\mathbb{X}}_{\partial \varphi }}·m_{\infty }=(a_k+{\partial }_k\varphi ,p^k).$$

(109)

In order for this action to be well-defined, we choose the space of gauge functions $\varphi$ to belong to ${\mathcal{H}}^2(\Sigma )$. Now, let us note that the following splitting of ${\mathcal{M}}_{\infty }$ exists:

$${\mathcal{M}}_{\infty }\simeq {\mathcal{H}}^1(\mathrm{div}0,\Sigma )\times \mathrm{grad}{\mathcal{H}}^2(\Sigma )\times \mathcal{H}(\mathrm{div}0,\Sigma ),$$

(110)

which comes from the the following decomposition of ${\mathcal{H}}^1(\Sigma )$ [50]:

$${\mathcal{H}}^1(\Sigma )={\mathcal{H}}^1(\mathrm{div}0,\Sigma )\oplus \mathrm{grad}{\mathcal{H}}^2(\Sigma ),$$

(111)

where $\mathrm{grad}{\mathcal{H}}^2(\Sigma )$ is the image of the $\mathrm{grad}$ operator acting on ${\mathcal{H}}^2(\Sigma )$. Accordingly with the latter decomposition, we denote points in ${\mathcal{M}}_{\infty }$ by $m_{\infty }=({\tilde{a}}_k,{\partial }_k\varphi ,p^k)$, where ${\tilde{a}}_k\in {\mathcal{H}}^1(\mathrm{div}0,\Sigma )$. By virtue of the decomposition above, the tangent space of ${\mathcal{M}}_{\infty }$ at some point $m_{\infty }$ also splits as:

$${\mathbf{T}}_{m_{\infty }}{\mathcal{M}}_{\infty }={\mathcal{H}}^1(\mathrm{div}0,\Sigma )\times \mathrm{grad}{\mathcal{H}}^2(\Sigma )\times \mathcal{H}(\mathrm{div}0,\Sigma ),$$

(112)

because of the natural identifications: ${\mathbf{T}}_{m_{\infty }}{\mathcal{H}}^1(\mathrm{div}0,\Sigma )\cong {\mathcal{H}}^1(\mathrm{div}0,\Sigma )$, ${\mathbf{T}}_{m_{\infty }}\mathrm{grad}{\mathcal{H}}^2(\Sigma )\cong \mathrm{grad}{\mathcal{H}}^2(\Sigma )$ and ${\mathbf{T}}_{m_{\infty }}\mathcal{H}(\mathrm{div}0,\Sigma )\cong \mathcal{H}(\mathrm{div}0,\Sigma )$. The second term in the right hand side of (112) clearly represents the kernel of ${\Omega }_{\infty }^{\Sigma }$, say K. A connection on the bundle ${\mathcal{M}}_{\infty }\to {\mathcal{M}}_{\infty }/\mathrm{grad}{\mathcal{H}}^2(\Sigma )$ exists whose horizontal vector fields lie, at each point, in the complement of K in the decomposition (112) and is the so called Coulomb connection:

$$\mathcal{R}:\mathfrak{X}({\mathcal{M}}_{\infty })\to {\mathfrak{X}}^H({\mathcal{M}}_{\infty })={\mathcal{H}}^1(\mathrm{div}0,\Sigma )\times \mathcal{H}(\mathrm{div}0,\Sigma ):\mathbb{X}\mapsto \mathcal{R}(\mathbb{X})=\tilde{\mathbb{X}},$$

(113)

where the tangent vector $\tilde{\mathbb{X}}$ is given by:

$$\tilde{\mathbb{X}}=\left({\tilde{\mathbb{X}}}_{a_k}={\mathbb{X}}_{a_k}-{\partial }_k{\int }_{\Sigma }{G}_{\Delta }{\delta }^{jl}{\partial }_j{\mathbb{X}}_{a_l}vo{l}_{\Sigma },{\tilde{\mathbb{X}}}_p^k={\mathbb{X}}_p^k\right),$$

(114)

and $G_{\Delta }$ represents the Green function of the Laplacian operator.

The coisotropic embedding theorem in this case leads to the following symplectic manifold:

$$\begin{array}{cc}\hfill \mathcal{P}& ={\mathcal{H}}^1(\mathrm{div}0,\Sigma )\times \mathrm{grad}{\mathcal{H}}^2(\Sigma )\times \mathcal{H}(\mathrm{div}0,\Sigma )\times K^{\star }\simeq \hfill \\ \hfill & \simeq {\mathcal{H}}^1(\mathrm{div}0,\Sigma )\times \mathrm{grad}{\mathcal{H}}^2(\Sigma )\times \mathcal{H}(\mathrm{div}0,\Sigma )\times \mathrm{grad}{\mathcal{H}}^2{(\Sigma )}^{\star },\hfill \end{array}$$

(115)

We denote points in $\mathcal{P}$ by ${\tilde{m}}_{\infty }=({\tilde{a}}_k,{\partial }_k\varphi ,p^k,{\mu }^k)$ and the symplectic structure ${\Omega }^{\mathcal{P}}$ reads:

$${\Omega }^{\mathcal{P}}(\mathbb{X}\otimes \kappa ,\mathbb{Y}\otimes {\kappa }^{\prime })={\int }_{\Sigma }\left({{\mathbb{X}}_{\tilde{a}}}_k{\mathbb{Y}}_p^k-{\mathbb{X}}_p^k{{\mathbb{Y}}_{\tilde{a}}}_k\right)vo{l}_{\Sigma }+\langle \kappa ,{\mathbb{Y}}_{\partial \varphi }\rangle -\langle {\kappa }^{\prime },{\mathbb{X}}_{\partial \varphi }\rangle ,$$

(116)

where $\langle ·,·\rangle$ represents the pairing between $\mathrm{grad}{\mathcal{H}}^2(\Sigma )$ and its dual. Now, let us consider the group of symmetries of the space–time $\mathbb{M}$, i.e., the Poincaré group. In particular, let us focus on the group of spatial rotations. They act on $\mathbb{M}$ by means of $SO(3)$ matrices:

$${\Phi }_{\mathcal{R}}^{\mathbb{M}}:\mathbb{M}\to \mathbb{M}:x^k\mapsto {\Phi }_{\mathcal{R}}^{\mathbb{M}}{(x)}^k={\mathcal{R}}_j^k{x}^j,$$

(117)

where ${\mathcal{R}}_j^k$ represent the matrix elements of the $SO(3)$ matrix ${\Phi }_{\mathcal{R}}^{\mathbb{M}}$. Since the fields a are 1-forms on $\mathbb{M}$ and the fields p are contravariant tensors on $\mathbb{M}$, they transform via the pull-back (via ${\Phi }_{{\mathcal{R}}^{-1}}^{\mathbb{M}}$) and via the push-forward (via ${\Phi }_{\mathcal{R}}^{\mathbb{M}}$), respectively. Therefore, the action of $\mathcal{R}$ is lifted to ${\mathcal{M}}_{\infty }$ as:

$$\begin{array}{cc}\hfill {\Phi }_{\mathcal{R}}^{{\mathcal{M}}_{\infty }}:{\mathcal{M}}_{\infty }\to {\mathcal{M}}_{\infty }:& ({\tilde{a}}_k(x),{\partial }_k\varphi (x),p^k(x))\mapsto \hfill \\ & \mapsto \left({{\mathcal{R}}^{-1}}_k^j{\tilde{a}}_j\left({\Phi }_{\mathcal{R}}^{\mathbb{M}}·x\right),{{\mathcal{R}}^{-1}}_k^j{\partial }_j\varphi \left({\Phi }_{\mathcal{R}}^{\mathbb{M}}·x\right),{\mathcal{R}}_j^k{p}^j({\Phi }_{\mathcal{R}}^{\mathbb{M}}·x)\right).\end{array}$$

(118)

This action can also be lifted to $\mathcal{P}$ via the procedure explained in Section 2 by computing the dual action of its tangent lift. A straightforward calculation gives the following action on $\mathcal{P}$:

$$\begin{array}{cc}\hfill {\Phi }_{\mathcal{R}}^{\mathcal{P}}:\mathcal{P}\to \mathcal{P}:& \left({\tilde{a}}_k(x),{\partial }_k\varphi (x),p^k(x),{\mu }^k(x)\right)\mapsto \hfill \\ & \mapsto \left({{\mathcal{R}}^{-1}}_k^j{\tilde{a}}_j\left({\Phi }_{\mathcal{R}}^{\mathbb{M}}·x\right),{{\mathcal{R}}^{-1}}_k^j{\partial }_j\varphi \left({\Phi }_{\mathcal{R}}^{\mathbb{M}}·x\right),{\mathcal{R}}_j^k{p}^j({\Phi }_{\mathcal{R}}^{\mathbb{M}}·x),{\mathcal{R}}_j^k{\mu }^j\left({\Phi }_{\mathcal{R}}^{\mathbb{M}}·x\right)\right).\end{array}$$

(119)

Let us focus for a moment in the case in which $\mathcal{R}$ is a rotation around the $x^3$-axis, denoted, for short, ${\mathcal{R}}^3$. Now, we prove that the action above is canonical and gives rise to a momentum map satisfying:

$${\Omega }^{\mathcal{P}}({\mathbb{X}}_{{\xi }_{{\mathcal{R}}^3}},\mathbb{Y}\oplus {\kappa }^{\prime })=\mathrm{d}{J}_{{\xi }_{{\mathcal{R}}^3}}(\mathbb{Y}\oplus {\kappa }^{\prime }),$$

(120)

where ${\mathbb{X}}_{{\xi }_{{\mathcal{R}}^3}}$ is the generator of the action (119). In the case considered, ${\xi }_{{\mathcal{R}}^3}$ is an element in $\mathfrak{so}(3)$ represented by the matrix:

$${\Phi }_{{\xi }_{{\mathcal{R}}^3}}=\left[\begin{array}{ccc}0& 0& -1\\ 0& 0& 0\\ 1& 0& 0\end{array}\right],$$

(121)

and the vector field ${\mathbb{X}}_{{\xi }_{{\mathcal{R}}^3}}$ is:

$$\begin{array}{c}\hfill {\mathbb{X}}_{{\xi }_{{\mathcal{R}}^3}}=\frac{d}{d\theta }{\left[{\Phi }_{e^{\theta {\xi }_{{\mathcal{R}}^3}}}^{\mathcal{P}}·{\tilde{m}}_{\infty }\right]}_{\theta =0}=\left({\left({\mathbb{X}}_{{\xi }_{{\mathcal{R}}^3}}\right)}_{{\tilde{a}}_k},{\left({\mathbb{X}}_{{\xi }_{{\mathcal{R}}^3}}\right)}_{\partial {\varphi }_k},{\left({\mathbb{X}}_{{\xi }_{{\mathcal{R}}^3}}\right)}_p^k,{\left({\mathbb{X}}_{{\xi }_{{\mathcal{R}}^3}}\right)}_{\mu }^k\right),\end{array}$$

(122)

where:

$${\left({\mathbb{X}}_{{\xi }_{{\mathcal{R}}^3}}\right)}_{{\tilde{a}}_k}=\left[\begin{array}{c}(x^2{\partial }_1-x^1{\partial }_2){\tilde{a}}_1+{\tilde{a}}_2\\ -{\tilde{a}}_1+(x^2{\partial }_1-x^1{\partial }_2){\tilde{a}}_2\\ (x^2{\partial }_1-x^1{\partial }_2){\tilde{a}}_3\end{array}\right]$$

(123)

$${\left({\mathbb{X}}_{{\xi }_{{\mathcal{R}}^3}}\right)}_{\partial {\varphi }_k}=\left[\begin{array}{c}(x^2{\partial }_1-x^1{\partial }_2){\partial }_1\varphi +{\partial }_2\varphi \\ -{\partial }_1\varphi +(x^2{\partial }_1-x^1{\partial }_2){\partial }_2\varphi \\ (x^2{\partial }_1-x^1{\partial }_2){\partial }_3\varphi \end{array}\right],$$

(124)

$${\left({\mathbb{X}}_{{\xi }_{{\mathcal{R}}^3}}\right)}_p^k=\left[\begin{array}{c}(x^2{\partial }_1-x^1{\partial }_2)p^1+p^2\\ -p^1+(x^2{\partial }_1-x^1{\partial }_2)p^2\\ (x^2{\partial }_1-x^1{\partial }_2)p^3\end{array}\right]$$

(125)

$${\left({\mathbb{X}}_{{\xi }_{{\mathcal{R}}^3}}\right)}_{\mu }^k=\left[\begin{array}{c}(x^2{\partial }_1-x^1{\partial }_2){\mu }^1+{\mu }^2\\ -{\mu }^1+(x^2{\partial }_1-x^1{\partial }_2){\mu }^2\\ (x^2{\partial }_1-x^1{\partial }_2){\mu }^3\end{array}\right].$$

(126)

Therefore, the left hand side of (120) is

$${\int }_{\Sigma }\left({\left({\mathbb{X}}_{{\xi }_{{\mathcal{R}}^3}}\right)}_{{\tilde{a}}_k}{\mathbb{Y}}_p^k-{\left({\mathbb{X}}_{{\xi }_{{\mathcal{R}}^3}}\right)}_p^k{{\mathbb{Y}}_{\tilde{a}}}_k\right)vo{l}_{\Sigma }+\langle {\left({\mathbb{X}}_{{\xi }_{{\mathcal{R}}^3}}\right)}_{\mu },{{\mathbb{Y}}_{\partial \varphi }}_k\rangle -\langle {\kappa }^{\prime },{\left({\mathbb{X}}_{{\xi }_{{\mathcal{R}}^3}}\right)}_{\partial \varphi }\rangle .$$

(127)

On the other hand, the right hand side of (120) reads

$${\int }_{\Sigma }\left(\frac{\delta J_{{\xi }_{{\mathcal{R}}^3}}}{\delta {\tilde{a}}_k}{{\mathbb{Y}}_{\tilde{a}}}_k+\frac{\delta J_{{\xi }_{{\mathcal{R}}^3}}}{\delta {\partial }_k\varphi }{{\mathbb{Y}}_{\partial \varphi }}_k+\frac{\delta J_{{\xi }_{{\mathcal{R}}^3}}}{\delta p^k}{\mathbb{Y}}_p^k\right)vo{l}_{\Sigma }+\langle \frac{\delta J_{{\xi }_{{\mathcal{R}}^3}}}{\delta \mu },{\kappa }^{\prime }\rangle ,$$

(128)

which gives:

$$\frac{\delta J_{{\xi }_{{\mathcal{R}}^3}}}{\delta {\tilde{a}}_k}=\left[\begin{array}{c}-(x^2{\partial }_1-x^1{\partial }_2)p^1-p^2\\ p^1-(x^2{\partial }_1-x^1{\partial }_2)p^2\\ -(x^2{\partial }_1-x^1{\partial }_2)p^3\end{array}\right]$$

(129)

$$\frac{\delta J_{{\xi }_{{\mathcal{R}}^3}}}{\delta {\partial }_k\varphi }=\left[\begin{array}{c}(x^2{\partial }_1-x^1{\partial }_2){\mu }^1+{\mu }^2\\ -{\mu }^1+(x^2{\partial }_1-x^1{\partial }_2){\mu }^2\\ (x^2{\partial }_1-x^1{\partial }_2){\mu }^3\end{array}\right]$$

(130)

$$\frac{\delta J_{{\xi }_{{\mathcal{R}}^3}}}{\delta p^k}=\left[\begin{array}{c}(x^2{\partial }_1-x^1{\partial }_2){\tilde{a}}_1+{\tilde{a}}_2\\ -{\tilde{a}}_1+(x^2{\partial }_1-x^1{\partial }_2){\tilde{a}}_2\\ (x^2{\partial }_1-x^1{\partial }_2){\tilde{a}}_3\end{array}\right]$$

(131)

$$\frac{\delta J_{{\xi }_{{\mathcal{R}}^3}}}{\delta {\mu }^k}=\left[\begin{array}{c}-(x^2{\partial }_1-x^1{\partial }_2){\partial }_1\varphi -{\partial }_2\varphi \\ {\partial }_1\varphi -(x^2{\partial }_1-x^1{\partial }_2){\partial }_2\varphi \\ -(x^2{\partial }_1-x^1{\partial }_2){\partial }_3\varphi \end{array}\right],$$

(132)

and, thus:

$$\begin{array}{cc}& J_{{\xi }_{{\mathcal{R}}^3}}({\tilde{a}}_k,{\partial }_k\varphi ,p^k,{\mu }^k)=\hfill \\ & ={\int }_{\Sigma }\left[(x^2{\partial }_1-x^1{\partial }_2){\tilde{a}}_1{p}^1+{\tilde{a}}_2{p}^1+(x^2{\partial }_1-x^1{\partial }_2){\tilde{a}}_2{p}^2-{\tilde{a}}_1{p}^2+(x^2{\partial }_1-x^1{\partial }_2){\tilde{a}}_3{p}^3\right]vo{l}_{\Sigma }\hfill \\ & +\langle {\mu }^1,(x^2{\partial }_1-x^1{\partial }_2){\partial }_1\varphi -{\partial }_2\varphi \rangle +\langle {\mu }^2,(x^2{\partial }_1-x^1{\partial }_2){\partial }_2\varphi +{\partial }_1\varphi \rangle +\langle {\mu }^3,(x^2{\partial }_1-x^1{\partial }_2){\partial }_3\varphi \rangle .\hfill \end{array}$$

(133)

Let us note that the quantities in the right arguments of the pairings above are the components of the vector field ${\mathbb{X}}_{{\xi }_{{\mathcal{R}}^3}}$ that correspond to the components of the vector field ${\mathbb{X}}_{{\xi }_{{\mathcal{R}}^3}}^H$, being the horizontal lifting of the vector field ${\mathbb{X}}_{{\xi }_{{\mathcal{R}}^3}}$, with respect to the connection ${\mathcal{R}}^{\uparrow }$ that extends the Coulomb connection $\mathcal{R}$ introduced above, Equation (113):

$${\mathcal{R}}^{\uparrow }:\mathfrak{X}(\mathcal{P})\to {\mathfrak{X}}^H(\mathcal{P}):\mathbb{X}\oplus \kappa \mapsto {\mathcal{R}}^{\uparrow }(\mathbb{X})={\mathbb{X}}^H=\tilde{\mathbb{X}}\oplus \tilde{\kappa }$$

(134)

where $\tilde{\mathbb{X}}=\mathcal{R}(\mathbb{X})$ and $\tilde{\kappa }=\kappa$. With this in mind, the function (133) has exactly the expression (22) for the connection $A={\mathcal{R}}^{\uparrow }$.

The currents $J_{{\xi }_{{\mathcal{R}}^{x^1}}}$ and $J_{{\xi }_{{\mathcal{R}}^{x^2}}}$ can be computed in the same way, obtaining:

$$\begin{array}{cc}\hfill J_{{\xi }_{{\mathcal{R}}^{x^1}}}& ={\int }_{\Sigma }\left[(x^1{\partial }_3-x^3{\partial }_1){\tilde{a}}_1{p}^1+(x^1{\partial }_3-x^3{\partial }_1){\tilde{a}}_2{p}^2+{\tilde{a}}_3{p}^2+(x^1{\partial }_3-x^3{\partial }_1){\tilde{a}}_3{p}^3-{\tilde{a}}_2{p}^3\right]vo{l}_{\Sigma }+\hfill \\ \hfill +& \langle {\mu }^1,(x^1{\partial }_3-x^3{\partial }_1){\partial }_1\varphi \rangle +\langle {\mu }^2,(x^1{\partial }_3-x^3{\partial }_1){\partial }_2\varphi -{\partial }_3\varphi \rangle +\langle {\mu }^3,(x^1{\partial }_3-x^3{\partial }_1){\partial }_3\varphi +{\partial }_2\varphi \rangle ,\hfill \end{array}$$

(135)

and:

$$\begin{array}{cc}\hfill J_{{\xi }_{{\mathcal{R}}^{x^2}}}& ={\int }_{\Sigma }\left[(x^3{\partial }_2-x^2{\partial }_3){\tilde{a}}_1{p}^1+{\tilde{a}}_3{p}^1+(x^3{\partial }_2-x^2{\partial }_3){\tilde{a}}_2{p}^2+(x^3{\partial }_2-x^2{\partial }_3){\tilde{a}}_3{p}^3-{\tilde{a}}_1{p}^3\right]vo{l}_{\Sigma }+\hfill \\ \hfill +& \langle {\mu }^1,(x^3{\partial }_2-x^2{\partial }_3){\partial }_1\varphi -{\partial }_3\varphi \rangle +\langle {\mu }^2,(x^3{\partial }_2-x^2{\partial }_3){\partial }_2\varphi \rangle +\langle {\mu }^3,(x^3{\partial }_2-x^2{\partial }_3){\partial }_3\varphi +{\partial }_1\varphi \rangle .\hfill \end{array}$$

(136)

The three currents computed so far can be pulled back to the physical space ${\mathcal{M}}_{\infty }$. As explained in the previous section the pull-back is done by taking the coordinate ${\mu }^k=0$, and it coincides with the standard components $0jk$ of the generalized angular momentum of the electromagnetic field. Thus, we obtain that the components of the momentum map ${\mathbb{J}}_{\mathcal{P}}$ corresponding to the subgroup $SO(3)$ of the Poincaré group $\mathcal{P}$ are exactly the three currents computed above

$${\mathbb{J}}_{\mathcal{P}}{({\tilde{m}}_{\infty })}_j=J_{{\xi }_{{\mathcal{R}}^{x^j}}}j=1,2,3.$$

(137)

We conclude this section by discussing how the conservation of the electric charge can be obtained via our construction by coupling the free electromagnetic field with an external source, say a quadri-current $J^{\mu }(x)$, and by considering the action of the symmetry group $U(1)$.

Consider the same theory discussed so far with the slightly modified Hamiltonian:

$$H=\frac{1}{2}{\eta }_{\mu \alpha }{\eta }_{\nu \beta }{\rho }^{\mu \nu }{\rho }^{\alpha \beta }+J^{\mu }{u}_{\mu },$$

(138)

where $J^{\mu }(x)$ is a fixed field in which the Hamiltonian depends and which belongs to the dual to the vector space, the vector potential $A_{\mu }$ belongs to. The Hamiltonian functional becomes:

$$\mathcal{H}={\int }_{\Sigma }\left[p^k{\partial }_k{a}_0+\frac{1}{2}{\beta }^{kj}\left({\partial }_k{a}_j-{\partial }_j{a}_k\right)+\frac{1}{4}{\delta }_{jl}{\delta }_{km}{\beta }^{jk}{\beta }^{lm}+\frac{1}{2}{\delta }_{jk}{p}^k{p}^j+j^{\mu }{a}_{\mu }\right]{\mathrm{vol}}_{\Sigma },$$

(139)

where $j^{\mu }$ is the restriction of $J^{\mu }$ to $\Sigma$.

In this case, the manifold ${\mathcal{M}}_{\infty }$ is easily seen to be:

$${\mathcal{M}}_{\infty }=\left\{(a_k,p^k):{\partial }_k{p}^k=j^0\right\}\subset {\mathcal{H}}^1(\Sigma )\times {\left[{\mathcal{L}}^2(\Sigma )\right]}^3,$$

(140)

where the $p^k$’s belongs to the subspace of ${\left[{\mathcal{L}}^2(\Sigma )\right]}^3$ selected by the constraint ${\partial }_k{p}^k=j^0$. The presymplectic structure ${\Omega }_{\infty }^{\Sigma }$ is again:

$${\Omega }_{\infty }^{\Sigma }(\mathbb{X},\mathbb{Y})={\int }_{\Sigma }\left({\mathbb{X}}_{a_k}{\mathbb{Y}}_p^k-{\mathbb{X}}_p^k{\mathbb{Y}}_{a_k}\right)vo{l}_{\Sigma }.$$

(141)

Now, denote by $({{\mathbb{X}}_{\tilde{a}}}_k,{{\mathbb{X}}_{a^{\nabla }}}_k,{{\mathbb{X}}_{\tilde{p}}}^k)$ the components of a vector field tangent to ${\mathcal{M}}_{\infty }$ according to the decomposition given in Equation (112). Then, the kernel of ${\Omega }_{\infty }^{\Sigma }$ are those with ${{\mathbb{X}}_{a^{\nabla }}}_k$ components only. In particular, vector fields of this type generate the action (109) of the $U(1)$ group on ${\mathcal{M}}_{\infty }$. This represent a symmetry group action, of which we may search for the corresponding conserved charge. In order to do it, we will use again the coisotropic embedding construction. Recall that the ${\mathcal{H}}^1(\Sigma )$ splits as ${\mathcal{H}}^1(\Sigma )={\mathcal{H}}^1(\mathrm{div}0,\Sigma )\oplus \mathrm{grad}{\mathcal{H}}^2(\Sigma )$. Analogously ${\left[{\mathcal{L}}^2(\Sigma )\right]}^3={\left[\mathcal{H}(\mathrm{div}0,\Sigma )\right]}^3\oplus \mathrm{grad}{\mathcal{H}}^1(\Sigma )$ (see [50]). Therefore, if we consider the Hilbert manifold:

$$\mathcal{P}={\mathcal{H}}^1(\mathrm{div}0,\Sigma )\times \mathrm{grad}{\mathcal{H}}^2(\Sigma )\times {\left[\mathcal{H}(\mathrm{div}0,\Sigma )\right]}^3\times \mathrm{grad}{\mathcal{H}}^1(\Sigma ),$$

(142)

whose points will be denoted by $({\tilde{a}}_k,a_k^{\nabla },{\tilde{p}}^k,p_{\nabla }^k)$, then the presymplectic manifold ${\mathcal{M}}_{\infty }$ can be considered the submanifold of $\mathcal{P}$ selected by the condition:

$${\partial }_k{p}_{\nabla }^k=j^0.$$

(143)

Now, let us note that $\mathcal{P}$ is a symplectic manifold equipped with the symplectic structure:

$${\Omega }^{\mathcal{P}}(\mathbb{X},\mathbb{Y})={\int }_{\Sigma }\left({{\mathbb{X}}_{\tilde{a}}}_k{\mathbb{Y}}_{\tilde{p}}^k-{\mathbb{X}}_{\tilde{p}}^k{{\mathbb{Y}}_{\tilde{a}}}_k\right)vo{l}_{\Sigma }+{\int }_{\Sigma }\left({{\mathbb{X}}_{a^{\nabla }}}_k{\mathbb{Y}}_{p_{\nabla }}^k-{\mathbb{X}}_{p_{\nabla }}^k{{\mathbb{Y}}_{a^{\nabla }}}_k\right)vo{l}_{\Sigma },$$

(144)

where the components ${{\mathbb{X}}_{a^{\nabla }}}_k$ are those defining the kernel of ${\Omega }_{\infty }^{\Sigma }$. Note that the latter structure pulls-back to ${\Omega }_{\infty }^{\Sigma }$ under the immersion map, $\mathfrak{j}$, of ${\mathcal{M}}_{\infty }$ into $\mathcal{P}$. Thus, ${\mathcal{M}}_{\infty }$ is a coisotropic submanifold of $\mathcal{P}$ and the symplectic manifold $\mathcal{P}$ was realized by “coupling” the kernel, $\mathrm{grad}{\mathcal{H}}^2$, of the original presymplectic structure with the complement of $\mathcal{H}(\mathrm{div}0,\Sigma )$ into ${\left[{\mathcal{L}}^2(\Sigma )\right]}^3$ associated with the splitting considered above.

Now, consider the generator of the symmetry group action considered above, i.e., the vector field $\mathbb{X}$ whose unique non-zero component is ${{\mathbb{X}}_{a^{\nabla }}}_k={\partial }_k\psi$. A straightforward computation shows that $\mathbb{X}$ is Hamiltonian, with respect to ${\Omega }^{\mathcal{P}}$ with Hamiltonian:

$$f=-{\int }_{\Sigma }\psi {\partial }_k{p}_{\nabla }^{k}vo{l}_{\Sigma },$$

(145)

which, restricted to the physical manifold ${\mathcal{M}}_{\infty }$ reads:

$${\mathfrak{j}}^{\star }f=-{\int }_{\Sigma }\psi j^{0}vo{l}_{\Sigma },$$

(146)

which says that the electric charge $j^0$ is the conserved charge associated with the $U(1)$ gauge symmetry of the system.

5. Conclusions

A global, covariant, geometric theory of symmetries was constructed directly on the space of solutions of first-order Hamiltonian field theories. The theory of symmetries of Hamiltonian systems, usually presented on an abstract setting on symplectic and presymplectic manifolds, is carried to the space of solutions of a first-order Hamiltonian field theory, which is naturally a presymplectic infinite-dimensional manifold. The case of gauge theories, i.e., theories such that the space of solutions carries a presymplectic structure with a non-trivial characteristic distribution, was dealt by constructing a symplectic regularization of it using the coisotropic embedding theorem.

In particular, the case of geometrical symmetries emerging from transformations on the bundle and/or space–time supporting the theory were considered, and we saw how, given a symmetry group of canonical transformations, it is possible to construct an algebra of conserved currents, which is directly defined on the space of solutions of the theory. We first considered a finite-dimensional, presymplectic case, i.e., the free relativistic particle for which we analyzed the consequences of the invariance under reparametrizations. Then, we moved to infinite-dimensional examples. In particular, we first considered the symplectic case where we analyzed the Klein–Gordon field theory as a guiding example. Then, we considered the “genuinely presymplectic” case exemplified by gauge theories, illustrated by electrodynamics. Here, we saw that a symmetry group may act both via dynamical and gauge symmetries and that the momentum map associated with such a symmetry group is reconstructed by the aid of a connection on the bundle associated with the gauge theory. In particular, we analyzed the action of the Poincaré group on the space of solutions of free electrodynamics giving rise to the usual energy–momentum tensor and the action of the $U(1)$ symmetry group on the space of solutions of electrodynamics with a fixed external source, giving rise to the conservation of the electrical charge.

The reconstruction, by using an appropriate extension of the standard BRST theory, of the final manifold of constraints ${\mathcal{M}}_{\infty }$ of the theory, from the symmetries on the extended symplectic space $\mathcal{P}$, obtained by using the coisotropic embedding theorem, will be discussed in further works. In order to do so, the algebra of currents in $\mathcal{P}$ associated to a symmetry group will be studied further.

The case of symmetries of a non-geometrical character, characteristic of hierarchies of integrable non-linear equations, will be discussed in a future paper.