Pedal Curves of Non-Lightlike Curves in Minkowski 3-Space

Abstract

We study the notions of pedal curves, contrapedal curves and $\mathit{B}$-Gauss maps of non-lightlike regular curves in Minkowski 3-space. Then we establish the relationships among the evolutes, the pedal and contrapedal curves. Moreover, we also investigate the singularities of these objects. Finally, we show some examples to comprehend the characteristics of the pedal and contrapedal curves in Minkowski 3-space.

1. Introduction

As one of the classical topics of differential geometry, pedal curves have been studied with great enthusiasm in recent years and scholars have achieved many results (cf. [1,2,3,4,5,6]). One found that the pedal curve has a symmetric relationship with the original curve. For any fixed curve, we can always give its pedal curve. This symmetry is also called dual in mathematics. There are many curves with symmetry, such as evolutes, involutes, Bertrand curves, Mannheim curves and so on. A lot of scholars are interested in geometric objects with symmetry in different spaces, and they study the different properties of them (cf. [7,8,9,10]).

In fact, there are many definitions of pedal curves in different spaces. According to [11], MacLaurin defined the trajectory of foot of the perpendicular from the given point to the tangent of the curve as the pedal curve. As an extension of the theory, Izumiya and Takeuchi gave the notions of the evolutoids and pedaloids in ${\mathbb{R}}^2$ in [12], where they showed that the pedal curve of the evolute is the contrapedal curve of the original curve. In 1907, Minkowski space was put forward by Minkowski, which is basically a combination of Euclidean 3-space and time into a four-dimensional manifold. Since Minkowski space was proposed, it has been studied by researchers domestically (cf. [13,14,15,16,17]). Bakurová introduced pedal curves in Minkowski plane in [18]. In [19], Izumiya and Takeuchi introduced families of relatives of pedal curves and evolutes and revealed some connections between these curve families. Moreover, Şekerci and Izumiya defined evolutoids and pedaloids in ${\mathbb{R}}_1^2$ and proved that the previous conclusions still hold in this plane. In [20], when the base curves have singularities, the pedal curves are defined by Li and Pei. They also investigated its singularity and calculated the relationships between the singular point of the pedal curves and inflection point.

Another important study was done by Izumiya, Pei and Sano in [5], they gave the notions of the lightcone pedal curves and lightcone Gauss map. They also established the relationships among singularities of these objects. Moreover, they proved that there is a correspondence between the singularity of the pedal curve and the lightcone Gauss map. However, at least as far as we know, there are not many papers about pedal curves related to regular space curves in ${\mathbb{R}}_1^3$. Therefore, this paper examines this issue.

This paper is structured as follows: We quickly review the necessary preparatory knowledge about Minkowski 3-space in Section 2. We define the pedal curves, contrapedal curves and $\mathit{B}$-Gauss maps of non-lightlike regular curves and consider the propositions of these objects in Section 3. Then, in Section 4, we show that when the pedal curve is singular, the relationships between the singularity of the pedal curves and original curves. In order to explain the main theorem, we show two examples in Section 5.

Without special instructions, all maps and manifolds are $C^{\infty }$ in this paper.

2. Preliminaries

In this section, we present some necessary preparatory knowledge that will help us to understand the main results.

Let ${\mathbb{R}}^3=\left\{({\alpha }_1,{\alpha }_2,{\alpha }_3)\right|{\alpha }_i\in \mathbb{R},i=1,2,3\}$ be the 3-dimensional vector space. For any $\mathit{\alpha }=({\alpha }_1,{\alpha }_2,{\alpha }_3)$ and $\mathit{\beta }=({\beta }_1,{\beta }_2,{\beta }_3)$ in ${\mathbb{R}}^3$, the pseudo scalar product of $\mathit{\alpha }$ and $\mathit{\beta }$ is defined by $⟨\mathit{\alpha },\mathit{\beta }⟩=-{\alpha }_1{\beta }_1+{\alpha }_2{\beta }_2+{\alpha }_3{\beta }_3.$ We call $({\mathbb{R}}^3,⟨,⟩)$ a Minkowski 3-space and denote it as ${\mathbb{R}}_1^3.$

We say that $\alpha \in {\mathbb{R}}_1^3\setminus \left\{\mathbf{0}\right\}$ is spacelike, lightlike and timelike if $⟨\mathit{\alpha },\mathit{\alpha }⟩>0,$$⟨\mathit{\alpha },\mathit{\alpha }⟩=0$ and $⟨\mathit{\alpha },\mathit{\alpha }⟩<0$, respectively.

We define the norm of $\mathit{\alpha }=({\alpha }_1,{\alpha }_2,{\alpha }_3)\in {\mathbb{R}}_1^3$ by $\left|\right|\mathit{\alpha }\left|\right|=\sqrt{|⟨\mathit{\alpha },\mathit{\alpha }⟩|}.$

For any $\mathit{\alpha }=({\alpha }_1,{\alpha }_2,{\alpha }_3)$ and $\mathit{\beta }=({\beta }_1,{\beta }_2,{\beta }_3)$ in ${\mathbb{R}}_1^3$, the pseudo vector product of $\mathit{\alpha }\mathrm{and}\mathit{\beta }$ is defined by

$$\mathit{\alpha }\wedge \mathit{\beta }=\left|\begin{array}{ccc}-{\mathit{e}}_1& {\mathit{e}}_2& {\mathit{e}}_3\\ {\alpha }_1& {\alpha }_2& {\alpha }_3\\ {\beta }_1& {\beta }_2& {\beta }_3\end{array}\right|=(-({\alpha }_2{\beta }_3-{\alpha }_3{\beta }_2),{\alpha }_3{\beta }_1-{\alpha }_1{\beta }_3,{\alpha }_1{\beta }_2-{\alpha }_2{\beta }_1),$$

where {${\mathit{e}}_1$,${\mathit{e}}_2$,${\mathit{e}}_3$} is the canonical basis of ${\mathbb{R}}_1^3.$ For the basic notions in Minkowski geometry see [21].

Let I be an open interval in $\mathbb{R},$$\gamma :I\to {\mathbb{R}}_1^3$ be a regular curve, we call $\gamma$ is spacelike, lightlike and timelike if ${\gamma }^{\prime }\left(t\right)$ is spacelike, lightlike and timelike, respectively, for any $t\in I.$

Let $\gamma :I\to {\mathbb{R}}_1^3$ be a non-lightlike regular curve, and s be the arc-length parameter. In this situation, $\mathit{T}\left(s\right)={\gamma }^{\prime }\left(s\right)$ is the unit tangent vector. The curvature is defined by $\kappa \left(s\right)=\sqrt{|⟨{\gamma }^{″}\left(s\right),{\gamma }^{″}\left(s\right)⟩|}.$ If $\kappa \left(s\right)\ne 0,$ then we can give the unit principal normal vector $\mathit{N}\left(s\right)$ by ${\gamma }^{\prime \prime }\left(s\right)=\kappa \left(s\right)\mathit{N}\left(s\right),$ and the unit binormal vector $\mathit{B}\left(s\right)$ by $\mathit{B}\left(s\right)=\mathit{T}\left(s\right)\wedge \mathit{N}\left(s\right).$ We denote that $⟨\mathit{T}\left(s\right),\mathit{T}\left(s\right)⟩={\delta }_1,⟨\mathit{N}\left(s\right),\mathit{N}\left(s\right)⟩={\delta }_2 \mathit{and} ⟨\mathit{B}\left(s\right),\mathit{B}\left(s\right)⟩=-{\delta }_1{\delta }_2.$ Then $\left\{\mathit{T}\right(s),\mathit{N}(s),\mathit{B}(s\left)\right\}$ is a pseudo orthonormal frame of $\gamma .$ Moreover, we have the following Frenet-Serret type formulas

$$\frac{d}{ds}\left[\begin{array}{c}\mathit{T}\left(s\right)\\ \mathit{N}\left(s\right)\\ \mathit{B}\left(s\right)\end{array}\right.=\left[\begin{array}{ccc}0& \kappa \left(s\right)& 0\\ -{\delta }_1{\delta }_2\kappa \left(s\right)& 0& {\delta }_1\tau \left(s\right)\\ 0& \tau \left(s\right)& 0\end{array}\right]\left[\begin{array}{c}\mathit{T}\left(s\right)\\ \mathit{N}\left(s\right)\\ \mathit{B}\left(s\right)\end{array}\right],$$

where $\tau \left(s\right)$ is the torsion of $\gamma$ (cf. [22]).

We define the hyperbolic 2-space by

$$H_0^2=\{\alpha \in {\mathbb{R}}_1^3|⟨\alpha ,\alpha ⟩=-1\},$$

the de Sitter 2-space by

$$S_1^2=\{\alpha \in {\mathbb{R}}_1^3|⟨\alpha ,\alpha ⟩=1\},$$

the evolute of a non-lightlike regular curve $\gamma$ without inflection points in ${\mathbb{R}}_1^3$ by

$$Ev\left(s\right)=\gamma \left(s\right)+\frac{1}{{\delta }_1{\delta }_2\kappa \left(s\right)}\mathit{N}\left(s\right)+\frac{{\kappa }^{\prime }\left(s\right)}{{\delta }_1{\delta }_2{\kappa }^2\left(s\right)\tau \left(s\right)}\mathit{B}\left(s\right).$$

(1)

3. Non-Lightlike Pedal Cueves in ${\mathbb{R}}_{\mathbf{1}}^{\mathbf{3}}$

According to [3], we call the locus of the closest point to the given point on the osculating plane of $\gamma$ the pedal curve in ${\mathbb{S}}^n$. Similarly, we obtain the pedal curve of a curve by projecting the given point $\mathit{p}$ to the osculating plane of the curve.

Definition 1.

Let $\gamma :I\to {\mathbb{R}}_1^3$ be a non-lightlike regular curve in ${\mathbb{R}}_1^3,$ and $\mathit{p}$ be an arbitrary fixed point in ${\mathbb{R}}_1^3$. We now define a curve $P{e}_{\gamma ,p}:I\to {\mathbb{R}}_1^3$ by

$$P{e}_{\gamma ,p}\left(s\right)={\delta }_1{\delta }_2⟨\mathit{P}\left(s\right),\mathit{B}\left(s\right)⟩\mathit{B}\left(s\right)+\mathit{p}.$$

(2)

We call $P{e}_{\gamma ,p}$ the pedal curve, $\mathit{p}$ the pedal point and $\mathit{P}\left(s\right)=\mathit{p}-\gamma \left(s\right)$ the pedal vector.

By straightforward calculations, the proposition below can be obtained.

Proposition 1.

Let $\gamma :I\to {\mathbb{R}}_1^3$ be a non-lightlike regular curve in ${\mathbb{R}}_1^3$. The pedal curve of γ is $P{e}_{\gamma ,p}$ and $s_0\in I,$ then the following hold.

$\left(1\right)$ If ${\delta }_2{\left(\tau ⟨\mathit{P},\mathit{B}⟩\right)}^2\left(s_0\right)>{\delta }_1{\delta }_2{\left(\tau ⟨\mathit{P},\mathit{N}⟩\right)}^2\left(s_0\right)$, then $s_0$ is a spacelike point on the pedal curve.

$\left(2\right)$ If ${\left(\tau ⟨\mathit{P},\mathit{B}⟩\right)}^2\left(s_0\right)={\delta }_1{\left(\tau ⟨\mathit{P},\mathit{N}⟩\right)}^2\left(s_0\right)\ne 0$, then $s_0$ is a lightlike point on the pedal curve.

$\left(3\right)$ If ${\delta }_2{\left(\tau ⟨\mathit{P},\mathit{B}⟩\right)}^2\left(s_0\right)<{\delta }_1{\delta }_2{\left(\tau ⟨\mathit{P},\mathit{N}⟩\right)}^2\left(s_0\right)$, then $s_0$ is a timelike point on the pedal curve.

Proof. 

By differentiating the Formula (2) with respect to s, we have

$$P{e}_{\gamma ,p}^{\prime }\left(s\right)={\delta }_1{\delta }_2\left(\tau ⟨\mathit{P},\mathit{B}⟩\mathit{N}\right)\left(s\right)+{\delta }_1{\delta }_2\left(\tau ⟨\mathit{P},\mathit{N}⟩\mathit{B}\right)\left(s\right).$$

It follows that

$$⟨P{e}_{\gamma ,p}^{\prime },P{e}_{\gamma ,p}^{\prime }⟩\left(s\right)={\delta }_2{\left(\tau ⟨\mathit{P},\mathit{B}⟩\right)}^2\left(s\right)-{\delta }_1{\delta }_2{\left(\tau ⟨\mathit{P},\mathit{N}⟩\right)}^2\left(s\right).$$

We have known that $s_0$ is a spacelike point, lightlike point and timelike point if $⟨P{e}_{\gamma ,p}^{\prime }\left(s_0\right),P{e}_{\gamma ,p}^{\prime }\left(s_0\right)⟩$ is positive, vanishing and negative, respectively. This completes the proof. □

According to [5], the singularities of lightcone Gauss map and lightcone pedal curve are dual. We can obtain a similar conclusion when we define the $\mathit{B}$-Gauss map as follows.

Let the $\mathit{B}$-Gauss map $G_{\delta }:I\to Q_{\delta }^2$ be defined by $G_{\delta }\left(s\right)=\mathit{B}\left(s\right),$ where

$$Q_{\delta }^2=\left\{\begin{array}{cc}{S}_1^2,\hfill & \mathit{if}\delta =1,\hfill \\ H_0^2,\hfill & \mathit{if}\delta =-1.\hfill \end{array}\right.$$

Meanwhile, $\delta =-{\delta }_1{\delta }_2=⟨\mathit{B}\left(s\right),\mathit{B}\left(s\right)⟩.$

In the following, we give the relation between the $\mathit{B}$-Gauss map and the pedal curve.

Theorem 1.

Let $\gamma :I\to {\mathbb{R}}_1^3$ be a non-lightlike regular curve in ${\mathbb{R}}_1^3.$ The pedal curve of γ is $P{e}_{\gamma ,p}$. Suppose that for any $\lambda \in \mathbb{R},$ $\mathit{p}\notin \gamma \left(s\right)\cup \lambda \mathit{T}\left(s\right),$ then

$\left(1\right)$$s_0$ is a fold point of the $\mathit{B}$-Gauss map $G_{\delta }$ if and only if $\tau \left(s_0\right)=0$ and $\left(\kappa {\tau }^{\prime }\right)\left(s_0\right)\ne 0.$

$\left(2\right)$$s_0$ is a cusp point of the pedal curve $P{e}_{\gamma ,p}$ if and only if $\tau \left(s_0\right)=0$ and $\left(\kappa {\tau }^{\prime }\right)\left(s_0\right)\ne 0.$

In Minkowski 3-space, the pedal curve also has a symmetrical relation with another curve, and we call this curve as the contrapedal curve. Following the Definition 1, we can get the contrapedal curve of $\gamma$ by projecting the point $\mathit{p}$ to the normal plane, where $\mathit{p}\in {\mathbb{R}}_1^3$ is an arbitrary fixed point.

Definition 2.

Let $\gamma :I\to {\mathbb{R}}_1^3$ be a non-lightlike regular curve in ${\mathbb{R}}_1^3.$ We now define a curve $CP{e}_{\gamma ,p}:I\to {\mathbb{R}}_1^3$ by

$$CP{e}_{\gamma ,p}\left(s\right)=\mathit{p}-{\delta }_1⟨\mathit{P}\left(s\right),\mathit{T}\left(s\right)⟩\mathit{T}\left(s\right).$$

We call $CP{e}_{\gamma ,p}$ as the contrapedal curve of $\gamma .$

The relationships among the evolutes, the pedal and contrapedal curves are given as following.

Theorem 2.

Let $\gamma :I\to {\mathbb{R}}_1^3$ be a non-lightlike regular curve in ${\mathbb{R}}_1^3$ without inflection points. Suppose that the evolute is regular, then we have

$$P{e}_{E{v}_{\gamma ,p}}\left(s\right)+{\delta }_{2}CP{e}_{\gamma ,p}\left(s\right)=(1+{\delta }_2)\mathit{p}.$$

Proof. 

By differentiating the Formula (1), we obtain

$\begin{array}{cc}& E{v}^{\prime }\left(s\right)=\left(\frac{{\kappa }^3{\tau }^3-{\kappa }^2{\kappa }^{\prime }{\tau }^{\prime }+{\kappa }^2{\kappa }^{″}\tau -2\kappa {{\kappa }^{\prime }}^2\tau }{{\delta }_1{\delta }_2{\kappa }^4{\tau }^2}\mathit{B}\right)\left(s\right),\hfill \\ & E{v}^{″}\left(s\right)=(\frac{{\kappa }^3{\tau }^3-{\kappa }^2{\kappa }^{\prime }{\tau }^{\prime }+{\kappa }^2{\kappa }^{″}\tau -2\kappa {{\kappa }^{\prime }}^2\tau }{{\delta }_1{\delta }_2{\kappa }^4\tau }\mathit{N}+b_3\mathit{B})\left(s\right),\hfill \end{array}$

$\mathrm{where}{b}_3\left(s\right)=\frac{{\kappa }^7{\tau }^4{\tau }^{\prime }-{\kappa }^6{\kappa }^{\prime }{\tau }^5+2{\kappa }^6{\kappa }^{\prime }\tau {{\tau }^{\prime }}^2-{\kappa }^6{\kappa }^{\prime }{\tau }^2{\tau }^{″}-2{\kappa }^6{\kappa }^{″}{\tau }^2{\tau }^{\prime }+{\kappa }^6{\kappa }^{″\prime }{\tau }^3+4{\kappa }^5{{\kappa }^{\prime }}^2{\tau }^2{\tau }^{\prime }-6{\kappa }^5{\kappa }^{\prime }{\kappa }^{″}{\tau }^3+6{\kappa }^4{{\kappa }^{\prime }}^3{\tau }^3}{{\delta }_1{\delta }_2{\kappa }^8{\tau }^4}\left(s\right).$

Then, we can get

$$E{v}^{\prime }\left(s\right)\wedge E{v}^{″}\left(s\right)=\left|\begin{array}{ccc}-\mathit{T}& \mathit{N}& \mathit{B}\\ 0& 0& \frac{{\kappa }^3{\tau }^3+{\kappa }^2{\kappa }^{\prime }{\tau }^{\prime }-{\kappa }^2{\kappa }^{\prime \prime }\tau +2\kappa {{\kappa }^{\prime }}^2\tau }{{\delta }_1{\delta }_2{\kappa }^4{\tau }^2}\\ 0& \frac{{\kappa }^3{\tau }^3-{\kappa }^2{\kappa }^{\prime }{\tau }^{\prime }+{\kappa }^2{\kappa }^{\prime \prime }\tau -2\kappa {{\kappa }^{\prime }}^2\tau }{{\delta }_1{\delta }_2{\kappa }^4\tau }& b_3\end{array}\right|\left(s\right).$$

We denote the unit binormal vector of the evolute as $\tilde{\mathit{B}},$ then

$$\tilde{\mathit{B}}\left(s\right)=\frac{E{v}^{\prime }\wedge E{v}^{″}}{\left|\right|E{v}^{\prime }\wedge E{v}^{″}\left|\right|}\left(s\right)=\mathrm{sgn}\left(\tau \left(s\right)\right)\mathit{T}\left(s\right),$$

where $\mathrm{sgn}\left(\tau \right(s\left)\right)$ is the signature of $\tau \left(s\right).$

The pedal curve of $Ev\left(s\right)$ is given by

$$P{e}_{E{v}_{\gamma ,p}}\left(s\right)={\delta }_1{\delta }_2⟨\mathit{P}\left(s\right),\tilde{\mathit{B}}\left(s\right)⟩\tilde{\mathit{B}}\left(s\right)+\mathit{p}.$$

Therefore, we obtain

$$P{e}_{E{v}_{\gamma ,p}}\left(s\right)+{\delta }_{2}CP{e}_{\gamma ,p}\left(s\right)=(1+{\delta }_2)\mathit{p}.$$

This completes the proof. □

The Theorem 2 is a generalization of the result for ${\mathbb{R}}^2.$ By restricting the conditions in this theorem, we can obtain a result similar to that for ${\mathbb{R}}^2$.

Corollary 1.

Let $\gamma :I\to {\mathbb{R}}_1^3$ be a spacelike regular curve in ${\mathbb{R}}_1^3$ without inflection points. Suppose that ${\delta }_2=-1$ and the evolute is regular, then we have

$$P{e}_{E{v}_{\gamma ,p}}\left(s\right)=CP{e}_{\gamma ,p}\left(s\right).$$

4. Singularities of 3-Dimensional Non-Lightlike Curves

In this section, we describe the singularity of a pedal curve and classify its singularities.

To consider the singular point, we quickly retrospect the criteria of singular points of curves (cf. [23,24,25]).

Proposition 2.

Let $\gamma :I\to {\mathbb{R}}_1^3$ be a non-lightlike curve and $s_0\in I$ be a singular point. Then, we have the following conclusions.

$\left(1\right)\gamma$ has a $3/2$-cusp at $s_0$ if and only if ${\gamma }^{″}\left(s_0\right)$ and ${\gamma }^{‴}\left(s_0\right)$ are linearly independent.

$\left(2\right)\gamma$ has a $4/3$-cusp at $s_0$ if and only if ${\gamma }^{\prime }\left(s_0\right)={\gamma }^{″}\left(s_0\right)=\mathbf{0}$ and ${\gamma }^{‴}\left(s_0\right)$ and ${\gamma }^{\left(4\right)}\left(s_0\right)$ are linearly independent.

$\left(3\right)\gamma$ has a $5/2$-cusp at $s_0$ if and only if ${\gamma }^{″}\left(s_0\right)\ne \mathbf{0},{\gamma }^{‴}\left(s_0\right)=c{\gamma }^{″}\left(s_0\right)$ for some constant $c\in \mathbb{R}$ and ${\gamma }^{″}\left(s_0\right)$ and $(3{\gamma }^{\left(5\right)}-10c{\gamma }^{\left(4\right)})\left(s_0\right)$ are linearly independent.

$\left(4\right)\gamma$ has a $5/3$-cusp at $s_0$ if and only if ${\gamma }^{″}\left(s_0\right)=\mathbf{0},$${\gamma }^{‴}\left(s_0\right)$ and ${\gamma }^{\left(4\right)}\left(s_0\right)$ are linearly dependent and ${\gamma }^{‴}\left(s_0\right)$ and ${\gamma }^{\left(5\right)}\left(s_0\right)$ are linearly independent.

Differentiating Equation (2) with respect to s, we have the following equations.

Lemma 1.

Let $\gamma :I\to {\mathbb{R}}_1^3$ be a non-lightlike regular curve in ${\mathbb{R}}_1^3$. The pedal curve of γ is $P{e}_{\gamma ,p}$, then we get

$\left(1\right)P{e}_{\gamma ,p}^{\prime }\left(s\right)=({\delta }_1{\delta }_2\tau ⟨\mathit{P},\mathit{B}⟩\mathit{N}+{\delta }_1{\delta }_2\tau ⟨\mathit{P},\mathit{N}⟩\mathit{B})\left(s\right).$

$\begin{array}{cc}\hfill \left(2\right)P{e}_{\gamma ,p}^{″}\left(s\right)=& \{-\kappa \tau ⟨\mathit{P},\mathit{B}⟩\mathit{T}+[2{\delta }_1{\delta }_2{\tau }^2⟨\mathit{P},\mathit{N}⟩+{\delta }_1{\delta }_2{\tau }^{\prime }⟨\mathit{P},\mathit{B}⟩]\mathit{N}\hfill \\ & +[-\kappa \tau ⟨\mathit{P},\mathit{T}⟩+{\delta }_1{\delta }_2{\tau }^{\prime }⟨\mathit{P},\mathit{N}⟩+2{\delta }_2{\tau }^2⟨\mathit{P},\mathit{B}⟩]\mathit{B}\}\left(s\right).\hfill \end{array}$

$\begin{array}{cc}\hfill \left(3\right)P{e}_{\gamma ,p}^{‴}\left(s\right)=& \{[-3\kappa {\tau }^2⟨\mathit{P},\mathit{N}⟩-(2\kappa {\tau }^{\prime }+{\kappa }^{\prime }\tau )⟨\mathit{P},\mathit{B}⟩]\mathit{T}\hfill \\ & +[-3\kappa {\tau }^2⟨\mathit{P},\mathit{T}⟩+6{\delta }_1{\delta }_2\tau {\tau }^{\prime }⟨\mathit{P},\mathit{N}⟩+(4{\delta }_2{\tau }^3-{\kappa }^2\tau +{\delta }_1{\delta }_2{\tau }^{\prime \prime })⟨\mathit{P},\mathit{B}⟩]\mathit{N}\hfill \\ & +[-(2\kappa {\tau }^{\prime }+{\kappa }^{\prime }\tau )⟨\mathit{P},\mathit{T}⟩+(4{\delta }_2{\tau }^3-{\kappa }^2\tau +{\delta }_1{\delta }_2{\tau }^{\prime \prime })⟨\mathit{P},\mathit{N}⟩+6{\delta }_2\tau {\tau }^{\prime }⟨\mathit{P},\mathit{B}⟩\hfill \\ & +{\delta }_1\kappa \tau \left]\mathit{B}\right\}\left(s\right).\hfill \end{array}$

$\begin{array}{cc}\hfill \left(4\right)P{e}_{\gamma ,p}^{\left(4\right)}\left(s\right)=& \left\{\right[6{\delta }_1{\delta }_2{\kappa }^2{\tau }^2⟨\mathit{P},\mathit{T}⟩+(-4{\kappa }^{\prime }{\tau }^2-14\kappa \tau {\tau }^{\prime })⟨\mathit{P},\mathit{N}⟩\hfill \\ & +(-7{\delta }_1\kappa {\tau }^3+{\delta }_1{\delta }_2{\kappa }^3\tau -{\kappa }^{\prime \prime }\tau -3{\kappa }^{\prime }{\tau }^{\prime }-3\kappa {\tau }^{\prime \prime })⟨\mathit{P},\mathit{B}⟩]\mathit{T}\hfill \\ & +[(-4{\kappa }^{\prime }{\tau }^2-14\kappa \tau {\tau }^{\prime })⟨\mathit{P},\mathit{T}⟩+(8{\delta }_2{\tau }^4-8{\kappa }^2{\tau }^2+8{\delta }_1{\delta }_2\tau {\tau }^{\prime \prime }+6{\delta }_1{\delta }_2{\tau }^{\prime 2})⟨\mathit{P},\mathit{N}⟩\hfill \\ & +(24{\delta }_2{\tau }^2{\tau }^{\prime }-3\kappa {\kappa }^{\prime }\tau -3{\kappa }^2{\tau }^{\prime }+{\delta }_1{\delta }_2{\tau }^{\prime \prime \prime })⟨\mathit{P},\mathit{B}⟩+4{\delta }_1\kappa {\tau }^2]\mathit{N}\hfill \\ & +[(-7{\delta }_1\kappa {\tau }^3+{\delta }_1{\delta }_2{\kappa }^3\tau -{\kappa }^{\prime \prime }\tau -3{\kappa }^{\prime }{\tau }^{\prime }-3\kappa {\tau }^{\prime \prime })⟨\mathit{P},\mathit{T}⟩\hfill \\ & +(24{\delta }_2{\tau }^2{\tau }^{\prime }-3\kappa {\kappa }^{\prime }\tau -3{\kappa }^2{\tau }^{\prime }+{\delta }_1{\delta }_2{\tau }^{\prime \prime \prime })⟨\mathit{P},\mathit{N}⟩\hfill \\ & +(8{\delta }_1{\delta }_2{\tau }^4-2{\delta }_1{\kappa }^2{\tau }^2+8{\delta }_2\tau {\tau }^{\prime \prime }+6{\delta }_2{\tau }^{\prime 2})⟨\mathit{P},\mathit{B}⟩+2{\delta }_1{\kappa }^{\prime }\tau +3{\delta }_1\kappa {\tau }^{\prime }\left]\mathit{B}\right\}\left(s\right).\hfill \end{array}$

$\begin{array}{cc}\hfill \left(5\right)P{e}_{\gamma ,p}^{\left(5\right)}\left(s\right)=& \left\{\right[(20{\delta }_1{\delta }_2\kappa {\kappa }^{\prime }{\tau }^5+40{\delta }_1{\delta }_2{\kappa }^2\tau {\tau }^{\prime })⟨\mathit{P},\mathit{T}⟩\hfill \\ & +(-15{\delta }_1\kappa {\tau }^4+15{\delta }_1{\delta }_2{\kappa }^3{\tau }^2-5{\kappa }^{\prime \prime }{\tau }^2-25{\kappa }^{\prime }\tau {\tau }^{\prime }-25\kappa \tau {\tau }^{\prime \prime }-20\kappa {\tau }^{\prime 2})⟨\mathit{P},\mathit{N}⟩\hfill \\ & +(-11{\delta }_1{\kappa }^{\prime }{\tau }^3-59{\delta }_1\kappa {\tau }^2{\tau }^{\prime }+6{\delta }_1{\delta }_2{\kappa }^2{\kappa }^{\prime }\tau +4{\delta }_1{\delta }_2{\kappa }^3{\tau }^{\prime }-{\kappa }^{‴}\tau -4{\kappa }^{″}{\tau }^{\prime }\hfill \\ & -6{\kappa }^{\prime }{\tau }^{″}-4\kappa {\tau }^{″})⟨\mathit{P},\mathit{B}⟩-10{\delta }_2{\kappa }^2{\tau }^2]\mathit{T}\hfill \\ & +[(-15{\delta }_1\kappa {\tau }^4+15{\delta }_1{\delta }_2{\kappa }^3{\tau }^2-5{\kappa }^{\prime \prime }{\tau }^2-25{\kappa }^{\prime }\tau {\tau }^{\prime }-25\kappa \tau {\tau }^{\prime \prime }-20\kappa {\tau }^{\prime 2})⟨\mathit{P},\mathit{T}⟩\hfill \\ & +(80{\delta }_2{\tau }^3{\tau }^{\prime }-30\kappa {\kappa }^{\prime }{\tau }^2-50{\kappa }^2\tau {\tau }^{\prime }+10{\delta }_1{\delta }_2\tau {\tau }^{\prime \prime \prime }+20{\delta }_1{\delta }_2{\tau }^{\prime }{\tau }^{\prime \prime })⟨\mathit{P},\mathit{N}⟩\hfill \\ & +(16{\delta }_1{\delta }_2{\tau }^5-17{\delta }_1{\kappa }^2{\tau }^3+40{\delta }_2{\tau }^2{\tau }^{″}+60{\delta }_2\tau {\tau }^{\prime 2}-3{\kappa }^{\prime 2}\tau -4\kappa {\kappa }^{″}\tau +{\delta }_1{\delta }_2{\kappa }^4\tau \hfill \\ & -12\kappa {\kappa }^{\prime }{\tau }^{\prime }-6{\kappa }^2{\tau }^{″}+{\delta }_1{\delta }_2{\tau }^{\left(4\right)})⟨\mathit{P},\mathit{B}⟩+10{\delta }_1{\kappa }^{\prime }{\tau }^2+25{\delta }_1\kappa \tau {\tau }^{\prime }]\mathit{N}\hfill \\ & +\left[\right(-11{\delta }_1{\kappa }^{\prime }{\tau }^3-59{\delta }_1\kappa {\tau }^2{\tau }^{\prime }+6{\delta }_1{\delta }_2{\kappa }^2{\kappa }^{\prime }\tau +4{\delta }_1{\delta }_2{\kappa }^3{\tau }^{\prime }-{\kappa }^{‴}\tau -4{\kappa }^{″}{\tau }^{\prime }\hfill \\ & -6{\kappa }^{\prime }{\tau }^{″}-4\kappa {\tau }^{″})⟨\mathit{P},\mathit{T}⟩\hfill \\ & +(16{\delta }_1{\delta }_2{\tau }^5-17{\delta }_1{\kappa }^2{\tau }^3+40{\delta }_2{\tau }^2{\tau }^{″}+60{\delta }_2\tau {\tau }^{\prime 2}-3{\kappa }^{\prime 2}\tau -4\kappa {\kappa }^{″}\tau \hfill \\ & +{\delta }_1{\delta }_2{\kappa }^4\tau -12\kappa {\kappa }^{\prime }{\tau }^{\prime }-6{\kappa }^2{\tau }^{″}+{\delta }_1{\delta }_2{\tau }^{\left(4\right)})⟨\mathit{P},\mathit{N}⟩\hfill \\ & +(80{\delta }_1{\delta }_2{\tau }^3{\tau }^{\prime }-10{\delta }_1\kappa {\kappa }^{\prime }{\tau }^2-10{\delta }_1{\kappa }^2\tau {\tau }^{\prime }+10{\delta }_2\tau {\tau }^{\prime \prime \prime }+20{\delta }_2{\tau }^{\prime }{\tau }^{\prime \prime })⟨\mathit{P},\mathit{B}⟩\hfill \\ & +11\kappa {\tau }^3+3{\delta }_1{\kappa }^{″}\tau -{\delta }_2{\kappa }^3\tau +8{\delta }_1{\kappa }^{\prime }{\tau }^{\prime }+6{\delta }_1\kappa {\tau }^{″}\left]\mathit{B}\right\}\left(s\right).\hfill \end{array}$

Based on the definition of pedal curve, we show the following theorem by using Propositon 2 and Lemma 1.

Theorem 3.

Let $\gamma :I\to {\mathbb{R}}_1^3$ be a non-lightlike regular curve in ${\mathbb{R}}_1^3$. The pedal curve of γ is $P{e}_{\gamma ,p},$ then we have

CASE 1: Suppose that for any $\lambda \in \mathbb{R},$ $\mathit{p}\notin \gamma \left(s_0\right)\cup \lambda \mathit{T}\left(s_0\right),$ and $s_0$ is a singular point of $P{e}_{\gamma ,p},$ that is, $\tau \left(s_0\right)=0.$

$\left(1\right)P{e}_{\gamma ,p}$ has a $3/2$-cusp at $s_0$ if and only if $\left(\kappa {\tau }^{\prime }\right)\left(s_0\right)\ne 0.$

$\left(2\right)P{e}_{\gamma ,p}$ has a $4/3$-cusp at $s_0$ if and only if $\left(\kappa {\tau }^{″}\right)\left(s_0\right)\ne 0$ and ${\tau }^{\prime }\left(s_0\right)=0.$

$\left(3\right)P{e}_{\gamma ,p}$ has a $5/2$-cusp at $s_0$ if and only if $\left({\tau }^{\prime }{\tau }^{″}\right)\left(s_0\right)\ne 0,$$({\kappa }^{\prime },{\kappa }^{″})\left(s_0\right)\ne (0,0)$ and $\kappa \left(s_0\right)=0.$

$\left(4\right)P{e}_{\gamma ,p}$ has a $5/3$-cusp at $s_0$ if and only if $\left({\kappa }^{\prime }{\tau }^{″}\right)\left(s_0\right)\ne 0$ and $\kappa \left(s_0\right)={\tau }^{\prime }\left(s_0\right)=0.$

CASE 2: Suppose that there exists $s_0\in I$ such that $\mathit{P}\left(s_0\right)=\mathbf{0},$ then $s_0$ is a singular point of $P{e}_{\gamma ,p}$ and we have

$\left(1\right)P{e}_{\gamma ,p}$ does not have $3/2$, $5/2$ and $5/3$-cusp at $s_0.$

$\left(2\right)P{e}_{\gamma ,p}$ has a $4/3$-cusp at $s_0$ if and only if $\left(\kappa \tau \right)\left(s_0\right)\ne 0.$

CASE 3: Suppose that there exists $\lambda \in \mathbb{R},$ such that $\mathit{p}\in \lambda \mathit{T}\left(s_0\right)\setminus \gamma \left(s_0\right),$ then $s_0$ is a singular point of $P{e}_{\gamma ,p},$ and we have

$\left(1\right)P{e}_{\gamma ,p}$ has a $3/2$-cusp at $s_0$ if and only if $\left(\kappa \tau \right)\left(s_0\right)\ne 0.$

$\left(2\right)P{e}_{\gamma ,p}$ has a $4/3$-cusp at $s_0$ if and only if $\left({\kappa }^{\prime }\tau \right)\left(s_0\right)\ne 0$ and $\kappa \left(s_0\right)=0.$

$\left(3\right)P{e}_{\gamma ,p}$ does not have $5/2$-cusp at $s_0.$

$\left(4\right)P{e}_{\gamma ,p}$ has a $5/3$-cusp at $s_0$ if and only if $\left(\kappa {\tau }^{\prime }\right)\left(s_0\right)\ne 0$ and $\tau \left(s_0\right)=0.$

Proof. 

CASE 1: Suppose that $\tau \left(s_0\right)=0,$ then

$P{e}_{\gamma ,p}^{″}\left(s_0\right)=\left({\delta }_1{\delta }_2{\tau }^{\prime }⟨\mathit{P},\mathit{B}⟩\right)\left(s_0\right)\mathit{N}\left(s_0\right)+\left({\delta }_1{\delta }_2{\tau }^{\prime }⟨\mathit{P},\mathit{N}⟩\right)\left(s_0\right)\mathit{B}\left(s_0\right).$

$\begin{array}{cc}\hfill P{e}_{\gamma ,p}^{‴}\left(s_0\right)=& -\left(2\kappa {\tau }^{\prime }⟨\mathit{P},\mathit{B}⟩\right)\left(s_0\right)\mathit{T}\left(s_0\right)+\left({\delta }_1{\delta }_2{\tau }^{\prime \prime }⟨\mathit{P},\mathit{B}⟩\right)\left(s_0\right)\mathit{N}\left(s_0\right)\hfill \\ & +(-2\kappa {\tau }^{\prime }⟨\mathit{P},\mathit{T}⟩+{\delta }_1{\delta }_2{\tau }^{\prime \prime }⟨\mathit{P},\mathit{N}⟩)\left(s_0\right)\mathit{B}\left(s_0\right).\hfill \end{array}$

$\begin{array}{cc}\hfill P{e}_{\gamma ,p}^{\left(4\right)}\left(s_0\right)=& [-(3{\kappa }^{\prime }{\tau }^{\prime }+3\kappa {\tau }^{\prime \prime })⟨\mathit{P},\mathit{B}⟩]\left(s_0\right)\mathit{T}\left(s_0\right)\hfill \\ & +[6{\delta }_1{\delta }_2{\tau }^{\prime 2}⟨\mathit{P},\mathit{N}⟩+(-3{\kappa }^2{\tau }^{\prime }+{\delta }_1{\delta }_2{\tau }^{\prime \prime \prime })⟨\mathit{P},\mathit{B}⟩]\left(s_0\right)\mathit{N}\left(s_0\right)\hfill \\ & +[(-3{\kappa }^{\prime }{\tau }^{\prime }-3\kappa {\tau }^{\prime \prime })⟨\mathit{P},\mathit{T}⟩+(-3{\kappa }^2{\tau }^{\prime }+{\delta }_1{\delta }_2{\tau }^{\prime \prime \prime })⟨\mathit{P},\mathit{N}⟩\hfill \\ & +6{\delta }_2{\tau }^{\prime 2}⟨\mathit{P},\mathit{B}⟩+3{\delta }_1\kappa {\tau }^{\prime }]\left(s_0\right)\mathit{B}\left(s_0\right).\hfill \end{array}$

$\begin{array}{cc}\hfill P{e}_{\gamma ,p}^{\left(5\right)}\left(s_0\right)=& [-20\kappa {\tau }^{\prime 2}⟨\mathit{P},\mathit{N}⟩+(4{\delta }_1{\delta }_2{\kappa }^3{\tau }^{\prime }-4{\kappa }^{\prime \prime }{\tau }^{\prime }-6{\kappa }^{\prime }{\tau }^{\prime \prime }-4\kappa {\tau }^{\prime \prime })⟨\mathit{P},\mathit{B}⟩]\left(s_0\right)\mathit{T}\left(s_0\right)\hfill \\ & +[-20\kappa {\tau }^{\prime 2}⟨\mathit{P},\mathit{T}⟩+20{\delta }_1{\delta }_2{\tau }^{\prime }{\tau }^{″}⟨\mathit{P},\mathit{N}⟩\hfill \\ & +(-12\kappa {\kappa }^{\prime }{\tau }^{\prime }-6{\kappa }^2{\tau }^{\prime \prime }+{\delta }_1{\delta }_2{\tau }^{\left(4\right)})⟨\mathit{P},\mathit{B}⟩]\left(s_0\right)\mathit{N}\left(s_0\right)\hfill \\ & +[(4{\delta }_1{\delta }_2{\kappa }^3{\tau }^{\prime }-4{\kappa }^{\prime \prime }{\tau }^{\prime }-6{\kappa }^{\prime }{\tau }^{\prime \prime }-4\kappa {\tau }^{\prime \prime })⟨\mathit{P},\mathit{T}⟩\hfill \\ & +(-12\kappa {\kappa }^{\prime }{\tau }^{\prime }-6{\kappa }^2{\tau }^{\prime \prime }+{\delta }_1{\delta }_2{\tau }^{\left(4\right)})⟨\mathit{P},\mathit{N}⟩+20{\delta }_2{\tau }^{\prime }{\tau }^{″}⟨\mathit{P},\mathit{B}⟩\hfill \\ & +8{\delta }_1{\kappa }^{\prime }{\tau }^{\prime }+6{\delta }_1\kappa {\tau }^{″}]\left(s_0\right)\mathit{B}\left(s_0\right).\hfill \end{array}$

In this situation, suppose $P{e}_{\gamma ,p}^{″}\left(s_0\right)\ne 0,$ that is, ${\tau }^{\prime }\left(s_0\right)\ne 0,$ then we have the following.

$P{e}_{\gamma ,p}^{″}\left(s_0\right)$ and $P{e}_{\gamma ,p}^{‴}\left(s_0\right)$ are linearly independent if and only if $\kappa \left(s_0\right)\ne 0.$

$P{e}_{\gamma ,p}^{″}\left(s_0\right)$ and $P{e}_{\gamma ,p}^{‴}\left(s_0\right)$ are linearly dependent if and only if $\kappa \left(s_0\right)=0.$ Thus, $P{e}_{\gamma ,p}^{‴}\left(s_0\right)=cP{e}_{\gamma ,p}^{‴}\left(s_0\right),$ where $c={\tau }^{″}\left(s_0\right)/{\tau }^{\prime }\left(s_0\right).$

Therefore, $P{e}_{\gamma ,p}$ has a $3/2$-cusp at $s_0$ if and only if $\left(\kappa {\tau }^{\prime }\right)\left(s_0\right)\ne 0.$ $P{e}_{\gamma ,p}$ has a $5/2$-cusp at $s_0$ if and only if $\left({\tau }^{\prime }{\tau }^{″}\right)\left(s_0\right)\ne 0,$$({\kappa }^{\prime },{\kappa }^{″})\left(s_0\right)\ne (0,0)$ and $\kappa \left(s_0\right)=0.$

Suppose $P{e}_{\gamma ,p}^{″}\left(s_0\right)=0,$ that is, ${\tau }^{\prime }\left(s_0\right)=0,$ then we have the following.

$P{e}_{\gamma ,p}^{‴}\left(s_0\right)\left(s_0\right)$ and $P{e}_{\gamma ,p}^{\left(4\right)}\left(s_0\right)\left(s_0\right)$ are linearly independent if and only if $\kappa \left(s_0\right){\tau }^{″}\left(s_0\right)\ne 0.$

$P{e}_{\gamma ,p}^{‴}\left(s_0\right)$ and $P{e}_{\gamma ,p}^{\left(4\right)}\left(s_0\right)$ are linearly dependent and $P{e}_{\gamma ,p}^{‴}\left(s_0\right)\ne 0$ if and only if ${\tau }^{″}\left(s_0\right)\ne 0$ and $\kappa \left(s_0\right)=0.$

Therefore, $P{e}_{\gamma ,p}$ has a $4/3$-cusp at $s_0$ if and only if $\kappa \left(s_0\right){\tau }^{″}\left(s_0\right)\ne 0$ and ${\tau }^{\prime }\left(s_0\right)=0.$ $P{e}_{\gamma ,p}$ has a $5/3$-cusp at $s_0$ if and only if ${\kappa }^{\prime }\left(s_0\right){\tau }^{″}\left(s_0\right)\ne 0$ and $\kappa \left(s_0\right)={\tau }^{\prime }\left(s_0\right)=0.$

CASE 2: Suppose that there exists $s_0\in I$ such that $\mathit{p}=\gamma \left(s_0\right),$ then

$\begin{array}{c}\hfill P{e}_{\gamma ,p}^{″}\left(s_0\right)=0.\end{array}$

$\begin{array}{c}\hfill P{e}_{\gamma ,p}^{‴}\left(s_0\right)=\left({\delta }_1\kappa \tau \right)\left(s_0\right)\mathit{B}\left(s_0\right).\end{array}$

$\begin{array}{c}\hfill P{e}_{\gamma ,p}^{\left(4\right)}\left(s_0\right)=\left(4{\delta }_1\kappa {\tau }^2\right)\left(s_0\right)\mathit{N}\left(s_0\right)+(2{\delta }_1{\kappa }^{\prime }\tau +3{\delta }_1\kappa {\tau }^{\prime })\left(s_0\right)\mathit{B}\left(s_0\right).\end{array}$

$\begin{array}{cc}\hfill P{e}_{\gamma ,p}^{\left(5\right)}\left(s_0\right)=& (-10{\delta }_2{\kappa }^2{\tau }^2)\left(s_0\right)\mathit{T}\left(s_0\right)+(10{\delta }_1{\kappa }^{\prime }{\tau }^2+25{\delta }_1\kappa \tau {\tau }^{\prime })\left(s_0\right)\mathit{N}\left(s_0\right)\hfill \\ & +(11\kappa {\tau }^3+3{\delta }_1{\kappa }^{\prime \prime }\tau -{\delta }_2{\kappa }^3\tau +8{\delta }_1{\kappa }^{\prime }{\tau }^{\prime }+6{\delta }_1\kappa {\tau }^{\prime \prime })\left(s_0\right)\mathit{B}\left(s_0\right).\hfill \end{array}$

In this situation, since $P{e}_{\gamma ,p}^{″}\left(s_0\right)\equiv 0,$ $P{e}_{\gamma ,p}$ does not have $3/2$ and $5/2$-cusp at $s_0.$ Moreover, $P{e}_{\gamma ,p}^{‴}\left(s_0\right)$ and $P{e}_{\gamma ,p}^{\left(4\right)}\left(s_0\right)$ are linearly dependent if and only if $\kappa \left(s_0\right)\tau \left(s_0\right)=0,$ it follows that $P{e}_{\gamma ,p}^{‴}\left(s_0\right)=0.$ So, $P{e}_{\gamma ,p}$ does not have $5/3$-cusp at $s_0.$ $P{e}_{\gamma ,p}^{‴}\left(s_0\right)$ and $P{e}_{\gamma ,p}^{\left(4\right)}\left(s_0\right)$ are linearly independent if and only if $\kappa \left(s_0\right)\tau \left(s_0\right)\ne 0,$ therefore, $P{e}_{\gamma ,p}$ has a $4/3$-cusp at $s_0$ if and only if $\kappa \left(s_0\right)\tau \left(s_0\right)\ne 0.$

The other case is similar to the above proofs. □

The following theorem shows the relationship between the singular points of the pedal curves and the intersection points of pedal and contrapedal curves.

Theorem 4.

Let $\gamma :I\to {\mathbb{R}}_1^3$ be a non-lightlike regular curve in ${\mathbb{R}}_1^3$, the pedal curve of γ is $P{e}_{\gamma ,p}$. Suppose that $\mathit{P}\left(s_0\right)=\mathbf{0}$, $s_0\in I,$ then $P{e}_{\gamma ,p}$ has a singular point at $s_0$ and we have

$$P{e}_{\gamma ,p}\left(s_0\right)=CP{e}_{\gamma ,p}\left(s_0\right)=\gamma \left(s_0\right)=\mathit{p}.$$

5. Examples

To demonstrate the characteristics of pedal and contrapedal curves in ${\mathbb{R}}_1^3$ better, we provide the following two examples. For the sake of the brevity of the example results, we use the parameter t instead of the arc-length parameter $s.$

Example 1.

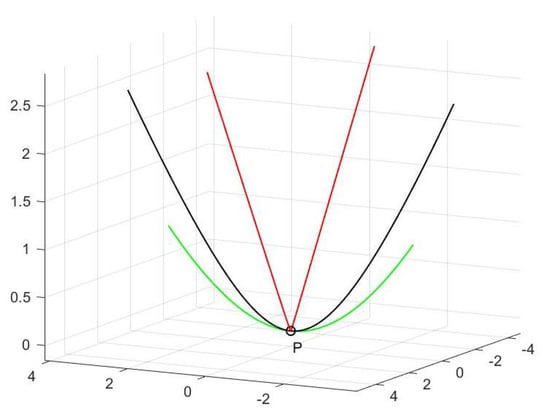
Let

$$\gamma \left(t\right)=(t^2,\frac{1}{3}{t}^3,3t),$$

then γ is a spacelike curve, and we obtain

$$\mathit{T}\left(t\right)=\frac{1}{\sqrt{t^4-4t^2+9}}(2t,t^2,3),$$

$$\mathit{B}\left(t\right)=\frac{1}{\sqrt{t^4-9t^2+9}}(3t,3,t^2).$$

If we take $\mathit{p}=(0,0,0)=\gamma \left(0\right),$ then

$$P{e}_{\gamma ,p}\left(t\right)=\frac{t^3}{t^4-9t^2+9}(3t,3,t^2).$$

According to Theorem 4, $P{e}_{\gamma ,p}$ has a singular point at $t=0.$ We draw it in Figure 1.

Figure 1. The curve $\gamma$ (green), its pedal (red) and contrapedal curve (black).

Example 2.

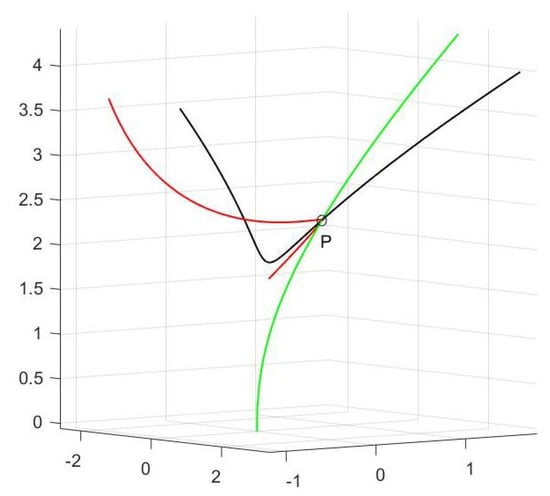
Let

$$\gamma \left(t\right)=(\frac{1}{3}{t}^3+2t,\frac{1}{3}{t}^3,t^2),$$

then γ is a timelike curve, and we obtain

$$\mathit{T}\left(t\right)=\frac{1}{2}(t^2+2,t^2,2t),$$

$$\mathit{B}\left(t\right)=\frac{1}{2}(t^2,t^2-2,2t).$$

If we take $\mathit{p}=(\frac{7}{3},\frac{1}{3},1)=\gamma \left(1\right),$ then

$$P{e}_{\gamma ,p}\left(t\right)=(-\frac{1}{6}{t}^5+\frac{1}{2}{t}^4-\frac{1}{2}{t}^3+\frac{1}{6}{t}^2+\frac{7}{3},-\frac{1}{6}{t}^5+\frac{1}{2}{t}^4-\frac{1}{6}{t}^3-\frac{5}{6}{t}^2+t,-\frac{1}{3}{t}^4+t^3-t^2+\frac{1}{3}t+1).$$

According to Theorem 4, $P{e}_{\gamma ,p}$ has a singular point at $t=1.$ We draw it in Figure 2.

Figure 2. The curve $\gamma$ (green), its pedal (red) and contrapedal curve (black).