Intelligent System for Estimation of the Spatial Position of Apples Based on YOLOv3 and Real Sense Depth Camera D415

Abstract

Despite the great possibilities of modern neural network architectures concerning the problems of object detection and recognition, the output of such models is the local (pixel) coordinates of objects bounding boxes in the image and their predicted classes. However, in several practical tasks, it is necessary to obtain more complete information about the object from the image. In particular, for robotic apple picking, it is necessary to clearly understand where and how much to move the grabber. To determine the real position of the apple relative to the source of image registration, it is proposed to use the Intel Real Sense depth camera and aggregate information from its depth and brightness channels. The apples detection is carried out using the YOLOv3 architecture; then, based on the distance to the object and its localization in the image, the relative distances are calculated for all coordinates. In this case, to determine the coordinates of apples, a transition to a symmetric coordinate system takes place by means of simple linear transformations. Estimating the position in a symmetric coordinate system allows estimating not only the magnitude of the shift but also the location of the object relative to the camera. The proposed approach makes it possible to obtain position estimates with high accuracy. The approximate root mean square error is 7–12 mm, depending on the range and axis. As for precision and recall metrics, the first is 100% and the second is 90%.

1. Introduction

Today, there is a rapid surge in the use of artificial intelligence systems in various spheres of the economy. Agriculture is one of the areas undergoing rapid digitalization [1,2,3]. According to the United Nations (UN) report [4], the number of the world’s population will grow rapidly in the next 30–50 years; in particular, by 2050, it is expected that the Earth population will reach 10 billion. At the same time, questions arise about providing such several people with provisions. The solution to this problem is impossible without increasing the efficiency in the field of agriculture. The work [5] pays great attention to the aspects of digitalization of sustainable agri-food systems and predicting risks, taking into account the new coronavirus infection in the Middle East and North Africa. It should be noted that along with the potential problems of future food shortages, today, there is another problem associated with the fact that part of the harvest remains unharvested. An important reason that unpicked apples rot in orchards, dachas, and agricultural holdings is the low return on investment.

All of the above allows us to conclude that one of the promising ways for the development of the agricultural industry is the introduction of robotic solutions, including fast, high-quality, and reliable harvesting [6,7]. At the same time, the key role in such robots should be played by an intelligent image analysis system, which is being developed, in particular, for the tasks of identifying damaged or diseased potatoes [8,9]. First, it is required to ensure high values of the apple recognition and detection metrics. Second, it is required to ensure low errors in determining the spatial position of the apple relative to the robot. Thirdly, efficient algorithms for bypassing the harvest are required, which allow harvesting fruits as much as possible without damage. This study is largely devoted to the first two indicated tasks. For the recognition system, the neural network architecture YOLOv3 was chosen [10], which includes an apple class in one of 80 recognizable classes. The solution of the second problem is based on the methods of computer optics [11] and the use of the Intel Real Sense Depth Camera D415 [12], which, in addition to registering an optical image in color channels of brightness, also constructs a depth map.

The second section will consider related works on neural networks used in detection and pattern recognition problems, including agriculture and apple recognition. The third section presents a hardware-software solution for the problem of estimating the apple coordinates in real space. Section 4 is devoted to the study of the errors obtained as a result of the presented solution. In the conclusion, the main results of the work are presented. It should be noted that a known neural network was used in this article, but in this work, we did not set the task of developing and training an algorithm for detecting apples but rather considered a new application of the YOLOv3 architecture modified for this task. The novelty of this paper is the assessment of the quality of the modified algorithm for detecting and positioning on apples.

2. Related Works

The task of detecting objects in computer vision is closely related to the task of pattern recognition. The first successful detectors using convolutional neural network technology were networks of the R-CNN architecture [13]. Inside the proposed solution, the CaffeNet architecture (a type of the AlexNet network) [14] was used to recognize objects in an arbitrarily selected rectangular region. At the same time, the algorithm worked rather slowly, and the proposal of regions for performing the recognition procedure was carried out using the selective search method. A modification of such a network was the Fast R-CNN network [15], which projected the regions proposed by selective search onto a once calculated feature map, and to refine the coordinates of the bounding rectangles, a regression block was additionally used since the sizes of the feature map and the original image were different and did not allow proportionally performing an integer projection of the regions. However, the performance of the selective selection method was poor. In this regard, the Fast R-CNN architecture was replaced by the Faster R-CNN architecture [16]. The main advantage of this approach was the proposal of regions already directly on the feature map, which made it possible, firstly, to use additional information of the feature space and knowingly avoid places with a low probability of the appearance of objects. This was achieved by introducing a specialized neural network into the image analysis process to suggest regions.

However, the accuracy of detector networks significantly decreased with the metrics of networks that solve only the recognition problem. At the same time, the speed of work was still unacceptable for use in real-time systems. A significant increase in computing performance relative to the R-CNN family was provided by the so-called Single Shot—Multibox Detector. Such networks perform localization and recognition procedures for a large number of regions in one iteration. An example is the neural networks of YOLO [17], SSD [18], RetinaNet [19] architectures, and others.

The networks of the YOLO (You Only Look Once) architecture should be emphasized [17]. Currently, there is a whole family of similar architectures, and significant progress in the quality of detection and performance has been achieved with the advent of the third version named YOLOv3 [20]. At the same time, by analogy with the idea of the R-CNN family, a separate pattern recognition task is also performed. YOLOv3 uses the DarkNet-53 neural network [21], which is a more complex convolutional network architecture compared to the previously discussed AlexNet. The selective region search method is not used in YOLO-based detection methods; instead, the input image is scaled and initially divided into square regions, in which recognition takes place using DarkNet-53. In each square, three bounding rectangles are constructed, and the object presence probability of each known type within such an area is estimated. In this case, the bounding rectangles can be of different sizes, and the use of square division allows leaving the detection area with the greatest confidence, cutting off those that capture only part of the object. For processing video sequences, YOLO allows processing each frame in one pass, which allows processing video images with sufficient computing power of the processor [22].

So, this network has also proved itself well in the problems of fruit recognition on trees [23]. Nevertheless, the authors of [23] consider only a part concerning the processing of individual image frames. Despite the rather high metrics of accuracy and completeness, YOLOv3 does not allow estimating the real distances to objects from the image received from one camera. Article [24] recommends many preliminary operations to improve the quality of detectors. However, the authors also do not consider the problem of determining the coordinates of apples in three-dimensional space. The authors of [25] show that customized training and the use of image augmentation [26] lead to an increase in the quality of such systems. Xuan G. et al. [27] achieve f-measure indices up to 91–94% under different illumination conditions on green apples and 94–95% on red apples. The authors of [28], in addition to apples, add pears to the recognition system based on YOLOv3 and suggest using Kalman filtering for tracking fruits while moving.

Work [29] is devoted to the use of the Intel Real Sense Depth Camera D435 for estimating the distance from the robot to obstacles when constructing a trajectory. Finally, in [30], a comparative analysis of the characteristics of the Real Sense camera line is presented, and in [31], a comparative analysis of depth cameras with laser scanning technologies is performed, showing the sensitivity of both approaches to noise.

Thus, this review shows that despite the presence of research in the field of computer vision algorithms for recognizing apples and works devoted to measuring the depth and assessing the coordinates of objects, the literature does not fully describe methods that combine data from the results of image processing and depth maps in this task. Next, it is worth considering the solution to this problem concerning an intelligent system for estimating the location of apples in 3D space. During the development phase of the primary solution, the YOLOv3 architecture (combination of speed and accuracy) and the Real Sense D415 camera (still available on the market for purchase) were chosen. At the same time, the technology for estimating coordinates when switching to another device for constructing depth maps, for example, Microsoft Kinnect, can also be used for the operation of the system, but it will be necessary to take into account the alignment of frames from different channels.

3. Materials and Methods

When describing the materials and methods used in the article, the hardware and software parts of the system should be distinguished separately. In particular, the Intel Real Sense Depth Camera D415 was used to record the video sequence of images. Image processing was carried out based on a laptop ASUS TUF FX504 (CPU Intel Core i7-8750, 2.2 GHz).

The software implementation was carried out in the Python programming language using the pre-trained YOLOv3 architecture and the TensorFlow deep learning library. In addition, the pyrealsense2 module was used, which provides convenient functions for working with Real Sense cameras, as well as the OpenCV library, which allows registering images and video providing convenient visualization of processing results in real time.

At this stage, the experiments were carried out in laboratory conditions, namely, on the territory of the engineering center of the Financial University under the Government of the Russian Federation (Moscow, Russia).

Figure 1 shows the architecture of the YOLOv3 convolutional neural network [20].

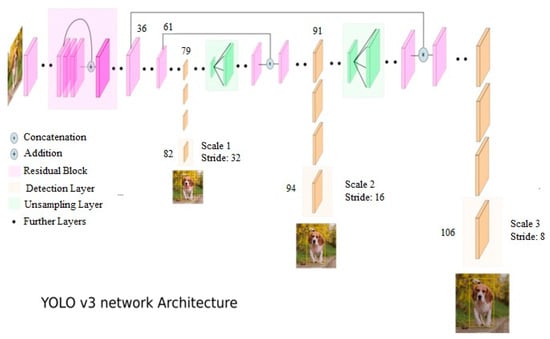
Figure 1. YOLOv3 network architecture.

From the presented figure, it can be seen that the selected model has 106 convolutional layers. This model can also detect objects of various sizes. It consists of standard convolutional layers, residual blocks, detection layers, and unsampling layers. It should be noted that in this article, the detector uses the weights of the pre-trained model, and there is no training process.

In the absence of sports balls and oranges on apple trees in Russia, these classes were also combined with the “apple” class. Figure 2 shows the camera used in the article.

Figure 2. Intel Real Sense Depth Camera D415.

Figure 3a,b show images of the color and depth channels of the camera, respectively, using the specialized software Intel Real Sense Viewer, and Figure 4 shows a frame with detections processed using OpenCV and the pyrealsense2 module.

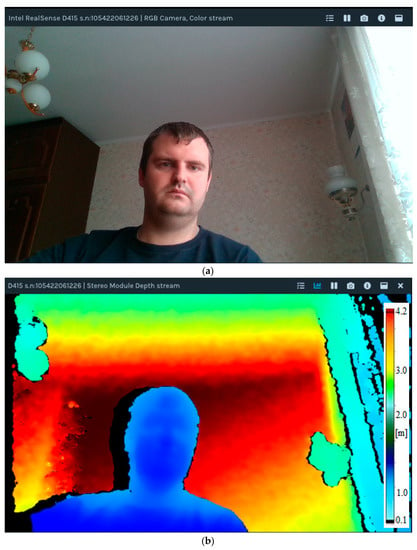
Figure 3. Image and depth registration in Intel Real Sense View. (a) RGB color channel; (b) Depth channel.

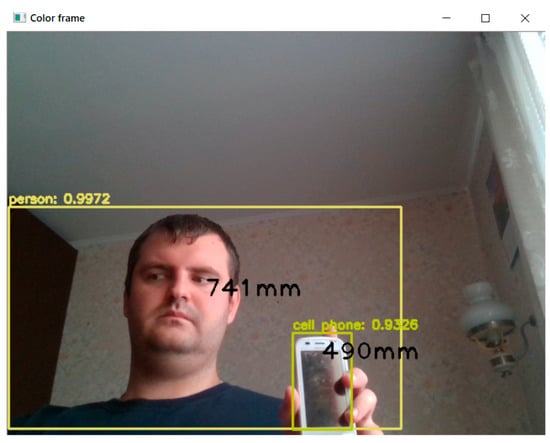
Figure 4. Image processing using Intel Real Sense Depth Camera D415 and YOLOv3.

It can be seen that the camera selects the distances to objects in the range of 0–4 m. Moreover, at each point of the depth map, the specialized color of the image corresponds to the distance to this point in space.

Figure 4 shows that using the YOLOv3 network and Real Sense camera allows detecting objects of different classes and calculating the distance to them. In this case, it is considered that the distance to the object is the distance to its center, i.e., to the center of the bounding rectangle of the detected object. In particular, for the image presented in Figure 4, the following objects were found: a person and a cell phone.

From Figure 4, it can be seen that the depth map is used to measure the distance from the center of the camera to a specific point. However, such a map lacks information about the object’s shifts relative to the camera in the X, Y, and Z planes. In this case, for the detected objects, there are the coordinates of the upper left point in pixels as well as the width and height of the bounding rectangle in pixels. The problem arises of converting the coordinates of objects in relative (to the upper left corner) pixels into millimeters relative to the center of the camera, since information about the distance in millimeters comes from the depth map. To solve this problem, it is possible to use the following relations [32]:

$$\begin{array}{l}X[mm]=d_{x_0,y_0}\frac{(C_x-x_0[px])}{f_x},\\ Y[mm]=d_{x_0,y_0}\frac{(C_y-y_0[px])}{f_y},\end{array}$$

(1)

where $X[mm]$ is the projection of the distance relative to the center of the image on the X axis (in mm), $Y[mm]$ is the projection of the distance relative to the center of the image on the Y axis (in mm), $d_{x_0,y_0}$ is the value of the depth map at a point with a coordinate $(x_0,y_0)$ (in mm), $C_x$ is the coordinate of the center of the image along the X axis (in pixels), $C_y$ is the coordinate of the center of the image along the Y axis (in pixels), $f_x$ and $f_y$ are internal parameters of the optical system of the camera used to obtain the image (focal lengths along the X and Y axes), $(x_0,y_0)$ is the coordinate of the center of the detected object in the image in pixels.

When calculating the distance to an object along the X-axis in accordance with Equation (1), it is necessary to take into account the offset of the RGB camera module from the center of Real Sense:

$$X^{\prime }[mm]=X[mm]-35$$

(2)

where $X^{\prime }[mm]$ is the unbiased projection of the distance from the center of the camera to the object along the X axis (in mm), 35 (mm) is the offset for the Intel Real Sense Depth Camera D415.

Finally, knowing the absolute distance to the object and calculating from (1) and (2) its projection on the X and Y axes, it is possible to calculate the projection on the Z-axis based on the geometric meaning of the distance:

$$Z[mm]=\sqrt{d_{x_0,y_0}^2-X^{\prime }{[mm]}^2-Y{[mm]}^2}.$$

(3)

Thus, Equations (1)–(3) fully describe the estimate of the coordinates of the detected apple relative to the center of the camera and can be used to correctly aim the grabber.

However, as can be seen from Figure 4, the detection and measurement of distances for all types of objects trained by YOLOv3 take place. In this regard, the algorithm was modified in such a way that after recognizing objects at each frame of the video sequence, it is checked whether it belongs to the classes “apple”, “orange”, and “sports ball”. The addition was made taking into account the existing probability that YOLOv3 takes an apple for these types of objects. The final processing scheme is shown in Figure 5.

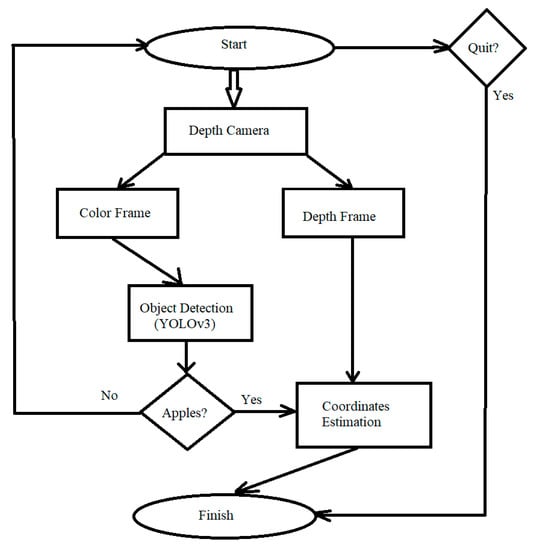
Figure 5. Apple detection and coordinate estimation system operation algorithm.

Based on the presented algorithm, the processing is carried out until the apples are found. The developed program provides for a forced interruption by the user.

It also should be noted that the transformation of the coordinate system in the image, in which the upper left point corresponds to zero on both axes, occurs in such a way that zero corresponds to the central position on the image, i.e., the absence of displacement of the object relative to the camera. This allows, through additional transformations, to use the properties of a symmetric coordinate system and to perceive positive deviations along the X axis as indicating that the object is to the right of the camera and negative ones indicating that it is to the left. The system works similarly with respect to the Y axis: with positive values, it is possible to say that the object is above the camera, and with negative values, it is lower.

In the next section, the main results of the proposed solution are considered.

4. Results

The proposed solution is based on YOLOv3 and an Intel Real Sense Depth Camera. The experiments were carried out in a laboratory, but in the future, the investigation of the algorithm on real apple trees is planned. Figure 6 shows an example of the result of detecting and estimating coordinates.

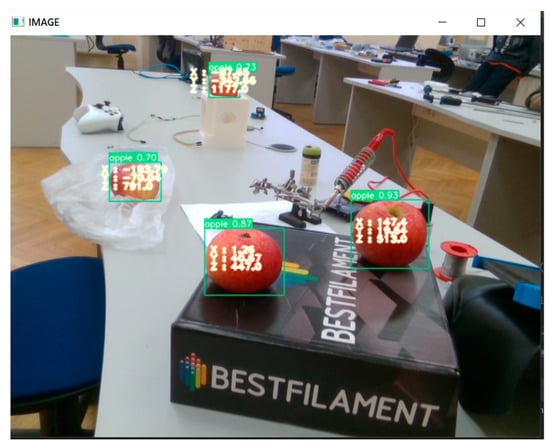
Figure 6. Detection, recognition, and estimation of apple coordinates.

In this case, in addition to the coordinates themselves, the probabilities of assigning an object to the class “apple” are also indicated. Table 1 presents such characteristics as Precision and Recall depending on the threshold at which it is decided that the detected object is indeed an apple. The analysis is performed for processing 200 frames at different positions of the apples. It should be noted that distance to apples during the experiment did not exceed 1.5 m.

Table 1. Precision and recall of recognition.

Probability Threshold, C	0.25	0.5	0.75
Precision	1.0	1.0	1.0
Recall	0.90	0.84	0.69

It should be noted that in binary classification (apple—not apple), the value of Precision is determined as $\frac{TP}{TP+FP}$, where TP is the number of True Positive detections of apples during 1 min of processing, FP is the number of False Positive detections of apples during 1 min of processing. Table 1 shows the maximum Precision, since our algorithm gives apple labels only for apples. As for Recall, it is determined as $\frac{TP}{TP+FN}$, where TP is the number of True Positive detections of apples during 1 min processing, FN is the number of False Negative detections of apples during 1 min processing. So, it is possible to see that using big probability thresholds, the algorithm skips many more apples on some frames of the video.

The low results of the Recall metric in Table 1 are associated not only with a decrease in the threshold but also with the fact that the detection worsens with the distance of apples from the camera. In the next experiment, the error in measuring the coordinates of apples relative to the camera was estimated. It should be noted that it is important to initially calibrate the camera so that the X, Y, and Z planes are in a perpendicular position relative to it. Otherwise, when calculating coordinates, it is worth taking into account the camera tilt angles along the corresponding axes. All measurements presented below were carried out based on the calculation of the zero angle, i.e., such that the projection coincides with the measured distance. Table 2 shows the coordinates (X, Y, Z) estimates obtained using measuring instruments (index 0) and using the Intel Real Sense Depth Camera D415 and YOLOv3 (index 1).

Table 2. Estimation of the coordinate measurement error.

Apple 1
Position	X1 mm	X0 mm	SEx mm2	Y1 mm	Y0 mm	SEy mm2	Z1 mm	Z0 mm	SEz mm2	D1 mm	D0 mm	SEd mm2
1	−114	−110	16	−33	−27	36	958	948	100	965	955	100
2	−56	−60	16	−14	−25	121	296	290	36	302	297	25
3	38	36	4	19	16	9	802	798	16	803	799	16
4	118	116	4	90	90	0	465	472	49	488	494	36
5	−128	−117	121	−106	−115	81	361	372	121	397	407	100
6	204	189	225	202	196	36	760	762	4	812	809	9
Apple 2
Position	X1 mm	X0 mm	SEx mm2	Y1 mm	Y0 mm	SEy mm2	Z1 mm	Z0 mm	SEz mm2	D1 mm	D0 mm	SEd mm2
1	−37	−31	36	−27	−20	49	941	936	25	942	937	25
2	69	68	1	−22	−17	25	449	436	169	455	442	169
3	−180	−168	144	130	122	64	1121	1096	625	1143	1115	784
4	318	322	16	286	294	64	765	754	121	876	871	25
5	−310	−317	49	−189	−195	36	526	531	25	639	648	81
6	98	104	36	−211	−200	121	355	360	25	424	425	1
Apple 3
Position	X1 mm	X0 mm	SEx mm2	Y1 mm	Y0 mm	SEy mm2	Z1 mm	Z0 mm	SEz mm2	D1 mm	D0 mm	SEd mm2
1	139	150	121	7	16	81	1101	1083	324	1110	1093	289
2	−20	−22	4	107	112	25	897	890	49	904	897	49
3	−212	−207	25	189	198	81	382	388	36	476	482	36
4	318	326	64	295	288	49	1308	1278	900	1378	1350	784
5	−188	−185	9	−212	−216	16	655	655	0	714	714	0
6	−312	−322	100	204	201	9	420	428	64	562	572	100
MSE(mm2)	55.06			50.17			149.39			146.06
RMSE(mm)	7.42			7.08			12.22			12.09

The column «position» indicates different apples’ locations during coordinates estimation. The new variables are introduced in Table 2. Let us explain them. In Table 2, the following parameters were calculated:

• Square Error along the X, Y and Z axes:

  $$S{E}_{xi}={(x_{0i}-x_{1i})}^2,S{E}_{yi}={(y_{0i}-y_{1i})}^2,S{E}_{zi}={(z_{0i}-z_{1i})}^2.$$

  (4)
• Euclidean distance to the apple using measuring instruments:

  $$D_{0i}=\sqrt{x_{0i}^2+y_{0i}^2+z_{0i}^2}.$$

  (5)
• Euclidean distance to the apple using Real Sense:

  $$D_{1i}=\sqrt{x_{1i}^2+y_{1i}^2+z_{1i}^2}.$$

  (6)
• Square Error of distance estimation:

  $$S{E}_{di}={(D_{0i}-D_{1i})}^2.$$

  (7)

The calculated values of the mean square errors and the root mean square errors show sufficiently the high accuracy of the coordinate estimation algorithm. In this case, the greatest errors occur along the Z axis, the distances along which can reach much larger values. To determine the influence of the absolute value of the displacement of objects relative to the camera, it is possible to construct the corresponding scatter diagrams between instrumental and software measurements. Figure 7 shows scatters for all axes and distance measurements.

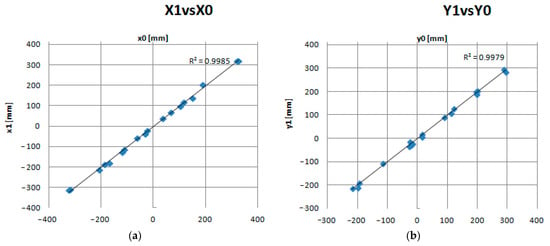
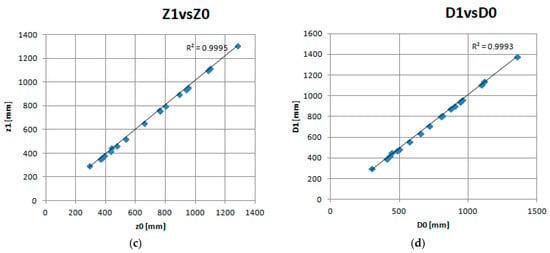
Figure 7. Estimates depending on real coordinate values. (a) X axis; (b) Y axis; (c) Z axis; (d) Distance.

The analysis of the dependencies presented in Figure 7 allows us to conclude that the estimation for all coordinates occurs with high accuracy (the index of determination between the estimates and the measured values of R² > 0.99 for all axes).

To estimate the homoscedasticity of the residuals, it is necessary to construct their scatter diagrams. The visualizations are shown in Figure 8. The analysis of scatter diagrams shows that concerning the X and Y axes, there is no correlation of errors with the real values of the distance projections. However, there is some negative correlation for the Z axis. In particular, there is an increase in the absolute value of the error with increasing distance. Moreover, this phenomenon also affects the errors in the estimation of the distance. This is probably due to several reasons. First, concerning the plane perpendicular to the Z axis, the camera was not completely calibrated to a zero angle. This is also confirmed by the fact that at small Z values, errors are also grouped above zero. In addition, the camera angle of view does not allow detecting apples at large offset distances X and Y.

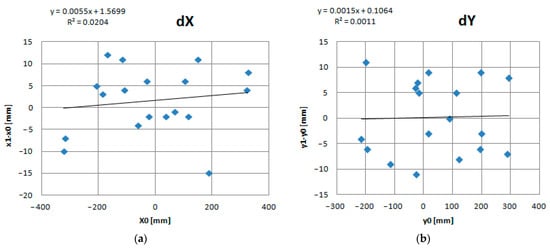
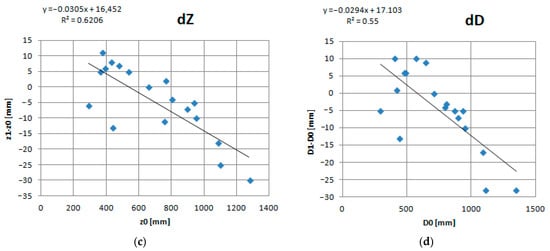
Figure 8. Errors depending on real coordinate values. (a) Residuals for X axis; (b) Residuals for Y axis; (c) Residuals for Z axis; (d) Residuals for distances.

Taking into account the dependencies shown in Figure 8c,d it is possible to adjust the accuracy of determining the coordinates and reduce the positioning error.

Finally, the average processing time of one frame containing apples was measured with the calculation of coordinates. On the CPU specified in Section 3, the performance was $2.52\pm 0.87$ frames per second. For the task of picking apples, this time is not critical, since the ratio of the time spent on detecting apples and estimating their coordinates to the time spent on picking is negligible. Since the Intel CPU was used in this research, it is possible to increase performance implementing the proposed solution in OpenVINO [33] and high-efficiency algorithms [34]. Another possibility is to use GPUs and YOLOv5 architecture.

5. Conclusions

The article presents an algorithm for joint detection, recognition of apples, and their relative coordinate estimation. As a result of the study, it was proposed to use the YOLOv3 neural network to solve the problem of image detection and recognition. At the same time, the “apple” class has been extended with some similar objects. The optimal probability threshold of getting high Precision and Recall scores is 0.2–0.3. At the same time, the value of the Recall metric is close to 90%, and there are no false positives. Object coordinates are calculated by the optical transformation of relative coordinates in the image pixel space to real coordinates using Intel Real Sense depth maps. The analysis showed that the root mean square errors are not large in measuring the coordinates. All errors are about 7–12 mm on average. However, the error increases with the distance of objects from the camera, which may be due to its tilt. In the future, it is planned to additionally take into account this error source. In addition, the average performance is about 2.5 frames per second. In the future, it is planned to use the YOLOv5 model to increase the processing speed.