Abstract
In this paper, we study the properties of a lower porosity of a set in . It turns out that the properties of the lower and upper porosity are symmetrical, except that the main tools for testing the lower porosity are not balls but cones. New families of topologies on generated by the lower porosity are defined. Furthermore, by applying the notion of the lower porosity, we introduce the definition of generalized continuity. Using defined topologies, we study properties of this continuity. We show that the properties of topologies generated by the lower and (upper) porosity are symmetrical.
Keywords:
porosity; lower porosity; lower porouscontinuity; topology generated by set and lower porosity; maximal additive class; maximal multiplicative class MSC:
54C30; 26A15; 54C08
1. Introduction
The porosity of a set, defined in [1], is the notion of smallness more restrictive than nowhere density and meagerness. It can be defined in arbitrary metric space. The main idea is that we modify the “ball” definition of nowhere density by the request that the sizes of holes should be estimated. Usually, the notion of the (upper) porosity of sets is used.
Recently, the concept of porosity is used not only to study subsets of a metric space but also to compare families of functions. By applying the notion of porosity one can describe how “small” one class of function in the other is, (see [2,3,4]). In the study of these comparison of classes of functions, it was found that it was possible to strengthen results by using the lower porosity instead of the (upper) porosity.
We deal with the lower porosity, which has also been considered in some papers. It is known that there are big differences between the lower and the upper porosities. In [5,6], some properties of the lower porosity in metric spaces are presented, whereas in [7], some properties of some kind of the lower porosity of subsets of are presented. The first aim of this paper is to investigate new properties of the lower porosity of subsets of . It turned out that there are many distinctions between porosity on and . For example, for every and , either or , while for every we can find a subset of whose porosity equals r. We limit our considerations to the case of because obtained results can be easily extended to the case of arbitrary . Properties of the lower porosity are symmetrical with properties of the (upper) porosity, but we apply cones instead of families of pairwise disjoint balls to estimate porosity.
The second aim of our paper is to describe some properties of lower porouscontinuous functions . Porouscontinuous functions were introduced by J. Borsík and J. Holos in [8]. Their properties and generalizations can be found, for example, in [9,10,11]. Lower porouscontinuity is much stronger than (upper) porouscontinuity. In [7], some properties of lower porouscontinuity of functions are studied. It turns out that there are big differences between lower porouscontinuity of functions defined on and functions defined on . Moreover, we present similarities and differences between lower porouscontinuity and (upper) porouscontinuity. For example, we show that lower porouscontinuous functions and (upper) porouscontinuous functions have the same maximal additive class and different maximal multiplicative class.
Let and denote the set of all positive integers and the set of all real numbers, respectively. For and , by we mean the restriction of f to . The symbols , , and denote the closure, the interior, and the boundary of with respect to the natural topology . The open ball with the center and the radius is denoted by . Similarly, by and we denote the sphere and the closed ball with the center A and the radius , respectively. For points , , , , we use the following notations:
- —the line passing through A and B;
- —the half-line beginning A through B;
- —the length of line segment ;
- —the measure of the angle between lines and ;
- —the distance between A and line .
2. Lower Porosity and Generalized Continuity
Now, we recall definitions of the (upper) porosity and the lower porosity. These notions can be defined in an arbitrary metric space but we present them only for subsets of because only such case is considered in this paper. Let , and . Then, according to [1,6], by we denote the supremum of the set of all for which there exists such that . The number is called the (upper) porosity of at A. Obviously, for and . The number is called the lower porosity of at A. Clearly, and for and . Moreover, for we have , and if .
Example 1.
Let be a decreasing sequence of positive reals convergent to 0 such that for each . Denote . Since for , we conclude that balls for are pairwise disjoint. Since , by Theorem 1.2 in [11] we obtain . On the other hand,
for every . Thus .
Example 2.
Let , and . Then for every .
Theorem 1.
Let , and . Then there exists a sequence of closed balls , not necessary pairwise disjoint, such that , for , and
Proof.
For every put and choose a closed ball such that . Denote . Since , we obtain . Fix and choose any . Then
and
We have shown that for each and for each the following inequalities
are true. Hence
and
Finally, □
Definition 1.
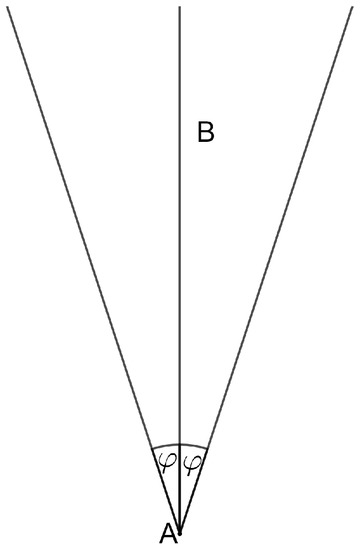
Let , and . The set
is called a cone appointed by two distinct points A, B, and the angle φ (see Figure 1).

Figure 1.
The cone .
Theorem 2.
Let be a cone, , and . Then .
Proof.
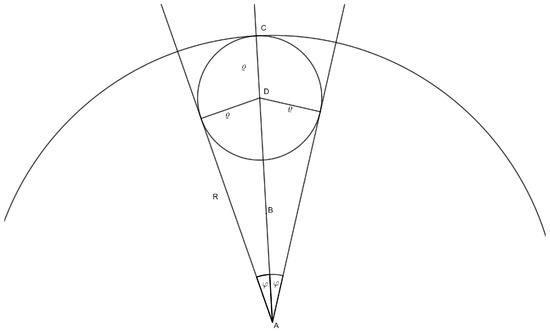
Take any and let C, D be points on the half-line such that and (see Figure 2). Then and the distance between D and the boundary of equals . Thus . Hence .

Figure 2.
The cone .
Let . Take a point such that the distance between E and is equal to . Put . Then and . Since defined by , where c is an arbitrary positive number, is strictly increasing, we obtain
Therefore for every . Finally,
□
Corollary 1.
Let , and . Since for every there exists such that , we have .
Lemma 1.
Let , , . For each we can find such that
where .
Proof.
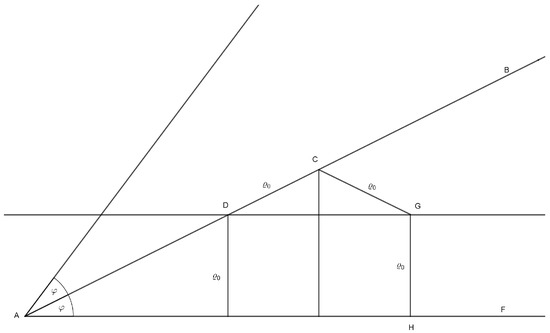
Let be any point on . Define by
For let be a point on the half-line such that . It is easy to see that if then
Let D be a point on the half-line such that and (see Figure 3).

Figure 3.
The cone .
Denote . Fix a point G, , lying on a straight line parallel to the straight line and passing through the point D such that . Let be such that . Obviously and
Let us compute and . Since and , we obtain and . Let H be a point on the half-line such that . It is easy to see that . Moreover, . Hence
Put
Moreover,
Therefore
For fixed we have . Thus . □
Theorem 3.
Let . There exists such that for each cone , , , and for each sequence satisfying conditions:
- ;
- for each ,
the equality
where , is fulfilled.
Proof.
Put . Let be any sequence of points from satisfying conditions and for each . Fix . Take a point on the half-line such that lines and are perpendicular. Let be a number from Lemma 1 chosen for the point . Then
Obviously
Hence
Since for each and , we obtain
□
In [8], J. Borsík and J. Holos defined families of porouscontinuous functions . Applying their ideas and replacing standard porosity in by the lower porosity in we transfer this concept for real functions defined on .
Definition 2.
Let , and . The function f will be called:
- -continuous at A if there exists a set such that , and is continuous at A;
- -continuous at A if for each there exists a set such that , and ;
- -continuous at A if there exists a set such that , and is continuous at A;
- -continuous at A if for each there exists a set such that , and .
By , , , and we denote the set of points at which f is -continuous, -continuous, -continuous, and -continuous, respectively.
Proposition 1.
Let , and . Then
- 1.
- if and only if for every ;
- 2.
- if and only if for every .
Similarly as in [8], we can easily check that f is -continuous at A if and only if it is -continuous at A.
Proposition 2.
Let , and , . Then
- 1.
- if then ;
- 2.
- if then ;
- 3.
- if then .
If f is -continuous, -continuous, -continuous at every point of for some then we say that f is -continuous, -continuous, -continuous, respectively. All of these functions are called lower porouscontinuous functions.
Obviously, if f is continuous at some A then f is lower porouscontinuous (in each sense) at A. We introduce for the following notations:
- ;
- ;
- .
In the sequel, we consider with several different topologies. Let be a topology on (in particular may be the natural topology). Then we say that is -continuous at if it is continuous at A as . Thus -continuity of f at A means that for each there exists -open set such that and . We say that f is -continuous if it is -continuous at each point. By and we denote the set of points at which f is continuous and f is -continuous, respectively. Denote
- ;
- .
Similarly, by and we denote the interior and the closure of in the topology . Finally, for any let .
3. Maximal Additive Families for Lower Porouscontinuous Functions
It is easily seen that the result of addition or multiplication of functions from one of discussed classes of functions, in general, need not belong to this class. Description of functions that can be represented as a final sum or product of lower porouscontinuous functions is still not known; therefore, we study the following similar notion.
Definition 3
([12]). Let be a family of real functions defined on . A set is called the maximal additive class for .
Remark 1.
Let , for , be a constant function. Clearly, if then .
Lemma 2.
Let , , and f be continuous at A. Then
- (1)
- if then ;
- (2)
- if then ;
- (3)
- if then .
Proof.
- (1)
- Since g is -continuous at A, there exists such that , is continuous at A and . Since f is continuous at A, and are continuous at A; therefore, .
- (2)
- Let . Since g is -continuous at A, there exists such that , and . By continuity of f at A, we can find such that for each . Let . Then andfor . This means that .
To prove the second condition, we consider the following two cases.
- . Take any . Since g is -continuous at A, there exists such that , and . By continuity of f at A, we can find such thatfor each . Let . Then andfor each . Then .
- . Let . Since g is -continuous at A, there exists such that ,and . By continuity of f at A, we can find such that for each . Let . Then andfor each . Hence .
- (3)
- The proof is similar to the proof of (1) and we omit it.
□
Lemma 3.
Let and . Then there exists a set such that
- ;
- is discrete;
- For each , if then .
Proof.
Let for . Applying the Zorn lemma, for every n we can choose a discrete set such that and for , . Let
Then is discrete, and . Take any such that . The inequality is obvious. If then certainly . Let . Choose any and such that . We can find such that . Since , there exists such that , and . Suppose that and take any . There exists such that , i.e., . Since
we obtain and . By construction of , there exists such that . Observe that and ; therefore , i.e., . Thus
This means that . By inequality , we obtain . Hence
and . Moreover,
Since was chosen arbitrarily, , which completed the proof. □
Theorem 4.
Let and . The following conditions are equivalent:
- (1)
- f is continuous at A;
- (2)
- ;
- (3)
- ;
- (4)
- ;
- (5)
- ;
- (6)
- ;
- (7)
- .
Proof.
Implications , , and are obvious. Implications , , and follow from Lemma 2.
. For every by we denote the unique number from such that . Let there exists such that for each we have . Choose such that for every , i.e., . Let and satisfy assertion of Theorem 3.
Suppose that f is not continuous at A. Then there exist and a sequence convergent to A such that for each . Clearly, we can find such that contains infinitely many elements of the sequence . Without loss of generality, we may assume that for every . Let be a set from Lemma 3 for and A. Then is discrete, and for each , if then . Define by
Clearly, for and is continuous, because is discrete and . Since is a closed subset of , by the Tietze theorem we can find a continuous extension of . Finally define by
Obviously, . Since , . Finally, .
On the other hand, , for every and for . Let
Then . By Lemma 3,
Moreover, . By Theorem 3,
Hence, , a contradiction.
and . Assume that there exists such that for each (, respectively) we have (, respectively). For every by we denote a number from such that . There exists such that . Choose such that for every , i.e., . Let and satisfy assertion of Theorem 3.
Suppose that f is not continuous at A. Then there exist and a sequence convergent to A such that for each . Again, we can find such that contains infinitely many elements of the sequence . Let be a set from Lemma 3 for and A. Then is discrete, and for each , if then . Define by
Clearly, for and is continuous. Since is a closed subset of , by the Tietze theorem we can find a continuous extension of . Define by
Obviously, . Since , . Finally, .
On the other hand, , for every and for . Let
Then . By Lemma 3,
Moreover, . By Theorem 3,
Hence, , a contradiction. □
Corollary 2.
For every we have
Remark 2.
One can defined , , and . It is easy to see that , , and . In [10], classes , , and are described using the notions of topologies p and s introduced in [5,13].
4. Maximal Multiplicative Families for Lower Porouscontinuous Functions
In this section, we describe maximal multiplicative classes for and . It turns out that aiming for this purpose we must define new topologies on generated by the lower porosity.
First, recall the definition of maximal multiplicative class for a family of functions.
Definition 4
([12]). Let be a family of real functions defined on . A set is called the maximal multiplicative class for .
Remark 3.
Let , for , be a constant function. If then .
Example 3.
Let , , and be defined by for and for . Clearly, f is not continuous. We will show that for each .
Take any . Obviously, for ; therefore, . On the other hand, f is continuous on an open set . Take and . If (or , or , respectively) then (or , or , respectively); therefore, for each .
Lemma 4.
Let , and . If f is not continuous at A and then there exists such that .
Proof.
As previously, for every by we denote a number from for which . There exists such that , where
Choose such that for every . Let and satisfy assertion of Theorem 3. Assume that and f is not continuous at A. Then there exist and a sequence convergent to A such that for each . We can find such that contains infinitely many elements of the sequence . Clearly, we may assume that for every . Let us define by
Obviously, . By Corollary 1, we obtain . Since , . Finally, .
On the other hand, , for every and for ; therefore,
By Theorem 3,
Hence, and the more . □
Theorem 5.
For every and the family of sets satisfying condition:
forms a topology. We denote it by . The topology is finer than the natural topology.
Proof.
Obviously, . For each and for each satisfying we obtain
Thus .
Let , and . Take such that . Then . Hence,
because . Thus .
Let for each . Fix . There exists such that . Take such that . Then and . Thus .
Hence is a topology on . The remaining part of the proof is obvious. □
Theorem 6.
Let and . The family of sets satisfying condition:
forms a topology. We denote it by . The topology is finer than the natural topology.
Proof.
The proof is very similar to the proof of the previous theorem and we omit it. □
Theorem 7.
Let and . The following conditions are equivalent:
- ;
- For every , if f is not continuous at A then and f is -continuous at A.
Proof.
First assume that condition (2) is fulfilled. Take and . If f is continuous at A then, obviously, is -continuous at A. Assume that f is not continuous at A. Then, by assumptions, and f is -continuous at A. Fix . Since , there exists such that and . By -continuity of f at A, there is for which and for each ; therefore and for each . Moreover, . Thus is -continuous at A. Since A and g were chosen arbitrary, .
Now assume that . Take any and assume that f is not continuous at A. By Lemma 4, . Aiming at a contradiction, suppose that f is not -continuous at A. Then there exists such that does not contain any -neighborhood of A. Hence . In particular, ; therefore, we can find such that and . Observe that if then and , because . Thus
On the other hand, since , we have , and . Suppose that . Then
which contradicts (4); therefore . Since , we have .
By Theorem 1, there exists a sequence of closed balls such that , , and
Since , for . Define by for and for . Clearly, for and is continuous, because is discrete and . Since is a closed subset of , by the Tietze theorem, we can find a continuous extension of . Finally, define by
By construction, g is continuous on an open set . By (5), we conclude that g is -continuous at A. Hence .
Moreover, and for each ; therefore . By (6),
Therefore is not -continuous at A, a contradiction. □
Theorem 8.
Let and . The following conditions are equivalent:
- ;
- For every , if f is not continuous at A then and f is -continuous at A.
Moreover, if then for every , if f is not continuous at A then and f is -continuous at A.
Proof.
Proof of the implication is very similar to the analogous part of the proof of the previous theorem and we omit it.
Now assume that (or , respectively). Take any A and assume that f is not continuous at A. By Lemma 4, . Suppose that f is not -continuous at A. Then repeating arguments from the proof of the previous theorem there exists and a sequence of closed balls such that ,
where and . Again, repeating previous arguments we can construct such that g is continuous on an open set , and for , where is the set from Lemma 3 for and the point A. Then and
which implies (and therefore ). This proves that if (or , respectively) then f is -continuous at A, which completes the proof. □
Problem 1.
Does ?
Remark 4.
Again, let us consider families of functions , and . Probably, in order to determine maximal multiplicative class for these families, we should use analogous of topologies p and s and modify them as in Theorems 5 and 6.
5. Properties of Topologies
We describe some properties of topologies and for different and for different sets . By we denote the set of accumulation points of in the natural topology.
Proposition 3.
Let , , . If then for each we have:
- if and only if ;
- if and only if .
Proof.
Since , we obtain for every . Hence, if then .
Let and assume that . Then we can find a sequence convergent to A such that for each . Choose such that for every , i.e., . Let and satisfy assertion of Theorem 3. Since , we may assume that for . Clearly, we can find such that contains infinitely many elements of the sequence . Without loss of generality, we may assume that for every . By assumption,
a contradiction. Hence, if then , which completed the proof.
The proof of the second statement is analogous and we omit it. □
The following two propositions follow directly from definitions of and .
Proposition 4.
Let , . If then
- ;
- .
Proposition 5.
Let and . If then
- ;
- ;
- Both topologies and are equal to the natural topology.
Proof.
It follows immediately from the fact that for every there exists such that . □
Theorem 9.
Let and . If then and .
Proof.
Let . Then there exist a sequence of elements of convergent to A and such that and for each . Put . Obviously, .
We will show that . Clearly, . Choose such that for every . Let and satisfy assertion of Theorem 3.
We can find such that contains infinitely many elements of the sequence . Without loss of generality, we may assume that for every . Then
Hence, .
In a similar way we can prove the second statement. □
Corollary 3.
Let , and . Then and .
Theorem 10.
Let , , . The following conditions are equivalent:
- (1)
- ;
- (2)
- ;
- (3)
- .
Proof.
Implication is obvious.
. Now assume that . Then
. Assume that . Take any such that . Then
Thus . □
In a similar way we can prove the following theorem.
Theorem 11.
Let , and . The following conditions are equivalent:
- (1)
- ;
- (2)
- ;
- (3)
- .
Example 4.
Let , , . Choose such that . Then, by Theorems 10 and 11, .
Corollary 4.
For every there exists such that and .
Example 5.
Let . Choose , and such that . Then, by Theorems 10 and 11, .
Remark 5.
By Example 5, for every we can find such that . The authors do not know whether for every we can find such that .
Problem 2.
Does for every there exist such that and ?
Corollary 5.
Let , . Then
- ;
- .
Proof.
Inclusion follows from Theorem 10, whereas inclusion follows from for each .
The proof of the second assertion is similar and we omit it. □
Problem 3.
It seems obvious that all properties of the lower porosity and lower porouscontinuity presented in the paper can be extended for sets in and functions for every . Does these properties can still be extended for the Hilbert spaces?
6. Summary
In the paper, we proved some properties of the lower porosity of subsets of . We found that the most useful tool for this is the notion of the cone. In Theorem 2, we showed that the lower porosity of the complement of a cone at the vertex can be expressed in the term of the angle of the cone. Moreover, we proved that the lower porosity of the union of the complement of the cone and elements of a sequence of points lying “close” to the axis of the cone at the vertex strictly decreases. It turns out that properties of the lower porosity of the complement of the cone are similar to properties of the (upper) porosity of the complement of a union of a sequence of pairwise disjoint balls, presented in [11]. Next, we introduced families of lower porouscontinuous functions. It generalizes the notion of (upper) porouscontinuity introduced by J. Borsík and J. Holos in [8]. There are three parameterized families of lower porouscontinuous functions , , and for .
In Section 3, we showed that maximal additive class for every family of lower porouscontinuous functions consists of continuous functions, similar to the case of (upper) porouscontinuity.
It turns out that maximal multiplicative classes for lower porouscontinuous functions have more complicated structure. To describe these classes, we introduced two families of new topologies and for and , symmetrical with topologies and generated by (upper) porosity introduced in [11]. In Theorems 7 and 8, we described maximal multiplicative classes for and for . Moreover, we proved inclusions .
In Section 5, some properties of topologies and are presented. It turns out that properties of topologies generated by the lower and (upper) porosity are symmetrical.
The whole work was devoted to sets and functions of the lower porosity from . Several natural questions remained unanswered. Moreover, it seems that properties of sets that lower porosity is just greater than 0 or is equal to 1 are more complicated and cones may not be a sufficient tool to characterize these types of porosity. It would be useful to find sets characterizing these kinds of the lower porosity. Similarly, the classes as well as and seem to have much different and more complicated properties than the corresponding classes for . Probably, the maximum additive classes of these families of functions consist of not only continuous functions and one need to define new topologies that are equivalent to the p and s topologies introduced by V. Kelar in [13] and L. Zajíček in [5]. Moreover, to determine the maximum multiplicative classes for , , and it will be necessary to modify these topologies, analogically as in Theorem 5 and Theorem 6.
Author Contributions
Conceptualization, S.K. and M.T.; methodology, S.K. and M.T.; validation, S.K. and M.T.; writing—review and editing, S.K. and M.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not aplicable.
Informed Consent Statement
Not aplicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Dolženko, E.P. Boundary properties of arbitrary functions. Math. USSR Izv. 1967, 31, 741–750. (In Russian) [Google Scholar] [CrossRef]
- Filipczak, M.; Ivanova, G.; Wódka, J. Comparison of some families of real functions in porosity terms. Math Slovaca 2017, 67, 1155–1164. [Google Scholar] [CrossRef]
- Ivanova, G.; Domnik, I. Dense and σ-porous subsets in some families of Darboux functions. Symmetry 2021, 13, 759. [Google Scholar] [CrossRef]
- Kowalczyk, S.; Turowska, M. Methods of comparison of families of real functions in porosity terms. Georgian Math. J. 2019, 26, 643–654. [Google Scholar] [CrossRef]
- Zajíček, L. Porosity, I-density topology and abstract density topologies. Real Anal. Exchange 1986, 12, 313–326. [Google Scholar] [CrossRef]
- Zajíček, L. Porosity and σ-porosity. Real Anal. Exchange 1987, 13, 314–350. [Google Scholar] [CrossRef]
- Kowalczyk, S.; Turowska, M. On some generalizations of porosity and porouscontinuity. Tatra Mt. Math. Publ. 2017, 68, 13–28. [Google Scholar] [CrossRef][Green Version]
- Borsík, J.; Holos, J. Some properties of porouscontinuous functions. Math. Slovaca 2014, 64, 741–750. [Google Scholar] [CrossRef]
- Borsík, J.; Kowalczyk, S.; Turowska, M. On points of porouscontinuity. Topol. Appl. 2020, 284, 107410. [Google Scholar] [CrossRef]
- Kowalczyk, S.; Turowska, M. Topologies generated by porosity and maximal additive and multiplicative families for porouscontinuous functions. Topol. Appl. 2018, 239, 1–13. [Google Scholar] [CrossRef]
- Kowalczyk, S.; Turowska, M. Topologies on normed spaces generated by porosity. Filomat 2019, 33, 335–352. [Google Scholar] [CrossRef]
- Bruckner, A.M. Differentation of Real Functions; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1978; Volume 659. [Google Scholar]
- Kelar, V. Topologies generated by porosity and strong porosity. Real Anal. Exchange 1990, 16, 255–267. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).