Coloring Properties of Mixed Cycloids

Abstract

In this paper, we investigate partitions of highly symmetrical discrete structures called cycloids. In general, a mixed hypergraph has two types of hyperedges. The vertices are colored in such a way that each C-edge has two vertices of the same color, and each D-edge has two vertices of distinct colors. In our case, a mixed cycloid is a mixed hypergraph whose vertices can be arranged in a cyclic order, and every consecutive p vertices form a C-edge, and every consecutive q vertices form a D-edge in the ordering. We completely determine the maximum number of colors that can be used for any $p\ge 3$ and any $q\ge 2$. We also develop an algorithm that generates a coloring with any number of colors between the minimum and maximum. Finally, we discuss the colorings of mixed cycloids when the maximum number of colors coincides with its upper bound, which is the largest cardinality of a set of vertices containing no C-edge.

1. Introduction

Many processes in different areas of science, technology, engineering, etc., have a circular nature and are modeled by circular structures using graphs and hypergraphs. They are important tools in finding optimal solutions to optimization problems (see [1] for a fresh random example).

In this paper, we investigate partitions of highly symmetrical discrete circular structures called cycloids. The general idea is that elements of the structure (called vertices) are placed in cyclic ordering, and intervals of elements in the ordering have a specified cardinality, and all are present. In this model, elements of a structure can be in a number of discrete states called colors. The partitions and restrictions on them are studied using the language of mixed hypergraph coloring, specifically termed as colorings, of complete $(p,q)$-uniform circular mixed hypergraphs of order n.

1.1. Mixed Hypergraphs and Their Coloring Parameters

The structure class of mixed hypergraphs was introduced in the mid-1990s [2,3]. The first decade of the theory is summarized in the monograph [4], and a regularly updated list of publications is maintained on the website [5]. Below, we give some basic definitions.

A mixed hypergraph is a triple $\mathcal{H}=(X,\mathcal{C},\mathcal{D})$, where X is the vertex set, and $\mathcal{C}$ and $\mathcal{D}$ are set systems over X. The members of $\mathcal{C}$ and $\mathcal{D}$ are termed C-edges and D-edges, respectively; their role is distinguished via vertex coloring. Throughout, we shall assume that X is finite, $\left|X\right|=n$, $X=\{x_0,x_1,\dots ,x_{n-1}\}$, and all C- and D-edges have size at least 2.

A proper k-coloring of $\mathcal{H}$ is a mapping $\phi :X\to \{1,\dots ,k\}$ such that

• every C-edge contains two (or more) vertices with a common color;
• every D-edge contains two (or more) vertices with distinct colors.

Some members of this rich structure class are uncolorable; $\mathcal{H}$ is said to be colorable if it admits at least one proper coloring. Various constructions of uncolorable mixed hypergraphs are described in [6].

Assume from now on that $\mathcal{H}$ is colorable. A strict k-coloring of $\mathcal{H}$ is a proper k-coloring that uses all the k colors. The feasible set of $\mathcal{H}$ is defined as

$$\mathsf{\Phi }\left(\mathcal{H}\right):=\{k\mid \mathcal{H} \mathrm{has} \mathrm{a} \mathrm{strict} k-\mathrm{coloring}\}.$$

The lower chromatic number $\chi \left(\mathcal{H}\right)$ is the smallest element of $\mathsf{\Phi }\left(\mathcal{H}\right)$, and the upper chromatic number $\overline{\chi }\left(\mathcal{H}\right)$ is the largest element of $\mathsf{\Phi }\left(\mathcal{H}\right)$. If $\mathcal{C}=⌀$, then $\overline{\chi }=\left|X\right|$, and we obtain the classical notion of proper vertex coloring, which directly generalizes from graphs to hypergraphs as studied since the mid-1960s. On the other hand, if $\mathcal{D}=⌀$, then $\chi =1$, and we obtain a coloring notion termed C-coloring. Its equivalents and particular cases have been studied under several names in various contexts; perhaps the earliest occurrence of the concept is published by Sterboul in [7]. The literature of C-coloring is surveyed in [8]. Evidently, uncolorable hypergraphs with $\mathcal{C}=⌀$ or $\mathcal{D}=⌀$ do not exist.

The feasible set is gap-free if it contains all integers between $\chi$ and $\overline{\chi }$; that means $\mathsf{\Phi }\left(\mathcal{H}\right)=\{k\mid \chi \left(\mathcal{H}\right)\le k\le \overline{\chi }\left(\mathcal{H}\right)\}$. The first mixed hypergraphs with gaps in their feasible sets were discovered in [9]. (With a related terminology, it is also said that the chromatic spectrum of $\mathcal{H}$ is gap-free (or, continuous). By definition, the chromatic spectrum of $\mathcal{H}$ is a vector of dimension $\left|X\right|$, whose kth entry is the number of partitions generated by strict k-colorings.)

1.2. Circular Mixed Hypergraphs

A mixed hypergraph is called circular if its vertices can be arranged in a cyclic order, $(x_1,\dots ,x_n)$, such that all C- and D-edges consist of consecutive vertices. In particular, the complete $(p,q)$-uniform circular mixed hypergraph of order n, which we denote by $\mathcal{KC}(n;p,q)$, is the mixed hypergraph $\mathcal{H}=(X,\mathcal{C},\mathcal{D})$ with

$$\begin{array}{ccc}\hfill \mathcal{C}& =& {\mathcal{C}}_p := \{x_i{x}_{i+1}\dots x_{i+p-1}\mid 0\le i\le n-1\},\hfill \\ \hfill \mathcal{D}& =& {\mathcal{D}}_q := \{x_i{x}_{i+1}\dots x_{i+q-1}\mid 0\le i\le n-1\},\hfill \end{array}$$

where the subscript addition is meant modulo n. Throughout, we shall assume $p\ge 3$ because ${\mathcal{C}}_2$ would make the entire X monochromatic and $\mathcal{H}$ uncolorable if $\mathcal{D}\ne ⌀$.

Circular mixed hypergraphs have been generalized in two different directions, structurally in [10] and in terms of color-bounding functions in [11]. The following result, which follows from both Theorem 9 of [10] and Theorem 6 of [11], is important in the current context.

Theorem 1

([10,11]). If a circular mixed hypergraph $\mathcal{H}$ is colorable, then its feasible set $\mathsf{\Phi }\left(\mathcal{H}\right)$ is gap-free.

A systematic study of circular mixed hypergraph coloring was carried out in the papers [12,13], with emphasis on $\chi$ in the former and on $\overline{\chi }$ in the latter. Combining some results from those works, the following theorem can be stated for complete circular mixed hypergraphs.

Theorem 2

([12,13]). Disregarding the unique exception of $(p,q)=(3,2)$ with $n\ge 3$ odd, all $\mathcal{KC}(n;p,q)$ are colorable for all $p\ge 3$ and all $q\ge 2$. Moreover, the lower chromatic number is 2 if $q\ge 3$ or n is even, and it is 3 if $q=2$ and $n\ge 3$ is odd.

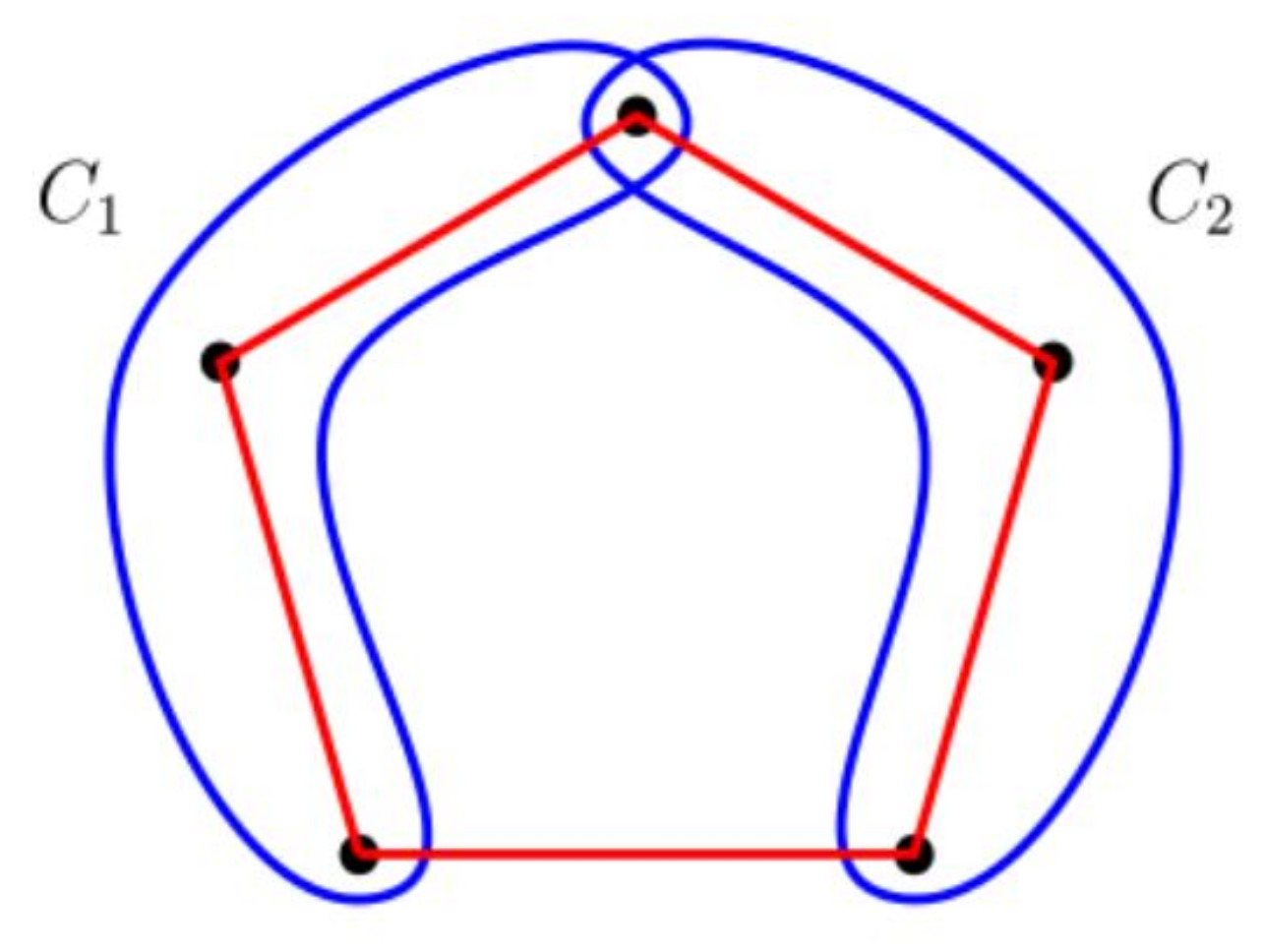
For any $n\ge 5$ odd, $\mathcal{KC}(n;3,2)$ is uncolorable but not minimal uncolorable. As was found in [12], $\mathcal{KC}(n;3,2)$ contains minimal uncolorable circular mixed hypergraph ${\mathcal{F}}_n$ as a partial sub-hypergraph. The smallest example ${\mathcal{F}}_5$ is shown in Figure 1.

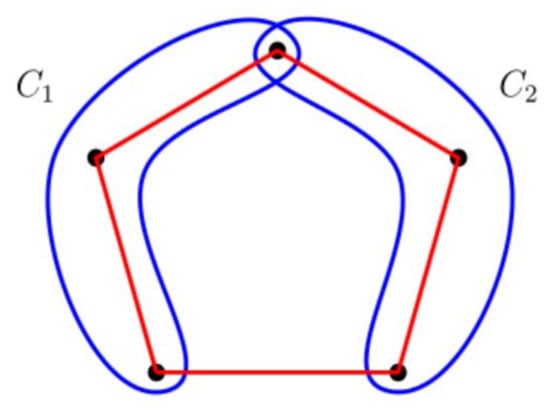
Figure 1. The minimal uncolorable circular mixed hypergraph ${\mathcal{F}}_5$.

Recent works deal with $\mathcal{KC}(n;p,p)$, namely [14] proves $\overline{\chi }=\lfloor \frac{n}{2}\rfloor$ for $p=q=3$, and the main theorem of [15] gives $n-s-1\le \overline{\chi }\le n-s$ if $p=q>3$, where s denotes the “sieve number”. We shall give the definition and some comments on this parameter in the concluding section.

At the end of the paper [15], its authors raise the problem of determining the feasible set of $\mathcal{KC}(n;p,q)$ for all p and q. Due to Theorem 1, this reduces to computing the upper chromatic number for all 3-tuples $n,p,q$. In the present work, we completely solve this problem as follows.

Theorem 3

(Main Theorem). For any integers $n\ge p\ge 3$ and $q\ge 2$, the upper chromatic number of $\mathcal{KC}(n;p,q)$ is as given in Table 1.

Table 1. The upper chromatic number of $\mathcal{KC}(n;p,q)$ for $n\ge p\ge 3$ and $q\ge 2$.

p	q	n	$\overline{\mathit{\chi }}$	Remark
3	2	n odd	—	uncolorable
3	2	n even	$n-\frac{n}{p-2}+2$	$=2$
$\ge 3$	$\ge 2$	$n=p$	$n-1$	$=p-1$ for
				$(p,q)\ne (3,2)$
4	2	n even	$n-\frac{n}{p-2}+1$	$=\frac{n}{2}+1$
5	2	$n=10$	$n-\lceil \frac{n}{p-2}\rceil +1$	$=7=n-\lfloor \frac{n}{3}\rfloor$
4	2	n odd	$n-\lceil \frac{n}{p-2}\rceil$	$=\frac{n-1}{2}$
5	2	$10\ne n\ge 6$	$n-\lceil \frac{n}{p-2}\rceil$	$=\lfloor \frac{2n}{3}\rfloor$
$p\ge 6$	2	$n>p$	$n-\lceil \frac{n}{p-2}\rceil$
$p\ge 3$	$q\ge 3$	$n>p$	$n-\lceil \frac{n}{p-1}\rceil$

The cases with $n<p$ are rather simple; we list them for completeness in the following assertion.

Proposition 1.

If $1\le n<p$, then

$$\mathrm{\Phi }\left(\mathcal{KC}(n;p,q)\right)=\left\{\begin{array}{ccc}\hfill \{1,\dots ,n\},& & 1\le n<q;\hfill \\ \hfill \{2,\dots ,n\},& & n\ge q, n \mathit{even} \mathit{or} q>2;\hfill \\ \hfill \{3,\dots ,n\},& & n\ge q=2, n \mathit{odd}.\hfill \end{array}\right.$$

Definition 1.

The color classes $X_1,\dots ,X_k$ of a strict k-coloring $\phi :X\to \{1,\dots ,k\}$ are defined as the sets $X_i={\phi }^{-1}\left(i\right)$, $i=1,\dots ,k$.

Remark 1.

If φ is a strict coloring of a mixed hypergraph $\mathcal{H}$ with $k=\overline{\chi }\left(\mathcal{H}\right)$ colors and with color classes $X_1,\dots ,X_k$, then $\overline{\chi }\left(\mathcal{H}\right)=n-{\sum }_{i=1}^k\left(\right|X_i|-1)$.

1.3. Structure of the Paper

For the sake of completeness, we include proofs also for simple cases that might be left to the reader. These are given in Section 2, which covers all combinations of parameters satisfying $n\le 2p-2$. From then on, $n\ge 2p-1$ will be assumed. In Section 3, we introduce the notion of the types of color classes and a weighting for monochromatic vertex pairs, which provides a basis for later proofs. Section 4 includes the proof of the Main Theorem for $q\ge 3$ and describes a coloring algorithm based on the “sieve number”, a parameter closely related to the upper chromatic number. Section 5 deals with $q=2$ and completes the proof of the Main Theorem. In Section 6, we characterize a special case of mixed cycloids, the so-called C-perfect mixed cycloids, and give concluding remarks.

2. Some Simple Cases: $\mathit{n}\le \mathbf{2}\mathit{p}-\mathbf{2}$

Here, we describe the solution for some fairly obvious combinations of the parameters. The next list deals with the cases of Proposition 1 and the first three lines of Table 1. After that, we consider the range $p+1\le n\le 2p-2$ in the case of $q\ge 3$.

Note that $n<p$ means $\mathcal{C}=⌀$, and then no monochromatic pair of vertices is required to occur, i.e., $\overline{\chi }=n$.

• For $1\le n<\min (p,q)$, we have $\mathcal{D}=⌀$; therefore, every color assignment to the vertices is a proper coloring, hence $\mathsf{\Phi }\left(\mathcal{KC}\right(n;p,q\left)\right)=\{1,\dots ,n\}$.
• For $q\le n<p$, if n is even or $q>2$, the color assignment $\phi :X\to \{1,2\}$, defined as $\phi \left(x_i\right)=1+i (\mathrm{mod} 2)$ for all $0\le i<n$, is a proper 2-coloring, and any number of vertices may be recolored with their private colors to obtain proper colorings with more colors, hence $\mathsf{\Phi }\left(\mathcal{KC}\right(n;p,q\left)\right)=\{2,\dots ,n\}$.
• For $q=2<n<p$ with n odd, $\mathcal{D}$ needs at least 3 colors, and the assignment $\phi \left(x_i\right)=1+i (\mathrm{mod} 2)$ for $0\le i\le n-2$ with $\phi \left(x_{n-1}\right)=3$ is a proper 3-coloring. Furthermore, here, we have the option to introduce private colors to any number of vertices, hence $\mathsf{\Phi }\left(\mathcal{KC}\right(n;p,q\left)\right)=\{3,\dots ,n\}$.
• If $p=3$ and $q=2$, then $\phi \left(x_{i-1}\right)\ne \phi \left(x_i\right)\ne \phi \left(x_{i+1}\right)$ due to the D-edges, but the C-edges $\{x_{i-1},x_i,x_{i+1}\}$ have to contain some color twice; thus, $\phi \left(x_{i-1}\right)=\phi \left(x_{i+1}\right)$ must hold for all i. This is impossible if n is odd—i.e., the hypergraph is uncolorable—and forces the 2-coloring with alternating colors if n is even.
• For $n=p\ge 3$, the coloring $\phi \left(x_i\right)=i$ for $i=1,\dots ,n-1$ with $\phi \left(x_0\right)=2$ is feasible unless $(p,q)=(3,2)$. Consequently, $\mathsf{\Phi }\left(\mathcal{KC}\right(p;p,q\left)\right)=\{2,\dots ,p-1\}$ if p is even or $q\ge 3$, and $\mathsf{\Phi }\left(\mathcal{KC}\right(p;p,q\left)\right)=\{3,\dots ,p-1\}$ if $p\ge 5$ is odd and $q=2$.

Proposition 2.

If $p+1\le n\le 2p-2$ and $q\ge 3$, then $\mathsf{\Phi }\left(\mathcal{KC}\right(n;p,q\left)\right)=\{2,\dots ,n-2\}$.

Proof. 

Since $p\ge 3$, we have $n\ge 4$. Then the partial assignment $\phi \left(x_0\right)=\phi \left(x_1\right)=1$, $\phi \left(x_{\lfloor n/2\rfloor }\right)=\phi \left(x_{\lfloor n/2\rfloor +1}\right)=2$ properly colors all C-edges. Then all the other vertices can get their private colors; therefore, $\overline{\chi }=n-2$. The feasible set is gap-free by Theorem 1, and the earler assignment $\phi \left(x_i\right)=1+i (\mathrm{mod} 2)$ is a proper 2-coloring. Hence, the assertion follows. □

3. Types of Color Classes

Assuming $n\ge 2p-1$, in this section, we introduce a weight associated with monochromatic pairs of vertices that are not far from each other in the circular order. These weights will be the main tool for proving tight upper bounds on the upper chromatic number.

Basic Definitions

We define the distance between two vertices $x_i$ and $x_j$ as

$$d(x_i,x_j):=min\left(\right|i-j|, n-|i-j\left|\right).$$

Assume for the moment that a proper coloring $\phi$ of $\mathcal{H}$ is also at hand. We say that $x_i$ and $x_j$ are related if $\phi \left(x_i\right)=\phi \left(x_j\right)$ and $d(x_i,x_j)<p$. It will be convenient to view related vertex pairs in the order $(x_i,x_j)$ such that

$$j=i+d(x_i,x_j) (\mathrm{mod} n).$$

This order is unique because $|i-j|=n/2$ would hold only if $n\le 2p-2$, which has already been handled in Proposition 2 and is disregarded here. For $|i-j|\ne n/2$, we shall write $i{<}_{n}j$ to express that $j=i+d(x_i,x_j) (\mathrm{mod} n)$ holds, i.e., walking around the cycle modulo n, the path from i to j is shorter than that from j to i.

Assuming $i{<}_{n}j$, the vertices $x_i$ and $x_j$ are said to form a next-related pair if they are related, and there does not exist any l such that they are related to $x_l$ and l is “between” i and j, that is $d(x_i,x_j)=d(x_i,x_l)+d(x_l,x_j)$. By definition, every C-edge must contain a related pair; then, it also contains a next-related pair. Therefore, it suffices to verify a proper coloring for the C-edges by restricting attention to the next-related pairs.

In this way, a proper coloring $\phi$ may contain two basic types of color classes:

• path-class: a sequence $x_{i_1},\dots ,x_{i_m}$ of vertices such that $x_{i_{j+1}}$ is next-related to $x_{i_j}$ for all $j=1,\dots ,m-1$, but $x_{i_1}$ and $x_{i_m}$ either are not related at all, or they are related in the direction from $i_1$ to $i_m$, i.e., $i_1{<}_n{i}_m$.
• cycle-class: a sequence $x_{i_1},\dots ,x_{i_m}$ of vertices such that $x_{i_{j+1}}$ is next-related to $x_{i_j}$ for all $j=1,\dots ,m-1$; moreover, $x_{i_1}$ is also next-related to $x_{i_m}$ in the direction from $i_m$ to $i_1$, i.e., $i_m{<}_n{i}_1$.

In either case, a color class of size m “loses” $m-1$ colors, in accordance with Remark 1.

Proposition 3.

Let $\phi :X\to \{1,\dots ,k\}$ be a proper vertex coloring of $\mathcal{H}$.

(i) 

The number of C-edges properly colored by a related pair $x_i,x_j$ is precisely $p-d(x_i,x_j)$.

(ii) 

If $X_i=\{x_{i_1},\dots ,x_{i_m}\}$ is a path-class, then the number of C-edges properly colored by $X_i$ is at most ${\sum }_{i=1}^{m-1}(p-d(x_i,x_j))\le (m-1)(p-1)$, with exactly $(m-1)(p-1)$ if and only if $m=2$ and $d(x_i,x_j)=1$. Moreover, if $q=2$, then the upper bound is at most $(m-1)(p-2)$.

(iii) 

If $X_i=\{x_{i_1},\dots ,x_{i_m}\}$ is a cycle-class, then the number of C-edges properly colored by $X_i$ is at most $mp-n$, with equality if and only if any two related vertex pairs are next-related.

Proof. 

$\left(i\right)$ There are exactly $p-d(x_i,x_j)$C-edges in the family ${\mathcal{C}}_p$, which contains the vertex pair $x_i,x_j$, for any $1\le d(x_i,x_j)\le p$.

$\left(ii\right)$ An upper bound is obtained by summing the formula of $\left(i\right)$ for the next-related pairs in $X_i$. We have $m-1$ terms, and each of them is at most $p-1$. To yield $(m-1)(p-1)$, each summand has to be $p-1$, which needs neighbor vertices. In the presence of more than two consecutive vertices $x_i,x_{i+1},x_{i+2}$, this computation would count the C-edge $x_i,\dots ,x_{i+p-1}$ twice because $p\ge 3$. If $q=2$, the distance between the next-related vertices is at least 2; hence, each of the $m-1$ terms in the upper bound is at most $p-2$.

$\left(iii\right)$ In the case of a cycle-class, we have to add $p-d(x_m,x_1)$ to the sum of $\left(ii\right)$. Then p occurs m times, and the sum of the $d(x_i,x_j)$ terms is equal to n because the next-related pairs form a complete cycle. If $x_i$ and $x_j$ with $i{<}_{n}j$ are related but not next-related, then $x_i,\dots ,x_{i+p-1}$ is properly colored by more than one pair of vertices. □

Corollary 1.

The average number of properly colored C-edges losing one color is

• at most, $p-1$ if $X_i$ is a path-class;
• at most, $p-2$ if $X_i$ is a path-class and $q=2$;
• at most, $p-\frac{n-p}{m-1}$ if $X_i$ is a cycle-class of size $m-1$.

Based on this observation, we assign colors to some of the vertices.

Definition 2.

In a vertex coloring $\phi :\{x_1,\dots ,x_n\}\to \{1,\dots ,k\}$ we say that $\phi \left(x_j\right)$ is a repeated color, and $x_j$ is a repeating vertex, if there is an index l with $1\le l<j$ and $\phi \left(x_j\right)=\phi \left(x_l\right)$. The weight of a repeated color $\phi \left(x_j\right)$, or of the repeating vertex $x_j$, is defined as

• $p-1$ if $q\ge 3$ and $x_j$ is in a path-class;
• $p-2$ if $q=2$ and $x_j$ is in a path-class;
• $p-\frac{n-p}{m-1}$ if $X_i$ is in a cycle-class of size $m-1$.

If all C-edges are properly colored, the weight sum taken over the repeating vertices is at least n; hence, the following inequalities are valid:

Corollary 2.

Let $\phi :X\to \{1,\dots ,k\}$ be a strict k-coloring of $\mathcal{KC}(n;p,q)$. Assume that $X_1,\dots ,X_j$ are path-classes and $X_{j+1},\dots ,X_k$ are cycle-classes.

(i) 

For any q, we have

$$(p-1)·\sum _{i=1}^j\left(\right|X_i|-1)+p·\sum _{i=j+1}^m\left|X_i\right|\ge (k-j+1)·n .$$

(ii) 

If $q=2$, then

$$(p-2)·\sum _{i=1}^j\left(\right|X_i|-1)+p·\sum _{i=j+1}^m\left|X_i\right|\ge (k-j+1)·n .$$

4. Proofs for $\mathit{q}\ge \mathbf{3}$

In this section, we first prove the Main Theorem in the case of $q\ge 3$. Then, in the second part, we point out a relation with the parameter called the sieve number, and based on it, we present an algorithm that properly colors $\mathcal{KC}(n;p,q)$ with any number of colors that belong to the feasible set.

4.1. The Upper Chromatic Number

The value $n-\lceil \frac{n}{p-1}\rceil$ for the upper chromatic number is stated in the last line of Table 1. Equivalently, it means that in every proper coloring of $\mathcal{KC}(n;p,q)$, there occur at least $\lceil \frac{n}{p-1}\rceil$ repeating vertices and that this bound is best possible. First, we show the easier part, the lower bound:

$$\overline{\chi }\left(\mathcal{KC}(n;p,q)\right)\ge n-\lceil \frac{n}{p-1}\rceil .$$

Indeed, for $j=0,1,\dots ,\lceil \frac{n}{p-1}\rceil -1$, assign color $j+1$ to the vertices $x_{j(p-1)}$ and $x_{j(p-1)+1}$; this is feasible unless $n\equiv 1$ (mod $(p-1)$) because the $2\lceil \frac{n}{p-1}\rceil$ vertices are all distinct. If $n\equiv 1$ (mod $(p-1)$) and $p\ge 4$, the simple modification $\phi \left(x_{n-2}\right)=\phi \left(x_{n-1}\right)=\frac{n-1}{p-1}+1$ can be done. Finally, if $p=3$ and n is odd, we recolor the last possible monochromatic pair $x_{n-3},x_{n-2}$ as $\phi \left(x_{n-3}\right)=\phi \left(x_{n-2}\right)=1$. These coloring patterns properly color all C-edges without creating any monochromatic D-edges. The number of colors can then be maximized by assigning a private new color to each vertex that has not been colored so far. This yields the claimed lower bound on $\overline{\chi }$.

The matching upper bound

$$\overline{\chi }\left(\mathcal{KC}(n;p,q)\right)\le n-\lceil \frac{n}{p-1}\rceil .$$

will be derived from the observations of the preceding section, estimating the number of repeated colors. For this, let $\phi$ be a proper coloring with $\overline{\chi }$ colors and color classes $X_1,\dots ,X_{\overline{\chi }}$. If all $X_i$ are path-classes, then it immediately follows from Corollary 2$\left(i\right)$ that the number ${\sum }_{i=1}^{\overline{\chi }}\left(\right|X_i|-1)$ of repeated colors is at least $\lceil \frac{n}{p-1}\rceil$. The same conclusion holds if the weight of every repeated color in the cycle-classes is at most $p-1$.

Assume that this is not the case, i.e., there is a cycle-class, say of size m, such that the weight $p-\frac{n-p}{m-1}$ of its repeating vertices is larger than $p-1$. Since all parameters are integers, this equivalently means

$$m-1\ge n-p+1 .$$

Moreover, since we already have a coloring with $n-\lceil \frac{n}{p-1}\rceil$ colors, for a better lower bound, it is also necessary that the number $m-1$ of lost colors be strictly smaller than $\lceil \frac{n}{p-1}\rceil$. However, we would then have

$$n-p+2\le \lceil \frac{n}{p-1}\rceil \le \frac{n}{p-1}+\frac{p-2}{p-1} ,$$

$$n·\left(1-\frac{1}{p-1}\right)\le (p-2)·\left(1+\frac{1}{p-1}\right) ,$$

$$n\le p ,$$

which is impossible because we have $n\ge 2p-1$. This contradiction completes the proof for $q\ge 3$.

4.2. The Sieve Number and a Coloring Algorithm

As introduced in [16], in a mixed hypergraph $\mathcal{H}$, a subfamily $\Sigma \subseteq \mathcal{C}$ of C-edges is a sieve if for every pair of vertices $x,y\in X$ and every pair of different C-edges $C,C^{\prime }\in \Sigma$ the following implication holds:

$$\{x,y\}\in C\cap C^{\prime }\Rightarrow \{x,y\}\in \mathcal{D}.$$

The maximum cardinality of a sieve in $\mathcal{H}$ is the sieve-number, denoted by $s\left(\mathcal{H}\right)$.

Algorithm 1 below will properly color the vertices of $\mathcal{H}=(X,{\mathcal{C}}_p,{\mathcal{D}}_q)$, with $n>p$ and $p,q\ge 3$, provided that $(p,q)\ne (3,3)$.

The main idea of the algorithm is to construct a maximum sieve $\Sigma$ and then color the vertices to satisfy all coloring constraints.

In general circular mixed hypergraphs, the intersection of two different C-edges of a sieve can only be empty, a common vertex, or two common vertices forming a D-edge. Let us call the intersection of two arbitrary C-edges good if and only if this intersection is empty, or a single vertex, or two vertices forming a D-edge. Otherwise, the intersection of two arbitrary C-edges is bad. Due to our particular family of hypergraphs, namely with $q\ge 3$, D-edges of size 2 do not occur; hence, we will always have a good nonempty intersection with a single vertex.

Algorithm 1. (Modified Algorithm from [15]).

INPUT: $\mathcal{H}=(X,{\mathcal{C}}_p,{\mathcal{D}}_q)=\mathcal{KC}(n;p,q)$, $n=\left|X\right|$, $n>p$, $p,q\ge 3$, both not equal to 3, and $X=\{x_0,x_1,\dots ,x_{n-1}\}$

OUTPUT: A proper coloring $c=(c\left(x_0\right),c\left(x_1\right),\dots ,c\left(x_{n-1}\right))$ of $\mathcal{KC}(n;p,q)$

Let $\mathcal{H}=(X,\mathcal{C},\mathcal{D})$ be a circular mixed hypergraph and $C_0$ one of its C-edges.

• Construction of a maximum sieve Σ through $C_0$. Let $\Sigma =\left\{C_0\right\}$, where $C_0=\{x_0,x_1,\dots$, $x_{p-1}\}$. Choose the C-edge $C_1$ nearest to $C_0$, having a “good intersection”. So, $C_1=\{x_{p-1},\dots ,x_{2p-2}\}$. Let $C_2$ have smallest distance from $C_1$ (measured in the cyclic order of the host cycle). Choose $C_3$ nearest to $C_2$, etc. Thus, a maximum sieve $\Sigma =\{C_0,C_1,...,C_{s-1}\}$ is obtained so that no new $C_s$ can be found.
• Assigning colors to some vertices of Σ. The vertices of the C-edge $C_i$ with p vertices are denoted by $x_0^i,x_1^i,\dots ,x_{p-1}^i$ according to the cyclic order of the host cycle. Next, we assign colors to some vertices of the C-edges of $\Sigma$ in the following way, where the coloring is denoted by c. Assign color 1 to the last two vertices $x_{p-1}^0$ and $x_{p-2}^0$. We then color some vertices of $C_1,\dots ,C_{s-1}$ in the following way: Color $x_{p-2}^i$ and $x_{p-1}^i$ a new color $c\left(x_{p-1}^{i-1}\right)+1$.
• Fixing the vertices to satisfy the C-condition. In step 2, we started coloring with the vertex $x_{p-1}^0\in C_0$, proceeded along the host cycle, and ended with coloring of the vertices of $C_{s-1}$.
  Let $V(\Sigma )$ denote the set of vertices belonging to edges of $\Sigma$.

  (a)

  If $V(\Sigma )=X$ and $x_{p-1}^{s-1}=x_0^0$, all C-conditions are satisfied.

  (b)

  If $V(\Sigma )=X$ and $x_{p-1}^{s-1}\ne x_0^0$, assign $c(x_0^0=x_0)=1$ and then all C-conditions are satisfied.

  (c)

  If $V(\Sigma )\ne X$ and $s-1=0$, assign 1 to $x_0$; otherwise, assign $c\left(x_{p-1}^{s-1}\right)+1$ to $x_0$ and $x_{n-1}$.

• Assign pairwise different colors to the remaining vertices of X. The cycloid is now colored with $c\left(\mathcal{H}\right)=n-s$ or $c\left(\mathcal{H}\right)=n-s-1$ colors, as shown in [15]. Let M denote this number. These may be values that reach $\overline{\chi }\left(\mathcal{H}\right)$ and near the upper bound found in [13].
• Downshifting colors: Let k be the number of colors desired, $2<k<M$. To construct a coloring using precisely k colors, start with the obtained coloring and do the following:

  (a)

  If more than $s+1$ colors are used, recolor all vertices with the largest color, a color 1 less. If this coloring violates the D-condition, recolor the unmodified, adjacent, previous vertex (or pair of vertices in the case which $x_{p-1}^i$ is the previous vertex) a color 1 less at each violated interval.

  (b)

  Repeat the above until the desired number of colors k is used for $k\ge s+1$.

  (c)

  If $k=s$ colors are desired, perform (b) until $s+1$ colors is obtained. Then begin with $C_1$ and color $x_{p-1}^1$ and $x_{p-2}^1$ both 1. Then, for all vertices assigned $s+1$, recolor these vertices 2. Now, s colors are used.

  (d)

  If $k<s$, use (b) and (c) to get to s colors. Then begin with $C_2$ and color $x_{p-1}^2$ and $x_{p-2}^2$ both 1. Then, for all vertices not assigned 1 or 2, recolor these vertices 1 less than the color already assigned. Repeat this process with $C_3$, $C_4$, and so on until the desired number of colors is met.

• End.

Again from [15], we have:

Lemma 1.

For $\mathcal{H}$=$(X,{\mathcal{C}}_r,{\mathcal{D}}_r)$, $r>3$, the sieve number is $s\left(\mathcal{H}\right)=\lfloor \frac{n}{r-1}\rfloor$.

Since $q>2$, the D-edges of $\mathcal{KC}(n;p,q)$ have no effect on the sieve number; therefore, $s\left(\mathcal{H}\right)=\lfloor \frac{n}{p-1}\rfloor$ for $\mathcal{H}$=$(X,{\mathcal{C}}_p,{\mathcal{D}}_q)$ with $p,q\ge 3$. As such, $\overline{\chi }\left(\mathcal{H}\right)=n-s$ or $n-s-1$ agrees with Table 1 with $n-s$ or $n-s-1$ operating the same as $n-\lceil \frac{n}{p-1}\rceil$.

Additionally, it should be noted that the algorithm has a runtime $\mathcal{O}\left(n^2\right)$ as the worst-case scenario will have a runtime of $\mathit{k}n$, where $\mathit{k}$ is an integer dependent on the number of colors required and $\overline{\chi }>n/2$.

5. Proofs for $\mathit{q}=\mathbf{2}$

Similar to the case of $q\ge 3$, here, the basic approach is also to analyze the possible weight distributions in proper vertex colorings of $\mathcal{KC}(n;p,2)$. The situation with $q=2$ is more complicated, however, than what we have seen with the previous larger q because, in some cases, the path-classes are not sufficient for an optimal coloring.

As we wrote in the introduction, the case of $p=3$ is well understood; therefore, we only consider $p\ge 4$ here. First, we describe some constructions and then prove that they are optimal. Table 1 shows that the general rule is $\overline{\chi }=n-\lceil \frac{n}{p-2}\rceil$, except for $p=4$ if n is even, and $p=5$ in the particular case of $n=10$, which has $\overline{\chi }=n-\lceil \frac{n}{p-2}\rceil +1$. This means $\lceil \frac{n}{p-2}\rceil$ repeated colors or $\lceil \frac{n}{p-2}\rceil -1$ in the exceptional cases.

5.1. Coloring Constructions

Recall that in the current case of $q=2$, neighbor vertices cannot get the same color.

5.2. General Case $p\ge 5$

For $j=0,1,\dots ,\lceil \frac{n}{p-2}\rceil -1$, assign color $j+1$ to the vertices $x_{j(p-2)}$ and $x_{j(p-2)+2}$; this is feasible unless $n\equiv 2$ (mod $(p-2)$) because $p-2\ge 3$, and so, the $2\lceil \frac{n}{p-1}\rceil$ vertices are all distinct (we view $x_{n+1}:=x_1$ if $n\equiv 1$ (mod $(p-2)$)). If $n\equiv 2$ (mod $(p-2)$), we set $\phi \left(x_{n-2}\right)=1$. After that, assign a private color to each vertex that has not been colored so far. We obtain a proper coloring with $\lceil \frac{n}{p-2}\rceil$ repeated colors for every $n\ge 2p-1$.

5.3. Exception $p=4$, n Even

Assign color 1 to every vertex of even index, i.e., $\phi \left(x_0\right)=\phi \left(x_2\right)=\dots =\phi \left(x_{n-2}\right)=1$, and assign a private color to every vertex of odd index. This coloring uses $n/2+1$ colors, and every C-edge (now of size 4) contains two vertices of color 1.

5.4. Exception $p=4$, n Odd

Assign $\phi \left(x_0\right)=\phi \left(x_2\right)=\dots =\phi \left(x_{n-3}\right)=1$, $\phi \left(x_{n-4}\right)=\phi \left(x_{n-2}\right)=2$, $\phi \left(x_{n-1}\right)=\phi \left(x_1\right)=3$. After that, assign a private color to each vertex that has not been colored so far. We obtain a proper coloring with $\frac{n+1}{2}$ repeated colors for every odd $n\ge 7$. Hence, the number of used colors is $\frac{n-1}{2}$.

5.5. Exception $p=5$, $n=10$

Let $\phi \left(x_0\right)=\phi \left(x_2\right)=\phi \left(x_5\right)=\phi \left(x_7\right)=1$, and assign a private color to each of the other six vertices. This coloring uses seven colors, which is more than $2n/3$, and every C-edge (now of size 5) contains two vertices of color 1.

5.6. Tight Upper ounds

Let $\phi$ again be a proper coloring with $\overline{\chi }$ colors and color classes $X_1,\dots ,X_{\overline{\chi }}$. In order to prove the upper bound

$$\overline{\chi }\left(\mathcal{KC}(n;p,q)\right)\le n-\lceil \frac{n}{p-2}\rceil \hspace{1em}\mathrm{or}\hspace{1em}\overline{\chi }\left(\mathcal{KC}(n;p,q)\right)\le n-\lceil \frac{n}{p-2}\rceil +1$$

we determine those cases in which there is a chance to use more colors if a cycle-class also occurs. For this, it is necessary that the weight $p-\frac{n-p}{m-1}$ in a cycle-class of size m exceeds the weight $p-2$ in a path-class. For this, we need:

$$\begin{array}{ccc}\hfill \frac{n-p}{m-1}& <& 2 ,\hfill \\ \hfill n-p+1& \le & 2m-2 ,\hfill \\ \hfill \lceil \frac{n-p+1}{2}\rceil & \le & m-1 .\hfill \end{array}$$

Moreover, the number $m-1$ of colors repeated so far has to be smaller than $\lceil \frac{n}{p-2}\rceil$. In this way, we obtain:

$$\frac{n-p+3}{2}\le \lceil \frac{n-p+1}{2}\rceil +1\le (m-1)+1\le \lceil \frac{n}{p-2}\rceil \le \frac{n+p-3}{p-2} .$$

Assuming $p\ge 5$ for the moment, the two ends of this inequality chain imply

$$n\le p+\frac{p}{p-4}<2p-1$$

for all $p\ge 6$, already settled in Section 2. If $p=5$, the range $2p-1\le n\le p+\frac{p}{p-4}$ means $9\le n\le 10$. Based on a rounding error, we can exclude $n=9$ because then we have $\lceil \frac{n-p+1}{2}\rceil +1=4>3=\lceil \frac{n}{p-2}\rceil$. For $n=10$, the number of repeated colors is at least $m-1\ge \lceil \frac{n-p+1}{2}\rceil =3$; hence, the number of used colors is at most $10-3=7$, which matches the construction described above.

Finally, let $p=4$. The distance between two next-related vertices is either 2 or 3 because $1<q$ and $4>p-1$. Assume without loss of generaliy that $X_1$ is a cycle-class. If there are no next-related pairs at distance 3 in $X_1$, then, of course, n is even; moreover, $|X_1|=n/2$, and there are $n/2-1$ repeating vertices in $X_1$. Hence, $\overline{\chi }\le n/2+1$ as claimed. On the other hand, if $x_i,x_{i+3}\in X_1$ are next-related, then the C-edges $\{x_{i-1},x_i,x_{i+1},x_{i+2}\}$ and $\{x_{i+1},x_{i+2},x_{i+3},x_{i+4}\}$ are not properly colored by $X_1$; moreover, they cannot be properly colored by just one further repeated color because $\{x_{i+1},x_{i+2}\}$ is not allowed to be monochromatic. In particular, if n is odd and all but one next-related pairs in $X_1$ are at distance 2, then beside the $\frac{n-3}{2}$ repeated colors in $X_1$, there must occur two further ones. Thus, no more than $n-\frac{n+1}{2}=\frac{n-1}{2}$ colors can occur.

In other words, if a “jump” $x_i,x_{i+3}\in X_1$ occurs, then two additional repeated colors have to occur in the interval $(x_{i-1},\dots ,x_{i+4})$. Similarly, if there are two consecutive jumps $x_i,x_{i+3},x_{i+6}\in X_1$, then three additional repeated colors are needed in $(x_{i-1},\dots ,x_{i+7})$ because among the four C-edges with respective first vertices $x_{i-1}$, $x_{i+1}$, $x_{i+2}$, $x_{i+4}$, which are not properly colored by $X_1$, only the second and third admit a common monochromatic vertex pair (namely $\{x_{i+2},x_{i+4}\}$). More generally, if there are t consecutive jumps $x_i,x_{i+3},\dots ,x_{3t}\in X_1$, then, depending on whether they close to a cycle or not,

• there are at least t additional repeated colors if $3t=n$;
• there are at least $t+1$ additional repeated colors if $3t<n$.

Note that n and t have the same parity. We have $|X_1|=\frac{n-t}{2}$; hence, the following lower bounds can be given by the number of repeated colors:

• $\left(\right|X_1|-1)+t=\frac{n+t-2}{2}\ge \frac{n+1}{2}$ if $3t=n$, with equality only if $t=3$ (as $n<2p-1$ holds for $t=2$);
• $\left(\right|X_1|-1)+(t+1)=\frac{n+t}{2}>n/2$ for all $t>0$ if $3t<n$.

This completes the proof for $q=2$.

6. Concluding Remarks

In this paper, we considered colorings of complete circular hypergraphs in which the “intervals” of any p consecutive vertices have to contain two vertices with a common color and any q consecutive vertices have to contain two distinct colors. The main result is the complete determination of the largest possible number of colors under these conditions for any number n of vertices, any $p\ge 3$, and any $q\ge 2$.

For $q\ge 3$, we also designed a procedure that can generate a coloring with any number of colors between minimum and maximum. The starting point of this algorithm is to take a sieve of maximum size in the hypergraph under consideration. In the hypergraphs $\mathcal{KC}(n;p,q)$ with $q\ge 3$, the sum of the sieve number and the “C-stability number” (see definition below) is very close to the number of vertices, and the C-stability number is very close to the upper chromatic number. In the rest of these conclusions, we mention some properties of circular hypergraphs in which the latter two parameters are equal in every induced subhypergraph.

C-Perfect Circular Hypergraphs

In a mixed hypergraph $\mathcal{H}$, a set of vertices is C-independent or C-stable if it contains no C-edge. The C-stability number ${\alpha }_{\mathcal{C}}\left(\mathcal{H}\right)$ is the maximum cardinality of a C-stable set of $\mathcal{H}$. Always, $\overline{\chi }\left(\mathcal{H}\right)\le {\alpha }_{\mathcal{C}}\left(\mathcal{H}\right)$ because a set with more distinct colors than ${\alpha }_{\mathcal{C}}\left(\mathcal{H}\right)$ would assign different colors to all the vertices of some C-edge. A mixed hypergraph $\mathcal{H}$ is C-perfect if $\overline{\chi }\left({\mathcal{H}}^{\prime }\right)={\alpha }_{\mathcal{C}}\left({\mathcal{H}}^{\prime }\right)$ for every induced subhypergraph ${\mathcal{H}}^{\prime }$ of $\mathcal{H}$, including $\mathcal{H}$ itself.

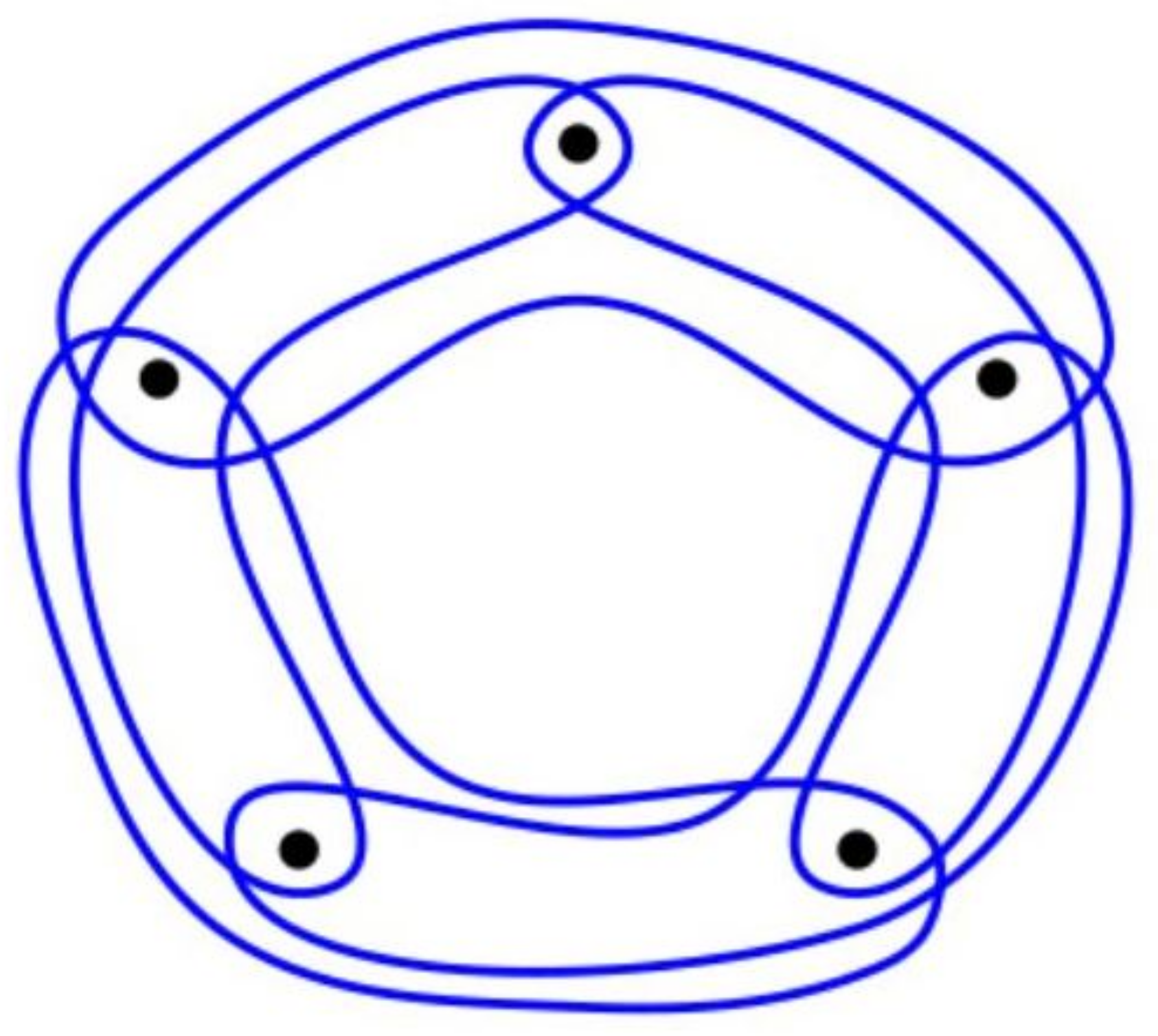
Several classes of C-perfect and minimal non-C-perfect mixed hypergraphs have been found. A polystar is a mixed hypergraph with at least two C-edges in which the set Y of vertices common to all C-edges (center) is nonempty, and every pair in Y forms a D-edge. When the center consists of one vertex, then the polystar is also called a monostar. Hence, each polystar in a C-hypergraph is a monostar. A bistar is a mixed hypergraph in which there exists a pair of distinct vertices common to all C-edges and not forming a D-edge. Bistars are C-perfect, whereas polystars are not. Among the first minimal non-C-perfect hypergraphs are the cycloids ${\mathcal{C}}_{2p-1}^p$, which, in the terminology of this article, is $\mathcal{KC}(2p-1;p,0)$, found first in [3]; for the smallest example, see Figure 2.

Figure 2. Cycloid ${\mathcal{C}}_5^3$=$\mathcal{KC}(5;3,0)$.

The characterization of C-perfect circular hypergraphs without D-edges was done in [17], proving that if no edge is a subset of another edge, the necessary and sufficient condition for C-perfectness of circular C-hypergraphs is to exclude monostars and cycloids. The situation with the presence of D-edges becomes more complicated, however, even in hypergraphs built upon host graphs without cycles, as was shown in [18].

Let ${\mathbf{S}}_n$ denote the class of all circular mixed hypergraphs of order $n\ge 7$ containing no induced monostar and no induced covered C-bistar with the following property: there is an ordering of the C-edges $C_0,C_1,C_2,\dots ,C_{s-1}$ so that $C_j\cup C_{j+1}=X$ and $C_j\cap C_{j+1}$ induces a $K_1$ or a $K_2, 0\le j\le s-1$ (indices modulo s). If $\mathcal{H}$ contains no D-edges of size 2, then ${\mathbf{S}}_n$ is empty for even n, and ${\mathbf{S}}_n$ is the cycloid ${\mathcal{C}}_{2p-1}^p$ for odd $n=2p-1$. An example for even $n=2s$ is $\mathcal{H}$ with $X=\{0,1,\dots ,2s-1\}, (X,\mathcal{D})$ is the $2s$-cycle, and $\mathcal{C}=\left\{\right\{0,1,\dots ,s\}+2t | 0\le t\le s-1\}$ indices taken modulo n. A non-uniform example of a hypergraph in ${\mathbf{S}}_7$ would have $\mathcal{C}=\left\{\right\{0,1,2,3\},\{2,3,4,5,6\},\{6,0,1\},\{1,2,3,4,5\},\{4,5,6,0\left\}\right\}$. The following general characterization of C-perfect circular mixed hypergraphs is proven in [19]:

Theorem 4.

A circular mixed hypergraph $\mathcal{H}$ is C-perfect if and only if $\mathcal{H}\notin {\mathbf{S}}_n$ and $\mathcal{H}$ does not contain induced C-monostars and induced covered C-bistars.

A $\mathcal{KC}(n;p,q)$ contains C-monostars if and only if $2p\le n$. If $q=2$, and $2p=n+1$, it contains covered C-bistars. If $q\ne 2$, and $2p=n+1$, then $\mathcal{KC}(n;p,q)\in {\mathbf{S}}_n$. These observations lead to the following characterization of C-perfect $\mathcal{KC}(n;p,q)$ hypergraphs:

Theorem 5.

A mixed cycloid $\mathcal{KC}(n;p,q)$ is C-perfect if and only if

$$2p\ge n+2.$$