Eulerian and Even-Face Graph Partial Duals

Abstract

Eulerian and bipartite graph is a dual symmetric concept in Graph theory. It is well-known that a plane graph is Eulerian if and only if its geometric dual is bipartite. In this paper, we generalize the well-known result to embedded graphs and partial duals of cellularly embedded graphs, and characterize Eulerian and even-face graph partial duals of a cellularly embedded graph by means of half-edge orientations of its medial graph.

1. Introduction

Geometric duality is a fundamental symmetric property among cellularly embedded graphs. “A plane graph G is Eulerian if and only if its geometric dual $G^{*}$ is bipartite” [1,2] is a classical theorem in graph theory. The sufficiency of this theorem is obvious and holds for any cellularly embedded graphs. With the help of Jordan Curve Theorem, the necessity of this theorem can be deduced by showing that a Eulerian plane graph is proper two-face-colourable. However, this does not hold for cellularly embedded graphs on the other surfaces, and one can easily find counter examples such as a cellularly embedding of the complete graph $K_5$ on the torus and the cellularly embedding of a cycle $C_n$ in the real projective plane.

A partial dual of a cellularly embedded graph, introduced by Chmutov [3], generalizes the geometric duality. It was introduced to unify Thistlethwaite theorems [3,4,5,6] in knot theory with a Tutte-like polynomial in graph theory. Partial duality is an impactful extension of geometric duality and has found numerous meaningful applications in mathematics and physics. For the basics of partial duality we refer the readers to the monograph [7].

Recently Huggett and Moffatt [8] gave an extension of the above dual symmetry between plane Eulerian and bipartite graphs to partial duality and characterized all bipartite partial duals of plane graphs by means of oriented circuits in their medial graphs. They left an open problem: Characterize all Eulerian partial duals of a plane graph. Basing on Huggett and Moffatt’s partial dual extension, Metsidik and Jin [9] solved this problem using half-edge orientations of medial graphs. Then Deng et al. generalized these results for ribbon graphs [10].

An even-face graph is a cellularly embedded graph without odd degree faces. There is a recent comprehensive research study of even-faced embeddings of complete graphs [11]. In this paper, we further study the following topics: Extending plane bipartite graphs to even-region graphs, we generalize the above classical result to embedded graphs and partial duals of cellularly embedded graphs, and characterize all Eulerian and all even-face graph partial duals of a cellularly embedded graph by using two methods.

2. Ribbon Graphs and Partial Duals

An embedded graph $G=\left(V\right(G),E(G\left)\right)\subset \Sigma$ is a graph drawn on a surface $\Sigma$ such that edges only intersect at their ends. Each path-connected component of $\Sigma \setminus G$ is a region of G. A face of G is a region of G homeomorphic to an open disc. G is cellularly embedded if each region of G is a face. There are several equivalent definitions for cellularly embedded graphs. In this paper, we use ribbon graphs.

Definition 1

([12]). A ribbon graph $\mathbf{G}=\left(V\right(\mathbf{G}),E(\mathbf{G}\left)\right)$ is a surface with boundary represented as the union of two sets of topological discs: A set $V\left(\mathbf{G}\right)$ of vertices, and a set $E\left(\mathbf{G}\right)$ of edges such that

• the vertices and edges intersect in disjoint line segments (we call such line segments common line segments since they belong to boundaries of both vertex discs and edge discs);
• each common line segment lies on the boundary of precisely one vertex and precisely one edge;
• every edge contains exactly two common line segments.

Notice that the notion of ribbon graphs corresponds to the reduced band decomposition mentioned in the classical book “Topological graph theory”of Gross and Tucker [13].

Definition 2

([14]). Edge line segments of an edge in a ribbon graph are the line segments obtained by deleting the common line segments from the boundary the edge. Vertex line segments of a vertex in a ribbon graph are the line segments that belong to the boundary of the vertex but not the boundary of its incident edges.

Notice that each edge contains exactly two edge line segments and the number of vertex line segments of a vertex equals the degree of the vertex.

The geometric dual ${\mathbf{G}}^{*}$ of a ribbon graph $\mathbf{G}$ has a precise description in the language of ribbon graphs. For each boundary component f of $\mathbf{G}$, we take a disc $f^{*}$ and identify f with the boundary of $f^{*}$, and thus we obtain a surface $\Sigma$ without boundary. Then ${\mathbf{G}}^{*}$ results when all the original vertex open discs of $\mathbf{G}$ are removed from $\Sigma$. See [7] for examples.

Definition 3

([8]). Let $\mathbf{G}\overrightarrow{-}A$ ($A\subseteq E\left(\mathbf{G}\right)$) denote the arrow-marked ribbon graph obtained as follows: For each edge $e\in A$, arbitrarily orient the boundary of e; place an arrow on each common line segment of e such that the directions of these arrows follow the orientation of the boundary of e; color the two arrows with e; and delete the edge e.

Marking arrows are illustrated locally at an edge in Figure 1. Let $\overrightarrow{+}$ be the inverse operation of the marking arrows $\overrightarrow{-}$. Then we have $\left(\mathbf{G}\overrightarrow{-}A\right)\overrightarrow{+}A=\mathbf{G}$ and $\left(\mathbf{G}\overrightarrow{-}A\right)\overrightarrow{+}B=\mathbf{G}\overrightarrow{-}(A\setminus B)$ for any edge subsets A and B with $B\subseteq A\subseteq E\left(\mathbf{G}\right)$. In particular, if we take the marking arrows $\overrightarrow{-}$ for all $E\left(\mathbf{G}\right)$, then we obtain an arrow presentation of $\mathbf{G}$.

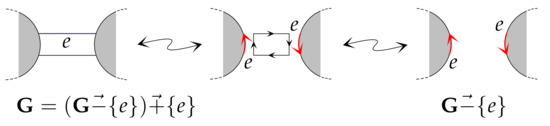
Figure 1. $\mathbf{G}=\left(\mathbf{G}\overrightarrow{-}\left\{e\right\}\right)\overrightarrow{+}\left\{e\right\}$ and $\mathbf{G}\overrightarrow{-}\left\{e\right\}$.

Definition 4

([8]). Let $\mathbf{G}$ be a ribbon graph and $A\subset E\left(\mathbf{G}\right),A^c=E\left(\mathbf{G}\right)\setminus A$. Then the partial dual of $\mathbf{G}$ with respect to A, denoted by ${\mathbf{G}}^A$, is given by

$${\mathbf{G}}^A:={\left(\mathbf{G}\overrightarrow{-}{A}^c\right)}^{*}\overrightarrow{+}{A}^c.$$

A few basic properties of partial duals are the following.

Proposition 1

([3]). Let $\mathbf{G}$ be a ribbon graph and $A,B\subset E\left(\mathbf{G}\right)$. Then

• ${\mathbf{G}}^{\varnothing }=\mathbf{G}$;
• ${\mathbf{G}}^{E\left(\mathbf{G}\right)}={\mathbf{G}}^{*}$;
• ${\mathbf{G}}^{A\cup B}={\left({\mathbf{G}}^A\right)}^{B\setminus A}$;
• $\mathbf{G}$ is orientable if only if ${\mathbf{G}}^A$ is orientable;
• partial duality acts disjointly on components.

For more details and examples refer to [7,15]. Here we also give an example to illustrate the definition.

Example 1.

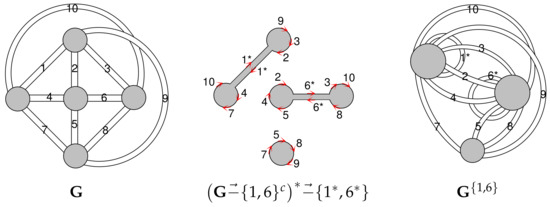
In Figure 2, the ribbon graph $\mathbf{G}$ on the left is equivalent to a cellular embedding of $K_5$ on torus, and the arrow-marked ribbon graph in the middle is the arrow presentation of ${\mathbf{G}}^{\{1,6\}}$. In the arrow presentation, the process of taking the geometric dual is the result of a local operation at each edge e that simply shifts the two arrows colored with e from the two common line segments of e to the two edge line segments of e.

Figure 2. A cellular embedding of $K_5$ on torus and one of its partial duals.

3. Generalizing a Classical Result of Plane Graphs to Embedded Graphs

The number of edge (or equivalently vertex) line segments lying on a boundary component of a ribbon graph is equal to the degree of the boundary component. A cellularly embedded graph G is even-face if the degree of each boundary component of its equivalent ribbon graph $\mathbf{G}$ is even. The degree of a region of an embedded graph is the sum of the degrees of the boundary components belonging to the region. Now we similarly define that an embedded graph is an even-region graph if the degree of each of its regions is even.

A dual $G^{⊛}$ of an embedded graph G in a surface $\Sigma$ is an embedded graph in the surface $\Sigma$ formed by placing one vertex in each region of G and embedding an edge between two vertices whenever the two regions of G they lie in share an edge in common. Note that in general $G^{⊛}$ is not unique, but isomorphic as abstract graphs. The vertices of $G^{⊛}$ corresponding to the faces of G have the fixed cyclic orderings of the edges incident to them and the fixed cyclic orders of the vertices are determined by the embedding of G. If G is cellularly embedded, then $G^{⊛}=G^{*}$ and $G^{⊛}$ is unique. A dual $G^{⊛}$ of the graph G embedded in the plane with components $G_1,G_2,\cdots ,G_p$ can be formed by one-vertex joins of $G_1^{*},G_2^{*},\cdots ,G_p^{*}$. Similar to geometric duals there is the standard immersion $G\uplus G^{⊛}$ of G and any fixed $G^{⊛}$, and therefore we use the natural bijection to its intersected edge $e^{*}$ in $G\uplus G^{⊛}$ to identify the edges of $G^{⊛}$.

Theorem 1.

Let G be an embedded graph in a connected closed surface. Then G is an even-region graph if and only if $G^{⊛}$ is Eulerian.

Proof. 

Without loss of generality we assume that G is a graph embedded in a connected closed surface $\Sigma$ such that if the connected sum ${\Sigma }_1\#{\Sigma }_2=\Sigma$ and $G\subset {\Sigma }_1$ then ${\Sigma }_2$ is homeomorphic to a sphere. Otherwise, the dual $G^{⊛}$ of G in ${\Sigma }_1$ is isomorphic to that of G in $\Sigma$ and G is an even-region graph in ${\Sigma }_1$ if and only if G is an even-region graph in $\Sigma$.

Let $\mathbf{G}$ be the fat graph in $\Sigma$ obtained by taking a small neighbourhood of G in $\Sigma$ such that the vertices and edges of $\mathbf{G}$ intersect in disjoint line segments. Then we can similarly define an edge line segment and a vertex line segment for the fat graph $\mathbf{G}$. Now we introduce an operation called amalgamating vertices by an edge as follows:

• choose two vertex line segments $l_v,l_{v^{\prime }}$ from vertex discs $v,v^{\prime }$ (possibly $v=v^{\prime }$);
• join the two vertex line segments $l_v,l_v^{\prime }$ by a new edge e;
• amalgamate $v,v^{\prime }$ by e to form a new vertex $v\cup e\cup v^{\prime }$;
• arbitrarily label the two line segments consisting of one part of $l_v$, one edge line segment of e and one part of $l_v^{\prime }$ with $l_v,l_{v^{\prime }}$.

If a region of $\mathbf{G}$ is not homeomorphic to a disc, then we can modify the region by a sequence of amalgamating vertices by an edge embedded in the surface $\Sigma$ into disjoint discs. Thus we modify $\mathbf{G}$ by a sequence of amalgamating vertices by an edge embedded in the surface $\Sigma$ such that very region of the modified fat graph is homeomorphic to a disc. Notice that the vertices of the modified fat graph may not be homeomorphic to discs. Removing the interior of all the vertices of the modified fat graph (removing all the original vertex discs of $\mathbf{G}$ and all new added edges) we obtain the fat graph ${\mathbf{G}}^{⊛}$ of an embedded graph $G^{⊛}$ in $\Sigma$.

Notice that there is a one to one correspondence between the vertex line segments lying on the boundary components of a region of $\mathbf{G}$ and the vertex line segments of the vertex of ${\mathbf{G}}^{⊛}$ corresponding to the region.

Recall that the degree of a vertex equals the number of vertex line segments of the vertex and then the result follows from a well-known theorem: A connected graph is Eulerian if and only if it has no vertex of odd degree. □

While ${\left(G^{⊛}\right)}^{⊛}$ is not necessarily equal to the embedded graph G, the words “even-region graph” and “Eulerian” can be interchanged in Theorem 1. Since $G^{⊛}=G^{*}$ for any cellularly embedded graph G, we have the following result obtained in [10,14,16] as a corollary.

Corollary 1.

Let G be a cellularly embedded graph. Then G is Eulerian if and only if its geometric dual $G^{*}$ is an even-face graph.

Since a connected plane graph is bipartite if and only if it is an even-face graph, we get the classical theorem mentioned in the introduction.

Corollary 2.

Let G be a connected plane graph. Then G is Eulerian if and only if its geometric dual $G^{*}$ is bipartite.

4. Eulerian Partial Duals

Let G be a cellularly embedded graph in $\Sigma$. Then $G^{*}$ has a natural cellular embedding in $\Sigma$, and therefore there is a standard immersion $G\uplus G^{*}$, where each edge of G intersects exactly one edge of $G^{*}$ at exactly one point. We again use the natural bijection of $e\in E\left(G\right)$ to its intersected edge $e^{*}$ in $G\uplus G^{*}$ to identify the edges of $G^{*}$ and set $A^{*}=\{e^{*}\mid e\in A\}$ for $A\subseteq E\left(G\right)$ accordingly.

Theorem 2

([8]). Let G be a connected and cellularly embedded graph, and $A\subseteq E\left(G\right)$. Then

$${\left[G\uplus G^{*}-(A^c\cup A^{*})\right]}^{⊛}\cong G^A.$$

Lemma 1.

Let G be a connected and cellularly embedded graph, and $A\subseteq E\left(G\right)$. Then $G^A$ is Eulerian if and only if $G\uplus G^{*}-(A^c\cup A^{*})$ is an even-region graph.

Proof. 

Let $G^A$ be Eulerian and $\mathsf{\Phi }:=G\uplus G^{*}-(A^c\cup A^{*})$. Then, by Theorem 2, ${\mathsf{\Phi }}^{⊛}$ is Eulerian. Then, by Theorem 1, $\mathsf{\Phi }$ is an even-region graph. □

Lemma 2.

Let G be a connected and cellularly embedded graph, and $A\subseteq E\left(G\right)$. Then $G\uplus G^{*}-(A^c\cup A^{*})$ is an even-region graph if and only if both ${G|}_A$ and $G^{*}{|}_{{A^c}^{*}}$ are even-region graphs, where ${G|}_A=G-A^c$ and ${A^c}^{*}={\left(A^c\right)}^{*}$.

Proof. 

⟹ We first claim that no region of ${G|}_A$ includes two components of $G^{*}{|}_{{A^c}^{*}}$ (equivalently no region of $G^{*}{|}_{{A^c}^{*}}$ includes two components of ${G|}_A$).

Consider a region f of ${G|}_A$. If f is a face of G, then f is an open disc. If f is not a face of G, then f contains some other edges and vertices of G. These edges and vertices divide f into faces of G. Then we can walk between any two of these faces via other such faces since G is connected. Notice that these faces correspond to vertices of $G^{*}{|}_{{A^c}^{*}}$ and our track from a face to the next one corresponds to an edge of $G^{*}{|}_{{A^c}^{*}}$. Thus, the part of $G^{*}{|}_{{A^c}^{*}}$ lying in f must be connected, and so the claim follows.

Suppose the degree of f is odd, then, by the claim, there is only one component C of $G^{*}{|}_{{A^c}^{*}}$ lying in f. Notice that the all boundary components of f and all boundary components of C consist of the all boundary components of some regions $R_1,R_2,\cdots ,R_s$ of $G\uplus G^{*}-(A^c\cup A^{*})$. Clearly the sum of the degrees of all boundary components of C is even. Hence the sum of the degrees of $R_1,R_2,\cdots ,R_s$ is odd. Thus at least one of $R_1,R_2,\cdots ,R_s$ has an odd degree, a contradiction to the assumption that $G\uplus G^{*}-(A^c\cup A^{*})$ is an even-region graph.

Thus ${G|}_A$ is an even-region graph. By the same argument, $G^{*}{|}_{{A^c}^{*}}$ is also an even-region graph.

⟸ Suppose that there is a region R of $G\uplus G^{*}-(A^c\cup A^{*})$ with an odd degree. Clearly R lies in a region, say again f, of ${G|}_A$. Then we again using a similar method of necessity showing that the degree of f is odd. □

From the proof of Lemma 2 we have already seen that the degree of each boundary component of $G^{*}{|}_{{A^c}^{*}}$ is even, similarly we can prove that if $G\uplus G^{*}-(A^c\cup A^{*})$ is an even-region graph then the degree of each boundary component of ${G|}_A$ is also even. Thus we have the following corollary.

Corollary 3.

Let G be a connected and cellularly embedded graph, and $A\subseteq E\left(G\right)$. Then $G\uplus G^{*}-(A^c\cup A^{*})$ is an even-region graph if and only if the degree of every boundary component of $G\uplus G^{*}-(A^c\cup A^{*})$ is even.

By Lemmas 1 and 2 we have

Theorem 3.

Let G be a connected and cellularly embedded graph, and $A\subseteq E\left(G\right)$. Then $G^A$ is Eulerian if and only if both ${G|}_A$ and $G^{*}{|}_{{A^c}^{*}}$ are even-region graphs.

By Lemma 1 and Corollary 3 we have

Theorem 4.

Let G be a connected and cellularly embedded graph, and $A\subseteq E\left(G\right)$. Then $G^A$ is Eulerian if and only if the degree of every boundary component of ${G|}_A$ and $G^{*}{|}_{{A^c}^{*}}$ is even.

5. Permissible Orientations and Eulerian Partial Duals

5.1. Permissible Orientations of Medial Graphs

Definition 5

([9]). By a half-edge orientation of a graph we mean an assignment of an orientation for each half-edge of the graph. An edge of a graph with a half-edge orientation is said to be consistent if the orientations of two half-edges of the edge define an orientation of the edge, otherwise it is an inconsistent edge.

Notice that a half-edge orientation of the graph with only consistent edges can be viewed as an orientation of a graph.

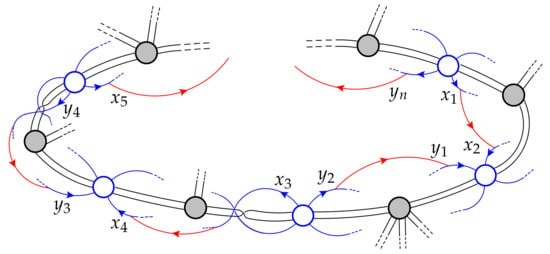
Let G be a cellularly embedded graph in a surface $\Sigma$. Then the medial graph $G_m$ of G is constructed as follows: In the first place, a vertex $v_e$ on each edge e of G; second, for each face f with boundary $v_1{e}_1{v}_2{e}_2\cdots v_t{e}_t{v}_1$, draw the edges $v_{e_1}{v}_{e_2},v_{e_2}{v}_{e_3},\cdots ,v_{e_t}{v}_{e_1}$ in a non-intersecting way inside the face f. It is easy to check that $G_m$ is a four-regular cellularly embedded graph in $\Sigma$.

A vertex $v_e$ of the medial graph $G_m$ of a ribbon graph $\mathbf{G}$ under a fixed half-edge orientation of $G_m$ is a semi-crossing if the directions of the four half-edges incident to $v_e$ are along one of the following three cyclic orders with respect to $v_e$: (incoming, incoming, outgoing, outgoing); (incoming, incoming, incoming, incoming); (outgoing, outgoing, outgoing, outgoing). There are two types of semi-crossing vertices of $G_m$ relative to edges of $\mathbf{G}$, see Figure 3. One is called c-vertices and the other is called d-vertices. An edge e of $\mathbf{G}$ is said to be a c-edge (respectively, d-edge) if $v_e$ in $G_m$ is a c-vertex (respectively, d-vertex).

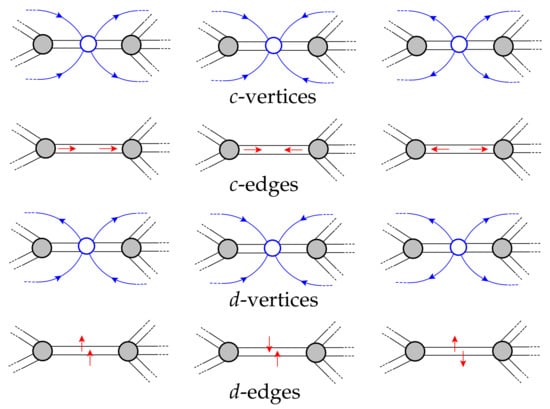
Figure 3. Definitions of c-, d-vertices and c-, d-edges.

An orientable loop l of an embedded graph G is called trivial if $l^{*}$ is a bridge of $G^{⊛}$. Note that an even-region graph contains no trivial loops. In this section we will consider half-edge orientations of $G_m$ satisfying the following three conditions:

Condition 1. Each vertex of $G_m$ is a semi-crossing;

Condition 2. Trivial loops of $\mathbf{G}$ are all c-edges and bridges of $\mathbf{G}$ are all d-edges;

Condition 3. Orientations of d-vertices of $G_m$ lying on the edges of $\mathbf{G}$ with a common end vertex and orientations of c-vertices of $G_m$ lying on the edges of a same boundary component of $\mathbf{G}$ must occur as shown in Figure 4 or their opposite.

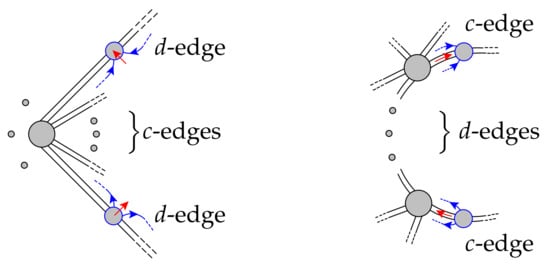
Figure 4. Configurations of orientations of d-edges with a common end vertex and c-edges lying on a same boundary component of $\mathbf{G}$.

For simplicity we call such a half-edge orientation of $G_m$ with the above three conditions a permissible orientation. Notice that these three conditions are all self-dual and $G_m={\left(G^{*}\right)}_m$, and therefore there is a one to one correspondence between c-edges (respectively, d-edges) of $\mathbf{G}$ and d-edges (respectively, c-edges) of ${\mathbf{G}}^{*}$.

While there are many permissible orientations for a medial graph, we are interested in the permissible orientations with different c-, d-vertex partitions. Let $t\left(G\right)$, b and l be the number of spanning trees, bridges and trivial loops of a cellularly embedded graph G, respectively. Then the medial graph $G_m$ of G admits at least $t\left(G\right)$ and at most $2^{\left|E\right(G\left)\right|-b-l}$ permissible such orientations. The upper bound is clear from the definition. Next we prove the lower bound. Let T be a spanning tree of the ribbon graph $\mathbf{G}$ equivalent to G and $A=E\left(T\right)$, $A^c=E\left(\mathbf{G}\right)\setminus A$. Then ${\mathbf{G}}^A$ is a bouquet, a graph with one vertex, i.e., ${\mathbf{G}}^A$ is Eulerian. By Theorem 4, each boundary component of ${G|}_A$ and $G^{*}{|}_{{A^c}^{*}}$ has an even degree. Alternately orient each edge line segment lying on each boundary component of ${\mathbf{G}|}_A$ and ${\mathbf{G}}^{*}{|}_{{A^c}^{*}}$ by incoming or outgoing arcs with respect to the boundary component, see Figure 11 for an example. Since there is no odd degree boundary component the orientation is consistent. Then we transfer the alternating transverse orientations of ${A^c}^{*}$ to the longitudinal orientations of the edges $A^c$ as in Figure 7. Hence all the edges of A are d-edges and the edges of $A^c$ are c-edges. The c- or d-status of the vertices of $G_m$ are inherited from the edges of $\mathbf{G}$; then, we direct the half-edges around each vertex as in Figure 3. Obviously, this half-edge orientation of $G_m$ is a permissible orientation. Since $t\left(G\right)=2^{\left|E\right(G\left)\right|-b-l}=1$ for a tree G, $G_m$ only admits one such permissible orientation, and thus the bounds are tight.

In the following section, we will show that the partial dual $G^A$ of a cellularly embedded graph G is Eulerian if and only if A is the set of d-edges determined by a permissible orientation of $G_m$. As in the example given in the following, we decrease the corresponding c-, d-edge partitions according to equivalent embeddings of G so that we gain all Eulerian partial duals of a cellularly embedded graph efficiently.

Example 2.

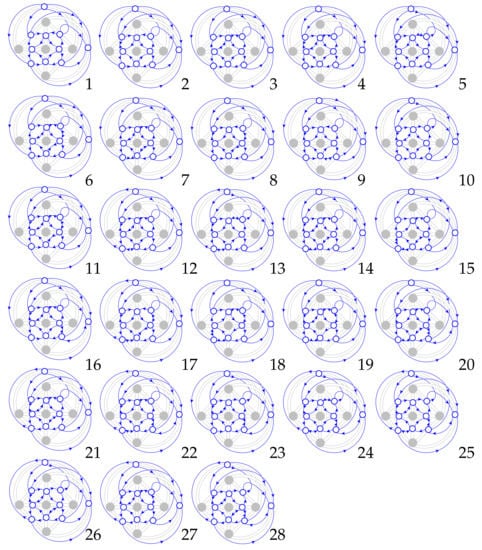
We first find a permissible orientation of the medial graph of a ribbon graph ${\mathbf{K}}_5$ with all c-vertices, see picture 1 in Figure 5. In order to obtain permissible orientations with different c-, d-edge partitions, we change some of the c-vertices to d-vertices considering equivalent ribbon graphs of ${\mathbf{K}}_5$. Since c-vertices satisfy the above three conditions, we only need to check the d-vertices in every changing process, see pictures 2–28 in Figure 5.

Figure 5. Picture 1 shows a permissible orientation of the medial graph of the ribbon graph ${\mathbf{K}}_5$ (equivalent to a five face embedding of $K_5$ on torus) with all c-vertices. Pictures 2–28 deriving from Picture 1 show some possible permissible orientations of the medial graph with different c-, d-edge partitions up to equivalent ribbon graphs of ${\mathbf{K}}_5$.

5.2. Characterizing all Eulerian Partial Duals of Cellularly Embedded Graphs

An embedded Eulerian graph with a half-edge orientation is alternating if we follow the cyclic order of the directed half-edges incident to each vertex, we find head–tail–⋯–head–tail. Notice that an embedded Eulerian graph G admits at most $2^{\left|V\right(G\left)\right|}$ alternating half-edge orientations and obviously admits at least one alternating half-edge orientation.

Theorem 5.

Let G be a connected and cellularly embedded graph. Then the partial dual $G^A$ is Eulerian if and only if A is the set of d-edges arising from a permissible orientation of $G_m$.

Proof. 

⟸ By Condition 2 of the definition of a permissible orientation we assume that ${\mathbf{G}|}_A$ contains no trivial loop.

Let C be a boundary component of ${\mathbf{G}|}_A$ and $e_1^{\prime },e_2^{\prime },\cdots ,$$e_n^{\prime }$ be the all edge line segments lying on C. Then, by Condition 3, the directions of the half-edges of $G_m$ incident to the half-vertex-discs $v_{e_1}^{\prime },v_{e_2}^{\prime },\cdots ,v_{e_n}^{\prime }$ identified by the edge line segments $e_1^{\prime },e_2^{\prime },\cdots ,$$e_n^{\prime }$ match up as in Figure 6, where ${\mathbf{G}|}_A$ is black and $G_m$ is blue and the red arcs join the half-edge of $v_{e_i}$ to the half-edge of $v_{e_{i+1}}$. Thus we have a half-edge cyclic sequence $x_1{x}_2{y}_1{y}_2\cdots x_{n-1}$$x_n{y}_{n-1}{y}_n$, where $x_i$ is a half edge with clockwise direction and $y_i$ with anticlockwise direction, and $x_i{y}_{i-1}$ and $y_j{x}_{j+1}$ with the subscript modulo n represent half-vertex discs $v_{e_i}^{\prime }$ and $v_{e_j}^{\prime }$, respectively. This in turn implies the half-vertex discs $v_{e_1}^{\prime },v_{e_2}^{\prime },\cdots ,v_{e_n}^{\prime }$ can be partitioned into two equal cardinality sets $\{v_{e_i}^{\prime }=x_i{y}_{i-1}\mid i=2,4,\cdots ,n\}$ and $\{v_{e_j}^{\prime }=y_j{x}_{j+1}\mid j=1,3,\cdots ,n-1\}$. Thus n is even. Hence any boundary component of ${G|}_A$ has an even degree. By the self-duality of the permissible direction, we know that any boundary component of $G^{*}{|}_{{\left(A^c\right)}^{*}}$ also has an even degree, i.e., ${G|}_A$ and $G^{*}{|}_{{\left(A^c\right)}^{*}}$ are even-region graphs. Then the result follows from Theorem 3.

Figure 6. A boundary component of a region of ${\mathbf{G}|}_A$ and its corresponding parts of $G_m$ with a permissible direction.

⟹ Let $\mathsf{\Phi }=G\uplus G^{*}-(A^c\cup A^{*})$. By Theorem 2, an embedded graph ${\mathsf{\Phi }}^{⊛}$ is Eulerian. Hence ${\mathsf{\Phi }}^{⊛}$ has alternating half-edge orientations. In the following, an alternating half-edge orientation of ${\mathsf{\Phi }}^{⊛}$ is transformed into a permissible orientation of $G_m$.

First, consider the fat graphs $\mathsf{\Phi }$ and ${\mathsf{\Phi }}^{⊛}$ in $\Sigma$ and then transfer longitudinal directions of the half-edges of ${\mathsf{\Phi }}^{⊛}$ to transverse directions of the edge line segments of $\mathsf{\Phi }$ as in Figure 7. Second, we transfer transverse directions of edge line segments of $\mathsf{\Phi }$ to directions of the edges of $\mathbf{G}$ as follows: Edge line segments of A are directed transversely and half-edges in $A^c$ are directed longitudinally. Then we will show that these transverse and longitudinal directions of the edges of $\mathbf{G}$ lead a permissible orientation of $G_m$.

Figure 7. Transfer directions lying on an edge to the dual edge.

The c- or d-status of the vertices of $G_m$ are inherited from the edges of $\mathbf{G}$, and the half-edges around each vertex were directed as in Figure 3. Condition 1 holds clearly.

By Theorem 3, ${G|}_A$ is an even-region graph. Hence ${G|}_A$ contains no trivial loops, i.e., d-edges (i.e., edges in A) cannot be trivial loops. By the self-duality of the definition, c-edges (i.e., edges in $A^c$) cannot be bridges and therefore Condition 2 holds.

Finally we show that Condition 3 also holds. Consider all d-edges incident to a vertex. Clearly d-edges incident to a same vertex correspond to the edges lying on a same boundary component of ${\mathsf{\Phi }}^{⊛}{|}_{A^{*}}$. Moreover, if the two edges are successive in the cyclic order of the end vertex then the two corresponding edges are adjacent on the boundary component. Recall that the half-edge orientation of ${\mathsf{\Phi }}^{⊛}$ is alternating, and by the construction of ${\mathsf{\Phi }}^{⊛}$ we have that ${\mathsf{\Phi }}^{⊛}{|}_{A^{*}}={\left({G|}_A\right)}^{⊛}$ is also an alternating half-edge direction, thus Condition 3 holds. Since the permissible orientation is self-dual, the directions of the c-edges on a same boundary component of $\mathbf{G}$ are satisfied concerning Condition 3. □

Example 3.

Edges of the ribbon graph ${\mathbf{K}}_5$ are numerated as in Figure 2. We take A to be the set of d-edges arising from the first seven permissible orientations of ${\left(K_5\right)}_m$ as shown in Figure 5, and obtain some Eulerian partial duals as shown in Figure 8. Since $K_5$ is cellularly embedded in torus, its all partial duals are also orientable (there is no half twist in the edges). In Figure 8, we contract all edges into line segments and paint the taking dual edges with blue.

Figure 8. Some Eulerian partial duals of $K_5$.

Since ${\left({\mathbf{G}}^A\right)}^{*}={\mathbf{G}}^{A^c}$ for $A\subseteq E\left(\mathbf{G}\right)$, and by Corollary 1, we have:

Proposition 2.

Let G be a connected and cellularly embedded graph, and $A\subseteq E\left(G\right)$. Then ${\mathbf{G}}^A$ is Eulerian if and only if ${\mathbf{G}}^{A^c}$ is an even-face graph.

Notice again that the words “Eulerian” and “even-face graph” can be interchanged in Proposition 2. Then the following corollary immediately follows from Theorem 5.

Corollary 4.

Let G be a connected and cellularly embedded graph. Then the partial dual $G^A$ is an even-face graph if and only if A is the set of c-edges arising from a permissible orientation of $G_m$.

6. Admissible Orientations and Even-Face Partial Duals

In this section, we provide another method to characterize even-face graph partial duals and also Eulerian partial duals of a cellularly embedded graph in terms of biseparations and half-edge orientations.

6.1. Admissible Orientations of Medial Graphs, 1-Sum, Join and Biseparation of Ribbon Graphs

A half-edge orientation of $G_m$ is admissible if it satisfies the following two conditions:

• each vertex of $G_m$ is a semi-crossing;
• inconsistent edge occurs only if the boundary of a face of G containing one of the end vertices of the inconsistent edge includes both a c-edge and a d-edge.

Definition 6

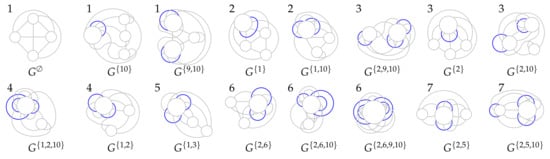
([17]). Let $\mathbf{G}$ be a connected ribbon graph, $v\in V\left(\mathbf{G}\right)$, and let $\mathbf{P}$ and $\mathbf{Q}$ be non-trivial, connected ribbon subgraphs of $\mathbf{G}$. Then $\mathbf{G}$ is said to be a 1-sum of $\mathbf{P}$ and $\mathbf{Q}$, written $\mathbf{G}=\mathbf{P}\oplus \mathbf{Q}$, if $\mathbf{G}=\mathbf{P}\cup \mathbf{Q}$ and $\mathbf{P}\cap \mathbf{Q}=\left\{v\right\}$ (see the picture on the left in Figure 9). The 1-sum is said to be involved at the vertex v. If there is an arc on the boundary of v with the property that all edges of $\mathbf{P}$ incident to v meet it on this arc, and no edges of $\mathbf{Q}$ do, then $\mathbf{G}$ is the join of $\mathbf{P}$ and $\mathbf{Q}$, written $\mathbf{G}=\mathbf{P}\vee \mathbf{Q}$ (see the picture on the right in Figure 9).

Figure 9. 1-sum and join.

We say that $\mathbf{G}$ can be written as a sequence of 1-sums if $\mathbf{G}$ contains subgraphs ${\mathbf{H}}_1,\cdots ,{\mathbf{H}}_l$ such that

$$\mathbf{G}={\mathbf{H}}_1\oplus {\mathbf{H}}_2\oplus {\mathbf{H}}_3\oplus \cdots \oplus {\mathbf{H}}_l=\left(\cdots \left(({\mathbf{H}}_1\oplus {\mathbf{H}}_2)\oplus {\mathbf{H}}_3\right)\oplus \cdots \oplus {\mathbf{H}}_l\right).$$

We say that an edge subset A of connected ribbon graph $\mathbf{G}$ defines a biseparation if either

• $A=E\left(\mathbf{G}\right)$ or $A=\varnothing$ (in which case the biseparation is trivial); or,
• $\mathbf{G}$ can be written as a sequence of 1-sums in which each 1-sum contains a component of ${\mathbf{G}|}_A$ and a component of ${\mathbf{G}|}_{A^c}$.

See [17,18] for more details and examples.

The biseparation of $\mathbf{G}$ defined by an edge subset A is even if the degree of each boundary component of $\mathbf{G}$ including a vertex line segment of the vertices of the sequence of 1-sums involved is even. See Figure 10 for an example in which the sequence of 1-sums is involved at the vertices $v_1,v_2,v_3$ and the degree of every boundary component of $\mathbf{G}$ including a vertex line segment of $\{v_1,v_2,v_3\}$ is even.

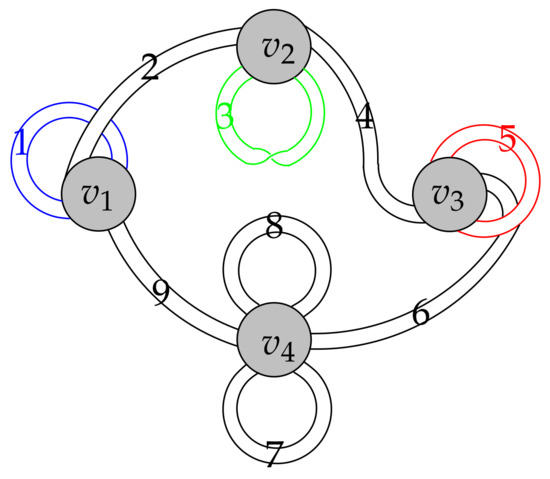
Figure 10. G = H₁ ⊕ H₂ ⊕ H₃ ⊕ H₄ = H₁ ⊕ H₂ ∨ H₃ ⊕ H₄ and $\{1,3,5\}$ defines an even biseparation of $\mathbf{G}$, where the color of the subgraph $H_i$ comes form the color of the edge-line-segments belonging to $H_i$.

6.2. Characterizing All Even-Face Partial Duals of Cellularly Embedded Graphs

Theorem 6.

Let G be a connected and cellularly embedded graph, and $A\subseteq E\left(G\right)$. Then $G^A$ is an even-face graph if and only if $A^c$ defines an even biseparation of $G^A$ and the degree of each vertex in $V\left(G{|}_A\right)\cup V\left(G^{*}{|}_{{A^c}^{*}}\right)\setminus C$ is even, where C is the set of all vertices lying on the boundaries of all regions of $G\uplus G^{*}-(A^c\cup A^{*})$ containing both vertices of ${G|}_A$ and $G^{*}{|}_{{A^c}^{*}}$.

Proof. 

Let $\mathsf{\Phi }=G\uplus G^{*}-(A^c\cup A^{*})$. By Theorem 2, ${\mathsf{\Phi }}^{⊛}\cong G^A$ and therefore there is an embedding $\widetilde{{\mathsf{\Phi }}^{⊛}}$ of ${\mathsf{\Phi }}^{⊛}$ equivalent to $G^A$. While $\widetilde{{\mathsf{\Phi }}^{⊛}}$ is cellularly embedded and ${\mathsf{\Phi }}^{⊛}$ possibly not, the only difference between the two embedded graphs is the orderings of the half edges of some vertices corresponding to the regions not homeomorphic to discs. By the proof of Lemma 2 the fat graph ${\mathsf{\Phi }}^{⊛}$ can be written as a sequence of joins, in which each join contains a component of ${\mathbf{G}}^{*}{|}_{A^{*}}$ and a component of ${\mathbf{G}|}_{A^c}$. Let the sequence of joins be involved at the vertices $v_1,\cdots ,v_s$. Then the ribbon graph $\widetilde{{\mathsf{\Phi }}^{⊛}}$ can be written as a sequence of 1-sums involved at the vertices $v_1,\cdots ,v_s$, in which each 1-sum contains a component of ${\mathbf{G}}^{*}{|}_{A^{*}}$ and a component of ${\mathbf{G}|}_{A^c}$. Thus $A^c$ defines a biseparation of $\widetilde{{\mathsf{\Phi }}^{⊛}}$, i.e., $A^c$ defines a biseparation of ${\mathbf{G}}^A$. Furthermore the faces of $\widetilde{{\mathsf{\Phi }}^{⊛}}$, which contain no vertex line segments of $\{v_1,\cdots ,v_s\}$ on their boundaries, correspond to the vertices of ${G|}_A$ and $G^{*}{|}_{{A^c}^{*}}$ that are not lying on the boundary of a region of $\mathsf{\Phi }$ containing both vertices of ${G|}_A$ and $G^{*}{|}_{{A^c}^{*}}$. Then the result follows from Corollary 1. □

Theorem 7.

Let G be a connected and cellularly embedded graph. Then the partial dual $G^A$ is an even-face graph if and only if $A^c$ defines an even biseparation of $G^A$ and A is the set of c-edges arising from an admissible orientation of $G_m$.

Proof. 

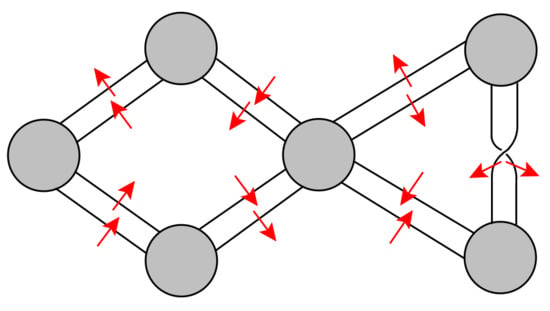
Let $C:={\bigcup }_B{\bigcup }_{v\in B}\left\{v\right\}$, where B is the boundary of a region of $G\uplus G^{*}-(A^c\cup A^{*})$ containing both vertices of ${G|}_A$ and $G^{*}{|}_{{A^c}^{*}}$.

⟸ Let $v\in V\left(G{|}_A\right)\setminus C$ and $e_1,e_2,\cdots ,e_n$ be the edge sequence incident to v. By the definition of the admissible orientation, the directions of the half edges of $v_{e_1},v_{e_2},\cdots ,v_{e_n}$ match up. Then we can show that n is even using a similar method as in the sufficiency of Theorem 5, i.e., the degree of v in $G|A$ is even. By the self-duality of the admissible orientation, we have that any vertex of $G^{*}{|}_{{A^c}^{*}}$ which is not lying on the boundary of a common region of ${G|}_A$ and $G^{*}{|}_{{A^c}^{*}}$ has an even degree. Then the result follows from Theorem 6.

⟹ Let $\mathsf{\Phi }=G\uplus G^{*}-(A^c\cup A^{*})$. By Theorem 6 we have that $A^c$ defines an even biseparation of $G^A$. By Theorem 2${\mathsf{\Phi }}^{⊛}\cong G^A$ and therefore there is an embedding $\widetilde{{\mathsf{\Phi }}^{⊛}}$ of ${\mathsf{\Phi }}^{⊛}$ equivalent to $G^A$. By the assumption $\widetilde{{\mathsf{\Phi }}^{⊛}}$ is an even-face graph.

We alternately orient each edge line segment lying on a boundary component of the ribbon graph $\widetilde{{\mathsf{\Phi }}^{⊛}}$ of $\widetilde{{\mathsf{\Phi }}^{⊛}}$ by incoming or outgoing arcs with respect to the boundary component, see Figure 11 for an example. Since $\widetilde{{\mathsf{\Phi }}^{⊛}}$ is an even-face graph the number of the edge line segments lying on a boundary component of $\widetilde{{\mathsf{\Phi }}^{⊛}}$ is even, and therefore the orientation is consistent.

Figure 11. Alternately orient each edge line segment lying on a boundary component.

Now we transversely orient each edge line segment of the fat graph ${\mathsf{\Phi }}^{⊛}$ according to the transverse direction of the corresponding edge line segment of $\widetilde{{\mathsf{\Phi }}^{⊛}}$. Recall that the two embedded graphs ${\mathsf{\Phi }}^{⊛}$ and $\widetilde{{\mathsf{\Phi }}^{⊛}}$ only differ from each other in the orderings of the half edges of some vertices corresponding to the regions not homeomorphic to discs.

First, we transfer transverse directions of the edge line segments of each edge of ${\mathsf{\Phi }}^{⊛}$ to longitudinal half-edge directions of the dual edge of $\mathsf{\Phi }$ as in Figure 6. Second, we transfer longitudinal half-edge directions of $\mathsf{\Phi }$ to directions of the edges of $\mathbf{G}$ as follows: Edge line segments belonging to $A^c$ are directed transversely and half-edges in A are directed longitudinally. Then we will show that the transverse and longitudinal directions of the edges of $\mathbf{G}$ lead an admissible orientation of $G_m$.

The c- or d-status of the vertices of $G_m$ are inherited from the edges of $\mathbf{G}$, and the half-edges around each vertex were oriented as in Figure 3. We only need to check that inconsistent edges have not occurred in the following two cases. Case 1: On the boundary of a face of $G_m$ corresponding to a boundary component of $\mathbf{G}$ consisting only of d-edges. Case 2: On the boundary of a face of $G_m$ encircling a vertex of $\mathbf{G}$ only incident to c-edges. Notice that a boundary component of $\mathbf{G}$ consisting only of d-edges corresponds to a boundary component of $\widetilde{{\mathsf{\Phi }}^{⊛}}$, and a vertex of $\mathbf{G}$ only incident to c-edges also corresponds to a boundary component of $\widetilde{{\mathsf{\Phi }}^{⊛}}$. So the result follows. □

The biseparation of $\mathbf{G}$ defined by an edge subset A is Eulerian if the degree of each vertex of the sequence of 1-sums involved is even.

Corollary 5.

Let G be a connected and cellularly embedded graph. Then the partial dual $G^A$ is Eulerian if and only if $A^c$ defines a Eulerian biseparation of $G^A$ and A is the set of d-edges arising from an admissible orientation of $G_m$.