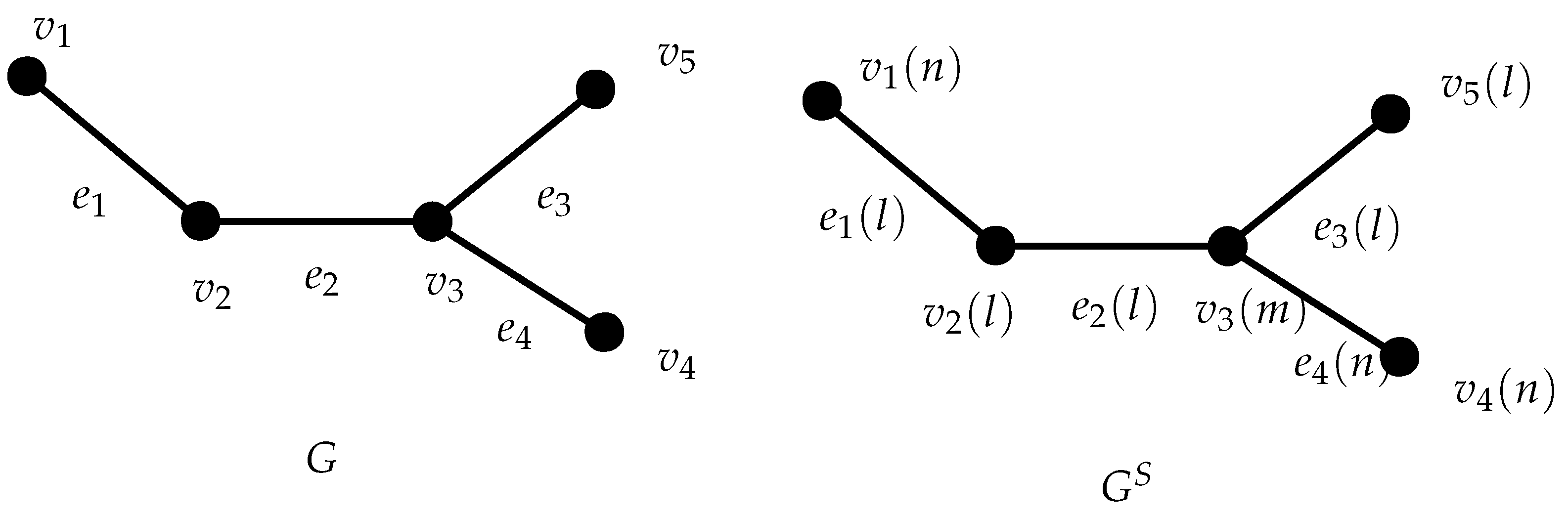Connectivity of Semiring Valued Graphs

Abstract

Graph connectivity theory is important in network implementations, transportation, network routing and network tolerance, among other things. Separation edges and vertices refer to single points of failure in a network, and so they are often sought-after. Chandramouleeswaran et al. introduced the principle of semiring valued graphs, also known as S-valued symmetry graphs, in 2015. Since then, works on S-valued symmetry graphs such as vertex dominating set, edge dominating set, regularity, etc. have been done. However, the connectivity of S-valued graphs has not been studied. Motivated by this, in this paper, the concept of connectivity in S-valued graphs has been studied. We have introduced the term vertex S-connectivity and edge S-connectivity and arrived some results for connectivity of a complete S-valued symmetry graph, S-path and S-star. Unlike the graph theory, we have observed that the inequality for connectivity $\kappa \left(G\right)\le {\kappa }^{\prime }\left(G\right)\le \delta \left(G\right)$ holds in the case of S-valued graphs only when there is a symmetry of the graph as seen in Examples 3–5.

1. Introduction

Connectivity of graphs plays an important role in network connections, network transportation, and network tolerance, etc. Critical vertices and edges correspond to single points of failure in every network, and thus we regularly want to spot them. The connectivity based on edges provides an additional stable form of a graph than a vertex based one. This happens because of every vertex of a connected graph that may be connected to at least one or additional edges. The removal of that vertex has an equivalent impact with the removal of all these attached edges. As a result, a graph that is one edge connected is one vertex connected too. Separation edges are also known as bridges and separation vertices are known as articulation points as shown in the figure within the Example 1. Algebraic graph theory is one of the main extensions of graph theory in which algebraic methods can be viewed in terms of graph theoretical concepts [1]. Chandramouleeswaran et al. [2] introduced the new graph theoretical concept known as semiring valued graphs (simply S-valued graphs). Since then, many works have been done in semiring valued graphs, such as regularity, degree-regular and connectedness of S-valued graphs [3,4,5]. In this article, the notions, the vertex S-connectivity and the edge S-connectivity in semiring valued graphs have been studied. Further, basic results on connectivity of few special graphs such as, S-complete, S-path and S-star have been proved. Symmetry of graphs has been measured and characterized by the automorphisms of graphs. This topic has been extensively studied over the past fifty years where automorphisms of graphs and group theory have played an important role, and promising and interesting results have been obtained, see for examples, [6,7]. The study of symmetry graph homomorphisms is over forty years old. It was pioneered by Sabidussi [8], and Hedrlin and Pultr [9] and other papers of these authors. Hahn and Tardif [10] gave a survey on symmetry graph homomorphisms. There is a chapter homomorphisms’ in the book [1] by Godsil and Royle. The special book [11] on graph homomorphisms by Hell and Nesetril appeared in 2004.

2. Preliminaries

In this Section, we will give some definitions that need for our main results.

Definition 1.

A vertex cut $V^{\prime }$ [12] of a graph $G=(V,E)$ is the subset of the vertex set V such that the removal of the set $V^{\prime }$ from G will disconnect the graph. That is, $G-V^{\prime }$ is disconnected. Similarly, we can define the edge cut $E^{\prime }$ of the graph $G=(V,E).$

Definition 2.

A $k-$vertex cut [12] of the graph G is a vertex cut that contains k elements. A k-edge cut [12] is an edge cut of graph G that contains k elements.

Definition 3.

The vertex connectivity of the graph G [12] is the minimum k for which G has a k-vertex cut. It is denoted by $\kappa \left(G\right).$ Similarly, the edge connectivity is defined by the minimum k such that G has a k-edge cut, and it is denoted by ${\kappa }^{\prime }\left(G\right).$

Definition 4.

A non-empty set S, together with two binary operations, addition and multiplication, is said to be a semiring [13] if $(S,+,0)$ is a monoid and $(S,·)$ is a semigroup. Furthermore, multiplication distributes over addition from both sides.

Definition 5.

The canonical pre-order ⪯ [13] is a relation in a semiring $(S,+,·)$ defined as follows: For any two elements $s_1,s_2\in S,s_1⪯s_2$ iff there exists an element $s_3\in S$ such that $s_1+s_3=s_2.$

Definition 6.

To compare the elements of $S\times \mathbb{N},$ we define ⪯ as follows:

1. 

$(s_1,n)⪯(s_2,m)\iff s_1⪯s_2$ and $n\le m.$

2. 

If $s_1⪯s_2$ and $n\ge m,$ that is, the comparision only with corresponding S-values

for all $s_1,s_2\in S$ and $n,m\in \mathbb{N},$

Definition 7.

The semiring valued graph [2] of a given graph $G=(V,E)$ is a graph $G^S=(V,E,\sigma ,\psi )$ with two S-valued functions, σ and ψ defined by $\sigma :V\to S$ and $\psi :E\to S$ by for all edges $\left((x,y)\right)\in E,$

$$\psi \left((x,y)\right)=\left\{\begin{array}{cc}min\left\{\sigma \left(x\right),\sigma \left(y\right)\right\}& if\sigma \left(y\right)⪯\sigma \left(x\right)or\sigma \left(x\right)⪯\sigma \left(y\right)\\ 0& otherwise\end{array}\right..$$

Definition 8.

The S-path $P^S\left(uv\right)$ [14] of a semiring valued graph $G^S$ is a path between the two vertices u and v in given graph $G,$ along with S-values in vertices and edges. Furthermore, $wt\left(P^S\left(uv\right)\right)=\underset{e\in P^S\left(uv\right)}{\Sigma }\psi \left(e\right)$ is the weight of the S- path in $G^S=(V,E,\sigma ,\psi ).$

Definition 9.

The semiring valued graph $G^S=(V,E,\sigma ,\psi )$ is said to be S-connected [4], if for every pair of vertices in $G^S$ have a S-path between them.

Definition 10.

The vertex degree [3] of the semiring valued graph $G^S,$ is defined as:

$${deg}_S\left(v_i\right)=\left(\sum _{v_j\in N_S\left(v_i\right)}\psi \left(v_i{v}_j\right),l\right),$$

where l is the number of incident edges of $v_i.$ Therefore, the minimum degree of $G^S$ is defined to be ${\delta }_S\left(G^S\right)=\underset{v_i\in V}{min}{deg}_S\left(v_i\right)$, and the maximum degree of $G^S$ is defined by ${\Delta }_S\left(G^S\right)=\underset{v_i\in V}{max}{deg}_S\left(v_i\right).$

Definition 11.

$p_S=({\Sigma }_{vs.\in V}\sigma \left(v\right),n)$ and $q_S=\left({\Sigma }_{(u,v)\in E}\psi (u,v),m\right)$ is defined as the order and size [5] of the semiring valued graph $G^S=(V,E,\sigma ,\psi )$, respectively, where n and m is the number of vertices and edges of the given graph $G=(V,E).$

3. Vertex S-Connectivity of Semiring Valued Graphs

In this Section, we have a tendency to discuss the vertex S-connectivity of semiring valued graphs and prove some straightforward results.

Definition 12.

Let $G^S=(V,E,\sigma ,\psi )$ be a semiring valued graph and let ${\mathcal{B}}_{G^S}=\left\{B_i\mid 1\le i\le k\right\}$ be the collection of S-connected components of $G^S.$ Then $B_i=(P_i,F_i),P_i\subseteq V,F_i\subseteq E,1\le i\le k.$ Therefore $|{\mathcal{B}}_{G^S}|=k$ and the graph $G^S$ is said to have k connected components. If $k=1,$ then $G^S$ is said to be a S-connected graph in which every pair of vertices has an S-path.

Definition 13.

The vertex strength of a semiring valued graph $G^S$ is the sum of the S-values of each vertices of $G^S.$ That is, $S{t}_V\left(G^S\right)=\underset{v_i\in V}{\Sigma }\sigma \left(v_i\right)=\mid V{\mid }_S.$

Definition 14.

A subset $P\subseteq V$ of a semiring valued graph $G^S=(V,E,\sigma ,\psi )$ is said to be vertex separating set if the removal of the set P from $G^S$ reduces the vertex strength of the graph $G^S$ and splits the graph into components. That is, $S{t}_V(G^S-P)⪯S{t}_V\left(G^S\right)$ and $|{\mathcal{B}}_{G^S-P}|>|{\mathcal{B}}_{G^S}|.$ In other words, ${|V-P|}_S⪯{\left|V\right|}_S$ and $|{\mathcal{B}}_{G^S-P}|>|{\mathcal{B}}_{G^S}|.$

Definition 15.

The vertex S-connectivity of $G^S$ denoted by ${\kappa }_V^S\left(G^S\right)$ is defined as the ${\kappa }_V^S=\underset{P\subseteq V}{min}\left\{\left(\right|P{|}_S,\left|P\right|)\right\},$ where $P\subseteq V$ such that $S{t}_V(G^S-P)⪯S{t}_V\left(G^S\right),$ and $|{\mathcal{B}}_{G^S-P}|>|{\mathcal{B}}_{G^S}|.$

From the definition, we observe that, ${\kappa }_V^S⪯p_S,$ where $p_S$ is the order of the graph $G^S.$

Example 1.

Take the semiring $S=(\left\{0,l,m,n\right\},+,·)$ with the binary operations ’+’ and ’·’, outlined by the subsequent Cayley tables.

+

0

l

m

n

·

0

l

m

n

⪯

Elements

0

0

m

m

n

0

0

0

0

0

0

0,l,m,n

l

l

l

m

n

l

0

0

l

n

l

l,m,n

m

m

m

m

m

m

0

l

m

n

n

n,m

n

n

n

m

n

n

0

0

n

n

m

m

Consider the graph G given in Figure 1

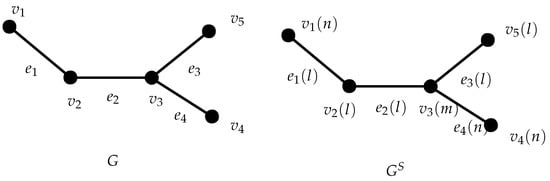
Figure 1. Graph G and its S-valued Graph $G^S$.

Define $\sigma :V\to S$ by $\sigma \left(v_1\right)=n,\sigma \left(v_2\right)=l,\sigma \left(v_3\right)=m,\sigma \left(v_4\right)=n,\sigma \left(v_5\right)=l.$

Then by definition of an S-valued graph, the edge valued function $\psi :E\to S$ is given by $\psi \left(e_1\right)=l,\psi \left(e_2\right)=l,\psi \left(e_3\right)=l,\psi \left(e_4\right)=n.$ Thus, we obtained the corresponding S-valued graph $G^S$ as in Figure 1

Using the definition for vertex strength of the semiring valued graph

we obtained, $S{t}_V\left(G^S\right)=n+l+m+l+n=m.$

Next, we consider the set, $P_1=\left\{v_3\left(m\right)\right\}.$ The graph $G^S-P_1$ has the following three components:

(1) 

$H_1^S=(\left\{v_1\left(n\right),v_2\left(l\right)\right\},\left\{e_1^2\left(l\right)\right\})$

(2) 

$H_2^S=(\left\{v_5\left(l\right)\right\},\varphi )$

(3) 

$H_3^S=(\left\{v_4\left(n\right)\right\},\varphi ).$

Therefore, $S{t}_V(G^S-P_1)=S{t}_V\left(H_1^S\right)+S{t}_V\left(H_2^S\right)+S{t}_V\left(H_3^S\right)=(l+n)+l+n=n.$ Since $S{t}_V(G^S-P_1)⪯S{t}_V\left(G^S\right),P_1$ is a vertex separating set such that $|P_1{|}_S=m,\left|P_1\right|=1.$

Similarly, we obtain the following sets are vertex separating sets of $G^S.$

(1) 

$P_2=\left\{v_2\left(l\right)\right\};$

(2) 

$P_3=\left\{v_2\left(l\right),v_3\left(m\right)\right\};$

(3) 

$P_4=\left\{v_2\left(l\right),v_5\left(l\right)\right\};$

(4) 

$P_5=\left\{v_2\left(l\right),v_4\left(n\right)\right\}$

(5) 

$P_6=\left\{v_3\left(m\right),v_4\left(n\right)\right\};$

(6) 

$P_7=\left\{v_3\left(m\right),v_5\left(l\right)\right\};$

(7) 

$P_8=\left\{v_3\left(m\right),v_1\left(n\right)\right\}.$

Then, by the definition of vertex S-connectivity, we have

$${\kappa }_V^S=\underset{P\subset V}{min}\left\{\left(\right|P{|}_S,\left|P\right|)\right\}=(l,1),$$

which corresponds to the vertex separating set $P_2=\left\{v_2\left(l\right)\right\}.$

Theorem 1.

Consider an S-valued graph $G^S=(V_S,E_S).$ Let $H^S=(P_S,F_S)$ be a subgraph of $G^S$ obtained by deleting a vertex v in $V.$ Then, $S{t}_V\left(H^S\right)⪯S{t}_V\left(G^S\right).$

Proof. 

Let $G^S=(V_S,E_S)$ be an S-valued graph with $V_S=\left\{(v_i,\sigma \left(v_i\right))\mid i=1,\cdots ,n\right\}$ and $E_S=\left\{\left(\left(v_i{v}_j\right)=e_i^j,\psi \left(e_i^j\right)\right)\mid i,j=1,\cdots ,n\right\}.$ Then for any $(v_i,\sigma \left(v_i\right))\in V_S$, let $H^S=\left(P_S=\left(V_S-\left\{(v_i,\sigma \left(v_i\right))\right\}\right),F_S\right)$ be a vertex deleted subgraph of $G^S.$ Then, $\left|V\right|=n$ and $\left|P\right|=n-1.$ By the definition of vertex strength of S-valued graph, we get $S{t}_V\left(G^S\right)=\underset{v_i\in V}{\Sigma }\sigma \left(v_i\right)=\sigma \left(v_1\right)+\cdots +\sigma \left(v_n\right)$ and $S{t}_V\left(H^S\right)=\underset{v_i\in P}{\Sigma }\sigma \left(v_i\right)=\sigma \left(v_1\right)+\cdots +\sigma \left(v_{n-1}\right).$ Thus, $S{t}_V\left(G^S\right)=S{t}_V\left(H^S\right)+\sigma \left(v_n\right).$ This implies that $S{t}_V\left(H^S\right)⪯S{t}_V\left(G^S\right).$ This completes the proof. □

The following corollaries can be easily proven by using the above theorem.

Corollary 1.

If $H^S=(P,F,{\sigma }_P,{\psi }_F)$ be a subgraph of $G^S$; then ${\kappa }_V^S\left(H^S\right)⪯{\kappa }_V^S\left(G^S\right).$

Corollary 2.

Let $G^S=(V_S,E_S)$ be a given S-valued graph. If $C^S$ is a clique of $G^S$, then $S{t}_V\left(C^S\right)⪯S{t}_V\left(G^S\right).$

Proof. 

Let $C^S$ be a clique of $G^S.$ Then, $C^S=(P_S,F_S)\subseteq (V_S,E_S)$ is a maximal subgraph of $G^S.$ Then, by the above theorem, $S{t}_V\left(C^S\right)⪯S{t}_V\left(G^S\right).$ □

Theorem 2.

If $G^S=(V_S,E_S)$ is a complete S-valued graph with $n-$vertices, then ${\kappa }_V^S\left(G^S\right)=\underset{P\subseteq V}{min}\left(\underset{v_i\in P}{\Sigma }\sigma \left(v_i\right),n-1\right),$ where P is the vertex separating set of $G^S.$

Proof. 

Let $G^S=(V_S,E_S)$ be a complete S-valued graph with n vertices. Clearly, $G^S$ is a connected S-valued graph. Deletion of one vertex $(v_1,\sigma \left(v_1\right))$ keeps the graph $G_1^S=G^S-\left(v_1,\sigma \left(v_1\right)\right)$ connected. Clearly, $G_1^S$ has $n-1$ vertices. Deleting one vertex, say $v_2$ from $G_1^S,$ gives a graph $G_2^S=G^S-\left\{(v_1,\sigma \left(v_1\right),(v_2,\sigma \left(v_2\right))\right\},$ which is again connected. Continuing this process, we observe that the graph

$$G_{n-1}^S=G^S-\left\{(v_1,\sigma \left(v_1\right)),(v_2,\sigma \left(v_2\right)),\cdots ,\left(v_{n-1},\sigma \left(v_{n-1}\right)\right)\right\}$$

leaves us only one vertex of $G^S.$ These $(n-1)$ vertices can be removed in $n{C}_1=n$ ways. Therefore, the vertex separating set P can have n choices, so that ${\left|P\right|}_S=\underset{v_i\in P}{\Sigma }\sigma \left(v_i\right),$$\left|P\right|=n-1.$ Hence, we have ${\kappa }_V^S\left(G^S\right)=\underset{P\subseteq V}{min}\left({\left|P\right|}_S,\left|P\right|\right)=\underset{P\subseteq V}{min}\left(\underset{v_i\in P}{\Sigma }\sigma \left(v_i\right),\left|P\right|\right).$

This completes the proof. □

Theorem 3.

If $G^S$ is an S-path, then ${\kappa }_V^S\left(G^S\right)=\underset{v_i\in V}{min}\left(\sigma \left(v_i\right),1\right).$

Proof. 

Let $G^S=(V,E,\sigma ,\psi )=(V_S,E_S)$ be a S-path with $V_S=\left\{\left(v_i,\sigma \left(v_i\right)\right)\mid i=1,2,\cdots ,n\right\}$ and $E_S=\left\{\left(e_1^2,\psi \left(e_1^2\right)\right),\cdots ,\left(e_{n-1}^n,\psi \left(e_{n-1}^n\right)\right)\right\}.$ Deletion of any vertex $\left(v_i,\sigma \left(v_i\right)\right),i=2,\cdots$, $n-1$ from $G^S$ disconnects the graph. Thus, each vertex $v_i,i=2,\cdots ,n-1$ is a vertex separting set $P_i$ of $G^S$ such that $|P_i{|}_S=\sigma \left(v_i\right)$ and $|P_i|=1.$ Hence, we have

$${\kappa }_V^S\left(G^S\right)=\underset{P\subseteq V}{min}\left({\left|P\right|}_S,\left|P\right|\right)=\underset{P\subseteq V}{min}\left(\sigma \left(v_i\right),1\right).$$

This completes the proof. □

Theorem 4.

If $K_{m,n}^S$ is a complete bipartite S-valued graph with two bipartition sets $V_1$ and $V_2$ such that $|V_1|=m;|V_2|=n$, then we have

$${\kappa }_V^S\left(G^S\right)=min\left\{(\underset{v_i\in V_1}{\Sigma }\sigma \left(v_i\right),m),(\underset{v_i\in V_2}{\Sigma }\sigma \left(v_i\right),n)\right\}.$$

Proof. 

Let $K_{m,n}^S$ be a complete bipartite S-valued graph with two bipartition sets $V_1$ and $V_2.$ Since it is complete bipartite S-valued graph removal of all vertices from $V_1$ or $V_2$ will make the graph disconnected. Hence, the vertex separating set P is either $V_1$ or $V_2$, which is minimum. Thus, ${\left|P\right|}_S=min\left\{|V_1{|}_S,{\left|V_2\right|}_S\right\}$ and $\left|P\right|=min\left\{|V_1|,|V_2|\right\}.$ Then, from the definition of vertex connectivity,

$${\kappa }_V^S\left(G^S\right)=min\left\{(\underset{v_i\in V_1}{\Sigma }\sigma \left(v_i\right),m),(\underset{v_i\in V_2}{\Sigma }\sigma \left(v_i\right),n)\right\}.$$

This completes the proof. □

The star graph can be realized as a complete bipartite graph $K_{1,n}^S,$ removing the pole leaves the graph disconnected. Hence, by using the above theorem, we obtain the following:

Corollary 3.

For a S-star $K_{1,n}^S$ with pole $v,$${\kappa }_V^S\left(K_{1,n}^S\right)=(\sigma \left(v\right),1).$

4. Edge S-Connectivity of Semiring Valued Graphs

Here, we have a tendency to introduce the notion of edge S-connectivity on S-valued graphs and prove some easy, however elegant, results.

Definition 16.

Consider the semiring valued graph $G^S=(V,E,\sigma ,\psi )$ with $V=\left\{v_i,\mid i=1,\cdots ,n\right\}$ and $E=\left\{\left(v_i{v}_j\right)=e_i^j\mid i,j=1,\cdots ,n\right\}.$ Then, the edge strength of $G^S$ is the sum of the S-values of edges of $G^S.$ That is,

$$S{t}_E\left(G^S\right)=\underset{e_i^j\in E}{\Sigma }\psi \left(e_i^j\right)=\mid E{\mid }_S.$$

Definition 17.

An edge separating set of a semiring valued graph $G^S=(V,E,\sigma ,\psi )$ is a subset $F\subseteq E$ whose removal from $G^S$ reduces the edge strength of the graph $G^S$ and increases the number of components in $G^S.$ That is,

$$S{t}_E(G^S-F)⪯S{t}_E\left(G^S\right)and|{\mathcal{B}}_{G^S-F}|>|{\mathcal{B}}_{G^S}|.$$

In other words, ${|E-F|}_S⪯{\left|E\right|}_S$ and $|{\mathcal{B}}_{G^S-F}|>|{\mathcal{B}}_{G^S}|.$

Definition 18.

The edge S-connectivity of $G^S,$ denoted by ${\kappa }_E^S\left(G^S\right),$ is defined as the ${\kappa }_E^S=\underset{F\subseteq E}{min}\left\{\left(\right|F{|}_S,\left|F\right|)\right\},$ where $F\subseteq E$ such that $S{t}_E(G^S-F)⪯S{t}_E\left(G^S\right),$ and $|{\mathcal{B}}_{G^S-F}|>|{\mathcal{B}}_{G^S}|.$

From the definition, we observe that, ${\kappa }_E^S⪯q_S,$ where $q_S$ is the size of the graph $G^S=(V,E,\sigma ,\psi ).$

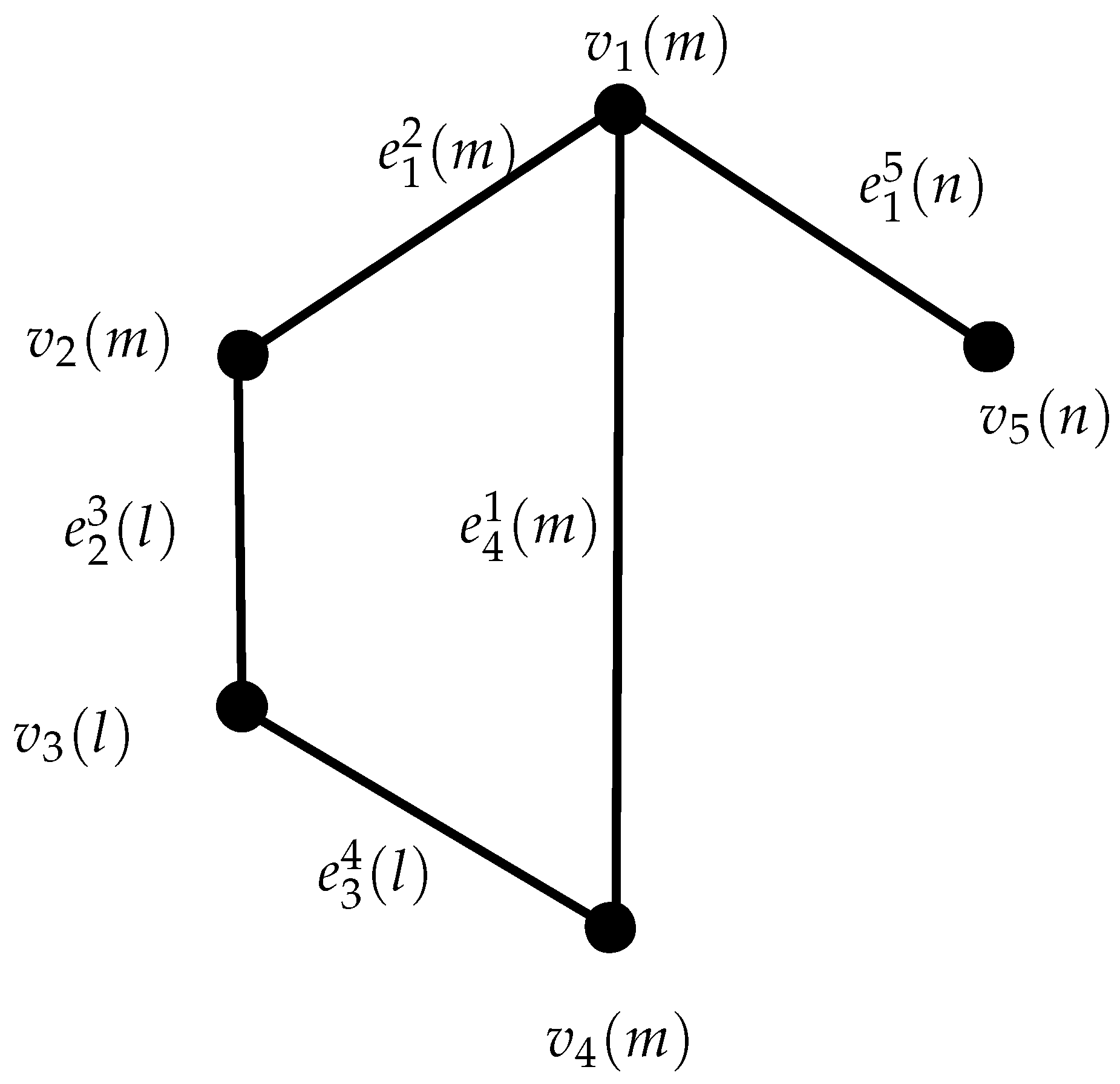
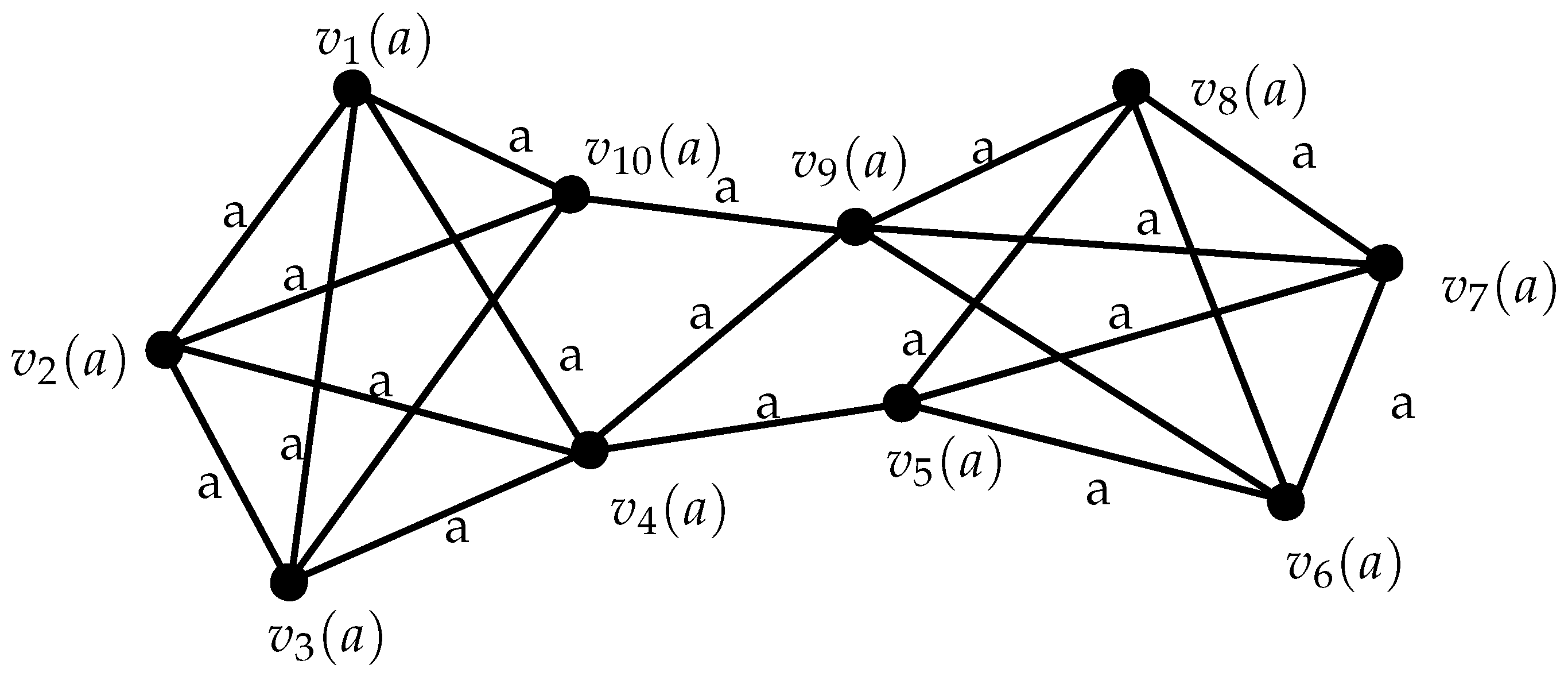
Example 2.

Take the semiring $S=(\left\{0,l,m,n\right\},+,·)$ as in the Example 1.The edge strength of the graph $G^S$ given in Figure 2 is $S{t}_E\left(G^S\right)=m+m+l+l+n=m.$ Consider the set, $F_1=\left\{e_1^5\left(n\right)\right\}.$ The graph $G^S-F_1$ has two components:

Figure 2. Semiring Valued Graph $G^S$.

(1) 

$H_1^S=(\left\{v_1\left(m\right),v_2\left(m\right),v_3\left(l\right),v_4\left(m\right)\right\},\left\{e_1^2\left(m\right),e_2^3\left(l\right),e_3^4\left(l\right),e_4^1\left(m\right)\right\})$;

(2) 

$H_2^S=(\left\{v_5\left(n\right)\right\},\varphi ).$

Therefore, we have $S{t}_E(G^S-F_1)=S{t}_E\left(H_1^S\right)+S{t}_E\left(H_2^S\right)=(m+l+l+m)+0=m.$ Since $S{t}_E(G^S-F_1)⪯S{t}_E\left(G^S\right),F_1$ is an edge-separating set such that $|F_1{|}_S=n,\left|F_1\right|=1.$

Similarly, we obtain the following sets that are edge-separating sets of $G^S$

(1) 

$F_2=\left\{e_1^2\left(m\right),e_4^1\left(m\right)\right\};$

(2) 

$F_3=\left\{e_1^2\left(m\right),e_2^3\left(l\right)\right\};$

(3) 

$F_4=\left\{e_1^2\left(m\right),e_3^4\left(l\right)\right\};$

(4) 

$F_5=\left\{e_1^2\left(m\right),e_1^5\left(n\right)\right\}$

(5) 

$F_6=\left\{e_2^3\left(l\right),e_3^4\left(l\right)\right\};$

(6) 

$F_7=\left\{e_2^3\left(l\right),e_4^1\left(m\right)\right\};$

(7) 

$F_8=\left\{e_2^3\left(l\right),e_1^5\left(n\right)\right\};$

(8) 

$F_9=\left\{e_1^5\left(n\right),e_4^1\left(m\right)\right\}.$

Then by the definition of edge S-connectivity, we have ${\kappa }_E^S=\underset{P\subseteq E}{min}\left\{\left(\right|P{|}_S,\left|P\right|)\right\}=(l,2).$

Even though $F_1=\left\{e_1^5\left(n\right)\right\}$ is an edge-separating set, which has null graph as its component, as per the definition of comparability, $F_6=\{e_2^3\left(l\right),e_3^4\left(l\right)\}$ will be the edge-separating set with the minimum cardinality $\left(|F_6{|}_S,\left|F_6\right|\right)=(l,2).$

Hence, ${\kappa }_E^S=(l,2).$

Analogous to the Theorem 1, we will simply prove the subsequent theorem and corollary.

Theorem 5.

Consider an S-valued graph $G^S=(V_S,E_S).$ Let $H^S=(P_S,F_S)$ be a subgraph of $G^S$ such that $H^S=\left(P_S,F_S=(E_S-\left\{(e,\psi (e\left)\right)\right\}\right)$ for some $(e,\psi \left(e\right)\in E_S.$ Then, $S{t}_E\left(H^S\right)⪯S{t}_E\left(G^S\right).$

Theorem 6.

Let $G^S=(V_S,E_S)$ be an S-valued graph and $H^S=(P_S,F_S)$ be a subgraph of $G^S$ such that $P_S\subseteq V_S$ and $F_S\subseteq E_S.$ Then, $S{t}_E\left(H^S\right)⪯S{t}_E\left(G^S\right).$

Proof. 

Let $G^S=(V_S,E_S)=(V,E,\sigma ,\psi )$ be a S-valued graph. Consider a subgraph $H^S=(P_S,F_S)=(P,F,{\sigma }_P,{\psi }_F)$ with $P\subseteq V$ and $F\subseteq E.$ Since $\left|F\right|\le {\left|E\right|,\left|F\right|}_S=\underset{e_i^j\in F}{\Sigma }\psi \left(e_i^j\right)⪯\underset{e_i^j\in E}{\Sigma }\psi \left(e_i^j\right)={\left|E\right|}_S.$ Thus, $S{t}_E\left(H^S\right)⪯S{t}_E\left(G^S\right).$ □

The following corollaries can be easily proved by using the above theorem.

Corollary 4.

For any subgraph, we have $H^S=(P,F,{\sigma }_P,{\psi }_F)$ of $G^S,$ and ${\kappa }_E^S\left(H^S\right)⪯{\kappa }_E^S\left(G^S\right).$

Corollary 5.

Let $G^S=(V,E,\sigma ,\psi )$ be a given S-valued graph. If $C^S$ is a clique of $G^S,$ then $S{t}_E\left(C^S\right)⪯S{t}_E\left(G^S\right)$ and ${\kappa }_E^S\left(C^S\right)⪯{\kappa }_E^S\left(G^S\right).$

Remark 1.

In graph theory, the inequality for connectivity $\kappa \left(G\right)\le {\kappa }^{\prime }\left(G\right)\le \delta \left(G\right)$ holds. However, in the theory of semiring valued graphs, the analogous inequality

$${\kappa }_V^S\left(G^S\right)⪯{\kappa }_E^S\left(G^S\right)⪯{\delta }_S\left(G^S\right)$$

(1)

need not be true in general. It is illustrated by the following examples.

Example 3.

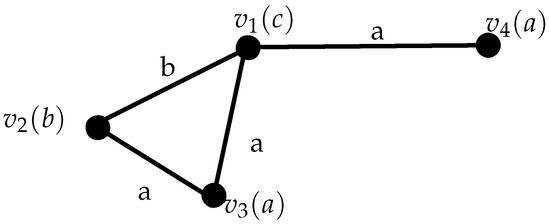
Take the semiring $S=(\left\{0,a,b,c\right\},+,·)$ with addition and multiplication as the

+

0

a

b

c

·

0

a

b

c

⪯

Elements

0

0

a

b

c

0

0

0

0

0

0

0,a,b,c

a

a

b

c

c

a

0

a

b

c

a

a,b,c

b

b

c

c

c

b

0

b

c

c

b

b,c

c

c

c

c

c

c

0

c

c

c

c

c

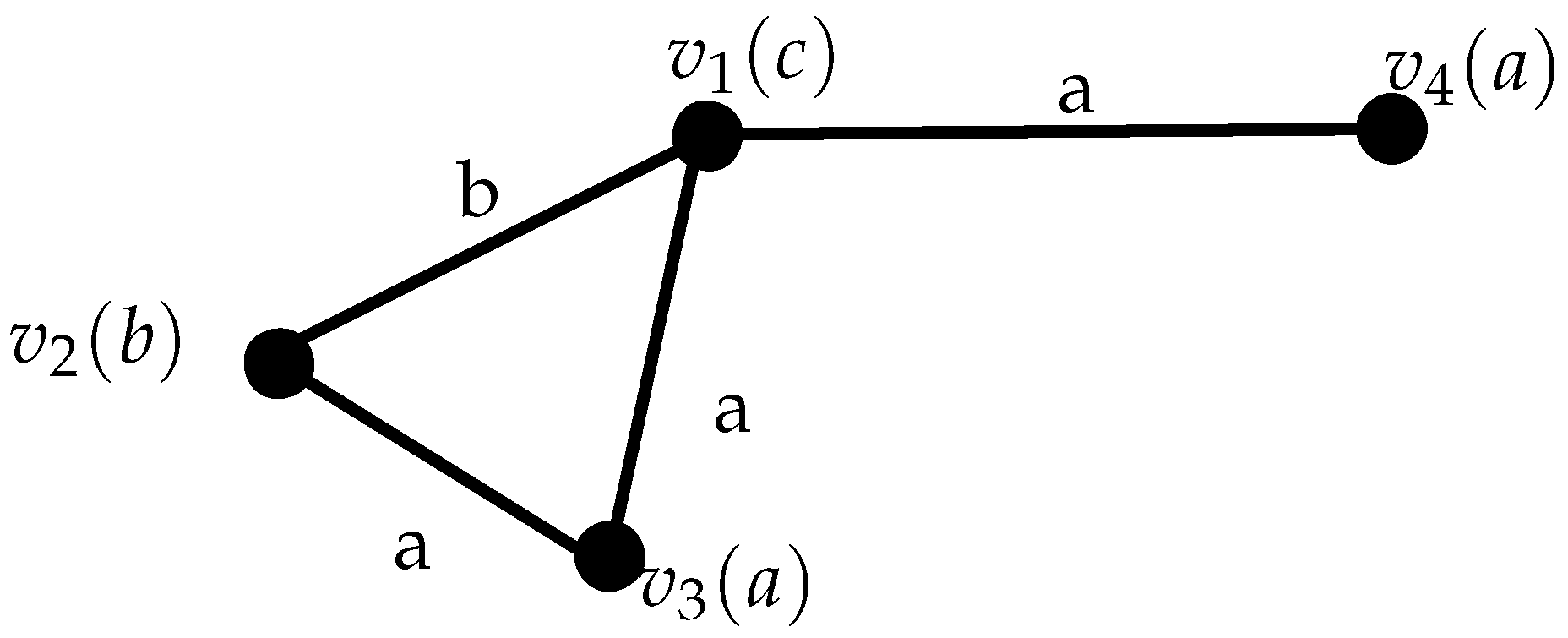
The minimum degree of $G^S$ given in Figure 3 $,$${\delta }_S\left(G^S\right)=(a,1)={deg}_S\left(v_4\right)$. The edge S- connectivity of $G^S,{\kappa }_E^S\left(G^S\right)=(a,1)$ and the vertex S-connectivity, ${\kappa }_V^S\left(G^S\right)=(c,1).$

Figure 3. Semiring valued graph $G^S$.

Thus, we have ${\delta }_S\left(G^S\right)⪯{\kappa }_E^S\left(G^S\right)⪯{\kappa }_V^S\left(G^S\right)$, which proves that the inequality (1) is not true.

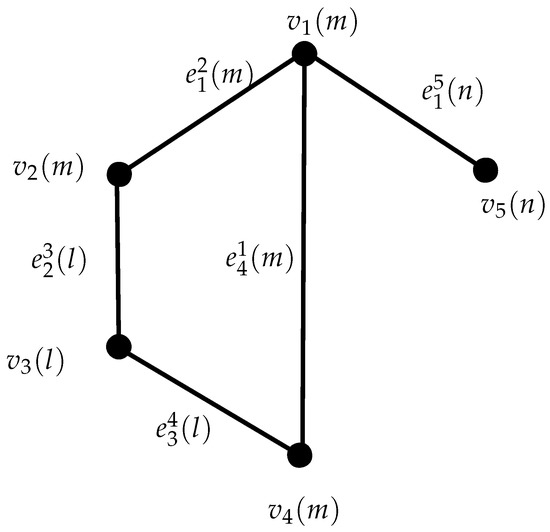
Example 4.

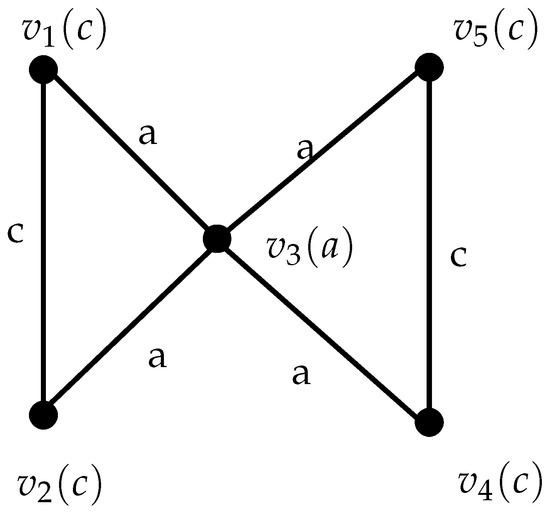
Let $S=(\left\{0,a,b,c\right\},+,·)$ be a semiring as in the Example 3.

In $G^S$ in Figure 4$,$${\delta }_S\left(G^S\right)=(c,2),{\kappa }_E^S\left(G^S\right)=(b,2)$ and ${\kappa }_V^S\left(G^S\right)=(a,1).$

Figure 4. Semiring Valued Graph $G^S$.

Thus, we have the inequality (1), and ${\kappa }_V^S\left(G^S\right)⪯{\kappa }_E^S\left(G^S\right)⪯{\delta }_S\left(G^S\right)$ holds.

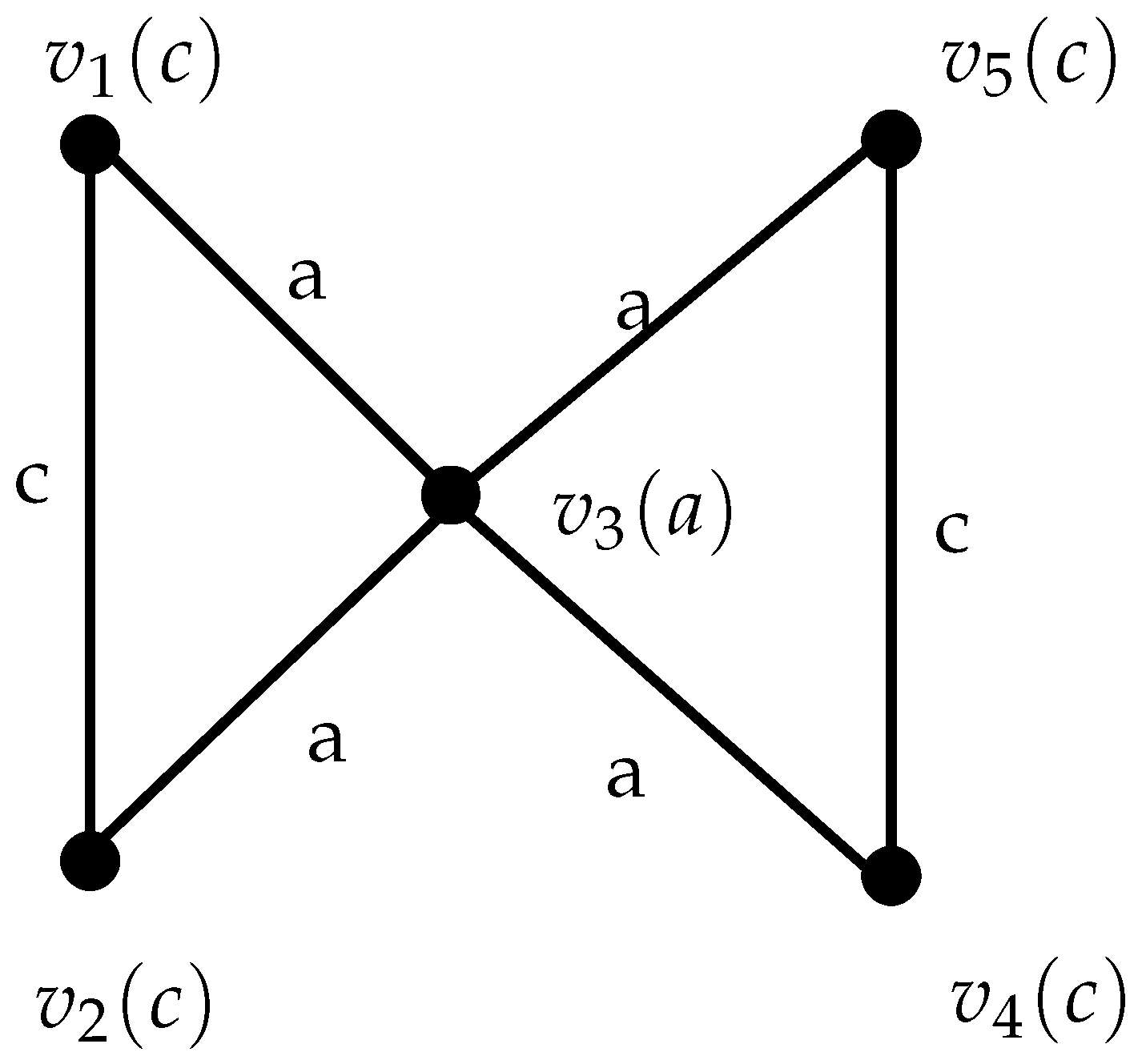
Example 5.

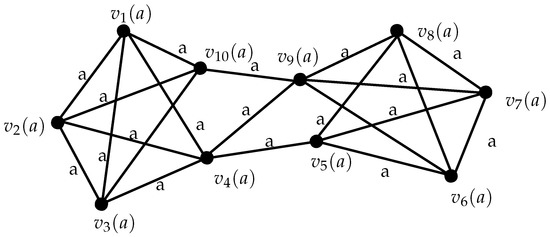
Let $S=(\left\{0,a,b,c\right\},+,·)$ be a semiring as in the Example 3.

In the graph $G^S$ given in Figure 5$,$ we can see ${\kappa }_V^S\left(G^S\right)=(a+a,2),{\kappa }_E^S\left(G^S\right)=(a+a+a,3)$ and ${\delta }_S\left(G^S\right)=(a+a+a+a,4)$, that is, ${\kappa }_V^S\left(G^S\right)=(b,2),{\kappa }_E^S\left(G^S\right)=(c,3)$ and ${\delta }_S\left(G^S\right)=(c,4).$ Thus, for this graph, the inequality ${\kappa }_V^S\left(G^S\right)⪯{\kappa }_E^S\left(G^S\right)⪯{\delta }_S\left(G^S\right)$ holds.

Figure 5. Semiring Valued Graph $G^S$.

Consider the S-valued graph $G^S$ given in Example 3; the inequality (1) fails for $G^S,$ as it is not S-vertex-regular. However, Examples 4 and 5 reveal that for some S-valued graphs, and in particular for S-vertex regular graphs, the inequality holds. We can generalize Example 5 for any S-vertex regular graphs, yielding the following:

Theorem 7.

For any S-vertex regular graph $G^S=(V_S,E_S),$ the inequality

$${\kappa }_V^S\left(G^S\right)⪯{\kappa }_E^S\left(G^S\right)⪯{\delta }_S\left(G^S\right)$$

holds.

Proof. 

The proof follows from the definition of S-vertex regular, vertex S-connectivity and edge S-connectivity of the S-valued graph.

For, in a S-vertex regular graph $G^S$ every vertex as well as edge will have the same S-value. However, the vertex S-connectivity edge S-connectivity depends on the number of vertices and edges to be removed which cannot exceed the minimum degree of the graph. □

5. Conclusions

In this paper, we have studied the vertex S-connectivity and the edge S-connectivity of semiring valued graphs. We observed through some examples that the inequality (1) holds when there is some symmetry of the S-valued graph under consideration. This differs from the theory of graphs. Further, we have established that the inequality (1) holds in the case of S-vertex regular graphs. In the future, we have proposed to study the vertex S-connectivity and the edge S-connectivity for different products of semiring valued graphs.