Multivariate Skew t-Distribution: Asymptotics for Parameter Estimators and Extension to Skew t-Copula

Abstract

Symmetric elliptical distributions have been intensively used in data modeling and robustness studies. The area of applications was considerably widened after transforming elliptical distributions into the skew elliptical ones that preserve several good properties of the corresponding symmetric distributions and increase possibilities of data modeling. We consider three-parameter p-variate skew t-distribution where p-vector $\mathbf{\mu }$ is the location parameter, $\mathsf{\Sigma }:p\times p$ is the positive definite scale parameter, p-vector $\mathbf{\alpha }$ is the skewness or shape parameter, and the number of degrees of freedom $\nu$ is fixed. Special attention is paid to the two-parameter distribution when $\mathbf{\mu }=\mathbf{0}$ that is useful for construction of the skew t-copula. Expressions of the parameters are presented through the moments and parameter estimates are found by the method of moments. Asymptotic normality is established for the estimators of $\mathsf{\Sigma }$ and $\mathbf{\alpha }$. Convergence to the asymptotic distributions is examined in simulation experiments.

1. Introduction

The idea of constructing multivariate skewed distributions from symmetric elliptical distributions has attracted many statisticians over last 25 years. This generalization preserves several good properties of corresponding symmetric distributions and in the same time increases possibilities of data modeling. In 1996, Azzalini and Dalla Valle introduced multivariate skew normal distribution [1]. Their idea of transforming multivariate normal distribution into a skewed distribution has been carried over to several other distributions and many generalizations have been made since 1996 (see for instance, Theodossiou [2], Arellano-Valle and Genton [3]). From these developments multivariate skew t-distribution has become most frequently used [4]. This distribution became an important tool in many data modeling applications because of heavier tail area than the normal and skew normal distributions (see, for instance, Lee and McLachan [5], Marchenko [6], Parisi and Liseo [7], Fernandez and Steel [8], Jones [9]). A review of applications in finance and insurance mathematics is given in Adcock et al. [10]. Multivariate skew t-distribution has also been successfully used as a data model in environmental studies and modelling coastal floodings (Ghizzolini et al. [11], Thompson and Shen [12]). Several other applications of skew elliptical distributions can be found in the collective monograph edited by Genton [13] and in the book by Azzalini and Capitanio [14] which includes a comprehensive list of references on the topic. Another useful property that makes multivariate t-distribution and skew t-distribution attractive in financial and actuarial applications is the possibility to take tail dependence between marginals into account. Tail dependence of multivariate t- and skew t-distributions has been intensively studied in recent years, see Fung and Seneta [15] or Joe and Li [16], for example. In Kollo et al. [17] it is shown that the upper tail dependence coefficient of the skew t-distribution can be several times bigger than the corresponding value of multivariate t-distribution. Moments and inferential aspects related to the multivariate skew t-distribution have been also actively studied in Padoan [18], Galarza et al. [19], Zhou and He [20], Lee and McLachlan [5], DiCiccio and Monti [21], for instance. A construction based on the skew t-distribution—skew t-copula—has made this distribution even more attractive in applications where correlated differently distributed marginals are joined into a multivariate distribution. Demarta and McNeil introduced skew t-copula based on multivariate generalized hyperbolic distribution [22], Kollo and Pettere [23] defined skew t-copula on the basis of the multivariate skew t-distribution following Azzalini and Capitanio [4].

The paper is organized as follows. In Section 2, we introduce necessary notation and notions from matrix algebra. In Section 3, skew t-distribution is defined through skew normal and inverse $\chi$-distribution and the first four central moments are found via the moments of skew normal and inverse $\chi$-distribution. The asymptotic normality for parameter estimators in the two-parameter case is also established in this section. In Section 4, obtained analytical results are illustrated by simulations for different scenarios and the speed of convergence to asymptotic distribution is also addressed. In Section 5, multivariate skew t-copula is defined and some properties are discussed. Technical proofs are presented in Appendix A. A comparison of density contours of Gaussian, skew normal and skew t-copula is presented in Supplementary Materials.

2. Notation and Preliminaries

To derive asymptotic normal distribution for the parameter estimators of skew t-distribution, we use matrix technique. Necessary notions and notation are presented in what follows.

Let us first denote the moments of a random vector $\mathbf{x}$ in the following matrix representation:

$$m_k\left(\mathbf{x}\right)=E\left[\underset{k\mathrm{times}}{\underbrace{\mathbf{x}\otimes {\mathbf{x}}^{\prime }\otimes \mathbf{x}\otimes {\mathbf{x}}^{\prime }\otimes \dots }}\right]=E\left[\mathbf{x}{\mathbf{x}}^{\prime }\otimes \mathbf{x}{\mathbf{x}}^{\prime }\otimes \dots \right].$$

The corresponding central moment is

$${\overline{m}}_k\left(\mathbf{x}\right)=m_k(\mathbf{x}-E\mathbf{x}).$$

We use notions $\mathrm{vec}$-operator, commutation matrix, Kronecker product, matrix derivative and their properties. For deeper insight into this technique we refer to Magnus and Neudecker [24], or Kollo and von Rosen [25]. If $\mathbf{A}$ is a $p\times q$ matrix, $\mathbf{A}=({\mathbf{a}}_1,\dots ,{\mathbf{a}}_q)$, the $pq$ column vector $\mathrm{vec}\mathbf{A}$ is formed by stacking the columns ${\mathbf{a}}_i$ under each other; that is

$$\mathrm{vec}\mathbf{A}=\left(\begin{array}{c}{\mathbf{a}}_1\\ \dots \\ {\mathbf{a}}_q\end{array}\right).$$

We denote a $p\times p$ identity matrix by ${\mathbf{I}}_p$ and a $pq\times pq$ commutation matrix by ${\mathbf{K}}_{p,q}$. Commutation matrix ${\mathbf{K}}_{p,q}$ is an orthogonal $pq\times pq$ partitioned matrix consisting of $q\times p$ blocks with the property

$${\mathbf{K}}_{p,q}\mathrm{vec}\mathbf{A}=\mathrm{vec}{\mathbf{A}}^{\prime }$$

where $\mathbf{A}$ is a $p\times q$-matrix. The Kronecker product $\mathbf{A}\otimes \mathbf{B}$ of a $p\times q$ matrix $\mathbf{A}$ and an $r\times s$ matrix $\mathbf{B}$ is a $pr\times qs$ partitioned matrix consisting of the $r\times s$ blocks

$$\mathbf{A}\otimes \mathbf{B}=\left[a_{ij}\mathbf{B}\right],i=1,\dots ,p;j=1,\dots ,q.$$

The following properties of the notions above are repeatedly used. It is assumed that the dimensions of the matrices match with the operations.

1.

$(\mathbf{A}\otimes \mathbf{B})(\mathbf{C}\otimes \mathbf{D})=\left(\mathbf{A}\mathbf{C}\right)\otimes \left(\mathbf{B}\mathbf{D}\right)$;

2.

$\mathbf{a}{\mathbf{b}}^{\prime }=\mathbf{a}\otimes {\mathbf{b}}^{\prime }={\mathbf{b}}^{\prime }\otimes \mathbf{a}$;

3.

$\mathrm{vec}\left(\mathbf{A}\mathbf{B}\mathbf{C}\right)=({\mathbf{C}}^{\prime }\otimes \mathbf{A})\mathrm{vec}\mathbf{B}$;

4.

${\mathbf{K}}_{p,1}={\mathbf{I}}_p,{\mathbf{K}}_{1,q}={\mathbf{I}}_q;$

5.

for $\mathbf{A}:p\times q$ and $\mathbf{B}:r\times s$, $\mathbf{A}\otimes \mathbf{B}={\mathbf{K}}_{p,r}(\mathbf{B}\otimes \mathbf{A}){\mathbf{K}}_{s,q}.$

Further, when deriving asymptotic distributions of the estimators of $\mathsf{\Sigma }$ and $\mathbf{\alpha }$ in Section 3, we use the matrix derivative where partial derivatives $\frac{\partial y_{kl}}{\partial x_{ij}}$ are ordered by the Kronecker product (see Magnus and Neudecker, [24])

$$\frac{d\mathbf{Y}}{d\mathbf{X}}=\frac{d}{d\mathrm{vec}{}^{\prime }\mathbf{X}}\otimes \mathrm{vec}\mathbf{Y},$$

with $\mathbf{X}:p\times q$ and $\mathbf{Y}=\mathbf{Y}\left(\mathbf{X}\right):r\times s$. It follows from the definition that

$$\frac{d\mathbf{Y}}{d\mathbf{X}}=\frac{d\mathrm{vec}\mathbf{Y}}{d\mathrm{vec}{}^{\prime }\mathbf{X}}=\frac{d\mathrm{vec}\mathbf{Y}}{d\mathbf{X}}=\frac{d\mathbf{Y}}{d\mathrm{vec}{}^{\prime }\mathbf{X}}.$$

The main properties of the matrix derivative are listed below.

(1)

$\frac{d\mathbf{X}}{d\mathbf{X}}={\mathbf{I}}_{pq}$;

(2)

$\frac{d(\mathbf{Y}+\mathbf{Z})}{d\mathbf{X}}=\frac{d\mathbf{Y}}{d\mathbf{X}}+\frac{d\mathbf{Z}}{d\mathbf{X}}$, $\mathbf{Z}=\mathbf{Z}\left(\mathbf{X}\right):r\times s$;

(3)

$\frac{d\mathbf{A}\mathbf{X}\mathbf{B}}{d\mathbf{X}}={\mathbf{B}}^{\prime }\otimes \mathbf{A}$;

(4)

If $\mathbf{Z}=\mathbf{Z}\left(\mathbf{Y}\right)$, $\mathbf{Y}=\mathbf{Y}\left(\mathbf{X}\right)$ then $\frac{d\mathbf{Z}}{d\mathbf{X}}=\frac{d\mathbf{Z}}{d\mathbf{Y}}\frac{d\mathbf{Y}}{d\mathbf{X}}$;

(5)

If $\mathbf{W}=\mathbf{Y}\mathbf{Z}$, $\mathbf{Z}=\mathbf{Z}\left(\mathbf{X}\right):s\times t$ then

$\frac{d\mathbf{W}}{d\mathbf{X}}=({\mathbf{Z}}^{\prime }\otimes {\mathbf{I}}_r)\frac{d\mathbf{Y}}{d\mathbf{X}}+({\mathbf{I}}_t\otimes \mathbf{Y})\frac{d\mathbf{Z}}{d\mathbf{X}}$;

(6)

If $\mathbf{X}:p\times p$ then $\frac{d{\mathbf{X}}^{-1}}{d\mathbf{X}}=-{\left({\mathbf{X}}^{\prime }\right)}^{-1}\otimes {\mathbf{X}}^{-1}$;

(7)

If $\mathbf{X}\in {\mathbb{R}}^{p\times p}$ then $\frac{d\left|\mathbf{X}\right|}{d\mathbf{X}}=\left|\mathbf{X}\right|\mathrm{vec}{\left({\mathbf{X}}^{-1}\right)}^{\prime }$, where $|·|$ denotes the determinant;

(8)

If $\mathbf{W}=\mathbf{Y}\otimes \mathbf{Z}$, $\mathbf{Z}=\mathbf{Z}\left(\mathbf{X}\right):m\times n$, then

$\frac{d\mathbf{W}}{d\mathbf{X}}=({\mathbf{I}}_s\otimes {\mathbf{K}}_{r,n}\otimes {\mathbf{I}}_m)\left[({\mathbf{I}}_{rs}\otimes \mathrm{vec}\mathbf{Z})\frac{d\mathbf{Y}}{d\mathbf{X}}+(\mathrm{vec}\mathbf{Y}\otimes {\mathbf{I}}_{mn})\frac{d\mathbf{Z}}{d\mathbf{X}}\right]$.

(9)

If $y=y\left(\mathbf{X}\right)$, $\mathbf{Z}=\mathbf{Z}\left(\mathbf{X}\right):m\times n$, then

$\frac{d\left(y\mathbf{Z}\right)}{d\mathbf{X}}=\mathrm{vec}\mathbf{Z}\frac{dy}{d\mathbf{X}}+y\frac{d\mathbf{Z}}{d\mathbf{X}}$.

3. Multivariate Skew $t_{\nu }$-Distribution

3.1. Definition

Multivariate skew t-distribution has been defined in different ways, see Kotz and Nadarajah [26] (Chapter 5). Kshirsagar [27] was the first to introduce a noncentral multivariate t-distribution, but the density expression was complicated and the distribution was not used in applications. From more recent definitions we refer to Fang et al. [28], but as the marginals in their definition have different degrees of freedom, the distribution had problems with practical use. Gupta [29] defined the multivariate skew t-distribution in a similar way like Azzalini and Capitanio [4], but their definition had several advantages and has become widely used in applications (for example, it is possible to use explicit expression of the moment generating function of skew normal distribution for calculating moments of skew t-distribution). We follow the approach by Azzalini and Capitanio [4].

A p-vector $\mathbf{x}$ has multivariate skew t-distribution with $\nu$ degrees of freedom if it is the ratio of a p-variate skew normal vector and a chi-distributed random variable with $\nu$ degrees of freedom. We have slightly modified their definition of the skew normal vector and use the covariance matrix as a parameter instead of the correlation matrix. Let $\mathbf{y}$ be a p-variate skew normal vector with density

$$f\left(\mathbf{y}\right)=2f_{N_p(\mathbf{0},\mathsf{\Sigma })}\left(\mathbf{y}\right)\mathsf{\Phi }\left({\mathbf{\alpha }}^{\prime }\mathbf{y}\right),$$

(1)

where $f_{N_p(\mathbf{0},\mathsf{\Sigma })}\left(\mathbf{y}\right)$ is the density function (density) of the p-variate normal distribution $N_p(\mathbf{0},\mathsf{\Sigma })$ and $\mathsf{\Phi }(·)$ is the cumulative distribution function (distribution function) of $N(0,1)$. Denote the distribution of vector $\mathbf{y}$ with density (1) by $\mathbf{y}\sim S{N}_p(\mathsf{\Sigma },\mathbf{\alpha })$, where $\mathsf{\Sigma }:p\times p$ is the scale parameter and $\mathbf{\alpha }\in {\mathbb{R}}^p$ is the shape or skewing parameter.

Definition 1. 

Let $\mathbf{y}$ be skew normally distributed with density (1) and let Z be χ-distributed with ν degrees of freedom, independent from $\mathbf{y}$. Then

$$\mathbf{x}=\mathbf{\mu }+\sqrt{\nu }\frac{\mathbf{y}}{Z}$$

(2)

is skew $t_{\nu }$-distributed, $\mathbf{x}\sim S{t}_{\nu }(\mathbf{\mu },\mathsf{\Sigma },\mathbf{\alpha })$.

The density function of $\mathbf{x}\sim S{t}_{\nu }(\mathbf{\mu },\mathsf{\Sigma },\mathbf{\alpha })$ is of the form (a modification of Azzalini and Capitanio [4])

$$f_{\mathbf{x}}\left(\mathbf{x}\right)=2f_{\nu ,p}\left(\mathbf{x}\right)F_{p+\nu }\left({\mathbf{\alpha }}^{\prime }(\mathbf{x}-\mathbf{\mu })\sqrt{\frac{p+\nu }{Q+\nu }}\right),$$

where $Q={(\mathbf{x}-\mathbf{\mu })}^{\prime }{\mathsf{\Sigma }}^{-1}(\mathbf{x}-\mathbf{\mu })$, $F_k$ is the distribution function of the univariate t-distribution with k degrees of freedom and $f_{\nu ,p}$ is the density function of the p-variate t-distribution with $\nu$ degrees of freedom and scale matrix $\mathsf{\Sigma }$

$$f_{\nu ,p}\left(\mathbf{x}\right)=\frac{\mathsf{\Gamma }\left(\frac{\nu +p}{2}\right)}{{\left(\nu \pi \right)}^{p/2}\mathsf{\Gamma }\left(\frac{\nu }{2}\right){\left|\mathsf{\Sigma }\right|}^{1/2}}{\left[1+\frac{{(\mathbf{x}-\mathbf{\mu })}^{\prime }{\mathsf{\Sigma }}^{-1}(\mathbf{x}-\mathbf{\mu })}{\nu }\right]}^{-\frac{\nu +p}{2}}.$$

3.2. Moments

By Formula (2), a skew t-distributed $\mathbf{x}$ is constructed using independent skew normal random vector $\mathbf{y}$ and $\chi$-distributed Z. Because of the independence of $\mathbf{y}$ and Z, the moments of $\mathbf{x}$ can be found as products of the moments of the skew normal and inverse $\chi$-distribution. The k-th moment, central moment and cumulant of a skew-normal random vector $\mathbf{y}$ are denoted by $m_k\left(\mathbf{y}\right)$, ${\overline{m}}_k\left(\mathbf{y}\right)$ and $c_k\left(\mathbf{y}\right)$, respectively. Explicit expressions of the raw moments, central moments and cumulants of $\mathbf{y}$ can be obtained by differentiating the moment generating function

$$M\left(\mathbf{t}\right)=2e^{\frac{1}{2}{\mathbf{t}}^{\prime }\mathsf{\Sigma }\mathbf{t}}\mathsf{\Phi }\left(\frac{{\mathbf{\alpha }}^{\prime }\mathsf{\Sigma }\mathbf{t}}{\sqrt{1+{\mathbf{\alpha }}^{\prime }\mathsf{\Sigma }\mathbf{\alpha }}}\right)$$

and the cumulant generating function

$$C\left(\mathbf{t}\right)=lnM\left(\mathbf{t}\right).$$

The first four cumulants for a skew-normal random vector $\mathbf{y}$ are (Kollo et al. [30])

$$c_1\left(\mathbf{y}\right)=E\mathbf{y}=\sqrt{\frac{2}{\pi }}\delta ,c_2\left(\mathbf{y}\right)=D\mathbf{y}=\mathsf{\Sigma }-\frac{2}{\pi }\delta {\delta }^{\prime },$$

(3)

$$c_3\left(\mathbf{y}\right)={\overline{m}}_3\left(\mathbf{y}\right)=\sqrt{\frac{2}{\pi }}\left(\frac{4}{\pi }-1\right)\delta \otimes {\delta }^{\prime }\otimes \delta ,$$

(4)

$$c_4\left(\mathbf{y}\right)=\frac{8}{\pi }\left(1-\frac{3}{\pi }\right)\delta \otimes {\delta }^{\prime }\otimes \delta \otimes {\delta }^{\prime },$$

where $\delta$ equals

$$\delta =\frac{\mathsf{\Sigma }\mathbf{\alpha }}{\sqrt{1+{\mathbf{\alpha }}^{\prime }\mathsf{\Sigma }\mathbf{\alpha }}}.$$

(5)

From general relation between the fourth order cumulants and central moments we have (see, e.g., Kollo and von Rosen [25] (p. 187))

$${\overline{m}}_4\left(\mathbf{y}\right)=c_4\left(\mathbf{y}\right)+({\mathbf{I}}_{p^2}+K_{p,p})(D\mathbf{y}\otimes D\mathbf{y})+\mathrm{vec}\left(D\mathbf{y}\right)\mathrm{vec}{}^{\prime }\left(D\mathbf{y}\right).$$

(6)

After some algebra, we get the expression for $\mathbf{\alpha }$ from (5):

$$\mathbf{\alpha }=\frac{{\mathsf{\Sigma }}^{-1}\delta }{\sqrt{1-{\delta }^{\prime }{\mathsf{\Sigma }}^{-1}\delta }}.$$

(7)

The quantity under square root in (7) influences the stability of parameter estimates and will be used later in a related discussion. Thus, we add a notation for it:

$$\eta =1-{\delta }^{\prime }{\mathsf{\Sigma }}^{-1}\delta .$$

(8)

Note also that each component ${\delta }_i$ in vector $\delta ={({\delta }_1,\dots ,{\delta }_p)}^{\prime }$ is directly connected to the corresponding marginal distribution, whereas this property does not hold for vector $\mathbf{\alpha }={({\mathbf{\alpha }}_1,\dots ,{\mathbf{\alpha }}_p)}^{\prime }$. For a more comprehensive discussion on parametrizations of skew-normal vector see Käärik et al. [31].

To derive the central moments of the multivariate skew $t_{\nu }$-distribution, we also need the moments of the skew normally distributed vector $\mathbf{y}$

$$m_2\left(\mathbf{y}\right)=\mathsf{\Sigma };$$

(9)

$$m_3\left(\mathbf{y}\right)=\sqrt{\frac{2}{\pi }}(\mathrm{vec}\mathsf{\Sigma }{\delta }^{\prime }+\delta \otimes \mathsf{\Sigma }+\mathsf{\Sigma }\otimes \delta -\delta {\delta }^{\prime }\otimes \delta ).$$

(10)

Recall that a random variable $V_{\nu }=\frac{1}{Z}$ is inverse ${\chi }_{\nu }$-distributed if its probability density function is (Lee [32] (p. 378))

$$f\left(x\right)=\frac{1}{2^{\nu /2-1}\mathsf{\Gamma }\left(\frac{\nu }{2}\right)}{x}^{-\nu -1}exp\left(-\frac{1}{2x^2}\right).$$

The moments of the inverse ${\chi }_{\nu }$-distribution can be obtained by integration.

Lemma 1. 

The moments of the inverse ${\chi }_{\nu }$-distribution are:

$$\begin{array}{cc}\hfill E{V}_{\nu }& =\frac{\mathsf{\Gamma }\left(\frac{\nu -1}{2}\right)}{\sqrt{2}\mathsf{\Gamma }\left(\frac{\nu }{2}\right)},\nu >1;\hfill \\ \hfill E{V}_{\nu }^k& =\frac{\mathsf{\Gamma }\left(\frac{\nu -k}{2}\right)}{2^{k/2}\mathsf{\Gamma }\left(\frac{\nu }{2}\right)},\nu >k.\hfill \end{array}$$

Proof. 

By standard integration technique, we can derive the expectation:

$$\begin{array}{cc}\hfill E{V}_{\nu }& ={\int }_0^{\infty }x\frac{1}{2^{\nu /2-1}\mathsf{\Gamma }\left(\frac{\nu }{2}\right)}{x}^{-\nu -1}exp\left(-\frac{1}{2x^2}\right)dx\hfill \\ \hfill & =\frac{1}{\mathsf{\Gamma }\left(\frac{\nu }{2}\right)}{\int }_0^{\infty }\frac{\mathsf{\Gamma }\left(\frac{\nu -1}{2}\right)}{2^{\frac{\nu -1}{2}-1}\sqrt{2}\mathsf{\Gamma }\left(\frac{\nu -1}{2}\right)}{x}^{-\nu }exp\left(-\frac{1}{2x^2}\right)dx=\frac{\mathsf{\Gamma }\left(\frac{\nu -1}{2}\right)}{\mathsf{\Gamma }\left(\frac{\nu }{2}\right)\sqrt{2}}.\hfill \end{array}$$

Following the same approach, the k-th order moment can be derived as follows

$$\begin{array}{cc}\hfill E{V}_{\nu }^k& ={\int }_0^{\infty }{x}^k\frac{1}{2^{\nu /2-1}\mathsf{\Gamma }\left(\frac{\nu }{2}\right)}{x}^{-\nu -1}exp\left(-\frac{1}{2x^2}\right)dx\hfill \\ \hfill & =\frac{2^{\frac{\nu -1}{2}-1}\mathsf{\Gamma }\left(\frac{\nu -1}{2}\right)}{2^{\frac{\nu }{2}-1}\mathsf{\Gamma }\left(\frac{\nu }{2}\right)}{\int }_0^{\infty }\frac{1}{2^{\frac{\nu -1}{2}-1}\mathsf{\Gamma }\left(\frac{\nu -1}{2}\right)}{x}^{-(\nu -1)-1}{x}^{k-1}exp\left(-\frac{1}{2x^2}\right)dx\hfill \\ \hfill & =\prod _{i=0}^{k-1}E{V}_{\nu -i}=\frac{\mathsf{\Gamma }\left(\frac{\nu -k}{2}\right)}{2^{\frac{k}{2}}\mathsf{\Gamma }\left(\frac{\nu }{2}\right)},\nu >k.\hfill \end{array}$$

□

The expressions of the second, third and fourth moment are special cases of this result:

$$E{V}_{\nu }^2=\frac{1}{\nu -2},\nu >2;$$

$$E{V}_{\nu }^3=\frac{E{V}_{\nu }}{\nu -3},\nu >3;$$

$$E{V}_{\nu }^4=\frac{1}{(\nu -2)(\nu -4)},\nu >4.$$

After some elementary algebra we get expressions of the corresponding central moments

$${\overline{m}}_3\left(V_{\nu }\right)=E{V}_{\nu }\left(\frac{7-2\nu }{(\nu -3)(\nu -2)}+2{\left(E{V}_{\nu }\right)}^2\right);$$

$${\overline{m}}_4\left(V_{\nu }\right)=\frac{1}{(\nu -2)(\nu -4)}+2\frac{\nu -5}{(\nu -2)(\nu -3)}{\left(E{V}_{\nu }\right)}^2-3{\left(E{V}_{\nu }\right)}^4.$$

To keep the notation simpler, we denote $V=V_{\nu }$.

In order to derive the asymptotic normality for parameter estimators of $S{t}_{\nu }$, we need the first 4 central moments of the distribution. Let us start with general expressions for central moments ${\overline{m}}_3\left(\mathbf{x}\right)$ and ${\overline{m}}_4\left(\mathbf{x}\right)$.

Lemma 2. 

Let $\mathbf{x}$ be a p-dimensional random vector with finite fourth order moments. Then the third and fourth central moment of $\mathbf{x}$ can be expressed as follows:

$$\begin{array}{cc}\hfill {\overline{m}}_3\left(\mathbf{x}\right)& =m_3\left(\mathbf{x}\right)-({\mathbf{I}}_{p^2}+{\mathbf{K}}_{p,p})(m_2\left(\mathbf{x}\right)\otimes E\mathbf{x})-\mathrm{vec}{m}_2\left(\mathbf{x}\right)E{\mathbf{x}}^{\prime }+2E\mathbf{x}E{\mathbf{x}}^{\prime }\otimes E\mathbf{x},\hfill \\ \hfill {\overline{m}}_4\left(\mathbf{x}\right)& =m_4\left(\mathbf{x}\right)-\mathbf{C}\left(\mathbf{x}\right)({\mathbf{I}}_{p^2}+{\mathbf{K}}_{p,p})-({\mathbf{I}}_{p^2}+{\mathbf{K}}_{p,p}){\left(\mathbf{C}\left(\mathbf{x}\right)\right)}^{\prime }-3E\mathbf{x}E{\mathbf{x}}^{\prime }\otimes E\mathbf{x}E{\mathbf{x}}^{\prime }\hfill \\ \hfill & +({\mathbf{I}}_{p^2}+{\mathbf{K}}_{p,p})\mathbf{A}\left(\mathbf{x}\right)+\mathbf{A}\left(\mathbf{x}\right){\mathbf{K}}_{p,p}+\mathbf{B}\left(\mathbf{x}\right)+{(\mathbf{A}\left(\mathbf{x}\right)+\mathbf{B}\left(\mathbf{x}\right))}^{\prime },\hfill \end{array}$$

where

$$\mathbf{A}\left(\mathbf{x}\right)=E{\mathbf{x}}^{\prime }\otimes m_2\left(\mathbf{x}\right)\otimes E\mathbf{x};\mathbf{B}\left(\mathbf{x}\right)=E{\mathbf{x}}^{\prime }\otimes \mathrm{vec}{m}_2\left(\mathbf{x}\right)\otimes E{\mathbf{x}}^{\prime };\mathbf{C}\left(\mathbf{x}\right)=m_3\left(\mathbf{x}\right)\otimes E{\mathbf{x}}^{\prime }.$$

Proof of the lemma is presented in Appendix A.1. Applying this lemma to skew t-distributed $\mathbf{x}$, the next result follows.

Lemma 3. 

Let $\mathbf{x}\sim S{t}_{\nu }(\mathbf{\mu },\mathsf{\Sigma },\mathbf{\alpha })$. Then its mean $E\mathbf{x}$, covariance matrix $D\mathbf{x}$, and central moments ${\overline{m}}_3\left(\mathbf{x}\right)$ and ${\overline{m}}_4\left(\mathbf{x}\right)$ can be expressed through the moments of inverse ${\chi }_{\nu }$-distributed V and $\mathbf{y}\sim S{N}_p(\mathsf{\Sigma },\mathbf{\alpha })$ in the following form:

$$E\mathbf{x}=\mathbf{\mu }+\sqrt{\nu }EVE\mathbf{y};$$

(11)

$$D\mathbf{x}=\nu m_2\left(V\right)m_2\left(\mathbf{y}\right)-E\mathbf{x}E{\mathbf{x}}^{\prime }=\nu (m_2\left(V\right)D\mathbf{y}+DVE\mathbf{y}E{\mathbf{y}}^{\prime });$$

(12)

$$\begin{array}{cc}\hfill & {\overline{m}}_3\left(\mathbf{x}\right)={\nu }^{3/2}\{E{V}^3{\overline{m}}_3\left(\mathbf{y}\right)-2(E{V}^3-{\left(EV\right)}^3)(E\mathbf{y}E{\mathbf{y}}^{\prime }\otimes E\mathbf{y})\hfill \\ \hfill & +(E{V}^3-EVE{V}^2)[({\mathbf{I}}_{p^2}+{\mathbf{K}}_{p,p})(m_2\left(\mathbf{y}\right)\otimes E\mathbf{y})+\mathrm{vec}{m}_2\left(\mathbf{y}\right)E{\mathbf{y}}^{\prime }]\};\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill {\overline{m}}_4\left(\mathbf{x}\right)& ={\nu }^2\{E{V}^4{\overline{m}}_4\left(\mathbf{y}\right)+(E{V}^4-EVE{V}^3)(\mathbf{C}\left(\mathbf{y}\right)({\mathbf{I}}_{p^2}+{\mathbf{K}}_{p,p})+({\mathbf{I}}_{p^2}+{\mathbf{K}}_{p,p})\mathbf{C}{\left(\mathbf{y}\right)}^{\prime })\hfill \\ \hfill & +3(E{V}^4-{\left(EV\right)}^4)E\mathbf{y}E{\mathbf{y}}^{\prime }\otimes E\mathbf{y}E{\mathbf{y}}^{\prime }\hfill \\ \hfill & -(E{V}^4-E{V}^2{\left(EV\right)}^2)[({\mathbf{I}}_{p^2}+{\mathbf{K}}_{p,p})\mathbf{A}\left(\mathbf{y}\right)+\mathbf{A}\left(\mathbf{y}\right){\mathbf{K}}_{p,p}+\mathbf{B}\left(\mathbf{y}\right)+{(\mathbf{A}\left(\mathbf{y}\right)+\mathbf{B}\left(\mathbf{y}\right))}^{\prime }]\}.\hfill \end{array}$$

(14)

Proof is straightforward and follows from Lemma 2 after substituting in the required moments of skew normal distribution from Formulas (9) and (10) and the moments of inverse $\chi$-distribution given in Lemma 1.

3.3. Point Estimates

Let us now focus on the case when $\mathbf{\mu }=\mathbf{0}$ and estimate the parameters of the two-parameter distribution $S{t}_{\nu }(\mathsf{\Sigma },\mathbf{\alpha })$ using the method of moments.

Let us have a sample of size n, $n>p$, from $S{t}_{\nu }(\mathsf{\Sigma },\mathbf{\alpha })$ with sample mean $\overline{\mathbf{x}}$ and unbiased sample covariance matrix $\mathbf{S}$. Now, the estimates for parameters $\mathsf{\Sigma }$ and $\mathbf{\alpha }$ through the moments of V and $\mathbf{y}$ can be obtained from Expressions (11) and (12):

$$E\mathbf{x}=\frac{\mathsf{\Gamma }\left(\frac{\nu -1}{2}\right)}{\mathsf{\Gamma }\left(\frac{\nu }{2}\right)}\sqrt{\frac{\nu }{\pi }}\delta ,$$

$$D\mathbf{x}=\nu \left[\frac{1}{\nu -2}\mathsf{\Sigma }-{\left(\frac{\mathsf{\Gamma }\left(\frac{\nu -1}{2}\right)}{\mathsf{\Gamma }\left(\frac{\nu }{2}\right)}\right)}^2\frac{1}{\pi }\delta {\delta }^{\prime }\right],$$

where $\delta$ is defined in (5). From here we get the following estimates

$$\widehat{\mathsf{\Sigma }}=\frac{\nu -2}{\nu }\left(\mathbf{S}+\overline{\mathbf{x}}{\overline{\mathbf{x}}}^{\prime }\right);$$

(15)

$$\widehat{\mathbf{\alpha }}=\frac{\frac{\nu }{\nu -2}{(\mathbf{S}+\overline{\mathbf{x}}{\overline{\mathbf{x}}}^{\prime })}^{-1}\overline{\mathbf{x}}}{\sqrt{\frac{\nu }{\pi }{\left(\frac{\mathsf{\Gamma }\left(\frac{\nu -1}{2}\right)}{\mathsf{\Gamma }\left(\frac{\nu }{2}\right)}\right)}^2-\frac{\nu }{\nu -2}{\overline{\mathbf{x}}}^{\prime }{(\mathbf{S}+\overline{\mathbf{x}}\overline{\mathbf{x}})}^{-1}\overline{\mathbf{x}}}}.$$

(16)

3.4. Asymptotic Normality

As the estimators depend on both, the sample mean and the sample covariance matrix, we need their joint distribution to find the asymptotic distributions of the parameter estimators. In general, the following convergence in distribution takes place for $\left(\begin{array}{c}\overline{\mathbf{x}}\\ \mathrm{vec}\mathbf{S}\end{array}\right)$ if ${\overline{m}}_4\left(\mathbf{x}\right)$ exists (Parring [33]):

$$\sqrt{n}\left[\left(\begin{array}{c}\overline{\mathbf{x}}\\ \mathrm{vec}\mathbf{S}\end{array}\right)-E\left(\begin{array}{c}\overline{\mathbf{x}}\\ \mathrm{vec}\mathbf{S}\end{array}\right)\right]\stackrel{D}{⟶}N(\mathbf{0},{\mathbf{D}}_{as}),$$

where

$${\mathbf{D}}_{as}=\left(\begin{array}{ccc}D\mathbf{x}& ⋮& {\overline{m}}_3{\left(\mathbf{x}\right)}^{\prime }\\ {\overline{m}}_3\left(\mathbf{x}\right)& ⋮& {\overline{m}}_4\left(\mathbf{x}\right)-\mathrm{vec}\left(D\mathbf{x}\right)\mathrm{vec}{}^{\prime }\left(D\mathbf{x}\right)\end{array}\right).$$

For the asymptotic covariance matrix of the joint distribution of sample mean and covariance matrix from skew t-distribution, ${\mathbf{D}}_{as}^{St}$, we get the expressions of necessary central moments from Equations (12)–(14). Derivation of asymptotic normality for estimators of parameters is based on Theorem 1 by Anderson [34] (pp. 132–133).

Theorem 1. 

Assume that for $\left\{{\mathbf{x}}_n\right\}$

$$\sqrt{n}({\mathbf{x}}_n-\mathbf{a})\stackrel{D}{⟶}{N}_p(\mathbf{0},\mathsf{\Sigma })$$

and

$${\mathbf{x}}_n\stackrel{P}{⟶}\mathbf{a},$$

if $n\to \infty$. Let the function $\mathbf{g}\left(\mathbf{x}\right):{\mathbb{R}}^p\to {\mathbb{R}}^q$ have continuous partial derivatives in a neighborhood of $\mathbf{a}$. Then, if $n\to \infty$

$$\sqrt{n}(\mathbf{g}\left({\mathbf{x}}_n\right)-\mathbf{g}\left(\mathbf{a}\right))\stackrel{D}{⟶}{N}_q(\mathbf{0},\xi \mathsf{\Sigma }{\xi }^{\prime }),$$

where

$$\xi =\frac{d\mathbf{g}\left(\mathbf{x}\right)}{d\mathbf{x}}{|}_{\mathbf{x}=\mathbf{a}}\ne \mathbf{0}$$

is the matrix derivative.

The vector ${({\overline{\mathbf{x}}}^{\prime },\mathrm{vec}{}^{\prime }\mathbf{S})}^{\prime }$ satisfies assumptions of ${\mathbf{x}}_n$ and we consider $\widehat{\mathsf{\Sigma }}$ and $\widehat{\mathbf{\alpha }}$ as the functions of ${({\overline{\mathbf{x}}}^{\prime },\mathrm{vec}{}^{\prime }\mathbf{S})}^{\prime }$ and derive asymptotic normality for the estimators. For $\widehat{\mathsf{\Sigma }}$ the following statement holds.

Theorem 2. 

Let us have a p-vector $\mathbf{x}\sim S{t}_{\nu }(\mathsf{\Sigma },\mathbf{\alpha })$, where ν is fixed. Then, for the estimator $\widehat{\mathsf{\Sigma }}$ in (15), the following convergence takes place, if $n\to \infty$

$$\sqrt{n}\mathrm{vec}(\widehat{\mathsf{\Sigma }}-\mathsf{\Sigma })\stackrel{D}{⟶}{N}_{p^2}(\mathbf{0},{\mathbf{D}}_{as}^{\mathsf{\Sigma }}),$$

where

$${\mathbf{D}}_{as}^{\mathsf{\Sigma }}={\left.\frac{d(\frac{\nu -2}{\nu }(\mathbf{S}+\overline{\mathbf{x}}{\overline{\mathbf{x}}}^{\prime }))}{d({\overline{\mathbf{x}}}^{\prime },\mathrm{vec}{}^{\prime }\mathbf{S})}\right|}_{\mathbf{E}\left(\begin{array}{c}\overline{\mathbf{x}}\\ \mathrm{vec}\mathbf{S}\end{array}\right)}{\mathbf{D}}_{as}^{St}{\left.{\left(\frac{d\left(\frac{\nu -2}{\nu }(\mathbf{S}+\overline{\mathbf{x}}{\overline{\mathbf{x}}}^{\prime })\right)}{d({\overline{\mathbf{x}}}^{\prime },\mathrm{vec}{}^{\prime }\mathbf{S})}\right)}^{\prime }\right|}_{\mathbf{E}\left(\begin{array}{c}\overline{\mathbf{x}}\\ \mathrm{vec}\mathbf{S}\end{array}\right)},$$

the matrix ${\mathbf{D}}_{as}^{St}$ is the asymptotic covariance matrix of $\left(\begin{array}{c}\overline{\mathbf{x}}\\ \mathrm{vec}\mathbf{S}\end{array}\right)$ and the derivative

$${\left.\frac{d(\frac{\nu -2}{\nu }(\mathbf{S}+\overline{\mathbf{x}}{\overline{\mathbf{x}}}^{\prime }))}{d({\overline{\mathbf{x}}}^{\prime },\mathrm{vec}{}^{\prime }\mathbf{S})}\right|}_{\mathbf{E}\left(\begin{array}{c}\overline{\mathbf{x}}\\ \mathrm{vec}\mathbf{S}\end{array}\right)}=\frac{\nu -2}{\nu }\left(({\mathbf{I}}_{p^2}+{\mathbf{K}}_{p,p})\left({\mathbf{I}}_p\otimes \sqrt{\frac{2}{\pi }}\delta \right)⋮{\mathbf{I}}_{p^2}\right).$$

Proof. 

To find the matrix derivative, we can rely on the corresponding expression for the skew normal distribution, derived by Kollo et al. [30] (Proposition 2) as the expression of the derivative for skew t-distribution differs only by a constant.

For $\mathbf{y}\sim S{N}_p(\mathsf{\Sigma },\mathbf{\alpha })$, the derivative of $\widehat{\mathsf{\Sigma }}$ is:

$$\left(({\mathbf{I}}_{p^2}+{\mathbf{K}}_{p,p})\left({\mathbf{I}}_p\otimes \sqrt{\frac{2}{\pi }}\delta \right)⋮{\mathbf{I}}_{p^2}\right).$$

From here, the derivative of $\widehat{\mathsf{\Sigma }}$ for $\mathbf{x}\sim S{t}_{\nu }(\mathsf{\Sigma },\mathbf{\alpha })$ is:

$${\left.\frac{d\widehat{\mathsf{\Sigma }}}{d({\overline{\mathbf{x}}}^{\prime },\mathrm{vec}{}^{\prime }\mathbf{S})}\right|}_{\mathbf{E}\left(\begin{array}{c}\overline{\mathbf{x}}\\ \mathrm{vec}\mathbf{S}\end{array}\right)}=\frac{\nu -2}{\nu }\left(({\mathbf{I}}_{p^2}+{\mathbf{K}}_{p,p})\left({\mathbf{I}}_p\otimes \sqrt{\frac{2}{\pi }}\delta \right)⋮{\mathbf{I}}_{p^2}\right).$$

This completes the proof. □

The proof of asymptotic normality of estimator for parameter $\mathbf{\alpha }$,

$$\sqrt{n}(\widehat{\mathbf{\alpha }}-\mathbf{\alpha })\stackrel{D}{⟶}{N}_p(\mathbf{0},{\mathbf{D}}_{as}^{\mathbf{\alpha }}),$$

is similar. In order to shorten the notation from (16), we define

$$M=\frac{\nu }{\pi }{\left(\frac{\mathsf{\Gamma }\left(\frac{\nu -1}{2}\right)}{\mathsf{\Gamma }\left(\frac{\nu }{2}\right)}\right)}^2-\frac{\nu }{\nu -2}{\overline{\mathbf{x}}}^{\prime }{(\mathbf{S}+\overline{\mathbf{x}}{\overline{\mathbf{x}}}^{\prime })}^{-1}\overline{\mathbf{x}}.$$

(17)

This allows us to express the estimator $\widehat{\mathbf{\alpha }}$ as

$$\widehat{\mathbf{\alpha }}=\frac{{\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}}{\sqrt{M}}.$$

(18)

Theorem 3. 

Let us have a p-vector $\mathbf{x}\sim S{t}_{\nu }(\mathsf{\Sigma },\mathbf{\alpha })$, where ν is fixed. Then, for the estimator $\widehat{\mathbf{\alpha }}$ in (18), the following convergence takes place, if $n\to \infty$

$$\sqrt{n}(\widehat{\mathbf{\alpha }}-\mathbf{\alpha })\stackrel{D}{⟶}{N}_p(\mathbf{0},{\mathbf{D}}_{as}^{\mathbf{\alpha }}),$$

where

$${\mathbf{D}}_{as}^{\mathbf{\alpha }}={\left.\frac{d\widehat{\mathbf{\alpha }}}{d({\overline{\mathbf{x}}}^{\prime },\mathrm{vec}{}^{\prime }\mathbf{S})}\right|}_{\mathbf{E}\left(\begin{array}{c}\overline{\mathbf{x}}\\ \mathrm{vec}\mathbf{S}\end{array}\right)}{\mathbf{D}}_{as}^{St}{\left.{\left(\frac{d\widehat{\mathbf{\alpha }}}{d({\overline{\mathbf{x}}}^{\prime },\mathrm{vec}{}^{\prime }\mathbf{S})}\right)}^{\prime }\right|}_{\mathbf{E}\left(\begin{array}{c}\overline{\mathbf{x}}\\ \mathrm{vec}\mathbf{S}\end{array}\right)},$$

(19)

matrix ${\mathbf{D}}_{as}^{St}$ is the asymptotic covariance matrix and the derivative

$$\frac{d\widehat{\mathbf{\alpha }}}{d({\overline{\mathbf{x}}}^{\prime },\mathrm{vec}{}^{\prime }\mathbf{S})}=\left(\frac{d\widehat{\mathbf{\alpha }}}{d\overline{\mathbf{x}}}⋮\frac{d\widehat{\mathbf{\alpha }}}{d\mathrm{vec}\mathbf{S}}\right),$$

where

$$\frac{d\widehat{\mathbf{\alpha }}}{d\overline{\mathbf{x}}}=M^{-\frac{1}{2}}{\widehat{\mathsf{\Sigma }}}^{-1}\left[\left(1-\frac{\nu -2}{\nu }{\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}\right){\mathbf{I}}_p+M^{-1}\left(\left(1-\frac{\nu -2}{\nu }\left({\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}+M\right)\right)\overline{\mathbf{x}}{\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\right)\right].$$

and

$$\frac{d\widehat{\mathbf{\alpha }}}{d\mathrm{vec}\mathbf{S}}=-\frac{\nu -2}{\nu }{M}^{-\frac{1}{2}}\left[({\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\otimes {\widehat{\mathsf{\Sigma }}}^{-1})+\frac{1}{2}{M}^{-1}({\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}{\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\otimes {\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1})\right].$$

The derivatives in (19) for the asymptotic covariance matrix ${\mathbf{D}}_{as}^{\mathbf{\alpha }}$ are obtained when the estimators $\overline{\mathbf{x}}$ and $\widehat{\mathsf{\Sigma }}$ are replaced by their expected values.

Derivations in the proof of Theorem 3 are more technical than in the proof of Theorem 2 and therefore the proof is presented in Appendix A.2.

4. Simulations and Discussion

To illustrate theoretical results, we consider a bivariate skew t-distribution $\mathbf{x}\sim S{t}_{\nu }(\mathsf{\Sigma },\mathbf{\alpha })$ and study the convergence speed of the estimates using several parameter sets. First we fix two values of $\eta$ in (8), since, by the construction, this quantity has effect on the stability of the moments-based estimate for $\mathbf{\alpha }$. Namely, values of $\eta$ close to zero make the moment-based estimates unstable (see, e.g., Formula (7)). Taking this into account, we choose one “problematic” value of $\eta$, $\eta \approx 0.03$, and one “safe” value, $\eta \approx 0.3$. Different values for $\mathsf{\Sigma }$ and $\mathbf{\alpha }$ are chosen to obtain given values of $\eta$. In both cases, two $\mathbf{\alpha }$ values of different magnitude are considered: small value is set to ${(0.5,1)}^{\prime }$ and moderate to ${(3,2)}^{\prime }$. Furthermore, the off-diagonal values in matrix parameter $\mathsf{\Sigma }$ are pre-set to achieve low or high absolute value of ${\sigma }_{12}/\sqrt{{\sigma }_{11}{\sigma }_{22}}$ with both signs. Thus, altogether 16 sets of parameters are used, the exact values can be found in Appendix A.3, Table A1. The number of degrees of freedom $\nu$ is taken equal to 4 in all cases considered.

With all parameter sets, the data is simulated using sample sizes n from 100 to ${10}^6$ (using sequence for the powers of 10 from 2 to 6 with 50 equally spaced points) and $k=3000$ repetitions for each sample size. The mean absolute percentage deviation between the estimate and the theoretical asymptotic value (MAPD) is used as an indicator of convergence. Given k generated samples, MAPD is calculated as

$$\mathrm{MAPD}\left(\theta \right)=\frac{1}{k}\sum _{j=1}^k\left|\frac{{\widehat{\theta }}_j-\theta }{\theta }\right|,$$

where $\theta$ is the theoretical asymptotic value of estimate and ${\widehat{\theta }}_j$ is the parameter estimate from the jth sample.

It must be noted that depending on the sample size and the value of $\eta$ there are occasions when it is not possible to find an eligible estimate for $\mathbf{\alpha }$ since the sample value for $\eta$ is negative. To achieve the planned 3000 estimates for parameter sets with $\eta \approx 0.03$ and small sample sizes there is up to $2.75$ times more samples needed altogether. For parameter sets with $\eta \approx 0.3$ the number of failed estimates is considerably smaller. Figure A1 in Appendix A.4 shows the ratio of the number of failed samples to the number of planned estimates from our simulations.

Figure 1 shows resulting MAPD values for parameters depending on the logarithm of sample size. Red tones represent $\eta \approx 0.03$ group and blue tones $\eta \approx 0.3$. Lighter tone is for smaller $\mathbf{\alpha }$ and dark for moderate size $\mathbf{\alpha }$. Line types represent different sign and magnitude combinations of ${\sigma }_{12}/\sqrt{{\sigma }_{11}{\sigma }_{22}}$.

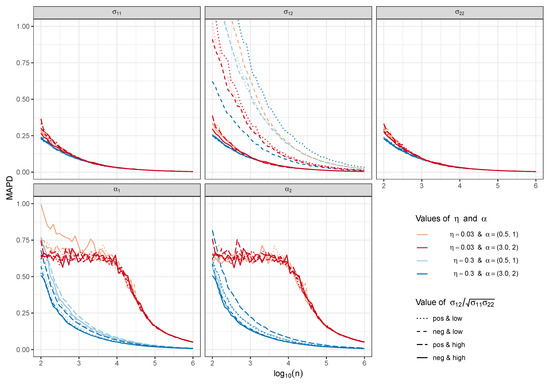
Figure 1. Convergence speed of parameter estimates.

As one can see, the convergence for diagonal elements of $\mathsf{\Sigma }$ is fastest and shows no remarkable differences for different parameter sets. However, MAPD for ${\widehat{\sigma }}_{11}$ and ${\widehat{\sigma }}_{22}$ is slightly bigger for sample sizes between 100 to 1000 if $\eta$ is small.

For the off-diagonal element of $\mathsf{\Sigma }$, the convergence speed varies with different parameter sets. If the absolute value of ${\sigma }_{12}/\sqrt{{\sigma }_{11}{\sigma }_{22}}$ is big, the pattern is actually similar to the convergence of diagonal elements, but for small values, the convergence is slower and MAPD can be close to or exceed value 1 even with sample sizes near 1000.

Most recognizable distinction is seen with the MAPD values of the estimates of $\mathbf{\alpha }$ and it is due to the $\eta$ value. If $\eta$ is small ($\eta \approx 0.03$), the MAPD value retains almost constantly high level with sample sizes from 100 up to 10,000, then starts to decrease with larger samples, but is still bigger than the MAPD value for the group with $\eta \approx 0.3$ with sample sizes near ${10}^6$. For $\eta \approx 0.3$, the convergence is faster and reaches smaller values.

Another aspect is the stability of estimates: with smaller $\eta$ ($\eta \approx 0.03$), the estimates are also more unstable for sample sizes under ${10}^4$ than the estimates corresponding to $\eta \approx 0.3$. Other variations (low and moderate $\mathbf{\alpha }$ elements and different ${\sigma }_{12}/\sqrt{{\sigma }_{11}{\sigma }_{22}}$ values) do not seem to have an effect on stability of the estimates.

Next we compare asymptotic covariance matrices of the estimators found in Theorems 2 and 3 with their estimates from simulated samples. Parameter sets 1 and 9 from Table A1 in Appendix A.3 were used. The former (set 1) corresponds to safe $\eta \approx 0.3$ value and the latter (set 9) to problematic $\eta \approx 0.03$ value and these parameter sets have the same value of $\mathbf{\alpha }$. For both cases $\widehat{\mathbf{\alpha }}$ and $\widehat{\mathsf{\Sigma }}$ were calculated 1000 times from samples of size 500. These parameter estimates were used to estimate $D_{as}^{\mathbf{\alpha }}$ and $D_{as}^{\mathsf{\Sigma }}$. For the simulations, the number of degrees of freedom $\nu =5$ was used, as it is the minimal value for calculating the asymptotic covariance matrices.

For the parameter set 9 with $\eta \approx 0.03$, the theoretical covariance matrix for $\sqrt{n}\widehat{\mathbf{\alpha }}$ is

$${\mathbf{D}}_{as}^{\mathbf{\alpha }}=\left(\begin{array}{cc}280.18& 503.84\\ 503.84& 993.65\end{array}\right)$$

and its estimate

$$\widehat{{\mathbf{D}}_{as}^{\mathbf{\alpha }}}=\left(\begin{array}{cc}230.93& 372.54\\ 372.54& 756.02\end{array}\right).$$

As the theoretical expected value is $\sqrt{n}\mathbf{\alpha }\approx {(11.2,22.4)}^{\prime }$ we can say that the variance of estimates is high in this case, but the theoretical and estimated covariance matrices are in agreement, although the theoretical values are higher. For the estimator $\sqrt{n}\mathrm{vec}\widehat{\mathsf{\Sigma }}$, the results are similar. In this case, the theoretical covariance matrix is

$${\mathbf{D}}_{as}^{\mathsf{\Sigma }}=\left(\begin{array}{cccc}200.00& -460.00& -460.00& 1213.50\\ -460.00& 1291.25& 1291.25& -3864.00\\ -460.00& 1291.25& 1291.25& -3864.00\\ 1213.50& -3864.00& -3864.00& \mathrm{14,112.00}\end{array}\right)$$

and the corresponding estimate:

$$\widehat{{\mathbf{D}}_{as}^{\mathsf{\Sigma }}}=\left(\begin{array}{cccc}182.98& -425.81& -425.81& 1044.01\\ -425.81& 1191.52& 1191.52& -3293.59\\ -425.81& 1191.52& 1191.52& -3293.59\\ 1044.01& -3293.59& -3293.59& \mathrm{11,819.03}\end{array}\right).$$

For the parameter set with $\eta \approx 0.3$, the same applies: theoretical and estimated covariance matrices are close while theoretical values are higher. Here the theoretical covariance matrix for $\sqrt{n}\widehat{\mathbf{\alpha }}$ is

$${\mathbf{D}}_{as}^{\mathbf{\alpha }}=\left(\begin{array}{cc}12.11& 13.01\\ 13.01& 21.38\end{array}\right)$$

and the estimate

$$\widehat{{\mathbf{D}}_{as}^{\mathbf{\alpha }}}=\left(\begin{array}{cc}9.59& 9.23\\ 9.23& 14.71\end{array}\right).$$

As these two parameter sets have the same value of $\mathbf{\alpha }$, we can see that for the second case the estimates vary much less. For $\eta \approx 0.3$, the theoretical covariance matrix for $\sqrt{n}\mathrm{vec}\widehat{\mathsf{\Sigma }}$ is

$${\mathbf{D}}_{as}^{\mathsf{\Sigma }}=\left(\begin{array}{cccc}32.00& -35.20& -35.20& 45.04\\ -35.20& 48.20& 48.20& -70.40\\ -35.20& 48.20& 48.20& -70.40\\ 45.04& -70.40& -70.40& 128.00\end{array}\right)$$

and its estimate

$$\widehat{{\mathbf{D}}_{as}^{\mathsf{\Sigma }}}=\left(\begin{array}{cccc}29.14& -30.29& -30.29& 36.03\\ -30.29& 39.30& 39.30& -54.62\\ -30.29& 39.30& 39.30& -54.62\\ 36.03& -54.62& -54.62& 97.27\end{array}\right).$$

Figure 2 presents scatterplots for estimates of ${\alpha }_1$ and ${\alpha }_2$ with theoretical 95% confidence ellipses. On the left panel ($\eta \approx 0.03$), the estimates of $\mathbf{\alpha }$ are more scattered as compared to the right panel, where $\eta \approx 0.3$, as expected. In addition, the placing of points does not correspond to an ellipse on the left panel, indicating the asymptotics does not work with sample size $n=500$ for distribution with $\eta \approx 0.03$. At the same time the result for $\eta \approx 0.3$ can be considered good.

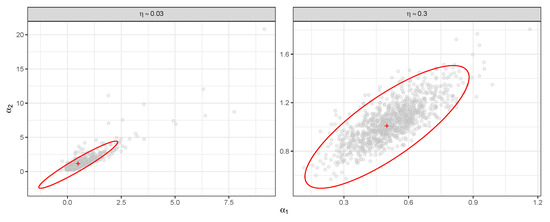
Figure 2. Comparison of estimates and theoretical confidence region: $\mathbf{\alpha }$.

Similar plots for the elements of $\widehat{\mathsf{\Sigma }}$ are presented in Figure 3. Here the estimates and ellipses again fit well for $\eta \approx 0.3$ case. For $\eta \approx 0.03$ the fit is also better compared to estimates of $\mathbf{\alpha }$ in the previous figure.

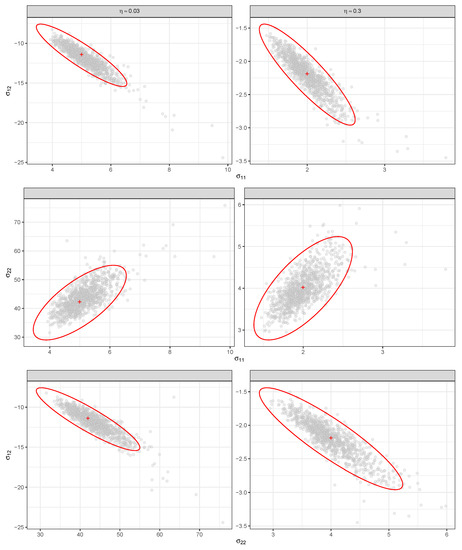
Figure 3. Comparison of estimates and theoretical confidence region: $\mathsf{\Sigma }$.

5. Skew t-Copula

5.1. Definition

The skew t-copula is introduced in Kollo and Pettere [23] (Chapter 15). When the location parameter $\mathbf{\mu }=\mathbf{0}$, the copula has the form

$$C_{p,\nu }(u_1,\dots ,u_p;\mathsf{\Sigma },\mathbf{\alpha })=F_{p,\nu }(F_{1,\nu }^{-1}(u_1;{\sigma }_{11},{\alpha }_1^{*}),\dots ,F_{1,\nu }^{-1}(u_p;{\sigma }_{pp},{\alpha }_p^{*});\mathsf{\Sigma },\mathbf{\alpha }),$$

where $F_{1,\nu }^{-1}(u_i;{\sigma }_{ii},{\alpha }_i^{*})$ denotes the inverse of the univariate skew $t_{1,\nu }$-distribution function and $F_{p,\nu }$ is the distribution function of the p-variate skew $t_{p,\nu }$-distribution. The arguments ${\sigma }_{ii}$ are the main diagonal elements of the covariance matrix $\mathsf{\Sigma }$ and ${\alpha }_i^{*}$ can be derived by the following simplification of (7):

$${\alpha }_i^{*}=\frac{{\sigma }_{ii}^{-1}{\delta }_i}{\sqrt{1-{\sigma }_{ii}^{-1}{\delta }_i^2}},i=1,\dots ,p.$$

(20)

Note that ${\alpha }_i^{*}$-s are not equal to the components ${\alpha }_i$ of the parameter vector $\mathbf{\alpha }$ of the multivariate distribution. The corresponding copula density is

$${\displaystyle c_{p,\nu }(\mathbf{u};\mathsf{\Sigma },\mathbf{\alpha })=\frac{f_{p,\nu }\left({(F_{1,\nu }^{-1}(u_1;{\sigma }_{11},{\alpha }_1^{*}),\dots ,F_{1,\nu }^{-1}(u_p;{\sigma }_{pp},{\alpha }_p^{*}))}^{\prime };\mathsf{\Sigma },\mathbf{\alpha }\right)}{{\displaystyle \prod _{i=1}^p}{f}_{1,\nu }\left(F_{1,\nu }^{-1}(u_i;{\sigma }_{ii},{\alpha }_i^{*});{\sigma }_{ii},{\alpha }_i^{*}\right)},}$$

where $f_{p,\nu }(\mathbf{u};\mathsf{\Sigma },\mathbf{\alpha })$ is the density function of $S{t}_{p,\nu }$ and the inverse functions $F_{1,\nu }^{-1}(u_i;{\sigma }_{ii},{\alpha }_i^{*})$ are as before.

In the standard case when $\mathbf{\mu }=\mathbf{0}$ and the covariance matrix $\mathsf{\Sigma }$ is equal to the correlation matrix $\mathbf{R}$, the density of the skew t-copula is of the form

$$c_{p,\nu }(\mathbf{u};\mathbf{R},\mathbf{\alpha })=\frac{f_{p,\nu }\left({(F_{1,\nu }^{-1}(u_1;{\alpha }_1^{*}),\dots ,F_{1,\nu }^{-1}(u_p;{\alpha }_p^{*}))}^{\prime };\mathbf{R},\mathbf{\alpha }\right)}{{\displaystyle {\prod }_{i=1}^p}{f}_{1,\nu }\left(F_{1,\nu }^{-1}(u_i;{\alpha }_i^{*});{\alpha }_i^{*}\right)},$$

(21)

where $F_{1,\nu }(u_i,{\alpha }_i^{*}),i=1,\dots ,p$ are the distribution functions of the univariate standard skew $t_{1,\nu }$-distribution. Density (21) is the most often used version of the skew t-copula density in data analysis.

As the numerator of the copula density consists of the density of multivariate skew t-distribution, the resulting copula is distribution function of a skewed multivariate distribution. When we want to apply skew t-copula in data analysis to join (possibly) differently distributed marginals into a multivariate distribution, we have to take into account the correlations between marginals. Pearson correlation matrix can easily be expressed through the parameter $\mathsf{\Sigma }$. Unfortunately Pearson correlations are not invariant under copula transformations (inverse distribution functions). We have to switch over to rank correlations. Fortunately for continuous elliptical distributions, Kendall’s $\tau$ can be expressed through the linear correlation (see Lindskog et al. [35])

$$\tau (X_i,X_j)=\frac{2}{\pi }arcsin\left(r_{ij}\right),$$

so we can switch over from linear correlations to rank correlations and vice versa.

5.2. Examples of Bivariate Skew t-Copula Densities

In the following we present some examples of two-dimensional copula densities to compare Gaussian, skew-normal and skew t-copulas using contour plots. First we present the formulas for the before mentioned copulas in bivariate case. The bivariate Gaussian copula has one parameter $\rho$ and using the general formula for multivariate Gaussian copula from Cherubini et al. [36] (p. 148) we can express bivariate density as

$$c_N(u_1,u_2;\rho )=\frac{1}{\sqrt{1-{\rho }^2}}exp\left(-\frac{{\rho }^2(z_1^2+z_2^2)-2\rho z_1{z}_2}{2(1-{\rho }^2)}\right),$$

where $z_i={\mathsf{\Phi }}^{-1}\left(u_i\right)$ and $u_i\in [0,1],i=1,2$. Skew-normal copula has in addition to $\rho$ parameter vector $\mathbf{\alpha }$ and following Käärik et al. [37] its density in bivaraite case is of form

$$c_{SN}(u_1,u_2;\rho ,\mathbf{\alpha })=\frac{1}{2\sqrt{1-{\rho }^2}}exp\left(-\frac{{\rho }^2(w_1^2+w_2^2)-2\rho w_1{w}_2}{2(1-{\rho }^2)}\right)\frac{\mathsf{\Phi }\left({\mathbf{\alpha }}^{\prime }{(w_1,w_2)}^{\prime }\right)}{\mathsf{\Phi }\left({\alpha }_1^{*}{w}_1\right)\mathsf{\Phi }\left({\alpha }_2^{*}{w}_2\right)},$$

where ${\alpha }_i^{*}$ are given by (20) and $w_i=F^{-1}(u_i;{\alpha }_i^{*})$ denotes inverse of the univariate skew-normal distribution function with parameter ${\alpha }_i^{*}$, as $u_i\in [0,1],i=1,2$. The bivariate skew t-copula has parameters $\rho$, $\mathbf{\alpha }$ and $\nu$ and using the general Formula (21) we get the bivariate density as

$$c_{2,\nu }(u_1,u_2;\rho ;\mathbf{\alpha })=\frac{\nu }{4\sqrt{1-{\rho }^2}}{\left(\frac{\mathsf{\Gamma }\left(\frac{\nu }{2}\right)}{\mathsf{\Gamma }\left(\frac{\nu +1}{2}\right)}\right)}^2\frac{{\left(1+\frac{Q}{(1-{\rho }^2)\nu }\right)}^{-\frac{\nu +2}{2}}}{{\displaystyle \prod _{i=1}^2}{(1+\frac{q_i^2}{\nu })}^{-\frac{\nu +1}{2}}}\frac{F_{2+\nu }\left({\mathbf{\alpha }}^{\prime }{(q_1,q_2)}^{\prime }\sqrt{\frac{2+\nu }{Q+\nu }}\right)}{{\displaystyle \prod _{i=1}^2}{F}_{1+\nu }\left({\alpha }_i^{*}{q}_i\sqrt{\frac{1+\nu }{q_i^2+\nu }}\right)},$$

where $q_i=F_{1,\nu }^{-1}(u_i;{\alpha }_i^{*}),u_i\in [0,1],i=1,2$, denotes inverse of the univariate skew t distribution function with parameter ${\alpha }_i^{*}$, $Q=q_1^2-2q_1{q}_2\rho +q_2^2$ and $F_k$ is the distribution function of the univariate $t_k$-distribution.

For a first example, we consider here the case were parameter $\rho$ is zero. Gaussian copula reduces to the product copula when $\rho =0$. If the corresponding parameter for skew-normal or skew t-copula equals zero, the resulting copula is not a product copula, this can be seen in Figure 4.

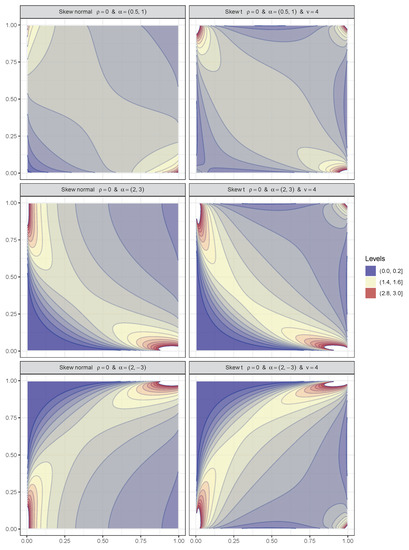
Figure 4. Examples of skew-normal and skew t-copulas when $\rho =0$.

In the figures, contours on the left correspond to skew-normal and on the right to skew t-copulas with different $\mathbf{\alpha }$ values (values are given in the header of the figure, note that the same number of degrees of freedom $\nu =4$ is used for all examples here). Contours are given with step size of $0.2$ starting from 0 and ending with 3. Dark blue, yellow and dark red colors represent the lowest, middle and highest contour levels for chosen scale.

If $\rho =0$ and both components of $\mathbf{\alpha }$ are positive, the densities of skew-normal and skew t-copulas tend to show negative dependence that grows stronger if ${\alpha }_i$ are bigger (see first and second row of Figure 4). If one ${\alpha }_i$ is negative, the copula represents positive dependence, but the direction of dependence also depends on the magnitude of ${\alpha }_i$, i.e., the direction is not so clear for ${\alpha }_i$ close to zero. When comparing contours in the second and third row we see that adding negative sign to the second component of $\mathbf{\alpha }$ results in rotation of the density by 90^o to the right. Rotation to the left would be the result if first element of $\mathbf{\alpha }$ is negative and the other positive. We note that the two skew copulas give the product copula if in addition to $\rho =0$ one element in the $\mathbf{\alpha }$ vector is also zero.

As a second example, we consider the case when $\rho \ne 0$. For Gaussian copula, the parameter $\rho$ gives the direction and strength of dependence between marginals. For the two skewed copulas, the additional parameter $\mathbf{\alpha }$ adds complexity to this relation. We can conclude from the Figures S1–S4. that if both ${\alpha }_i$ are positive and $\rho$ is negative as given here, the dependence for skewed copulas can be stronger as compared to Gaussian copula. For positive $\rho$, the opposite may happen: the skew-normal and skew t represent weaker dependence as compared to Gaussian copula or the dependence changes direction, see Figure S2 for $\rho =0.2$, for example. The effect of parameter $\mathbf{\alpha }$ is more notable if its elements have high absolute values.

6. Conclusions

Our main theoretical results, presented in Theorems 2 and 3, assure the asymptotic normality for the moment based parameter estimators of the two-parameter multivariate skew t-distribution. We can make the following observations based on the simulations used to illustrate the analytical results. First, the behaviour of the estimates of $\mathbf{\alpha }$ depends on the value of $\eta$: if the value of $\eta$ is close to zero (we used value $0.03$), the estimates of $\mathbf{\alpha }$ are unstable and the convergence is really slow, MAPD values are greater than $0.5$ with sample sizes up to ${10}^4$. For parameter sets with $\eta$ value $0.3$, the results are more stable and, for the aforementioned sample size, the MAPD values were already less than $0.1$. Second, it occurs that the combination of small sample size and low $\eta$ value can result in ineligible estimates of $\mathbf{\alpha }$. As a third point, we note that the estimates of $\mathsf{\Sigma }$ are stable and the convergence is faster than the convergence of the estimates of $\mathbf{\alpha }$. Furthermore, the value of $\eta$ does not affect the estimates of $\mathsf{\Sigma }$. As the two considered values of $\eta$ were chosen arbitrarily, its effect needs further investigation. Finally we also define skew t-copula, a powerful and flexible tool that can be used to model dependent data with differently distributed marginals in fields like finance, actuarial science and more.

Appendix A.1. Proof of Lemma 2

Proof. 

We have to express the third and fourth central moments through raw moments.

$$\begin{array}{ccc}\hfill {\overline{m}}_3\left(\mathbf{x}\right)& =& E[(\mathbf{x}-E\mathbf{x}){(\mathbf{x}-E\mathbf{x})}^{\prime }\otimes (\mathbf{x}-E\mathbf{x})]\hfill \\ & =& E[(\mathbf{x}{\mathbf{x}}^{\prime }-E\mathbf{x}{\mathbf{x}}^{\prime }-\mathbf{x}E\mathbf{x}+E\mathbf{x}E\mathbf{x})\otimes (\mathbf{x}-E\mathbf{x})]\hfill \\ & =& E[\mathbf{x}{\mathbf{x}}^{\prime }\otimes \mathbf{x}-\mathbf{x}{\mathbf{x}}^{\prime }\otimes E\mathbf{x}-E\mathbf{x}{\mathbf{x}}^{\prime }\otimes \mathbf{x}+E\mathbf{x}{\mathbf{x}}^{\prime }\otimes E\mathbf{x}\hfill \\ & -& \mathbf{x}E{\mathbf{x}}^{\prime }\otimes \mathbf{x}+\mathbf{x}E{\mathbf{x}}^{\prime }\otimes E\mathbf{x}+E\mathbf{x}E{\mathbf{x}}^{\prime }\otimes \mathbf{x}-E\mathbf{x}E{\mathbf{x}}^{\prime }\otimes E\mathbf{x}]\hfill \\ & =& E(\mathbf{x}{\mathbf{x}}^{\prime }\otimes \mathbf{x})-E\left(\mathbf{x}{\mathbf{x}}^{\prime }\right)\otimes E\mathbf{x}-E\mathbf{x}E({\mathbf{x}}^{\prime }\otimes \mathbf{x})+E\mathbf{x}E{\mathbf{x}}^{\prime }\otimes E\mathbf{x}\hfill \\ & -& E(\mathbf{x}E{\mathbf{x}}^{\prime }\otimes \mathbf{x})+E\mathbf{x}E{\mathbf{x}}^{\prime }\otimes E\mathbf{x}\hfill \\ & =& m_3\left(\mathbf{x}\right)-m_2\left(\mathbf{x}\right)\otimes E\mathbf{x}-E\mathbf{x}\otimes m_2\left(\mathbf{x}\right)+2E\mathbf{x}E{\mathbf{x}}^{\prime }\otimes E\mathbf{x}-E{\mathbf{x}}^{\prime }\otimes E(\mathbf{x}\otimes \mathbf{x})\hfill \\ & =& m_3\left(\mathbf{x}\right)-m_2\left(\mathbf{x}\right)\otimes E\mathbf{x}-E\mathbf{x}\otimes m_2\left(\mathbf{x}\right)+2E\mathbf{x}E{\mathbf{x}}^{\prime }\otimes E\mathbf{x}-E{\mathbf{x}}^{\prime }\otimes \mathrm{vec}{m}_2\left(\mathbf{x}\right).\hfill \end{array}$$

Finally

$${\overline{m}}_3\left(\mathbf{x}\right)=m_3\left(\mathbf{x}\right)-({\mathbf{I}}_{p^2}+{\mathbf{K}}_{p,p})(m_2\left(\mathbf{x}\right)\otimes E\mathbf{x})-\mathrm{vec}{m}_2\left(\mathbf{x}\right)E{\mathbf{x}}^{\prime }+2E\mathbf{x}E{\mathbf{x}}^{\prime }\otimes E\mathbf{x}.$$

Derivation of the fourth central moment is longer. We can use the intermediate expression from derivation of ${\overline{m}}_3\left(\mathbf{x}\right)$ after the third equality sign above

$$\begin{array}{ccc}\hfill {\overline{m}}_4\left(\mathbf{x}\right)& =& E[(\mathbf{x}-E\mathbf{x}){(\mathbf{x}-E\mathbf{x})}^{\prime }\otimes (\mathbf{x}-E\mathbf{x}){(\mathbf{x}-E\mathbf{x})}^{\prime }]\hfill \\ & =& E\left\{\right[\mathbf{x}{\mathbf{x}}^{\prime }\otimes \mathbf{x}-\mathbf{x}{\mathbf{x}}^{\prime }\otimes E\mathbf{x}-E\mathbf{x}{\mathbf{x}}^{\prime }\otimes \mathbf{x}+E\mathbf{x}{\mathbf{x}}^{\prime }\otimes E\mathbf{x}\hfill \\ & & -\mathbf{x}E{\mathbf{x}}^{\prime }\otimes \mathbf{x}+\mathbf{x}E{\mathbf{x}}^{\prime }\otimes E\mathbf{x}+E\mathbf{x}E{\mathbf{x}}^{\prime }\otimes \mathbf{x}-E\mathbf{x}E{\mathbf{x}}^{\prime }\otimes E\mathbf{x}]\otimes {\mathbf{x}}^{\prime }\}\hfill \\ & & -E\left\{\right[\mathbf{x}{\mathbf{x}}^{\prime }\otimes \mathbf{x}-\mathbf{x}{\mathbf{x}}^{\prime }\otimes E\mathbf{x}-E\mathbf{x}{\mathbf{x}}^{\prime }\otimes \mathbf{x}+E\mathbf{x}{\mathbf{x}}^{\prime }\otimes E\mathbf{x}\hfill \\ & & -\mathbf{x}E{\mathbf{x}}^{\prime }\otimes \mathbf{x}+\mathbf{x}E{\mathbf{x}}^{\prime }\otimes E\mathbf{x}+E\mathbf{x}E{\mathbf{x}}^{\prime }\otimes \mathbf{x}-E\mathbf{x}E{\mathbf{x}}^{\prime }\otimes E\mathbf{x}]\otimes E{\mathbf{x}}^{\prime }\}\hfill \\ & =& m_4\left(\mathbf{x}\right)-{\overline{m}}_3\left(\mathbf{x}\right)\otimes E{\mathbf{x}}^{\prime }-E(\mathbf{x}{\mathbf{x}}^{\prime }\otimes E\mathbf{x}\otimes {\mathbf{x}}^{\prime })-E(E\mathbf{x}{\mathbf{x}}^{\prime }\otimes \mathbf{x}\otimes {\mathbf{x}}^{\prime })\hfill \\ & & +E(E\mathbf{x}{\mathbf{x}}^{\prime }\otimes E\mathbf{x}\otimes {\mathbf{x}}^{\prime })-E(\mathbf{x}E{\mathbf{x}}^{\prime }\otimes \mathbf{x}\otimes {\mathbf{x}}^{\prime })+E(\mathbf{x}E{\mathbf{x}}^{\prime }\otimes E\mathbf{x}\otimes {\mathbf{x}}^{\prime })\hfill \\ & & +E\mathbf{x}E{\mathbf{x}}^{\prime }\otimes m_2\left(\mathbf{x}\right)-E\mathbf{x}E{\mathbf{x}}^{\prime }\otimes E\mathbf{x}\otimes E{\mathbf{x}}^{\prime }.\hfill \end{array}$$

The expectations in the last equality can be presented through moments when we use the property of the Kronecker product for vectors $\mathbf{a}{\mathbf{b}}^{\prime }=\mathbf{a}\otimes {\mathbf{b}}^{\prime }={\mathbf{b}}^{\prime }\otimes \mathbf{a}$

$$\begin{array}{ccc}\hfill E(\mathbf{x}{\mathbf{x}}^{\prime }\otimes E\mathbf{x}{\mathbf{x}}^{\prime })& =& E(\mathbf{x}\otimes {\mathbf{x}}^{\prime }\otimes E\mathbf{x}\otimes {\mathbf{x}}^{\prime })=E({\mathbf{x}}^{\prime }\otimes \mathbf{x}\otimes {\mathbf{x}}^{\prime }\otimes E{\mathbf{x}}^{\prime })=m_3^{\prime }\left(\mathbf{x}\right)\otimes E\mathbf{x};\hfill \\ \hfill E(E\mathbf{x}{\mathbf{x}}^{\prime }\otimes \mathbf{x}{\mathbf{x}}^{\prime })& =& E\mathbf{x}\otimes m_3^{\prime }\left(\mathbf{x}\right);\hfill \\ \hfill E(E\mathbf{x}{\mathbf{x}}^{\prime }\otimes E\mathbf{x}{\mathbf{x}}^{\prime })& =& E(E\mathbf{x}\otimes {\mathbf{x}}^{\prime }\otimes {\mathbf{x}}^{\prime }\otimes E\mathbf{x})=E\mathbf{x}\otimes \mathrm{vec}{}^{\prime }{m}_2\left(\mathbf{x}\right)\otimes E\mathbf{x};\hfill \\ \hfill E(\mathbf{x}E{\mathbf{x}}^{\prime }\otimes \mathbf{x}{\mathbf{x}}^{\prime })& =& E(\mathbf{x}\otimes E{\mathbf{x}}^{\prime }\otimes \mathbf{x}\otimes {\mathbf{x}}^{\prime })=E(E{\mathbf{x}}^{\prime }\otimes \mathbf{x}\otimes {\mathbf{x}}^{\prime }\otimes \mathbf{x})=E{\mathbf{x}}^{\prime }\otimes m_3\left(\mathbf{x}\right);\hfill \\ \hfill E(\mathbf{x}E{\mathbf{x}}^{\prime }\otimes E\mathbf{x}{\mathbf{x}}^{\prime })& =& E(\mathbf{x}\otimes E{\mathbf{x}}^{\prime }\otimes E\mathbf{x}\otimes {\mathbf{x}}^{\prime })=E(E{\mathbf{x}}^{\prime }\otimes \mathbf{x}\otimes {\mathbf{x}}^{\prime }\otimes E{\mathbf{x}}^{\prime })\hfill \\ & =& E{\mathbf{x}}^{\prime }\otimes m_2\left(\mathbf{x}\right)\otimes E\mathbf{x}.\hfill \end{array}$$

After plugging in the expression of ${\overline{m}}_3\left(\mathbf{x}\right)$ we have

$$\begin{array}{cc}\hfill {\overline{m}}_4\left(\mathbf{x}\right)& =m_4\left(\mathbf{x}\right)-m_3\left(\mathbf{x}\right)\otimes E{\mathbf{x}}^{\prime }+m_2\left(\mathbf{x}\right)\otimes E\mathbf{x}E{\mathbf{x}}^{\prime }+E\mathbf{x}\otimes m_2\left(\mathbf{x}\right)\otimes E{\mathbf{x}}^{\prime }\hfill \\ \hfill & +E{\mathbf{x}}^{\prime }\otimes \mathrm{vec}{m}_2\left(\mathbf{x}\right)\otimes E{\mathbf{x}}^{\prime }-3E\mathbf{x}E{\mathbf{x}}^{\prime }\otimes E\mathbf{x}E{\mathbf{x}}^{\prime }-m_3^{\prime }\left(\mathbf{x}\right)\otimes E\mathbf{x}-E\mathbf{x}\otimes m_3^{\prime }\left(\mathbf{x}\right)\hfill \\ \hfill & +E\mathbf{x}\otimes \mathrm{vec}{}^{\prime }{m}_2\left(\mathbf{x}\right)\otimes E\mathbf{x}-E{\mathbf{x}}^{\prime }\otimes m_3\left(\mathbf{x}\right)+E{\mathbf{x}}^{\prime }\otimes m_2\left(\mathbf{x}\right)\otimes E\mathbf{x}\hfill \\ \hfill & +E\mathbf{x}E{\mathbf{x}}^{\prime }\otimes m_2\left(\mathbf{x}\right).\hfill \end{array}$$

Applying notation in Lemma 2

$$\begin{array}{ccc}\hfill \mathbf{A}\left(\mathbf{x}\right)& =& E{\mathbf{x}}^{\prime }\otimes m_2\left(\mathbf{x}\right)\otimes E\mathbf{x};\hfill \\ \hfill \mathbf{B}\left(\mathbf{x}\right)& =& E{\mathbf{x}}^{\prime }\otimes \mathrm{vec}{m}_2\left(\mathbf{x}\right)\otimes E{\mathbf{x}}^{\prime };\hfill \\ \hfill \mathbf{C}\left(\mathbf{x}\right)& =& m_3\left(\mathbf{x}\right)\otimes E{\mathbf{x}}^{\prime }\hfill \end{array}$$

we get the statement after using property 5 of the Kronecker product

$$\begin{array}{cc}\hfill {\overline{m}}_4\left(\mathbf{x}\right)& =m_4\left(\mathbf{x}\right)-\mathbf{C}\left(\mathbf{x}\right)({\mathbf{I}}_{p^2}+{\mathbf{K}}_{p,p})-({\mathbf{I}}_{p^2}+{\mathbf{K}}_{p,p}){\left(\mathbf{C}\left(\mathbf{x}\right)\right)}^{\prime }-3E\mathbf{x}E{\mathbf{x}}^{\prime }\otimes E\mathbf{x}E{\mathbf{x}}^{\prime }\hfill \\ \hfill & +\mathbf{A}\left(\mathbf{x}\right)+\mathbf{B}\left(\mathbf{x}\right)+{(\mathbf{A}\left(\mathbf{x}\right)+\mathbf{B}\left(\mathbf{x}\right))}^{\prime }+m_2\left(\mathbf{x}\right)\otimes E\mathbf{x}E{\mathbf{x}}^{\prime }+E\mathbf{x}E{\mathbf{x}}^{\prime }\otimes m_2\left(\mathbf{x}\right).\hfill \end{array}$$

□

Appendix A.2. Proof of Theorem 3

Proof. 

Let us start from Expression (18) for $\widehat{\mathbf{\alpha }}$:

$$\widehat{\mathbf{\alpha }}=\frac{{\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}}{\sqrt{M}},$$

where M is given in (17), which, taking (15) into account, can also be expressed as follows:

$$M=\frac{\nu }{\pi }{\left(\frac{\mathsf{\Gamma }\left(\frac{\nu -1}{2}\right)}{\mathsf{\Gamma }\left(\frac{\nu }{2}\right)}\right)}^2-{\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}.$$

Let us now derive the needed derivatives step by step.

$$\frac{d\widehat{\mathbf{\alpha }}}{d\overline{\mathbf{x}}}=\frac{d\left({\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}{M}^{-\frac{1}{2}}\right)}{d\overline{\mathbf{x}}}=M^{-\frac{1}{2}}\frac{d\left({\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}\right)}{d\overline{\mathbf{x}}}+{\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}\frac{d{M}^{-\frac{1}{2}}}{d\overline{\mathbf{x}}}.$$

(A1)

Let us find the two derivatives in (A1).

(a)

The first derivative can be expressed as

$$\frac{d\left({\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}\right)}{d\overline{\mathbf{x}}}={\widehat{\mathsf{\Sigma }}}^{-1}+({\overline{\mathbf{x}}}^{\prime }\otimes {\mathbf{I}}_p)\frac{d{\widehat{\mathsf{\Sigma }}}^{-1}}{d\overline{\mathbf{x}}}.$$

(A2)

Now the derivative $\frac{d{\widehat{\mathsf{\Sigma }}}^{-1}}{d\overline{\mathbf{x}}}$ can be found as

$$\begin{array}{cc}\hfill \frac{d{\widehat{\mathsf{\Sigma }}}^{-1}}{d\overline{\mathbf{x}}}& =\frac{d{\widehat{\mathsf{\Sigma }}}^{-1}}{d\widehat{\mathsf{\Sigma }}}\frac{d\widehat{\mathsf{\Sigma }}}{d\overline{\mathbf{x}}}=-({\widehat{\mathsf{\Sigma }}}^{-1}\otimes {\widehat{\mathsf{\Sigma }}}^{-1})\frac{d\left(\frac{\nu -2}{\nu }(\mathbf{S}+\overline{\mathbf{x}}{\overline{\mathbf{x}}}^{\prime })\right)}{d\overline{\mathbf{x}}}\hfill \\ \hfill & =-\frac{\nu -2}{\nu }\left({\widehat{\mathsf{\Sigma }}}^{-1}\otimes {\widehat{\mathsf{\Sigma }}}^{-1}\right)\left(\overline{\mathbf{x}}\otimes {\mathbf{I}}_p+{\mathbf{I}}_p\otimes \overline{\mathbf{x}}\right)\hfill \\ \hfill & =-\frac{\nu -2}{\nu }\left({\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}\otimes {\widehat{\mathsf{\Sigma }}}^{-1}+{\widehat{\mathsf{\Sigma }}}^{-1}\otimes {\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}\right).\hfill \end{array}$$

(A3)

The Equations (A2) and (A3) imply that

$$\begin{array}{cc}\hfill \frac{d\left({\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}\right)}{d\overline{\mathbf{x}}}& ={\widehat{\mathsf{\Sigma }}}^{-1}-({\overline{\mathbf{x}}}^{\prime }\otimes {\mathbf{I}}_p)\frac{\nu -2}{\nu }\left({\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}\otimes {\widehat{\mathsf{\Sigma }}}^{-1}+{\widehat{\mathsf{\Sigma }}}^{-1}\otimes {\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}\right)\hfill \\ \hfill & ={\widehat{\mathsf{\Sigma }}}^{-1}-\frac{\nu -2}{\nu }\left({\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}{\widehat{\mathsf{\Sigma }}}^{-1}+{\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\otimes {\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}\right)\hfill \\ \hfill & ={\widehat{\mathsf{\Sigma }}}^{-1}-\frac{\nu -2}{\nu }\left({\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}{\widehat{\mathsf{\Sigma }}}^{-1}+{\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}{\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\right).\hfill \end{array}$$

(b)

The second derivative in (A1) is

$$\begin{array}{cc}\hfill \frac{d{M}^{-\frac{1}{2}}}{d\overline{\mathbf{x}}}& =\frac{d{M}^{-\frac{1}{2}}}{dM}\frac{dM}{d\overline{\mathbf{x}}}=-\frac{1}{2}{M}^{-\frac{3}{2}}\frac{d(-{\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}})}{\overline{\mathbf{x}}}\hfill \\ \hfill & =\frac{1}{2}{M}^{-\frac{3}{2}}\left({\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}+\overline{\mathbf{x}}\frac{d\left({\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}\right)}{d\overline{\mathbf{x}}}\right)\hfill \\ \hfill & =\frac{1}{2}{M}^{-\frac{3}{2}}\left({\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}+{\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}-{\overline{\mathbf{x}}}^{\prime }\frac{\nu -2}{\nu }\left({\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}{\widehat{\mathsf{\Sigma }}}^{-1}+{\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}{\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\right)\right)\hfill \\ \hfill & =\frac{1}{2}{M}^{-\frac{3}{2}}\left(2{\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}-\frac{\nu -2}{\nu }\left({\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}{\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}+{\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}{\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\right)\right)\hfill \\ \hfill & =M^{-\frac{3}{2}}\left(\left(1-\frac{\nu -2}{\nu }{\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}\right){\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\right).\hfill \end{array}$$

Now, applying the results of parts (a) and (b) into Equation (A1), yields

$$\begin{array}{cc}\hfill \frac{d\widehat{\mathbf{\alpha }}}{d\overline{\mathbf{x}}}& =M^{-\frac{1}{2}}\left({\widehat{\mathsf{\Sigma }}}^{-1}-\frac{\nu -2}{\nu }\left({\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}{\widehat{\mathsf{\Sigma }}}^{-1}+{\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}{\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\right)\right)\hfill \\ \hfill & +{\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}{M}^{-\frac{3}{2}}\left(\left(1-\frac{\nu -2}{\nu }{\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}\right){\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\right)\hfill \\ \hfill & =M^{-\frac{1}{2}}[\left({\widehat{\mathsf{\Sigma }}}^{-1}-\frac{\nu -2}{\nu }\left({\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}{\widehat{\mathsf{\Sigma }}}^{-1}+{\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}{\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\right)\right)\hfill \\ \hfill & +M^{-1}\left(\left(1-\frac{\nu -2}{\nu }{\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}\right){\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}{\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\right)]\hfill \\ \hfill & =M^{-\frac{1}{2}}[\left(1-\frac{\nu -2}{\nu }{\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}\right){\widehat{\mathsf{\Sigma }}}^{-1}\hfill \\ \hfill & +M^{-1}\left(\left(1-\frac{\nu -2}{\nu }\left({\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}+M\right)\right){\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}{\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\right)].\hfill \end{array}$$

Taking the derivative of $\widehat{\mathbf{\alpha }}$ by $\mathrm{vec}\mathbf{S}$ is similar, but simpler. First of all, following Equality (A1), we can write

$$\frac{d\widehat{\mathbf{\alpha }}}{d\mathrm{vec}\mathbf{S}}=M^{-\frac{1}{2}}\frac{d\left({\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}\right)}{d\mathrm{vec}\mathbf{S}}+{\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}\frac{d{M}^{-\frac{1}{2}}}{d\mathrm{vec}\mathbf{S}}.$$

Let us find the two derivatives in the last sum.

(a)

The first derivative can be expressed as

$$\frac{d\left({\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}\right)}{d\mathrm{vec}\mathbf{S}}=({\overline{\mathbf{x}}}^{\prime }\otimes {\mathbf{I}}_p)\frac{d{\widehat{\mathsf{\Sigma }}}^{-1}}{d\widehat{\mathsf{\Sigma }}}\frac{d\widehat{\mathsf{\Sigma }}}{d\mathrm{vec}\mathbf{S}}=-\frac{\nu -2}{\nu }({\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\otimes {\widehat{\mathsf{\Sigma }}}^{-1}),$$

(b)

The second derivative is

$$\begin{array}{ccc}\hfill \frac{d{M}^{-\frac{1}{2}}}{d\mathrm{vec}\mathbf{S}}& =& \frac{d{M}^{-\frac{1}{2}}}{dM}\frac{dM}{d\mathrm{vec}\mathbf{S}}=-\frac{1}{2}{M}^{-\frac{3}{2}}\frac{d(-{\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}})}{d\mathrm{vec}\mathbf{S}}\hfill \\ & =& -\frac{1}{2}{M}^{-\frac{3}{2}}({\overline{\mathbf{x}}}^{\prime }\otimes {\overline{\mathbf{x}}}^{\prime })({\widehat{\mathsf{\Sigma }}}^{-1}\otimes {\widehat{\mathsf{\Sigma }}}^{-1})\frac{\nu -2}{\nu }\hfill \\ & =& -\frac{\nu -2}{2\nu }{M}^{-\frac{3}{2}}({\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\otimes {\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}).\hfill \end{array}$$

The full expression of the derivative $\frac{d\widehat{\mathbf{\alpha }}}{d\mathrm{vec}\mathbf{S}}$ is

$$\frac{d\widehat{\mathbf{\alpha }}}{d\mathrm{vec}\mathbf{S}}=-\frac{\nu -2}{\nu }{M}^{-\frac{1}{2}}\left[({\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\otimes {\widehat{\mathsf{\Sigma }}}^{-1})+\frac{1}{2}{M}^{-1}({\widehat{\mathsf{\Sigma }}}^{-1}\overline{\mathbf{x}}{\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1}\otimes {\overline{\mathbf{x}}}^{\prime }{\widehat{\mathsf{\Sigma }}}^{-1})\right].$$

□

Appendix A.3. Parameter Sets

Table A1. Parameter sets for simulations.

	$\mathit{\eta }$	${\mathit{\alpha }}_1$	${\mathit{\alpha }}_2$	${\mathit{\sigma }}_{11}$	${\mathit{\sigma }}_{22}$	${\mathit{\sigma }}_{12}$	${\mathit{\sigma }}_{12}/\sqrt{{\mathit{\sigma }}_{11}{\mathit{\sigma }}_{22}}$
Set 1	0.3030	0.5	1	2.0	4.00	−2.20	−0.78
Set 2	0.3030	0.5	1	1.0	2.20	−0.15	−0.10
Set 3	0.2999	0.5	1	1.5	1.00	0.96	0.78
Set 4	0.3030	0.5	1	3.0	1.35	0.20	0.10
Set 5	0.3049	3.0	2	0.6	1.50	−0.76	−0.80
Set 6	0.3049	3.0	2	0.2	0.30	−0.06	−0.24
Set 7	0.3067	3.0	2	0.1	0.10	0.08	0.80
Set 8	0.3012	3.0	2	0.2	0.10	0.01	0.07
Set 9	0.0305	0.5	1	5.0	42.00	−11.50	−0.79
Set 10	0.0301	0.5	1	28.0	28.00	−2.80	−0.10
Set 11	0.0300	0.5	1	16.0	16.00	12.30	0.77
Set 12	0.0298	0.5	1	15.0	25.00	3.80	0.20
Set 13	0.0301	3.0	2	7.0	22.00	−9.90	−0.80
Set 14	0.0305	3.0	2	3.0	3.00	−0.60	−0.20
Set 15	0.0301	3.0	2	1.1	2.00	1.19	0.80
Set 16	0.0302	3.0	2	2.2	2.00	0.36	0.17

Table A1. Parameter sets for simulations.

	$\mathit{\eta }$	${\mathit{\alpha }}_1$	${\mathit{\alpha }}_2$	${\mathit{\sigma }}_{11}$	${\mathit{\sigma }}_{22}$	${\mathit{\sigma }}_{12}$	${\mathit{\sigma }}_{12}/\sqrt{{\mathit{\sigma }}_{11}{\mathit{\sigma }}_{22}}$
Set 1	0.3030	0.5	1	2.0	4.00	−2.20	−0.78
Set 2	0.3030	0.5	1	1.0	2.20	−0.15	−0.10
Set 3	0.2999	0.5	1	1.5	1.00	0.96	0.78
Set 4	0.3030	0.5	1	3.0	1.35	0.20	0.10
Set 5	0.3049	3.0	2	0.6	1.50	−0.76	−0.80
Set 6	0.3049	3.0	2	0.2	0.30	−0.06	−0.24
Set 7	0.3067	3.0	2	0.1	0.10	0.08	0.80
Set 8	0.3012	3.0	2	0.2	0.10	0.01	0.07
Set 9	0.0305	0.5	1	5.0	42.00	−11.50	−0.79
Set 10	0.0301	0.5	1	28.0	28.00	−2.80	−0.10
Set 11	0.0300	0.5	1	16.0	16.00	12.30	0.77
Set 12	0.0298	0.5	1	15.0	25.00	3.80	0.20
Set 13	0.0301	3.0	2	7.0	22.00	−9.90	−0.80
Set 14	0.0305	3.0	2	3.0	3.00	−0.60	−0.20
Set 15	0.0301	3.0	2	1.1	2.00	1.19	0.80
Set 16	0.0302	3.0	2	2.2	2.00	0.36	0.17

Appendix A.4. Samples with Failed Estimates

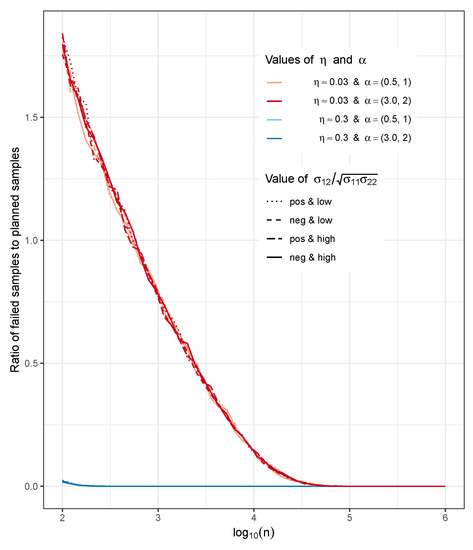
Figure A1. Ratio of the number of failed samples to the number of planned estimates from our simulations for all parameter sets.