Split Casimir Operator and Universal Formulation of the Simple Lie Algebras

Abstract

We construct characteristic identities for the split (polarized) Casimir operators of the simple Lie algebras in adjoint representation. By means of these characteristic identities, for all simple Lie algebras we derive explicit formulae for invariant projectors onto irreducible subrepresentations in $T^{\otimes 2}$ in the case when T is the adjoint representation. These projectors and characteristic identities are considered from the viewpoint of the universal description of the simple Lie algebras in terms of the Vogel parameters.

1. Introduction

In this paper, we demonstrate the usefulness of the $\mathfrak{g}$-invariant split Casimir operator $\widehat{C}$ (see definition in Section 2) in the representation theory of Lie algebras (see also [1]). Namely, for all simple Lie algebras $\mathfrak{g}$, explicit formulas can be found for invariant projectors onto irreducible representations that appear in the expansion of the tensor product $T\otimes T^{\prime }$ of two representations T and $T^{\prime }$. In particular, these invariant projectors are constructed in terms of the $\mathfrak{g}$-invariant operator $\widehat{C}$. It is natural to find invariant projectors in terms of $\mathfrak{g}$-invariant operators, which in general are images of special elements of the so-called centralizer algebra.

In the paper, we consider a very particular problem of constructing invariant projectors in representation spaces of $T^{\otimes 2}$, where $T\equiv ad$ is the adjoint representation but for all simple Lie algebras $\mathfrak{g}$. Our approach is closely related to the one outlined in [1,2]. In [2], such invariant projectors were obtained in terms of several special invariant operators and the calculations were performed using a peculiar diagram technique. In our approach, we try to construct invariant projectors in the representation space $V^{\otimes 2}$ of $T^{\otimes 2}$ by using only one $\mathfrak{g}$-invariant operator, which is the split Casimir operator $\widehat{C}$.

It turns out (see [3]) that for all simple Lie algebras $\mathfrak{g}$ in the defining representations all invariant projectors in $V^{\otimes 2}$ are constructed as polynomials in $\widehat{C}$. This is not the case for the adjoint representation, i.e., not for all algebras $\mathfrak{g}$ the invariant projectors in $V_{ad}^{\otimes 2}$ are constructed as polynomials of only one operator ${\widehat{C}}_{ad}\equiv {ad}^{\otimes 2}\widehat{C}$. Namely, in the case of $s\ell \left(N\right)$ and $so\left(8\right)$ algebras there are additional $\mathfrak{g}$-invariant operators that are independent of ${\widehat{C}}_{ad}$ and act, respectively, in the anti-symmetrized and symmetrized parts of the space $V_{ad}^{\otimes 2}$. In [3], we constructed such additional operators explicitly.

Our study of the split Casimir operator $\widehat{C}$ was motivated by the works [4,5,6,7], and by the idea that the knowledge of the characteristic identities for ${\widehat{C}}_{ad}$ turns out to be a key point for understanding the so-called universal formulation of the simple Lie algebras [8] (see also the historical notes in [2], Section 21.2). Though some characteristic identities and formulas for certain $\mathfrak{g}$-invariant projectors can be found in a different form in [2], we believe that the methods we used and the results obtained can be useful for future research, e.g., from the viewpoint of technical applications of the split Casimir operator.

The split Casimir operator ${\widehat{C}}_{ad}$ for the Lie algebras of the classical series in the adjoint representation and for the exceptional algebras was considered in detail in [3,9]. Here, we present only a universal description of these results.

In our paper, to simplify the notation, we always write $s\ell \left(N\right)$, $so\left(N\right)$ and $sp\left(2n\right)$ instead of $s\ell (N,\mathbb{C})$, $so(N,\mathbb{C})$ and $sp(2n,\mathbb{C})$, respectively.

2. Split Casimir Operator for Simple Lie Algebras

2.1. General Definitions

Let $\mathfrak{g}$ be a simple Lie algebra with the basis $X_a$ and defining relations

$$[X_a,X_b]=C_{ab}^d{X}_d,$$

(1)

where $C_{ab}^d$ are the structure constants. The Cartan–Killing metric is defined in the standard way:

$${\mathsf{g}}_{ab}\equiv C_{ac}^d{C}_{bd}^c=\mathbf{Tr}(ad\left(X_a\right)·ad\left(X_b\right)),$$

(2)

where ad denotes adjoint representation: $ad{\left(X_a\right)}_b^d=C_{ab}^d$. Recall that the structure constants $C_{abc}\equiv C_{ab}^d{\mathsf{g}}_{dc}$ are antisymmetric under permutation of indices $(a,b,c)$. We denote an enveloping algebra of the Lie algebra $\mathfrak{g}$ as $\mathcal{U}\left(\mathfrak{g}\right)$.

Let ${\mathsf{g}}^{df}$ be the inverse matrix to the Cartan–Killing metric (2). We use this matrix and construct the operator

$$\widehat{C}={\mathsf{g}}^{ab}{X}_a\otimes X_b\in \mathfrak{g}\otimes \mathfrak{g}\subset \mathcal{U}\left(\mathfrak{g}\right)\otimes \mathcal{U}\left(\mathfrak{g}\right),$$

(3)

which is called the split (or polarized) Casimir operator of the Lie algebra $\mathfrak{g}$. This operator is related to the usual quadratic Casimir operator

$$C_{\left(2\right)}={\mathsf{g}}^{ab}{X}_a·X_b\in \mathcal{U}\left(\mathfrak{g}\right),$$

(4)

by means of the formula

$$\Delta \left(C_{\left(2\right)}\right)=C_{\left(2\right)}\otimes I+I\otimes C_{\left(2\right)}+2\widehat{C},$$

(5)

where $\Delta$ is the standard co-multiplication for enveloping algebras $\mathcal{U}\left(\mathfrak{g}\right)$:

$$\Delta \left(X_a\right)=(X_a\otimes I+I\otimes X_a).$$

(6)

The following statement holds (see, for example, [10,11]).

Proposition 1.

The operator $\widehat{C}$, given in (3), does not depend on the choice of the basis in $\mathfrak{g}$ and satisfies the condition (which is called ad-invariance or $\mathfrak{g}$-invariance):

$$[\Delta \left(A\right),\widehat{C}]=[(A\otimes I+I\otimes A),\widehat{C}]=0,\forall A\in \mathfrak{g},$$

(7)

where Δ is co-multiplication (6). In addition, the operator $\widehat{C}$ obeys the equations

$$[{\widehat{C}}_{12},{\widehat{C}}_{13}+{\widehat{C}}_{23}]=0\Rightarrow [{\widehat{C}}_{13},{\widehat{C}}_{23}]=\frac{1}{2}[{\widehat{C}}_{12},{\widehat{C}}_{13}-{\widehat{C}}_{23}],$$

(8)

which use the standard notation

$${\widehat{C}}_{12}={\mathsf{g}}^{ab}{X}_a\otimes X_b\otimes I,{\widehat{C}}_{13}={\mathsf{g}}^{ab}{X}_a\otimes I\otimes X_b,{\widehat{C}}_{23}={\mathsf{g}}^{ab}I\otimes X_a\otimes X_b.$$

(9)

Here I is the unit element in $\mathcal{U}\left(\mathfrak{g}\right)$ and ${\widehat{C}}_{ij}\in \mathcal{U}\left(\mathfrak{g}\right)\otimes \mathcal{U}\left(\mathfrak{g}\right)\otimes \mathcal{U}\left(\mathfrak{g}\right)$.

Relations (8) indicate that the split Casimir operator (3) realizes the Kono–Drinfeld Lie algebra and can be used as a building block for constructing solutions to the quantum and semi-classical Yang–Baxter equations (see, e.g., [12,13] and references therein).

2.2. The Split Casimir Operator for Simple Lie Algebras in the Adjoint Representation

The generators $X_a$ of a simple Lie algebra $\mathfrak{g}$ satisfy the defining relations (1) and, in the adjoint representation, $X_a$ are implemented as matrices ad${\left(X_a\right)}_b^d=C_{ab}^d$. In this case the split Casimir operator (3) is written as

$${\left({\widehat{C}}_{ad}\right)}_{b_1{b}_2}^{a_1{a}_2}\equiv {(ad\otimes ad)}_{b_1{b}_2}^{a_1{a}_2}\left(\widehat{C}\right)=C_{h{b}_1}^{a_1}{C}_{f{b}_2}^{a_2}{\mathsf{g}}^{hf}.$$

(10)

By definition, this operator satisfies identities (8). Below we need one more ad-invariant rank-1 operator:

$${\left(\mathbf{K}\right)}_{b_1{b}_2}^{a_1{a}_2}={\mathsf{g}}^{a_1{a}_2}{\mathsf{g}}_{b_1{b}_2}.$$

(11)

The operators (10) and (11) act in the tensor product $V_{ad}\otimes V_{ad}$ of two spaces $V_{ad}=\mathfrak{g}$ of the adjoint representation and have the symmetry properties ${\left({\widehat{C}}_{ad}\right)}_{b_1{b}_2}^{a_1{a}_2}={\left({\widehat{C}}_{ad}\right)}_{b_2{b}_1}^{a_2{a}_1}$ and ${\mathbf{K}}_{b_1{b}_2}^{a_1{a}_2}={\mathbf{K}}_{b_2{b}_1}^{a_2{a}_1}$, which are conveniently written in the form

$${\left({\widehat{C}}_{ad}\right)}_{21}=\mathbf{P}{\left({\widehat{C}}_{ad}\right)}_{12}\mathbf{P}={\left({\widehat{C}}_{ad}\right)}_{12},{\mathbf{K}}_{21}=\mathbf{P}{\mathbf{K}}_{12}\mathbf{P}={\mathbf{K}}_{12},$$

where $1,2$ are numbers of spaces $V_{ad}$ in the product $(V_{ad}\otimes V_{ad})$ and $\mathbf{P}$ is a permutation matrix in $(V_{ad}\otimes V_{ad})$:

$$\mathbf{P}(X_{a_1}\otimes X_{a_2})=(X_{a_2}\otimes X_{a_1})=(X_{b_1}\otimes X_{b_2}){\mathbf{P}}_{a_1{a}_2}^{b_1{b}_2},{\mathbf{P}}_{a_1{a}_2}^{b_1{b}_2}={\delta }_{a_2}^{b_1}{\delta }_{a_1}^{b_2}.$$

(12)

Here $(X_a\otimes X_b)$ is the basis in the space $(V_{ad}\otimes V_{ad})$. Define the symmetrized and anti-symmetrized parts of the operator ${\widehat{C}}_{ad}$

$${\left({\widehat{C}}_{\pm }\right)}_{b_1{b}_2}^{a_1{a}_2}=\frac{1}{2}({\left({\widehat{C}}_{ad}\right)}_{b_1{b}_2}^{a_1{a}_2}\pm {\left({\widehat{C}}_{ad}\right)}_{b_1{b}_2}^{a_2{a}_1}),{\widehat{C}}_{\pm }={\mathbf{P}}_{\pm }^{\left(ad\right)}{\widehat{C}}_{ad}={\widehat{C}}_{ad}{\mathbf{P}}_{\pm }^{\left(ad\right)},$$

(13)

where ${\mathbf{P}}_{\pm }^{\left(ad\right)}=\frac{1}{2}(\mathbf{I}\pm \mathbf{P})$ and $\mathbf{I}$ is the unit operator in ${\left(V_{ad}\right)}^{\otimes 2}$.

Proposition 2.

The operators ${\widehat{C}}_{ad}$, ${\widehat{C}}_{\pm }$ and $\mathbf{K}$, given in (10), (11) and (13), satisfy the identities

$${\widehat{C}}_{-}^2=-\frac{1}{2}{\widehat{C}}_{-},$$

(14)

$${\widehat{C}}_{-}\mathbf{K}=0=\mathbf{K}{\widehat{C}}_{-},{\widehat{C}}_{ad}\mathbf{K}=\mathbf{K}{\widehat{C}}_{ad}=-\mathbf{K},$$

(15)

$${\widehat{C}}_{+}\mathbf{K}=\mathbf{K}{\widehat{C}}_{+}=-\mathbf{K}.$$

(16)

The proof was presented in [3].

Now we take into account Definitions (10)–(12), Relations (14),

$${\left({\widehat{C}}_{-}\right)}_{b_1{b}_2}^{a_1{a}_2}=-\frac{1}{2}{C}_d^{a_1{a}_2}{C}_{b_1{b}_2}^d,C_d^{a_1{a}_2}\equiv C_{d{b}_2}^{a_1}{\mathsf{g}}^{b_2{a}_2}.$$

(17)

$$C_{b_1{b}_2}^d{C}_a^{b_1{b}_2}={\delta }_a^d\iff \mathrm{ad}{\left(C_{\left(2\right)}\right)}_r^f={\mathsf{g}}^{ab}{C}_{ad}^f{C}_{br}^d={\delta }_r^f,$$

(18)

and $C_{ba}^a=0$, which is valid for all simple Lie algebras, and obtain general formulas for the traces

$$\begin{array}{c}\mathbf{Tr}\left({\widehat{C}}_{ad}\right)=0,\mathbf{Tr}\left({\widehat{C}}_{\pm }\right)=\pm \frac{1}{2}dim\mathfrak{g},\mathbf{Tr}\left({\widehat{C}}_{ad}^2\right)=dim\mathfrak{g},\\ \mathbf{Tr}\left({\widehat{C}}_{-}^2\right)=-\frac{1}{2}\mathbf{Tr}\left({\widehat{C}}_{-}\right)=\frac{1}{4}dim\mathfrak{g},\\ \mathbf{Tr}\left({\widehat{C}}_{+}^2\right)=\mathbf{Tr}({\widehat{C}}_{ad}^2-{\widehat{C}}_{-}^2)=\frac{3}{4}dim\mathfrak{g},\\ \mathbf{Tr}\left(\mathbf{K}\right)=dim\mathfrak{g},\mathbf{Tr}\left(\mathbf{I}\right)={(dim\mathfrak{g})}^2,\mathbf{Tr}\left(\mathbf{P}\right)=dim\mathfrak{g}.\end{array}$$

(19)

where $\mathbf{Tr}\equiv {\mathrm{Tr}}_1{\mathrm{Tr}}_2$ is the trace in the space $V_{ad}\otimes V_{ad}$ (as usual the indices 1 and 2 are attributed to factors in the product $V_{ad}\otimes V_{ad}$). These formulas will be used in what follows.

Using the characteristic identity (14) for the operator ${\widehat{C}}_{-}$, one can construct two mutually orthogonal projectors

$$P_1=-2{\widehat{C}}_{-},P_2=2{\widehat{C}}_{-}+{\mathbf{P}}_{-}^{(ad)}\Rightarrow P_i{P}_k=P_i{\delta }_{ik},$$

(20)

which decompose the anti-symmetrized part ${\mathbf{P}}_{-}^{\left(ad\right)}(ad\otimes ad)$ of the representation $(ad\otimes ad)$ into two sub-representations ${\mathsf{X}}_{1,2}=P_{1,2}(ad\otimes ad)$. The dimensions of these sub-representations are equal to the traces of corresponding projectors (20):

$$dim{\mathsf{X}}_1=\mathbf{Tr}\left(P_1\right)=dim\mathfrak{g},dim{\mathsf{X}}_2=\mathbf{Tr}\left(P_2\right)=\frac{1}{2}dim\mathfrak{g}(dim\mathfrak{g}-3),$$

(21)

where we use the general formulae (19). Since the constants $C_{b_1{b}_2}^d$ play the role of the Clebsch–Gordan coefficients for the fusion ${ad}^{\otimes 2}\to ad$, we see from the explicit form (17) of the operator ${\widehat{C}}_{-}$ that the projector $P_1$, given in (20), extracts the adjoint representation ${\mathsf{X}}_1=ad$ in ${\mathbf{P}}_{-}^{\left(ad\right)}\left({ad}^{\otimes 2}\right)$. Thus, the adjoint representation is always contained in the anti-symmetrized part ${\mathbf{P}}_{-}^{\left(ad\right)}\left({ad}^{\otimes 2}\right)$. The first formula in (21) confirms the equivalence of ${\mathsf{X}}_1$ and ad. Note also that ${\mathsf{X}}_2$ is not necessarily an irreducible representation for all simple Lie algebras (for the details, see [3]).

2.3. Universal Characteristic Identities for Operator ${\widehat{\mathit{C}}}_{+}$ in the Case of Lie Algebras of Classical Series

It was shown in [3] that for the algebras of the classical series $A_n,B_n,C_n,D_n$ the characteristic identities for the operator ${\widehat{C}}_{+}$ in the adjoint representation can be written in a generic form:

$${\widehat{C}}_{+}^3+\frac{1}{2}{\widehat{C}}_{+}^2={\mu }_1{\widehat{C}}_{+}+{\mu }_2({\mathbf{I}}^{\left(ad\right)}+{\mathbf{P}}^{\left(ad\right)}-2\mathbf{K}),$$

(22)

where ${\mu }_1$ and ${\mu }_2$ are the parameters of the simple Lie algebras as we define these parameters at the moment. Multiplying both sides of Equation (22) by $\mathbf{K}$ and using the relations

$$\mathbf{K}({\mathbf{I}}^{\left(ad\right)}+{\mathbf{P}}^{\left(ad\right)})=2\mathbf{K},\mathbf{K}{\widehat{C}}_{+}=-\mathbf{K},\mathbf{K}·\mathbf{K}=dim\mathfrak{g}·\mathbf{K},$$

one may express the dimension of the Lie algebra $\mathfrak{g}$ through the parameters ${\mu }_1$ and ${\mu }_2$:

$$dim\mathfrak{g}=\frac{2{\mu }_2-{\mu }_1+1/2}{2{\mu }_2}.$$

(23)

Then, we multiply both sides of (22) by ${\mathbf{P}}_{+}^{\left(ad\right)}({\widehat{C}}_{+}+1)$ and deduce the characteristic identity for ${\widehat{C}}_{+}$ projected onto the subspace ${\mathbf{P}}_{+}^{\left(ad\right)}\left(V_{ad}^{\otimes 2}\right)\equiv \frac{1}{2}({\mathbf{I}}^{(ad)}+{\mathbf{P}}^{(ad)})\left(V_{ad}^{\otimes 2}\right)$:

$${\mathbf{P}}_{+}^{\left(ad\right)}({\widehat{C}}_{+}+1)({\widehat{C}}_{+}^3+\frac{1}{2}{\widehat{C}}_{+}^2-{\mu }_1{\widehat{C}}_{+}-2{\mu }_2)=0,$$

(24)

which can be written in a factorized form:

$${\mathbf{P}}_{+}^{\left(ad\right)}({\widehat{C}}_{+}+1)({\widehat{C}}_{+}+\frac{\alpha }{2t})({\widehat{C}}_{+}+\frac{\beta }{2t})({\widehat{C}}_{+}+\frac{\gamma }{2t})=0\iff {\mathbf{P}}_{+}^{\left(ad\right)}\prod _{i=1}^4({\widehat{C}}_{+}-a_i)=0.$$

(25)

Here, we introduce the notation for the roots of the identity (24)

$$a_1=-1,a_2=-\frac{\alpha }{2t},a_3=-\frac{\beta }{2t},a_4=-\frac{\gamma }{2t},t=\alpha +\beta +\gamma ,$$

(26)

and the last equation follows from the condition $(a_2+a_3+a_4)=-1/2$, which is obtained from the comparison of (24) and (25). The parameter t normalizes the eigenvalues of the operator ${\widehat{C}}_{+}$. For each simple Lie algebra $\mathfrak{g}$ we choose $t^{-1}$ such that

$$\left(\theta ,\theta \right)=\frac{1}{t},$$

(27)

where $\theta$ is the highest root of $\mathfrak{g}$. Thus, t coincides with the dual Coxeter number $h^{\vee }$ of the algebra $\mathfrak{g}$. The parameters $\alpha ,\beta ,\gamma$ were introduced by Vogel [8]. The values of these parameters for the algebras $A_n,B_n,C_n,D_n$ are summarized in Table 1.

Table 1. The Vogel parameters for the Lie Algebras of Classical Series.

	$\mathit{s}\mathit{\ell }(\mathit{n}+1)$	$\mathit{so}(2\mathit{n}+1)$	$\mathit{sp}\left(2\mathit{n}\right)$	$\mathit{so}\left(2\mathit{n}\right)$
t	$n+1$	$2n-1$	$n+1$	$2n-2$
$\frac{\alpha }{2t}$	$-1/(n+1)$	$-1/(2n-1)$	$-1/(n+1)$	$-1/(2n-2)$
$\frac{\beta }{2t}$	$1/(n+1)$	$2/(2n-1)$	$1/(2n+2)$	$1/(n-1)$
$\frac{\gamma }{2t}$	$1/2$	$(2n-3)/(4n-2)$	$(n+2)/(2n+2)$	$(n-2)/(2n-2)$

Here we encounter an interesting non-linear diophantine problem of finding all integers $dim\mathfrak{g}$ in (29) for which the parameters $\alpha ,\beta$,$\gamma$ and $dim{V}_{\left(a_i\right)}$ are integers. The partial solutions of this problem are given in Table 1. The analogous diophantine problems were considered in [14,15].

Comparison of Equations (24) and (25) implies that the parameters ${\mu }_1$ and ${\mu }_2$ are expressed via the Vogel parameters as

$${\mu }_1=-\frac{\alpha \beta +\alpha \gamma +\beta \gamma }{4t^2},{\mu }_2=-\frac{\alpha \beta \gamma }{16t^3},$$

(28)

and the dimensions (23) of the simple Lie algebras acquire a remarkable universal form obtained by Deligne and Vogel [8,16]:

$$dim\mathfrak{g}=\frac{(\alpha -2t)(\beta -2t)(\gamma -2t)}{\alpha \beta \gamma }.$$

(29)

Now, by using the characteristic identity (25), one can obtain the universal form of the projectors $P_{\left(a_i\right)}^{(+)}$ on the invariant subspaces $V_{\left(a_i\right)}$ in the symmetrized space ${\mathbf{P}}_{+}^{(ad)}\left(V_{ad}^{\otimes 2}\right)$:

$$\begin{array}{c}{P}_{(-\frac{\alpha }{2t})}^{(+)}=\frac{4t^2}{(\beta -\alpha )(\gamma -\alpha )}\left({\widehat{C}}_{+}^2+\left(\frac{1}{2}-\frac{\alpha }{2t}\right){\widehat{C}}_{+}+\frac{\beta \gamma }{8t^2}\left({\mathbf{I}}^{(ad)}+{\mathbf{P}}^{(ad)}-\frac{2\alpha }{(\alpha -2t)}\mathbf{K}\right)\right)\equiv P^{(+)}\left(\alpha \right|\beta ,\gamma ),\hfill \end{array}$$

$$P_{(-\frac{\beta }{2t})}^{(+)}=P^{(+)}\left(\beta \right|\alpha ,\gamma ),P_{(-\frac{\gamma }{2t})}^{(+)}=P^{(+)}\left(\gamma \right|\alpha ,\beta ),P_{(-1)}^{(+)}=\frac{1}{dim\mathfrak{g}}\mathbf{K}.$$

The irreducible representations that act in the subspaces $V_{(-1)}$, $V_{(-\frac{\alpha }{2t})}$, $V_{(-\frac{\beta }{2t})}$, $V_{(-\frac{\gamma }{2t})}$ were respectively denoted in [8] as ${\mathsf{X}}_0$, $Y_2\left(\alpha \right)$, $Y_2\left(\beta \right)$, $Y_2\left(\gamma \right)$; see Section 3 below. Finally, we calculate (by means of trace Formulas (19)) the universal expressions [8] for the dimensions of the invariant eigenspaces $V_{\left(a_i\right)}$:

$$\begin{array}{ccc}& & dim{V}_{(-1)}=\mathbf{Tr}{P}_{(-1)}^{(+)}=1,\hfill \end{array}$$

$$\begin{array}{ccc}& & dim{V}_{(-\frac{\alpha }{2t})}=\mathbf{Tr}{P}_{(-\frac{\alpha }{2t})}^{(+)}=-\frac{(3\alpha -2t)(\beta -2t)(\gamma -2t)t(\beta +t)(\gamma +t)}{{\alpha }^2(\alpha -\beta )\beta (\alpha -\gamma )\gamma },\hfill \end{array}$$

(30)

$$\begin{array}{ccc}\hfill & & dim{V}_{(-\frac{\beta }{2t})}=\mathbf{Tr}{P}_{(-\frac{\beta }{2t})}^{(+)}=-\frac{(3\beta -2t)(\alpha -2t)(\gamma -2t)t(\alpha +t)(\gamma +t)}{{\beta }^2(\beta -\alpha )\alpha (\beta -\gamma )\gamma },\hfill \end{array}$$

(31)

$$\begin{array}{ccc}& & dim{V}_{(-\frac{\gamma }{2t})}=\mathbf{Tr}{P}_{(-\frac{\gamma }{2t})}^{(+)}=-\frac{(3\gamma -2t)(\beta -2t)(\alpha -2t)t(\beta +t)(\alpha +t)}{{\gamma }^2(\gamma -\beta )\beta (\gamma -\alpha )\alpha }.\hfill \end{array}$$

(32)

2.4. Universal Characteristic Identities for Operator $\widehat{C}$ in the Case of Exceptional Lie Algebras

The antisymmetric parts of the split Casimir operators ${\widehat{C}}_{-}$ for all simple Lie algebras in the adjoint representation obey the same identity (14):

$${\widehat{C}}_{-}\left({\widehat{C}}_{-}+\frac{1}{2}\right)=0.$$

(33)

The symmetric parts of the split Casimir operators ${\widehat{C}}_{+}$ in the adjoint representation for the exceptional Lie algebras obey identities that have a similar structure (The universal formulae (34) were obtained in [2], eq. (17.10), under the assumption that ${\widehat{C}}_{+}^2$ is expressed as a linear combination of $\mathfrak{g}$-invariant operators $(\mathbf{I}+\mathbf{P})$, $\mathbf{K}$ and ${\widehat{C}}_{+}$. We explicitly checked this assumption for all exceptional Lie algebras [3].)

$${\widehat{C}}_{+}^2=-\frac{1}{6}{\widehat{C}}_{+}+\mu \left(\mathbf{I}+\mathbf{P}+\mathbf{K}\right),$$

(34)

where the universal parameter $\mu$ is fixed as follows:

$$\mu =\frac{5}{6(2+dim(\mathfrak{g}\left)\right)}.$$

(35)

Note that the identities for the algebras $s\ell \left(3\right)$ and $so\left(8\right)$ have the same structure.

From (34) one can obtain the universal characteristic identity on the symmetric part of the split Casimir operator ${\widehat{C}}_{+}$ projected onto the subspace ${\mathbf{P}}_{+}^{\left(ad\right)}\left(V_{ad}^{(\otimes 2}\right)$:

$${\mathbf{P}}_{+}^{\left(ad\right)}({\widehat{C}}_{+}+1)({\widehat{C}}_{+}^2+\frac{1}{6}{\widehat{C}}_{+}-2\mu )\equiv {\mathbf{P}}_{+}^{\left(ad\right)}({\widehat{C}}_{+}+1)({\widehat{C}}_{+}+\frac{\alpha }{2t})({\widehat{C}}_{+}+\frac{\beta }{2t})=0,$$

(36)

where we introduced the notation for two eigenvalues of the ${\widehat{C}}_{+}$:

$$\frac{\alpha }{2t}=\frac{1-{\mu }^{\prime }}{12},\frac{\beta }{2t}=\frac{1+{\mu }^{\prime }}{12},{\mu }^{\prime }:=\sqrt{1+288\mu }=\sqrt{\frac{dim\mathfrak{g}+242}{dim\mathfrak{g}+2}}.$$

(37)

According to (36), these parameters are related as

$$3(\alpha +\beta )=t.$$

With the fixed value of the parameter $\alpha$, this relation defines the line of the exceptional Lie algebras on the $\beta ,t$ plane (see Equation (47) below). Following [2], note that ${\mu }^{\prime }$ is a rational number only for a certain sequence of dimensions $dim\mathfrak{g}$. It turns out that this sequence is finite (We thank D. O. Orlov who proved the finiteness of this sequence):

$$\begin{array}{c}dim\mathfrak{g}=3,8,14,28,47,52,78,96,119,133,190,248,287,336,\\ 484,603,782,1081,1680,3479,\end{array}$$

(38)

which includes the dimensions $14,52,78,133,248$ of the exceptional Lie algebras ${\mathfrak{g}}_2,{\mathfrak{f}}_4,{\mathfrak{e}}_6,{\mathfrak{e}}_7,{\mathfrak{e}}_8$, and the dimensions 8 and 28 of the algebras $s\ell \left(3\right)$ and $so\left(8\right)$, which are sometimes also referred to as exceptional. Thus, for these algebras, using (37), we calculate the values of the parameters $\frac{\alpha }{2t},\frac{\beta }{2t}$ given in Table 2.

Table 2. The Vogel parameters for the exceptional Lie algebras.

	$\mathit{s}\mathit{\ell }\left(3\right)$	$\mathit{so}\left(8\right)$	${\mathfrak{g}}_2$	${\mathfrak{f}}_4$	${\mathfrak{e}}_6$	${\mathfrak{e}}_7$	${\mathfrak{e}}_8$
$\frac{\alpha }{2t}$	$-1/3$	$-1/6$	$-1/4$	$-1/9$	$-1/12$	$-1/18$	$-1/30$
$\frac{\beta }{2t}$	$1/2$	$1/3$	$5/12$	$5/18$	$1/4$	$2/9$	$1/5$

Taking into account that ${\widehat{C}}_{-}$ satisfies (14) and ${\widehat{C}}_{+}$ satisfies (36), we obtain the following identities for the total split Casimir operator ${\widehat{C}}_{ad}=({\widehat{C}}_{+}+{\widehat{C}}_{-})$ in the case of the exceptional Lie algebras:

$${\widehat{C}}_{ad}\left({\widehat{C}}_{ad}+\frac{1}{2}\right)\left({\widehat{C}}_{ad}+1\right)\left({\widehat{C}}_{ad}^2+\frac{1}{6}{\widehat{C}}_{ad}-2\mu \right)=0\Rightarrow$$

(39)

$${\widehat{C}}_{ad}\left({\widehat{C}}_{ad}+\frac{1}{2}\right)\left({\widehat{C}}_{ad}+1\right)\left({\widehat{C}}_{ad}+\frac{\alpha }{2t}\right)\left({\widehat{C}}_{ad}+\frac{\beta }{2t}\right)=0.$$

(40)

Here $\mu$ is defined in (35) and $\frac{\alpha }{2t},\frac{\beta }{2t}$ are given in Table 2.

Remark 1.

The sequence (38) contains dimensions $dim{\mathfrak{g}}^{*}=(10m-122+360/m)$, $(m\in \mathbb{N})$ referring to the adjoint representations of the so-called $E_8$ family of algebras ${\mathfrak{g}}^{*}$; see [2], eq. (21.1). For these dimensions we have the relation ${\mu }^{\prime }=|(m+6)/(m-6)|$. The two numbers 47 and 119 from the sequence (38) do not belong to the sequence $dim{\mathfrak{g}}^{*}$. Thus, the interpretation of these two numbers as dimensions of some algebras is missing. Moreover, for values $dim\mathfrak{g}$ given in (38), using (37), one can calculate dimensions (30) of the corresponding representations $Y\left(\alpha \right)$:

$$\begin{array}{c}dim{V}_{(-\frac{\alpha }{2t})}=\left\{5,27,77,300,\frac{14553}{17},1053,2430,\frac{48608}{13},\frac{111078}{19},7371,15504,27000,\right.\\ \left.\frac{841279}{23},\frac{862407}{17},107892,\frac{2205225}{13},\frac{578151}{2},559911,\frac{42507504}{31},\frac{363823677}{61}\right\}\end{array}$$

Since $dim{V}_{(-\frac{\alpha }{2t})}$ should be an integer, we conclude that no Lie algebras exist with dimensions $47,96,119,287,336,603,782,1680,3479$, for which we assume characteristic identity (36) and the trace Formulas (19).

3. Universal Characteristic Identities for Operator $\widehat{\mathbf{C}}$ and Vogel Parameters

In Section 2.2 and Section 2.3 we constructed the projectors onto the spaces of irreducible sub-representations in the representation ${ad}^{\otimes 2}$ for all simple Lie algebras of classical series $A_n,B_n,C_n,D_n$. In all cases, the construction was carried out by finding the characteristic identities for the split Casimir operators. We note that the construction of projectors in terms of the split Casimir operator and finding the dimensions of the corresponding subspaces can be obtained by using the Vogel parameters $\alpha ,\beta$ and $\gamma$, which were introduced in [8] (see also [5,17]). The values of the Vogel parameters specify simple Lie algebras and we present these values in Table 3 (see below). Since all universal formulas for the simple Lie algebras are written as homogeneous and symmetric functions of the parameters $\alpha ,\beta$ and $\gamma$, one can consider simple Lie algebras as points in the space ${\mathbb{RP}}^3/{\mathbb{S}}_3$. It is convenient to choose a normalization of the parameters such that $\alpha =-2$, see Table 3. Note that the data in the first six lines of Table 3 coincide with the data given in Table 1 of Section 2.3. We list the Vogel parameters for the algebras $s\ell \left(3\right)$ and $so\left(8\right)$ in the separate lines of Table 3, since the characteristic identities for the symmetric part ${\widehat{C}}_{+}$ of the split Casimir operator in the adjoint representations have the same order and the same structure as for the exceptional Lie algebras (see [3]).

Table 3. The Vogel parameters for the simple Lie algebras.

Type	Lie Algebra	$\mathit{\alpha }$	$\mathit{\beta }$	$\mathit{\gamma }$	t	$-\frac{\mathit{\alpha }}{2\mathit{t}}=\frac{1}{\mathit{t}}$	$-\frac{\mathit{\beta }}{2\mathit{t}}$	$-\frac{\mathit{\gamma }}{2\mathit{t}}$
$A_n$	$s\ell (n+1)$	$-2$	2	$n+1$	$n+1$	$\frac{1}{n+1}$	$-\frac{1}{n+1}$	$-1/2$
$B_n$	$so(2n+1)$	$-2$	4	$2n-3$	$2n-1$	$\frac{1}{2n-1}$	$-\frac{2}{2n-1}$	$-\frac{2n-3}{2(2n-1)}$
$C_n$	$sp\left(2n\right)$	$-2$	1	$n+2$	$n+1$	$\frac{1}{n+1}$	$-\frac{1}{2(n+1)}$	$-\frac{n+2}{2(n+1)}$
$D_n$	$so\left(2n\right)$	$-2$	4	$2n-4$	$2n-2$	$\frac{1}{2n-2}$	$-\frac{1}{n-1}$	$-\frac{n-2}{2(n-1)}$
$A_2$	$s\ell \left(3\right)$	$-2$	2	3	3	$1/3$	$-1/3$	$-1/2$
$D_4$	$so\left(8\right)$	$-2$	4	4	6	$1/6$	$-1/3$	$-1/3$
$G_2$	${\mathfrak{g}}_2$	$-2$	$10/3$	$8/3$	4	$1/4$	$-5/12$	$-1/3$
$F_4$	${\mathfrak{f}}_4$	$-2$	5	6	9	$1/9$	$-5/18$	$-1/3$
$E_6$	${\mathfrak{e}}_6$	$-2$	6	8	12	$1/12$	$-1/4$	$-1/3$
$E_7$	${\mathfrak{e}}_7$	$-2$	8	12	18	$1/18$	$-2/9$	$-1/3$
$E_8$	${\mathfrak{e}}_8$	$-2$	12	20	30	$1/30$	$-1/5$	$-1/3$

As usual, we split the tensor product of two adjoint representations into the symmetric and antisymmetric parts:

$$ad\otimes ad={\mathbf{P}}_{+}^{\left(ad\right)}(ad\otimes ad)+{\mathbf{P}}_{-}^{\left(ad\right)}(ad\otimes ad).$$

(41)

In the general case of the Lie algebras of the classical series (the algebras $s\ell \left(3\right)$ and $so\left(8\right)$ are exceptional cases), the symmetric part ${\mathbf{P}}_{+}^{\left(ad\right)}\left({ad}^{\otimes 2}\right)$ decomposes into four irreducible representations (see, e.g., [8]): a singlet, denoted as ${\mathsf{X}}_0$, with a zero eigenvalue of the quadratic Casimir operator $C_{\left(2\right)}$ (which corresponds to the eigenvalue $(-1)$ for the split operator $\widehat{C}$), and three representations that we denote as $Y_2\left(\alpha \right),Y_2\left(\beta \right) \mathrm{and} Y_2\left(\gamma \right)$. Their dimensions, as well as the corresponding values of the quadratic Casimir operator $C_{\left(2\right)}$ (defined in (4)) and split Casimir operator $\widehat{C}$ are equal to:

$$\begin{array}{cc}\hfill dim{Y}_2\left(\alpha \right)& =dim{V}_{(-\frac{\alpha }{2t})},C_{\left(2\right)}=2-\frac{\alpha }{t},\widehat{C}=-\frac{\alpha }{2t},\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill dim{Y}_2\left(\beta \right)& =dim{V}_{(-\frac{\beta }{2t})},C_{\left(2\right)}=2-\frac{\beta }{t},\widehat{C}=-\frac{\beta }{2t},\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill dim{Y}_2\left(\gamma \right)& =dim{V}_{(-\frac{\gamma }{2t})},C_{\left(2\right)}=2-\frac{\gamma }{t},\widehat{C}=-\frac{\gamma }{2t}.\hfill \end{array}$$

(44)

where the explicit expressions for $dim{V}_{(-\frac{\alpha }{2t})}$, $dim{V}_{(-\frac{\beta }{2t})}$ and $dim{V}_{(-\frac{\gamma }{2t})}$ are given in (30)–(32), respectively, and the eigenvalues of the operators $C_{\left(2\right)}$ and $\widehat{C}$ are related by the condition:

$$\widehat{C}=\frac{1}{2}{C}_{\left(2\right)}-1.$$

(45)

The eigenvalues of the operator $\widehat{C}$ on the representations $Y_2\left(\alpha \right),Y_2\left(\beta \right),Y_2\left(\gamma \right)$ in ${\mathbf{P}}_{+}^{\left(ad\right)}(ad\times ad)$ are presented in the three last columns of Table 3. Therefore, taking into account that ${\widehat{C}}_{+}$ has four eigenvalues $(-1,-\frac{\alpha }{2t},-\frac{\beta }{2t},-\frac{\gamma }{2t})$ and ${\widehat{C}}_{-}$ has two eigenvalues $(0,-\frac{1}{2})$, the generic characteristic identity for the split Casimir operator reads:

$${\widehat{C}}_{ad}({\widehat{C}}_{ad}+\frac{1}{2})({\widehat{C}}_{ad}+1)({\widehat{C}}_{ad}+\frac{\alpha }{2t})({\widehat{C}}_{ad}+\frac{\beta }{2t})({\widehat{C}}_{ad}+\frac{\gamma }{2t})=0.$$

(46)

In the case of the $s\ell \left(N\right)$ algebras, the eigenvalue $(-1/2)$ of the operator ${\widehat{C}}_{ad}$ is doubly degenerated, since $\frac{\gamma }{2t}=1/2$; therefore, in the identity (46) one should keep only one factor $({\widehat{C}}_{ad}+\frac{1}{2})$ of two.

We now turn to the discussion of the case of the exceptional Lie algebras. Note that all exceptional Lie algebras are distinguished in Table 3 by the value of the parameter $\gamma /\left(2t\right)$ being equal to $1/3$ (all other parameters of the exceptional Lie algebras in Table 3 are in agreement with the parameters listed in Table 2 of Section 2.4). Thus, all exceptional Lie algebras in the three-dimensional space of the Vogel parameters $(\alpha ,\beta ,\gamma )$ lie in the plane $\alpha =-2$ on the line:

$$3\gamma =2t\Rightarrow \gamma =2\beta -4.$$

(47)

We chose the coordinates $(\beta ,\gamma )$ on this plane and visualized all simple Lie algebras as points on this plane (Vogel map):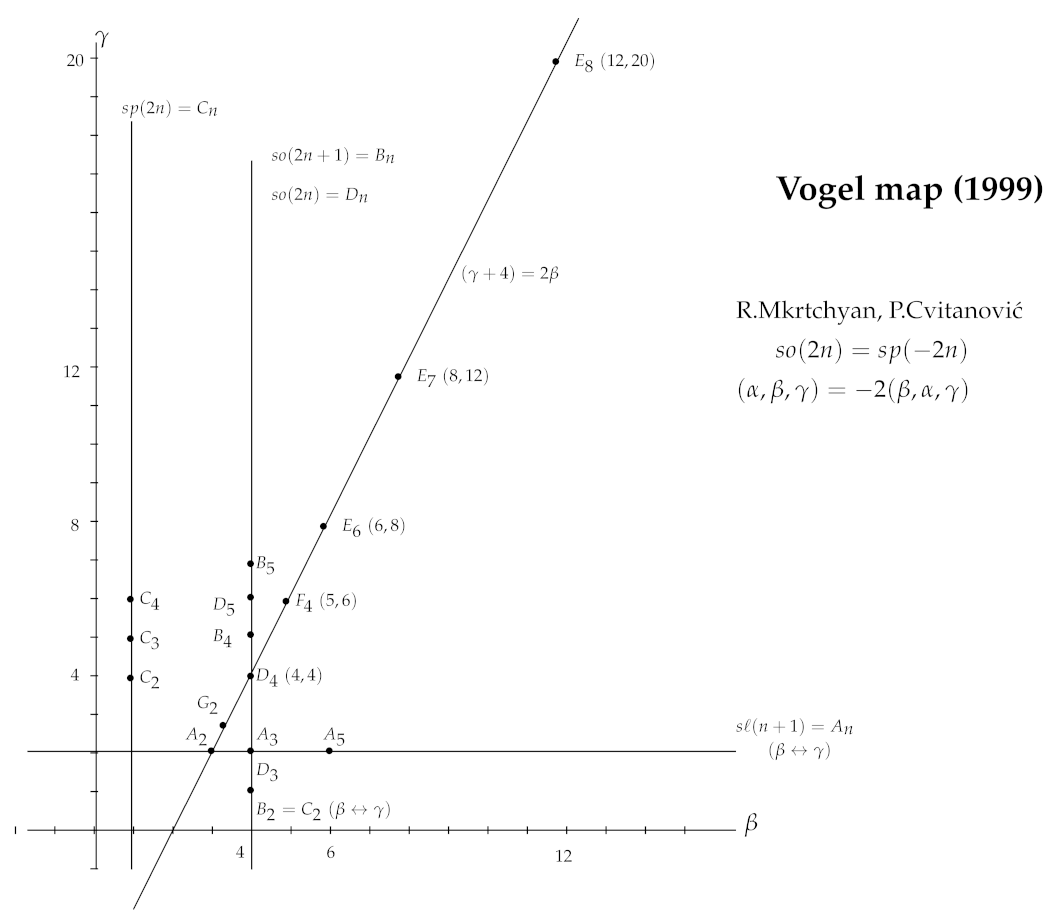

When Condition (47) is fulfilled, Dimension (32) and (44) of the space of the representation $Y_2\left(\gamma \right)$ is zero in view of the factor $(3\gamma -2t)$ in the numerator of (32). Hence the corresponding projector $P_{(-\frac{\gamma }{2t})}$ on this space is also equal to zero and the parameter $-\gamma /\left(2t\right)$ cannot be an eigenvalue of ${\widehat{C}}_{ad}$. In this case, in the general characteristic identity (46) for the operator ${\widehat{C}}_{ad}=(ad\otimes ad)\left(\widehat{C}\right)$, the last factor $({\widehat{C}}_{ad}+\frac{\gamma }{2t})$ will be absent and the universal characteristic identity coincides with (40):

$${\widehat{C}}_{ad}({\widehat{C}}_{ad}+\frac{1}{2})({\widehat{C}}_{ad}+1)({\widehat{C}}_{ad}+\frac{\alpha }{2t})({\widehat{C}}_{ad}+\frac{\beta }{2t})=0.$$

(48)

As we showed in Section 2.4, identity (48) for the values of the parameters $\alpha ,\beta$ given in Table 2 and Table 3 exactly reproduces the characteristic identities for the split Casimir operator ${\widehat{C}}_{ad}$ in the case of the exceptional Lie algebras. Note that both algebras $so\left(8\right)$ and $s\ell \left(3\right)$ (the latter one has to replace the parameters $\beta \leftrightarrow \gamma$) lie on the line (47) and the characteristic identities are also given by the generic Formula (48). Indeed, for the algebra $s\ell \left(3\right)$, we have $\frac{\gamma }{2t}=\frac{1}{2}$; therefore, the eigenvalue $(-1/2)$ of the operator ${\widehat{C}}_{ad}$ is doubly degenerated and one of the factors $({\widehat{C}}_{ad}+1/2)$ in (46) must be omitted. By contrast, for the algebra $so\left(8\right)$ both parameters $\frac{\beta }{2t}$ and $\frac{\gamma }{2t}$ are equal to the critical value $\frac{1}{3}$, which gives zero in denominators of Expressions (31), (43) and (32), (44) for the dimensions $dim{V}_{(-\frac{\beta }{2t})}$ and $dim{V}_{(-\frac{\gamma }{2t})}$ of the representations $Y_2\left(\beta \right)$ and $Y_2\left(\gamma \right)$, respectively. However, these zeros are cancelled by zeros coming from the terms $(3\beta -2t)$ and $(3\gamma -2t)$ in the numerators of the expressions for $dim{V}_{(-\frac{\beta }{2t})}$, $dim{V}_{(-\frac{\gamma }{2t})}$ and these dimensions turn out to be 35. Since the eigenvalue $-\frac{\beta }{2t}=-\frac{\gamma }{2t}=-\frac{1}{3}$ of the operator ${\widehat{C}}_{ad}$ is doubly degenerated, we must omit one of the factors $({\widehat{C}}_{ad}+1/3)$ in (46) and this identity is transformed into identity (48).

The antisymmetric part ${\mathbf{P}}_{-}^{\left(ad\right)}(ad\otimes ad)$ decomposes for all simple Lie algebras into a direct sum of two terms, ${\mathsf{X}}_1$ and ${\mathsf{X}}_2$ (see Section 2.2), one of which, ${\mathsf{X}}_1$, is the adjoint representation ad with the value of the quadratic Casimir $C_{\left(2\right)}^{(ad)}=1$, and the other representation, ${\mathsf{X}}_2$, has the value of the quadratic Casimir $C_{\left(2\right)}^{\left({\mathsf{X}}_2\right)}=2$. The representation ${\mathsf{X}}_2$ is reducible for the case of algebras $s\ell \left(N\right)$ and irreducible for all other simple Lie algebras. The dimension of the representations ${\mathsf{X}}_1,{\mathsf{X}}_2$ and the corresponding eigenvalues ${\widehat{C}}^{(ad)}$ and ${\widehat{C}}^{\left({\mathsf{X}}_2\right)}$ of the split Casimir operator are equal to (cf. (21)):

$$\begin{array}{c}dim{\mathsf{X}}_1=dim\mathfrak{g},{\widehat{C}}^{(ad)}=-1/2,\\ dim{\mathsf{X}}_2=\frac{1}{2}dim\mathfrak{g}(dim\mathfrak{g}-3),{\widehat{C}}^{\left({\mathsf{X}}_2\right)}=0.\end{array}$$

The values ${\widehat{C}}^{(ad)}$ and ${\widehat{C}}^{\left({\mathsf{X}}_2\right)}$ agree with the characteristic identity (14) for the antisymmetrized part of ${\widehat{C}}_{-}$, which is valid for all simple Lie algebras.

4. Conclusions

In this paper, we demonstrated the usefulness of the $\mathfrak{g}$-invariant split Casimir operator $\widehat{C}$ in the representation theory of Lie algebras. Namely, for all simple Lie algebras $\mathfrak{g}$, explicit formulas were found for invariant projectors onto irreducible representations that appear in the expansion of the tensor product $T^{\otimes 2}$ of two adjoint representations. These projectors are constructed in terms of the operator $\widehat{C}$. The key role of this approach is to play the characteristic identities for the split Casimir operator. It is quite remarkable that these identities have the generic form (46), which depends on Vogel parameters only. If for some algebra one of the factor becomes equal to zero, it has to be omitted and the corresponding identity has a lower degree in terms of the split Casimir operator.

One hope the proposed approach will also be useful for the analysis of the structure of the tensor product of $T^{\otimes 3}$ of three adjoint representations. The dimensions of the irreducible representations that appear in the expansion of the tensor product $T^{\otimes 3}$ are well known [8], whereas the structure of the projectors is missing. We are planning to report the corresponding results elsewhere.