A 2D Hyperchaotic Map: Amplitude Control, Coexisting Symmetrical Attractors and Circuit Implementation

Abstract

An absolute value function was introduced for chaos construction, where hyperchaotic oscillation was found with amplitude rescaling. The nonlinear absolute term brings the convenience for amplitude control. Two regimes of amplitude control including total and partial amplitude control are discussed, where the attractor can be rescaled separately by two independent coefficients. Symmetrical pairs of coexisting attractors are captured by corresponding initial conditions. Circuit implementation by the platform STM32 is consistent with the numerical exploration and the theoretical observation. This finding is helpful for promoting discrete map application, where amplitude control is realized in an easy way and coexisting symmetrical sequences with opposite polarity are obtained.

1. Introduction

Chaos has been widely used in image encryption [1,2,3,4,5,6] and secure communication [7,8,9]. Adjusting the amplitude of chaos without damaging its engineering application is an important issue because of the butterfly effect. However, there is still much work to do for the rescaling of broadband chaotic sequences. Difficulty modulation with broadband chaotic signal, amplitude [10,11,12,13], symmetry [14,15,16,17], and multistability [18,19,20,21] have been extensively studied in a nonlinear field. In practical engineering applications, linear transformations are usually necessary but sometimes are unpermitted to obtain the required geometric scale in designed hardware. The difficulty hidden in circuit design and debugging increases the value of amplitude control in chaos.

The non-bifurcation parameter is usually applied in the dynamical system to rescale the signal amplitude without changing the Lyapunov exponents, which is significant for the application of chaos. Appropriate signal control can save the modulator in chaos-based applications, including amplitude control [22,23,24] and offset control [25,26,27,28]. In continuous systems, amplitude control with independent control knobs and coexisting symmetric attractors have been widely studied, but in discrete mapping the amplitude control with a single parameter has not received enough attention. For example [29,30,31,32], the multi-stable phenomenon of the map has been discussed in detail, and the position of the phase trajectory through the multistability to achieve the purpose of amplitude control was given, but this ignored a method of directly adjusting the signal amplitude with a single knob. Besides, in many discrete maps like [33], although there are abundant attractor coexistence phenomena, there are no symmetrical coexisting attractors.

In this paper, a two-dimensional hyperchaotic map was given with two independent amplitude knobs, and the map also had a pair of symmetrical coexisting attractors in some cases. The amplitude control characteristics of the map and the symmetry of the coexisting attractors are analyzed. In Section 2, the hyperchaotic mapping model is constructed and the basic chaotic dynamics behavior is analyzed. In Section 3, the realization method of amplitude control is discussed. The symmetry of the coexisting attractors is discussed in Section 4. In Section 5, the map is implemented through a digital platform. Finally, we give the conclusions and discussion.

2. A New 2D Hyperchaotic Map and Its Dynamic Analysis

2.1. Model and Its Fixed Points Analysis

Absolute value function is often applied to realize chaos in continuous systems [34,35], and here adding absolute value function into discrete mapping as follows

$$\{\begin{array}{l}{x}_{n+1}=a{x}_n+b{x}_n\left|y_n\right|\\ y_{n+1}=c{x}_n-1.25y_n\end{array}$$

(1)

where x_n, y_n (n = 1, 2, 3, …) are system state variables; a, b, c, are system parameters, and none of them is zero.

The stability of the above discrete mapping (1) can be analyzed by means of fixed points. The fixed points of discrete mapping are the elements that map to itself in its domain. The fixed points S* = (x*, y*) of the two-dimensional mapping (1) can be solved by the following Equation (2)

$$\{\begin{array}{l}{x}^{\ast }=a{x}^{\ast }+b{x}^{\ast }\left|y^{\ast }\right|\\ y^{\ast }=c{x}^{\ast }-1.25y^{\ast }\end{array}$$

(2)

By solving Equation (2), we can get $\left|y^{\ast }\right|=\frac{1-a}{b}\to b(1-a)>0$.

The Jacobian matrix of map (1) is

$$J=\left[\begin{array}{cc}1& b{x}^{\ast }\mathrm{sgn}(y^{\ast })\\ c& -1.25\end{array}\right]$$

(3)

Substitute the fixed points S* = (x*, y*) = (2.25y*/c, y*) into Equation (3)

$$J^{\ast }=\left[\begin{array}{cc}1& \frac{2.25b{y}^{\ast }\mathrm{sgn}(y^{\ast })}{c}\\ c& -1.25\end{array}\right]$$

(4)

The map characteristic equation corresponds to the matrix J written as follows

$$P(\lambda )=(\lambda +1.25)(\lambda -1)-2.25(1-a)$$

(5)

λ_1,2 are the two eigenvalues of Equation (5). When P(λ) = 0, we can get Δ = 14.0625 − 9a. Then ${\lambda }_{1,2}=\frac{-0.25\pm \sqrt{\mathsf{\Delta }}}{2}$. When $-1<{\lambda }_{1,2}=\frac{-0.25\pm \sqrt{\mathsf{\Delta }}}{2}<1$, we can get 1< a < 11/9. Therefore, if a < 1, b > 0 or a > 11/9, b < 0 the map has unstable fixed points, and if 1 < a < 11/9, b < 0, the map has stable fixed points.

When a = 2.35, b = −1, c = −1, IC = (0.1, 0.1) in map (1), the time series of variables x, y are shown in Figure 1a,b and the phase trajectory is shown in Figure 1c.

Figure 1. The sequence and phase trajectory of map (1) with a = 2.35, b = −1, c = −1, IC = (0.1, 0.1): (a) x(n) sequence, (b) y(n) sequence, and (c) the phase trajectory.

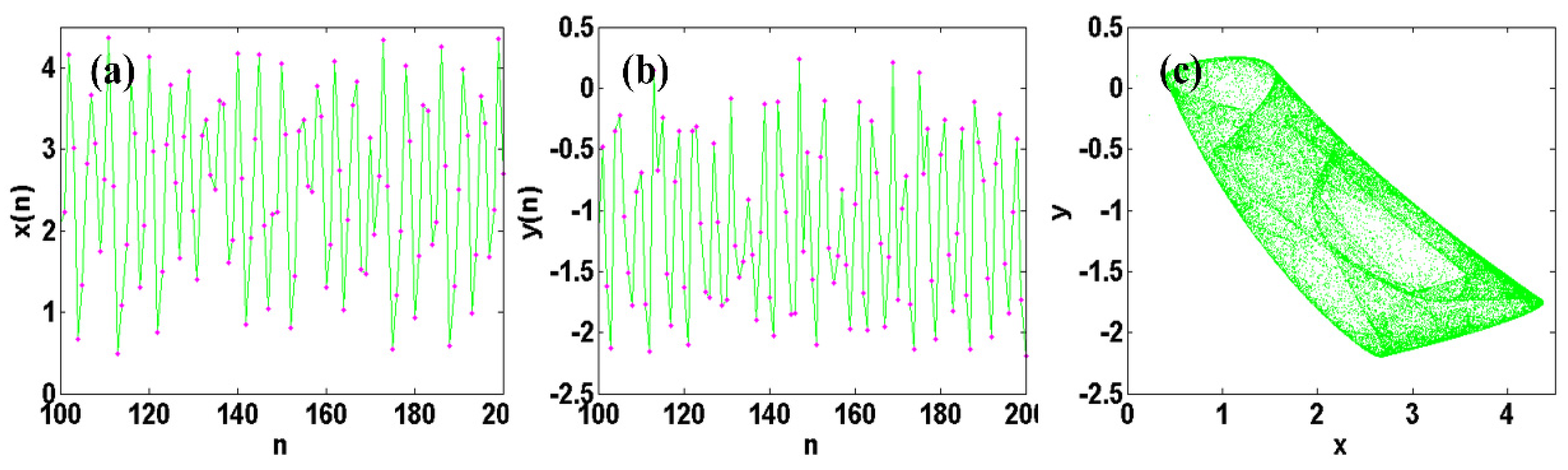
2.2. Bifurcation Analysis

To analyze the nonlinear characteristics of map (1), we set b = −1 and c = −1 and let initial condition IC = (0.1, 0.1), the Lyapunov exponent spectra and bifurcation diagram for the region of a in (−2, 2.4) are shown in Figure 2. When the parameter a varies in ([2, 2.4), it can be seen that when a є (2, 2.15), LE1 = 0, LE2 < 0, the map is in a quasi-periodical state, and its typical coexisting phase trajectories are shown in Figure 3a. When a є (2.2, 2.234), both exponents are negative, the map is in a periodic state, and its typical coexisting phase trajectories are shown in Figure 3b; when a є (2.247, 2.255), (2.257, 2.32), (2.3256, 2.3259), LE1 > 0, LE2 < 0, the map is chaotic, and its typical coexisting phase trajectories are shown in Figure 3c–e; when a є (2.283, 2.4), both Lyapunov exponents are greater than zero, therefore the map is hyperchaotic, and its typical coexisting phase trajectories are shown in Figure 3f. The corresponding Lyapunov exponents under different parameters are shown in Table 1.

Figure 2. Dynamical behavior of map (1) with b = −1, c = −1 and initial conditions IC = (0.1, 0.1): (a) Lyapunov exponents, (b) bifurcation diagram.

Figure 3. Symmetrical coexisting attractors of map (1) with b = −1, c = −1 when (a) a = 2.15, (b) a = 2.23, (c) a = 2.25, (d) a = 2.28, (e) a = 2.3, (f) a = 2.3259.

Table 1. Phase trajectory types and Lyapunov exponents of map (1) when b = −1, c = −1, IC = (−0.1, −0.1).

a	Phase Trajectory Type	LEs
a = 2.15	quasi-period	(0, −0.1914)
a = 2.23	period	(−0.002709, −0.1558)
a = 2.25	chaos	(0.05989, −0.1648)
a = 2.28	chaos	(0.1041, −0.01998)
a = 2.3	hyperchaos	(0.1403, 0.07291)
a = 2.3259	chaos	(0.04464, −0.02)

3. Amplitude Control

3.1. Total Amplitude Control

The parameter b in the map (1) is a single non-bifurcation knob used for total amplitude control [21]. Let u_n+1 = x_n+1/b, v_n+1 = y_n+1/b, map (1) is changed as follows

$$\{\begin{array}{l}{u}_{n+1}=a{u}_n+b^2{u}_n\left|v_n\right|\\ v_{n+1}=c{u}_n-1.25v_n\end{array}$$

(6)

When b = 1, Equation (6) is equivalent to Equation (1), which indicates that the parameter b of Equation (1) rescales the amplitude of x and y according to 1/b; that is, b is the total amplitude parameter.

Therefore, the output sequences are controlled by the non-bifurcation parameter b. As shown in Figure 4, the amplitude of x, y are rescaled by the non-bifurcation parameter b. When b = −1, the amplitudes of x and y are very large; and with the change of b, it decreases inversely proportional to the absolute value of b. Figure 4c shows the phase trajectory when the control parameter b changes.

Figure 4. Signals and phase trajectories of map (1) with a = 2.35, c = −1, IC = (−0.1, −0.1) under different rescaling parameter b: (a) x(n), (b) y(n), and (c) phase trajectory.

It can be seen from Figure 5 that when the parameter b changes in the range of (−10, 0), the average value of the absolute values of x, y decreases accordingly in inverse proportion to the absolute value of b. The Lyapunov exponents spectrum corresponding to the parameter b in (−10, 0) remain constant as shown in Figure 5a. It further proves that b of map (1) only rescales the amplitude of x without changing the frequency.

Figure 5. Dynamical behavior of map (1) with a = 2.35, c = −1, IC = (−0.1, −0.1) when b varies in [–10, 0]: (a) Lyapunov exponents, (b) average variables of |x| and |y|.

3.2. Partial Amplitude Control

In map (1), the parameter c is a single parameter used for partial amplitude control [15]. Here, let u_n+1 = x_n+1/c, v_n+1 = y_n+1

$$\{\begin{array}{l}{u}_{n+1}=a{u}_n+b{u}_n\left|v_n\right|\\ v_{n+1}=c^2{u}_n-1.25v_n\end{array}$$

(7)

When c =1, Equation (7) is equivalent to Equation (1), which shows that the parameter c rescales the amplitude of x according to 1/c, that is, c is the partial amplitude parameter.

Therefore, the amplitude of output signal x is controlled by the parameter c of map (1). As shown in Figure 6, the amplitude of the signal x is rescaled by c. When c = −1, the amplitude of the x signal is very large, and as c changes, it decreases in inverse proportion to the absolute value of c. Figure 6b shows the phase trajectories when the control parameter c changes.

Figure 6. Feature of amplitude control in map (1) with a = 2.35, b = −1 and IC = (−0.1, −0.1) for the scaling variable c: (a) x signal waveform (b) phase trajectories.

It can also be seen from Figure 7b that when the parameter c changes within the range of (−15, 0), the average value of the absolute value of the state variables x decreases accordingly in inverse proportion to the absolute value of c. The Lyapunov exponents spectrum corresponding to parameter c is shown in Figure 7a, showing that the parameter c of map (1) only rescales the amplitude of the state variable x without adjusting the frequency of it.

Figure 7. Dynamical behavior of map (1) with a = 2.35, b = −1 and IC = (−0.1, −0.1), when c varies in (−15, 0]: (a) Lyapunov exponents, (b) average value of the state variable x.

4. Bistability with Coexisting Symmetrical Attractors

In the following section, we focus on the multistability of the map. Typically, for the special structure of symmetrical maps, there are coexisting attractors in their basins of attraction in the phase space. Map (1) is a symmetric map, which can be proved by the invariance under the transforming x → −x, y → −y. At this time, the polarities on both sides of the map equation remain balanced.

Figure 8 shows the basin of attraction of map (1) with a = 2.35, b = −1, c = −1, which proves its bistability. Here we use the same color to mark the basin of attraction. There are two areas in different colors in the picture, clearly showing the two types of attractors.

Figure 8. Symmetric basins of attraction for map (1) with a = 2.35, b = −1, c = 1, Dark turquoise for IC = (0.1, 0.1), and Light cyan is for IC = (−0.1, −0.1).

The bifurcation of parameter b for the state variable y under different initial values is shown in Figure 9, and Figure 10 shows typical phase trajectories of coexisting symmetric attractors. It can also be seen that the parameter b can modify the symmetric modes of the coexisting attractors under a set of fixed initial conditions. From Figure 10a,b, we can see the parameter b can freely control the polarity of the sequence of y.

Figure 9. Coexisting bifurcation diagrams of map (1) with different initial conditions and a = 2.35, c = −1.

Figure 10. Coexisting symmetric attractors of map (1) with a = 2.35, c = −1: (a) b = −1, and (b) b = 1.

To verify the bistability of map (1), we analyze it in terms of the signal waveforms. Figure 11 shows the signal waveforms of the state variables x, y. The symmetric attractors are controlled under various parameter b and c as shown in Figure 12.

Figure 11. Signal waveforms of map (1) with a = 2.35, b = −1, c = −1, under various initial values: (a) the state variable x, (b) the state variable y.

Figure 12. Symmetric attractors of map (1) at different amplitude parameters: (a) total amplitude control with c = −1, and (b) partial amplitude control with b = −1.

5. Circuit Implementation

In this work, the digital technique is used to demonstrate the dynamic characteristics of map (1). The experimental device mainly includes STM32F103 and 12-bit digital-to-analog conversion module TLV5618. Two signals of the map (1) are output through two 12-bit digital-to-analog converter (DAC) modules. The experimental circuit platform is shown in Figure 13. Given the corresponding parameter values and initial conditions, the typical phase diagram of the chaotic map can be observed in the oscilloscope, as shown in Figure 14.

Figure 13. Experimental platform.

Figure 14. Two modes of the symmetric coexisting attractors in map (1) from the oscilloscope with a = 2.35, c = −1, (a) b = −1, (b) b = 1.

6. Discussion and Conclusions

In this paper, the dynamical properties of a two-dimensional hyperchaotic map with absolute value function are discussed, and the stability of its fixed points are analyzed in detail. The map can not only realize the global amplitude control by a single controller but can also realize the partial amplitude control by a single knob. These dynamic characteristics are proved by the platform based on STM32F103 chip and the digital-to-analog converter, where the experimental results are in good agreement with the simulation analysis. The special symmetry mode is a new passage for providing coexisting oscillation with inverse polarity of the chaotic signal, which shows great potential in chaos application and deserve further exploration. In future, the simple hyperchaotic map could be applied to the design of random number generators for chaos-based engineering.