Abstract
Establishing a node importance ranking is a problem that has attracted the attention of many researchers in recent decades. For unweighted networks where the edges do not have any attached weight, many proposals have been presented, considering local or global information of the networks. On the contrary, it occurs in undirected edge-weighted networks, where the proposals to address this problem have been more scarce. In this paper, a ranking method of node importance for undirected and edge-weighted is provided, generalizing the measure of line importance (DIL) based on the centrality degree proposed by Opsahl. The experimentation was done on five real networks and the results illustrate the benefits of our proposal.
1. Introduction
Networks study, in the form of mathematical graph theory, is one of the most important objects from discrete mathematics [1]. The importance of its various applications in issues of traffic, economy, brain networks, spread of diseases, social networks, electrical power grid, etc. has made this field of research gain the attention of many researchers in the last 20 years (see for instance [2,3,4,5,6,7,8]).
In a complex network there are some more important vertices than others that influence or have a greater impact on their structure or function. This importance establishes some vertices rankings that can be based on different viewpoints, this is to say, we can have an importance based on the neighborhood, on the paths, on the link, connectivity or sensibility (more details in [9]). For example, the degree of a vertex allows ordering or making a vertices ranking according to the number of neighbors it has. In general, we have the well known centrality measures that give us a vertices importance ranking. However, identifying vital nodes is not an easy job because the criteria for vital nodes are diverse due to their context-dependent nature, and consequently it is not possible to find a universal index that better quantifies the importance of nodes in all situations. Even harder, if you want to find a set of important nodes, it is an NP-Hard problem (see [10]).
In this context, other criteria have emerged to determine the importance of a node. For instance, in [11] there are taken into account the characteristics of the scale, tightness and topology of the local area network where the node and its neighbors are located. Liu et al. [12] proposed an effective ranking method based on degree value and the importance of edges. Saxena et al. designed a method to identify the best ranked nodes in order to control an epidemic through immunizations [13]. On the other hand, the conscious centrality of the community is addressed by Magelinski et al., who propose the relevance of the bridge node in the network quantified in modular vitality [14]. Along the same lines, Ghalmane et al. analyze the nonoverlapping community structure network based on an immunization strategy, recognizing the relevance of the node given the characteristics of the communities [15], while the same author asserts that modular centrality must include the influences of the nodes both in their own communities and in others [16]. Gupta et al. also agree that community structure is important for understanding the spread of an epidemic [17].
In [18] the authors proposed a method based on degree and degree of their neighborhoods. Ren et al. in [19] proposed a measure based on degree and clustering coefficient. For its part, Ref. [20] is based on combining the existing centrality criteria, where the weight for each criterion is calculated by the entropy weighting method which overcomes the impact of the subjective factor, and the Vlsekriterijumska Optimizacija I Kompromisno Resenje (VIKOR) method is used for ranking nodes’ importance. Jia-Sheng et al. improved the method of node importance evaluation based on node contraction [21]. Recently, a new multievidence centrality is proposed based on evidence theory. The existing measures of degree centrality, betweenness centrality, efficiency centrality and correlation centrality are taken into consideration in [22].
Edge-weighted graphs are not exempt from this discussion. For example, there are the rankings which are natural extensions of unweighted graphs, that we could call more representative, they are the strength of the node [23], weighted H-index [24], weighted degree [25,26], the weighted closeness centrality [27], weighted betweenness centrality [28], weighted PageRank and leaderRank [29]. Furthermore, Opsahl in [30] proposed a generalization of degree for weighted graph that combines the strength and the number of neighbors.
In addition, on this type of networks new methods have been proposed to establish the importance or influence of the nodes. Among them, Yang et al. [31] proposed the Two-Way-PageRank method based on PageRank and analyzed the importance of two important factors that affect the importance of the nodes and gave a definition and expression of the importance of the nodes. A new centrality measure (Laplacian centrality) for undirected and edge-weighted graph is proposed in [32] as well. Tang [33] proposed the weighted K-order propagation number algorithm to extract the disease propagation based on the network topology to evaluate the node importance. In the field of maximization of influence, Ahmad proposes an approach that includes the weighted sum and a multicriteria decision method [34]. All this generates the recognition of influential nodes in the network. The authors, through experimentation, conclude that their model is competitive to other similar ones [34]. Even axiomatic approaches have been proposed (see [35,36]).
In the framework of modeling complex biological systems Almasi & Hu provide a measure from the importance of vertices in a weighted human disease network [2]. They propose a vertex importance measure by extending a centrality measure for unweighted networks proposed by Liu et al. They named their extension on weighted graphs, the DIL-W centrality.
In this paper, a ranking method for undirected and edge-weighted graph is provided. Particularly, the aim of this article is to generalize the vertex importance measure (DIL) of an undirected and unweighted network given by Liu et al., to an undirected and edge-weighted graph using the generalization of degree centrality proposed by Opsahl in [30]. Our proposal is slightly different from Almasi & Hu’s one, but when we compare both generalizations in real networks, with respect to the measure the network efficiency, we can see that we obtain a better or the same efficiency measure, as we will show in the following sections.
The paper is organized as follows. Section 2 contains generalities about graph theory and the definition of degree centrality proposed by Opsahl. In Section 3 the generalization of the importance vertex measure, denoted by DIL-W, is given. In Section 4, we compare our proposal DIL-W with the one given by Almasi & Hu (denoted by DIL-W) considering and on some real networks (Zacharys karate club network, US air transport network, meta-analysis network of human whole-brain functional coactivations, colony of ants network and wild birds network). Moreover, we analyze the DIL-W rank with different values of and provide a discussion about the results. Finally, in Section 5, we give the final conclusions.
2. Basic Definitions
Graphs
The following definitions come from [37,38].
Definition 1.
A graph G is a finite nonempty set V of objects called vertices together with a possibly empty set E of 2-element subsets of V called edges.
To indicate that a graph G has vertex set V and edge set E, we write . If the set of vertices is , then the edge between vertex and vertex is denoted by .
If is an edge of G, then and are adjacent vertices. Two adjacent vertices are referred to as neighbors of each other. The set of neighbors of a vertex v is called the open neighborhood of v (or simply the neighborhood of v) and is denoted by . If and are distinct edges in G, then and are adjacent edges.
Definition 2.
The number of vertices in a graph G is the order of G and the number of edges is the size of G.
Definition 3.
The degree of a vertex v in a graph G, denoted by , is the number of vertices in G that are adjacent to v. Thus, the degree of v is the number of vertices in its neighborhood .
On the other hand, an important generalization of the simple graph consists in the definition of weighted graph, more specifically edge-weighted graph. Informally, an edge-weighted graph is a graph whose edges have been assigned a weight.
Definition 4.
An edge-weighted graph is a pair where is a graph and is a weight function. If then .
The adjacency matrix of G is the matrix , or simply , where
Definition 5.
The strength of a vertex , denoted by , is defined as the sum of the weights of all edges incident to it, this is to say
The following definition comes from [30] and it is very important in our work.
Definition 6
(Degree centrality). The degree centrality of of an edge-weighted graph , denoted by , is defined as
where .
The parameter is called tuning parameter. It is clear that when then and when then .
3. Measuring Vertex Importance on an Undirected Weighted Graph
In this section the generalization of the importance vertex measure is given, denoted by DIL-W.
Let us consider an undirected weighted graph with and . Let be the tuning parameter.
Definition 7
(Importance edge). The importance of an edge , denoted by , is defined as
where, for , with p is the number of triangles, one edge of the triangle is , is the weight of the sum of the edges incident to that form a triangle with and .
Definition 8
(Contribution). The contribution that makes to the importance of the edge , denoted by , is defined as
where is the weight of .
Definition 9
(Importance of vertex DIL-W). The importance of a vertex , denoted by , is defined as
From the definition of degree centrality (Definition 6) proposed by Opsahl in [30], we can see that when the tuning parameter is 0 the Definitions 7–9 of importance edge, contribution and importance of vertex respectively, are the same as that proposed by Liu et al. in [12] for an undirected and unweighted network. However, when , our proposal is slightly different from Almasi & Hu’s proposal in [2]. In the latter, the authors define the contribution as
Notice that, if the strength of the vertex is the traditional degree centrality as in the case of the undirected and unweighted graph, it is not possible to get the proposal of Liu et al. from the Equation (2). This slight difference between the generalization of the vertex importance method of [2] and our generalization is relevant when we compare both generalizations in real networks with respect to the measure of the network efficiency as we will show in the next section.
On the other hand, a possibility to extend the vertex importance based on degree and the importance of lines from an unweighted network to the proposed by Almasi & Hu, is to consider the contribution as
Indeed, when we obtain the original proposal and when we get the generalization given in [2]. Despite the above, we do not consider Equation (3) because, in our opinion, it is not a good generalization proposal since it does not improve the one done by Almasi & Hu.
One of the good qualities of the DIL ranking is that it recognizes the importance of bridge nodes (see more in [39]). This quality is not lost in our extension to weighted graphs. For instance, we can see in Figure 1 that when applying the DIL-W ranking with , vertex 10 has a better ranking than vertex 4; this is due to the vertex 10 being a bridge node. Indeed, from Definitions 9 we get
and
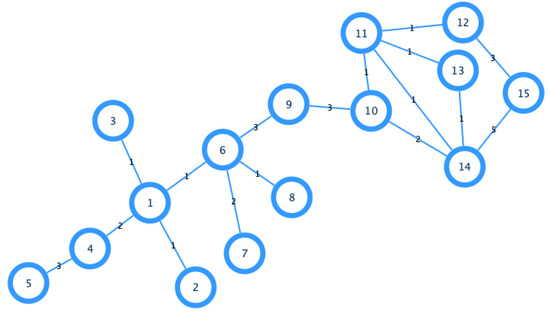
Figure 1.
Simple network example.
Therefore, .
On the other hand, the consideration of the centrality measure that combines degree and strength, picks up the main idea of the original measure, which is the number of neighbors of a vertex, an idea that is lost when considering only the strength.
4. Comparison and Analysis Results
4.1. Data and Source Code
In our research, we compare our proposal DIL-W for and with DIL-W on some real networks, these are: Zacharys karate club network [40] (with 34 vertices and 78 edges), US air transport network [41] (with 500 vertices and 2980 edges), meta-analysis network of human whole-brain functional coactivations [5] (with 638 vertices and 18,625 edges), colony of ants network [42] (with 113 vertices and 4550 edges) and wild bird network [43] (with 131 vertices and 1444 edges).
For the databases of colony of ants and wild birds networks, see [44]. For US air transport network see [45]. For brain functional coactivactions network database, see [46]. The source code of our analysis and network files can be found at https://github.com/RonaldManriquez/DIL-W-alpha.git from 8 March 2021.
4.2. Evaluation
According to [47], network efficiency is an index used to indicate the quality of network connectivity. A high connectivity indicates a higher efficiency of the graph. The efficiency of a graph, denoted by , is defined as follows:
where is the distance between the vertex and the vertex , defined as,
where h are the indices of the intermediary vertices on paths between and , and the weights of the edges . (see more details in [27,28]). We consider and to compare DIL-W with DIL-W, according to what was discussed at the end of Section 3.
The authors in [48] show that between 5% and 10% of important nodes may cause the entire network to falter. To compare the DIL-W proposal with DIL-W, the 10% of the vertices are deleted one by one from the networks according to the importance ranking produced by DIL-W and DIL-W, and we compute the decline rate of network efficiency, denoted by , and defined by
where is the efficiency of the original graph, and is the graph efficiency after some vertices are removed [19]. We expect a greater decline rate of the network efficiency if we delete a more important vertex of the obtained DIL-W ranking.
In Figure 2, we see the ranking done by DIL-W, DIL-W and DIL-W on the example networks versus the decline rate of the network efficiency. There exists a correlation between the rankings DIL-W, DIL-W and DIL-W and the decline rate of the network efficiency in Zacharys karate club, US air transport and colony of ants networks, whereas in the case of wild birds and brain functional coactivations networks, the correlation is not evident.
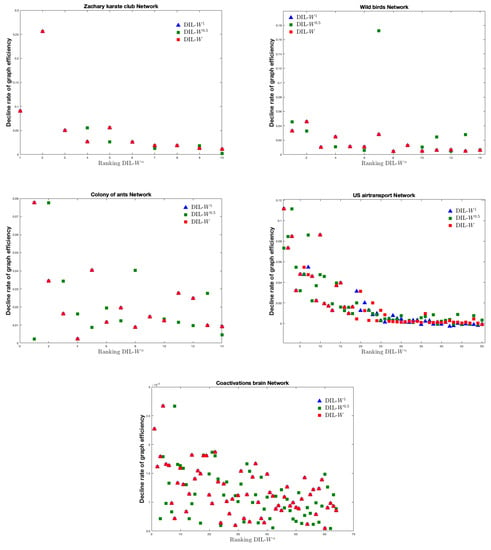
Figure 2.
The relation between decline rate of network efficiency and the ranking DIL-W, DIL-W and DIL-W on the example networks.
In each implementation only one node is removed according to the importance ranking list, then we compute the decline rate of the network efficiency.
In Figure 3, we can see the relation between the decline rate of network efficiency and the number of vertices deleted from five real networks.
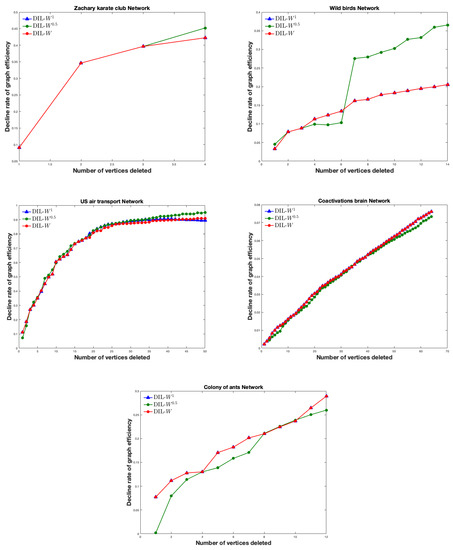
Figure 3.
The decline rate of the network efficiency as a function of deleting the top 10% of the vertices ranked by DIL-W, DIL-W and DIL-W from five real networks (Zacharys karate club, wild birds, US air transport, brain functional coactivations and colony of ants).
In Zachary karate club, US air transport and wild birds networks, DIL-W performs the best between all three rankings. In brain functional coactivations and colony of ants networks, DIL-W and DIL-W perform the best. Notice that, only in the case of US air transport, DIL-W does not match completely with DIL-W. Table 1 shows the nodes ranking on the wild bird and US air transport networks, making evident the same ranking of importance of nodes for DIL-W and DIL-W in wild birds network and the slight difference of ranking in US air transport network.

Table 1.
The ranking results of DIL-W and DIL-W on wild birds and US air transport networks.
4.3. Ranking DIL-W for Different Values of
In the previous section we could see that, with respect to efficiency, DIL-W performs better rankings in brain functional coactivations and colony of ants networks, when , whereas in US air transport, Zachary karate club and wild birds’ networks the ranking is better with .
In this section we compare the different rankings that DIL-W performs for different values of . We have considered the values , , , , and 1. Figure 4 shows the results.
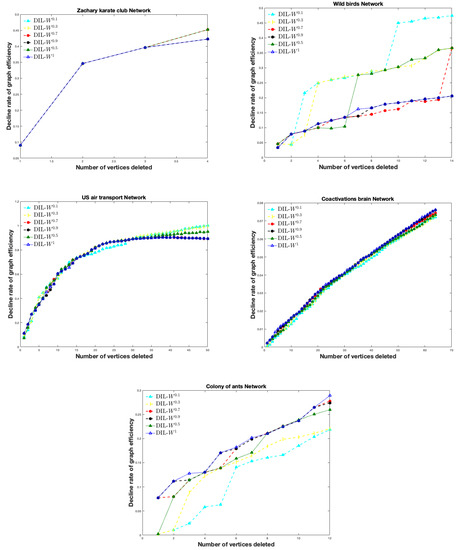
Figure 4.
The decline rate of the network efficiency as a function of deleting the top 10% of the vertices ranked by DIL-W, DIL-W, DIL-W, DIL-W, DIL-W and DIL-W from five real networks (Zacharys karate club, wild birds, US air transport, brain functional coactivations and colony of ants).
For the US air transport, Zachary karate club and wild birds networks, it is observed that the smaller the , the better the efficiency ranking is performed. Conversely, in colony of ants and brain coactivations networks the best performance for efficiency is with or close to 1. In conclusion, we can see that DIL-W is equal to or better in efficiency than the DIL-W proposal given in [2] in the five networks that we have considered. In particular, they coincide in efficiency in brain coactivations and colony of ants networks for and cannot be improved with another value of as we concluded from Figure 4. In contrast, DIL-W performs better than DIL-W on the US air transport, Zachary karate club and wild birds networks, as soon as .
Moreover, we deepen into the possible relations between DIL and DIL-W for the different values of seen previously (i.e., and 1) on all the networks that we have tested. Figure 5 shows the relations. In each network it is observed that the correlation coefficient between both rankings are very close to 1. In particular, for the Zachary karate club network we have all coefficients above 0.988. While for US air transport we have the largest range of correlation coefficients among all networks (between 0.7308 and 0.9998).
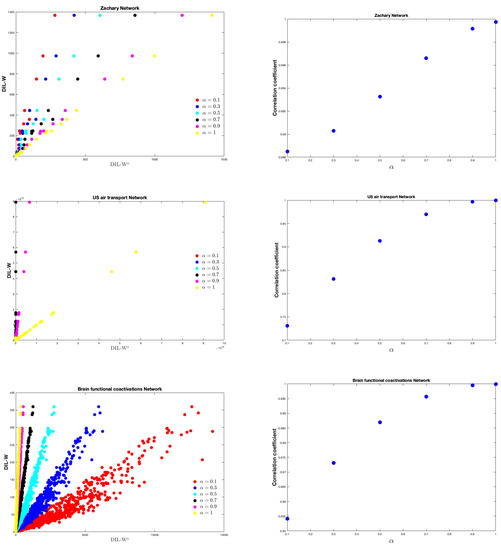
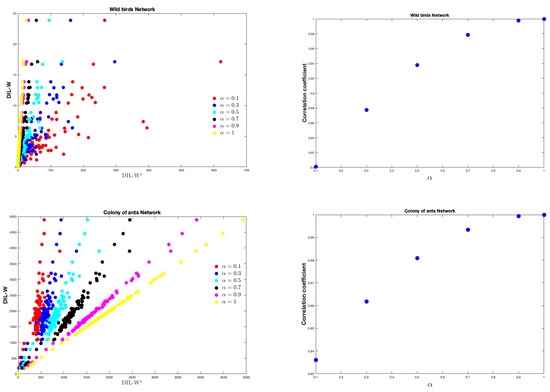
Figure 5.
On the left the relationship between the DIL-W and DIL-W αrankings for different values of α. On the right the correlation coefficient for the different values of α.
4.4. Computational Complexity
In general the real complex networks have many vertices, then the computational complexity plays an important role. DIL-W has a computational complexity of , where n is the total numbers of vertices of the graph and is the average degree of vertices in a network. Moreover, DIL-W uses local information of a vertex for its importance evaluation. By the above, we believe that DIL-W can be efficient to compute in large networks.
5. Conclusions
In this paper, we propose a ranking of importance of nodes which is applicable to undirected and edge-weighted networks. We can see that DIL-W is equal to or better in efficiency than the DIL-W proposal given in [2] in the five networks that we have considered.
We assess effectiveness by comparing the rate of decrease of network efficiency caused by node removal. The higher the rate of decrease of network efficiency caused by node removal, the more important will be the node. In Figure 4, the results show that DIL-W can evaluate the importance of nodes better in the US air transport, Zachary karate club and wild birds networks, when is less than one. Conversely, in colony of ants and brain coactivations networks, the best performance for efficiency is with or close to 1. In consequence, when modifying the parameter it is possible to obtain better rankings for the network in the sense of effectiveness.
From the above, we are presented with an important task or challenge, which is to establish what value of makes the ranking perform more optimally. It is difficult to determine the exact value of to use. We think that there may be a dependency on the weights at the edges. For instance, is it better to have many edges with weights between 0 and 1 or few edges with weights greater than 1? Such answers would allow a better understanding of the optimal in certain networks.
From Table 1 we can see that only in the US air transport network the rankings made by DIL-W and DIL-W do not match completely, since there is a small difference in positions 6 and 7 of the rankings.
With respect to the computational complexity, we believe that DIL-W can be efficient to compute in large networks because it uses local information of a vertex for its importance evaluation.
In summary, our research provides a way to generalize the classification method for edge-weighted and undirected graphs. This turns out to be an element for the discussion around the usefulness of the concept of degree of centrality and its standard use has limitations in complex networks, as pointed out by Sciarra et al. [49].
Author Contributions
The authors R.M., C.G.-N., F.M., and C.T. contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported and funded by Agencia Nacional de Investigación y Desarrollo (ANID), COVID0739 project.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We thank the two anonymous reviewers for their helpful comments that helped improve this manuscript.
Conflicts of Interest
The authors declare that they have no conflict of interest. The funders had no role in the design of the study; in the collection, analysis, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Newman, M. The structure and function of complex networks. SIAM Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef]
- Almasi, S.; Hu, T. Measuring the importance of vertices in the weighted human disease network. PLoS ONE 2019, 14, e0205936. [Google Scholar] [CrossRef]
- An, X.L.; Zhang, L.; Li, Y.Z.; Zhang, J.G. Synchronization analysis of complex networks with multi-weights and its application in public traffic network. Phys. A Stat. Mech. Its Appl. 2014, 412, 149–156. [Google Scholar] [CrossRef]
- Manríquez, R.; Guerrero-Nancuante, C.; Martínez, F.; Taramasco, C. Spread of Epidemic Disease on Edge-Weighted Graphs from a Database: A Case Study of COVID-19. Int. J. Environ. Res. Public Health 2021, 18, 4432. [Google Scholar] [CrossRef]
- Crossley, N.; Mechelli, A.; Vértes, P.; Winton-Brown, T.; Patel, A.; Ginestet, C.; McGuire, P.; Bullmore, E. Cognitive relevance of the community structure of the human brain functional coactivation network. Proc. Natl. Acad. Sci. USA 2013, 110, 11583–11588. [Google Scholar] [CrossRef]
- Wang, G.; Cao, Y.; Bao, Z.Y.; Han, Z.X. A novel local-world evolving network model for power grid. Acta Phys. Sin. 2009, 6, 58. [Google Scholar]
- Montenegro, E.; Cabrera, E.; González, J.; Manríquez, R. Linear representation of a graph. Bol. Soc. Parana. Matemática 2019, 37, 97–102. [Google Scholar] [CrossRef]
- Pastor-Satorras, R.; Vespignani, A. Epidemic Spreading in Scale-Free Networks. Phys. Rev. Lett. 2001, 86, 3200–3203. [Google Scholar] [CrossRef]
- Lü, L.; Chen, D.; Ren, X.L.; Zhang, Q.M.; Zhang, Y.C.; Zhou, T. Vital nodes identification in complex networks. Phys. Rep. 2016, 650, 1–63. [Google Scholar] [CrossRef]
- Vinterbo, S.A. Privacy: A machine learning view. IEEE Trans. Knowl. Data Eng. 2004, 16, 939–948. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, J.; Yang, J.; Lun, L. Node Importance Ranking of Complex Network based on Degree and Network Density. Int. J. Perform. Eng. 2019, 15, 850. [Google Scholar] [CrossRef]
- Liu, J.; Xiong, Q.; Shi, W.; Shi, X.; Wang, K. Evaluating the importance of nodes in complex networks. Phys. A Stat. Mech. Its Appl. 2016, 452, 209–219. [Google Scholar] [CrossRef]
- Saxena, C.; Doja, M.N.; Ahmad, T. Group based centrality for immunization of complex networks. Phys. A Stat. Mech. Its Appl. 2018, 508, 35–47. [Google Scholar] [CrossRef]
- Magelinski, T.; Bartulovic, M.; Carley, K.M. Measuring Node Contribution to Community Structure with Modularity Vitality. IEEE Trans. Netw. Sci. Eng. 2021, 8, 707–723. [Google Scholar] [CrossRef]
- Ghalmane, Z.; Hassouni, M.E.; Cherifi, H. Immunization of networks with non-overlapping community structure. Soc. Netw. Anal. Min. 2019, 9, 1–22. [Google Scholar] [CrossRef]
- Ghalmane, Z.; Cherifi, C.; Cherifi, H.; Hassouni, M.E. Centrality in complex networks with overlapping community structure. Sci. Rep. 2019, 9, 1–29. [Google Scholar] [CrossRef] [PubMed]
- Gupta, N.; Singh, A.; Cherifi, H. Community-based immunization strategies for epidemic control. In Proceedings of the 2015 7th International Conference on Communication Systems and Networks (COMSNETS), Bangalore, India, 6–10 January 2015; pp. 1–6. [Google Scholar]
- Wang, J.W.; Rong, L.; Guo, T.Z. A new measure method of network node importance based on local characteristics. J. Dalian Univ. Technol. 2010, 50, 822–826. [Google Scholar]
- Ren, Z.; Shao, F.; Liu, J.; Guo, Q.; Wang, B.H. Node importance measurement based on the degree and clustering coefficient information. Acta Phys. Sin. 2013, 62, 128901. [Google Scholar]
- Yang, Y.; Yu, L.; Wang, X.; Zhou, Z.; Chen, Y.; Kou, T. A novel method to evaluate node importance in complex networks. Phys. A Stat. Mech. Its Appl. 2019, 526, 121118. [Google Scholar] [CrossRef]
- Wang, J.; Wu, X.; Yan, B.; Guo, J. Improved method of node importance evaluation based on node contraction in complex networks. Procedia Eng. 2011, 15, 1600–1604. [Google Scholar]
- Mo, H.; Deng, Y. Identifying node importance based on evidence theory in complex networks. Phys. A Stat. Mech. Its Appl. 2019, 529, 121538. [Google Scholar] [CrossRef]
- Barrat, A.; Barthelemy, M.; Pastor-Satorras, R.; Vespignani, A. The architecture of complex weighted networks. Proc. Natl. Acad. Sci. USA 2004, 101, 3747–3752. [Google Scholar] [CrossRef] [PubMed]
- Lü, L.; Zhou, T.; Zhang, Q.M.; Stanley, H.E. The H-index of a network node and its relation to degree and coreness. Nat. Commun. 2016, 7, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Garas, A.; Schweitzer, F.; Havlin, S. A k-shell decomposition method for weighted networks. New J. Phys. 2012, 14, 083030. [Google Scholar] [CrossRef]
- Wei, B.; Liu, J.; Wei, D.; Gao, C.; Deng, Y. Weighted k-shell decomposition for complex networks based on potential edge weights. Phys. A Stat. Mech. Its Appl. 2015, 420, 277–283. [Google Scholar] [CrossRef]
- Newman, M. Scientific collaboration networks. II. Shortest paths, weighted networks, and centrality. Phys. Rev. E 2001, 64, 016132. [Google Scholar] [CrossRef] [PubMed]
- Brandes, U. A faster algorithm for betweenness centrality. J. Math. Sociol. 2001, 25, 163–177. [Google Scholar] [CrossRef]
- Ou, Q.; Jin, Y.; Zhou, T.; Wang, B.H.; Yin, B.Q. Power-law strength-degree correlation from resource-allocation dynamics on weighted networks. Phys. Rev. E 2007, 75, 021102. [Google Scholar] [CrossRef]
- Opsahl, T.; Agneessens, F.; Skvoretz, J. Node centrality in weighted networks: Generalizing degree and shortest paths. Soc. Netw. 2010, 32, 245–251. [Google Scholar] [CrossRef]
- Yang, Y.; Xie, G.; Xie, J. Mining important nodes in directed weighted complex networks. Discret. Dyn. Nat. Soc. 2017, 2017, 9741824. [Google Scholar] [CrossRef]
- Qi, X.; Fuller, E.; Wu, Q.; Wu, Y.; Zhang, C.Q. Laplacian centrality: A new centrality measure for weighted networks. Inf. Sci. 2012, 194, 240–253. [Google Scholar] [CrossRef]
- Tang, P.; Song, C.; Ding, W.; Ma, J.; Dong, J.; Huang, L. Research on the node importance of a weighted network based on the k-order propagation number algorithm. Entropy 2020, 22, 364. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, A.; Ahmad, T.; Bhatt, A. HWSMCB: A community-based hybrid approach for identifying influential nodes in the social network. Phys. A Stat. Mech. Its Appl. 2020, 545, 123590. [Google Scholar] [CrossRef]
- Skibski, O.; Rahwan, T.; Michalak, T.; Yokoo, M. Attachment centrality: Measure for connectivity in networks. Artif. Intell. 2019, 274, 151–179. [Google Scholar] [CrossRef]
- Sosnowska, J.; Skibski, O. Attachment Centrality for Weighted Graphs. In Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence (IJCAI-17), Melbourne, Australia, 19–25 August 2017; pp. 416–422. [Google Scholar]
- Chartrand, G.; Lesniak, L. Graphs and Digraphs, 1st ed.; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- West, D.B. Introduction to Graph Theory, 2nd ed.; Prentice Hall: Englewood Cliffs, NY, USA, 2001. [Google Scholar]
- Musial, K.; Juszczyszyn, K. Properties of bridge nodes in social networks. In International Conference on Computational Collective Intelligence; Springer: Berlin/Heidelberg, Germany, 2019; pp. 357–364. [Google Scholar]
- Zachary, W.W. An Information Flow Model for Conflict and Fission in Small Groups. J. Anthropol. Res. 1977, 33, 452–473. [Google Scholar] [CrossRef]
- Colizza, V.; Pastor-Satorras, R.; Vespignani, A. Reaction–diffusion processes and metapopulation models in heterogeneous networks. Nat. Phys. 2007, 3, 276–282. [Google Scholar] [CrossRef]
- Mersch, D.P.; Crespi, A.; Keller, L. Tracking individuals shows spatial fidelity is a key regulator of ant social organization. Science 2013, 340, 1090–1093. [Google Scholar] [CrossRef]
- Firth, J.A.; Sheldon, B.C. Experimental manipulation of avian social structure reveals segregation is carried over across contexts. Proc. R. Soc. B Biol. Sci. 2015, 282, 20142350. [Google Scholar] [CrossRef]
- Rossi, R.; Ahmed, N.K. The Network Data Repository with Interactive Graph Analytics and Visualization. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015. [Google Scholar]
- Latora, V.; Nicosia, V.; Russo, G. Complex Networks: Principles, Methods and Applications, 1st ed.; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Rubinov, M.; Sporns, O. Complex network measures of brain connectivity: Uses and interpretations. NeuroImage 2010, 52, 1059–1069. [Google Scholar] [CrossRef]
- Latora, V.; Marchiori, M. Efficient Behavior of Small-World Networks. Phys. Rev. Lett. 2001, 87, 198701. [Google Scholar] [CrossRef]
- Lai, Y.; Motter, A.; Nishikawa, T. Attacks and cascades in complex networks. In Complex Networks; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2004; Volume 650. [Google Scholar]
- Sciarra, C.; Chiarotti, G.; Laio, F.; Ridolfi, L. A change of perspective in network centrality. Sci. Rep. 2018, 8, 1–9. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).