Exact Likelihood Inference for a Competing Risks Model with Generalized Type II Progressive Hybrid Censored Exponential Data

Abstract

In many situations of survival and reliability test, the withdrawal of units from the test is pre-planned in order to to free up testing facilities for other tests, or to save cost and time. It is known that several risk factors (RiFs) compete for the immediate failure cause of items. In this paper, we derive an inference for a competing risks model (CompRiM) with a generalized type II progressive hybrid censoring scheme (GeTy2PrHCS). We derive the conditional moment generating functions (CondMgfs), distributions and confidence interval (ConfI) of the scale parameters of exponential distribution (ExDist) under GeTy2PrHCS with CompRiM. A real data set is analysed to illustrate the validity of the method developed here. From the data, it can be seen that the conditional PDFs of MLEs is almost symmetrical.

1. Introduction

In many situations of survival and reliability test, the tester might not obtain complete information on failure times for all items. The withdrawal of units from the test is pre-planned in order to to free up testing facilities for other tests, or to save cost and time. Type I censoring scheme (Ty1CS) and type II censoring scheme (Ty2CS) cannot be used if the teste wants to eliminate the live items at a point other than the end point of the test. Therefore, progressive type II censoring scheme (PrTy2CS) has become popular censoring scheme in a survival and reliability analysis problem (Refs. [1,2,3,4,5]). Though the PrTy2CS assure a number of observed failures, it has the drawback that it might take a long time to terminate the test and to observe a pre-fixed number of failures. In this motivation, Ref. [6] suggest a GeTy2PrHCS in which the test is assured to end at a pre-assigned time. These are designed to fix the drawbacks inherent in the type II progressive hybrid censoring scheme (Ty2PrHCS). The survival and reliability analysis based on the GeTy2PrHCS can save time and costs. GeTy2PrHCS may arise in a situation when the tester has prepaid for the use of the facility.

GeTy2PrHCS can be explained as follows. The m, PrTy2CS (${\Re }_1,{\Re }_2,\cdots ,{\Re }_m$; ${\sum }_{i=1}^m{\Re }_i+m=n$), and times ${\mathcal{T}}_1$ and ${\mathcal{T}}_2$ are pre-assigned integers such that $m\le n$ and $0<{\mathcal{T}}_1<{\mathcal{T}}_2<\infty$. Let ${\mathcal{D}}_1$ and ${\mathcal{D}}_2$ denote the number of failures up to time ${\mathcal{T}}_1$ and ${\mathcal{T}}_2$, respectively. Randomly, ${\Re }_1$ of the surviving units are removed from the test at the time of 1st failure ($X_{1:m:n}$). Randomly, the ${\Re }_2$ of the surviving units are removed at the time of 2nd failure ($X_{2:m:n}$). If m-th failure ($X_{m:m:n}$) occurs before the ${\mathcal{T}}_1$, we continue to observe failures (${\Re }_m={\Re }_{m+1}=\cdots ={\Re }_{d_1}=0$; without any further withdrawals) up to time ${\mathcal{T}}_1$ (Case (a)). If ${\mathcal{T}}_1<X_{m:m:n}<{\mathcal{T}}_2$, end the test at m-th failure (Case (b)). If $X_{m:m:n}>{\mathcal{T}}_2$, end the test at time ${\mathcal{T}}_2$ (Case (c)). This GeTy2PrHCS modifies the Ty2PrHCS by assuring that the test will be finished by ${\mathcal{T}}_2$. For the GeTy2PrHCS, there are three possible scenarios (Figure 1).

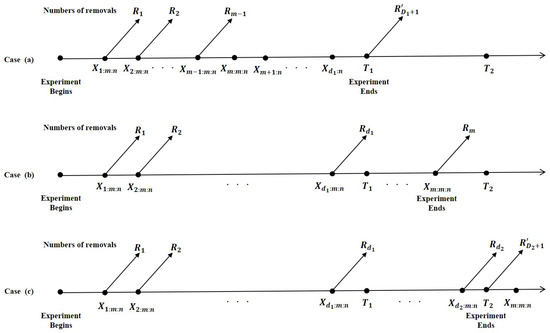
Figure 1. GeTy2PrHCS. Case (a): $\{X_{1:m:n},X_{2:m:n},\cdots ,X_{m:m:n},X_{m+1:n},\cdots ,x_{d_1:n}\}$, if $X_{m:m:n}<{\mathcal{T}}_1$, ${\Re }_m={\Re }_{m+1}=\cdots ={\Re }_{d_1}=0$. Case (b): $\{X_{1:m:n},X_{2:m:n},\cdots ,X_{d_1:m:n},\cdots ,X_{m:m:n}\}$, if ${\mathcal{T}}_1<X_{m:m:n}<{\mathcal{T}}_2$. Case (c): $\{X_{1:m:n},X_{2:m:n},\cdots ,X_{d_1:m:n},\cdots ,X_{d_2:m:n}\}$, if ${\mathcal{T}}_2<X_{m:m:n}$.

In Case (c), $X_{d_1:m:n}<{\mathcal{T}}_1<X_{d_1+1:m:n}$, $X_{d_2:m:n}<{\mathcal{T}}_2<X_{d_2+1:m:n}$, and $X_{d_2+1:m:n},\cdots ,$ $X_{m:m:n}$ are not observed.

Due to the complication of external environment and internal structure, it is known that the breakdown of a item results by several reasons of failure. These reasons of breakdown are called the competing risks data (CompD) that compete with each other in life cycle and can be encountered in survival and reliability study, and it has been discussed by many authors (Refs. [7,8,9,10,11]). From Ref. [11], it can be seen that the conditional PDFs of MLEs under CompRiM with censored data is almost symmetrical. In CompRiM, it is assumed that the among RiFs are statistically independent. A CompD and indicator denoting the RiF of failure consists of an observed failure time. In Section 2, we will prove the CondMgf, distributions and ConfI of the scale parameters of ExDist under GeTy2PrHCS with CompRiM. We will present a simulation results to investigate the biases, root mean squared error (rMSE), coverage percentages (CovP) and confidence lengths (ConfL) of the MLEs of parameters of ExDist under GeTy2PrHCS with CompRiM in Section 3. An illustrative example is presented. Finally, in Section 4, the conclusion and summary are presented. The meanings of abbreviations and symbols are listed in Abbreviations Section.

2. Model Description and Conditional Inference for MLEs

2.1. Model Description and MLEs

We suppose that n randomly selected items with CompD for an ExDist data were put on a survival and reliability test. We suppose that the $X_1,X_2,\cdots ,X_n$ are iid with an ExDist. Here, $X_i=min\{X_{i1},X_{i2},\cdots ,X_{ik}\}$, $X_{ik}$ denotes the life-time of the i-th item under the k-th RiF with cumulative distribution function (CDF) such as $G_k\left(x\right)=1-exp(-{\lambda }_k^{-1}x)$. Recently, researchers are interested with specific factor in the presence of other RiFs. Therefore, in this paper, we suppose that there are two RiFs for the failures. Then, it is to obtain the CDF of life-time as

$$\begin{array}{cc}\hfill & \mathcal{F}(x;\mathbf{\lambda })=1-exp\left[-{\left(\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}\right)}^{-1}x\right],x>0,{\lambda }_1>0,{\lambda }_2>0,\hfill \end{array}$$

where $\mathbf{\lambda }=({\lambda }_1,{\lambda }_2)$.

Let $\mathit{X}=\{x_1,x_2,\cdots ,x_n\}$ denote the data of n items, and $\mathsf{\Delta }=\{{\delta }_1,{\delta }_2,\cdots ,{\delta }_n\}$ denote the indicator of RiF. Here ${\delta }_i=1$ denotes the i-th failure caused by 1st RiF. On the other hands, ${\delta }_i=0$ denotes that other RiF is responsible for the i-th failure. Each life-time is composed of life-time and the reason for failure under the CompRiM $(\mathit{X},\mathsf{\Delta })$. Therefore, the joint PDF (jPDF) of failure life-time and RiF is

$$\begin{array}{c}\hfill f_{\mathit{X},\mathsf{\Delta }}(x,k)={{\lambda }_k}^{-1}exp\left[-{\left(\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}\right)}^{-1}x\right],k=1,2.\end{array}$$

From GeTy2PrHCS, we have the following data;

Case (a)

$\{(x_{1:m:n},{\delta }_{1:m:n}),(x_{2:m:n},{\delta }_{2:m:n}),\cdots ,(x_{m:m:n},{\delta }_{m:m:n}),(x_{m+1:n},{\delta }_{m+1:n})\cdots ,(x_{d_1:n},$${\delta }_{d_1:n}\left)\right\}$.

Case (b)

$\{(x_{1:m:n},{\delta }_{1:m:n}),(x_{2:m:n},{\delta }_{2:m:n}),\cdots ,(x_{d_1:m:n},{\delta }_{d_1:m:n}),\cdots ,(x_{m:m:n},{\delta }_{m:m:n})\}$.

Case (c)

$\{(x_{1:m:n},{\delta }_{1:m:n}),(x_{2:m:n},{\delta }_{2:m:n}),\cdots ,(x_{d_1:m:n},{\delta }_{d_1:m:n}),\cdots ,(x_{d_2:m:n},{\delta }_{d_2:m:n})\}$.

Based on the GeTy2PrHCS, the likelihood function (see, Ref. [6]) is

$$\begin{array}{c}\hfill \mathcal{L}\left(\mathbf{\lambda }\right|x)=\left\{\begin{array}{c}{\varsigma }_{{\mathcal{D}}_1}^{\prime }\prod _{j=1}^{{\mathcal{D}}_1}{f}_{\mathit{X},\mathsf{\Delta }}{\left(x_{j:m:n},1\right)}^{{\delta }_j}{f}_{\mathit{X},\mathsf{\Delta }}{\left(x_{j:m:n},2\right)}^{1-{\delta }_j}{\left[1-\mathcal{F}\left(x_{j:m:n}\right)\right]}^{{\Re }_j}{\left[1-\mathcal{F}\left({\mathcal{T}}_1\right)\right]}^{{\Re }_{{\mathcal{D}}_1+1}^{\prime }},\hfill \\ {\mathcal{D}}_1=m,m+1,\cdots ,n,\hfill \\ \\ {\varsigma }_m^{\prime }\prod _{j=1}^m{f}_{\mathit{X},\mathsf{\Delta }}{\left(x_{j:m:n},1\right)}^{{\delta }_j}{f}_{\mathit{X},\mathsf{\Delta }}{\left(x_{j:m:n},2\right)}^{1-{\delta }_j}{\left[1-\mathcal{F}\left(x_{j:m:n}\right)\right]}^{{\Re }_j},\hfill \\ {\mathcal{D}}_1=0,1,\cdots ,m-1,{\mathcal{D}}_2=m,\hfill \\ \\ {\varsigma }_{{\mathcal{D}}_2}^{\prime }\prod _{j=1}^{{\mathcal{D}}_2}{f}_{\mathit{X},\mathsf{\Delta }}{\left(x_{j:m:n},1\right)}^{{\delta }_j}{f}_{\mathit{X},\mathsf{\Delta }}{\left(x_{j:m:n},2\right)}^{1-{\delta }_j}{\left[1-\mathcal{F}\left(x_{j:m:n}\right)\right]}^{{\Re }_j}{\left[1-\mathcal{F}\left({\mathcal{T}}_2\right)\right]}^{{\Re }_{{\mathcal{D}}_2+1}^{\prime }},\hfill \\ {\mathcal{D}}_2=1,2,\cdots ,m-1,\hfill \end{array}\right.\end{array}$$

(1)

where ${\Re }_{{\mathcal{D}}_1+1}^{\prime }=n-{\sum }_{i=1}^{m-1}{\Re }_i-{\mathcal{D}}_1$, ${\Re }_{{\mathcal{D}}_2+1}^{\prime }=n-{\sum }_{i=1}^{{\mathcal{D}}_2}{\Re }_i-{\mathcal{D}}_2$ and ${\varsigma }_{\mathcal{D}}^{\prime }={\prod }_{j=1}^{\mathcal{D}}{\sum }_{k=j}^m\left({\Re }_k+1\right)$.

Using (1), then, we can obtain the MLEs of ${\lambda }_k$ ($k=1,2$) as

$$\begin{array}{c}\hfill {\widehat{\lambda }}_k=\left\{\begin{array}{cc}\frac{1}{n_k}\left[\sum _{j=1}^{{\mathcal{D}}_1}\left(1+{\Re }_j\right)x_{j:m:n}+{\mathcal{T}}_1{\Re }_{{\mathcal{D}}_1+1}^{\prime }\right],\hfill & {\mathcal{D}}_1=m,m+1,\cdots ,n,\hfill \\ \hfill & \\ \frac{1}{n_k}\left[\sum _{j=1}^m\left(1+{\Re }_j\right)x_{j:m:n}\right],\hfill & {\mathcal{D}}_1=0,1,\cdots ,m-1,{\mathcal{D}}_2=m,\hfill \\ \hfill & \\ \frac{1}{n_k}\left[\sum _{j=1}^{{\mathcal{D}}_2}\left(1+{\Re }_j\right)x_{j:m:n}+{\mathcal{T}}_2{\Re }_{{\mathcal{D}}_2+1}^{\prime }\right],\hfill & {\mathcal{D}}_2=1,\cdots ,m-1.\hfill \end{array}\right.\end{array}$$

(2)

Here, we denote the total failure number of units due to the RiF k by $n_k$, $k=1,2$, then it is easy to obtain $n_1={\sum }_{i=1}^u{\delta }_i$ and $n_2={\sum }_{i=1}^u(1-{\delta }_i)=u-n_1$, where $u=d_1$ for Case (a), $u=m$ for Case (b) and $u=d_2$ for Case (c).

From (2), the ${\widehat{\lambda }}_1$ and ${\widehat{\lambda }}_2$ do not exist when $n_1=0$ and $n_2=0$, respectively. In order to estimate ${\lambda }_1$ and ${\lambda }_2$, we have to observe at least one failure caused by each RiF. That is,

$$\begin{array}{c}\hfill {\zeta }^{\left(u\right)}=\left\{n_1\ge 1,n_2\ge 1,n_1+n_2=u\right\}.\end{array}$$

2.2. Conditional Inference for MLEs

To find the exact conditional inference for ${\widehat{\lambda }}_1$ and ${\widehat{\lambda }}_2$, we first derive the CondMgf of ${\widehat{\lambda }}_1$ and ${\widehat{\lambda }}_2$, respectively. In order to obtain CondMgf of ${\widehat{\lambda }}_1$ and ${\widehat{\lambda }}_2$, we need the following Lemma in Ref. [12].

Lemma 1.

Let ${\eta }_j>0$ ($j=1,2,\cdots ,m$), and let X denote the absolutely continuous RV with $f\left(x\right)$ (PDF) and $\mathcal{F}\left(x\right)$ (CDF). For $m\ge 1$, then, we have

$$\begin{array}{c}\hfill {\int }_{\mathcal{T}}^{x_{m+1}}\cdots {\int }_{\mathcal{T}}^{x_3}{\int }_{\mathcal{T}}^{x_2}\prod _{j=1}^{m}f\left(x_j\right){\left\{1-\mathcal{F}\left(x_j\right)\right\}}^{{\eta }_j-1}d{x}_{1}d{x}_2\cdots d{x}_m\\ \hfill =\sum _{i=0}^m{\varsigma }_{i,m}\left({\mathbf{\eta }}_{\mathit{m}}\right){\left\{1-\mathcal{F}\left(x_{m+1}\right)\right\}}^{{\kappa }_{i,m}\left({\eta }_m\right)}{\left\{1-\mathcal{F}\left(\mathcal{T}\right)\right\}}^{{\sum }_{j=1}^{m-i}{\eta }_j},\end{array}$$

where ${\mathbf{\eta }}_{\mathit{m}}=\left({\eta }_1,{\eta }_2,\cdots ,{\eta }_m\right)$; ${\varsigma }_{i,m}\left({\mathbf{\eta }}_{\mathit{m}}\right)=\frac{{\left(-1\right)}^i}{\left\{{\prod }_{j=1}^i{\sum }_{k=m-i+1}^{m-i+j}{\eta }_k\right\}\left\{{\prod }_{j=1}^{m-i}{\sum }_{k=j}^{m-i}{\eta }_k\right\}}$, ${\kappa }_{i,m}\left({\mathbf{\eta }}_{\mathit{m}}\right)={\sum }_{j=m-i+1}^m{\eta }_j$ with the usual conventions that ${\prod }_{j=1}^0{a}_j\equiv 1$ and ${\sum }_{j=i}^0{a}_j\equiv 0$.

Using Lemma 1, we have the CondMgf of ${\widehat{\lambda }}_1$, given ${\zeta }^{\left(u\right)}$, as follow Theorem.

Theorem 1.

The CondMgf of ${\widehat{\lambda }}_1$, given ${\zeta }^{\left(u\right)}$, is

$$\begin{array}{cc}\hfill M_{{\widehat{\lambda }}_1}& \left(t\right)\hfill \\ \hfill =& E\left(e^{t{\widehat{\lambda }}_1}|{\zeta }^{\left(u\right)}\right)\hfill \\ \hfill =& \sum _{d_1=m}^{n-({\Re }_1+\cdots +{\Re }_{m-1})}\sum _{i=1}^{d_1-1}\frac{{\varsigma }_{d_1}^{\prime }}{P\left({\zeta }^{\left(d_1\right)}\right|{\mathcal{D}}_1=d_1)}\left(\begin{array}{c}{d}_1\\ i\end{array}\right)\frac{{\lambda }_1^{d_1-i}{\lambda }_2^i}{{({\lambda }_1+{\lambda }_2)}^{d_1}}{\left(1-\frac{t}{i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}\right)}^{-d_1}\hfill \\ \hfill & \times \sum _{j=0}^{d_1}{\varsigma }_{j,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1)q_1^{\left(1-\frac{t}{i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}\right)\left[{\Re }_{{\mathcal{D}}_1+1}^{\prime }+{\kappa }_{j,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1)\right]}\hfill \\ \hfill & +\sum _{d_1=0}^{m-1}\sum _{i=1}^{m-1}\frac{{\varsigma }_m^{\prime }}{P\left({\zeta }^{\left(m\right)}\right|{\mathcal{D}}_1=d_1,{\mathcal{D}}_2=m)}\left(\begin{array}{c}m\\ i\end{array}\right)\frac{{\lambda }_1^{m-i}{\lambda }_2^i}{{({\lambda }_1+{\lambda }_2)}^m}{\left(1-\frac{t}{i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}\right)}^{-m}\hfill \\ \hfill & \times \sum _{i_1=0}^{d_1}\sum _{i_2=0}^{m-d_1}{\varsigma }_{i_1,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1){\varsigma }_{i_2,m-d_1}({\Re }_{d_1+1},\cdots ,{\Re }_m+1)q_1^{\left(1-\frac{t}{i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}\right){\sum }_{j=d_1-i_1+1}^{d_1}({\Re }_j+1)}\hfill \\ \hfill & \times q_2^{\left(1-\frac{t}{i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}\right){\sum }_{j=m-i_2+1}^m({\Re }_j+1)}+\sum _{d_2=1}^{m-1}\sum _{i=1}^{d_2-1}\frac{{\varsigma }_{d_2}^{\prime }}{P\left({\zeta }^{\left(d_2\right)}\right|{\mathcal{D}}_2=d_2)}\left(\begin{array}{c}{d}_2\\ i\end{array}\right)\frac{{\lambda }_1^{d_2-i}{\lambda }_2^i}{{({\lambda }_1+{\lambda }_2)}^{d_2}}{\left(1-\frac{t}{i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}\right)}^{-d_2}\hfill \\ \hfill & \times \sum _{j=0}^{d_2}{\varsigma }_{j,d_2}({\Re }_1+1,\cdots ,{\Re }_{d_2}+1)q_2^{\left(1-\frac{t}{i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}\right){\Re }_{d_2-i+1}^{\ast }},\hfill \end{array}$$

where ${\Re }_j^{\ast }={\sum }_{i=j}^m({\Re }_i+1)$, $q_1=exp\left[-\left(\frac{1}{{\lambda }_1}+\frac{1}{{\lambda }_2}\right){\mathcal{T}}_1\right]$ and $q_2=exp\left[-\left(\frac{1}{{\lambda }_1}+\frac{1}{{\lambda }_2}\right){\mathcal{T}}_2\right]$.

Theorem 2.

The CondMgf of ${\widehat{\lambda }}_2$, given ${\zeta }^{\left(u\right)}$, is

$$\begin{array}{cc}\hfill M_{{\widehat{\lambda }}_1}& \left(t\right)\hfill \\ \hfill =& E\left(e^{t{\widehat{\lambda }}_1}|{\zeta }^{\left(u\right)}\right)\hfill \\ \hfill =& \sum _{d_1=1}^{n-({\Re }_1+\cdots +{\Re }_{m-1})}\sum _{i=1}^{d_1-1}\frac{{\varsigma }_{d_1}^{\prime }}{P\left({\zeta }^{\left(d_1\right)}\right|{\mathcal{D}}_1=d_1)}\left(\begin{array}{c}{d}_1\\ i\end{array}\right)\frac{{\lambda }_1^{d_1-i}{\lambda }_2^i}{{({\lambda }_1+{\lambda }_2)}^{d_1}}{\left(1-\frac{t}{d_1-i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}\right)}^{-d_1}\hfill \\ \hfill & \times \sum _{j=0}^{d_1}{\varsigma }_{j,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1)q_2^{\left(1-\frac{t}{d_1-i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}\right)\left[{\Re }_{{\mathcal{D}}_1+1}^{\prime }+{\kappa }_{j,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1)\right]}\hfill \\ \hfill & +\sum _{d_1=0}^{m-1}\sum _{i=1}^{m-1}\frac{{\varsigma }_m^{\prime }}{P\left({\zeta }^{\left(m\right)}\right|{\mathcal{D}}_1=d_1,{\mathcal{D}}_2=m)}\left(\begin{array}{c}m\\ i\end{array}\right)\frac{{\lambda }_1^{m-i}{\lambda }_2^i}{{({\lambda }_1+{\lambda }_2)}^m}{\left(1-\frac{t}{m-i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}\right)}^{-m}\hfill \\ \hfill & \times \sum _{i_1=0}^{d_1}\sum _{i_2=0}^{m-d_1}{\varsigma }_{i_1,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1){\varsigma }_{i_2,m-d_1}({\Re }_{d_1+1},\cdots ,{\Re }_m+1)q_1^{\left(1-\frac{t}{m-i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}\right){\sum }_{j=d_1-i_1+1}^{d_1}({\Re }_j+1)}\hfill \\ \hfill & \times q_2^{\left(1-\frac{t}{m-i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}\right){\sum }_{j=m-i_2+1}^m({\Re }_j+1)}+\sum _{d_2=1}^{m-1}\sum _{i=1}^{d_2-1}\frac{{\varsigma }_{d_2}^{\prime }}{P\left({\zeta }^{\left(d_2\right)}\right|{\mathcal{D}}_2=d_2)}\left(\begin{array}{c}{d}_2\\ i\end{array}\right)\frac{{\lambda }_1^{d_2-i}{\lambda }_2^i}{{({\lambda }_1+{\lambda }_2)}^{d_2}}{\left(1-\frac{t}{d_2-i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}\right)}^{-d_2}\hfill \\ \hfill & \times \sum _{j=0}^{d_1}{\varsigma }_{j,d_2}({\Re }_1+1,\cdots ,{\Re }_{d_2}+1)q_2^{\left(1-\frac{t}{d_2-i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}\right){\Re }_{d_2-i+1}^{\ast }}.\hfill \end{array}$$

Using Theorems 1 and 2, then, we readily obtain the first and second moments of ${\widehat{\lambda }}_1$ and ${\widehat{\lambda }}_2$, respectively.

Corollary 1.

The $E_{{\lambda }_1}\left({\widehat{\lambda }}_1\right)$ and $E_{{\lambda }_1}\left({{\widehat{\lambda }}_1}^2\right)$ are given by

$$\begin{array}{cc}\hfill E_{{\lambda }_1}& \left({\widehat{\lambda }}_1\right)=M_{{\widehat{\lambda }}_1}^{\prime }\left(0\right)\hfill \\ \hfill =& \sum _{d_1=m}^{n-({\Re }_1+\cdots +{\Re }_{m-1})}\sum _{i=1}^{d_1-1}\frac{{\varsigma }_{d_1}^{\prime }}{P\left({\zeta }^{\left(d_1\right)}\right|{\mathcal{D}}_1=d_1)}\left(\begin{array}{c}{d}_1\\ i\end{array}\right)\frac{{\lambda }_1^{d_1-i}{\lambda }_2^i}{{({\lambda }_1+{\lambda }_2)}^{d_1}}\sum _{j=0}^{d_1}{\varsigma }_{j,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1)\hfill \\ \hfill & \times q_1^{{\Re }_{{\mathcal{D}}_1+1}^{\prime }+{\kappa }_{j,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1)}\left\{\frac{d_1}{i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}+\frac{{\mathcal{T}}_1}{i}\left[{\Re }_{{\mathcal{D}}_1+1}^{\prime }+{\kappa }_{j,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1)\right]\right\}\hfill \\ \hfill & +\sum _{d_1=0}^{m-1}\sum _{i=1}^{m-1}\frac{{\varsigma }_m^{\prime }}{P\left({\zeta }^{\left(m\right)}\right|{\mathcal{D}}_1=d_1,{\mathcal{D}}_2=m)}\left(\begin{array}{c}m\\ i\end{array}\right)\frac{{\lambda }_1^{m-i}{\lambda }_2^i}{{({\lambda }_1+{\lambda }_2)}^m}\hfill \\ \hfill & \times \sum _{i_1=0}^{d_1}\sum _{i_2=0}^{m-d_1}{\varsigma }_{i_1,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1){\varsigma }_{i_2,m-d_1}({\Re }_{d_1+1},\cdots ,{\Re }_m+1)q_1^{{\sum }_{j=d_1-i_1+1}^{d_1}({\Re }_j+1)}\hfill \\ \hfill & \times q_2^{{\sum }_{j=m-i_2+1}^m({\Re }_j+1)}\left\{\frac{m}{i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}+\frac{{\mathcal{T}}_1}{i}\sum _{j=d_1-i_1+1}^{d_1}({\Re }_j+1)+\frac{{\mathcal{T}}_2}{i}\sum _{j=m-i_2+1}^m({\Re }_j+1)\right\}\hfill \\ \hfill & +\sum _{d_2=1}^{m-1}\sum _{i=1}^{d_2-1}\frac{{\varsigma }_{d_2}^{\prime }}{P\left({\zeta }^{\left(d_2\right)}\right|{\mathcal{D}}_2=d_2)}\left(\begin{array}{c}{d}_2\\ i\end{array}\right)\frac{{\lambda }_1^{d_2-i}{\lambda }_2^i}{{({\lambda }_1+{\lambda }_2)}^{d_2}}\hfill \\ \hfill & \times \sum _{j=0}^{d_2}{\varsigma }_{j,d_2}({\Re }_1+1,\cdots ,{\Re }_{d_2}+1)q_2^{{\Re }_{d_2-i+1}^{\ast }}\left\{\frac{d_2}{i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}+\frac{{\mathcal{T}}_2}{i}{\Re }_{d_2-i+1}^{\ast }\right\},\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill E_{{\lambda }_1}& \left({{\widehat{\lambda }}_1}^2\right)=M_{{\widehat{\lambda }}_1}^{″}\left(0\right)\hfill \\ \hfill =& \sum _{d_1=m}^{n-({\Re }_1+\cdots +{\Re }_{m-1})}\sum _{i=1}^{d_1-1}\frac{{\varsigma }_{d_1}^{\prime }}{P\left({\zeta }^{\left(d_1\right)}\right|{\mathcal{D}}_1=d_1)}\left(\begin{array}{c}{d}_1\\ i\end{array}\right)\frac{{\lambda }_1^{d_1-i}{\lambda }_2^i}{{({\lambda }_1+{\lambda }_2)}^{d_1}}\sum _{j=0}^{d_1}{\varsigma }_{j,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1)\hfill \\ \hfill & \times q_1^{{\Re }_{{\mathcal{D}}_1+1}^{\prime }+{\kappa }_{j,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1)}\left[\frac{d_1}{i}{\left(\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}\right)}^2+{\left\{\frac{d_1}{i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}+\frac{{\mathcal{T}}_1}{i}\left[{\Re }_{{\mathcal{D}}_1+1}^{\prime }+{\kappa }_{j,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1)\right]\right\}}^2\right]\hfill \\ \hfill & +\sum _{d_1=0}^{m-1}\sum _{i=1}^{m-1}\frac{{\varsigma }_m^{\prime }}{P\left({\zeta }^{\left(m\right)}\right|{\mathcal{D}}_1=d_1,{\mathcal{D}}_2=m)}\left(\begin{array}{c}m\\ i\end{array}\right)\frac{{\lambda }_1^{m-i}{\lambda }_2^i}{{({\lambda }_1+{\lambda }_2)}^m}\hfill \\ \hfill & \times \sum _{i_1=0}^{d_1}\sum _{i_2=0}^{m-d_1}{\varsigma }_{i_1,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1){\varsigma }_{i_2,m-d_1}({\Re }_{d_1+1},\cdots ,{\Re }_m+1)q_1^{{\sum }_{j=d_1-i_1+1}^{d_1}({\Re }_j+1)}\hfill \\ \hfill & \times q_2^{{\sum }_{j=m-i_2+1}^m({\Re }_j+1)}\left[\frac{m}{i}{\left(\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}\right)}^2+{\left\{\frac{m}{i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}+\frac{{\mathcal{T}}_1}{i}\sum _{j=d_1-i_1+1}^{d_1}({\Re }_j+1)+\frac{{\mathcal{T}}_2}{i}\sum _{j=m-i_2+1}^m({\Re }_j+1)\right\}}^2\right]\hfill \\ \hfill & +\sum _{d_2=1}^{m-1}\sum _{i=1}^{d_2-1}\frac{{\varsigma }_{d_2}^{\prime }}{P\left({\zeta }^{\left(d_2\right)}\right|{\mathcal{D}}_2=d_2)}\left(\begin{array}{c}{d}_2\\ i\end{array}\right)\frac{{\lambda }_1^{d_2-i}{\lambda }_2^i}{{({\lambda }_1+{\lambda }_2)}^{d_2}}\sum _{j=0}^{d_2}{\varsigma }_{j,d_2}({\Re }_1+1,\cdots ,{\Re }_{d_2}+1)q_2^{{\Re }_{d_2-i+1}^{\ast }}\hfill \\ \hfill & \times \left[\frac{d_2}{i}{\left(\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}\right)}^2+{\left\{\frac{d_2}{i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}+\frac{{\mathcal{T}}_2}{i}{\Re }_{d_2-i+1}^{\ast }\right\}}^2\right].\hfill \end{array}$$

Corollary 2.

The $E_{{\lambda }_2}\left({\widehat{\lambda }}_2\right)$ and $E_{{\lambda }_2}\left({{\widehat{\lambda }}_2}^2\right)$ are given by

$$\begin{array}{cc}\hfill E_{{\lambda }_2}& \left({\widehat{\lambda }}_2\right)=M_{{\widehat{\lambda }}_2}^{\prime }\left(0\right)\hfill \\ \hfill =& \sum _{d_1=m}^{n-({\Re }_1+\cdots +{\Re }_{m-1})}\sum _{i=1}^{d_1-1}\frac{{\varsigma }_{d_1}^{\prime }}{P\left({\zeta }^{\left(d_1\right)}\right|{\mathcal{D}}_1=d_1)}\left(\begin{array}{c}{d}_1\\ i\end{array}\right)\frac{{\lambda }_1^{d_1-i}{\lambda }_2^i}{{({\lambda }_1+{\lambda }_2)}^{d_1}}\sum _{j=0}^{d_1}{\varsigma }_{j,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1)\hfill \\ \hfill & \times q_1^{{\Re }_{{\mathcal{D}}_1+1}^{\prime }+{\kappa }_{j,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1)}\left\{\frac{d_1}{d_1-i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}+\frac{{\mathcal{T}}_1}{d_1-i}\left[{\Re }_{{\mathcal{D}}_1+1}^{\prime }+{\kappa }_{j,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1)\right]\right\}\hfill \\ \hfill & +\sum _{d_1=0}^{m-1}\sum _{i=1}^{m-1}\frac{{\varsigma }_m^{\prime }}{P\left({\zeta }^{\left(m\right)}\right|{\mathcal{D}}_1=d_1,{\mathcal{D}}_2=m)}\left(\begin{array}{c}m\\ i\end{array}\right)\frac{{\lambda }_1^{m-i}{\lambda }_2^i}{{({\lambda }_1+{\lambda }_2)}^m}\hfill \\ \hfill & \times \sum _{i_1=0}^{d_1}\sum _{i_2=0}^{m-d_1}{\varsigma }_{i_1,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1){\varsigma }_{i_2,m-d_1}({\Re }_{d_1+1},\cdots ,{\Re }_m+1)q_1^{{\sum }_{j=d_1-i_1+1}^{d_1}({\Re }_j+1)}\hfill \\ \hfill & \times q_2^{{\sum }_{j=m-i_2+1}^m({\Re }_j+1)}\left\{\frac{m}{m-i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}+\frac{{\mathcal{T}}_1}{m-i}\sum _{j=d_1-i_1+1}^{d_1}({\Re }_j+1)+\frac{{\mathcal{T}}_2}{m-i}\sum _{j=m-i_2+1}^m({\Re }_j+1)\right\}\hfill \\ \hfill & +\sum _{d_2=1}^{m-1}\sum _{i=1}^{d_2-1}\frac{{\varsigma }_{d_2}^{\prime }}{P\left({\zeta }^{\left(d_2\right)}\right|{\mathcal{D}}_2=d_2)}\left(\begin{array}{c}{d}_2\\ i\end{array}\right)\frac{{\lambda }_1^{d_2-i}{\lambda }_2^i}{{({\lambda }_1+{\lambda }_2)}^{d_2}}\hfill \\ \hfill & \times \sum _{j=0}^{d_2}{\varsigma }_{j,d_2}({\Re }_1+1,\cdots ,{\Re }_{d_2}+1)q_2^{{\Re }_{d_2-i+1}^{\ast }}\left\{\frac{d_2}{d_2-i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}+\frac{{\mathcal{T}}_2}{d_2-i}{\Re }_{d_2-i+1}^{\ast }\right\},\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill E_{{\lambda }_2}& \left({{\widehat{\lambda }}_2}^2\right)=M_{{\widehat{\lambda }}_2}^{″}\left(0\right)\hfill \\ \hfill =& \sum _{d_1=m}^{n-({\Re }_1+\cdots +{\Re }_{m-1})}\sum _{i=1}^{d_1-1}\frac{{\varsigma }_{d_1}^{\prime }}{P\left({\zeta }^{\left(d_1\right)}\right|{\mathcal{D}}_1=d_1)}\left(\begin{array}{c}{d}_1\\ i\end{array}\right)\frac{{\lambda }_1^{d_1-i}{\lambda }_2^i}{{({\lambda }_1+{\lambda }_2)}^{d_1}}\sum _{j=0}^{d_1}{\varsigma }_{j,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1)\hfill \\ \hfill & \times q_1^{{\Re }_{{\mathcal{D}}_1+1}^{\prime }+{\kappa }_{j,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1)}\hfill \\ \hfill & \times \left[\frac{d_1}{d_1-i}{\left(\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}\right)}^2+{\left\{\frac{d_1}{d_1-i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}+\frac{{\mathcal{T}}_1}{d_1-i}\left[{\Re }_{{\mathcal{D}}_1+1}^{\prime }+{\kappa }_{j,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1)\right]\right\}}^2\right]\hfill \\ \hfill & +\sum _{d_1=0}^{m-1}\sum _{i=1}^{m-1}\frac{{\varsigma }_m^{\prime }}{P\left({\zeta }^{\left(m\right)}\right|{\mathcal{D}}_1=d_1,{\mathcal{D}}_2=m)}\left(\begin{array}{c}m\\ i\end{array}\right)\frac{{\lambda }_1^{m-i}{\lambda }_2^i}{{({\lambda }_1+{\lambda }_2)}^m}\hfill \\ \hfill & \times \sum _{i_1=0}^{d_1}\sum _{i_2=0}^{m-d_1}{\varsigma }_{i_1,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1){\varsigma }_{i_2,m-d_1}({\Re }_{d_1+1},\cdots ,{\Re }_m+1)q_1^{{\sum }_{j=d_1-i_1+1}^{d_1}({\Re }_j+1)}{q}_2^{{\sum }_{j=m-i_2+1}^m({\Re }_j+1)}\hfill \\ \hfill & \times \left[\frac{m}{m-i}{\left(\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}\right)}^2+{\left\{\frac{m}{m-i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}+\frac{{\mathcal{T}}_1}{m-i}\sum _{j=d_1-i_1+1}^{d_1}({\Re }_j+1)+\frac{{\mathcal{T}}_2}{m-i}\sum _{j=m-i_2+1}^m({\Re }_j+1)\right\}}^2\right]\hfill \\ \hfill & +\sum _{d_2=1}^{m-1}\sum _{i=1}^{d_2-1}\frac{{\varsigma }_{d_2}^{\prime }}{P\left({\zeta }^{\left(d_2\right)}\right|{\mathcal{D}}_2=d_2)}\left(\begin{array}{c}{d}_2\\ i\end{array}\right)\frac{{\lambda }_1^{d_2-i}{\lambda }_2^i}{{({\lambda }_1+{\lambda }_2)}^{d_2}}\sum _{j=0}^{d_2}{\varsigma }_{j,d_2}({\Re }_1+1,\cdots ,{\Re }_{d_2}+1)q_2^{{\Re }_{d_2-i+1}^{\ast }}\hfill \\ \hfill & \times \left[\frac{d_2}{d_2-i}{\left(\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}\right)}^2+{\left\{\frac{d_2}{d_2-i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}+\frac{{\mathcal{T}}_2}{i}{\Re }_{d_2-i+1}^{\ast }\right\}}^2\right].\hfill \end{array}$$

In order to obtain CondPDF of ${\widehat{\lambda }}_1$ and ${\widehat{\lambda }}_2$, respectively, we need the following Lemma in Ref. [13].

Lemma 2.

If RV $Y\sim \gamma (a,b)$, let $X=Y+\delta$, then the Mgf or RV X is

$$\begin{array}{c}\hfill M_X\left(t\right)=e^{t\delta }{(1-bt)}^{-a},t<1/b,\end{array}$$

where $\gamma (x-\delta ;a,b)$ is a gamma distribution with shift (δ), shape ($a>0$) and rate ($b>0$) parameters.

Using Lemma 2, we have the CondPDF of ${\widehat{\lambda }}_1$, given as ${\zeta }^{\left(u\right)}$, as in the following theorem.

Theorem 3.

The CondPDF of ${\widehat{\lambda }}_1$, given ${\zeta }^{\left(u\right)}$, is

$$\begin{array}{cc}\hfill f_{{\widehat{\lambda }}_1}& \left(x\right)\hfill \\ \hfill =& \sum _{d_1=m}^{n-({\Re }_1+\cdots +{\Re }_{m-1})}\sum _{i=1}^{d_1-1}\frac{{\varsigma }_{d_1}^{\prime }}{P\left({\zeta }^{\left(d_1\right)}\right|{\mathcal{D}}_1=d_1)}\left(\begin{array}{c}{d}_1\\ i\end{array}\right)\frac{{\lambda }_1^{d_1-i}{\lambda }_2^i}{{({\lambda }_1+{\lambda }_2)}^{d_1}}\sum _{j=0}^{d_1}{\varsigma }_{j,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1)\hfill \\ \hfill & \times q_1^{{\Re }_{{\mathcal{D}}_1+1}^{\prime }+{\kappa }_{j,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1)}\gamma \left(x-\frac{{\mathcal{T}}_1}{i}\left[{\Re }_{{\mathcal{D}}_1+1}^{\prime }+{\kappa }_{j,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1)\right];d_1,\frac{1}{i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}\right)\hfill \\ \hfill & +\sum _{d_1=0}^{m-1}\sum _{i=1}^{m-1}\frac{{\varsigma }_m^{\prime }}{P\left({\zeta }^{\left(m\right)}\right|{\mathcal{D}}_1=d_1,{\mathcal{D}}_2=m)}\left(\begin{array}{c}m\\ i\end{array}\right)\frac{{\lambda }_1^{m-i}{\lambda }_2^i}{{({\lambda }_1+{\lambda }_2)}^m}\hfill \\ \hfill & \times \sum _{i_1=0}^{d_1}\sum _{i_2=0}^{m-d_1}{\varsigma }_{i_1,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1){\varsigma }_{i_2,m-d_1}({\Re }_{d_1+1},\cdots ,{\Re }_m+1)q_1^{{\sum }_{j=d_1-i_1+1}^{d_1}({\Re }_j+1)}\hfill \\ \hfill & \times q_2^{{\sum }_{j=m-i_2+1}^m({\Re }_j+1)}\gamma \left(x-\frac{{\mathcal{T}}_1}{i}\sum _{j=d_1-i_1+1}^{d_1}({\Re }_j+1)-\frac{{\mathcal{T}}_2}{i}\sum _{j=m-i_2+1}^m({\Re }_j+1);m,\frac{1}{i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}\right)\hfill \\ \hfill & +\sum _{d_2=1}^{m-1}\sum _{i=1}^{d_2-1}\frac{{\varsigma }_{d_2}^{\prime }}{P\left({\zeta }^{\left(d_2\right)}\right|{\mathcal{D}}_2=d_2)}\left(\begin{array}{c}{d}_2\\ i\end{array}\right)\frac{{\lambda }_1^{d_2-i}{\lambda }_2^i}{{({\lambda }_1+{\lambda }_2)}^{d_2}}\sum _{j=0}^{d_2}{\varsigma }_{j,d_2}({\Re }_1+1,\cdots ,{\Re }_{d_2}+1)q_2^{{\Re }_{d_2-i+1}^{\ast }}\hfill \\ \hfill & \times \gamma \left(x-\frac{{\mathcal{T}}_2}{i}{\Re }_{d_2-i+1}^{\ast };d_2,\frac{1}{i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}\right),\hfill \end{array}$$

Theorem 4.

The CondPDF of ${\widehat{\lambda }}_2$, given ${\zeta }^{\left(u\right)}$, is

$$\begin{array}{cc}\hfill f_{{\widehat{\lambda }}_2}& \left(x\right)\hfill \\ \hfill =& \sum _{d_1=m}^{n-({\Re }_1+\cdots +{\Re }_{m-1})}\sum _{i=1}^{d_1-1}\frac{{\varsigma }_{d_1}^{\prime }}{P\left({\zeta }^{\left(d_1\right)}\right|{\mathcal{D}}_1=d_1)}\left(\begin{array}{c}{d}_1\\ i\end{array}\right)\frac{{\lambda }_1^{d_1-i}{\lambda }_2^i}{{({\lambda }_1+{\lambda }_2)}^{d_1}}\sum _{j=0}^{d_1}{\varsigma }_{j,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1)\hfill \\ \hfill & \times q_1^{{\Re }_{{\mathcal{D}}_1+1}^{\prime }+{\kappa }_{j,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1)}\gamma \left(x-\frac{{\mathcal{T}}_1}{d_1-i}\left[{\Re }_{{\mathcal{D}}_1+1}^{\prime }+{\kappa }_{j,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1)\right];d_1,\frac{1}{d_1-i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}\right)\hfill \\ \hfill & +\sum _{d_1=0}^{m-1}\sum _{i=1}^{m-1}\frac{{\varsigma }_m^{\prime }}{P\left({\zeta }^{\left(m\right)}\right|{\mathcal{D}}_1=d_1,{\mathcal{D}}_2=m)}\left(\begin{array}{c}m\\ i\end{array}\right)\frac{{\lambda }_1^{m-i}{\lambda }_2^i}{{({\lambda }_1+{\lambda }_2)}^m}\hfill \\ \hfill & \times \sum _{i_1=0}^{d_1}\sum _{i_2=0}^{m-d_1}{\varsigma }_{i_1,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1){\varsigma }_{i_2,m-d_1}({\Re }_{d_1+1},\cdots ,{\Re }_m+1)q_1^{{\sum }_{j=d_1-i_1+1}^{d_1}({\Re }_j+1)}\hfill \\ \hfill & \times q_2^{{\sum }_{j=m-i_2+1}^m({\Re }_j+1)}\gamma \left(x-\frac{{\mathcal{T}}_1}{m-i}\sum _{j=d_1-i_1+1}^{d_1}({\Re }_j+1)-\frac{{\mathcal{T}}_2}{m-i}\sum _{j=m-i_2+1}^m({\Re }_j+1);m,\frac{1}{m-i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}\right)\hfill \\ \hfill & +\sum _{d_2=1}^{m-1}\sum _{i=1}^{d_2-1}\frac{{\varsigma }_{d_2}^{\prime }}{P\left({\zeta }^{\left(d_2\right)}\right|{\mathcal{D}}_2=d_2)}\left(\begin{array}{c}{d}_2\\ i\end{array}\right)\frac{{\lambda }_1^{d_2-i}{\lambda }_2^i}{{({\lambda }_1+{\lambda }_2)}^{d_2}}\sum _{j=0}^{d_2}{\varsigma }_{j,d_2}({\Re }_1+1,\cdots ,{\Re }_{d_2}+1)q_2^{{\Re }_{d_2-i+1}^{\ast }}\hfill \\ \hfill & \times \gamma \left(x-\frac{{\mathcal{T}}_2}{d_2-i}{\Re }_{d_2-i+1}^{\ast };d_2,\frac{1}{d_2-i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}\right).\hfill \end{array}$$

Corollary 3.

The tail probabilities of ${\widehat{\lambda }}_1$ and ${\widehat{\lambda }}_2$, given ${\zeta }^{\left(u\right)}$, are

$$\begin{array}{cc}\hfill P_{{\lambda }_1}& \left({\widehat{\lambda }}_1>w\right)\hfill \\ \hfill =& \sum _{d_1=m}^{n-({\Re }_1+\cdots +{\Re }_{m-1})}\sum _{i=1}^{d_1-1}\frac{{\varsigma }_{d_1}^{\prime }}{P\left({\zeta }^{\left(d_1\right)}\right|{\mathcal{D}}_1=d_1)}\left(\begin{array}{c}{d}_1\\ i\end{array}\right)\frac{{\lambda }_1^{d_1-i}{\lambda }_2^i}{{({\lambda }_1+{\lambda }_2)}^{d_1}}\sum _{j=0}^{d_1}{\varsigma }_{j,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1)\hfill \\ \hfill & \times q_1^{{\Re }_{{\mathcal{D}}_1+1}^{\prime }+{\kappa }_{j,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1)}\Gamma \left(d_1,\frac{1}{i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}⟨d_1-\frac{{\mathcal{T}}_1}{i}\left[{\Re }_{{\mathcal{D}}_1+1}^{\prime }+{\kappa }_{j,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1)\right]⟩\right)\hfill \\ \hfill & +\sum _{d_1=0}^{m-1}\sum _{i=1}^{m-1}\frac{{\varsigma }_m^{\prime }}{P\left({\zeta }^{\left(m\right)}\right|{\mathcal{D}}_1=d_1,{\mathcal{D}}_2=m)}\left(\begin{array}{c}m\\ i\end{array}\right)\frac{{\lambda }_1^{m-i}{\lambda }_2^i}{{({\lambda }_1+{\lambda }_2)}^m}\hfill \\ \hfill & \times \sum _{i_1=0}^{d_1}\sum _{i_2=0}^{m-d_1}{\varsigma }_{i_1,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1){\varsigma }_{i_2,m-d_1}({\Re }_{d_1+1},\cdots ,{\Re }_m+1)q_1^{{\sum }_{j=d_1-i_1+1}^{d_1}({\Re }_j+1)}\hfill \\ \hfill & \times q_2^{{\sum }_{j=m-i_2+1}^m({\Re }_j+1)}\Gamma \left(m,\frac{1}{i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}⟨m-\frac{{\mathcal{T}}_1}{i}\sum _{j=d_1-i_1+1}^{d_1}({\Re }_j+1)-\frac{{\mathcal{T}}_2}{i}\sum _{j=m-i_2+1}^m({\Re }_j+1)⟩\right)\hfill \\ \hfill & +\sum _{d_2=1}^{m-1}\sum _{i=1}^{d_2-1}\frac{{\varsigma }_{d_2}^{\prime }}{P\left({\zeta }^{\left(d_2\right)}\right|{\mathcal{D}}_2=d_2)}\left(\begin{array}{c}{d}_2\\ i\end{array}\right)\frac{{\lambda }_1^{d_2-i}{\lambda }_2^i}{{({\lambda }_1+{\lambda }_2)}^{d_2}}\sum _{j=0}^{d_2}{\varsigma }_{j,d_2}({\Re }_1+1,\cdots ,{\Re }_{d_2}+1)q_2^{{\Re }_{d_2-i+1}^{\ast }}\hfill \\ \hfill & \times \Gamma \left(d_2,\frac{1}{i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}⟨d_2-\frac{{\mathcal{T}}_2}{i}{\Re }_{d_2-i+1}^{\ast }⟩\right),\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill P_{{\lambda }_2}& \left({\widehat{\lambda }}_2>w\right)\hfill \\ \hfill =& \sum _{d_1=m}^{n-({\Re }_1+\cdots +{\Re }_{m-1})}\sum _{i=1}^{d_1-1}\frac{{\varsigma }_{d_1}^{\prime }}{P\left({\zeta }^{\left(d_1\right)}\right|{\mathcal{D}}_1=d_1)}\left(\begin{array}{c}{d}_1\\ i\end{array}\right)\frac{{\lambda }_1^{d_1-i}{\lambda }_2^i}{{({\lambda }_1+{\lambda }_2)}^{d_1}}\sum _{j=0}^{d_1}{\varsigma }_{j,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1)\hfill \\ \hfill & \times q_1^{{\Re }_{{\mathcal{D}}_1+1}^{\prime }+{\kappa }_{j,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1)}\Gamma \left(d_1,\frac{1}{d_1-i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}⟨d_1-\frac{{\mathcal{T}}_1}{d_1-i}\left[{\Re }_{{\mathcal{D}}_1+1}^{\prime }+{\kappa }_{j,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1)\right]⟩\right)\hfill \\ \hfill & +\sum _{d_1=0}^{m-1}\sum _{i=1}^{m-1}\frac{{\varsigma }_m^{\prime }}{P\left({\zeta }^{\left(m\right)}\right|{\mathcal{D}}_1=d_1,{\mathcal{D}}_2=m)}\left(\begin{array}{c}m\\ i\end{array}\right)\frac{{\lambda }_1^{m-i}{\lambda }_2^i}{{({\lambda }_1+{\lambda }_2)}^m}\hfill \\ \hfill & \times \sum _{i_1=0}^{d_1}\sum _{i_2=0}^{m-d_1}{\varsigma }_{i_1,d_1}({\Re }_1+1,\cdots ,{\Re }_{d_1}+1){\varsigma }_{i_2,m-d_1}({\Re }_{d_1+1},\cdots ,{\Re }_m+1)q_1^{{\sum }_{j=d_1-i_1+1}^{d_1}({\Re }_j+1)}\hfill \\ \hfill & \times q_2^{{\sum }_{j=m-i_2+1}^m({\Re }_j+1)}\Gamma \left(m,\frac{1}{m-i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}⟨m-\frac{{\mathcal{T}}_1}{m-i}\sum _{j=d_1-i_1+1}^{d_1}({\Re }_j+1)-\frac{{\mathcal{T}}_2}{m-i}\sum _{j=m-i_2+1}^m({\Re }_j+1)⟩\right)\hfill \\ \hfill & +\sum _{d_2=1}^{m-1}\sum _{i=1}^{d_2-1}\frac{{\varsigma }_{d_2}^{\prime }}{P\left({\zeta }^{\left(d_2\right)}\right|{\mathcal{D}}_2=d_2)}\left(\begin{array}{c}{d}_2\\ i\end{array}\right)\frac{{\lambda }_1^{d_2-i}{\lambda }_2^i}{{({\lambda }_1+{\lambda }_2)}^{d_2}}\sum _{j=0}^{d_2}{\varsigma }_{j,d_2}({\Re }_1+1,\cdots ,{\Re }_{d_2}+1)q_2^{{\Re }_{d_2-i+1}^{\ast }}\hfill \\ \hfill & \times \Gamma \left(d_2,\frac{1}{d_2-i}\frac{{\lambda }_1{\lambda }_2}{{\lambda }_1+{\lambda }_2}⟨d_2-\frac{{\mathcal{T}}_2}{d_2-i}{\Re }_{d_2-i+1}^{\ast }⟩\right),\hfill \end{array}$$

respectively, where w is the arbitrary constant, $<x>=max\{x,0\}$ and $\Gamma (a,b)={\int }_b^{\infty }(1/(a-1)!)x^{a-1}{e}^{-x}dx$.

The proofs of Theorems are given in Appendix A and Appendix B. Based on Corollary 3, we derive $100(1-\alpha )\%$ ConfI of ${\widehat{\lambda }}_k$. Here, when the other parameter is fixed, we suppose that $P({\widehat{\lambda }}_k>w)$ is an increasing function of ${\lambda }_k$. Then, we can derive the ConfP for ${\lambda }_k$, denoted by $({\lambda }_k^{\left(L\right)},{\lambda }_k^{\left(U\right)})$, satisfying the following equation with ${\widehat{\lambda }}_k^{\left(obs\right)}$ being the observed value of ${\widehat{\lambda }}_k$:

$$\begin{array}{c}\hfill P_{{\lambda }_k^{\left(L\right)}}({\widehat{\lambda }}_k^{\left(L\right)}>{\widehat{\lambda }}_k^{\left(obs\right)})=\frac{\alpha }{2},P_{{\lambda }_k^{\left(U\right)}}({\widehat{\lambda }}_k^{\left(U\right)}>{\widehat{\lambda }}_k^{\left(obs\right)})=1-\frac{\alpha }{2},k=1,2.\end{array}$$

3. Data Analysis and Simulation Results

3.1. Data Analysis

In order to analyze the illustrative example data, we use the data in Ref. [14]. The full data are presented in Table 1. This data was analyzed by Refs. [11,15,16]. From the data (Table 1), ${\delta }_i=1$ denotes the failure of the i-th unit caused by 9th RiF, and ${\delta }_i=0$ denotes the failure of the i-th unit caused by other RiFs. Here, we suppose that this data follow the ExDist based on the PrTy2CS (i.e., $n=36$, $m=24$, ${\Re }_1=6,{\Re }_{24}=6$ and ${\Re }_i=0$ for $i=2,\dots ,23$). Then, PrTy2CS data are presented in Table 2.

Table 1. Full data for illustrative example.

xi	11	35	49	170	329	381	708	958	1062
${\delta }_i$	0	0	0	0	0	0	0	0	0
$x_i$	1167	1594	1925	1990	2223	2327	2400	2451	2471
${\delta }_i$	1	0	1	1	1	0	1	0	1
$x_i$	2551	2565	2831	2568	2694	2702	2761	3034	3059
${\delta }_i$	1	0	1	1	0	0	0	1	0
$x_i$	3112	3214	3478	3504	4329	6367	6976	7846	13403
${\delta }_i$	1	1	1	1	1	0	1	1	0

Table 2. PrTy2CS data for illustrative example.

$x_i$	11	35	49	170	329	381	708	958
${\delta }_i$	0	0	0	0	0	0	0	0
${\Re }_i$	6	0	0	0	0	0	0	0
$x_i$	1062	1167	1594	1925	1990	2223	2327	2400
${\delta }_i$	0	1	0	1	1	1	0	1
${\Re }_i$	0	0	0	0	0	0	0	0
$x_i$	2451	2471	2551	2565	2568	2694	2702	2761
${\delta }_i$	0	1	1	0	1	1	0	0
${\Re }_i$	0	0	0	0	0	0	0	6

We set three GeTy2PrHCS (Case (a): ${\mathcal{T}}_1=3000$ and ${\mathcal{T}}_2=4000$, Case (b): ${\mathcal{T}}_1=2000$ and ${\mathcal{T}}_2=3000$, and Case (c): ${\mathcal{T}}_1=2000$ and ${\mathcal{T}}_1=2500$). Table 3 presents the each $95\%$ ConfIs for ${\widehat{\lambda }}_1$ and ${\widehat{\lambda }}_2$, and we have contained the standard error (StE) and MSE calculated from Corollary 1–3. Each PDF of ${\widehat{\lambda }}_1$ and ${\widehat{\lambda }}_2$ based on the illustrative example data is shown in Figure 2.

Table 3. Inference of ${\widehat{\lambda }}_1$ and ${\widehat{\lambda }}_2$ for illustrative example.

${\mathcal{T}}_1$	${\mathcal{T}}_2$	${\mathit{n}}_1$	${\mathit{n}}_2$	${\widehat{\mathit{\lambda }}}_1$	SE(${\widehat{\mathit{\lambda }}}_1$)	95% ConfI for ${\widehat{\mathit{\lambda }}}_1$
				${\widehat{\mathit{\lambda }}}_2$	SE(${\widehat{\mathit{\lambda }}}_2$)	95% ConfI for ${\widehat{\mathit{\lambda }}}_2$
3000	4000	9	16	6221.000	2073.667	(3236.839, 11,956.370)
				3499.312	874.828	(2143.771, 5711.985)
2000	3000	9	15	6080.444	2026.815	(3163.707, 11,686.230)
				3648.267	941.978	(2199.395, 6051.596)
2000	2500	6	12	8719.500	3559.721	(3917.271, 19,408.840)
				4359.750	1258.551	(2475.919, 7676.917)

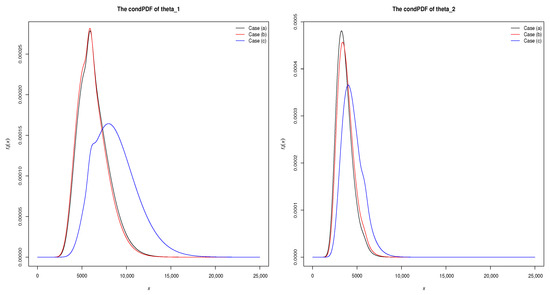
Figure 2. The CondPDFs of ${\widehat{\lambda }}_1$ and ${\widehat{\lambda }}_2$ for example.

3.2. Simulation Results

In this Section, we consider various GeTy2PrHCS. First of all, we have used four PrTy2CS as; Sch (a): ${\Re }_m=n-m$ and ${\Re }_1={\Re }_2=\cdots ={\Re }_{m-1}=0$, Sch (b): ${\Re }_1=n-m$ and ${\Re }_2={\Re }_3=\cdots ={\Re }_m=0$, Sch (c): ${\Re }_1={\Re }_m=(n-m)/2$ and ${\Re }_2={\Re }_3=\cdots ={\Re }_{m-1}=0$, Sch (d): ${\Re }_{m/2}=n-m$ and ${\Re }_1={\Re }_2=\cdots ={\Re }_{m/2-1}={\Re }_{m/2+1}=\cdots ={\Re }_m=0$.

First of all, for four PrTy2CS, we generate PrTy2CS data. We generate new RV $\mathit{U}=(u_1,u_2,\cdots ,u_n)$. Now if $u_i<{\theta }_1/({\theta }_1+{\theta }_2)$, then assign ${\delta }_i=1$, otherwise ${\delta }_i=0$. Then, the corresponding GeTy2PrHCS CompD is $\{(x_{1:m:n},{\delta }_1),(x_{2:m:n},{\delta }_2),\cdots ,(x_{d_1:n},{\delta }_{d_1})\}$ for Case (a) ($x_{m:m:n}<{\mathcal{T}}_1$), $\{(x_{1:m:n},{\delta }_1),(x_{2:m:n},{\delta }_2),\cdots ,(x_{m:m:n},{\delta }_m)\}$ for Case (b) (${\mathcal{T}}_1<x_{m:m:n}<{\mathcal{T}}_2$), and $\{(x_{1:m:n},{\delta }_1),(x_{2:m:n},{\delta }_2),\cdots ,(x_{d_2:m:n},{\delta }_{d_2})\}$ for Case (c) (${\mathcal{T}}_2<x_{m:m:n}$). Without loss of generality, we take ${\lambda }_1=0.4$ and ${\lambda }_2=0.6$ in each case. We replicate the process 1000 times in each GeTy2PrHCS. We calculate the rMSEs, biases, ConfL and CovP of the estimator. The simulation results are presented in Figure 3 (Table 4) and Figure 4 (Table 5).

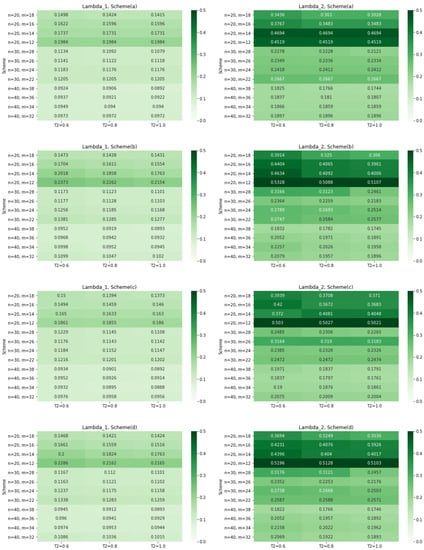
Figure 3. Relative rMSEs for ${\widehat{\lambda }}_1$ and ${\widehat{\lambda }}_2$

Table 4. Relative rMSEs and biases for ${\widehat{\lambda }}_1$ and ${\widehat{\lambda }}_2$.

n	${\mathcal{T}}_1$	m	Scheme	${\mathcal{T}}_2=0.6$		${\mathcal{T}}_2=0.8$		${\mathcal{T}}_2=1.0$
				${\widehat{\mathbf{\lambda }}}_{\mathbf{1}}$	${\widehat{\mathbf{\lambda }}}_{\mathbf{2}}$	${\widehat{\mathbf{\lambda }}}_{\mathbf{1}}$	${\widehat{\mathbf{\lambda }}}_{\mathbf{2}}$	${\widehat{\mathbf{\lambda }}}_{\mathbf{1}}$	${\widehat{\mathbf{\lambda }}}_{\mathbf{2}}$
20	0.3	18	(a)	0.1498(0.0233) ${}^{†}$	0.3436(0.0678)	0.1424(0.0198)	0.3030(0.0606)	0.1415(0.0195)	0.3028(0.0601)
			(b)	0.1473(0.0224)	0.3914(0.0792)	0.1428(0.0203)	0.3250(0.0616)	0.1431(0.0205)	0.3060(0.0560)
			(c)	0.1500(0.0240)	0.3939(0.0891)	0.1394(0.0196)	0.3708(0.0797)	0.1373(0.0182)	0.3710(0.0790)
			(d)	0.1468(0.0217)	0.3694(0.0733)	0.1421(0.0198)	0.3249(0.0610)	0.1424(0.0201)	0.3036(0.0555)
		16	(a)	0.1622(0.0276)	0.3767(0.0819)	0.1596(0.0268)	0.3483(0.0786)	0.1596(0.0268)	0.3483(0.0786)
			(b)	0.1704(0.0313)	0.4404(0.0958)	0.1611(0.0256)	0.4065(0.0813)	0.1554(0.0232)	0.3961(0.0762)
			(c)	0.1494(0.0211)	0.4200(0.0794)	0.1459(0.0189)	0.3672(0.0659)	0.1460(0.0187)	0.3683(0.0661)
			(d)	0.1661(0.0300)	0.4231(0.0891)	0.1559(0.0234)	0.4076(0.0799)	0.1516(0.0219)	0.3926(0.0743)
		14	(a)	0.1737(0.0346)	0.4694(0.1370)	0.1731(0.0344)	0.4694(0.1037)	0.1731(0.0344)	0.4694(0.1037)
			(b)	0.2018(0.0393)	0.4634(0.1251)	0.1858(0.0342)	0.4092(0.1059)	0.1763(0.0302)	0.4006(0.1004)
			(c)	0.1650(0.0279)	0.3720(0.0814)	0.1633(0.0258)	0.4081(0.0906)	0.1630(0.0257)	0.4048(0.0897)
			(d)	0.2000(0.0365)	0.4396(0.1154)	0.1824(0.0329)	0.4040(0.1038)	0.1763(0.0301)	0.4017(0.1003)
		12	(a)	0.1984(0.0437)	0.4519(0.1122)	0.1984(0.0437)	0.4519(0.1122)	0.1984(0.0437)	0.4519(0.1122)
			(b)	0.2373(0.0486)	0.5328(0.1392)	0.2262(0.0441)	0.5088(0.1223)	0.2154(0.0401)	0.5107(0.1183)
			(c)	0.1861(0.0338)	0.5030(0.1113)	0.1855(0.0336)	0.5027(0.1114)	0.1860(0.0336)	0.5021(0.1111)
			(d)	0.2286(0.0443)	0.5196(0.1302)	0.2162(0.0415)	0.5128(0.1228)	0.2165(0.0401)	0.5103(0.1180)
30	0.3	28	(a)	0.1134(0.0126)	0.2278(0.0358)	0.1092(0.0103)	0.2228(0.0315)	0.1079(0.0097)	0.2121(0.0301)
			(b)	0.1173(0.0182)	0.3166(0.0582)	0.1123(0.0161)	0.3123(0.0517)	0.1101(0.0146)	0.2461(0.0463)
			(c)	0.1229(0.0144)	0.2485(0.0483)	0.1145(0.0116)	0.2306(0.0430)	0.1108(0.0103)	0.2265(0.0404)
			(d)	0.1167(0.0182)	0.3176(0.0581)	0.1120(0.0158)	0.3121(0.0515)	0.1101(0.0145)	0.2457(0.0462)
		26	(a)	0.1141(0.0111)	0.2349(0.0390)	0.1122(0.0101)	0.2336(0.0381)	0.1118(0.0100)	0.2334(0.0380)
			(b)	0.1177(0.0177)	0.2364(0.0398)	0.1128(0.0150)	0.2259(0.0358)	0.1103(0.0141)	0.2183(0.0333)
			(c)	0.1176(0.0172)	0.3164(0.0565)	0.1143(0.0152)	0.3190(0.0517)	0.1142(0.0149)	0.3183(0.0505)
			(d)	0.1163(0.0166)	0.2352(0.0387)	0.1121(0.0148)	0.2253(0.0353)	0.1102(0.0140)	0.2176(0.0328)
		24	(a)	0.1183(0.0130)	0.2418(0.0433)	0.1176(0.0127)	0.2412(0.0430)	0.1176(0.0127)	0.2412(0.0430)
			(b)	0.1256(0.0165)	0.2789(0.0582)	0.1185(0.0140)	0.2693(0.0518)	0.1168(0.0129)	0.2514(0.0465)
			(c)	0.1184(0.0151)	0.2385(0.0382)	0.1152(0.0137)	0.2328(0.0356)	0.1147(0.0135)	0.2326(0.0353)
			(d)	0.1237(0.0160)	0.2738(0.0555)	0.1175(0.0134)	0.2668(0.0502)	0.1158(0.0126)	0.2503(0.0462)
		22	(a)	0.1205(0.0138)	0.2667(0.0547)	0.1205(0.0138)	0.2667(0.0547)	0.1205(0.0138)	0.2667(0.0547)
			(b)	0.1381(0.0208)	0.2747(0.0479)	0.1285(0.0148)	0.2584(0.0423)	0.1277(0.0139)	0.2577(0.0411)
			(c)	0.1216(0.0183)	0.2472(0.0396)	0.1201(0.0178)	0.2472(0.0394)	0.1202(0.0179)	0.2474(0.0394)
			(d)	0.1338(0.0186)	0.2587(0.0432)	0.1283(0.0147)	0.2588(0.0424)	0.1259(0.0133)	0.2571(0.0403)
40	10.0	38	(a)	0.0924(0.0084)	0.1825(0.0237)	0.0906(0.0072)	0.1766(0.0191)	0.0892(0.0065)	0.1744(0.0179)
			(b)	0.0952(0.0102)	0.1832(0.0183)	0.0919(0.0081)	0.1782(0.0161)	0.0893(0.0070)	0.1745(0.0145)
			(c)	0.0934(0.0076)	0.1971(0.0300)	0.0901(0.0059)	0.1837(0.0237)	0.0892(0.0049)	0.1791(0.0207)
			(d)	0.0945(0.0099)	0.1822(0.0173)	0.0912(0.0077)	0.1766(0.0156)	0.0893(0.0070)	0.1746(0.0143)
		36	(a)	0.0937(0.0079)	0.1837(0.0230)	0.0921(0.0068)	0.1810(0.0208)	0.0922(0.0069)	0.1807(0.0206)
			(b)	0.0968(0.0101)	0.2052(0.0293)	0.0942(0.0093)	0.1971(0.0253)	0.0932(0.0096)	0.1891(0.0222)
			(c)	0.0952(0.0097)	0.1837(0.0180)	0.0926(0.0081)	0.1797(0.0149)	0.0914(0.0078)	0.1761(0.0142)
			(d)	0.0960(0.0098)	0.2052(0.0297)	0.0941(0.0093)	0.1957(0.0242)	0.0929(0.0095)	0.1892(0.0221)
		34	(a)	0.0949(0.0076)	0.1866(0.0239)	0.0940(0.0072)	0.1859(0.0235)	0.0940(0.0072)	0.1859(0.0235)
			(b)	0.0998(0.0100)	0.2257(0.0370)	0.0952(0.0083)	0.2026(0.0293)	0.0945(0.0081)	0.1958(0.0271)
			(c)	0.0932(0.0095)	0.1900(0.0239)	0.0895(0.0070)	0.1876(0.2019)	0.0888(0.0067)	0.1861(0.0214)
			(d)	0.0974(0.0088)	0.2158(0.0350)	0.0953(0.0086)	0.2022(0.0293)	0.0944(0.0081)	0.1962(0.0274)
		32	(a)	0.0973(0.0081)	0.1897(0.0257)	0.0972(0.0080)	0.1896(0.0258)	0.0972(0.0080)	0.1896(0.0258)
			(b)	0.1099(0.0130)	0.2079(0.0236)	0.1047(0.0104)	0.1957(0.0212)	0.1020(0.0104)	0.1896(0.0197)
			(c)	0.0976(0.0080)	0.2075(0.0261)	0.0958(0.0072)	0.2009(0.0231)	0.0956(0.0071)	0.2004(0.0229)
			(d)	0.1086(0.0121)	0.2069(0.0232)	0.1036(0.0103)	0.1922(0.0199)	0.1015(0.0102)	0.1893(0.0197)

${}^{†}$ rMSE(Bias).

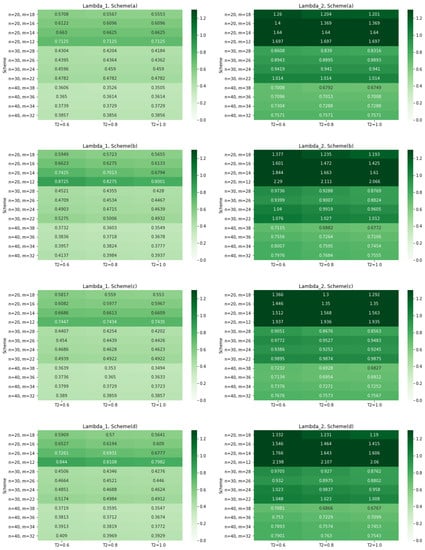
Figure 4. Relative ConfL for ${\widehat{\lambda }}_1$ and ${\widehat{\lambda }}_2$.

Table 5. Relative ConfL and CovP for ${\widehat{\lambda }}_1$ and ${\widehat{\lambda }}_2$.

n	${\mathcal{T}}_1$	m	Scheme	${\mathcal{T}}_2=0.6$		${\mathcal{T}}_2=0.8$		${\mathcal{T}}_2=1.0$
				${\widehat{\mathbf{\lambda }}}_{\mathbf{1}}$	${\widehat{\mathbf{\lambda }}}_{\mathbf{2}}$	${\widehat{\mathbf{\lambda }}}_{\mathbf{1}}$	${\widehat{\mathbf{\lambda }}}_{\mathbf{2}}$	${\widehat{\mathbf{\lambda }}}_{\mathbf{1}}$	${\widehat{\mathbf{\lambda }}}_{\mathbf{2}}$
20	0.3	18	(a)	0.5708(940.1) †	10.2596(960.1)	0.5567(940.1)	10.2036(960.0)	0.5553(940.0)	10.2010(950.9)
			(b)	0.5949(940.7)	10.3765(940.7)	0.5723(940.8)	10.2353(950.1)	0.5655(940.5)	10.1928(950.3)
			(c)	0.5817(940.9)	10.3657(950.3)	0.5590(950.2)	10.3001(950.6)	0.5530(950.2)	10.2922(950.2)
			(d)	0.5909(940.7)	10.3323(950.0)	0.5700(940.8)	10.2307(950.1)	0.5641(940.5)	10.1896(950.3)
		16	(a)	0.6122(940.0)	10.3998(950.5)	0.6096(940.1)	10.3694(950.5)	0.6096(940.1)	10.3694(950.5)
			(b)	0.6623(940.8)	10.6005(950.7)	0.6275(940.5)	10.4725(950.4)	0.6133(940.5)	10.4249(950.5)
			(c)	0.6082(950.1)	10.4458(940.6)	0.5977(950.1)	10.3503(950.2)	0.5967(950.2)	10.3503(950.2)
			(d)	0.6527(940.7)	10.5460(950.4)	0.6194(940.7)	10.4641(950.5)	0.6090(940.6)	10.4145(950.6)
		14	(a)	0.6630(940.8)	10.6396(950.7)	0.6625(940.8)	10.6396(950.7)	0.6625(940.8)	10.6396(950.7)
			(b)	0.7425(950.0)	10.8444(950.4)	0.7013(950.0)	10.6625(950.2)	0.6794(950.3)	10.6101(950.1)
			(c)	0.6686(940.5)	10.5124(950.1)	0.6613(930.7)	10.5683(940.9)	0.6609(930.8)	10.5634(950.0)
			(d)	0.7261(940.9)	10.7664(950.2)	0.6931(940.7)	10.6427(950.0)	0.6777(950.3)	10.6064(950.1)
		12	(a)	0.7125(940.5)	10.6972(960.1)	0.7125(940.5)	10.6972(960.1)	0.7125(940.5)	10.6972(960.1)
			(b)	0.8725(940.8)	20.2903(940.6)	0.8275(950.0)	20.1114(940.6)	0.8001(940.8)	20.0659(940.4)
			(c)	0.7447(940.5)	10.9367(960.0)	0.7434(940.6)	10.9358(960.0)	0.7435(940.6)	10.9347(960.0)
			(d)	0.8440(940.8)	20.1976(940.7)	0.8108(940.9)	20.1065(940.6)	0.7982(940.8)	20.0598(940.6)
30	0.3	28	(a)	0.4304(950.5)	0.8608(950.7)	0.4204(950.7)	0.8390(950.6)	0.4184(950.6)	0.8316(950.6)
			(b)	0.4521(940.6)	0.9736(950.7)	0.4355(940.2)	0.9288(950.2)	0.4280(940.6)	0.8769(950.2)
			(c)	0.4407(940.0)	0.9051(950.0)	0.4254(940.1)	0.8676(940.5)	0.4202(940.0)	0.8563(940.7)
			(d)	0.4506(940.4)	0.9705(950.4)	0.4346(940.3)	0.9270(950.4)	0.4276(940.7)	0.8762(950.3)
		26	(a)	0.4395(950.5)	0.8943(950.2)	0.4364(950.4)	0.8895(950.2)	0.4362(950.4)	0.8893(950.3)
			(b)	0.4709(950.6)	0.9399(950.9)	0.4534(950.4)	0.9007(950.6)	0.4467(950.4)	0.8824(950.7)
			(c)	0.4540(940.5)	0.9772(960.1)	0.4439(940.2)	0.9527(950.6)	0.4426(940.2)	0.9483(950.7)
			(d)	0.4664(950.5)	0.9320(950.8)	0.4521(950.5)	0.8975(950.8)	0.4460(950.3)	0.8802(950.7)
		24	(a)	0.4596(950.7)	0.9419(940.7)	0.4590(950.8)	0.9410(940.8)	0.4590(950.8)	0.9410(940.8)
			(b)	0.4903(940.1)	10.0400(940.7)	0.4715(940.7)	0.9919(940.7)	0.4639(940.7)	0.9605(940.9)
			(c)	0.4686(940.7)	0.9386(940.7)	0.4628(940.7)	0.9252(940.6)	0.4623(940.7)	0.9245(940.5)
			(d)	0.4851(940.2)	10.0230(940.8)	0.4688(940.6)	0.9837(940.8)	0.4624(940.6)	0.9580(940.9)
		22	(a)	0.4782(950.7)	10.0145(950.1)	0.4782(950.7)	10.0145(950.1)	0.4782(950.7)	10.0145(950.1)
			(b)	0.5275(940.0)	10.0762(940.1)	0.5006(930.8)	10.0271(940.8)	0.4932(930.8)	10.0124(940.4)
			(c)	0.4939(960.2)	0.9895(950.9)	0.4922(960.2)	0.9874(950.8)	0.4922(960.2)	0.9875(950.8)
			(d)	0.5174(930.9)	10.0478(940.6)	0.4984(930.8)	10.0232(940.5)	0.4912(930.9)	10.0082(940.5)
40	10.0	38	(a)	0.3606(940.9)	0.7008(940.2)	0.3526(950.0)	0.6792(940.0)	0.3505(940.9)	0.6749(940.0)
			(b)	0.3732(950.0)	0.7115(930.8)	0.3603(940.9)	0.6882(940.2)	0.3549(940.9)	0.6772(940.3)
			(c)	0.3639(960.0)	0.7232(930.8)	0.3530(940.7)	0.6928(940.6)	0.3494(940.7)	0.6827(940.5)
			(d)	0.3719(940.6)	0.7081(930.9)	0.3595(940.6)	0.6866(940.1)	0.3547(940.8)	0.6767(940.2)
		36	(a)	0.3650(940.1)	0.7096(930.6)	0.3614(940.0)	0.7013(930.5)	0.3614(930.9)	0.7008(930.4)
			(b)	0.3836(940.8)	0.7556(930.9)	0.3718(940.5)	0.7264(930.6)	0.3678(940.7)	0.7106(930.7)
			(c)	0.3736(940.8)	0.7134(930.8)	0.3650(950.1)	0.6954(930.7)	0.3633(940.8)	0.6912(930.8)
			(d)	0.3813(950.0)	0.7530(930.3)	0.3712(940.6)	0.7229(930.9)	0.3674(940.8)	0.7099(930.8)
		34	(a)	0.3739(940.5)	0.7304(940.4)	0.3729(940.7)	0.7288(940.6)	0.3729(940.7)	0.7288(940.6)
			(b)	0.3957(940.2)	0.8007(940.8)	0.3824(950.3)	0.7595(950.1)	0.3777(940.8)	0.7454(950.0)
			(c)	0.3799(950.6)	0.7376(940.4)	0.3729(960.1)	0.7271(940.5)	0.3723(960.0)	0.7252(940.6)
			(d)	0.3913(940.4)	0.7893(940.6)	0.3819(950.3)	0.7574(950.0)	0.3772(940.9)	0.7453(950.1)
		32	(a)	0.3857(940.7)	0.7571(940.3)	0.3856(940.7)	0.7571(940.3)	0.3856(940.7)	0.7571(940.3)
			(b)	0.4137(940.3)	0.7976(940.4)	0.3984(940.5)	0.7684(940.3)	0.3937(940.3)	0.7555(940.6)
			(c)	0.3890(950.1)	0.7676(930.9)	0.3859(940.9)	0.7573(940.0)	0.3857(950.0)	0.7567(940.0)
			(d)	0.4090(940.2)	0.7901(940.3)	0.3969(940.3)	0.7630(940.5)	0.3929(940.2)	0.7543(940.6)

${}^{†}$ ConfL (CovP).

From Table 4 and Table 5, the MSEs and ConfL increase as n decreases. For fixed n, the MSEs and ConfL increase generally as the number of m decreases. For fixed n and m, the rMSEs and ConfL increases generally as the pre-fixed time ${\mathcal{T}}_2$ decreases. From Figure 3 and Figure 4, it can be seen that the concentration becomes thicker. Therefore, we can make it easy to grasp the simulation results. The estimaor for Sch (a) has smaller rMSE and ConfL than the corresponding estimaor for the other three Sch (a, b, c). We can observe that the ConfI works well for all GeTy2PrHCS.

Frome Table 4, it can be seen that ${\widehat{\lambda }}_1$ is more precise compared to the ${\widehat{\lambda }}_2$ in terms of the rMSE and bias. It is because, when ${\lambda }_2$ is bigger than ${\lambda }_1$, we may observe smaller failure number due to the 2nd RiF than those due to the 1st RiF. Therefore, ${\widehat{\lambda }}_1$ is more efficient than ${\widehat{\lambda }}_2$.

4. Conclusions

In many situations of survival and reliability tests, the withdrawal of units from the test is pre-planned in order to to free up testing facilities for other tests, or to save cost and time. Recently, Ref. [6] suggest a GeTy2PrHCS. It is known that more than one RiF may be present at the same time. Therefore, we derive inference for CompRiM with GeTy2PrHCS ExDist data. We derive the CondMgf of the ${\widehat{\lambda }}_1$ and ${\widehat{\lambda }}_2$ of ExDist and the resulting ConfI under GeTy2PrHCS. Consequently, for fixed n (sample size) and m (PrTy2CS sample size), the rMSEs and ConfL increase as the time ${\mathcal{T}}_2$ decreases. ${\widehat{\lambda }}_1$ is more efficient compared to the ${\widehat{\lambda }}_2$ in terms of the rMSE and bias. Although we focused on the inference for CompRiM with GeTy2PrHCS ExDist data, the suggested GeTy2PrHCS CompRiM can be extended to other distributions. In these cases, the exact condPDF of the MLEs under GeTy2PrHCS CompRiM cannot be explicitly obtained.