A New Analysis of Fractional-Order Equal-Width Equations via Novel Techniques

Abstract

In this paper, the new iterative transform method and the homotopy perturbation transform method was used to solve fractional-order Equal-Width equations with the help of Caputo-Fabrizio. This method combines the Laplace transform with the new iterative transform method and the homotopy perturbation method. The approximate results are calculated in the series form with easily computable components. The fractional Equal-Width equations play an essential role in describe hydromagnetic waves in cold plasma. Our object is to study the nonlinear behaviour of the plasma system and highlight the critical points. The techniques are very reliable, effective, and efficient, which can solve a wide range of problems arising in engineering and sciences.

1. Introduction

Many researchers have studied fractional evaluation equations in the last decade because of their significant applicability in various fields of modern technology and science. It has been demonstrated that time-fractional equations define certain physical processes and that their application solves different problems. In this regard, it is critical to develop more implementations of innovative for fractional calculus [1,2,3,4,5,6]. Ford and Simpson found the fractional Caputo derivative [7] to be the best technique for finding time-fractional problems since it consistently contains the initial specifications that are missing in different individual models [8]. According to Spanier and Oldham, integrals and fractional derivatives can be utilized to demonstrate much more useful synthetic models than traditional approaches [9]. Furthermore, later on, fractional theory commitments and implementation, such as fractal mathematics, can be discussed in the literature. Readers interested are referred to [10,11,12,13,14,15,16,17,18].

Many researchers have focused on partial differential equations in recent years due to their wide range of technology and research implementations. These fractional equations are appropriate for identifying different important inventions in fluid dynamics, magnetic fields, nuclear physics, acoustics, electrodynamics, particle physics, optical structures, viscoelasticity, and other fields [19,20,21]. The fractional-order nonlinear Equal-Width equations are fundamental partial differential equations that show the various complex nonlinear phenomenon in the field of sciences, usually in plasma physics, plasma waves, fluid mechanics, chemical physics, solid-state physics, etc. The Equal-Width equations described the behavior of nonlinear waves in a variety of nonlinear systems, including hydromagnetic waves in acoustic waves in plasma, surface waves incompressible fluids, cold plasma, shallow water waves, acoustic waves in enharmonic crystals, and so on [22,23,24,25].

The general fractional-order equal width (EW) equation has the following form for long waves traveling in the positive $\varphi$ direction [26,27,28,29,30,31,32,33]:

$$D_{\Im }^{\varrho }\omega =\alpha {\omega }^p{\omega }_{\varphi }-\beta {\omega }_{\varphi \varphi \Im }=0,\Im >0,\varphi \in R,0<\varrho \le 1,$$

where p is a positive integer; $\alpha$ and $\beta$ are the positive constant, which require the boundary conditions $\omega \to 0$ as $\varphi \to \pm \infty$; and $\varrho$ is a parameter presenting order of fractional derivative. The derivative is understood in Caputo–Fabrizio form. Function $\omega (\varphi ,\Im )$ is probability density function, $\varphi$ is the spatial coordinate, and ℑ is the temporal coordinate. This expression carries a parameter that describes fractional-order derivative. For $\varrho =1$, fractional-order equations convert into classical equations. In this paper, we shall incorporate periodic boundary conditions for a region $a\le \varphi \le b$. The form of the initial wave will be taken so that at large distances from the wave, $\left|\omega \right|$ is very small and follows the free-space boundary conditions $\omega =0$.

Numerous researchers have used various techniques to solve nonlinear fractional differential equations. Many investigators have used various methods to solve a variety of problems in previously implemented different analytical and numerical methods, such as the Adomian decomposition technique, finite difference method, generalized differential transform technique, finite element technique, perturbation methods, fractional differential transform technique, homotopy analysis strategy, iterative technique, etc., see [26,27,28,29,30,31,34,35,36] for more details. The homotopy analysis method (HAM) is a brilliant mathematical strategy proposed and applied by Liao [32,33,37]. Some scientists have shown the promise of using the HAM to study different mathematical modeling [38]. Furthermore, a good fundamental method identified as the homotopy analysis transform technique is as an important example of the homotopy analysis method that is used by combining the Laplace transformation technique. This inventive convergence of HAM and Laplace transformation is used to examine a wide variety of different problems [39,40]. When compared to traditional methods, these changes promote and strengthen the problem-solving methodology.

Several authors have suggested techniques for find the solution of fractional partial differential equations applying the fractional order Caputo and Fabrizio operators. The fractional-order wave equations was analyzed analytically by Xu in [41], who reduced the governing equation to two fractional ordinary differential equations. Dehghan et al. in [42], for example, used the HAM to solve linear partial differential equations; fractional derivatives are expressed by Liouville-Caputo sense in this work. Using the CF fractional derivative, Goufo et al. [43] developed a mathematical analysis of a model of rock fracture in the environment and achieved computational and analytical techniques. In [44], Jafari et al. utilized the HAM to solve a multi-order fractional differential equation investigated by Diethelm and Ford [45]. The chinese mathemation JH He introduce the homotopy perturbation method in 1998 [46]. This technique is efficient and accurate and eliminates an unconditione matrix, complicate integrals, and infinite series form. This method does not need of the problem a specific parameters. The homotopy perturbation transformation method (HPTM) combines the Elzaki transformation and the Homotopy perturbation method. Many researcher have been implemented HPTM to solving differential equations, such as Navier-Stokes problems [47], heat-like problems [48], gas dynamic model [49], Fisher’s and hyperbolic equation [50].

Daftardar-Gejji and Jafari [51,52] developed a new iterative approach for solving nonlinear equations in 2006. Jafari et al. [53] first applied Laplace transform in the iterative technique. They proposed a new straightforward method called the iterative Laplace transform method to look for the numerical solution of the fractional partial differential equation (FPDE) system. the iterative Laplace transform method to solve linear and non-linear partial differential equations such as time-fractional Fokker Planck equation [54], Zakharov Kuznetsov equation [55] and Fornberg Whitham equation [56], etc.

In this paper, we use the Iterative and homotopy perturbation transform methods to solved fractional Equal-Width equations with the help of Caputo-Fabrizio. The fractional calculus fundamental definitions are defined in Section 2, write the general methodologies in Section 3 and Section 4, many test models to show the effectiveness of suggested techniques are given in Section 5 and Section 6, and finally, the conclusion is given in Section 7.

2. Preliminaries Concepts

This section provides some fundamental concepts of fractional calculus.

Definition 1

([57]). The Liouville–Caputo fractional derivative of order ϱ is given as:

$$D_{\Im }^{\varrho }\omega (\varphi ,\Im )=\frac{1}{\Gamma (n-\varrho )}{\int }_0^{\Im }{(\Im -\theta )}^{n-\varrho -1}{\omega }^{\left(n\right)}(\varphi ,\theta )d\theta ,n-1<\varrho <n,\Im >0,$$

(1)

where $\omega (\varphi ,\Im )\in L_1(a,b),{\omega }^{\left(n\right)}(\varphi ,\theta )$ is the integer n-th order derivative of $\omega (\varphi ,\theta )$ and $n\in \mathbb{N}$.

For $0<\varrho \le 1$, we defined the Laplace transform for the Liouville–Caputo fractional derivative of order ϱ as:

$$\mathcal{L}\left[D_{\Im }^{\varrho }\omega (\varphi ,\Im )\right]\left(s\right)=s^{\varrho }\mathcal{L}\left[\omega (\varphi ,\Im )\right]\left(s\right)-s^{\varrho -1}\left[\omega (\varphi ,0)\right].$$

(2)

Definition 2

([57]). The Caputo–Fabrizio fractional derivative of order ϱ is defined by

$$D_{\Im }^{\varrho }\omega (\varphi ,\Im )=\frac{(2-\varrho )M\left(\varrho \right)}{2(n-\varrho )}{\int }_0^{\Im }exp\left(-\frac{\varrho }{n-\varrho }(\Im -\theta )\right){\omega }^{\left(n\right)}(\varphi ,\theta )d\theta ,$$

(3)

where $M\left(\alpha \right)$ is a normalization form such that $M\left(0\right)=M\left(1\right)=1$. The exponential law is used as the nonsingular kernel in this fractional derivative.

For $0<\varrho \le 1$, we defined the Laplace transform for the Caputo–Fabrizio fractional derivative of order ϱ as:

$$\mathcal{L}\left[D_{\Im }^{\varrho }\omega (\varphi ,\Im )\right]\left(s\right)=\frac{s\mathcal{L}\left[\omega \right(\varphi ,\Im \left)\right]\left(s\right)-\omega (\varphi ,0)}{s+\varrho (1-s)}.$$

(4)

3. Homotopy Perturbation Transform Method

Consider the general form fractional-order partial differential equation of the form

$${}^{CF}{D}_{\Im }^{\varrho }\omega (\varphi ,\Im )+M\omega (\varphi ,\Im )+N\omega (\varphi ,\Im )=h(\varphi ,\Im ),\Im >0,0<\varrho \le 1$$

(5)

with the initial condition

$$\omega (\varphi ,0)=g\left(\varphi \right),$$

(6)

where is ${}^{CF}{D}_{\Im }^{\varrho }\mu =\frac{{\partial }^{\varrho }\mu (\varrho ,\Im )}{\partial {\Im }^{\varrho }}$ the fractional-order Caputo operator of $\varrho ,M$ and N are linear and nonlinear functions, and the source term is $h(\varrho ,\Im )$.

Next, we apply the Laplace transform to (5), and we get

$$\mathcal{L}[D_{\Im }^{\varrho }\omega (\varphi ,\Im )+M\omega (\varphi ,\Im )+N\omega (\varphi ,\Im )]=\mathcal{L}\left[h(\varphi ,\Im )\right].$$

Further, simplification through Laplace differentiation leads to

$$\frac{s^{\varrho }\mathcal{L}\left(\omega (\varphi ,\Im )\right)-s^{-1}\omega (\varphi ,0)}{s+\varrho (1-s)}=\mathcal{L}\left[M\omega (\varphi ,\Im )+N\omega (\varphi ,\Im )]+h((\varphi ,\Im ))\right],$$

$$\mathcal{L}\left[\omega (\varphi ,\Im )\right]=s^{-1}g\left(\varphi \right)+\frac{s+\varrho (1-s)}{s}\mathcal{L}\left[h(\varphi ,\Im )\right]-\frac{s+\varrho (1-s)}{s}\mathcal{L}[M\omega (\varphi ,\Im )+N\omega (\varphi ,\Im )].$$

(7)

Now, taking inverse Laplace transform converts (7) into

$$\omega (\varphi ,\Im )={\mathcal{L}}^{-1}\left\{s^{-1}g\left(\varphi \right)+\frac{s+\varrho (1-s)}{s}\mathcal{L}\left[h(\varphi ,\Im )\right]\right\}-{\mathcal{L}}^{-1}\left\{\frac{s+\varrho (1-s)}{s}\mathcal{L}[M\omega (\varphi ,\Im )+N\omega (\varphi ,\Im )]\right\},$$

(8)

or

$$\omega (\varphi ,\Im )=g\left(\varphi \right)+{\mathcal{L}}^{-1}\left\{\frac{s+\varrho (1-s)}{s}\mathcal{L}\left[h(\varphi ,\Im )\right]\right\}-{\mathcal{L}}^{-1}\left\{\frac{s+\varrho (1-s)}{s}\mathcal{L}[M\omega (\varphi ,\Im )+N\omega (\varphi ,\Im )]\right\}.$$

(9)

Now, the perturbation procedure in terms of power series with parameter p is presented as

$$\omega (\varphi ,\Im )=\sum _{k=0}^{\infty }{p}^k{\omega }_k(\varphi ,\Im ),$$

(10)

where perturbation term is p and $p\in [0,1]$.

The nonlinear terms can be defined as

$$N\omega (\varphi ,\Im )=\sum _{k=0}^{\infty }{p}^k{H}_k\left({\omega }_k\right),$$

(11)

where $H_m$ are He’s polynomials of ${\omega }_0,{\omega }_1,{\omega }_2,\dots ,{\omega }_m,$ and can be determined as [46]

$$H_m({\omega }_0,{\omega }_1,\dots ,{\omega }_m)=\frac{1}{m!}\frac{{\partial }^m}{\partial p^m}{\left[N\left(\sum _{k=0}^{\infty }{p}^k{\omega }_k\right)\right]}_{p=0},$$

(12)

where $m\in \mathbb{N}\cup \left\{0\right\}.$

Putting (11) and (12) into (9), we have

$$\begin{array}{cc}\hfill \sum _{k=0}^{\infty }{p}^k{\omega }_k(\varphi ,\Im )& =g\left(\varphi \right)+{\mathcal{L}}^{-1}\left\{\frac{s+\varrho (1-s)}{s}\mathcal{L}\left[h(\varphi ,\Im )\right]\right\}\hfill \\ \hfill & -p\left[{\mathcal{L}}^{-1}\left\{\frac{s+\varrho (1-s)}{s}\mathcal{L}\left\{M\sum _{k=0}^{\infty }{p}^k{\omega }_k(\varphi ,\Im )+\sum _{k=0}^{\infty }{p}^k{H}_k\left({\omega }_k\right)\right\}\right\}\right].\hfill \end{array}$$

(13)

By comparing the coefficient of p on both sides of (13), we get

$$\begin{array}{cc}\hfill p^0:{\omega }_0(\varphi ,\Im )& =g\left(\varphi \right)+{\mathcal{L}}^{-1}\left\{\frac{s+\varrho (1-s)}{s}\mathcal{L}\left[h(\varphi ,\Im )\right]\right\},\hfill \\ \hfill p^1:{\omega }_1(\varphi ,\Im )& ={\mathcal{L}}^{-1}\left\{\frac{s+\varrho (1-s)}{s}\mathcal{L}[M{\omega }_0(\varphi ,\Im )+H_0\left(\omega \right)]\right\},\hfill \\ \hfill p^2:{\omega }_2(\varphi ,\Im )& ={\mathcal{L}}^{-1}\left\{\frac{s+\varrho (1-s)}{s}\mathcal{L}[M{\omega }_1(\varphi ,\Im )+H_1\left(\omega \right)]\right\},\hfill \\ \hfill & ⋮\hfill \\ \hfill p^k:{\omega }_k(\varphi ,\Im )& ={\mathcal{L}}^{-1}\left\{\frac{s+\varrho (1-s)}{s}\mathcal{L}[M{\omega }_{k-1}(\varphi ,\Im )+H_{k-1}\left(\omega \right)]\right\},k>0,k\in \mathbb{N},\hfill \end{array}$$

(14)

where

$$\omega (\varphi ,\Im )=\underset{M\to \infty }{lim}\sum _{k=1}^M{\omega }_k(\varphi ,\Im ).$$

(15)

4. The New Iterative Transform Method Basic Procedure

Consider a particular type of a FPDE of the form

$${}^{CF}{D}_{\Im }^{\varrho }\omega (\varphi ,\Im )+M\omega (\varphi ,\Im )+N\omega (\varphi ,\Im )=h(\varphi ,\Im ),n-1<\varrho \le n,n\in \mathbb{N}$$

(16)

with the initial conditions

$${\omega }^k(\varphi ,0)=g_k\left(\varphi \right),k=0,1,2,\dots ,n-1,$$

(17)

where M and N are linear and nonlinear functions, respectively.

By applying the Laplace transformation to (16), we get

$$\mathcal{L}\left[D_{\Im }^{\varrho }\omega (\varphi ,\Im )\right]+\mathcal{L}[M\omega (\varphi ,\Im )+N\omega (\varphi ,\Im )]=\mathcal{L}\left[h(\varphi ,\Im )\right].$$

(18)

Applying the Laplace differentiation is given as

$$\mathcal{L}\left[\omega (\varphi ,\Im )\right]=\frac{1}{s}\omega (\varphi ,0)+\frac{s+\varrho (1-s)}{s^2}\mathcal{L}\left[h(\varphi ,\Im )\right]-\frac{s+\varrho (1-s)}{s^2}\mathcal{L}[M\omega (\varphi ,\Im )+N\omega (\varphi ,\Im )],$$

(19)

using inverse Laplace transformation to (19) into

$$\omega (\varphi ,\Im )={\mathcal{L}}^{-1}\left\{\frac{1}{s}\omega (\varphi ,0)+\frac{s+\varrho (1-s)}{s^2}\mathcal{L}\left[h(\varphi ,\Im )\right]\right\}-{\mathcal{L}}^{-1}\left\{\frac{s+\varrho (1-s)}{s^2}\mathcal{L}[M\omega (\varphi ,\Im )+N\omega (\varphi ,\Im )]\right\}.$$

(20)

Using the iterative technique, we obtain

$$\omega (\varphi ,\Im )=\sum _{m=0}^{\infty }{\omega }_m(\varphi ,\Im ).$$

(21)

Further, the operator M is linear; therefore,

$$M\left(\sum _{m=0}^{\infty }{\omega }_m(\varphi ,\Im )\right)=\sum _{m=0}^{\infty }M\left[{\omega }_m(\varphi ,\Im )\right],$$

(22)

and the operator N is nonlinear, so we have

$$N\left(\sum _{m=0}^{\infty }{\omega }_m(\varphi ,\Im )\right)={\omega }_0(\varphi ,\Im )+M\left(\sum _{k=0}^m{\omega }_k(\varphi ,\Im )\right)-N\left(\sum _{k=0}^m{\omega }_k(\varphi ,\Im )\right).$$

(23)

By substituting (21), (22) and (23) into (20), we obtain

$$\begin{array}{cc}\hfill \sum _{m=0}^{\infty }{\omega }_m(\varphi ,\Im )& ={\mathcal{L}}^{-1}\left\{\frac{1}{s}\omega (\varphi ,0)+\frac{s+\varrho (1-s)}{s^2}\mathcal{L}\left[h(\varphi ,\Im )\right]\right\}\hfill \\ \hfill & -{\mathcal{L}}^{-1}\left\{\frac{s+\varrho (1-s)}{s^2}\mathcal{L}\left\{M\left(\sum _{k=0}^m{\omega }_k(\varphi ,\Im )\right)-N\left(\sum _{k=0}^m{\omega }_k(\varphi ,\Im )\right)\right\}\right\}.\hfill \end{array}$$

(24)

The new iterative transform method is defined as

$$\begin{array}{cc}\hfill {\omega }_0(\varphi ,\Im )& ={\mathcal{L}}^{-1}\left\{\frac{1}{s}\omega (\varphi ,0)+\frac{s+\varrho (1-s)}{s^2}\mathcal{L}\left(g(\varphi ,\Im )\right)\right\},\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill {\omega }_1(\varphi ,\Im )& =-{\mathcal{L}}^{-1}\left\{\frac{s+\varrho (1-s)}{s^2}\mathcal{L}\left\{M\left[{\omega }_0(\varphi ,\Im )\right]+N\left[{\omega }_0(\varphi ,\Im )\right]\right\}\right\},\hfill \end{array}$$

(26)

and

$$\begin{array}{cc}\hfill {\omega }_{m+1}(\varphi ,\Im )& =-{\mathcal{L}}^{-1}\left\{\frac{s+\varrho (1-s)}{s^2}\mathcal{L}\left\{-M\left(\sum _{k=0}^m{\omega }_k(\varphi ,\Im )\right)-N\left(\sum _{k=0}^m{\omega }_k(\varphi ,\Im )\right)\right\}\right\},m\ge 1.\hfill \end{array}$$

(27)

Lastly, (16) and (17) provide the m-term solution in series form, defined as

$$\omega (\varphi ,\Im )\cong {\omega }_0(\varphi ,\Im )+{\omega }_1(\varphi ,\Im )+{\omega }_2(\varphi ,\Im )+\cdots +{\omega }_m(\varphi ,\Im ),m\in \mathbb{N}.$$

(28)

5. Implementation of the HPTM

Example 1.

Consider the fractional-order nonlinear Equal-Width equation; if $\alpha =1$, $\beta =1$ and $p=1$ is given as

$${}^{CF}{D}_{\Im }^{\varrho }\omega +\omega {\omega }_{\varphi }-{\omega }_{\varphi \varphi \Im }=0,\Im >0,\varphi \in \mathbb{R},0<\varrho \le 1$$

(29)

with the initial condition

$$\omega (\varphi ,0)=3{\mathrm{sech}}^2\left(\frac{\varphi -15}{2}\right).$$

(30)

Applying the Laplace transform to (29) with initial condition (30), we have

$$\frac{s^{\varrho }\mathcal{L}\left(\omega (\varphi ,\Im )\right)-s^{-1}\omega (\varphi ,0)}{s+\varrho (1-s)}=\mathcal{L}\left[{\omega }_{\varphi \varphi \Im }-\omega {\omega }_{\varphi }\right],$$

(31)

or

$$\mathcal{L}\left[\omega (\varphi ,\Im )\right]=s^{-1}3{\sec \mathrm{h}}^2\left(\frac{\varphi -15}{2}\right)+\frac{s+\varrho (1-s)}{s}\mathcal{L}\left[{\omega }_{\varphi \varphi \Im }-\omega {\omega }_{\varphi }\right].$$

(32)

Now, using the inverse Laplace transform to (32), we have

$$\omega (\varphi ,\Im )=3{\mathrm{sech}}^2\left(\frac{\varphi -15}{2}\right)+{\mathcal{L}}^{-1}\left\{\frac{s+\varrho (1-s)}{s}\mathcal{L}\left[{\omega }_{\varphi \varphi \Im }-\omega {\omega }_{\varphi }\right]\right\}.$$

(33)

Now, by implementing HPM, we get

$$\begin{array}{cc}\hfill \sum _{m=0}^{\infty }{p}^m{\omega }_m(\varphi ,\Im )& =3{\mathrm{sech}}^2\left(\frac{\varphi -15}{2}\right)\hfill \\ \hfill & +p\left[{\mathcal{L}}^{-1}\left\{\frac{s+\varrho (1-s)}{s}\mathcal{L}\left\{\left(\sum _{m=0}^{\infty }{p}^m{\omega }_m{(\varphi ,\Im )}_{\varphi \varphi \Im }\right)-\left(\sum _{m=0}^{\infty }{p}^m{H}_m\left(\omega \right)\right)\right\}\right\}\right].\hfill \end{array}$$

(34)

The nonlinear terms can be defined with the help of He’s polynomials

$$\sum _{m=0}^{\infty }{p}^m{H}_m\left(\omega \right)=\omega {\omega }_{\varphi }.$$

(35)

He’s polynomials are defined as

$$\begin{array}{cc}\hfill H_0\left(\omega \right)& ={\omega }_0{\left({\omega }_0\right)}_{\varphi },\hfill \\ \hfill H_1\left(\omega \right)& ={\omega }_0{\left({\omega }_1\right)}_{\varphi }+{\omega }_1{\left({\omega }_0\right)}_{\varphi },\hfill \\ \hfill & ⋮.\hfill \end{array}$$

With the coefficients comparing p-like, we get

$$\begin{array}{cc}\hfill p^0:{\omega }_0(\varphi ,\Im )& =3{\mathrm{sech}}^2\left(\frac{\varphi -15}{2}\right),\hfill \\ \hfill p^1:{\omega }_1(\varphi ,\Im )& ={\mathcal{L}}^{-1}\left\{\frac{s+\varrho (1-s)}{s}\mathcal{L}\left[{\left({\omega }_0\right)}_{\varphi \varphi \Im }-H_0\right]\right\},\hfill \\ \hfill p^1:{\omega }_1(\varphi ,\Im )& =9{\mathrm{sech}}^4\left(\frac{\varphi -15}{2}\right)tanh\left(\frac{\varphi -15}{2}\right)\left(\varrho \Im +(1-\varrho )\right),\hfill \\ \hfill p^2:{\omega }_2(\varphi ,\Im )& ={\mathcal{L}}^{-1}\left\{\frac{s+\varrho (1-s)}{s}L\left[{\left({\omega }_1\right)}_{\varphi \varphi \Im }-H_1\right]\right\},\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill p^2:{\omega }_2(\varphi ,\Im )& =\frac{9}{4}\frac{1}{{cosh}^{12}\left(\frac{1}{2}\varphi -\frac{15}{2}\right)}\left[sinh\left(\frac{1}{2}\varphi -\frac{15}{2}\right)\left\{-24\left({(1-\varrho )}^2+2\varrho (1-\varrho )\Im +\frac{1}{2}{\varrho }^2{\Im }^2\right){cosh}^3\left(\frac{1}{2}\varphi -\frac{15}{2}\right)\right.\right.\hfill \\ \hfill & +30\left({(1-\varrho )}^2+2\varrho (1-\varrho )\Im +\frac{{\varrho }^2{\Im }^2}{2}\right)cosh\left(\frac{1}{2}\varphi -\frac{15}{2}\right)\hfill \\ \hfill & -72\left(\varrho \Im +(1-\varrho )\right)sinh\left(\frac{1}{2}\varphi -\frac{15}{2}\right)cosh\left(\frac{1}{2}\varphi -\frac{15}{2}\right)\hfill \\ \hfill & \left.\left.+135\left(\varrho \Im +(1-\varrho )\right)sinh\left(\frac{1}{2}\varphi -\frac{15}{2}\right)+4{cosh}^7\left(\frac{1}{2}\varphi -\frac{15}{2}\right)\right\}\left(\varrho \Im +(1-\varrho )\right)\right],\hfill \\ \hfill & ⋮.\hfill \end{array}$$

Provided the series form solution is

$$\omega (\varphi ,\Im )=\sum _{k=0}^{\infty }{\omega }_k(\varphi ,\Im ).$$

Then, we have

$$\begin{array}{cc}\hfill \omega (\varphi ,\Im )& =3{\mathrm{sech}}^2\left(\frac{\varphi -15}{2}\right)+9{\mathrm{sech}}^4\left(\frac{\varphi -15}{2}\right)tanh\left(\frac{\varphi -15}{2}\right)\left(\varrho \Im +(1-\varrho )\right)\hfill \\ \hfill & +\frac{9}{4}\frac{1}{{cosh}^{12}\left(\frac{1}{2}\varphi -\frac{15}{2}\right)}\left[sinh\left(\frac{1}{2}\varphi -\frac{15}{2}\right)\left\{-24\left({(1-\varrho )}^2+2\varrho (1-\varrho )\Im +\frac{{\varrho }^2{\Im }^2}{2}\right){cosh}^3\left(\frac{1}{2}\varphi -\frac{15}{2}\right)\right.\right.\hfill \\ \hfill & +30\left({(1-\varrho )}^2+2\varrho (1-\varrho )\Im +\frac{{\varrho }^2{\Im }^2}{2}\right)cosh\left(\frac{1}{2}\varphi -\frac{15}{2}\right)\hfill \\ \hfill & -72\left(\varrho \Im +(1-\varrho )\right)sinh\left(\frac{1}{2}\varphi -\frac{15}{2}\right)cosh\left(\frac{1}{2}\varphi -\frac{15}{2}\right)\hfill \\ \hfill & \left.\left.+135\left(\varrho \Im +(1-\varrho )\right)sinh\left(\frac{1}{2}\varphi -\frac{15}{2}\right)+4{cosh}^7\left(\frac{1}{2}\varphi -\frac{15}{2}\right)\right\}\left(\varrho \Im +(1-\varrho )\right)\right]+\cdots .\hfill \end{array}$$

(36)

Putting $\varrho =1$ into (36), we obtain the solution of this problem as

$$\begin{array}{cc}\hfill \omega (\varphi ,\Im )& =3{\mathrm{sech}}^2\left(\frac{\varphi -15}{2}\right)+9{\mathrm{sech}}^4\left(\frac{\varphi -15}{2}\right)tanh\left(\frac{\varphi -15}{2}\right)\Im \hfill \\ \hfill & +\frac{9}{4}\frac{1}{{cosh}^{12}\left(\frac{1}{2}\varphi -\frac{15}{2}\right)}\left[sinh\left(\frac{1}{2}\varphi -\frac{15}{2}\right)\left\{-24{\Im }^2{cosh}^3\left(\frac{1}{2}\varphi -\frac{15}{2}\right)\right.\right.\hfill \\ \hfill & +30{\Im }^{2}cosh\left(\frac{1}{2}\varphi -\frac{15}{2}\right)-72\Im sinh\left(\frac{1}{2}\varphi -\frac{15}{2}\right)cosh\left(\frac{1}{2}\varphi -\frac{15}{2}\right)\hfill \\ \hfill & \left.\left.+135\Im sinh\left(\frac{1}{2}\varphi -\frac{15}{2}\right)+4{cosh}^7\left(\frac{1}{2}\varphi -\frac{15}{2}\right)\right\}\Im \right]+\cdots .\hfill \end{array}$$

(37)

The exact solution of this problem as follows:

$$\omega (\varphi ,\Im )=3{\mathrm{sech}}^2\left(\frac{\varphi -15-\Im }{2}\right).$$

(38)

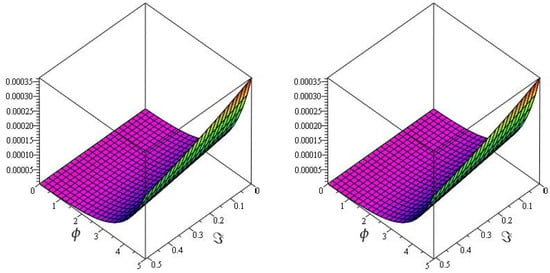
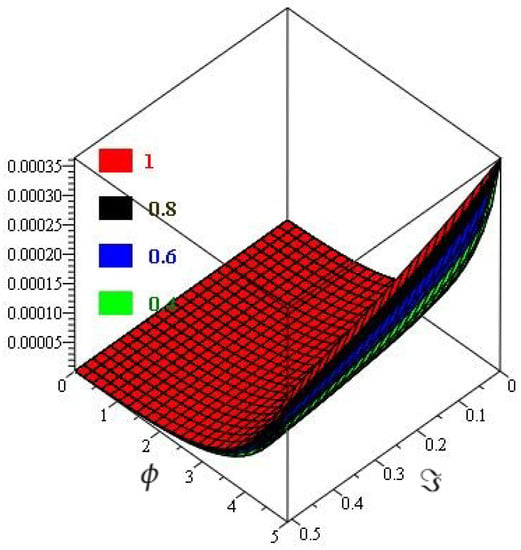
In Figure 1, the exact and the HPTM solutions of Example 1 at $\varrho =1$ are shown by subgraphs. From the given figure, it can be seen that both the HPTM and exact results are in close contact with each other. Furthermore, in Figure 2, the HPTM results of Example 1 are investigated at different fractional-order at $\varrho =1,0.8,0.6$ and $0.4$ of the 3D graph. It is analyzed that fractional-order problem solutions converge to an integer-order effect as fractional-order analysis to integer-order.

Figure 1. The actual and HPTM solution graphs at $\varrho =1$ of Example 1.

Figure 2. The HPTM solution of different fractional-order ϱ graph of Example 1.

Example 2.

Consider the fractional nonlinear Equal-Width equation of the form: if $\alpha =3$, $\beta =-1$ and $p=2$ are given as

$${}^{CF}{D}_{\Im }^{\varrho }\omega +3{\omega }^2{\omega }_{\varphi }-{\omega }_{\varphi \varphi \Im }=0,\Im >0,\varphi \in \mathbb{R},0<\varrho \le 1$$

(39)

with the initial condition

$$\omega (\varphi ,0)=\frac{1}{4}\mathrm{sech}(\varphi -30).$$

(40)

Applying Laplace transform to (39), we get

$$\mathcal{L}\left[\omega (\varphi ,\Im )\right]=s^{-1}\omega (\varphi ,0)+\frac{s+\varrho (1-s)}{s}\mathcal{L}\left[{\omega }_{\varphi \varphi \Im }-3{\omega }^2{\omega }_{\varphi }\right].$$

(41)

Using the initial condition (40) into (41), we get

$$\mathcal{L}\left[\omega (\varphi ,\Im )\right]=s^{-1}\frac{1}{4}\mathrm{sech}(\varphi -30)+\frac{s+\varrho (1-s)}{s}\mathcal{L}\left[{\omega }_{\varphi \varphi \Im }-3{\omega }^2{\omega }_{\varphi }\right].$$

(42)

By applying inverse Laplace transform to (42), we get

$$\omega (\varphi ,\Im )=\frac{1}{4}\mathrm{sech}(\varphi -30)+{\mathcal{L}}^{-1}\left\{\frac{s+\varrho (1-s)}{s}\mathcal{L}\left[{\omega }_{\varphi \varphi \Im }-3{\omega }^2{\omega }_{\varphi }\right]\right\}.$$

(43)

Now, we implement HPM, and we get

$$\begin{array}{cc}\hfill \sum _{m=0}^{\infty }{p}^m{\omega }_m(\varphi ,\Im )& =\frac{1}{4}\mathrm{sech}(\varphi -30)\hfill \\ \hfill & +p\left[{\mathcal{L}}^{-1}\left\{\frac{s+\varrho (1-s)}{s}\mathcal{L}\left(\sum _{m=0}^{\infty }{p}^m{\omega }_m{(\varphi ,\Im )}_{\varphi \varphi \Im }-\sum _{m=0}^{\infty }{p}^m{H}_m\left(\omega \right)\right)\right\}\right].\hfill \end{array}$$

(44)

The nonlinear terms can be defined with the help of He’s polynomials

$$\sum _{m=0}^{\infty }{p}^m{H}_m\left(\omega \right)=3{\omega }^2{\omega }_{\varphi }.$$

(45)

He’s polynomial are defined as

$$\begin{array}{cc}\hfill H_0\left(\omega \right)& =3{\left({\omega }_0\right)}^2{\left({\omega }_0\right)}_{\varphi },\hfill \\ \hfill H_1\left(\omega \right)& =3{\left({\omega }_0\right)}^2{\left({\omega }_1\right)}_{\varphi }+6{\omega }_0{\omega }_1{\left({\omega }_0\right)}_{\varphi },\hfill \\ \hfill & ⋮.\hfill \end{array}$$

By comparing p-like coefficients, we get

$$\begin{array}{cc}\hfill p^0:{\omega }_0(\varphi ,\Im )& =\frac{1}{4}\mathrm{sech}(\varphi -30),\hfill \\ \hfill p^1:{\omega }_1(\varphi ,\Im )& ={\mathcal{L}}^{-1}\left\{\frac{s+\varrho (1-s)}{s}\mathcal{L}\left[{\left({\omega }_0\right)}_{\varphi \varphi \Im }-H_0\left(\omega \right)\right]\right\},\hfill \\ \hfill p^1:{\omega }_1(\varphi ,\Im )& =\frac{3}{64}{\mathrm{sech}}^3(\varphi -30)tanh(\varphi -30)\left(\varrho \Im +(1-\varrho )\right),\hfill \\ \hfill & ⋮.\hfill \end{array}$$

The series form solution is

$$\omega (\varphi ,\Im )=\sum _{m=0}^{\infty }{\omega }_m(\varphi ,\Im ).$$

Then, we have

$$\omega (\varphi ,\Im )=\frac{1}{4}\mathrm{sech}(\varphi -30)+\frac{3}{64}{\mathrm{sech}}^3(\varphi -30)tanh(\varphi -30)\left(\varrho \Im +(1-\varrho )\right)+\cdots .$$

(46)

Putting $\varrho =1$ in (46), we obtain the solution of this problem as

$$\omega (\varphi ,\Im )=\frac{1}{4}\mathrm{sech}(\varphi -30)+\frac{3}{64}{\mathrm{sech}}^3(\varphi -30)tanh(\varphi -30)+\cdots .$$

(47)

The exact solution of this problem is

$$\omega (\varphi ,\Im )=\frac{1}{4}\mathrm{sech}\left(\varphi -30-\frac{\Im }{4}\right).$$

(48)

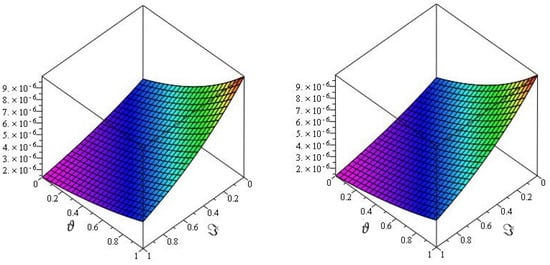
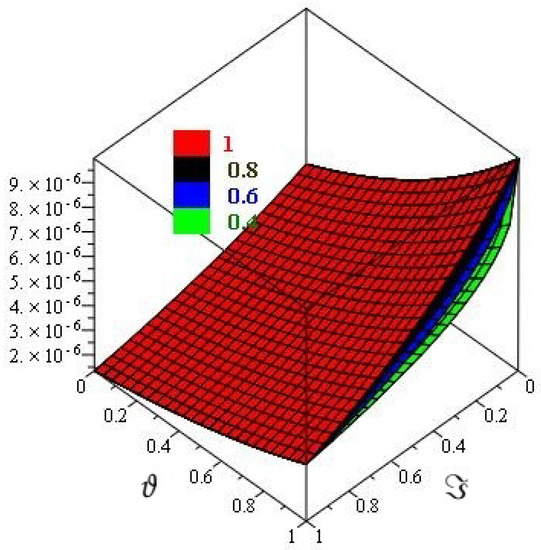
In Figure 3, the exact and the HPTM solutions of Example 2 at $\varrho =1$ are shown by subgraphs. From the given figure, it can be seen that both the HPTM and exact results are in close contact with each other. Furthermore, in Figure 4, the HPTM results of Example 2 are investigated at different fractional-order at $\varrho =1,0.8,0.6$ and $0.4$ of 3D graph. According to the analysis, that fractional-order problem solutions converge to an integer-order effect as fractional-order analysis to integer-order.

Figure 3. The actual and HPTM solution graphs at $\varrho =1$ of Example 2.

Figure 4. The HPTM solution of different fractional-order ϱ graph of Example 2.

Example 3.

Consider the fractional nonlinear fractional-order modified equal width equation is given as follows. Consider the fractional nonlinear Equal-Width equation of the form

$${}^{CF}{D}_{\Im }^{\varrho }\omega +\frac{12}{7}{\left({\omega }^6\right)}_{\varphi }-\frac{3}{7}{\left({\omega }^6\right)}_{\varphi \varphi \Im }=0,\Im >0,\varphi \in \mathbb{R},0<\varrho \le 1$$

(49)

with the initial condition

$$\omega (\varphi ,0)={cosh}^{2/5}\left(\frac{5\varphi }{6}\right).$$

(50)

Using Laplace transform to (49), we get

$$\mathcal{L}\left[\omega (\varphi ,\Im )\right]=s^{-1}\omega (\varphi ,0)+\frac{s+\varrho (1-s)}{s}\mathcal{L}\left[\frac{12}{7}{\left({\omega }^6\right)}_{\varphi }-\frac{3}{7}{\left({\omega }^6\right)}_{\varphi \varphi \Im }\right].$$

(51)

Putting the initial condition (50) into (51), we have

$$\mathcal{L}\left[\omega (\varphi ,\Im )\right]=s^{-1}{cosh}^{2/5}\left(\frac{5\varphi }{6}\right)+\frac{s+\varrho (1-s)}{s}\mathcal{L}\left[\frac{12}{7}{\left({\omega }^6\right)}_{\varphi }-\frac{3}{7}{\left({\omega }^6\right)}_{\varphi \varphi \Im }\right].$$

(52)

By applying inverse Laplace transform to (52), we have

$$\omega (\varphi ,\Im )={cosh}^{2/5}\left(\frac{5\varphi }{6}\right)+{\mathcal{L}}^{-1}\left\{\frac{s+\varrho (1-s)}{s}\mathcal{L}\left[\frac{12}{7}{\left({\omega }^6\right)}_{\varphi }-\frac{3}{7}{\left({\omega }^6\right)}_{\varphi \varphi \Im }\right]\right\}.$$

(53)

Now, we implement HPM, and we get

$$\sum _{m=0}^{\infty }{p}^m{\omega }_m(\varphi ,\Im )={cosh}^{2/5}\left(\frac{5\varphi }{6}\right)+p\left[{\mathcal{L}}^{-1}\left\{\frac{s+\varrho (1-s)}{s}\mathcal{L}\left(\sum _{m=0}^{\infty }{p}^m{\omega }_m{(\varphi ,\Im )}_{\varphi \varphi \Im }\right)\right\}\right].$$

(54)

The nonlinear terms can be defined with the help of He’s polynomials

$$\sum _{m=0}^{\infty }{p}^m{H}_m\left(\omega \right)=\frac{12}{7}{\left({\omega }^6\right)}_{\varphi }-\frac{3}{7}{\left({\omega }^6\right)}_{\varphi \varphi \Im }.$$

(55)

He’s polynomials are defined as

$$\begin{array}{cc}\hfill H_0\left(\omega \right)& =\frac{12}{7}{\left({\omega }_0^6\right)}_{\varphi }-\frac{3}{7}{\left({\omega }_0^6\right)}_{\varphi \varphi \Im }\hfill \\ \hfill & ⋮.\hfill \end{array}$$

By comparing p-like coefficients, we get

$$\begin{array}{cc}\hfill p^0:{\omega }_0(\varphi ,\Im )& ={cosh}^{2/5}\left(\frac{5\varphi }{6}\right),\hfill \\ \hfill p^1:{\omega }_1(\varphi ,\Im )& ={\mathcal{L}}^{-1}\left\{\frac{s+\varrho (1-s)}{s}\mathcal{L}\left[H_0\left(\omega \right)\right]\right\},\hfill \\ \hfill p^1:{\omega }_1(\varphi ,\Im )& =-\frac{24}{7}{cosh}^{7/5}\left(\frac{5\varphi }{6}\right)sinh\left(\frac{5\varphi }{6}\right)\left(\varrho \Im +(1-\varrho )\right),\hfill \\ \hfill & ⋮.\hfill \end{array}$$

The series form solution is

$$\omega (\varphi ,\Im )=\sum _{m=0}^{\infty }{\omega }_m(\varphi ,\Im ).$$

Then, we have

$$\omega (\varphi ,\Im )={cosh}^{2/5}\left(\frac{5\varphi }{6}\right)-\frac{24}{7}{cosh}^{2/5}\left(\frac{5\varphi }{6}\right)sinh\left(\frac{5\varphi }{6}\right)\left(\varrho \Im +(1-\varrho )\right)+\cdots .$$

(56)

Putting $\varrho =1$ into (56), we obtain the solution of this problem as

$$\omega (\varphi ,\Im )={cosh}^{2/5}\left(\frac{5\varphi }{6}\right)-\frac{24}{7}{cosh}^{7/5}\left(\frac{5\varphi }{6}\right)sinh\left(\frac{5\varphi }{6}\right)\Im +\cdots .$$

(57)

The exact solution of this problem is

$$\omega (\varphi ,\Im )={cosh}^{2/5}\left\{\frac{5}{6}(\varphi -\Im )\right\}.$$

(58)

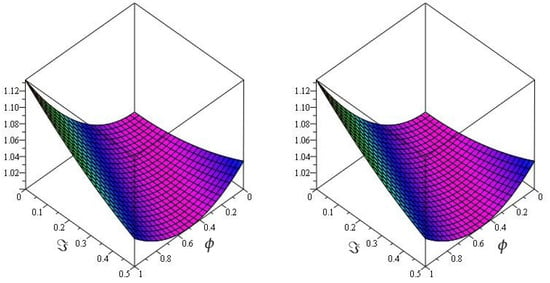
In Figure 5, the exact and the HPTM solutions of Example 3 at $\varrho =1$ are showm by subgraphs, respectively. From the given figure, it can be seen that both the HPTM and exact results are in close contact with each other. Furthermore, in Figure 6, the HPTM results of Example 3 are investigated at different fractional-order at $\varrho =1,0.8,0.6$ and $0.4$ of 3D graph. Analysis shows that fractional-order problem solutions converge to an integer-order effect as fractional-order analysis to integer-order.

Figure 5. The actual and HPTM solution graphs at $\varrho =1$ of Example 3.

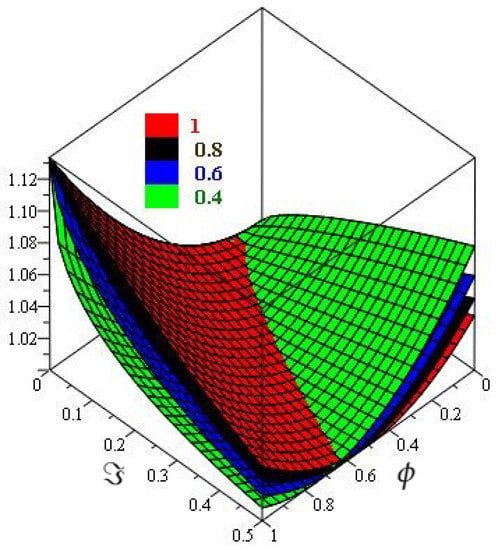
Figure 6. The HPTM solution of different fractional-order ϱ graph of Example 3.

6. Implementation of Iterative Transform Method

Example 4.

Consider the fractional nonlinear Equal-Width equation of the form

$${}^{CF}{D}_{\Im }^{\varrho }\omega +\omega {\omega }_{\varphi }-{\omega }_{\varphi \varphi \Im }=0,\Im >0,\varphi \in \mathbb{R},0<\varrho \le 1$$

(59)

with the initial condition

$$\omega (\varphi ,0)=3{\mathrm{sech}}^2\left(\frac{\varphi -15}{2}\right).$$

(60)

Applying the Laplace transform to (59), we get

$$\mathcal{L}\left[\omega (\varphi ,\Im )\right]=s^{-1}\omega (\varphi ,0)-\frac{s+\varrho (1-s)}{s}\mathcal{L}\left[\omega {\omega }_{\varphi }-{\omega }_{\varphi \varphi \Im }\right].$$

(61)

Applying inverse Laplace transform to (61), we have

$$\omega (\varphi ,\Im )={\mathcal{L}}^{-1}\left\{s^{-1}\omega (\varphi ,0)\right\}-{\mathcal{L}}^{-1}\left\{\frac{s+\varrho (1-s)}{s}\mathcal{L}\left[\omega {\omega }_{\varphi }-{\omega }_{\varphi \varphi \Im }\right]\right\}.$$

(62)

Now, by using the suggested analytical method, we get

$$\begin{array}{cc}\hfill {\omega }_0(\varphi ,\Im )& =3{\mathrm{sech}}^2\left(\frac{\varphi -15}{2}\right),\hfill \\ \hfill {\omega }_1(\varphi ,\Im )& =-{\mathcal{L}}^{-1}\left\{\mathcal{L}\left[{\omega }_0{\omega }_{\varphi 0}-{\omega }_{0\varphi \varphi \Im }\right]\right\}\hfill \\ \hfill & =9{\mathrm{sech}}^4\left(\frac{\varphi -15}{2}\right)tanh\left(\frac{\varphi -15}{2}\right)\left(\varrho \Im +(1-\varrho )\right),\hfill \\ \hfill {\omega }_2(\varphi ,\Im )& =-{\mathcal{L}}^{-1}\left\{\frac{s+\varrho (1-s)}{s}\mathcal{L}\left[{\omega }_1{\omega }_{\varphi 1}-{\omega }_{1\varphi \varphi \Im }\right]\right\},\hfill \\ \hfill & =\frac{9}{4}\frac{1}{{cosh}^{12}\left(\frac{1}{2}\varphi -\frac{15}{2}\right)}\left[sinh\left(\frac{1}{2}\varphi -\frac{15}{2}\right)\left\{-24\left({(1-\varrho )}^2+2\varrho (1-\varrho )\Im +\frac{{\varrho }^2{\Im }^2}{2}\right){cosh}^3\left(\frac{1}{2}\varphi -\frac{15}{2}\right)\right.\right.\hfill \\ \hfill & +30\left({(1-\varrho )}^2+2\varrho (1-\varrho )\Im +\frac{{\varrho }^2{\Im }^2}{2}\right)cosh\left(\frac{1}{2}\varphi -\frac{15}{2}\right)\hfill \\ \hfill & -72\left(\varrho \Im +(1-\varrho )\right)sinh\left(\frac{1}{2}\varphi -\frac{15}{2}\right)cosh\left(\frac{1}{2}\varphi -\frac{15}{2}\right)\hfill \\ \hfill & \left.\left.+135\left(\varrho \Im +(1-\varrho )\right)sinh\left(\frac{1}{2}\varphi -\frac{15}{2}\right)+4{cosh}^7\left(\frac{1}{2}\varphi -\frac{15}{2}\right)\right\}\left(\varrho \Im +(1-\varrho )\right)\right]\hfill \\ \hfill & ⋮\hfill \\ \hfill {\omega }_{n+1}(\varphi ,\Im )& ={\mathcal{L}}^{-1}\left\{\frac{{(s+\varrho (1-s))}^n}{s^n}\mathcal{L}\left[{\omega }_n{\omega }_{\varphi n}-{\omega }_{n\varphi \varphi \Im }\right]\right\}.\hfill \end{array}$$

The series form result is

$$\omega (\varphi ,\Im )={\omega }_0(\varphi ,\Im )+{\omega }_1(\varphi ,\Im )+{\omega }_2(\varphi ,\Im )+{\omega }_3(\varphi ,\Im )+\cdots +{\omega }_n(\varphi ,\Im ).$$

Then, we have

$$\begin{array}{cc}\hfill \omega (\varphi ,\Im )& =3{\mathrm{sech}}^2\left(\frac{\varphi -15}{2}\right)+9{\mathrm{sech}}^4\left(\frac{\varphi -15}{2}\right)tanh\left(\frac{\varphi -15}{2}\right)\left(\varrho \Im +(1-\varrho )\right)\hfill \\ \hfill & +\frac{9}{4}\frac{1}{{cosh}^{12}\left(\frac{1}{2}\varphi -\frac{15}{2}\right)}\left[sinh\left(\frac{1}{2}\varphi -\frac{15}{2}\right)\left\{-24\left({(1-\varrho )}^2+2\varrho (1-\varrho )\Im +\frac{{\varrho }^2{\Im }^2}{2}\right){cosh}^3\left(\frac{1}{2}\varphi -\frac{15}{2}\right)\right.\right.\hfill \\ \hfill & +30\left({(1-\varrho )}^2+2\varrho (1-\varrho )\Im +\frac{{\varrho }^2{\Im }^2}{2}\right)cosh\left(\frac{1}{2}\varphi -\frac{15}{2}\right)\hfill \\ \hfill & -72\left(\varrho \Im +(1-\varrho )\right)sinh\left(\frac{1}{2}\varphi -\frac{15}{2}\right)cosh\left(\frac{1}{2}\varphi -\frac{15}{2}\right)\hfill \\ \hfill & \left.\left.+135\left(\varrho \Im +(1-\varrho )\right)sinh\left(\frac{1}{2}\varphi -\frac{15}{2}\right)+4{cosh}^7\left(\frac{1}{2}\varphi -\frac{15}{2}\right)\right\}\left(\varrho \Im +(1-\varrho )\right)\right]+\cdots .\hfill \end{array}$$

(63)

Putting $\varrho =1$ into (63), we obtain the solution of this problem as

$$\begin{array}{cc}\hfill \omega (\varphi ,\Im )& =3{\mathrm{sech}}^2\left(\frac{\varphi -15}{2}\right)+9{\mathrm{sech}}^4\left(\frac{\varphi -15}{2}\right)tanh\left(\frac{\varphi -15}{2}\right)\Im \hfill \\ \hfill & +\frac{9}{4}\frac{1}{{cosh}^{12}\left(\frac{1}{2}\varphi -\frac{15}{2}\right)}\left[sinh\left(\frac{1}{2}\varphi -\frac{15}{2}\right)\left\{-24{\Im }^2{cosh}^3\left(\frac{1}{2}\varphi -\frac{15}{2}\right)\right.\right.\hfill \\ \hfill & +30{\Im }^{2}cosh\left(\frac{1}{2}\varphi -\frac{15}{2}\right)-72\Im sinh\left(\frac{1}{2}\varphi -\frac{15}{2}\right)cosh\left(\frac{1}{2}\varphi -\frac{15}{2}\right)\hfill \\ \hfill & \left.\left.+135\Im sinh\left(\frac{1}{2}\varphi -\frac{15}{2}\right)+4{cosh}^7\left(\frac{1}{2}\varphi -\frac{15}{2}\right)\right\}\Im \right]+\cdots .\hfill \end{array}$$

(64)

The exact solution of this problem is

$$\omega (\varphi ,\Im )=3{\mathrm{sech}}^2\left(\frac{\varphi -15-\Im }{2}\right).$$

(65)

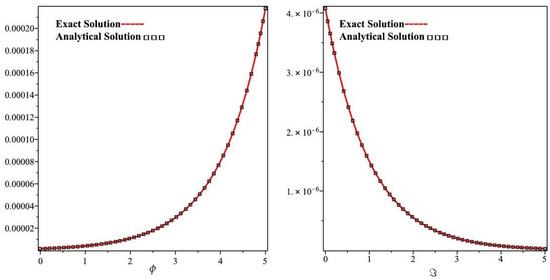
In Figure 7, it is shown that the exact and the NITM solutions graph with respect to ϕ and ℑ of Example 4 at $\varrho =1$. From the given figures, it can be seen that both the NITM and exact results are in close contact with each other. Furthermore, in Figure 8, the NITM results of Example 4 are investigated at different fractional-order at $\varrho =1,0.8,0.6$ and $0.4$ of 2D graph with respect to ϕ and ℑ.

Figure 7. The actual and ITM solution graphs at $\varrho =1$ with respect to ϕ and ℑ of Example 4.

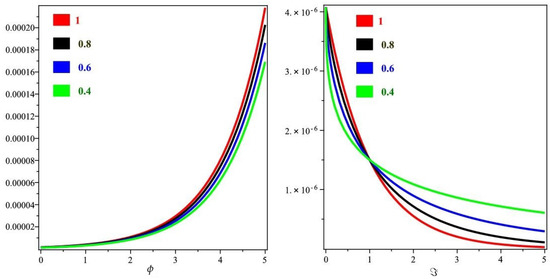
Figure 8. The ITM solution of different fractional-order ϱ graphs with respect to ϕ and ℑ of Example 4.

Example 5.

Consider the fractional nonlinear Equal-Width equation of the form

$${}^{CF}{D}_{\Im }^{\varrho }\omega +3{\omega }^2{\omega }_{\varphi }-{\omega }_{\varphi \varphi \Im }=0,\Im >0,\varphi \in \mathbb{R},0<\varrho \le 1$$

(66)

with the initial condition

$$\omega (\varphi ,0)=\frac{1}{4}\mathrm{sech}(\varphi -30).$$

(67)

Applying the Laplace transform to (66), we get

$$\mathcal{L}\left[\omega (\varphi ,\Im )\right]=s^{-1}\omega (\varphi ,0)-\frac{s+\varrho (1-s)}{s}\mathcal{L}\left[3{\omega }^2{\omega }_{\varphi }-{\omega }_{\varphi \varphi \Im }\right].$$

(68)

Applying inverse Laplace transform to (68), we have

$$\omega (\varphi ,\Im )={\mathcal{L}}^{-1}\left\{s^{-1}\omega (\varphi ,0)\right\}-{\mathcal{L}}^{-1}\left\{\frac{s+\varrho (1-s)}{s}\mathcal{L}\left[3{\omega }^2{\omega }_{\varphi }-{\omega }_{\varphi \varphi \Im }\right]\right\}.$$

(69)

Now, by using the suggested analytical method, we get

$$\begin{array}{cc}\hfill {\omega }_0(\varphi ,\Im )& =\frac{1}{4}\mathrm{sech}(\varphi -30),\hfill \\ \hfill {\omega }_1(\varphi ,\Im )& =-{\mathcal{L}}^{-1}\left\{\frac{s+\varrho (1-s)}{s}\mathcal{L}\left[3{\omega }_0^2{\omega }_{0\varphi }-{\omega }_{0\varphi \varphi \Im }\right]\right\},\hfill \\ \hfill {\omega }_1(\varphi ,\Im )& =\frac{3}{64}{\mathrm{sech}}^3(\varphi -30)tanh(\varphi -30)\left(\varrho \Im +(1-\varrho )\right),\hfill \\ \hfill & ⋮\hfill \\ \hfill {\omega }_{n+1}(\varphi ,\Im )& ={\mathcal{L}}^{-1}\left\{\frac{{(s+\varrho (1-s))}^n}{s^n}\mathcal{L}\left[3{\omega }_n^2{\omega }_{n\varphi }-{\omega }_{n\varphi \varphi \Im }\right]\right\}.\hfill \end{array}$$

The series form result is

$$\omega (\varphi ,\Im )={\omega }_0(\varphi ,\Im )+{\omega }_1(\varphi ,\Im )+{\omega }_2(\varphi ,\Im )+{\omega }_3(\varphi ,\Im )+\cdots +{\omega }_n(\varphi ,\Im ).$$

Then, we have

$$\omega (\varphi ,\Im )=\frac{1}{4}\mathrm{sech}(\varphi -30)+\frac{3}{64}{\mathrm{sech}}^3(\varphi -30)tanh(\varphi -30)\left(\varrho \Im +(1-\varrho )\right)+\cdots .$$

(70)

Putting $\varrho =1$ into (70), we obtain the solution of this problem as

$$\omega (\varphi ,\Im )=\frac{1}{4}\mathrm{sech}(\varphi -30)+\frac{3}{64}{\mathrm{sech}}^3(\varphi -30)tanh(\varphi -30)\Im +\cdots .$$

(71)

The exact solution of this problem is

$$\omega (\varphi ,\Im )=\frac{1}{4}\mathrm{sech}\left(\varphi -30-\frac{\Im }{4}\right).$$

(72)

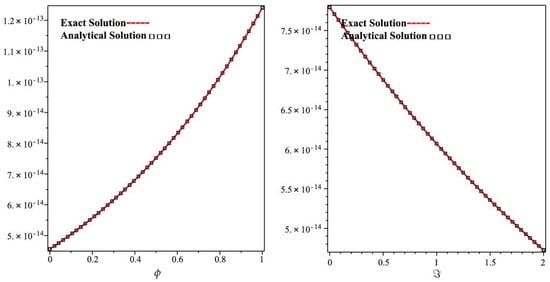
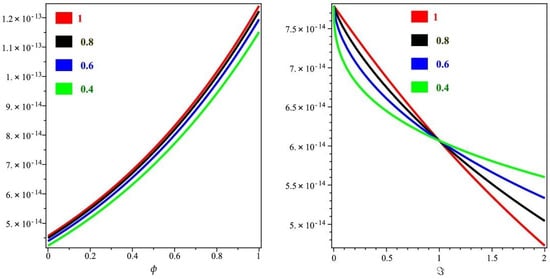
In Figure 9, it is shown that the exact and the NITM solutions graph with respect to ϕ and ℑ of Example 5 at $\varrho =1$. From the given figures, it can be seen that both the NITM and exact results are in close contact with each other. Furthermore, in Figure 10, the NITM results of Example 5 are investigated at different fractional-order at $\varrho =1,0.8,0.6$, and $0.4$ of 2D graph with respect to ϕ and ℑ.

Figure 9. The actual and ITM solution graphs at $\varrho =1$ with respect to ϕ and ℑ of Example 5.

Figure 10. The ITM solution of different fractional-order ϱ graphs with respect to ϕ and ℑ of Example 5.

Example 6.

Consider the fractional nonlinear Equal-Width equation of the form

$${}^{CF}{D}_{\Im }^{\varrho }\omega +\frac{12}{7}{\left({\omega }^6\right)}_{\varphi }-\frac{3}{7}{\left({\omega }^6\right)}_{\varphi \varphi \Im }=0,\Im >0,\varphi \in \mathbb{R},0<\varrho \le 1$$

(73)

with the initial condition

$$\omega (\varphi ,0)={cosh}^{2/5}\left(\frac{5\varphi }{6}\right).$$

(74)

Applying the Laplace transform to (73), we get

$$\mathcal{L}\left[\omega (\varphi ,\Im )\right]=s^{-1}\omega (\varphi ,0)-\frac{s+\varrho (1-s)}{s}\mathcal{L}\left[\frac{12}{7}{\left({\omega }^6\right)}_{\varphi }-\frac{3}{7}{\left({\omega }^6\right)}_{\varphi \varphi \Im }\right].$$

(75)

Applying inverse Laplace transform to (75), we have

$$\omega (\varphi ,\Im )={\mathcal{L}}^{-1}\left\{s^{-1}\omega (\varphi ,0)\right\}-{\mathcal{L}}^{-1}\left\{\frac{s+\varrho (1-s)}{s}\mathcal{L}\left[\frac{12}{7}{\left({\omega }^6\right)}_{\varphi }-\frac{3}{7}{\left({\omega }^6\right)}_{\varphi \varphi \Im }\right]\right\}.$$

(76)

Now, by using the suggested analytical method, we get

$$\begin{array}{cc}\hfill {\omega }_0(\varphi ,\Im )& ={cosh}^{2/5}\left(\frac{5\varphi }{6}\right),\hfill \\ \hfill {\omega }_1(\varphi ,\Im )& =-{\mathcal{L}}^{-1}\left\{\mathcal{L}\left[\frac{12}{7}{\left({\omega }_0^6\right)}_{\varphi }-\frac{3}{7}{\left({\omega }^6\right)}_{0\varphi \varphi \Im }\right]\right\},\hfill \\ \hfill {\omega }_1(\varphi ,\Im )& =-\frac{24}{7}{cosh}^{7/5}\left(\frac{5\varphi }{6}\right)sinh\left(\frac{5\varphi }{6}\right)\left(\varrho \Im +(1-\varrho )\right),\hfill \\ \hfill & ⋮\hfill \\ \hfill {\omega }_{n+1}(\varphi ,\Im )& ={\mathcal{L}}^{-1}\left\{\frac{{(s+\varrho (1-s))}^n}{s^n}\mathcal{L}\left[\frac{12}{7}{\left({\omega }_n^6\right)}_{\varphi }-\frac{3}{7}{\left({\omega }^6\right)}_{n\varphi \varphi \Im }\right]\right\}.\hfill \end{array}$$

The series form result is

$$\omega (\varphi ,\Im )={\omega }_0(\varphi ,\Im )+{\omega }_1(\varphi ,\Im )+{\omega }_2(\varphi ,\Im )+{\omega }_3(\varphi ,\Im )+\cdots +{\omega }_n(\varphi ,\Im ).$$

Then, we have

$$\omega (\varphi ,\Im )={cosh}^{2/5}\left(\frac{5\varphi }{6}\right)-\frac{24}{7}{cosh}^{2/5}\left(\frac{5\varphi }{6}\right)sinh\left(\frac{5\varphi }{6}\right)\left(\varrho \Im +(1-\varrho )\right)+\cdots .$$

(77)

Putting $\varrho =1$ into (77), we obtain the solution of this problem as

$$\omega (\varphi ,\Im )={cosh}^{2/5}\left(\frac{5\varphi }{6}\right)-\frac{24}{7}{cosh}^{7/5}\left(\frac{5\varphi }{6}\right)sinh\left(\frac{5\varphi }{6}\right)\Im +\cdots .$$

(78)

The exact solution of this problem is

$$\omega (\varphi ,\Im )={cosh}^{2/5}\left(\frac{5}{6}(\varphi -\Im )\right).$$

(79)

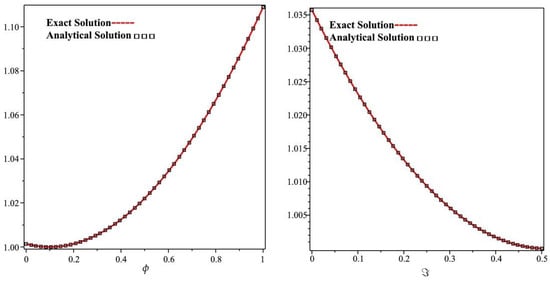
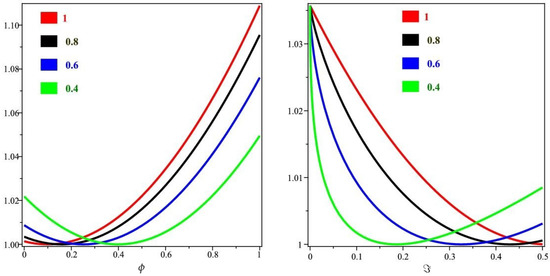
In Figure 11, it is shown that the exact and the NITM solutions graph with respect to ϕ and ℑ of Example 6 at $\varrho =1$. From the given figures, it can be seen that both the NITM and exact results are in close contact with each other. Furthermore, in Figure 12, the NITM results of Example 6 are investigated at different fractional-order at $\varrho =1,0.8,0.6$, and $0.4$ of the 2D graph with respect to ϕ and ℑ.

Figure 11. The actual and ITM solution graphs at $\varrho =1$ with respect to ϕ and ℑ of Example 6.

Figure 12. The ITM solution of different fractional-order ϱ graphs with respect to ϕ and ℑ of Example 6.

7. Conclusions

In this paper, we have presented a homotopy perturbation transform method and iterative transform method for solving fractional-order Equal-Width equations. The derivative is considered in the Caputo–Fabrizio sense. The figures analysis of the fractional-order results achieved has verified the convergence towards the results of the integer order. Finally, some examples have been shown to demonstrate the efficiency and accuracy of the current technique.