On 2-Rainbow Domination Number of Generalized Petersen Graphs P(5k,k)

Abstract

We obtain new results on 2-rainbow domination number of generalized Petersen graphs $P(5k,k)$. In some cases (for some infinite families), exact values are established, and in all other cases lower and upper bounds are given. In particular, it is shown that, for $k>3$, ${\gamma }_{r2}\left(P(5k,k)\right)=4k$ for $k\equiv 2,8mod10$, ${\gamma }_{r2}\left(P(5k,k)\right)=4k+1$ for $k\equiv 5,9mod10$, $4k+1\le {\gamma }_{r2}\left(P(5k,k)\right)\le 4k+2$ for $k\equiv 1,6,7mod10$, and $4k+1\le {\gamma }_{r2}\left(P(5k,k)\right)\le 4k+3$ for $k\equiv 0,3,4mod10$.

1. Introduction

Inspired by several facility location problems, Brešar, Henning and Rall [1,2,3] initiated the study of the k-rainbow domination problem. The problem is proved to be NP-complete even if the input graph is a chordal graph or a bipartite graph [2]. This variation of the general domination problem has already attracted considerable attention. The growing interest in domination problems [4] is based on a variety of practical applications on one hand, and, on the other hand, expected (and usually proven) intractability on general graphs.

1.1. Graphs and Rainbow Domination

A (simple) graph $G=\left(V\right(G),E(G\left)\right)$ is a combinatorial object, where $V=V\left(G\right)$ is a set whose elements are called vertices and $E=E\left(G\right)$ is a set of edges. Edges are pairs of vertices, $e=\{u,v\}$. The interval of integers is denoted by $[i,j]=\{k\in \mathbb{N}|i\le k\le j\}$. All subscripts in this paper will be taken modulo n.

Given a graph G and a positive integer t, the goal is to assign a subset of the color set $\{1,2,\cdots ,t\}$ to every vertex of G such that every vertex with the empty set assigned has all t colors in its neighborhood. Such an assignment is called a t-rainbow dominating function ($tRDF$) of the graph G. The weight of assignment g, a $tRDF$ of a graph G, is the value $w\left(g\right)={\sum }_{v\in V\left(G\right)}\left|g\left(v\right)\right|$. We say that G is tRD-colored (or simply, colored) by g, and that each vertex is tRD-dominated (or simply dominated) by its neighbors under g. The t-rainbow domination number${\gamma }_{rt}\left(G\right)$ is the minimum weight over all $tRDF$s in G.

1.2. Generalized Petersen Graphs

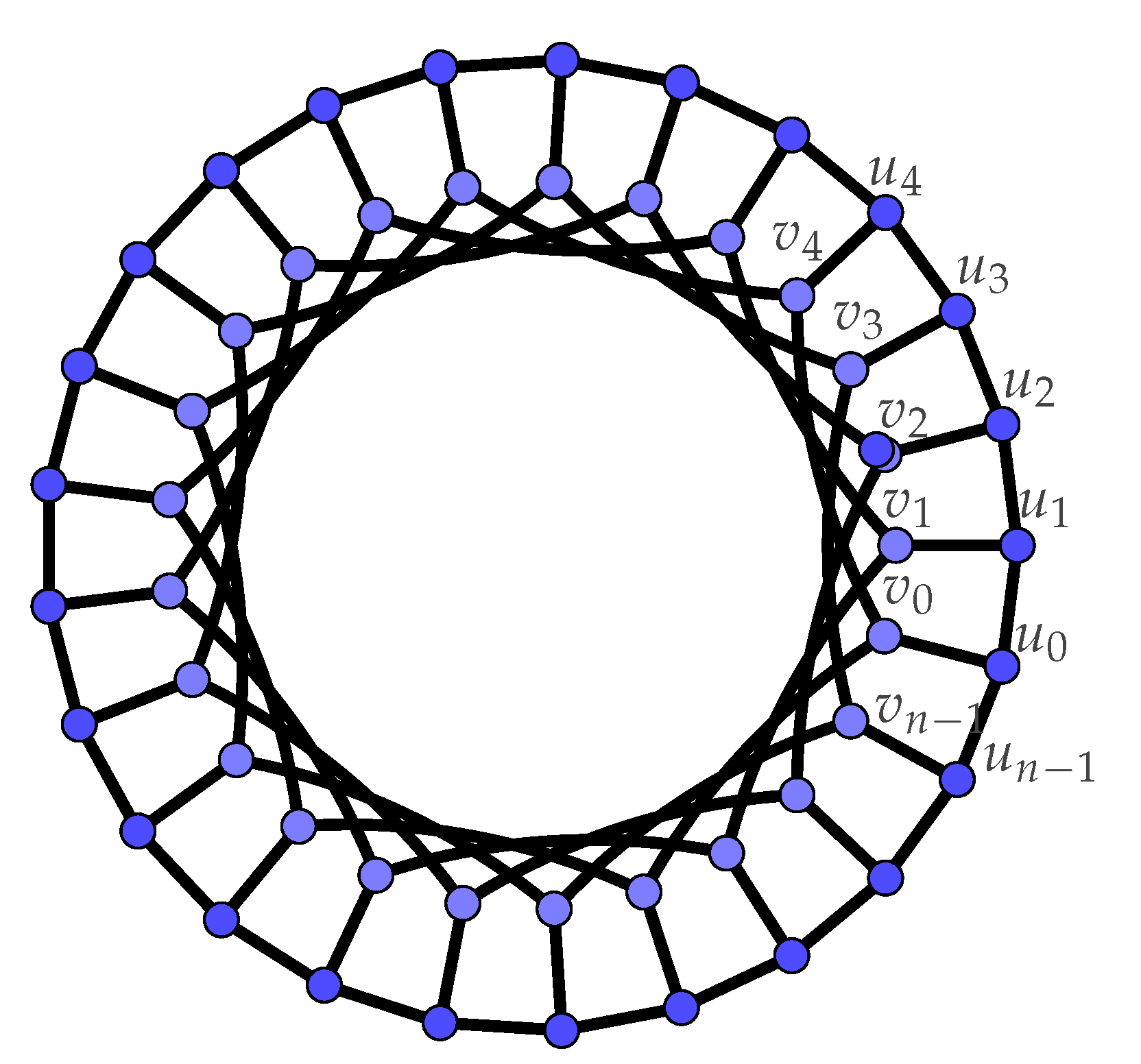
For $n\ge 3$ and k, $1\le k\le n-1$, the generalized Petersen graph $P(n,k)$, is a graph on $2n$ vertices with $V\left(P(n,k)\right)=\{v_i,u_i\mid 0\le i\le n-1\}$ and $E\left(P(n,k)\right)=\{\{u_i,u_{i+1}\},\{u_i,v_i\},\{v_i,v_{i+k}\}\mid 0\le i\le n-1\}$. This standard notation was introduced by Watkins [5] (see Figure 1).

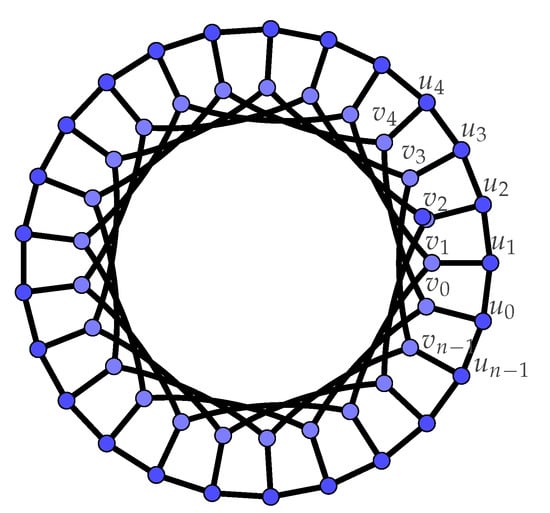
Figure 1. A generalized Petersen graph $P(n,k)$.

It is well known that the graphs $P(n,k)$ are 3-regular unless $k=\frac{n}{2}$ and that $P(n,k)$ are higly symmetric [5,6]. As $P(n,k)$ and $P(n,n-k)$ are isomorphic, it is natural to restict attention to $P(n,k)$ with $n\ge 3$ and k, $1\le k<\frac{n}{2}$. In this work, we will implicitly make use of another symmetry of Petersen graphs. It is well-known that the mapping that maps $v_i\to v_{i+1}$ and $u_i\to u_{i+1}$ is an authomorphism. Hence any rotation along the long cycle is an authomorphism.

1.3. Related Previous Work

The early papers [1,2,3] already provide various results on k-rainbow domination. The special case, 2-rainbow domination, has been studied in a number of works where 2-rainbow domination numbers of several graph classes were established; see [7,8,9,10,11] and the references there.

Generalized Petersen graphs have been studied extensively in the past, often as very interesting examples in research of various graph invariants. The interest seems to be even more intensive recently, including domination [12], independent rainbow domination [13,14], Italian domination [15], Roman and double Roman domination [11,16,17], to name just a few. Many papers focus on subfamilies of Petersen graphs. Popular examples are $P(n,c)$, for fixed (and usually small) c, and $P(ck,k)$, for fixed c and arbitrary k (hence infinitely many $n=ck$).

2-rainbow domination has been established for several families of Petersen graphs: $P(n,1)$ in [8,18], $P(n,2)$ in [19], $P(n,3)$ in [20].

Here, we will also use the general bound $\lceil \frac{4n}{5}\rceil \le {\gamma }_{r2}\left(P(n,k)\right)\le n$ that has been proved in [2] and directly implies the next proposition.

Proposition 1.

$4k\le {\gamma }_{r2}\left(P(5k,k)\right)\le 5k$.

In [18] (see also [8]), it is shown that ${\gamma }_{r2}\left(P(n,k)\right)\le n-1$ for all $n\ge 13$ except $n=2k+2$, and ${\gamma }_{r2}\left(P(n,k)\right)=n$ if and only if $k=1$, or $n=2k+2$ for $k\ge 3$, or $(n,k)\in \left\{\right(5,2),(7,2),(7,3),(10,3),(11,3),(11,4\left)\right\}$. In cases when $n=5k$, the next proposition follows.

Proposition 2.

${\gamma }_{r2}\left(P(5k,k)\right)\le 5k-1$ for all $k>1$.

In [19], is proved that ${\gamma }_{r2}\left(P(n,2)\right)=\lceil \frac{4n}{5}\rceil +\alpha$, where $\alpha =0$ for $n\equiv 0,3,4,9(mod10)$, and $\alpha =1$ otherwise. The odd n case already appears in [2]. In [20], it is shown that ${\gamma }_{r2}\left(P(n,3)\right)\le n-\lfloor \frac{n}{8}\rfloor +\alpha$, where $\alpha =0$ for $n\equiv 0,2,4,5,6,7,13,14,15(mod16)$, and $\alpha =1$ otherwise. In particular, we have ${\gamma }_{r2}\left(P(10,2)\right)=8$ and ${\gamma }_{r2}\left(P(15,3)\right)\le 14$.

1.4. Our Results

We prove the next theorem that gives exact values of 2-rainbow domination number for some, and bounds with gap at most 2 for all other infinite subfamilies of Petersen graphs $P(5k,k)$.

Theorem 1.

Let $k>3$. Then

$${\gamma }_{r2}\left(P(5k,k)\right)=\left\{\begin{array}{cc}4k,\hfill & k\equiv 2,8mod10\hfill \\ 4k+1,\hfill & k\equiv 5,9mod10\hfill \end{array}\right.$$

(1)

$$4k+1\le {\gamma }_{r2}\left(P(5k,k)\right)\le \left\{\begin{array}{cc}4k+2,\hfill & k\equiv 1,6,7mod10\hfill \\ 4k+3,\hfill & k\equiv 0,3,4mod10\hfill \end{array}\right.$$

(2)

The cases when $k\le 3$ are summarized below.

Theorem 2.

${\gamma }_{r2}\left(P(5,1)\right)=5$, ${\gamma }_{r2}\left(P(10,4)\right)=10$, $13\le {\gamma }_{r2}\left(P(15,3)\right)\le 14$.

Theorem 1 follows from Propositions 4–7. The small cases of Theorem 2 recall previously known facts (see Examples 1–3).

Note that the previously known values ${\gamma }_{r2}\left(P(5k,k)\right)$ for $k=1$ and $k=3$ in Theorem 1 improve the general values that hold for the infinite families. For the case $k=1$, this is expected because of the general upper bound [2]. The upper bound for $k=3$ is obtained by a special construction recalled from [20].

2. Constructions and Proofs

We start by examples that recall some well-known facts.

Example 1.

Observe that $P(5,1))$ is the Cartesian product of $C_5$ and $P_2$. It is well known that ${\gamma }_{r2}\left(P(5,1)\right)=5$; see [8,18].

Example 2.

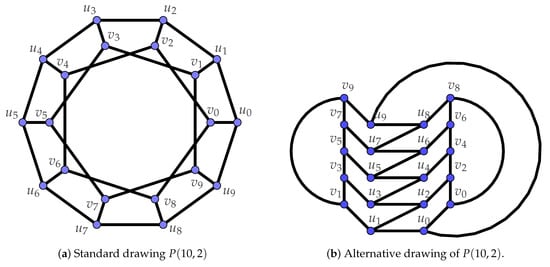
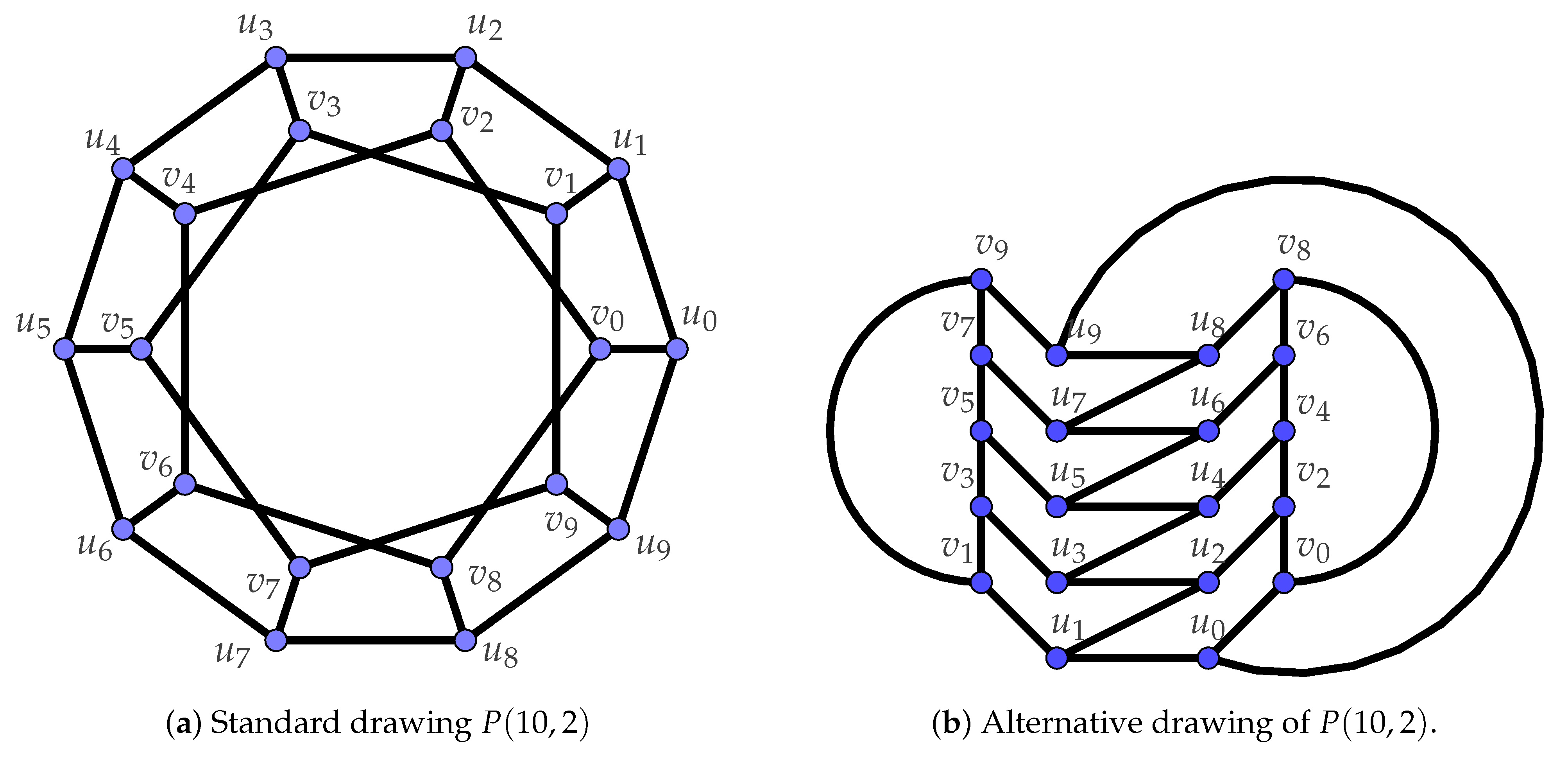
It is well known that ${\gamma }_{r2}\left(P(10,2)\right)=8$ [19]. A 2RD-coloring of $P(10,2))$ of weight 8 is shown on two alternative drawings of Petersen graph on Figure 2.

Figure 2. Two drawings of $P(10,2)$ with a 2RDF.

Example 3.

A 2RD function of $P(15,3)$ is given by

$$\left(\begin{array}{cccc}f\left(u_0\right)& f\left(u_1\right)& \cdots & f\left(u_{14}\right)\\ f\left(v_0\right)& f\left(v_1\right)& \cdots & f\left(v_{14}\right)\end{array}\right)=\left(\begin{array}{ccccc}100& 300& 202& 020& 010\\ 020& 001& 010& 101& 202\end{array}\right).$$

The elements in rows are written in triples for easier reading. The symbol “3” stands for the set $\{1,2\}$. Hence, ${\gamma }_{r2}\left(P(15,3)\right)\le 14$ [20].

We continue with some formal arguments that will motivate and approve introduction of reduced tables that will be used later for representing the 2RD-colorings. We use the fact that in any 2RD-coloring of weight $4k$, each vertex is either assigned a color or has exactly two neighbors that are colored by distinct colors.

Lemma 1.

Assume $P(5k,k)=4k$. Let $C_i=\{v_i,v_{k+i},v_{2k+i},v_{3k+i},v_{4k+i}\}$ and $V_i=\{u_i,u_{k+i},$$u_{2k+i},$$u_{3k+i},u_{4k+i}\}$, for any $i\in [0,k-1]$. Then, for an 2RD-coloring of weight $4k$, we have

(1) 

exactly one vertex of $C_i$ receives color 1 and exactly one vertex receives color 2;

(2) 

the two vertices on the cycle $v_i{v}_{k+i}{v}_{2k+i}{v}_{3k+i}{v}_{4k+i}$ that receive colors are not adjacent;

(3) 

exactly one vertex of $V_i$ receives color 1 and exactly one vertex receives color 2;

(4) 

assume (wlog) $f\left(v_{k+i}\right)=1$ and $f\left(v_{3k+i}\right)=2$. Then $f\left(u_{4k+i}\right)=1$ and $f\left(u_{0+i}\right)=2$.

Proof .

(1) and (2). Each vertex of $C_i$ has exactly one neighbor outside $C_i$. Hence (at least) two nonadjacent vertices of $C_i$ must be in S. If both vertices are of the same color, say 1, then we must have at least three vertices in $V_i$ of color 2. We conclude that $C_i$ must include exactly one vertex of color 1 and one vertex of color 2 (statement (1)), and these two vertices are not adjacent (statement (2)).

(3) and (4). From above, we can assume that we have two nonadjacent vertices in $C_i$ that are of different colors. Without loss of generality, say $f\left(v_{k+i}\right)=1$ and $f\left(v_{3k+i}\right)=2$. Then $v_{2k+i}$ is dominated by $v_{k+i}$ and $v_{3k+i}$, while $v_{4k+i}$ must have a neighbor of color 1 outside $C_i$, and $v_{5k+i}=v_i$ must have a neighbor of color 2 outside $C_i$. Consequently, $f\left(u_{4k+i}\right)=1$ and $f\left(u_i\right)=2$. If any other vertex of $V_i$ is assigned a color, then clearly some vertex of $C_i$ would be overdominated, and consequently, the total number of colors used would be more than $4k=\frac{4n}{5}$. Hence, in any 2RD-coloring, exactly one vertex of $V_i$ receives color 1 and exactly one vertex of $V_i$ receives color 2 (statement (3)), and if $f\left(v_{k+i}\right)=1$ and $f\left(v_{3k+i}\right)=2$, then $f\left(u_{4k+i}\right)=1$ and $f\left(u_{0+i}\right)=2$ (statement (4)). □

Futhermore, due to symmetry, the minimal 2RD-colorings are exactly determined by the coloring of (any) one inner cycle. In other words, assuming ${\gamma }_{r2}\left(P(5k,k)\right)=4k$, the coloring of any inner cycle forces the 2RD-coloring on the whole graph. This is formally stated in the next Proposition.

Proposition 3.

Assume $P(5k,k)=4k$. Let $C_i=\{v_i,v_{k+i},v_{2k+i},v_{3k+i},v_{4k+i}\}$, for $i\in [0,k-1]$, be the set of vertices of the i-th inner cycle. Let C be any inner cycle; i.e., $V\left(C\right)=C_i$ for some $i\in [0,k-1]$. Given a fixed assignment of colors on C, there are exactly two ways to extend the coloring to $P(5k,k)$.

Proof. 

By Lemma 1, coloring of $C_i$ forces the coloring of $V_i$. Let us write the values of 2RD-coloring f on $V_i$ in a column. Furthermore, recall that in this column there are exactly two (adjacent) positions that are colored by 1 and 2. Wlog, assume the column is shown in Table 1, Table 2 and Table 3.

Table 1. (a) Column structure.

$f\left(u_i\right)$	$\downarrow f\left(v_i\right)$
$f\left(u_{k+i}\right)$	$\downarrow f\left(v_{k+i}\right)$
$f\left(u_{2k+i}\right)$	$\downarrow f\left(v_{2k+i}\right)$
$f\left(u_{3k+i}\right)$	$\downarrow f\left(v_{3k+i}\right)$
$f\left(u_{4k+i}\right)$	$\downarrow f\left(v_{4k+i}\right)$
i

Table 2. (b) Complete column.

0	$\downarrow 2$
0	$\downarrow 0$
0	$\downarrow 1$
2	$\downarrow 0$
1	$\downarrow 0$
i

Table 3. (c) Reduced column.

0

0

0

2

1

i

By the properties of the 2RD-coloring (see Lemma 1), the three positions without a color must be in three consecutive rows. The vertex at the middle row clearly needs both colors, and the other two vertices need one color (the other color is provided from the cycle $C_i$). See Table 4 below. As each column in a 2RD-coloring of weight $4k$ has exactly two vertices that are assigned two distinct colors, the two neighboring columns are exactly determined. However, the two neighboring columns can be put to positions $i-1$ and $i+1$ in two ways (see Table 5 and Table 6). This concludes the proof. □

Table 4. (d) i-th column.

0	← 1
0	← 1,2
0	← 2
2
1
i	neighbors

Table 5. (e) First extension.

	0	← 1
1→	0	← 2
2→	0
	2
	1
$i-1$	i	$i+1$

Table 6. (f) Second extension.

1→	0
2→	0	← 1
	0	← 2
	2
	1
$i-1$	i	$i+1$

The proof of Proposition 3 directly implies the next statement.

Corollary 1.

${\gamma }_{r2}\left(P(40,8)\right)=32$, ${\gamma }_{r2}\left(P(60,12)\right)=48$.

Proof. 

Start with any column, say $i=2$. By Lemma 3, the first and the third column are determined. Choose one of the possible extensions; see tables below. Continue until all columns $i\in [0,8]$ in one and $i\in [0,12]$ in the second table are filled in. Observe that $8=0(mod8)$ and $12=0(mod12)$, so the last and the first columns in the tables refer to the same sets of vertices. Note, however, that the entries in the two columns are shifted, which means that the colors assigned to column 0 and 8 in Table 7 and columns 0 and 12 in Table 8 exactly match.

Table 7. (g) A 2RD-coloring of $V_i$ for $P(40,8)$.

0	0	1	0	2	0	0	2	0
0	1	0	0	1	0	2	0	0
0	2	0	1	0	0	1	0	2
2	0	0	2	0	1	0	0	1
1	0	2	0	0	2	0	1	0
0	1	2	3	4	5	6	7	8

Table 8. (h) A 2RD-coloring of $V_i$ for $P(60,12)$.

2	0	1	0	0	1	0	2	0	0	2	0	1
1	0	0	1	0	2	0	0	2	0	1	0	0
0	1	0	2	0	0	2	0	1	0	0	1	0
0	2	0	0	2	0	1	0	0	1	0	2	0
0	0	2	0	1	0	0	1	0	2	0	0	2
0	1	2	3	4	5	6	7	8	9	10	11	12

Hence, the columns 0 to 7 in the first table define a 2RD-coloring of $P(40,8)$, and we have ${\gamma }_{r2}\left(P(40,8)\right)=32$. Similarly, columns 0 to 11 in the second table define a 2RD-coloring of $P(60,12))$, implying ${\gamma }_{r2}\left(P(60,12)\right)=48$. □

The last proof gives a general idea to see which graphs among $P(5k,k))$ allow 2RD-coloring with $4k$ colors. This will hold exactly when columns 0 and k will match, taking into account the shift of rows as indicated below (Table 9).

Table 9. (i) A 2RD-coloring of $V_i$ for $P(5k,k)$.

$f\left(u_0\right)$	$f\left(u_1\right)$	...	$f\left(u_i\right)$	...	$f\left(u_{k-1}\right)$	$f\left(u_k\right)$	$f\left(u_{k+1}\right)$	...
$f\left(u_k\right)$	$f\left(u_{k+1}\right)$	...	$f\left(u_{k+i}\right)$	...	$f\left(u_{2k-1}\right)$	$f\left(u_{2k}\right)$	$f\left(u_{2k+1}\right)$	...
$f\left(u_{2k}\right)$	$f\left(u_{2k+1}\right)$	...	$f\left(u_{2k+i}\right)$	...	$f\left(u_{3k-1}\right)$	$f\left(u_{3k}\right)$	$f\left(u_{3k+1}\right)$	...
$f\left(u_{3k}\right)$	$f\left(u_{3k+1}\right)$	...	$f\left(u_{3k+i}\right)$	...	$f\left(u_{4k-1}\right)$	$f\left(u_{4k}\right)$	$f\left(u_{4k+1}\right)$	...
$f\left(u_{4k}\right)$	$f\left(u_{4k+1}\right)$	...	$f\left(u_{4k+i}\right)$	...	$f\left(u_{5k-1}\right)$	$f\left(u_{5k}\right)=f\left(u_0\right)$	$f\left(u_1\right)$	...
0	1	...	i	...	$k-1$	k	$k+1$	...

It is straightforward to check that if either the Table 7 or Table 8 would be extended to larger indices, the columns will eventually repeat in the pattern. It can readily be seen from Table 8 that columns 0 and 1 exactly repeat as columns 10 and 11. So obviously, the patterns are periodic with period 10. We write this observation formally as a Lemma.

Lemma 2.

${\gamma }_{r2}\left(P(5(k+10),k+10)\right)\le {\gamma }_{r2}\left(P(5k,k)\right)+40$.

Lemma 2 and Proposition 1 imply Proposition 4.

Proposition 4.

For $k=2(mod10)$ and $k=8(mod10)$ it holds ${\gamma }_{r2}\left(P(5k,k)\right)=4k$.

Due to uniqueness of the 2RD-colorings of weight $4k$ (see Lemma 3), we also have the next Lemma.

Lemma 3.

If $k\not\equiv 2,8$ (mod 10) then ${\gamma }_{r2}\left(P(5k,k)\right)>4k$.

Proof. 

Starting with any column, it has been shown above that there are exactly two possible extensions to potentially infinite pattern with the property that the minimal possible number of colors is used. As observed in Proposition 4, $k\equiv 2,8$ (mod 10) are the only possibilities in which the extensions match when the two ends of pattern are identified. □

In the continuation, we give several constructions that provide upper bounds for ${\gamma }_{r2}\left(P(5k,k)\right)$. In the first case, the upper bound clearly equals the lower bound and is at the same time also the exact value.

Proposition 5.

If $k\equiv 5,9$ (mod 10) then ${\gamma }_{r2}\left(P(5k,k)\right)=4k+1$.

Proof. 

By Lemma 3, ${\gamma }_{r2}\left(P(5k,k)\right)\ge 4k+1$. So it is sufficient to provide constructions of colorings showing that if $k\equiv 5,9$ (mod 10) then ${\gamma }_{r2}\left(P(5k,k)\right)\le 4k+1$. Because of Lemma 2, we only need a coloring of $P(25,5)$ of weight 21 and a coloring of $P(45,9)$ of weight 37, and the general statement follows by induction.

A coloring of $P(25,5)$ of weight 21 can be constructed as follows. Table 10 below is obtained by first taking five consecutive columns of the general pattern in columns 0 to 4. The columns 5, 6, and 7 repeat the values of columns 1, 2, and 3 using the fact that cf. $f\left(u_5\right)$ appears in the first row of column 5 but also in the second row of column 0. We only alter column 5 of Table 10 by putting $f\left(u_{14}\right)=2$, an additional color to the previously uncolored vertex $u_{14}$. It is straightforward to check that this assures that all the vertices are 2RD-colored.

Table 10. (j) A 2RD-coloring of $P(25,5)$.

0	1	0	2	0	1	0	0
1	0	0	1	0	2	0	1
2	0	1	0	2	0	0	2
0	0	2	0	1	0	2	0
0	2	0	0	2	0	1	0
0	1	2	3	4	5	6	7

The very same idea is used to obtain Table 11 that provides a coloring of $P(45,9)$ of weight 37. □

Table 11. (k) A 2RD-coloring of $P(45,9)$.

2	0	1	0	0	1	0	2	0	1	0	0
1	0	0	1	0	2	0	0	2	0	1	0
0	1	0	2	0	0	2	0	1	0	2	0
0	2	0	0	2	0	1	0	2	0	0	2
0	0	2	0	1	0	0	1	0	2	0	1
0	1	2	3	4	5	6	7	8	9	10	11

Following the idea of the last proof, we provide further constructions below. In all cases, only one column is altered by updating the values of a 2RD-coloring. In one case, $P(50,10)$, one of the vertices is assigned two colors. An alternative solution that assigns at most one color to each vertex is given in Table 12.

Table 12. (r) Another 2RD-coloring of $P(50,10)$.

1	0	0	1	0	2	0	0	2	1	2	0	1
2	0	1	0	0	1	0	2	0	2	0	0	2
0	0	2	0	1	0	0	1	0	2	1	2	0
1	2	0	0	2	0	1	0	0	1	0	1	0
0	1	0	2	0	0	2	0	1	0	1	0	0
0	1	2	3	4	5	6	7	8	9	10	11	12

Note however that in this case, two columns are altered; thus the consistency check would have to include four consecutive columns in this case. The constructions imply the following two propositions.

Proposition 6.

Assume $k>3$. If $k\equiv 1,6,7$ (mod 10) then ${\gamma }_{r2}\left(P(5k,k)\right)\le 4k+2$.

Proof. 

The proof is by induction, using Lemma 2, and construction of the basic cases. Table 13, Table 14 and Table 15 below provide 2RD-colorings of $\left(P\right(5k,k\left)\right)$ for k= 6, 7, and 11. Since we can observe that it is sufficient to check only three columns around the altered column, the proof is straightforward. □

Table 13. (l) A 2RD-coloring of $P(30,6)$.

1	0	2	0	0	2	2	0	0
2	0	0	2	0	1	0	2	0
0	2	0	1	0	2	0	1	0
0	1	0	0	1	1	0	0	1
0	0	1	0	2	0	1	0	2
0	1	2	3	4	5	6	7	8

Table 14. (m) A 2RD-coloring of $P(35,7)$.

1	0	0	1	0	2	0	2	0	1
2	0	1	0	0	1	2	0	0	2
0	0	2	0	1	0	1	0	2	0
0	2	0	0	2	0	1	0	1	0
0	1	0	2	0	0	2	1	0	0
0	1	2	3	4	5	6	7	8	9

Table 15. (n) A 2RD-coloring of $P(55,11)$.

1	0	2	0	0	2	0	1	0	0	1	2	0	0
2	0	0	2	0	1	0	0	1	0	2	0	2	0
0	2	0	1	0	0	1	0	2	0	2	0	1	0
0	1	0	0	1	0	2	0	0	2	1	0	0	1
0	0	1	0	2	0	0	2	0	1	0	1	0	2
0	1	2	3	4	5	6	7	8	9	10	11	12	13

Proposition 7.

Assume $k>3$. If $k\equiv 0,3,4$ (mod 10) then ${\gamma }_{r2}\left(P(5k,k)\right)\le 4k+3$.

Proof. 

The proof is analogous to the proof of Proposition 6. In Table 16, Table 17 and Table 18, 2RD-colorings of $P(5k,k)$ for k = 4, 10, and 13 are given. As in the proof of Proposition 6, we start with k consecutive columns using one of the two infinite patterns given before. We add some columns to the right that repeat the colorings of the columns 0, 1, and 2 that are shifted one row up. (This is because cf. the vertex in row 1 of column k also appears in row 2 of column 0.) Next, the column $k-1$ is considered, and some additional colors are used so that all the vertices in columns $k-1$ and k are 2RD-colored (this colors are emphasized in the tables). We omit the details. Note that in all other columns, the construction used already assures that those vertices are 2RD-colored. □

Table 16. (o) A 2RD-coloring of $P(20,4)$.

1	0	0	1	2	0	1
2	0	1	2	0	0	2
0	0	2	1	0	2	0
0	2	0	1	0	1	0
0	1	0	2	1	0	0
0	1	2	3	4	5	6

Table 17. (p) A 2RD-coloring of $P(50,10)$.

1	0	0	1	0	2	0	0	2	1	2	0	1
2	0	1	0	0	1	0	2	0	2	0	0	2
0	0	2	0	1	0	0	1	0	2,1	0	2	0
0	2	0	0	2	0	1	0	0	1	0	1	0
0	1	0	2	0	0	2	0	1	0	1	0	0
0	1	2	3	4	5	6	7	8	9	10	11	12

Table 18. (q) A 2RD-coloring of $P(65,13)$.

1	0	2	0	0	2	0	1	0	0	1	0	2	2	0	0
2	0	0	2	0	1	0	0	1	0	2	0	1	0	2	0
0	2	0	1	0	0	1	0	2	0	0	2	2	0	1	0
0	1	0	0	1	0	2	0	0	2	0	1	1	0	0	1
0	0	1	0	2	0	0	2	0	1	0	0	1	1	0	2
0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15

3. Conclusions

Exact values of 2-rainbow domination number for some, and bounds with gap at most 2 for all other infinite subfamilies of Petersen graphs $P(5k,k)$, are provided. We conjecture that the upper bounds proved here are in fact the exact values. It is a challenging research task to prove this conjecture, or, in other words, to obtain better lower bounds for the remaining cases. The present authors see two possible approaches. One is the application of the algebraic approach, see for example [14,21,22,23]. As an alternative, the discharging method [16], which has been applied to a domination problem recently, may give improved lower bounds. Formal elaboration of either of these ideas is expected to demand substantial effort, so it is left for future work.

On the other hand, in cases where the upper and lower bounds do not match, it is possible that that the upper bounds may be improved because we have used ad hoc constructions. The constructions used in proofs of Propositions 1 and 5–7 are all based on the same idea: start with the optimal pattern and alter one column if needed. Here, we note two consequences of the limitations of our constructions.

• As we are only altering one column, in one case it forced one vertex to be colored by two colors (see Table 17). It is possible to find an alternative 2RD-coloring where each vertex is assigned at most one color. However, two columns need to be changed in this case.
• Updating only one column may not provide the best possible 2RD-coloring. In other words, it may be possible that altering more than one column can improve the bounds.

Therefore, as long as we do not have a proof that the upper bounds are indeed the exact values, it is still possible that some better constructions exist that would improve the upper bounds.

Due to well-known symmetries of generalized Petersen graphs, it is straightforward that the results of this paper directly apply to the family $P(5k,4k)$ as $P(5k,4k)\approx P(5k,k)$ (≈denotes graph isomorphism). Furthermore, analysis of the family $P(5k,2k)$ (and at the same time $P(5k,3k)$) can be done along the same lines. For example, we state without proof

Conjecture 1.

${\gamma }_{r2}\left(P(20,8)\right)=16$, ${\gamma }_{r2}\left(P(30,12)\right)=24$. ${\gamma }_{r2}\left(P(5,2)\right)=5$, ${\gamma }_{r2}\left(P(10,4)\right)=10$.

And we also conjecture that

Conjecture 2.

Let $k\ge 3$. Then

$${\gamma }_{r2}\left(P(5k,2k)\right)=\left\{\begin{array}{cc}4k,\hfill & k\equiv 4,6mod10\hfill \\ 4k+1,\hfill & k\equiv 1,3mod10\hfill \end{array}\right.$$

(3)

$$4k+1\le {\gamma }_{r2}\left(P(5k,2k)\right)\le \left\{\begin{array}{cc}4k+2,\hfill & k\equiv 0,5,7,8,9mod10\hfill \\ 4k+3,\hfill & k\equiv 2mod10\hfill \end{array}\right.$$

(4)

There are a number of interesting related questions worth further investigation; for example:

• It is easy to see that there is no 2RD-coloring of weight $\frac{4}{5}n$ of graphs in the families $P(3k,k)$, $P(4k,k)$, $P(6k,k)$. We claim that the families that may allow 2RD-domination of weight $\frac{4}{5}n$ are $P(10k,k)$, $P(15k,k)$,..., or, in general, $P(n,k)$, where n is a multiple of $5k$.
• Petersen graphs are 3-regular; hence k-rainbow dominations can only be considered for $k=2$ and 3. An interesting avenue of research therefore is to find values or good bounds for 3-rainbow domination of Petersen graphs.