Network Analyzing by the Aid of Orbit Polynomial

Abstract

This article aims to be a further contribution to the research on structural complexity networks. Here, we emphasize measures to determine symmetry. The so-called “orbit polynomial” is defined by $O_G\left(x\right)={\sum }_i{a}_i{x}^i$, where $a_i$ is the number of orbits of size i. Furthermore, the graph polynomial $1-O_G\left(x\right)$ has a unique positive root in the interval $(0,1)$, which can be considered as a relevant measure of the symmetry of a graph. In the present paper, we studied some properties of the orbit polynomial with respect to the stabilizer elements of each vertex. Furthermore, we constructed graphs with a small number of orbits and characterized some classes of graphs in terms of calculating their orbit polynomials. We studied the symmetry structure of well-known real-world networks in terms of the orbit polynomial.

1. Introduction

The length of orbits or similar vertices gives useful information about the components in a network. For example, the degree of nodes in each orbit is the same, which produces important information concerning the number of component interconnections. Studying the counting polynomial [1] enables us to determine the structural properties of a graph. One of them is the orbit polynomial [2], which uses the cardinalities of the size of vertex orbits. The vertex (or edge) orbits capture the symmetry structure of the graph by constituting a partition on the set of vertices; see [3,4,5,6,7,8,9]. Furthermore, the decomposition of vertices in such a way defines an equivalence relation in which two vertices are similar if they are in the same orbit.

It is a well-known fact that this polynomial has a unique positive root in the interval $(0,1]$, and this value can be considered as a relevant measure of the symmetry of a graph; see [2].

Furthermore, a set of graphs has been used to analyze the branching, symmetry, cyclicity, and connectedness of graphs. In this paper, we used the apparatus of [2] and introduced two novel graph concepts based on the orbits of graphs; see [10]. The typical terms of the orbit polynomials are of the form $c{x}^n$, where c is the number of orbits of $\mathrm{Aut}\left(\mathit{G}\right)$ of size n in the orbit polynomial. The coefficients of this polynomial are all positive, so subtracting these polynomials from one results in a new polynomial that has a unique positive root; see [3,10,11,12,13,14,15]. Although all graphs considered in this paper are finite, connected, and simple, namely graphs without loops and directed or multiple edges, the definition of the orbit polynomial can be generalized to non-simple graphs, especially for graphs with weights associated with vertices or edges. For instance, this polynomial can be computed for a molecular graph with heteroatoms and multiple bonds [16].

The main contribution of this paper is to investigate the orbit polynomials of special graph classes. Section 2 is devoted to introducing the concepts and definitions. In Section 3, we calculate the orbit polynomials for special classes of graphs. In Section 4, we construct graphs with a small number of orbits. As a result, we determine the structure of graphs with a given orbit of sizes one, m, and n, where m and n are two positive integers. Finally, in Section 5, we apply our results to analyze symmetry structures or real-world networks. However, an examination of the relationship between the size of the automorphism group and the positive real root of the orbit polynomial for certain classes of real-world networks is beyond the scope of this paper.

2. Preliminaries

Our notation is standard and mainly taken from standard books of graph theory such as [17]. The vertex and edge sets of a graph G are denoted by $V\left(G\right)$ and $E\left(G\right)$, respectively. All graphs considered in this paper are simple, connected, and finite.

For a graph G with automorphism group $\mathrm{Aut}\left(\mathit{G}\right)$ and an arbitrary vertex $v\in V\left(G\right)$, the vertex-orbit of v (or orbit of v) is the set of all $\alpha \left(v\right)$’s, where $\alpha$ is an automorphism of G. If a graph has exactly one orbit, then we say it is vertex-transitive. Equivalently, a graph G is vertex-transitive, if for two arbitrary vertices, there is an automorphism that maps them together. An edge-transitive graph can similarly be defined.

Finding the automorphism group of a graph could take exponential time, since, for example, the complete graph $K_n$ has ${\mathbb{S}}_n$ as its automorphism group. Let $A=A\left(G\right)$ be the adjacency matrix of graph G and $P_{\sigma }$ be a permutation matrix, corresponding to the permutation $\sigma \in {\mathbb{S}}_n$. Then, $\sigma$ is an automorphism of graph G if and only if $P_{\sigma }^{T}A{P}_{\sigma }=A$ or $P_{\sigma }A=A{P}_{\sigma }$. Here, computing the automorphism group, as well as the orbits of our graphs was done with the aid of the Nauty package [18].

3. Methods and Results

In this section, we introduce the orbit polynomial, which was firstly defined in [2]. The coefficients of this polynomial come from the automorphism group of the graph, and they reflect the structure of the automorphism group regarding the graph. Furthermore, we define an edge version of the orbit polynomial, and some algebraic properties of this polynomial are given. We also applied both definitions to characterize some classes of graphs.

Creating polynomials on the set of orbits of a graph would help to distinguish vertices having different properties and thus to separate them into different orbits; see [19,20].

Let $\Gamma$ be a group and X a non-empty set. The action of group $\Gamma$ on the set X induces a group homomorphism $\phi$ from $\Gamma$ into the symmetric group ${\mathbb{S}}_X$ on X, where $g.x=x$ for all $g\in \Gamma$ and $x\in X$. The stabilizer of element $x\in X$ is defined as ${\Gamma }_x=\{g\in \Gamma :g.x=x\}.$ Furthermore, the orbit of element $x\in X$ is denoted by $x^{\Gamma }$ or $\left[x\right]$, which is $\left\{g\right(x):g\in \Gamma \}$. The orbit-stabilizer theorem implies that $|x^{\Gamma }|\times |{\Gamma }_x|=|\Gamma |$.

Orbit Polynomial

The orbit polynomial [3,21,22] is defined as $O_G\left(x\right)={\sum }_{i=1}^t{x}^{|O_i|},$ where $O_1,\dots ,O_t$ are all orbits of graph G under the action of $\mathrm{Aut}\left(\mathit{G}\right)$ on the set of vertices. Then, the modified orbit polynomial is $O_G^{\star }\left(x\right)=1-O_G\left(x\right).$ In [2], the authors proved several inequalities using these unique positive roots of different graphs. In addition, they defined a new symmetry measure based on the unique positive root of $O_G^{\star }$.

Example 1.

For the path graph $P_n$, we obtain:

$$\begin{array}{c}\hfill O_{P_n}\left(x\right)=\left\{\begin{array}{cc}\frac{n}{2}{x}^2,\hfill & 2\mid n\\ x+\frac{n-1}{2}{x}^2,\hfill & 2\nmid n\end{array}\right.,\end{array}$$

and:

$$\begin{array}{c}\hfill O_{P_n}^{\star }\left(x\right)=\left\{\begin{array}{cc}1-\frac{n}{2}{x}^2,\hfill & 2\mid n\\ 1-x-\frac{n-1}{2}{x}^2,\hfill & 2\nmid n\end{array}\right..\end{array}$$

To proceed with this section, we introduce some algebraic properties of the elements of a graph by the orbit polynomial.

In general, if the edge-transitive graph G is not vertex-transitive, then G is bipartite with partition $V\left(G\right)=V_1\left(G\right)\cup V_2\left(G\right)$, and so:

$$\begin{array}{ccc}\hfill O_G\left(x\right)& =& x^{|V_1|}+x^{|V_2|},\hfill \\ \hfill O_G^{\star }\left(x\right)& =& 1-(x^{|V_1|}+x^{|V_2|}).\hfill \end{array}$$

Example 2.

Consider the graph $S_{n,m}$ as depicted in Figure 1. This graph has three orbits, which are a singleton set containing the central vertex, the set of neighbors of the central vertex, and the set of pendant vertices. Hence,

$$\begin{array}{ccc}\hfill O_{S_{n,m}}\left(x\right)& =& x+x^n+x^{nm},\hfill \\ \hfill O_{S_{n,m}}^{\star }\left(x\right)& =& 1-(x+x^n+x^{nm}).\hfill \end{array}$$

Figure 1. Graph $S_{n,m}$, where $n=6$ and $m=2$.

The bi-star graph $B_{n,n}$ is a graph constructed by the union of two star graphs $S_n$ by joining their central vertices. Furthermore, by a two-graph is a graph, we mean a graph with exactly two vertex-orbits.

Theorem 1.

Let T be a tree on n vertices. Then:

• $T\cong S_n$ if and only if $O_T\left(x\right)=x+x^{n-1}$.
• $T\cong B_{\frac{n}{2},\frac{n}{2}}$ if and only if $O_T\left(x\right)=x^2+x^{n-2}$.
• $T\cong S_{n,m}$ if and only if $O_T\left(x\right)=x+x^n+x^{nm}$, where $n=2m$.

Proof. 

• If $T\cong S_n$, then we obtain $O_T\left(x\right)=x+x^{n-1}$. Conversely, if $O_T\left(x\right)=x+x^{n-1}$, then T has two orbits of sizes one and $n-1$, which yields that $T\cong S_n$.
• If $O_T\left(x\right)=x^2+x^{n-2}$, then T has two orbits, and similar to Example 1, we can prove that T has a central edge and that the other vertices are in the same orbit. It is a well-known fact that a two-tree with a central edge is isomorphic to $B_{\frac{n}{2},\frac{n}{2}}$.
• If $B\cong S_{n,m}$, then by Example 2, the proof is straightforward. If $O_T\left(x\right)=x+x^n+x^{nm}$, then T has three orbits. A singleton orbits consists of the central vertex, an orbit of size n, and an orbit of size $nm$. Clearly, all pendant edges are in the same orbit, and necessarily, T has an orbit whose vertices are adjacent to both the central vertex and the pendant vertices. This yields that $T\cong S_{n,m}$.

□

4. Construction of Graphs with a Small Number of Orbits

Here, we study graphs with a few orbits. A graph is vertex-transitive if and only if it has only one orbit. The structure of graphs with two orbits is more complicated, but the problem is completely solved for trees. In other words, if T is a tree with two orbits, then $T\cong S_n$ or $T\cong S_{n,n}$. For an arbitrary vertex-transitive graph G, the graph $G+K_1$ is a graph with exactly two orbits, but not all two-graphs can be constructed in this way; for example, see Figure 2. However, the orbit polynomial of a two-graph G is $O_G\left(x\right)=x^{|O_1|}+x^{|O_2|}$, where $|O_1|+|O_2|=n$ and $|O_i|$ divides $\left|\mathrm{Aut}\right(\mathit{G}\left)\right|$, where $i=1,2$.

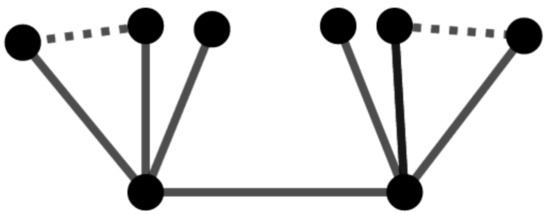
Figure 2. A caterpillar graph with four distinct orbits.

The characterization of graphs is an important topic in algebraic graph theory, and finding the orbit polynomial is a new method to analyze the structure of the graphs.

Definition 1.

A caterpillar graph is a graph obtained by a path graph $P_r$ in which $n_i(1\le i\le r)$ pendant edges are attached to the i-th vertex.

Suppose $n_1$ and $n_2$ are two distinct numbers. Then, the caterpillar graph G depicted in Figure 2 has four orbits of sizes $1,1,n_1$, and $n_2$.

Example 3.

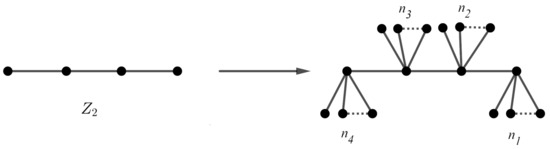
Similar to the above discussion, in Figure 3, we can construct a graph from $P_4$ with four singleton sets and four non-singleton orbits, where $n_1$, $n_2$, $n_3$, and $n_4$ are distinct natural numbers.

Figure 3. A graph with four non-singleton orbits constructed by the path graph $P_4$.

It is not difficult to prove that $\mathrm{Aut}\left(\mathit{G}\right)\cong {\mathbb{S}}_{{\mathit{n}}_{\mathit{1}}}\times {\mathbb{S}}_{{\mathit{n}}_{\mathit{2}}}$. Following this method, suppose $(n_1,n_2,\dots ,n_r)$ is a sequence of distinct arbitrary integers, where $n_i\ge 1(1\le i\le r)$. Then, the caterpillar graph $G=C(n_1,n_2,\dots ,n_r)$ has $2r$ orbits of sizes $\stackrel{rtimes}{\overbrace{1,\dots ,1}}$ and $n_1,n_2,\dots ,n_r$ in which $\mathrm{Aut}\left(\mathit{G}\right)\cong {\prod }_{\mathit{i}=\mathit{1}}^{\mathit{r}}{\mathbb{S}}_{{\mathit{n}}_{\mathit{i}}}$. If some of the $n_i$’s are the same, then the structure of $Aut\left(G\right)$ is more complicated. The caterpillar graph G in Figure 4 has $n-r$ singleton orbits, and the other orbits are of sizes $n_1,n_2,\dots ,n_r$, while the underlying graph is the path graph $P_n$ with automorphism group ${\mathbb{Z}}_2$. Following this method, suppose G is a graph with an identity automorphism group. Add $n_i$ pendant edges to each vertex of G. The automorphism group of the resulting graph is isomorphic to group ${\mathbb{S}}_{n_1}\times \dots \times {\mathbb{S}}_{n_r}$, where $\left|V\right(G\left)\right|=r$.

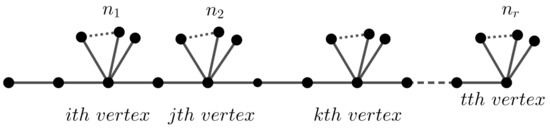
Figure 4. A caterpillar graph with n singleton and r non-singleton orbits.

Example 4.

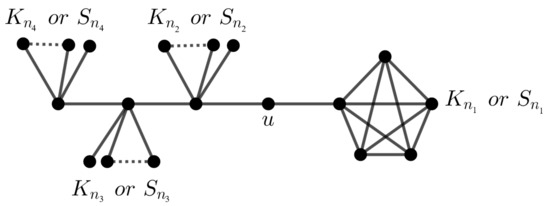
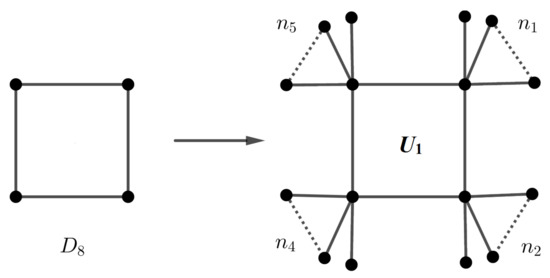
Consider a graph G as depicted in Figure 5. Attach $n_i(1\le i\le 4)$ pendent vertices to each leaf of G; see Figure 6. The orbit sizes of the new graph $G^{\prime }$ are $|O_1|=n_1,$$|O_2|=n_2,\left|O_3\right|=n_3$, $|O_4|=n_4$, and $|O_5|=\dots =|O_{\left|V\right(G\left)\right|-4}|=1$. Consider the graph H in Figure 7. The orbit size sequence of H is $(1,1,1,1,1,n_1,n_2,n_3,n_4)$. If we remove the vertex u from H and join its neighbors by an edge, then the resulting graph has four non-singleton orbits of sizes $n_1-1,n_2,n_3$, and $n_4$. In general, choose a graph of order r with the identity symmetric group, and each vertex coincides to either $S_{{\mathit{n}}_{\mathit{i}}}$ or $K_{n_i+1}$$(1\le i\le rand{n}_i\ne n_j)$. Then, the resulting graph has $2r$ orbits of sizes $(\stackrel{rtimes}{\overbrace{1,\dots ,1}},n_1,n_2,\dots ,n_r)$. Moreover, the automorphism group of the resulting graph is isomorphic to ${\mathbb{S}}_{n_1-1}\times {\mathbb{S}}_{n_2-1}\times \dots \times {\mathbb{S}}_{n_r-1}$. For example, the cycle graph $C_4$ in Figure 8 is vertex-transitive with dihedral automorphism group $D_8$. Attach $n_1,n_2,n_3$, and $n_4$ (all of them are distinct) pendent edges to each vertex. Then, the graph $U_1$ has four non-singleton orbits and four singleton orbits. Hence, the orbit polynomial is $4x+x^{n_1}+x^{n_2}+x^{n_3}+x^{n_4}$. Two graphs $U_1$ and $U_2$ in Figure 8 and Figure 9 have the same orbit polynomial.

Figure 5. A graph with the identity automorphism group.

Figure 6. The graph $G^{\prime }$ in Example 4.

Figure 7. The graph H with $2r$ orbits.

Figure 8. The graph $H^{\prime }$ in Example 4.

Figure 9. A graph with the same orbit polynomial with the graph $G^{\prime }$ in Figure 8.

Theorem 2.

[9] Let the graph G be decomposed to the subgraphs $G_1,\dots ,G_r$, where $G_i$ and $G_j$ are vertex-disjoint of different sizes, then:

$$\mathrm{Aut}\left(\mathit{G}\right)\cong \mathrm{Aut}\left({\mathit{G}}_{\mathit{1}}\right)\times \dots \times \mathrm{Aut}\left({\mathit{G}}_{\mathit{r}}\right)$$

and each orbit $O_i$ of $G_i$ is an orbit of G. In addition, $O_G\left(x\right)={\sum }_{i=1}^r{O}_{G_i}\left(x\right)+\left|V\left(G\right)\right|x$.

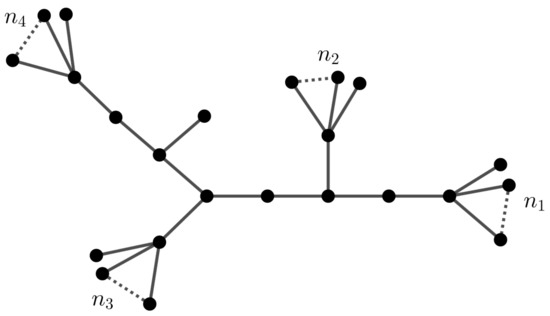
Example 5.

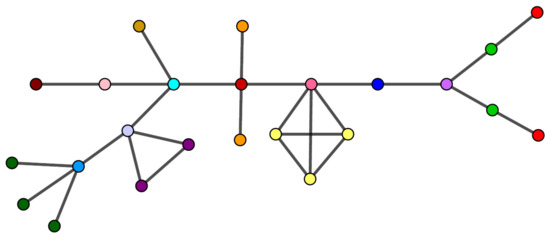
Consider the graph G in Figure 10. The vertices in the same orbit are colored the same. $O_G\left(x\right)=10x+4x^2+2x^3$

Figure 10. The graph G in Example 5.

Construction of Graphs with Few Vertex-Orbits

Theorem 3.

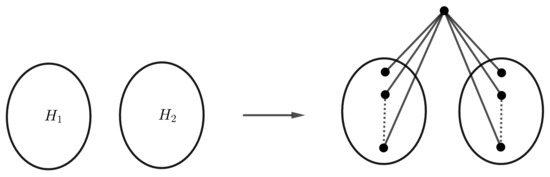
If G is the union of two vertex-transitive graphs $H_1$ and $H_2$ of orders respectively $m,n$$(m\ne n)$, then $K_1+(H_1\cup H_2)$ (as depicted in Figure 11) is a graph with three orbits of sizes $1,m,n$.

Figure 11. The graph $K_1+(H_1\cup H_2)$.

Proof. 

By Corollary 14.6 of [17], $\mathrm{Aut}\left({\mathit{K}}_{\mathit{1}}+\mathit{G}\right)\cong \mathrm{Aut}\left(\mathit{G}\right)$. This completes the proof. □

Theorem 4.

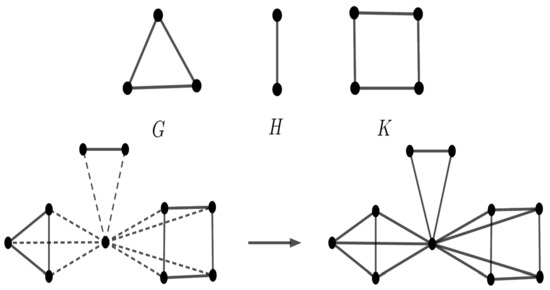
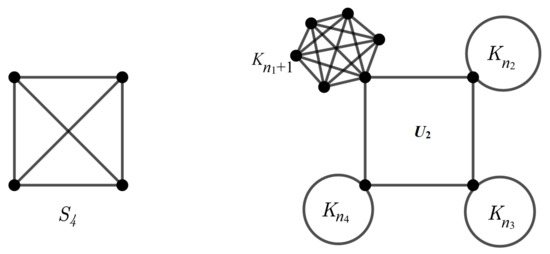
Suppose $G,H$ and K are three vertex-transitive graphs of orders $n_1,n_2$, and $n_3$, respectively, (distinct); see Figure 12. Then, the graph $\mathcal{L}=K_1+(G\cup H\cup K)$ has four orbits of sizes $1,n_1,n_2$, and $n_3$. In general, $K_m+(H\cup G\cup K)$, where $m\notin \{n_1,n_2,n_3\}$ has four orbits of sizes $m,n_1,n_2$, and $n_3$.

Figure 12. $G,H$, and K are three vertex-transitive graphs of orders $n_1,n_2$, and $n_3$, respectively.

Proof. 

The proof is similar to that of Theorem 3. □

Corollary 1.

We yield that:

$$O_{\mathcal{L}}\left(x\right)=x+O_G\left(x\right)+O_H\left(x\right)+O_K\left(x\right).$$

Example 6.

Consider the graph G as depicted in Figure 10. The vertices in the same orbit have the same color.

Theorem 5.

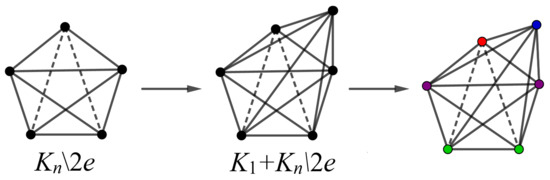
Let $K_{2n}$ be a complete graph on $2n$ vertices. Put $n_1$ pendent edge into $n-k$$(k\in \mathbb{N})$ vertices of $K_{2n}$ and $n_2$ pendent edges on the other vertices ($n+k$ vertices); see Figure 13. Then, the resulting graph has four orbits of sizes $n-k$, $n+k$, $(n-k)n_1$, $(n+k)n_2$.

Figure 13. The graph $K_1+K_n\setminus 2e$, for $n=5$.

Proof. 

All $n_i$ pendant vertices attached to vertex $v_i(1\le i\le n)$ are in the same orbit. By Theorem 2, the proof is complete. □

Example 7.

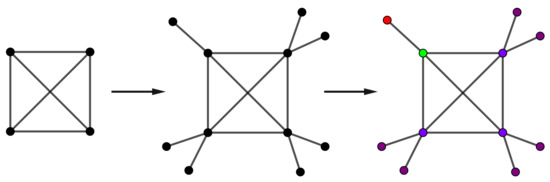
Consider the complete graph $K_4$ and the new graph H in Figure 14 by attaching pendant edges to graph $K_4$. Then, by Theorem 2, we obtain $O_H\left(x\right)=5x+3x^2$.

Figure 14. The orbit polynomial of graph H is $O_H\left(x\right)=5x+3x^2$.

Example 8.

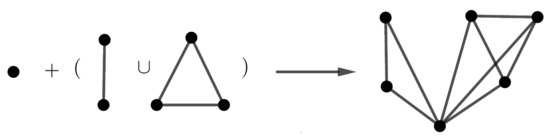
The orbit polynomial of graph $K_1+(K_2\cup K_3)$, depicted in Figure 15, is $x+x^2+x^3$.

Figure 15. The graph $K_1+(K_2\cup K_3)$.

Theorem 6.

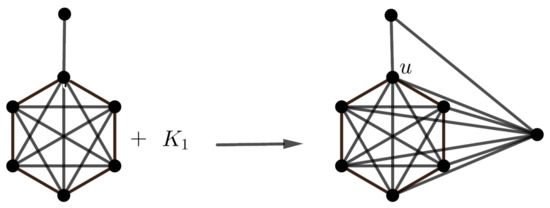
If $G=K_{n-1}+e$, then $K_1+G$ (as depicted in Figure 16) has three orbits of sizes $1,1,n-1$.

Figure 16. The graph $(K_6+e)+K_1$.

Proof. 

It is not difficult to show that $\mathrm{Aut}\left({\mathit{K}}_{\mathit{1}}+\mathit{G}\right)\cong \mathrm{Aut}\left(\mathit{G}\right)$. If $G=K_{n-1}+e$, then $\mathrm{Aut}\left(\mathit{G}\right)\cong {\mathbb{S}}_{\mathit{n}-\mathit{1}}$. This completes the proof. □

Corollary 2.

If $G=(K_{n-1}+e)+K_1$, then $O_G\left(x\right)=2x+x^{n-1}$.

5. Application in Real-World Networks

Many complex systems can be modeled as networks consisting of components and relations between them. We need information about large real-world networks to study the structural properties and dynamical complexity of networks; see [23]. Furthermore, graph complexity and network complexity have applications in the wider field of spatial complexity. Spatial complexity is the main problem of the exploration of the world’s large-scale structure and of the “cosmic web” of spiderweb-like conglomerates of galaxies that develop in it; see [24]. The fact that the vertex set of a network can be partitioned into orbits is very important since similar vertices will have the same properties, and thus, the network structure can be regarded as a quotient graph in which the vertices are orbits. Hence, for computing most of the graph invariants such as the entropy, the distance between vertices, the PageRank vector, etc., we should calculate these values for each orbit instead of a vertex.

In this section, we study the symmetry structure of well-known real-world networks in terms of orbit polynomials. To do this, first, we determined the structure of the automorphism group of some real-world complex networks. Consider the graph $\mathcal{G}$ as depicted in Figure 17. In [9], the authors showed that $O_{\mathcal{G}}\left(x\right)=12x+5x^2+x^3+2x^4$ and $O_{\mathcal{G}}^{\star }\left(x\right)=1-[11x+6x^2+x^3+2x^4]$. Furthermore, they showed that $\delta \left(O_{\mathcal{G}}^{\star }\right)=0.46$.

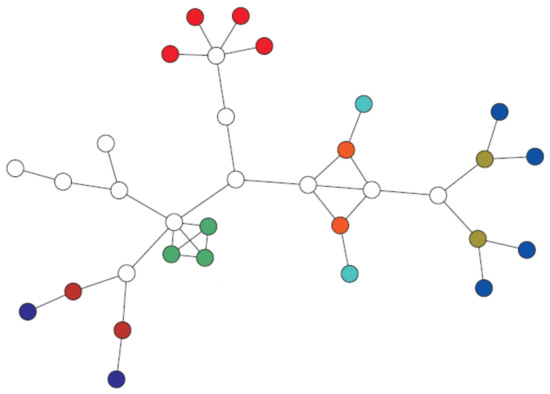
Figure 17. Vertices with the same color are in the same orbit, and singleton orbits are shown in white color.

The karate graph $\mathcal{K}$ [25] has 34 vertices and 78 edges; see Figure 18. It is not dfficult to see that the automorphism group of this graph is:

$$\mathrm{Aut}\left(\mathcal{K}\right)\cong {\mathbb{S}}_{|{\mathit{X}}_{\mathit{1}}|}\times {\mathbb{S}}_{|{\mathit{X}}_{\mathit{2}}|}\times {\mathbb{S}}_{\mathit{2}},$$

where $X_1=\{1,2,3,4,5\}$, $X_2=\{6,7\}$, and ${\mathbb{S}}_2=⟨(8,10)(9,11)⟩$. Hence, the order of its automorphism group is $\left|\mathrm{Aut}\right(\mathcal{K}\left)\right|=$ 480. The orbit and the modified orbit polynomials are as follows:

$$O_{\mathcal{K}}\left(x\right)=23x+2x^2+x^{5}and{O}_{\mathcal{K}}^{\star }\left(x\right)=1-23x-2x^2-x^5.$$

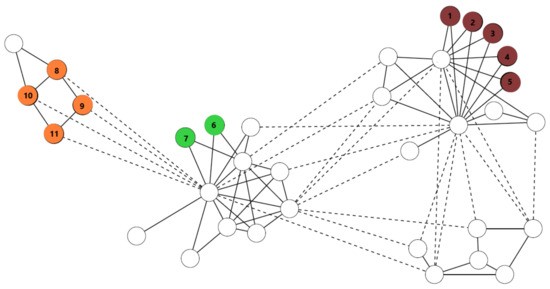
Figure 18. Zachary’s karate graph $\mathcal{K}$.

By the R program [26], we explored that $\delta =0.043$.

The automorphism group of the dolphins network [27] is isomorphic with the abelian group ${\mathbb{S}}_2\times {\mathbb{S}}_2$ of order four, and the regarded polynomials are $O_{\mathcal{D}}\left(x\right)=30x+2x^2$ and $O_{\mathcal{D}}^{\star }\left(x\right)=1-2x^2-30x^2$. This yields that $\delta =0.017$.

Another graph is word adjacency; see [28]. The automorphism group of this graph is ${\mathbb{S}}_2$ with orbit polynomial $O_{\mathcal{W}}\left(x\right)=60x+x^2$ and modified orbit polynomial $O_{\mathcal{W}}^{\star }\left(x\right)=1-x^2-60x$, and thus, $\delta =0.009$. Finally, consider the American football games network; see [27]. The automorphism group of this graph is ${\mathbb{S}}_1$, which implies that $O_{\mathcal{F}}\left(x\right)=115x$ and $O_{\mathcal{F}}^{\star }\left(x\right)=1-115x$, which yield that $\delta =0.008$. In Table 1, some results including the sizes of the networks, the orders of the automorphism groups, and the positive roots of the modified orbit polynomials [22] are summarized. In this table, the symbol $\delta$ denotes the unique positive root of the modified orbit polynomial.

Table 1. Unique positive roots of modified orbit polynomials of some real-world networks.

Networks	$(\mathit{V},\mathit{E})$	$\left|\mathbf{Aut}\right(\mathit{G}\left)\right|$	$\mathit{\delta }$
Graph $\mathcal{G}$	(33,37)	4608	0.46
Karate Club	(34,78)	480	0.043
Dolphins	(62,159)	4	0.017
Word Adjacency	(112,425)	2	0.009
Football Game	(115,613)	1	0.008

Actually, the order of the maximal orbit in the graphs $\mathcal{G}$, $\mathcal{K}$, $\mathcal{D}$, and $\mathcal{F}$, is 4, 5, 2, 2, 1, respectively. We say a measure is degenerate if it fails to distinguish between two graphs that are not isomorphic [29,30]. Our results showed that, as the value of the unique positive roots in Table 1 decreased, the order of the automorphism groups also decreased, but this is not true in general. Continuing, a set of well-known real-world networks with distinct topologies were collected, and analyzing the reported data showed that the symmetry measure $\delta$ was not highly correlated with the size of the automorphism group; see Table 1. Furthermore, in [2,31], it was shown that $\delta$ was a degenerate measure for sorting distinct graphs with the same vertex-orbits. Finally, in [2], six classes of trees of orders 15–19 were chosen, and the results indicated a weak correlation between $\delta$ and S.

6. Summary and Conclusions

In this paper, we investigated the orbit polynomial for several graph/network classes. Then, we analyzed the value of the unique zeros of the modified version of these polynomials. Moreover, we established many properties of both orbit polynomials. We proved that some classes of trees can be characterized by their orbit polynomials. We also determined the structures of the automorphism group of some real-world networks in terms of local symmetry elements. Applying the automorphism group method enabled us to analyze networks by capturing information about the number of interconnections of components.

It is clear that if a graph G on n vertices is asymmetric, then $O_G^{\star }=1-nx$, and thus, $\delta =\frac{1}{n}$. On the other hand, for vertex-transitive graphs with the same number of vertices, we obtained $O_G^{\star }=1-x^n$, which implies that $\delta =1$. This yielded that for a graph G with n vertices, the unique positive root lied in the interval $[\frac{1}{n},1]$. As $\delta$ increased to one, the graph G would be more symmetric; see [32]. Furthermore, $\delta$ tended to zero if n were sufficiently large. In addition, if $\mathcal{G}$ and $\mathcal{H}$ were two asymmetric random networks of order n, then $\delta \left(\mathcal{G}\right)=\delta \left(\mathcal{H}\right)=\frac{1}{n}$. This yielded that for two equally sized graphs with the same automorphism group, the positive root of the modified orbit polynomial may not capture meaningful structural information.