Abstract
Online environments have evolved from the early-stage technical systems to social platforms with social communication mechanisms resembling the interactions which can be found in the real world. Online marketers are using the close relations between the users of social networks to more easily propagate the marketing contents in their advertising campaigns. Such viral marketing campaigns have proven to provide better results than traditional online marketing, hence the increasing research interest in the topic. While the majority of the up-to-date research focuses on maximizing the global coverage and influence in the complete network, some studies have been conducted in the area of budget-constrained conditions as well as in the area of targeting particular groups of nodes. In this paper, a novel approach to targeting multi-attribute nodes in complex networks is presented, in which an MCDA method with various preference weights for all criteria is used to select the initial seeds to best reach the targeted nodes in the network. The proposed approach shows some symmetric characteristics—while the global coverage in the network is decreased, the coverage amongst the targeted nodes grows.
1. Introduction
The analysis of social networks has evolved from early-stage sociograms based on small graphs into mainstream multi-billion node social networks with high business potential [1]. Social platforms let their users easily connect to their friends or acquaintances and easily maintain relationships. These close relations between social network users have been widely used by online marketers to improve the engagement of potential consumers to benefit from their services and products [2]. Viral marketing campaigns in social networks have proven to bring better effects in engaging potential consumers than traditional online advertising [3].
This performance of viral marketing resulted in increased research on information propagation in complex networks. While the majority of the research focuses exclusively on increasing the network coverage with information, as the only factor and performance measure, some works aim their attention at a targeted approach [4,5], also with a focus on user preferences [6]. From a different perspective, other approaches avoid repeated messages due to lowered performance causing a habituation effect [7], information overload [8] or the need for delays between messages for multi-product campaigns [9]. Efforts towards targeting specific users have mainly been focused on single attributes or network metrics for the seed selection [10]. The real-life applications of social networks in viral marketing campaigns are often based on selecting multiple attributes such as age, gender and localization of the target group [11].
To better address the aforementioned needs, the authors’ main contribution in this paper is to provide an approach in which multi-attribute targeted groups of users can be reached in social networks by providing the initial seeding information to a limited number of selected network users. In the proposed approach, contrary to other studies, the selection of the seeded nodes of the social network is based on multiple, often conflicting, criteria and nodes’ attributes. Moreover, by virtue of the MCDA (Multi-Criteria Decision Analysis) foundations of the proposed approach, the importance of each criterion considered in the selection process can be adjusted to meet the marketer’s needs. MCDA tools, such as sensitivity analysis [12], also allow us to further study and understand the effect each seeded nodes’ attribute has on the planned viral marketing campaign’s capacity to reach the targeted group of the network nodes [13]. Some symmetric characteristics of the proposed approach are assumed—whilst the global coverage in the network can decrease, the proposed approach strives to maximize coverage amongst the targeted nodes.
2. Literature Review
The early stage research in the area of information spreading assumed that all nodes within the network have the same interest in the product or the propagated content. The network coverage was the main assumed factor and performance measure for influence maximisation problem identified firstly in [14]. From this point of view, the most central nodes, having a high influence on others, had the highest potential to be selected as seeds. Most of the seed selection methods focused on node network characteristics and heuristics improving the performance [15]. Usually, only the whole network structures are taken into account for seed selection.
While real campaigns take into account various node characteristics, the problem was emphasized by [5] and a targeted approach to viral marketing was proposed. It was based on assigning nodes to a potential market and searching for a local centrality score during the seeding process. For each user, the average importance factor was calculated to determine the impact on target group. Another study focused on targeting with the use of costs assigned to users within the network, together with the benefits related to the user interests [4]. It extends the typical approaches focused on assumption that users are acquired at the same costs with same benefits for marketers. As a result, the authors proposed a cost-aware targeted viral marketing with an effective computational approach, making the seeds selection within billion-scale networks possible. From the perspective of practical applications the authors took into account the number of posts under specific topics are a representation of user interest and potential benefits. While the earlier methods focused on influence maximisation based solely on centralities and influence, the study in [16] distinguished two classes of methods, taking into account more complex structural relations like overlap, and other group focused on user features and social information. They use, among others, trust between the users and cost. The study emphasises the lack of methods taking into account the user interest. The approach is based on the interest in the message. The experimental study was based on randomly assigned interest vectors within well-known datasets, without nodes’ attributes. An integrated marketing approach was proposed in [6] for combining targeted marketing with viral marketing. The approach took into account users with revealed preferences and users with potentially high utility scores for the marketer. One of the goals was the maximization of information awareness and constraints focused on reaching the targeted users. The study [17] explored Cost-aware Targeted Viral Marketing model, with focus on the cost of the nodes’ acquisition and potential benefits. Integer programming was used with the potential to search for close to exact solutions within large scale networks. From other perspective, the authors of [18] introduced a Targeted Influence Maximization problem, using an objective function and penalization parameter for adoption of non-target nodes. The proposed approaches focused on general target groups characterized by benefits or knowledge acquired from user posts.
While targeting can be based on various performance evaluation criteria and campaign goals it creates space for applications or multi-criteria decision support methods. In the recent years some preliminary research has began in the area of utilising multi-criteria decision analysis (MCDA) techniques in the social network studies. Zareie et al. [19] used the TOPSIS method (Technique for Order Preference by Similarity to Ideal Solution) to reduce overlap and maximize coverage while influencing social networks. Yang et al. [20] used TOPSIS in the Susceptible-Infected-Recovered (SIR) model to dynamically identify influential nodes in complex networks, and in [21] used entropy weighting for setting the weights values. Liu et al. [22] used TOPSIS to evaluate the importance of nodes in Shanxi water network and Beijing subway networks by comparing each node’s close degree to an ideal object. Robles et al. [23] used multiobjective optimization algorithms to maximize the revenue of viral marketing campaigns while reducing the costs. Wang et al. [24] proposed a Similarity Matching-based weighted reverse influence sampling for influence maximization in geo-social location-aware networks. Gandhi and Muruganantham [25,26] used TOPSIS to provide a framework for Social Media Analytics for finding influencers in selected networks. Montazerolghaem [27] used separately AHP and TOPSIS to provide rankings of effective factors in network marketing success in Iran. In their prior research, Karczmarczyk et al. [28] used the PROMETHEE II method (Preference Ranking Organization METHod for Enrichment of Evaluations) for evaluation of performance of viral marketing campaigns in social networks, as well as for decision support in the planning of such campaigns.
The up-to-date literature studies show a multitude of available MCDA methods [29]. Some examples of known and widely used MCDA methods include AHP, TOPSIS [30,31], or methods from the ELECTRE and PROMETHEE families [32]. The methods can be divided into three groups, based on the used approach. The first group, also known as the American school of MCDA methods, use the axiom of full variants comparability and two basic relations are available—indifference and preference of variants. The resulting model is aggregated into a single criterion [33]. The methods from the second group, also known as the European school of MCDA methods, are based on the axiom of partial comparability of variants. The aggregation takes place using the outranking relation. The third group consists of methods based on the foundations from both the aforementioned groups. The current taxonomy of the available MCDA methods can be found, for example, in [29,32,34].
The analysis of the existing works shows that among the large number of studies related to the information propagation and influence maximization, only a small fraction is focused on the very common real-life problem of targeting users with specific characteristics. The discussed approaches focused on single attributes and node characteristics for the seed selection to reach the assumed audiences or communities. Nonetheless, the social media skyrocketing is usually based on selection of parameters of the target group with various values of the attributes such as age, gender or localization, with different importance from the perspective of the campaign performance. This forms an interesting research gap, which is addressed in this paper with the proposed new approach. The approach is based on the assumption that, in order to maximize reaching a multi-attribute target group in the network, the seed selection process is also based on a multi-criteria evaluation of nodes. The seed selection process is supported with MCDA methods, allowing us to assign weights to individual attributes of the network nodes and produce rankings of seeds with the potential to increase the coverage in the addressed multi-attribute target group.
3. Methodology
In this section, the methodological framework of the approach proposed in this paper is presented. In Section 3.1, the assumptions regarding the multi-attribute nature of the targeted nodes are presented. Subsequently, in Section 3.2, the problem of multi-criteria seed selection for targeting heterogeneous multi-attribute nodes is explained. Then, in Section 3.3, the MCDA foundations of the proposed approach are presented and the selection of the TOPSIS method is justified. Finally, in Section 3.4 the TOPSIS foundations and its adaptation for seed selection for targeting multi-attribute nodes are presented. The conceptual framework of the proposed approach is also visually presented on Figure 1.
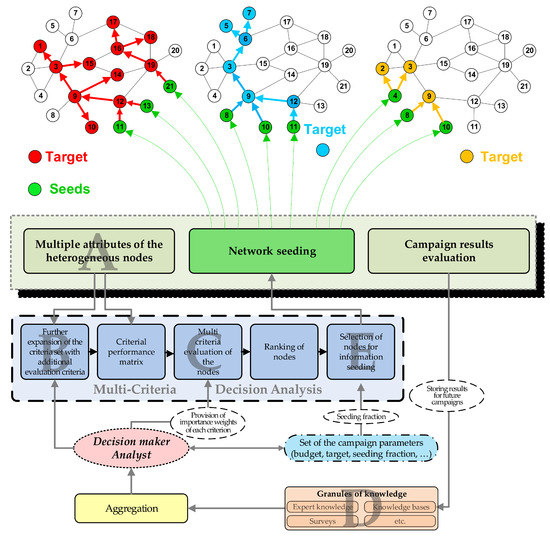
Figure 1.
Conceptual framework of the proposed approach. Marks A–E provide anchors to be referred in the main text of the paper.
3.1. Multi-Attribute Nature of the Targeted Nodes
The proposed methodology complements the widely-used Independent Cascade (IC) model [14] for modeling the spread within the complex networks by taking into account the problem of reaching targeted multi-attribute nodes in social networks by the information propagation processes. In the proposed approach, it is assumed that the network nodes are characterized not only by the centrality relations between them and other nodes [35,36,37], but also by a set of custom attributes (see Figure 1A).
The values of these attributes for individual vertices can be expressed as precise numerical values, such as age [years] or income [dollars]. Alternatively, if the attributes represent qualitative properties of the nodes, their values can be converted to numeric values with the use of 5-point Likert scale [38,39] (1—strongly disagree, 5—strongly agree) or enumerations (e.g., age: 1—young, 2—midle-aged, 3—old; or sex: 1—male, 2—female).
The nodes can also be characterized by the computed attributes derived from the network characteristics and measures. These include the centrality measures such as degree [35], closeness [40], betweenness [41] or eigenvector [36,37]. Additional attributes can also be derived as a composite of the two aforementioned types of attributes, by computing centrality measures based on limited subsets of the nodes’ neighbors (see Figure 1B). For example, if attribute represented the degree of a node, that is, the total count of its neighbors, the could represent the count of its male neighbors, and the count of its female neighbors.
The aim of the proposed methodological framework is to reach the targeted network nodes with multi-attribute characteristics, based on the multi-criteria process of selecting nodes for seeding in the process of information propagation.
3.2. Multi-Attribute Seed Selection
As was described in Section 3.1, in the proposed approach an attempt is made to reach the nodes with specific values of the selected attributes. For example, in preventive oncological social campaigns, an attempt is made to reach middle-aged women, that is, aged between 50 and 69.
In the independent cascade model [14], the information propagation process in a complex network is preceded by the selection of seeds. That means choosing a subset of network vertices, to which the information is provided at the beginning of the process, in order for them to pass the information further through the network. Normally, the seeds represent a given fraction of all network nodes. For example, the seeding fraction can be set to 5% of the network. There are numerous approaches to selecting the initial seeds, which generally result in producing a ranking of all network nodes and seeding information to the ones on top of the list.
Whilst other approaches focus on generating the ranking based on a single centrality measure, such as degree [35] or eigencentrality [36], in the authors’ proposed approach, multiple attributes are considered in order to select the seeds with the highest potential to eventually propagate the information to the targeted nodes.
It is important to note, that in the proposed approach, the final coverage of the network, i.e., the fraction of nodes to which the information was eventually delivered, can be lower than in case of the traditional centrality-based approaches. However, the proposed method increases the chances to maximize the coverage within the targeted nodes’ groups.
3.3. MCDA Foundations of the Proposed Approach and the Research Method Justification
The approach presented in this paper is based on the MCDA methodology foundations [42]. The adaptation of the MCDA methodology for the needs of seed selection resulted directly from the formal and practical assumptions of the research. First, the assumed modeling goal was an attempt to reach only the targeted set of multi-attribute nodes. Therefore, any attempt to obtain the optimal solution in a global sense (such as maximization of the global coverage) was disregarded in this research. Second, the fulfillment of the goals adopted in this research requires considering a number of attributes in the process of seed selection. Third, it was established that a compromise maximizing matching the required goals would be searched for, at the expense of the global network coverage.
The aforementioned premises of the multi-criteria modeling environment and goals, as well as the analysis of the formal components of the MCDA model at the stage of the model structuring and preference modeling, are the starting point for the selection of the appropriate MCDA method. It is worth noting that this is a significant problem, and an improper selection of the MCDA method can lead to incorrect results in the final decision model [29,32].
In this paper, the assumed effect of the construction and operation of the MCDA model is a ranking of variants [43]. The criterial performance of the variants will be expressed on a quantitative scale [44]. The expected result is a complete ranking of variants [45]. The deterministic simulation data environment present in this paper, shows the quantitative character of the input data. The research assumptions require that different weights of the individual criteria are taken into account, and their nature will also be quantitative. There is no need to use relative or absolute weighting criteria [46]. In the modeling process, it was also assumed that due to the deterministic nature of the simulation model being developed, there is no natural uncertainty of the preferential information. In practice, this implies the use of the methods from the “American school” [45]. Based on [29,44], as well as the MCDA methods’ set discussed in [32], using the expert system provided in [47], it is easy to show that aforementioned requirements are fully met only by the following set of MCDA methods: MAUT (Multi-Attribute Utility Theory), MAVT (Multi-Attribute Value Theory), SAW (Simple Additive Weighing), SMART (Simple Multi-Attribute Ranking Technique), TOPSIS (Technique for Order Preference by Similarity to an Ideal Solution), UTA (Utilites Additives), VIKOR (VIsekriterijumska optimizacija i KOmpromisno Resenje).
On the foundations of the aforementioned analysis, as well as based on the [32] formal recommendations, two groups of MCDA methods can be indicated as valid for solving the problem stated in this paper. The first one is based on an additive/multiplicative form of a utility/value function (MAUT, MAVT, SAW, SMART, UTA), and the second one is based on reference points (TOPSIS, VIKOR).
The former group of methods is founded on a very trivial mathematical principles—a simple aggregation of data and partial utilities. In practice, this results in transferring into the final models an undesirable effect of linear substitution of criteria. Consequently, this directly implies the possibility of obtaining incorrect rankings (failure to meet the level of individual criteria to a satisfactory degree).
Among the latter group, there is a significant level of similarity between both the TOPSIS and VIKOR methods. They both are based on the same assumptions and differ only in the chosen technique of normalization and aggregation of data. The TOPSIS method assumes minimizing the distance to the ideal solution and maximizing the distance to the anti-ideal solution, whereas in VIKOR only the distance to the ideal solution is minimized.
The principles of the TOPSIS and VIKOR methods, along with the fact that TOPSIS uses vector normalization (compared to linear normalization in VIKOR), expedite the selection of the TOPSIS method as the one which has the best potential in the considered problem of seeds’ selection [48]. Consequently, it was the TOPSIS method that was chosen for the further stages of this research. Moreover, it is important to note that the chosen TOPSIS method does not require the attribute preferences to be independent [49,50,51]. This further strengthens the potential of using this method in the considered problem, in which, due to its preliminary character, we do not yet have full knowledge in the area of dependence or independence of the model attributes.
3.4. Multi-Criteria Seed Selection for Multi-Attribute Nodes Targeting
The Technique for Order Performance by Similarity to Ideal Solution (TOPSIS) is a widely-used MCDA method, originating from the American MCDA school. Originally formed by Hwang and Yoon [52], it is based on the concept that given a set of criteria and their possible values, a positive ideal solution (PIS), and negative ideal solution (NIS) can be indicated. These are a two hypothetical, non-existent, alternatives, whose all values for all criteria are either maximized (PIS) or minimized (NIS). When a set of alternatives are compared, in the TOPSIS method they are ranked based on their relative distance to the PIS and NIS. The best alternative should be as close as possible in terms of criteria values to the PIS, and as far as possible from NIS.
In the proposed approach, the TOPSIS method is used for multi-criteria evaluation of the nodes (see Figure 1C). First of all, the criteria for evaluation of the potential seeding nodes need to be chosen. Then, a decision matrix is built based on the criteria values of all vertices in the studied network, in which the m rows represent the vertices and n columns represent the criteria (see Equation (1)):
In the second step of the algorithm, the decision matrix is normalized. Different formulae are used for the benefit criteria (2) and different for the cost criteria (3):
The MCDA-based approaches extend the traditional aggregating approaches by the fact that the weights of individual decision attributes can be adjusted to varying values. The analyst adjusts the weights of each decision criterion to the preferences of the decision maker. In the case of the considered problem of seed selection, the marketer adjusts the weights of individual criteria to increase as much as possible the potential to reach to the targeted network nodes through the seeded network nodes. The weights are chosen based on the analyst’s knowledge, skills and experience (see Figure 1D). Therefore, in the third step of the TOPSIS algorithm used in the authors’ proposed approach, the weights are imposed on the decision matrix and, consequently, a weighted normalized decision matrix is constructed:
In the fourth step of the algorithm, the positive and negative ideal solutions ( and respectively) are computed (Equations (5) and (6)). In the case of the studied seed selection problem, the positive ideal solution would represent a vertex, which for all criteria has the best possible values, whereas the negative ideal solution would be a vertex with the worst possible values for each criterion.
In the penultimate, fifth, step of the TOPSIS method, the Euclidean distances between each network vertex and the positive and negative ideal solutions are computed:
Eventually, the relative closeness of each vertex to the ideal solution is computed:
The obtained scores are then used to rank the vertices and build the final ranking, which then can be used for selecting the vertices for the initial network seeding (see Figure 1E).
All in all, the MCDA foundations of the proposed approach facilitate obtaining network nodes’ rankings with the highest, according to the analyst, potential to reach the targeted nodes in the social network. Moreover, the use of MCDA allows us to study the stability of the obtained ranking with sensitivity analyses. This, in turn, allows us to study the effect of each individual criterion on the final ranking and, therefore, allows us to iteratively improve the obtained solution.
4. Empirical Study
4.1. Real-Life Usage Example
In this section, a brief real-life usage example of the proposed approach will be presented, explaining every step of the proposed framework on a small real network. In further sections, a more in-depth analysis is performed on a larger synthetic network.
The empirical example in this section will be performed on a real network. Enron emails network [53] was selected due to its limited size (143 nodes and 623 edges), which allows us to study in detail the status of every single node of the network. It is important to keep in mind that the proposed approach is intended for networks with nodes characterized by multiple attributes. Due to the fact that the publicly available network repositories principally provide only edge lists of networks, the attributes had to be overlaid on the network artificially. Therefore, artificial values for two attributes were generated for the network, based on [54]: gender (69 nodes male, and 74 nodes female), and age (0–29 years—62 nodes, 30–59 years—55 nodes, over 60 years—26 nodes).
For such a network, for illustrative purposes, two complete scenarios with two different targets will be presented. In both, a constant propagation probability (0.1) and seeding fraction (0.05, i.e., 7 vertices) is assumed.
4.1.1. Target 1: Male Aged 0–29
In this scenario, the aim of the viral marketing campaign is to reach men aged 0–29, that is, the targets are described by specific values of two criteria: gender (C2) and age (C5). The target group, therefore, consists of 28 nodes (see Figure 2). Apart from the two target-describing attributes, some other criteria are also available: degree (C1), degree male (C3), degree female (C4), degree aged 0–29 (C6), degree aged 30–59 (C7), degree aged 60+ (C8). The decision maker (DM)/analyst, based on their expertise, provide the preference weights for all criteria: C1: 8.20, C2: 25.40, C3: 12.60, C4: 3.80, C5: 28.40, C6: 14, C7: 3.80, C8: 3.80. These weights are provided by the DM as input data to the proposed approach, as the ones which, according to the DM, allow to rank the nodes in order to find the seeds potentially best for maximizing influence in the targeted group. In order to provide such weights, the analyst can refer to archival knowledge and use decision support systems or MCDA methods such as AHP [39].
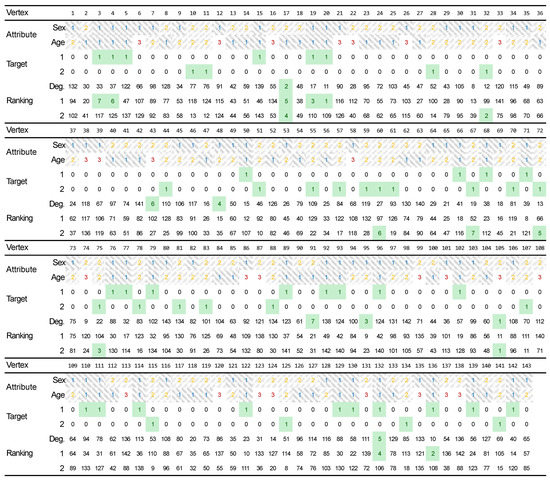
Figure 2.
Visual presentation of two real-life usage scenarios for targeting male aged 0–29 (target 1) or female aged 30–59 (target 2). The table contains: values of the sex and age attributes, information on targeted nodes for both scenarios, and the rankings of nodes for seeding.
Once the preference weights are known, the TOPSIS method is used to evaluate all vertices. The top seven (seeding fraction 0.05) are chosen as seeds and the campaign is started.
For this scenario, the simulations (see Figure A1 in Appendix A) have shown the campaign averagely reached 9/28 targeted nodes (32.14%), with global coverage 0.2224. A traditional degree-based approach for the same network results averagely in reaching 7.7/28 targeted nodes (27.5%), with global coverage 0.2881. The multi-criteria approach reached 4.64% more of the targeted nodes with global coverage lower by 0.0657.
4.1.2. Target 2: Female Aged 30–59
In this scenario, the aim of the viral marketing campaign is to reach women aged 30–59. The target group consists of 24 nodes (see Figure 2). Again, apart from the two target-describing attributes, some other criteria are also available: degree (C1), degree male (C3), degree female (C4), degree aged 0–29 (C6), degree aged 30–59 (C7), degree aged 60+ (C8). It is important to note that, contrary to other approaches [4], in the proposed approach the criteria values are reused and only the preference weights are adjusted. This time, the decision maker, based on their expertise, provide the following preference weights for the criteria: C1: 4.4, C2: 30.4, C3: 4, C4: 10.4, C5: 30.40, C6: 5.4, C7: 10.4, C8: 4.4.
Once the preference weights are known, the TOPSIS method is used to evaluate all vertices. The top seven (seeding fraction 0.05) are chosen as seeds, and the campaign is started.
For this scenario, the simulations (see Figure A2 in Appendix A) have shown the campaign on average reached 9.5/24 targeted nodes (39.58%), with global coverage 0.2552. A traditional degree-based approach for the same network results averagely in reaching 6.8/24 targeted nodes (28.33%), with global coverage 0.2881. The multi-criteria approach reached 11.25% more of the targeted nodes with global coverage lower by 0.0329.
4.1.3. Real-Life Example Discussion
In the real-life example, two complete scenarios with two different targets were presented. As expected, in both cases the proposed approach resulted in lowering the global coverage but increasing the influence in the targeted set of nodes. In both cases, it was the decision-maker (DM) who first determined the values for weights. This is a subjective assessment, based on the DM’s knowledge, skills and experience. In case the weights would have been estimated improperly, the ranking of the nodes would be ordered differently, and, therefore, different 7 nodes would be selected as seeds (see Section 3.4). This, in turn, could result in reaching fewer targeted nodes in the network (see Section 4.8). The actual participation of the decision-maker in the process of solving the task is very important in MCDA, and the actual performance of the obtained solution is dependent on both the quality of the attributes and the proper selection of the values of the vector of the relative importance of the decision model criteria. Attempting to obtain the maximum potential to reach through the seeded nodes to the targeted nodes requires searching for the most satisfying values of the vector of the relative importance of the decision model criteria.
4.2. Setup of the Comprehensive Experiment
The basic usage example presented above is followed by a set of three more in-depth analysis scenarios, performed on a larger synthetic network. In order to illustrate the proposed approach, the empirical study was performed on a Barabasi-Albert (BA) synthetic network [55]. The Barabasi-Albert network model was created as an outcome of a research of the structure of the WWW in the 90’s. Two complementary mechanisms drive the construction of BA networks: network growth and preferential attachment. In the BA synthetic networks, several selected nodes (hubs) have an unusually high degree compared to the other vertices in the network.
Over the recent years, there has been an abundance of research showing that a vast number of social networks, both virtual and real, are scale-free in their nature [55,56,57,58]. Their degree k follows a power law and exponent is typically . The sample network was generated with exponent with value in the middle of this range . Moreover, in order to allow clear visualisation of the network, the vertices count was set to 1000. The resulting network was characterized by the following the average values of its centrality metrics:
- Betweenness—1687.295;
- Degree—3.994;
- Closeness—0.0002310899;
- Eigen Centrality—0.03661858.
Since the proposed approach is intended for networks whose nodes are described with multiple attributes, the subsequent step was to assign a set of attributes to each of the vertices of the obtained network. The most of publicly available network datasets are based mainly on set of nodes and edges, without node attributes. To overcome this problem, we used node attributes following distributions from demographic data. It is similar to approach presented in [16]. The information on sex distribution from demographic data was overlaid on the network to obtain the first attribute [54]. This resulted in 470 network nodes marked as male and 530 marked as female. Subsequently, the age distribution information [54] was used to add to the network the second attribute, with three possible values:
- young, i.e., aged 0–49, of the population;
- mid-aged, i.e., aged 50–69, of the population;
- elderly, i.e., aged 70 and above, of the population.
Finally, the goal of the information spreading campaign was chosen for the empirical research. For illustrative purposes, it was decided that a real-life example of social campaign for a breast cancer prevention program (mammography) would be used [59]. This campaign targets women aged 50–69, which in the case of the network generated for this experiment translated to 130 out of the total of 1000 nodes of the network.
4.3. Criteria for Seed Selection
As was described in Section 3, in the proposed approach the initial seeds were selected from the network based on multiple criteria. In the case of the studied synthetic network, apart from the sex and age attributes, the general degree of each node was also taken into account, as well as the degree measurements based on each value of the two attributes. This resulted in a total of eight evaluation criteria, presented in Table 1.

Table 1.
Seed selection criteria.
The criterion C1 represents the number of neighbors of each evaluated vertex. Criterion C2 is based on the sex attribute and is equal to 0 if there is a match between the targeted and actual sex or 1 in the case of a mismatch. Criterion C3 represents the count of male neighbors of a vertex, whereas criterion C4 represents female neighbors of a vertex. In turn, criterion C5 indicates the difference between the targeted and actual age group of a vertex. For example, if the targeted age group was young, vertices from age groups young, mid-aged and elderly would obtain the values of 0, 1 and 2 respectively. Since the targeted group in this experiment is in the middle, that is, mid-aged, vertices from this group would obtain value 0 and from other groups would obtain value 1 for criterion C5. Last, but not least, criteria C6, C7 and C8 represent the count of respectively young, mid-aged and elderly neighbors of a vertex. All criteria C1–C8 were then assembled to create a single decision matrix for the TOPSIS method. At this stage, it is important to note that during the research the authors decided to follow the degree-based criteria, as the degree is the most basic measure which can be used for benchmarking of the approach. If other measure, such as closeness, betweenness, eigencentrality, and so forth, was used as criterion C1, also the remaining criteria C3, C4, C6, C7, C8 would need to be modified to use the selected metric.
The last step required for the seed-selection setup was specifying the preference direction of all evaluation criteria C1–C8. Because criteria C2 and C5 represent difference between the targeted and actual values, the lowest possible values were preferred. On the other hand, since the remaining criteria are based on the degree network centrality measure, the preference direction for these criteria was maximum.
After the experiment was set up, three scenarios based on various weights of individual criteria were studied. Their description and results are presented in the following sections.
4.4. Scenario 1: Single Criterion
The first scenario studied was intended to be similar to the approaches that are based solely on a single centrality measure, here—the degree. Therefore, the preference weights for the TOPSIS ranking-generation method were set to a significant value of 100 for C1, and a negligible value of 1 for all other criteria. All vertices were evaluated and ordered by rank. It was decided, that in the simulations the seeding fraction of 0.05 and propagation of 0.3 will be used. Therefore, the 50 vertices with the highest CCi scores were selected as seeds (see Table 2).

Table 2.
Seeds selected for Scenario 1, ordered by their rank and CCi score obtained in the applied TOPSIS method.
The analysis of Table 2 allows us to observe that the best vertex, labelled 3 obtained significantly more score than any other vertex (0.9975 compared to 0.6800 and 0.6000 for vertices 4 and 2 ranked 2 and 3, respectively). It is also noticeable that the score of the best vertex 3 was over two-fold higher than the score of vertices 24 and 1 ranked 6/7, with an equal score of 0.4400. These scores can be confirmed, when the degree measure of each of the nodes is verified. The degree of the leading vertex 3 is equal to 52, followed by 36, 32, 29, 28 for vertices 4, 2, 12, 5 respectively and 24 for vertices 1 and 24. Last, but not least, it can be observed that because the degree was used as the main criteria for the selection of seeds, multiple of the selected nodes are scored equally, for example all nodes ranked 40–45 are scored 0.1800 and all nodes ranked 46–50 are scored 0.1600.
After the seeds were selected, the campaign was simulated over the same network, with the same seeds for 10 consecutive times. In order to allow repeatability of the simulation conditions, a set of 10 pre-drawn weights for each connection (edge) in the network was used. The outcomes of each simulation were stored and presented in the form of a visual graph (see Figure A3 in Appendix A). On average, the simulation took 8.6 iterations and resulted in 433.6 nodes being infected (0.4336 coverage). However, only 50.5 nodes of the 130 targeted nodes were infected (0.3885 target coverage).
4.5. Scenario 2: Two Criteria
In the second scenario, the preference weight of the degree measure was reduced in favor of the more accurate female degree (C4) and mid-aged degree (C7). Therefore the weights of C4 and C7 were set to 100 while the weights of the rest of the criteria was set to 1. All vertices were evaluated again, under the new conditions and their ranking was built. The correlation coefficient between the rankings for both scenarios is equal to 0.9022 for the scores and 0.7510 for the ranks of the vertices. The results of the top 50 vertices, selected as seeds, are presented in Table 3.

Table 3.
Seeds selected for Scenario 2, ordered by their rank and CCi score obtained in the applied TOPSIS method.
When Table 3 is analyzed, it is clearly visible that the scores obtained by the best vertices are much more diversified than in case of the first scenario. The three leading vertices are still the ones labelled 3, 4 and 2; however, the order of the subsequent two has changed. The vertex 5 is now ranked 4 with the score of 0.5836 (previously 0.5200), followed by the vertex 12 now scored 0.5392 (previously 0.5400). The vertex 24 remained on position 6; however, it is now followed by vertex 6, scored 0.4741, which in the previous scenario was ranked 12th with the score of 0.4000. A detailed analysis of the differences between ranks obtained by vertices in the rankings for scenarios 1 and 2 is presented on Figure 3A. The horizontal axis presents the consecutive ranks of all 1000 vertices of the studied network in scenario 1, whereas the vertical axis shows how these vertices were then ranked in scenario 2. The closer the point representing a vertex is to the diagonal line on the chart, the smaller the change in the rank occurred. It can be observed, that while in case of the top-ranked vertices only small changes in rank occur, as it can be confirmed in Table 3, in the case of the vertices further down the list, changes of even hundreds of levels in rank can be observed.
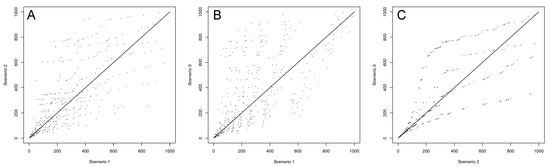
Figure 3.
Visual comparison of ranks of nodes obtained in rankings for various scenarios: (A) scenarios 1 and 2; (B) scenarios 1 and 3; (C) scenarios 2 and 3.
Subsequent to the selection of the seeds, ten simulations were performed with the same conditions as in the first scenario. The visual representation of the outcomes of the simulations are presented in Figure A4 in Appendix A. In this scenario, the simulations averagely lasted 9.1 iterations, that is, longer by 0.5 iteration and resulted in 435.6 nodes infected (0.4356 coverage, 0.0020 more). What is interesting, the usage of two criteria allowed us to increase the coverage in the target group. Averagely 52 targeted nodes were infected, that is, 0.4 target coverage, which is 0.0115 more than in the first scenario.
4.6. Scenario 3: Four Criteria
In the third scenario, it was decided to focus on seeding information not only to vertices with high values of female degree (C4) and mid-aged degree (C7), but also to nodes which are already in the target group, that is, the right sex (C2, female) and age (C5, mid-aged). The seeds selected for this scenario are presented in Table 4.

Table 4.
Seeds selected for Scenario 3, ordered by their rank and CCi score obtained in the applied TOPSIS method.
The analysis of Table 4 shows that the vertex 3 is still the leading one, however its score is much lower in case of this scenario (0.9069, compared to 0.9975 and 0.9980 in scenarios 1 and 2 respectively). Some minor changes in ranks can also be observed for the remaining seeds. Figure 3B visualizes the comparison of ranks between scenarios 1 and 3, whereas Figure 3C between scenarios 2 and 3. The analysis of these figures allows us to visually observe that the ranking obtained in scenario 3 is more similar to the one obtained in scenario 2 than to the one in scenario 1. This can be confirmed, indeed, by comparing the correlation coefficients between all scenarios (see Table 5).

Table 5.
Correlation matrix between the three scenarios’ ranks (A) and scores (B).
The results of the ten simulations performed for this scenario under the same conditions as used previously, are visually presented in Figure A5 in Appendix A. The average duration of the simulations was 8.7 iterations, which is slightly longer than in scenario 1 but shorter than that in scenario 2. On average, 435 nodes were infected (0.4350 coverage), which, similarly, is better than scenario 1 but worse than scenario 2. Finally, averagely 52.7 targeted nodes were infected, that is, 0.4054 targeted coverage, which is 0.0054 better than in scenario 2 and 0.0169 better than in the traditional approach, mimicked in scenario 1 (see Table 6 and Table 7).

Table 6.
Average simulation results for scenarios 1–3.

Table 7.
Comparison of differences between the average simulation results for scenarios 1–3.
4.7. Sensitivity Analysis
As it was observed in Section 4.4, Section 4.5 and Section 4.6, depending on the preference weights regarding evaluation criteria, the evaluation score of each vertex varied, resulting in differences in the obtained rankings and diverse sets of initial seeds for performing the information propagation campaign. The MCDA methodological foundations of the proposed approach allow to perform sensitivity analysis of the obtained rankings, and thus recognize how changes in the criteria preference affect the final rankings and, in turn, the selected seeds.
In this section, a sensitivity analysis for the seed selection problem for the studied network is presented. For clarity, the subset of analyzed vertices was limited to the ones which were selected as seeds in any of the scenarios 1–3. This resulted in a subset comprising of a total of 63 vertices: 1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 14, 16, 17, 18, 19, 20, 21, 24, 26, 29, 30, 33, 34, 36, 37, 40, 42, 45, 47, 48, 49, 53, 55, 56, 57, 59, 65, 69, 74, 82, 93, 97, 101, 103, 104, 113, 116, 122, 130, 135, 143, 151, 152, 153, 170, 172, 174, 185, 195, 238, 295, 464.
In order to perform the sensitivity analysis, at first the weights of all criteria were set to 1. Then, the weight of each criterion was gradually changed to 1, 25, 50, 75 and 100, while the rest of criteria remained at an unchanged level. Afterwards, the level of all criteria was increased to 25, and each criterion was tested again with the weight of 1, 25, 50, 75 and 100, while the rest of the criteria remained at an unchanged level. The same was then repeated for the levels of 50 and 75. At each combination of weights, the TOPSIS method was used to compute a ranking. The score and ranks of each of the 63 studied vertices was stored, and plotted afterwards. The plots representing the changes of score of each vertex is presented in Figure 4. The changes of ranks are presented in Figure 5.
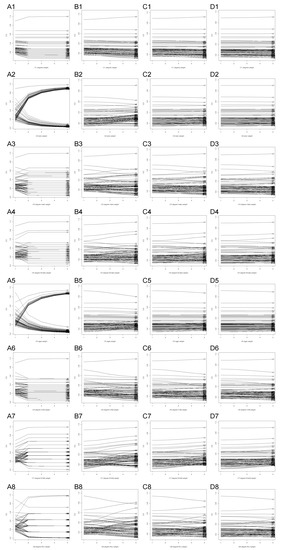
Figure 4.
Sensitivity analysis on the subset of 63 network vertices. The charts represent how changes in a single criterion (1–8) affect the score obtained by the analysed vertices, when the weights of the other criteria are set to 1 (A), 25 (B), 50 (C) or 75 (D).
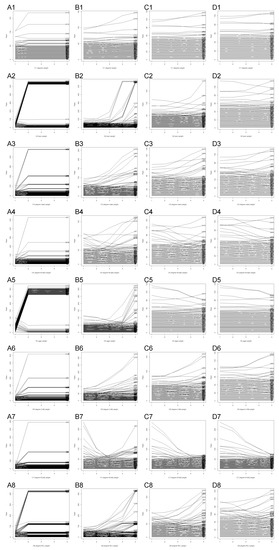
Figure 5.
Sensitivity analysis on the subset of 63 network vertices. The charts represent how changes in a single criterion (1–8) affect the ranks obtained by the analysed vertices, when the weights of the other criteria are set to 1 (A), 25 (B), 50 (C) or 75 (D).
The analysis of Figure 4A shows how each of the criteria support or conflict with individual vertices. It is particularly clear because, while the weight of each criterion is increased in the range 1–100, the weights of the remaining criteria are locked at the level of 1. The chart A8 demonstrates that, in some cases, the vertex 3, which was the leading one in all three exemplary scenarios, in some cases can be outran by other vertices. If the weight of criterion C8 (elderly degree) was increased to 25, while the weights of the other criteria remained negligible at the value of 1, the score of vertex 3 would drop below 0.8 and it would be ranked 3rd. However, if the weights of the other criteria were levelled at 25, the vertex would be the leader again, unless the weight of criterion C8 was increased close to 100. Then the vertex 3 would be ranked second.
Similarly, as can be observed in chart A5, if the weight of criterion C5 (age) was increasing, yet the other weights remained at 1, the vertex 3 would lose score very fast, down to a level of approximately 0.2. However, if the weights of the other criteria were increasing, the downfall of the score would be reduced to 0.8 (B5) or even 0.9 (C5, D5).
An interesting observation can be made looking at charts A1–A8. As was seen in Table 2 in Section 4.4, many vertices obtained the same score, and therefore their rank could vary. During the sensitivity analysis, this resulted in plots for multiple vertices being superimposed one on another. For example, on chart A1, only vertices 3, 4, 2, 12 and 5 can be located easily, while the remaining vertices are stacked together on the chart.
Because criterion C1 is based on the degree centrality measure, the vertices’ plots cluster in multiple score-groups, based on a plentiful, yet enumerable set of possible degree values, in the case of the studied network. On the other hand, due to the fact that the criteria C7 and C8 are based on the degrees of less numerous social groups (mid-aged and elderly), the possible values of the degree measure are more limited in this case and, therefore, there are less possible score values, which can be observed on the charts A7 and A8. In case of the chart A2, it can be observed that if the vertices are appraised based on the criterion C2 (sex), where only two values are possible, the vertices cluster in two groups. Since both sexes are distributed in the studied network at a roughly even probability level, it can be observed on the chart that both groups of vertices’ plots are similar in size. On the other hand, however, in case of criterion C5, also only two values are possible, so the vertices are plotted in two groups too. However, because only about a quarter of the studied network is in the targeted middle-aged group, a clear disproportion between the groups of plots can be observed on the chart A5.
Whilst in the case of Figure 4, the values on the vertical axis were limited to the range from 0 to 1, and multiple vertices were allowed to have the same value, in case of Figure 5 each value can be assigned only to a single vertex at a time. As was mentioned earlier, the set of analyzed vertices is limited to 63 for readability. The charts on Figure 5 are scaled to show ranks from 1 (best) to the worst one obtained by any of the 63 studied vertices. It is important to reiterate, that each of the 63 studied nodes was in the group of 50 best vertices in one of the scenarios described above. Therefore it is very unforeseen to observe that the chart C1 ends at about rank 120, obtained by the worst vertex 130, and the chart A6 ends around rank 600 for vertices 104 and 130. These observations emphasize the importance of proper selection of seeds for information spreading campaigns in social networks.
4.8. Full Range Analysis
The empirical study was concluded by performing a comprehensive set of 65,610 simulations based on the full range of the seed selection preference weights. For each of the eight decision criteria, the weights of 1, 50 and 100 were assigned. That resulted in possible sets of criteria preference weights and, consequently, 6561 sets of seeds, for each of which ten simulations under invariable conditions were performed. The results of the performed 65,610 simulations were then stored and aggregated for further analysis.
For the studied synthetic network, the highest number of infected vertices was reached for the seeds indicated by rankings based on high weights of the C5 (age) criterion, and negligible weights of the other criteria. It was equal to 459.7 infected nodes, that is, 0.4597 coverage. For such scenarios, averagely 61.3 targeted nodes were infected, that is, 0.4715 coverage of the targets.
On the other hand, the highest coverage within the targeted nodes was achieved in the simulations originating from the rankings produced by the scenarios in which high weight values were assigned to criteria C2 (sex) and C5 (age). On average 75.8 targeted nodes were infected in these simulations, that is, 0.5831 targets’ coverage. For these scenarios, on average 458.6 vertices were infected, that is, 0.4586 coverage. This substantial increase in the count of the infected targets might be caused by the fact, that for this scenario, all seeds were part of the target group themselves (resulting in on average 25.8 non-seed targets infected, i.e., 0.1985), whereas in the scenario described in Section 4.6, only 5 of the initial seeds were from the target group (resulting in, on average, 47.7 non-seed targets infected, i.e., 0.3669 of the targets).
All in all, the simulation results have shown that the use of a multi-attribute seed selection approach, proposed in this paper, at the cost of reducing the coverage on the studied network by 0.0011, allowed us to increase the coverage within the targeted nodes by 0.1116 compared to the approach oriented on maximizing the global network coverage.
5. Conclusions
Large-scale networks used daily by billions of users [60] create a medium for transmitting information and content. While most influence maximisation methods focus on increasing coverage, it is also important to reach users interested in content or services to avoid the distribution of unwanted messages, decrease information overload and habituation effect and, as a result, increase campaign performance. Earlier research in the area of information spreading focused mainly on influence maximisation. Only limited number of studies discussed targeting nodes with specific characteristics with main focus on their single attributes.
This paper proposes a novel approach to seeding information in multi-attribute social networks, in order to target multi-attribute groups of nodes. In the proposed approach, the seeds for initializing the campaign are chosen based on the ranking obtained with an MCDA method. During information spreading initialization, it is possible to adjust the weights assigned to each attribute. This, in turn, allows to manipulate the symmetry between the global coverage and coverage within the targeted group of nodes. Particularly, the coverage within the targeted multi-attribute nodes’ group can be increased, at the cost of potentially reducing the global coverage. The experimental research has shown a superior performance of the proposed approach, compared to traditional approaches focused on the degree centrality measure.
Although the empirical research has shown that the multi-attribute approach to the seed selection allowed us to significantly increase the coverage within the targeted group of nodes, the full-scope study has shown that even higher increase could be obtained if the higher weights were assigned to the criteria which were not initially selected for research in the empirical study. Therefore, grasping this experimental domain knowledge, especially in form of creation of an ontology for selection of criteria for targeting particular types of targets, is a very promising possible future field of research. Such ontology could provide guidelines for the marketer, for assigning weights to the multi-attribute seed rank generation.
Moreover, during the research, finding a multi-attribute model of a real network proved to be very problematic and it was necessary to perform the empirical study on networks with attributes superimposed artificially, based on the known distributions of these attributes in population. This allowed us to study the efficiency of the proposed approach, but comparing to other similar works in this field was not possible. It would be beneficial to include in future work the collection of knowledge about a real multi-attribute social network, in order to allow benchmarking of the proposed approach on a real model. This, in turn, implies additional methodical challenges, as proper reflecting of the non-deterministic nature of performance data in complex networks requires proper adjusting of the MCDA-based decision models and methods used. In practice, the usage of fuzzy extensions of MCDA methods (which proved to be powerful tools for dealing with data uncertainty) seems to be very promising.
Last, but not least, this research focused only on the multiple values of the network attributes. Future work should include a more profound look into the main aspects of the multi-attributed complex network itself.
Author Contributions
Conceptualization, A.K., J.J. and J.W.; Data curation, A.K. and J.J.; Formal analysis, A.K., J.J. and J.W.; Funding acquisition, J.J. and J.W.; Investigation, J.J.; Methodology, A.K., J.J. and J.W.; Project administration, J.J.; Resources, A.K.; Software, A.K.; Supervision, J.J., J.W.; Validation, J.J.; Visualization, A.K. and J.J.; Writing—original draft, A.K., J.J. and J.W.; Writing—review and editing, J.J. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Science Centre of Poland, the decision no. 2017/27/B/HS4/01216 (A.K., J.J.) and within the framework of the program of the Minister of Science and Higher Education under the name “Regional Excellence Initiative” in the years 2019–2022, project number 001/RID/2018/19, the amount of financing PLN 10,684,000.00 (J.W.).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The final steps of each of the 10 simulations from various scenarios are presented below. The blue “s” vertices represent the seeds. The green “i” nodes represent the non-targeted vertices which were infected. The empty vertices with red outline represent the targets of the campaign. The fully-colored red vertices represent the targets which were successfully reached in the campaign.
Figure A1 presents the target 1, and Figure A2 the target 2 of the real-life usage example from Section 4.1. Subsequently, Figure A3, Figure A4 and Figure A5 present scenarios on the synthetic network simulations from Section 4.4, Section 4.5 and Section 4.6 respectively.
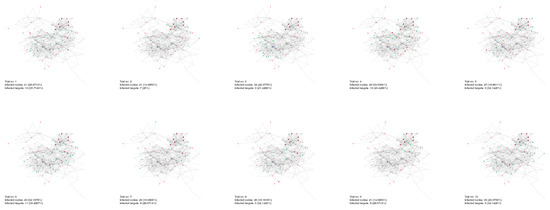
Figure A1.
Visual representation of the real-life usage example—target 1.

Figure A2.
Visual representation of the real-life usage example—target 2.

Figure A3.
Visual representation of 10 trials for Scenario 1.

Figure A4.
Visual representation of 10 trials for Scenario 2.

Figure A5.
Visual representation of 10 trials for Scenario 3.
References
- Dunbar, R.I. Do online social media cut through the constraints that limit the size of offline social networks? R. Soc. Open Sci. 2016, 3, 150292. [Google Scholar] [CrossRef] [PubMed]
- Vinerean, S. Importance of strategic social media marketing. Expert J. Mark. 2017, 5. Available online: http://hdl.handle.net/11159/1381 (accessed on 27 June 2020).
- Iribarren, J.L.; Moro, E. Impact of Human Activity Patterns on the Dynamics of Information Diffusion. Phys. Rev. Lett. 2009, 103, 038702. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.T.; Dinh, T.N.; Thai, M.T. Cost-aware targeted viral marketing in billion-scale networks. In Proceedings of the IEEE INFOCOM 2016—The 35th Annual IEEE International Conference on Computer Communications, San Francisco, CA, USA, 10–15 April 2016; pp. 1–9. [Google Scholar]
- Mochalova, A.; Nanopoulos, A. A targeted approach to viral marketing. Electron. Commer. Res. Appl. 2014, 13, 283–294. [Google Scholar] [CrossRef]
- Liu, Q.; Dong, Z.; Liu, C.; Xie, X.; Chen, E.; Xiong, H. Social marketing meets targeted customers: A typical user selection and coverage perspective. In Proceedings of the 2014 IEEE International Conference on Data Mining, Shenzhen, China, 14–17 December 2014; pp. 350–359. [Google Scholar]
- Voss, G.; Godfrey, A.; Seiders, K. Do satisfied customers always buy more? The roles of satiation and habituation in customer repurchase. In Marketing Science Institute Working Paper Series 2010; Marketing Science Institute: Cambridge, MA, USA, 2010; pp. 10–101. [Google Scholar]
- Luo, C.; Lan, Y.; Wang, C.; Ma, L. The Effect of Information Consistency and Information Aggregation on eWOM Readers’ Perception of Information Overload. In Proceedings of the PACIS 2013, Jeju Island, Korea, 18–22 June 2013; p. 180. [Google Scholar]
- Datta, S.; Majumder, A.; Shrivastava, N. Viral marketing for multiple products. In Proceedings of the 2010 IEEE International Conference on Data Mining, Sydney, Australia, 13–17 December 2010; pp. 118–127. [Google Scholar]
- Thakur, N.; Han, C.Y. An approach to analyze the social acceptance of virtual assistants by elderly people. In Proceedings of the 8th International Conference on the Internet of Things, Santa Barbara, CA, USA, 15–18 October 2018; pp. 1–6. [Google Scholar]
- Thakur, N.; Han, C.Y. Framework for an intelligent affect aware smart home environment for elderly people. Int. J. Recent Trends Hum. Comput. Interact. (IJHCI) 2019, 9, 23–43. [Google Scholar]
- Pamučar, D.S.; Božanić, D.; Ranđelović, A. Multi-criteria decision making: An example of sensitivity analysis. Serbian J. Manag. 2017, 12, 1–27. [Google Scholar] [CrossRef]
- Mukhametzyanov, I.; Pamucar, D. A sensitivity analysis in MCDM problems: A statistical approach. Decis. Mak. Appl. Manag. Eng. 2018, 1, 51–80. [Google Scholar] [CrossRef]
- Kempe, D.; Kleinberg, J.; Tardos, É. Maximizing the spread of influence through a social network. In Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 24–27 August 2003; pp. 137–146. [Google Scholar]
- Hinz, O.; Skiera, B.; Barrot, C.; Becker, J.U. Seeding strategies for viral marketing: An empirical comparison. J. Mark. 2011, 75, 55–71. [Google Scholar] [CrossRef]
- Zareie, A.; Sheikhahmadi, A.; Jalili, M. Identification of influential users in social networks based on users’ interest. Inf. Sci. 2019, 493, 217–231. [Google Scholar] [CrossRef]
- Li, X.; Smith, J.D.; Dinh, T.N.; Thai, M.T. Why approximate when you can get the exact? Optimal targeted viral marketing at scale. In Proceedings of the IEEE INFOCOM 2017—IEEE Conference on Computer Communications, Atlanta, GA, USA, 1–4 May 2017; pp. 1–9. [Google Scholar]
- Pasumarthi, R.; Narayanam, R.; Ravindran, B. Near optimal strategies for targeted marketing in social networks. In Proceedings of the 2015 International Conference on Autonomous Agents and Multiagent Systems, Paris, France, 10–15 July 2015; pp. 1679–1680. [Google Scholar]
- Zareie, A.; Sheikhahmadi, A.; Khamforoosh, K. Influence maximization in social networks based on TOPSIS. Expert Syst. Appl. 2018, 108, 96–107. [Google Scholar] [CrossRef]
- Yang, P.; Liu, X.; Xu, G. A dynamic weighted TOPSIS method for identifying influential nodes in complex networks. Mod. Phys. Lett. B 2018, 32, 1850216. [Google Scholar] [CrossRef]
- Yang, Y.; Yu, L.; Zhou, Z.; Chen, Y.; Kou, T. Node Importance Ranking in Complex Networks Based on Multicriteria Decision Making. Math. Probl. Eng. 2019, 2019. [Google Scholar] [CrossRef]
- Liu, Z.; Jiang, C.; Wang, J.; Yu, H. The node importance in actual complex networks based on a multi-attribute ranking method. Knowl. Based Syst. 2015, 84, 56–66. [Google Scholar] [CrossRef]
- Robles, J.F.; Chica, M.; Cordon, O. Evolutionary Multiobjective Optimization to Target Social Network Influentials in Viral Marketing. Expert Syst. Appl. 2020, 113183. [Google Scholar] [CrossRef]
- Wang, L.; Yu, Z.; Xiong, F.; Yang, D.; Pan, S.; Yan, Z. Influence Spread in Geo-Social Networks: A Multiobjective Optimization Perspective. IEEE Trans. Cybern. 2019. [Google Scholar] [CrossRef]
- Gandhi, M.; Muruganantham, A. Potential influencers identification using multi-criteria decision making (MCDM) methods. Procedia Comput. Sci. 2015, 57, 1179–1188. [Google Scholar] [CrossRef][Green Version]
- Muruganantham, A.; Gandhi, G.M. Framework for Social Media Analytics based on Multi-Criteria Decision Making (MCDM) Model. Multimed. Tools Appl. 2020, 79, 3913–3927. [Google Scholar] [CrossRef]
- Montazerolghaem, M. Effective Factors in Network Marketing Success and Ranking Using Multi-criteria Decision Making Techniques. Int. J. Appl. Optim. Stud. 2019, 2, 73–89. [Google Scholar]
- Karczmarczyk, A.; Jankowski, J.; Wątróbski, J. Multi-criteria decision support for planning and evaluation of performance of viral marketing campaigns in social networks. PLoS ONE 2018, 13, e0209372. [Google Scholar] [CrossRef] [PubMed]
- Cinelli, M.; Kadziński, M.; Gonzalez, M.; Słowiński, R. How to Support the Application of Multiple Criteria Decision Analysis? Let Us Start with a Comprehensive Taxonomy. Omega 2020, 102261. [Google Scholar] [CrossRef] [PubMed]
- Pamučar, D.S.; Božanić, D.I.; Kurtov, D.V. Fuzzification of the Saaty’s scale and a presentation of the hybrid fuzzy AHP-TOPSIS model: An example of the selection of a brigade artillery group firing position in a defensive operation. Vojnoteh. Glas. 2016, 64, 966–986. [Google Scholar] [CrossRef]
- Chatterjee, P.; Stević, Ž. A two-phase fuzzy AHP-fuzzy TOPSIS model for supplier evaluation in manufacturing environment. Oper. Res. Eng. Sci. Theory Appl. 2019, 2, 72–90. [Google Scholar] [CrossRef]
- Wątróbski, J.; Jankowski, J.; Ziemba, P.; Karczmarczyk, A.; Zioło, M. Generalised framework for multi-criteria method selection. Omega 2019, 86, 107–124. [Google Scholar] [CrossRef]
- Stević, Ž.; Tanackov, I.; Vasiljević, M.; Novarlić, B.; Stojić, G. An integrated fuzzy AHP and TOPSIS model for supplier evaluation. Serbian J. Manag. 2016, 11, 15–27. [Google Scholar] [CrossRef]
- Mardani, A.; Jusoh, A.; Zavadskas, E.K. Fuzzy multiple criteria decision-making techniques and applications—Two decades review from 1994 to 2014. Expert Syst. Appl. 2015, 42, 4126–4148. [Google Scholar] [CrossRef]
- Freeman, L.C. Centrality in social networks conceptual clarification. Soc. Netw. 1978, 1, 215–239. [Google Scholar] [CrossRef]
- Bonacich, P. Technique for analyzing overlapping memberships. Sociol. Methodol. 1972, 4, 176–185. [Google Scholar] [CrossRef]
- Valente, T.W.; Coronges, K.; Lakon, C.; Costenbader, E. How correlated are network centrality measures? Connections 2008, 28, 16. [Google Scholar]
- Likert, R. A technique for the measurement of attitudes. Arch. Psychol. 1932, 22, 55. [Google Scholar]
- Saaty, T.L.; Vargas, L.G. The legitimacy of rank reversal. Omega 1984, 12, 513–516. [Google Scholar] [CrossRef]
- Sabidussi, G. The centrality index of a graph. Psychometrika 1966, 31, 581–603. [Google Scholar] [CrossRef]
- Freeman, L.C. A set of measures of centrality based on betweenness. Sociometry 1977, 35–41. [Google Scholar] [CrossRef]
- Roy, B.; Vanderpooten, D. The European school of MCDA: Emergence, basic features and current works. J. Multi Criteria Decis. Anal. 1996, 5, 22–38. [Google Scholar] [CrossRef]
- Roy, B. Paradigms and challenges. In Multiple Criteria Decision Analysis: State of the Art Surveys; Springer: Berlin/Heidelberg, Germany, 2005; pp. 3–24. [Google Scholar]
- Guitouni, A.; Martel, J.M. Tentative guidelines to help choosing an appropriate MCDA method. Eur. J. Oper. Res. 1998, 109, 501–521. [Google Scholar] [CrossRef]
- Roy, B.; Słowiński, R. Questions guiding the choice of a multicriteria decision aiding method. EURO J. Decis. Process. 2013, 1, 69–97. [Google Scholar] [CrossRef]
- Vansnick, J.C. On the problem of weights in multiple criteria decision making (the noncompensatory approach). Eur. J. Oper. Res. 1986, 24, 288–294. [Google Scholar] [CrossRef]
- Wątróbski, J.; Jankowski, J.; Ziemba, P.; Karczmarczyk, A.; Zioło, M. Generalised framework for multi-criteria method selection: Rule set database and exemplary decision support system implementation blueprints. Data Brief 2019, 22, 639. [Google Scholar] [CrossRef] [PubMed]
- Stević, Ž.; Alihodžić, A.; Božičković, Z.; Vasiljević, M.; Vasiljević, Đ. Application of combined AHP-TOPSIS model for decision making in management. In Proceedings of the 5th International Conference Economics and Management-Based on New Technologies “EMONT”, Vrnjačka Banja, Serbia, 18–21 June 2015; pp. 33–40. [Google Scholar]
- Behzadian, M.; Otaghsara, S.K.; Yazdani, M.; Ignatius, J. A state-of the-art survey of TOPSIS applications. Expert Syst. Appl. 2012, 39, 13051–13069. [Google Scholar] [CrossRef]
- Chen, S.J.; Hwang, C.L. Fuzzy multiple attribute decision making methods. In Fuzzy Multiple Attribute Decision Making; Springer: Berlin/Heidelberg, Germany, 1992; pp. 289–486. [Google Scholar]
- Yoon, K.P.; Hwang, C.L. Multiple Attribute Decision Making: An Introduction; Sage Publications: Thousand Oaks, CA, USA, 1995; Volume 104. [Google Scholar]
- Hwang, C.L.; Yoon, K. Multiple criteria decision making. In Lecture Notes in Economics and Mathematical Systems; Springer: Berlin/Heidelberg, Germany, 1981; Volume 186, pp. 58–191. [Google Scholar]
- Rossi, R.A.; Ahmed, N.K. The Network Data Repository with Interactive Graph Analytics and Visualization. In Proceedings of the AAAI 2015, Austin, TX, USA, 25–30 January 2015. [Google Scholar]
- Gus. Ludność. Stan i Struktura Ludności Oraz Ruch Naturalny w Przekroju Terytorialnym; Statistics Poland: Warsaw, Poland, 2016. [Google Scholar]
- Barabási, A.L.; Bonabeau, E. Scale-free networks. Sci. Am. 2003, 288, 60–69. [Google Scholar] [CrossRef] [PubMed]
- Chiasserini, C.F.; Garetto, M.; Leonardi, E. Social network de-anonymization under scale-free user relations. IEEE ACM Trans. Netw. 2016, 24, 3756–3769. [Google Scholar] [CrossRef]
- Luo, Y.; Ma, J. The influence of positive news on rumor spreading in social networks with scale-free characteristics. Int. J. Mod. Phys. C 2018, 29, 1850078. [Google Scholar] [CrossRef]
- Liu, W.; Li, T.; Liu, X.; Xu, H. Spreading dynamics of a word-of-mouth model on scale-free networks. IEEE Access 2018, 6, 65563–65572. [Google Scholar] [CrossRef]
- Ministerstwo Zdrowia. Program Profilaktyki Raka Piersi (Mammografia); www.gov.pl; Ministerstwo Zdrowia: Warsaw, Poland, 2018. [Google Scholar]
- WeAreSocial Digital 2020. Available online: https://wearesocial.com/digital-2020 (accessed on 27 June 2020).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).