Abstract
The class of log-elliptical distributions is well used and studied in risk measurement and actuarial science. The reason is that risks are often skewed and positive when they describe pure risks, i.e., risks in which there is no possibility of profit. In practice, risk managers confront a system of mutually dependent risks, not only one risk. Thus, it is important to measure risks while capturing their dependence structure. In this short paper, we compute the multivariate risk measures, multivariate tail conditional expectation, and multivariate tail covariance measure for the family of log-elliptical distributions, which captures the dependence structure of the risks while focusing on the tail of their distributions, i.e., on extreme loss events. We then study our result and examine special cases, as well as the optimal portfolio selection using such measures. Finally, we show how the given multivariate tail moments can also be computed for log-skew elliptical models based on similar approaches given for the log-elliptical case.
1. Introduction
The family of log-elliptical (LE) distributions is a family of continuous distributions that includes the log-normal (LN) distribution as a special case. This family of distributions is extensively used in quantitative finance to model financial returns and losses (Chriss [1], Valdez and Dhaene [2], Hamada and Valdez [3], Valdez et al. [4], Klebaner and Landsman [5], Kortschak and Hashorva [6], Landsman-Makov-Shushi [7]). Let be an random vector with the multivariate LE distribution. Then, its probability density function (pdf) takes the form (see, for instance, Valdez et al. [4])
Here is an vector of locations, is an scale matrix, and is called the density generator which satisfies the following condition
The LN pdf is obtained by taking the density generator Another important example is the log-Laplace distribution which is obtained by taking where
The LE family of distributions can be derived from the transformation of an elliptical random vector whose pdf takes the form
with the characteristic function
for some function , called the characteristic generator. For the normal distribution, the characteristic generator is the exponential function For the Laplace distribution and for the generalized stable laws distributions
Any log-elliptical random vector has a unique density generator and thus has a unique characteristic generator ; this can be shown from the existence and uniqueness theorem. If the expectation of exists, the characteristic generator can be extended on the negative part and the expectation has the following explicit form
where and are the location and scale parameters of respectively (see, Klebaner and Landsman [5], formula (2.13). Furthermore, if the covariance between two log-elliptical random variables exists, then, the covariance follows the form (see Valdez et al. [4])
where and are the location and scale parameter of respectively, and
is the scale matrix of the log-elliptical bivariate random vector
The following are some special members of the class of log-elliptical distributions.
- 1
- Multivariate log-normal distribution: In the case that the density generator is , the pdf of the multivariate log-normal distribution isand we write
- 2
- Multivariate log-Student-t distribution: The pdf of the log-Student-t distribution is given bywith degrees of freedom, and we write
- 3
- Multivariate log-logistic distribution: An elliptical vector is log-logistic distributed if its pdf takes the formand we write is
- 4
- Multivariate log-Laplace distribution: we say that is a multivariate log-Laplace random vector if its pdf is
A well-known property of the LE family of distributions is that the moments of this family can be computed explicitly using the elliptical characteristic generator .
The moments of LE distributions can be computed explicitly, by the following celebrated Lemma:
Lemma 1.
Let . Then, if moment of exists then the characteristic generator ψ can be extended on the negative part and the mentioned moment takes the form
where and ψ is the characteristic generator of the associated elliptical random vector .
In this paper, we focus on the following projection of a random vector of risks
where
is vector, where is the value at risk of under the quantile, For simplicity, we also write , having in mind that we have a vector of q-th quantiles.
Following the asymptotic expansion of the conditional characteristic function we have
The first measure, has been introduced in Landsman–Makov–Shushi [8] and is called the multivariate tail conditional (MTCE) measure, where the second measure centralized around MTCE was introduced in Landsman–Makov–Shushi [9] in order to capture the dispersion of the random vector of risks when focusing on extreme losses. Analyzing the moments and the tail moments of random variables has been studied and well investigated in the literature, and there is a still active research in this area—in its applications in different fields, from data analysis to actuarial science (Loperfido [10], Loperfido-Mazur-Podgórski [11], Ogasawara [12]).
2. Multivariate Tail Conditional Expectation for Log-Elliptical Models
The multivariate tail conditional expectation (MTCE) measure is a risk measure that naturally extends the tail conditional expectation (TCE) from a univariate risk into a multivariate system of mutually depend risks. This multivariate risk measure has been introduced in Landsman–Makov–Shushi [8]. For additional literature about the MTCE measure we refer to Cai–Wang–Mao [13], Hashorva [14], Mousavi et al. [14], Frei [15], Ling [16], Shushi and Yao [17], among others. Define an vector of random risks that are mutually dependent on each other with cumulative distribution function . Using this notation, for two n-variate random vectors and means that We now introduce the MTCE measure with varied quantiles
This definition is essentially more realistic than that introduced in Landsman–Makov–Shushi [8], where all the quantile levels were the same. Now each risk or loss may exceed its own VaR, which can be large, small, or even equal to 0, implying total flexibility as to the degree of riskiness of any of the underlying risks. The TCE, which is the tail conditional expectation measure,
Proposition 1.
The measure satisfies the following expression,
Proof.
Please see Landsman–Makov–Shushi [9]. □
Let We introduce a new random vector associated with the element of vector with the pdf
Theorem 1.
Let be an random vector of risks with characteristic generator which can be extended on the negative part. Then, the MTCE measure is given by
Here
is the tail function of the random vector associated with and symbol ∘ is the Hadamard product.
Proof.
From the definition of MTCE, and using the transformation we have
where
Now, notice that the following integral is, in fact, the moment generated function of an associated elliptical distribution,
allowing us to introduce a new random vector associated with the random vector with the pdf (a similar technique can be found in Valdez et al. (2009)).Thus, for the component, we have
where □
Example 1.
Log-normal distribution. Let be a log-elliptical random vector of risks.Then, the density function and the characteristic generator are given by and , respectively. Then where is the identity matrix and
whereis the tail function of n-variate standard normal random vector. This result well conforms with Valdez et al. [4], Equation (39).
Example 2.
Log-Laplace distribution. We say that is multivariate Log Laplace random vector if its characteristic generator
The density generator is equaled to
where is the modified Bessel function of the third kind. Then the density of the multivariate Log Laplace distribution is equal
For
and
that coincides with univariate Log-Laplace distribution. (Eltoft et al. [18], Equation (9)).
The MTCE of multivariate Log-Laplace can be calculated as follows
Here the random vector has the pdf
Numerical Illustration
Let us now examine a random vector of five risks with the multivariate log-normal distribution where
and
Then, the graph of vector MTCE corresponded to vector of levels
is presented in Figure 1 (solid line).
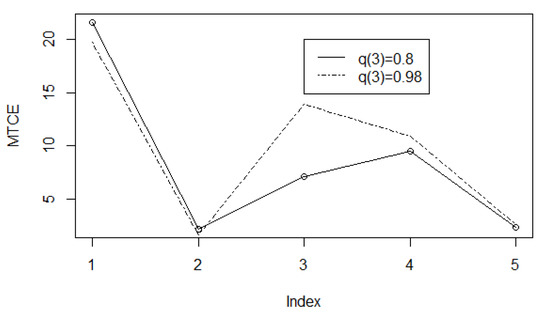
Figure 1.
Graphs of MTCE for Log-normal dependence structure for and
One can see that as it is expected the value of the components of the vector MTCE is increased if the level of the corresponded observation increased but is increased not proportionally. On the same graph we presented MTCE for (dot-dashed line), i.e., we changed only level from to , and we can see that all system of components of vector MTCE stretched out mostly in the direction of increasing.
3. Multivariate Tail Covariance for Log-Elliptical Models
The multivariate tail covariance (MTCov) measure provides a variation of the MTCE measure for the dispersion of the random vector of risks. This measure was introduced in Landsman–Makov–Shushi [9]. While we have established that the proposed multivariate tail covariance (MTCov) measure is given by
meaning that
Theorem 2.
Let be an random vector of risks with characteristic generator ψ, which can be extended on the negative part. Then, the component of the MTCov measure is given by
Here is the tail function of vector associated with the vector and having density
Proof.
From the definition of MTCov with the form (17), we have
and using the transformation we have
for the component,
The proof of the Theorem follows from (19) and Theorem 1. □
Extensions to the Class of Log-Elliptical Models
We note that the MTCE and MTCOV measures can naturally be extended to the class of log-skew-elliptical distributions
Here such that
In particular, after some calculations one would find that the formulas remain the same, but, with new random vectors with the same pdfs as the log-elliptical case multiplied by the associated skewness term, as follows:
and
4. Optimal Portfolio Selection with Log-Elliptical Distributions
In risk management, the optimal portfolio selection problem is one of the most profound and well studied areas in both the theoretical and also the practical aspects of portfolio decision making (Castellano and Cerqueti [19], Li and Hoi [20], Shen et al. [21], and Fletcher [22]).
Modern portfolio theory (MPT), developed by Markowitz in the year 1952 provided the foundations of optimal portfolio theory based on the moments of the portfolio risk (see, Markowitz, Elton, and Gruber [23], and Francis and Kim [24]). In MPT the classical mean-variance (MV) is introduced and is given by
where is the portfolio loss, and are a vectors of weights and losses (equaled the minus portfolio returns), respectively, and where is vector of n ones. , where is the vector of expected losses and where is the covariance matrix of the vector of portfolio losses. Here is the risk aversion parameter, which can be interpreted as the parameter of a trade-off between the expected loss, and the variance, or the standard deviation, of the portfolio.
Suppose that we have a system of n risks of losses such that Such considered risks that are having LE distributions describe pure risks, i.e., risks that can only bring losses without the possibility of profit. Then, we aim at finding the optimal weights that would minimize such a portfolio of risks. Since the classical MV model only focuses on the mean and variance of the risk, it does not capture the skewness appearing in the LE distribution. To avoid this problem, we suggest taking the MTCE and MTCov measures instead of the expectation and covariance matrix of the portfolio risk, i.e.,
Thus, we focus on the tails of the risks, leading to the following projection of the portfolio risk
so and In that case, instead of the classical MV, we would have the following measure
which the both capture the skewness of the distribution and focusing on extreme loss events, much like the optimal portfolio problem with value-at-risk, and expected-shortfall Our goal is to minimize the MV measure of the losses
Theorem 3.
The optimal solution of (23) subject to is given by
Proof.
The proof relies on the classical MV optimal solution if and substitute with and See also Landsman-Makov-Shushi [25], Remark 3.1. □
Another well-known measure is the mean-standard deviation measure, which takes the form where In that case, we also have explicit solution for the OPS problem.
Theorem 4.
The solution of the minimization of functional
subject to is given by
if
Proof.
The proof of the Theorem straightforwardly follows from Landsman–Makov–Shushi [25], Table 3, where instead of taking and we take and respectively. □
Resuming this section we would point out that the most optimal results listed in Table 3 [25] can be provided here and can be outspread in the context of and
5. Conclusions
In this paper we derived the MTCE and MTCov measures for the class of log-elliptical distributions. The importance of the results stems from the fact that in risk management, risks are often skewed and non-negative, but their logarithms can still preserve the symmetric property. We found the analytic forms for MTCE and MTCov multivariate functionals and also used these measures in the formulation and solving the problem of the optimal portfolio selection.
Author Contributions
Both authors contributed equally. Both authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Israel Science Foundation (Grant No. 1686/17).
Institutional Review Board Statement
Not applicable
Informed Consent Statement
Not applicable
Data Availability Statement
Not applicable
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chriss, N. Black Scholes and Beyond: Option Pricing Models; McGraw-Hill: New York, NY, USA, 1996. [Google Scholar]
- Valdez, E.A.; Dhaene, J. Bounds for sums of non-independent log-elliptical random variables. In Proceedings of the 7th International Congress on Insurance: Mathematics and Economics, Lyon, France, 25–27 June 2003. [Google Scholar]
- Hamada, M.; Valdez, E.A. CAPM and option pricing with elliptically contoured distributions. J. Risk Insur. 2008, 75, 387–409. [Google Scholar] [CrossRef]
- Valdez, E.A.; Dhaene, J.; Maj, M.; Vanduffel, S. Bounds and approximations for sums of dependent log-elliptical random variables. Insur. Math. Econ. 2009, 44, 385–397. [Google Scholar] [CrossRef]
- Klebaner, F.C.; Landsman, Z. Option pricing for log-Symmetric distributions of returns. Methodol. Comput. Appl. Probab. 2009, 11, 339–357. [Google Scholar] [CrossRef]
- Kortschak, D.; Hashorva, E. Second order asymptotics of aggregated log-elliptical risk. Methodol. Comput. Appl. Probab. 2014, 16, 969–985. [Google Scholar] [CrossRef][Green Version]
- Landsman, Z.; Makov, U.; Shushi, T. Tail conditional moments for elliptical and log-elliptical distributions. Insur. Econ. 2016, 71, 179–188. [Google Scholar] [CrossRef]
- Landsman, Z.; Makov, U.; Shushi, T. Multivariate tail conditional expectation for elliptical distributions. Insur. Econ. 2016, 70, 216–223. [Google Scholar] [CrossRef]
- Landsman, Z.; Makov, U.; Shushi, T. A multivariate tail covariance measure for elliptical distributions. Insur. Math. Econ. 2018, 81, 27–35. [Google Scholar] [CrossRef]
- Loperfido, N. Singular value decomposition of the third multivariate moment. Linear Algebra Appl. 2015, 473, 202–216. [Google Scholar] [CrossRef]
- Loperfido, N.; Mazur, S.; Podgórski, K. Third cumulant for multivariate aggregate claim models. Scand. Actuar. J. 2018, 2018, 109–128. [Google Scholar] [CrossRef]
- Ogasawara, H. Unified and non-recursive formulas for moments of the normal distribution with stripe truncation. Commun. Stat. Theory Methods 2020, 10, 1–38. [Google Scholar]
- Cai, J.; Wang, Y.; Mao, T. Tail subadditivity of distortion risk measures and multivariate tail distortion risk measures. Insur. Math. Econ. 2017, 75, 105–116. [Google Scholar] [CrossRef]
- Hashorva, E. Approximation of some multivariate risk measures for Gaussian risks. J. Multivar. Anal. 2019, 169, 330–340. [Google Scholar] [CrossRef]
- Frei, C. A New Approach to Risk Attribution and Its Application in Credit Risk Analysis. Risks 2020, 8, 65. [Google Scholar] [CrossRef]
- Ling, C. Asymptotics of multivariate conditional risk measures for Gaussian risks. Insur. Math. Econ. 2019, 86, 205–215. [Google Scholar] [CrossRef]
- Shushi, T.; Yao, J. Multivariate risk measures based on conditional expectation and systemic risk for Exponential Dispersion Model. Insur. Math. Econ. 2020, 93, 178–186. [Google Scholar] [CrossRef]
- Eltoft, T.; Kim, T.; Lee, T.-W. On the Multivariate Laplace Distribution. IEEE Signal Process. Lett. 2006, 13, 300–303. [Google Scholar] [CrossRef]
- Castellano, R.; Cerqueti, R. Mean–Variance portfolio selection in presence of infrequently traded stocks. Eur. J. Oper. Res. 2014, 234, 442–449. [Google Scholar] [CrossRef]
- Li, B.; Hoi, S.C. Online portfolio selection: A survey. ACM Comput. Surv. 2014, 46, 35. [Google Scholar] [CrossRef]
- Shen, Y.; Zhang, X.; Siu, T.K. Mean–variance portfolio selection under a constant elasticity of variance model. Oper. Res. Lett. 2014, 42, 337–342. [Google Scholar] [CrossRef]
- Fletcher, J. Exploring the benefits of using stock characteristics in optimal portfolio strategies. Eur. J. Financ. 2015, 23, 1–19. [Google Scholar] [CrossRef]
- Elton, E.J.; Gruber, M.J. Modern Portfolio Theory and Investment Analysis; Wiley: New York, NY, USA, 1987. [Google Scholar]
- Francis, J.C.; Kim, D. Modern Portfolio Theory: Foundations, Analysis, and New Developments; John Wiley & Sons: Hoboken, NJ, USA; New York, NY, USA, 2013; Volume 795. [Google Scholar]
- Landsman, Z.; Makov, U.E.; Shushi, T. Portfolio Optimization by a Bivariate Functional of the Mean and Variance. J. Optim. Theory Appl. 2020, 185, 622–651. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).