Semigroups of Terms, Tree Languages, Menger Algebra of n-Ary Functions and Their Embedding Theorems

Abstract

The concepts of terms and tree languages are significant tools for the development of research works in both universal algebra and theoretical computer science. In this paper, we establish a strong connection between semigroups of terms and tree languages, which provides the tools for studying monomorphisms between terms and generalized hypersubstitutions. A novel concept of a seminearring of non-deterministic generalized hypersubstitutions is introduced and some interesting properties among subsets of its are provided. Furthermore, we prove that there are monomorphisms from the power diagonal semigroup of tree languages and the monoid of generalized hypersubstitutions to the power diagonal semigroup of non-deterministic generalized hypersubstitutions and the monoid of non-deterministic generalized hypersubstitutions, respectively. Finally, the representation of terms using the theory of n-ary functions is defined. We then present the Cayley’s theorem for Menger algebra of terms, which allows us to provide a concrete example via full transformation semigroups.

1. Introduction and Preliminaries

In the classical theory of theoretical computer science, an automaton is a finite state machine which accepts certain strings of letters from a fixed base alphabet. Such strings are usually called words, and sets of words are called languages. Formal language theory is the study of properties of languages and automata. One of a generalized study of formal languages is the study of tree languages, i.e., the words of the classical case can be considered as a particular kind of terms. Since terms are commonly represented by tree diagrams, such formal languages are also called tree languages. For more details in this background, see [1,2,3]. We now recall the fundamental notion of terms as follows: Let $X_n=\{x_1,\dots ,x_n\}$, for n a natural number, be a finite set which elements are called variables and $X=\{x_1,\dots ,x_n,\dots \}$ be countably infinite. The variable $x_i$ in $X_n$ is an alphabet of formal languages. To define terms from this alphabet, we use a set $\{f_i\mid i\in I\}$ of operation symbols, indexed by the set I. The type is the sequence $\tau ={\left(n_i\right)}_{i\in I}$ of the natural numbers which are arities of the operation symbols $f_i$. An n-ary term of type τ is defined inductively by: Every variable $x_j\in X_n$ is an n-ary term of type $\tau$ and $f_i(t_1,\dots ,t_{n_i})$ is an n-ary term of type $\tau$ where $t_1,\dots ,t_{n_i}$ are n-ary terms of type $\tau$ and $f_i$ is an $n_i$-ary operation symbol. The set of all n-ary terms of type $\tau$ is denoted by $W_{\tau }\left(X_n\right)$. Let $W_{\tau }\left(X\right):={\bigcup }_{n\in {\mathbf{N}}^{+}}{W}_{\tau }\left(X_n\right)$ be the set of all terms of type $\tau$. See [4,5,6,7,8,9,10] for other related topics of terms.

Every term can be represented by a tree diagram, i.e., we consider term as a rooted tree whose vertices correspond to the operation symbols and variables that occur in it. We call this tree the tree representation of a term t. For instance, a tree representation of a term

$$f(x_4,g\left(h(x_1,x_2)\right),h(x_9,x_5))$$

can be shown in the below diagram.

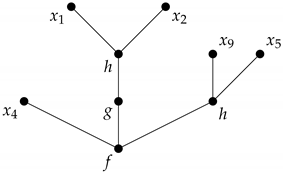
Substituting the variables that appear in a term by the other terms, one obtains a new term. This can be described by the $(n+1)$-generalized superpostion $S^n$, $n\ge 1,$

$$S^n:W_{\tau }{\left(X\right)}^{n+1}\to W_{\tau }\left(X\right)$$

defined inductively by the following steps: for $t,t_1,\dots ,t_n\in W_{\tau }\left(X\right)$

(1)

If $t=x_i$; $1\le i\le n$, then $S^n(x_i,t_1,\dots ,t_n):=t_i.$

(2)

If $t=x_i$; $n<i$, then $S^n(x_i,t_1,\dots ,t_n):=x_i$.

(3)

If $t=f_i(s_1,\dots ,s_{n_i})$, then

$S^n(t,t_1,\dots ,t_n):=f_i(S^n(s_1,t_1,\dots ,t_n),\dots ,S^n(s_{n_i},t_1,\dots ,t_n)).$

Then, we can form the algebraic structure, $(n+1)$-ary algebra $(W_{\tau }\left(X\right),S^n)$ consisting the universe $W_{\tau }\left(X\right)$ together with one $(n+1)$-ary operation $S^n$. In [11], the algebra in this form is known as a Menger algebra with infinitely many nullary operations. It is not hard to show that this algebra satisfies the superassociative law:

$$S^n(S^n(t,t_1,\dots ,t_n),s_1,\dots ,s_n)=S^n(t,S^n(t_1,s_1,\dots ,s_n),\dots ,S^n(t_n,s_1,\dots ,s_n))$$

for all arbitrary terms $t,t_1,\dots ,t_n,s_1,\dots ,s_n\in W_{\tau }\left(X\right).$

Using the concepts of terms and generalized superposition, the following ideas are essentially recalled. It was known from [12] that a formal definition of a strong hyperidentity and a strong solid variety can be given using the concept of a generalized hypersubstitution. We now recall such concept as follows: Let $\{f_i\mid i\in I\}$ be an indexed set of operation symbols of type $\tau$ where $f_i$ is $n_i$-ary, $n_i$ is a natural number. Let $Hy{p}_G\left(\tau \right)$ be the set of all arbitrary mappings $\sigma :\{f_i\mid i\in I\}\to W_{\tau }\left(X\right),$ which is called a generalized hypersubstitution of type τ. To define a binary operation on this set, the essential defining is necessary. Any $\sigma \in Hy{p}_G\left(\tau \right)$ can be uniquely extended to a mapping

$$\widehat{\sigma }:W_{\tau }\left(X\right)\to W_{\tau }\left(X\right),$$

which is defined by

(1)

$\widehat{\sigma }\left[x_i\right]:=x_i\in X,$

(2)

$\widehat{\sigma }\left[f_i(t_1,\dots ,t_{n_i})\right]:=S^{n_i}(\sigma \left(f_i\right),\widehat{\sigma }\left[t_1\right],\dots ,\widehat{\sigma }\left[t_{n_i}\right])$ where $\widehat{\sigma }\left[t_j\right]$, $1\le j\le n_i$ are already defined.

Using the extension of generalized hypersubstitution of type $\tau$, the binary operation ${\circ }_G$ is defined by ${\sigma }_1{\circ }_G{\sigma }_2:={\widehat{\sigma }}_1\circ {\sigma }_2$ where ∘ denotes the usual composition of mappings. The generalized hypersubstitution ${\sigma }_{id}$, which sends each $f_i$ to the term $f_i(x_1,x_2,\dots ,x_{n_i})$, is an identity element for ${\circ }_G$. Then, $(Hy{p}_G\left(\tau \right),{\circ }_G,{\sigma }_{id})$ is a monoid. See the following references for the research topics and current trends in this direction [13,14,15,16,17,18].

Let $P\left(W_{\tau }\left(X\right)\right)$ be the power set of all the set of all terms of type $\tau$. An inductive definition of an $(n+1)$-ary operation on $P\left(W_{\tau }\left(X\right)\right)$ is completely defined in [19]. Let n be a natural number, $B,B_1,\dots ,B_n$ are arbitrary subsets of $W_{\tau }\left(X\right)$. Then, an $(n+1)$-ary generalized superposition operation

$${\widehat{S}}^n:P{\left(W_{\tau }\left(X\right)\right)}^{n+1}\to P\left(W_{\tau }\left(X\right)\right)$$

is defined inductively by

(1)

If $B=\left\{x_i\right\}$; $1\le i\le n$, then ${\widehat{S}}^n(\left\{x_i\right\},B_1,\dots ,B_n):=B_i$.

(2)

If $B=\left\{x_i\right\}$; $n<i$, then ${\widehat{S}}^n(\left\{x_i\right\},B_1,\dots ,B_n):=\left\{x_i\right\}$.

(3)

If $B=\left\{f_i(t_1,\dots ,t_{n_i})\right\}$, and suppose that ${\widehat{S}}^n(\left\{t_k\right\},B_1,\dots ,B_n)$ for all $k=1,\dots ,n_i$ are already defined, then ${\widehat{S}}^n(\left\{f_i(t_1,\dots ,t_{n_i})\right\},B_1,\dots ,B_n):=\{f_i(r_1,\dots ,r_{n_i})\mid r_k\in {\widehat{S}}^n(\left\{t_k\right\},B_1,\dots ,B_n),1\le k\le n_i\}$.

(4)

If B is an arbitrary nonsingleton subset of $W_{\tau }\left(X\right)$, then

$${\widehat{S}}^n(B,B_1,\dots ,B_n):=\bigcup _{b\in B}{\widehat{S}}^n(\left\{b\right\},B_1,\dots ,B_n).$$

If one of the sets $B,B_1,\dots ,B_n$ is empty, we define ${\widehat{S}}^n(B,B_1,\dots ,B_n):=\varnothing$. It turns out that the following algebra of type $(n+1)$, $(P\left(W_{\tau }\left(X\right)\right),{\widehat{S}}^n)$ is a Menger algebra and called a power Menger algebra with infinitely many nullary operations. Then, it was proved that this algebra satisfies the superassociative law [19].

A non-deterministic generalized hypersubstitution of type $\tau$ [19] is a mapping $\sigma :\{f_i\mid i\in I\}\to P\left(W_{\tau }\left(X\right)\right)$. The set of all such mappings is denoted by $Hy{p}_G^{nd}\left(\tau \right)$. It is well-known that every $\sigma$ generates a mapping $\widehat{\sigma }$ which takes a tree language into itself by the following inductive way:

(1)

$\widehat{\sigma }[\varnothing ]:=\varnothing$,

(2)

$\widehat{\sigma }\left[\left\{x_i\right\}\right]:=\left\{x_i\right\}$ where $x_i$ is a variable from X,

(3)

$\widehat{\sigma }\left[\left\{f_i(t_1,\dots ,t_{n_i})\right\}\right]:={\widehat{S}}^{n_i}(\sigma \left(f_i\right),\widehat{\sigma }\left[\left\{t_1\right\}\right],\dots ,\widehat{\sigma }\left[\left\{t_{n_i}\right\}\right])$ if $\widehat{\sigma }\left[\left\{t_k\right\}\right],1\le k\le n_i$ are already defined,

(4)

$\widehat{\sigma }\left[B\right]:={\displaystyle \bigcup _{b\in B}}\widehat{\sigma }\left[\left\{b\right\}\right]$ if B is an arbitrary nonsingleton subset of $W_{\tau }\left(X\right).$

The algebraic properties of $\widehat{\sigma }$ were proved in [19] that every extension $\widehat{\sigma }$ of non-deterministic generalized hypersubstitution $\sigma$ is an endomorphism of the algebra $(P\left(W_{\tau }\left(X\right)\right),{\widehat{S}}^n)$. Applying an extension $\widehat{\sigma }$, in [20], the binary operation ${\circ }_G^{nd}:Hy{p}_G^{nd}{\left(\tau \right)}^2\to Hy{p}_G^{nd}\left(\tau \right)$ was introduced by setting ${\sigma }_1{\circ }_G^{nd}{\sigma }_2:={\widehat{\sigma }}_1\circ {\sigma }_2$. Moreover, the non-deterministic generalized hypersubstitution ${\sigma }_{id}$ was defined to be an identity element where ${\sigma }_{id}\left(f_i\right):=\left\{f_i(x_1,\dots ,x_{n_i})\right\}$ for all $i\in I$. As a consequence, the structure $(Hy{p}_G^{nd}\left(\tau \right),{\circ }_G^{nd},{\sigma }_{id})$ forms a monoid.

As we mentioned above, there are many authors who studied the concepts of terms and tree languages in various structures. The lack of relationships among the algebras of terms and tree languages allows us to study in this paper. Thus, two potential questions natually arise: Firstly, are there interactions between several algebras of terms and tree languages? Secondly, how can these connections be described in terms of embedding, if any? In the present paper, these problems are answered in Section 2. Particularly, in Section 3, we define another binary operation for the set of all non-deterministic generalized hypersubstitutions and provide their interesting properties. An embedding theorem of a Menger algebra with infinitely many nullary operations in a suitable algebra is studied in Section 4. We also give a concrete example of this representation.

2. Monomorphisms between Semigroups of Terms and Tree Languages

In any Menger algebra $(G,\circ )$, i.e., the structure consisting of a nonempty set with an $(n+1)$-operation satisfying the superassociative law, a binary operation + on G can be defined by $a+b:=\circ (a,\underset{n\mathrm{times}}{\underbrace{b,\dots ,b}})$. It is not difficult to see that + is associative. The algebra $(G,+)$ is called the diagonal semigroup. Moreover, on the Cartesian power $G^n$, one can define a binary operation ∗ by $((x_1,\dots ,x_n)\ast (y_1,\dots ,y_n)):=(\circ (x_1,y_1,\dots ,y_n),\dots ,\circ (x_n,y_1,\dots ,y_n)).$ It turns out that $(G^n,\ast )$ forms a semigroup, which is called the binary comitant. In 2006, Denecke and Jampachon [11] defined these two semigroups for the set of terms and characterized the regularity and Green’s relations. The situation for tree languages was studied in [21].

In order to study the connection between the semigroups of terms and tree languages, we need the following lemma:

Lemma 1.

For any terms $t,s_1,\dots ,s_n\in W_{\tau }\left(X\right)$, we have

$$\left\{S^n(t,s_1,\dots ,s_n)\right\}={\widehat{S}}^n(\left\{t\right\},\left\{s_1\right\},\dots ,\left\{s_n\right\}).$$

Proof. 

We give a proof by induction on the complexity of the term t. The proof is easy to verify if t is a variable. Assume that $t=f_i(t_1,\dots ,t_{n_i})$ and

$$\left\{S^n(t_k,s_1,\dots ,s_n)\right\}={\widehat{S}}^n(\left\{t_k\right\},\left\{s_1\right\},\dots ,\left\{s_n\right\})$$

for every $k=1,\dots ,n_i$. Then,

• $\left\{S^n(t,s_1,\dots ,s_n)\right\}$
• $\hspace{1em}=\hspace{1em}\left\{S^n(f_i(t_1,\dots ,t_{n_i}),s_1,\dots ,s_n)\right\}$
• $\hspace{1em}=\hspace{1em}\left\{f_i(S^n(t_1,s_1,\dots ,s_n),\dots ,S^n(t_{n_i},s_1,\dots ,s_n))\right\}$
• $\hspace{1em}=\hspace{1em}\{f_i(r_1,\dots ,r_{n_i})\mid r_k\in \left\{S^n(t_k,s_1,\dots ,s_n)\right\},1\le k\le n_i\}$
• $\hspace{1em}=\hspace{1em}\{f_i(r_1,\dots ,r_{n_i})\mid r_k\in {\widehat{S}}^n(\left\{t_k\right\},\left\{s_1\right\},\dots ,\left\{s_n\right\}),1\le k\le n_i\}$
• $\hspace{1em}=\hspace{1em}{\widehat{S}}^n(\left\{f_i(t_1,\dots ,t_{n_i})\right\},\left\{s_1\right\},\dots ,\left\{s_{n_i}\right\})$
• $\hspace{1em}=\hspace{1em}{\widehat{S}}^n(\left\{t\right\},\left\{s_1\right\},\dots ,\left\{s_{n_i}\right\}).$

 □

Let I be a nonempty indexed set. The symbol ${\tau }_n^{\left|I\right|}$ means a fixed n-ary type with operation symbols ${\left(f_i\right)}_{i\in I}$. That is, ${\tau }_n^{\left|I\right|}$ is a sequence of $\left|I\right|$-tuple of fixed n-ary operation symbols. For instance, if $\left|I\right|=3$, ${\tau }_2^3=(2,2,2)$. This means that we have three binary operation symbols.

On the set $W_{{\tau }_n^{\left|I\right|}}\left(X\right)$, the binary operation ${+}_g$ can be defined by $s{+}_{g}t=S^n(s,t,\dots ,t)$ for all $s,t\in W_{{\tau }_n^{\left|I\right|}}\left(X\right)$. Similarly, the binary operation ${\oplus }_g$ on $P(W_{{\tau }_n^{\left|I\right|}}\left(X\right)$ is defined by setting $A{\oplus }_{g}B={\widehat{S}}^n(A,B,\dots ,B)$ for all $A,B\in P(W_{{\tau }_n^{\left|I\right|}}\left(X\right).$ Then, we have

Proposition 1.

The diagonal semigroup $(W_{{\tau }_n^{\left|I\right|}}\left(X\right),{+}_g)$ can be embedded into the diagonal power semigroup $(P\left(W_{{\tau }_n^{\left|I\right|}}\left(X\right)\right),{\oplus }_g)$.

Proof. 

It follows immediately from the superassociativity of $S^n$ and ${\widehat{S}}^n$ that $(W_{{\tau }_n^{\left|I\right|}}\left(X\right),{+}_g)$ and $(P\left(W_{{\tau }_n^{\left|I\right|}}\left(X\right)\right),{\oplus }_g)$ are semigroups. For any term t in $W_{{\tau }_n^{\left|I\right|}}\left(X\right)$, we define a mapping $\phi :W_{{\tau }_n^{\left|I\right|}}\left(X\right)\to P\left(W_{{\tau }_n^{\left|I\right|}}\left(X\right)\right)$ by $\phi \left(t\right)=\left\{t\right\}$. Obviously, $\phi$ is injective. Moreover, the homomorphism property is also true by applying Lemma 1. Since, for all $s,t\in W_{{\tau }_n^{\left|I\right|}}\left(X\right)$, we have $\phi \left(s{+}_{g}t\right)=\phi \left(S^n(s,t\dots ,t)\right)=\left\{S^n(s,t\dots ,t)\right\}={\widehat{S}}^n(\left\{s\right\},\left\{t\right\},\dots ,\left\{t\right\})={\widehat{S}}^n(\phi \left(s\right),\phi \left(t\right),\dots ,\phi \left(t\right))=\phi \left(s\right){\oplus }_g\phi \left(t\right).$  □

Proposition 2.

The binary comitant semigroup $(W_{{\tau }_n^{\left|I\right|}}{\left(X\right)}^n,{\ast }_g)$ where ${\ast }_g$ on $W_{{\tau }_n^{\left|I\right|}}{\left(X\right)}^n$ is defined by

$$\left((s_1,\dots ,s_n){\ast }_g(t_1,\dots ,t_n)\right):=(S^n(s_1,t_1,\dots ,t_n),\dots ,S^n(s_n,t_1,\dots ,t_n))$$

can be embedded into the semigroup $(P{\left(W_{{\tau }_n^{\left|I\right|}}\left(X\right)\right)}^n,{\otimes }_g)$ where the operation ${\ast }_g$ on $P{\left(W_{{\tau }_n^{\left|I\right|}}\left(X\right)\right)}^n$ is defined by

$\left((A_1,\dots ,A_n){\otimes }_{g}g(B_1,\dots ,B_n)\right):=({\widehat{S}}^n(A_1,B_1,\dots ,B_n),\dots ,{\widehat{S}}^n(A_n,B_1,\dots ,B_n)).$

Proof. 

Clearly, $(W_{{\tau }_n^{\left|I\right|}}{\left(X\right)}^n,{\ast }_g)$ and $(P{\left(W_{{\tau }_n^{\left|I\right|}}\left(X\right)\right)}^n,{\otimes }_g)$ are semigroups since the operations $S^n$ and ${\widehat{S}}^n$ satisfy the superassociative law, respectively. A mapping $\phi :W_{{\tau }_n^{\left|I\right|}}{\left(X\right)}^n\to P{\left(W_{{\tau }_n^{\left|I\right|}}\left(X\right)\right)}^n$ can be defined by $\phi \left((t_1,\dots ,t_n)\right)=(\left\{t_1\right\},\dots ,\left\{t_n\right\})$ for all terms $t_1,\dots ,t_n$ of type ${\tau }_n^{\left|I\right|}$. It is clearly that $\phi$ is injective. To prove that $\phi$ is homomorphism, we let $s_1,\dots ,s_n,t_1,\dots ,t_n$ be elements in $W_{{\tau }_n^{\left|I\right|}}\left(X\right)$. Then, by Lemma 1, we obtain

• $\phi \left((s_1,\dots ,s_n){\ast }_g(t_1,\dots ,t_n)\right)$
• $\hspace{1em}=\hspace{1em}\phi \left((S^n(s_1,t_1,\dots ,t_n),\dots ,S^n(s_n,t_1,\dots ,t_n))\right)$
• $\hspace{1em}=\hspace{1em}(\left\{S^n(s_1,t_1,\dots ,t_n)\right\},\dots ,\left\{S^n(s_n,t_1,\dots ,t_n)\right\})$
• $\hspace{1em}=\hspace{1em}({\widehat{S}}^n(\left\{s_1\right\},\left\{t_1\right\},\dots ,\left\{t_n\right\}),\dots ,{\widehat{S}}^n(\left\{s_n\right\},\left\{t_1\right\},\dots ,\left\{t_n\right\}))$
• $\hspace{1em}=\hspace{1em}(\left\{s_1\right\},\dots ,\left\{s_n\right\}){\ast }_g(\left\{t_1\right\},\dots ,\left\{t_n\right\})$
• $\hspace{1em}=\hspace{1em}\phi \left((s_1,\dots ,s_n)\right){\otimes }_g\phi \left((t_1,\dots ,t_n)\right).$

This finishes the proof.  □

A relationship between the diagonal semigroup $(W_{{\tau }_n^{\left|I\right|}}\left(X\right),{+}_g)$ and the binary comitant semigroup $(W_{{\tau }_n^{\left|I\right|}}{\left(X\right)}^n,{\ast }_g)$ is now provided.

Proposition 3.

Let $\phi :W_{{\tau }_n^{\left|I\right|}}\left(X\right)\to W_{{\tau }_n^{\left|I\right|}}{\left(X\right)}^n$ be a mapping which is defined by $\phi \left(t\right)=(t,\dots ,t)$ for all $t\in W_{{\tau }_n^{\left|I\right|}}\left(X\right)$. Then, φ is a monomorphism from $(W_{{\tau }_n^{\left|I\right|}}\left(X\right),{+}_g)$ into $(W_{{\tau }_n^{\left|I\right|}}{\left(X\right)}^n,{\ast }_g)$, i.e., it satisfies the identity $\phi \left(s{+}_{g}t\right)=\phi \left(s\right){\ast }_g\phi \left(t\right)$ for all $s,t\in W_{{\tau }_n^{\left|I\right|}}\left(X\right)$.

Proof. 

Injectivity of $\phi$ is clearly obtained. In addition, $\phi$ is homomorphism since $\phi \left(s{+}_{g}t\right)=\phi \left(S^n(s,t,\dots ,t)\right)=(S^n(s,t,\dots ,t),\dots ,S^n(s,t,\dots ,t))=(s,\dots ,s){\ast }_g(t,\dots ,t)=\phi \left(s\right){\ast }_g\phi \left(t\right)$.  □

Using the generalized superposition $S^n$ for every $1\le i\le n$, we define a binary operation ${·}_{x_i}$ on $W_{{\tau }_n^{\left|I\right|}}\left(X\right)$ in the following way:

$$s{·}_{x_i}t:=S^n(s,x_1,\dots ,x_{i-1},t,x_{i+1},\dots ,x_n)$$

for all $s,t\in W_{{\tau }_n^{\left|I\right|}}\left(X\right)$. Then, we have

Proposition 4.

The set $W_{{\tau }_n^{\left|I\right|}}\left(X\right)$ with a binary operation ${·}_{x_i}$ forms a monoid.

Proof. 

Because the generalized superposition $S^n$ satisfies the superassociative law, then a binary operation ${·}_{x_i}$ is associative. We see that a variable $x_i$ acts as the identity element, by the property of the generalized superposition $S^n$, we have $s{·}_{x_i}{x}_i=S^n(s,x_1,\dots ,x_{i-1},x_i,x_{i+1},\dots ,x_n)=s=S^n(x_i,x_1,\dots ,x_{i-1},s,x_{i+1},\dots ,x_n)=x_i{·}_{x_i}s$.  □

The situation for tree languages was already defined in [22], i.e., for any subsets $A,B$ of $W_{{\tau }_n^{\left|I\right|}}\left(X\right)$, the binary operation ${·}_{x_i}$ on $P\left(W_{{\tau }_n^{\left|I\right|}}\left(X\right)\right)$ is defined by

$$A{\odot }_{x_i}B:={\widehat{S}}^n(A,\left\{x_1\right\},\dots ,\left\{x_{i-1}\right\},B,\left\{x_{i+1}\right\},\dots ,\left\{x_n\right\}).$$

Furthermore, $(P\left(W_{{\tau }_n^{\left|I\right|}}\left(X\right)\right),{\odot }_{x_i})$ is a monoid, since the singleton $\left\{x_i\right\}$ is an identity with respect to ${·}_{x_i}$.

Proposition 5.

The monoid $(W_{{\tau }_n^{\left|I\right|}}\left(X\right),{·}_{x_i})$ can be embedded into $(P\left(W_{{\tau }_n^{\left|I\right|}}\left(X\right)\right),{\odot }_{x_i})$.

Proof. 

Firstly, we define a mapping $\phi :(W_{{\tau }_n^{\left|I\right|}}\left(X\right),{·}_{x_i})\to (P\left(W_{{\tau }_n^{\left|I\right|}}\left(X\right)\right),{\odot }_{x_i})$ by $\phi \left(t\right)=\left\{t\right\}$ for all $t\in W_{{\tau }_n^{\left|I\right|}}\left(X\right)$. Clearly, $\phi$ is injective. It can be shown straightforwardly that a mapping $\phi$ is a homomorphism.  □

3. The Left Seminearring of Non-Deterministic Generalized Hypersubstitutions

In this section, we investigate the structural properties of non-deterministic generalized hypersubstitutions. One of the algebraic structures that we are interested in is a seminearring.

Definition 1.

A left (right) seminearring is a triple of a nonempty set R together with two binary operations, denoted by + and ·, respectively, such that + and · is associative on R, and satisfying the left (right) distributive law, i.e., for all $a,b,c\in R,a·(b+c)=a·b+a·c\left(\right(a+b)·c=a·c+b·c).$

It was proved in [23] that, under suitable two binary operations, i.e., ${\circ }_G$ and ${+}_G$, which are defined by $\left({\sigma }_1{+}_G{\sigma }_2\right)\left(f_i\right):=S^{n_i}({\sigma }_2\left(f_i\right),{\sigma }_1\left(f_i\right),\dots ,{\sigma }_1\left(f_i\right))$ for all ${\sigma }_1,{\sigma }_2\in Hy{p}_G\left(\tau \right)$; the set of all generalized hypersubstitutions of type $\tau$ forms a left seminearring.

On the diagonal semigroup $(W_{{\tau }_n^{\left|I\right|}}\left(X\right),{+}_g)$ as we mentioned in the previous section, we now establish the relationship between the diagonal semigroup and the semigroup $(Hy{p}_G\left(\tau \right),{+}_G)$. To do this, we improve a definition of a binary operation ${+}_g$ by the following

$$s{+}_g^{\prime }t:=S^n(t,s,\dots ,s).$$

It can be proved by a direct calculation and the superassociativity of the generalized superposition $S^n$ that this defining operation is associative. Then, we have that

Proposition 6.

$(W_{{\tau }_n^{\left|I\right|}}\left(X\right),{+}_g^{\prime })$ is a semigroup.

A strong connection between the diagonal semigroup and the semigroup of all generalized hypersubstitutions is provided in the following theorem:

Theorem 1.

The diagonal semigroup $(W_{{\tau }_n^{\left|I\right|}}\left(X\right),{+}_g^{\prime })$ can be embedded into $(Hy{p}_G\left({\tau }_n^{\left|I\right|}\right),{+}_G)$.

Proof. 

For any generalized hypersubstitution of type ${\tau }_n^{\left|I\right|}$$\sigma$ and any term t, the mapping ${\sigma }_t$ is defined by ${\sigma }_t\left(f_i\right)=t$, where $f_i$ is an n-ary operation symbol. To prove this theorem, we define a mapping $\phi$ which takes each n-ary term t to a generalized hypersubstitution of type ${\tau }_n^{\left|I\right|}$ by $\phi \left(t\right)={\sigma }_t$ for all $t\in W_{{\tau }_n^{\left|I\right|}}\left(X\right)$. It is obvious that $\phi$ is injective. Now, let $s,t\in W_{{\tau }_n^{\left|I\right|}}\left(X\right)$. Then, $\phi \left(s{+}_g^{\prime }t\right)=\phi \left(S^n(t,s,\dots ,s)\right)={\sigma }_{S^n(t,s,\dots ,s)}={\sigma }_s{+}_G{\sigma }_t=\phi \left(s\right){+}_G\phi \left(t\right).$ In fact, we have ${\sigma }_{S^n(t,s,\dots ,s)}\left(f_i\right)=S^n(t,s,\dots ,s)=S^n({\sigma }_t\left(f_i\right),{\sigma }_s\left(f_i\right),\dots ,{\sigma }_s\left(f_i\right))=\left(\phi \left(s\right){+}_G\phi \left(t\right)\right)\left(f_i\right).$  □

The next purpose of this section is to define another binary operation on the set of all non-deterministic generalized hypersubstitutions. This leads us to form a novel semigroup. Now, we introduce a novel definition of the binary operation ${+}_G^{nd}$ on the set of all non-deterministic generalized hypersubstitutions of type $\tau$ by setting

$$\left({\sigma }_1{+}_G^{nd}{\sigma }_2\right)\left(f_i\right):={\widehat{S}}^{n_i}({\sigma }_2\left(f_i\right),{\sigma }_1\left(f_i\right),\dots ,{\sigma }_1\left(f_i\right)).$$

Then, $Hy{p}_G^{nd}\left(\tau \right)$ forms a semigroup with respect to the binary operation ${+}_G^{nd}$, which is presented in the following proposition:

Proposition 7.

$(Hy{p}_G^{nd}\left(\tau \right),{+}_G^{nd})$ is a semigroup.

Proof. 

Let ${\sigma }_1^{nd},{\sigma }_2^{nd}$ and ${\sigma }_3^{nd}$ be elements in $Hy{p}_G^{nd}\left(\tau \right)$. Because of the superassociativity of the generalized superposition ${\widehat{S}}^n$, we have

$\left(\left({\sigma }_1{+}_G^{nd}{\sigma }_2\right){+}_G^{nd}{\sigma }_3\right)\left(f_i\right)$	=	${\widehat{S}}^{n_i}({\sigma }_3\left(f_i\right),\left({\sigma }_1{+}_G^{nd}{\sigma }_2\right)\left(f_i\right),\dots ,\left({\sigma }_1{+}_G^{nd}{\sigma }_2\right)\left(f_i\right))$
	=	${\widehat{S}}^{n_i}({\widehat{S}}^{n_i}({\sigma }_3\left(f_i\right),{\sigma }_2\left(f_i\right),\dots ,{\sigma }_2\left(f_i\right)),{\sigma }_1\left(f_i\right),\dots ,{\sigma }_1\left(f_i\right))$
	=	${\widehat{S}}^{n_i}(\left({\sigma }_2{+}_G^{nd}{\sigma }_3\right)\left(f_i\right),{\sigma }_1\left(f_i\right),\dots ,{\sigma }_1\left(f_i\right))$
	=	$\left({\sigma }_1{+}_G^{nd}\left({\sigma }_2{+}_G^{nd}{\sigma }_3\right)\right)\left(f_i\right).$

The proof is finished.  □

Then, we have

Theorem 2.

$(Hy{p}_G^{nd}\left(\tau \right),{+}_G^{nd},{\circ }_G^{nd})$ is a left seminearring.

Proof. 

It is well known that $(Hy{p}_G^{nd}\left(\tau \right),{\circ }_G^{nd})$ is a semigroup and by Proposition 7 $(Hy{p}_G^{nd}\left(\tau \right),$ ${+}_G^{nd})$ is also a semigroup. Now, we show the left distributivity. For this, let ${\sigma }_1,{\sigma }_2$ and ${\sigma }_3$ be non-deterministic generalized hypersubstitutions of type ${\tau }_n^{\left|I\right|}$. Then, by the fact that any extension of non-deterministic generalized hypersubstitutions of type ${\tau }_n^{\left|I\right|}$ is endomorphism on the set of tree languages, we have

$\left({\sigma }_1{\circ }_G^{nd}\left({\sigma }_2{+}_G^{nd}{\sigma }_3\right)\right)\left(f_i\right)$	=	${\widehat{\sigma }}_1\left[\left({\sigma }_2{+}_G^{nd}{\sigma }_3\right)\left(f_i\right)\right]$
	=	${\widehat{\sigma }}_1\left[{\widehat{S}}^n({\sigma }_3\left(f_i\right),{\sigma }_2\left(f_i\right),\dots ,{\sigma }_2\left(f_i\right))\right]$
	=	${\widehat{S}}^n({\widehat{\sigma }}_1\left[{\sigma }_3\left(f_i\right)\right],{\widehat{\sigma }}_1\left[{\sigma }_2\left(f_i\right)\right],\dots ,{\widehat{\sigma }}_1\left[{\sigma }_2\left(f_i\right)\right])$
	=	${\widehat{S}}^n(\left({\sigma }_1{\circ }_G^{nd}{\sigma }_3\right)\left(f_i\right),\left({\sigma }_1{\circ }_G^{nd}{\sigma }_2\right)\left(f_i\right),\dots ,\left({\sigma }_1{\circ }_G^{nd}{\sigma }_2\right)\left(f_i\right))$
	=	$\left(\left({\sigma }_1{\circ }_G^{nd}{\sigma }_2\right){+}_G^{nd}\left({\sigma }_1{\circ }_G^{nd}{\sigma }_3\right)\right)\left(f_i\right).$

This shows that the left distributive law is valid.  □

The following counterexample shows that the right distributive law is not satisfied.

Example 1.

Let I be a singleton and the type ${\tau }_2^1=\left(2\right)$ with one binary operation symbol f. Define non-deterministic generalized hypersubstitutions of type ${\tau }_2^1$, say ${\sigma }_1,{\sigma }_2$ and ${\sigma }_3$ by

$${\sigma }_1\left(f\right)=\left\{f(x_1,f(x_2,x_5))\right\},{\sigma }_2\left(f\right)=\{x_4,f(x_3,x_2)\},{\sigma }_3\left(f\right)=\left\{f(x_2,x_1)\right\}.$$

Consider

$\left(\left({\sigma }_1{+}_G^{nd}{\sigma }_2\right){\circ }_G^{nd}{\sigma }_3\right)\left(f\right)$	=	${\left({\sigma }_1{+}_G^{nd}{\sigma }_2\right)}^{\widehat{}}\left[\left\{f(x_2,x_1)\right\}\right]$
	=	${\widehat{S}}^2(\left({\sigma }_1{+}_G^{nd}{\sigma }_2\right)\left(f\right),\left\{x_2\right\},\left\{x_1\right\})$
	=	${\widehat{S}}^2(\{x_4,f(x_3,f(x_1,f(x_2,x_5)))\},\left\{x_2\right\},\left\{x_1\right\})$
	=	$\{x_4,f(x_3,f(x_2,f(x_1,x_5)))\}$

and

• $\left(\left({\sigma }_1{\circ }_G^{nd}{\sigma }_3\right){+}_G^{nd}\left({\sigma }_2{\circ }_G^{nd}{\sigma }_3\right)\right)\left(f\right)$
• $\hspace{1em}=\hspace{1em}{\widehat{S}}^2(\left({\sigma }_2{\circ }_G^{nd}{\sigma }_3\right)\left(f\right),\left({\sigma }_1{\circ }_G^{nd}{\sigma }_3\right)\left(f\right),\left({\sigma }_1{\circ }_G^{nd}{\sigma }_3\right)\left(f\right))$
• $\hspace{1em}=\hspace{1em}{\widehat{S}}^2(\{x_4,f(x_1,x_5)\},\left\{f(x_2,f(x_1,x_5))\right\},\left\{f(x_2,f(x_1,x_5))\right\})$
• $\hspace{1em}=\hspace{1em}\{x_4,f(f(x_2,f(x_1,x_5)),x_5)\}$

Thus, $\left(\left({\sigma }_1{+}_G^{nd}{\sigma }_2\right){\circ }_G^{nd}{\sigma }_3\right)\ne \left(\left({\sigma }_1{\circ }_G^{nd}{\sigma }_3\right){+}_G^{nd}\left({\sigma }_2{\circ }_G^{nd}{\sigma }_3\right)\right).$ This means that the right distributive law is not true.

Based on the monoid $(Hy{p}_G\left(\tau \right),{\circ }_G,{\sigma }_{id})$, various algebraic structural properties of some submonoids were investigated by Leeratanavalee in [24]. Now, we extend these concepts to non-deterministic generalized hypersubstitutions and study some interesting relationships.

Definition 2.

Let $\tau ={\left(n_i\right)}_{i\in I}$ be a type with operation symbols $f_i$ having the arity $n_i$ for each $i\in I$. A non-deterministic generalized hypersubstitution σ is said to be

(1) 

projection non-deterministic generalized hypersubstitution if the image $\sigma \left(f_i\right)$ is a nonempty subset of X. Let $P_G^{nd}\left(\tau \right)$ be the set of all projection non-deterministic generalized hypersubstitutions of type τ.

(2) 

a pre-non-deterministic generalized hypersubstitution if $\sigma \left(f_i\right)$ is a nonempty subset of $W_{\tau }\left(X\right)\backslash X$. Let $Pr{e}_G^{nd}\left(\tau \right)$ be the set of all pre-non-deterministic generalized hypersubstitutions of type τ.

Theorem 3.

$P_G^{nd}\left(\tau \right)\cup \left\{{\sigma }_{id}\right\}$ and $Pr{e}_G^{nd}\left(\tau \right)$ are submonoids of $(Hy{p}_G^{nd}\left(\tau \right),{\circ }_G^{nd},{\sigma }_{id})$.

Proof. 

Obviously, the identity non-deterministic generalized hypersubstitution ${\sigma }_{id}$ belongs to the sets $P_G^{nd}\left(\tau \right)\cup \left\{{\sigma }_{id}\right\}$ and $Pr{e}_G^{nd}\left(\tau \right)$. Now, we let ${\sigma }_1,{\sigma }_2\in P_G^{nd}\left(\tau \right)\cup \left\{{\sigma }_{id}\right\}$. To prove that ${\sigma }_1{\circ }_G{\sigma }_2\in P_G^{nd}\left(\tau \right)\cup \left\{{\sigma }_{id}\right\}$, we consider the following four cases:

Case 1: ${\sigma }_1\in P_G^{nd}\left(\tau \right)$ and ${\sigma }_2={\sigma }_{id}$. Then, ${\sigma }_1\left(f_i\right)=B$ where $\varnothing \ne B\subseteq X$. Consider $\left({\sigma }_1{\circ }_G{\sigma }_{id}\right)\left(f_i\right)={\widehat{\sigma }}_1\left[{\sigma }_{id}\left(f_i\right)\right]={\widehat{S}}^{n_i}({\sigma }_1\left(f_i\right),\left\{x_1\right\},\dots ,\left\{x_{n_i}\right\})$. By the assumption, we have $\left({\sigma }_1{\circ }_G{\sigma }_{id}\right)\left(f_i\right)={\widehat{S}}^{n_i}(B,\left\{x_1\right\},\dots ,\left\{x_{n_i}\right\})={\displaystyle \bigcup _{b\in B}}{\widehat{S}}^n(\left\{b\right\},\left\{x_1\right\},\dots ,\left\{x_{n_i}\right\})\subseteq X.$ Thus, ${\sigma }_1{\circ }_G^{nd}{\sigma }_2\in P_G^{nd}\left(\tau \right)\cup \left\{{\sigma }_{id}\right\}.$

Case 2: ${\sigma }_1={\sigma }_{id}$ and ${\sigma }_2\in P_G^{nd}\left(\tau \right)$. Then, ${\sigma }_2\left(f_i\right)=B$ where $\varnothing \ne B\subseteq X$. Thus, $\left({\sigma }_{id}{\circ }_G{\sigma }_2\right)\left(f_i\right)={\widehat{\sigma }}_{id}\left[{\sigma }_2\left(f_i\right)\right]={\widehat{\sigma }}_{id}\left[B\right]=B$.

Case 3: ${\sigma }_1={\sigma }_{id}={\sigma }_2$. Obvious.

Case 4: ${\sigma }_1,{\sigma }_2\in P_G^{nd}\left(\tau \right)$. Then, both ${\sigma }_1\left(f_i\right)$ and ${\sigma }_2\left(f_i\right)$ are nonempty subsets of X. Thus, $\left({\sigma }_1{\circ }_G{\sigma }_2\right)\left(f_i\right)={\widehat{\sigma }}_1\left[{\sigma }_2\left(f_i\right)\right]={\widehat{\sigma }}_1\left[B\right]=B$ for some $\varnothing \ne B\subseteq X$ and ${\sigma }_2\left(f_i\right)=B$.

Finally, it is not difficult to verify that the composition of two pre-non-deterministic generalized hypersubstitutions is again a pre-non-deterministic generalized hypersubstitution:  □

Theorem 4.

$P_G^{nd}\left(\tau \right)$ and $Pr{e}_G^{nd}\left(\tau \right)$ form sub-left seminearrings of $(Hy{p}_G^{nd}\left(\tau \right),{+}_G^{nd},{\circ }_G^{nd})$.

Proof. 

Our goal is to show that the sets $P_G^{nd}\left(\tau \right)$ and $Pr{e}_G^{nd}\left(\tau \right)$ are closed under the binary operation ${+}_G^{nd}$. Let ${\sigma }_1,{\sigma }_2\in P_G^{nd}\left(\tau \right)$. Then, the images of them are nonempty subsets of X. Since $\left({\sigma }_1{+}_G^{nd}{\sigma }_2\right)\left(f_i\right)={\widehat{S}}^{n_i}({\sigma }_2\left(f_i\right),{\sigma }_1\left(f_i\right),\dots ,{\sigma }_1\left(f_i\right))$ and ${\sigma }_1\left(f_i\right),{\sigma }_2\left(f_i\right)$ are nonempty subsets of X, $\left({\sigma }_1{+}_G^{nd}{\sigma }_2\right)\left(f_i\right)$ is also a set of some variables from X. Thus, ${\sigma }_1{+}_G^{nd}{\sigma }_2\in P_G^{nd}\left(\tau \right)$. Next, let ${\sigma }_1,{\sigma }_2\in Pr{e}_G^{nd}\left(\tau \right)$. Then, the images of them are nonempty subsets of $W_{\tau }\left(X\right)\backslash X$. Since $\left({\sigma }_1{+}_G^{nd}{\sigma }_2\right)\left(f_i\right):={\widehat{S}}^{n_i}({\sigma }_2\left(f_i\right),{\sigma }_1\left(f_i\right),\dots ,{\sigma }_1\left(f_i\right))$ and ${\sigma }_1\left(f_i\right),{\sigma }_2\left(f_i\right)$ are nonempty subsets of $W_{\tau }\left(X\right)\backslash X$, $\left({\sigma }_1{+}_G^{nd}{\sigma }_2\right)\left(f_i\right)$ is a nonempty subset of $W_{\tau }\left(X\right)\backslash X$. This shows that ${\sigma }_1{+}_G^{nd}{\sigma }_2$ is a pre-non-deterministic generalized hypersubstitution.  □

Similar to Theorem 1, the situation for tree languages is given. To do this, the following tool is needed. For every subsets $A,B$ of terms of type ${\tau }_n^{\left|I\right|}$, a binary operation ${\oplus }_g^{\prime }:P\left(W_{{\tau }_n^{\left|I\right|}}\left(X\right)\right)\times P\left(W_{{\tau }_n^{\left|I\right|}}\left(X\right)\right)\to P\left(W_{{\tau }_n^{\left|I\right|}}\left(X\right)\right)$ is defined by

$$A{\oplus }_g^{\prime }B:={\widehat{S}}^n(B,A,\dots ,A).$$

Using the fact that the generalized superposition ${\widehat{S}}^n$ over tree languages satisfies the superassociative law, then we get

Lemma 2.

$(P\left(W_{{\tau }_n^{\left|I\right|}}\left(X\right)\right),{\oplus }_g^{\prime })$ forms a semigroup, and called the diagonal power semigroup.

We now investigate the relationship between the diagonal power semigroup which is constructed in Proposition 2 and the semigroup $(Hy{p}_G^{nd}\left({\tau }_n^{\left|I\right|}\right),{+}_G^{nd})$.

Theorem 5.

The diagonal power semigroup $(P\left(W_{{\tau }_n^{\left|I\right|}}\left(X\right)\right),{\oplus }_g^{\prime })$ can be embedded into $(Hy{p}_G^{nd}\left({\tau }_n^{\left|I\right|}\right)$, ${+}_G^{nd})$.

Proof. 

Let $\sigma$ be a non-deterministic generalized hypersubstitution of type ${\tau }_n^{\left|I\right|}$ and B be a subset of $W_{{\tau }_n^{\left|I\right|}}\left(X\right)$. Then, we associate a mapping ${\sigma }_B:\{f_i\mid i\in I\}\to P\left(W_{{\tau }_n^{\left|I\right|}}\left(X\right)\right)$ by ${\sigma }_B\left(f_i\right)=B$, where $f_i$ is an n-ary operation symbol. Then, a mapping $\phi$ from the powerset of n-ary terms to the non-deterministic generalized hypersubstitution of type ${\tau }_n^{\left|I\right|}$ is defined by $\phi \left(B\right)={\sigma }_B$ for all $B\subseteq W_{{\tau }_n^{\left|I\right|}}\left(X\right)$. It is commonly seen that $\phi$ is injective. Now, let $A,B\subseteq W_{{\tau }_n^{\left|I\right|}}\left(X\right)$. Then, $\phi \left(A{+}_g^{\prime }B\right)=\phi \left({\widehat{S}}^n(B,A,\dots ,A)\right)={\sigma }_{{\widehat{S}}^n(B,A,\dots ,A)}={\sigma }_A{+}_G^{nd}{\sigma }_B=\phi \left(A\right){+}_G^{nd}\phi \left(B\right).$ In fact, ${\sigma }_{{\widehat{S}}^n(B,A,\dots ,A)}\left(f_i\right)={\widehat{S}}^n(B,A,\dots ,A)={\widehat{S}}^n({\sigma }_B\left(f_i\right),{\sigma }_A\left(f_i\right),\dots ,{\sigma }_A\left(f_i\right))=\left(\phi \left(A\right){+}_B^{nd}\phi \left(t\right)\right)\left(f_i\right).$ Now, the proof is completed.  □

We complete this section by giving a significant connection between generalized hypersubstitutions and non-deterministic generalized hypersubstitutions. For convenient, a non-deterministic generalized hypersubstitution will be denoted by ${\sigma }^{nd}$.

Lemma 3.

For any term t, a generalized hypersubstitution of type τ σ, and a non-deterministic generalized hypersubstitution ${\sigma }^{nd}$,

$$\left\{\widehat{\sigma }\left[t\right]\right\}=\widehat{{\sigma }^{nd}}\left[\left\{t\right\}\right].$$

Proof. 

We give a proof on the complexity of the term t. If t is a variable, we are done. The proof follows directly from Lemma 1 if $t=f_i(t_1,\dots ,t_{n_i}):$  □

Theorem 6.

$(Hy{p}_G\left(\tau \right),{\circ }_G,{\sigma }_{id})$ can be embedded into $(Hy{p}_G^{nd}\left(\tau \right),{\circ }_G^{nd},{\sigma }_{id}).$

Proof. 

Let $f_i$ be an $n_i$-ary operation symbol and $\sigma$ a generalized hypersubstitution of type $\tau$. Then, we define $\overline{{\sigma }^{nd}}:\{f_i\mid i\in I\}\to P\left(W_{\tau }\left(X\right)\right)$ by $\overline{{\sigma }^{nd}}\left(f_i\right)=\left\{\sigma \left(f_i\right)\right\}$. It is clear that $\overline{{\sigma }^{nd}}$ belongs to $Hy{p}_G^{nd}\left(\tau \right)$. In order to prove that there is a monomorphism from $Hy{p}_G\left(\tau \right)$ to $Hy{p}_G^{nd}\left(\tau \right)$, we define a mapping $\theta :Hy{p}_G\left(\tau \right)\to Hy{p}_G^{nd}\left(\tau \right)$ by

$$\theta \left(\sigma \right)=\overline{{\sigma }^{nd}}$$

for all $\sigma \in Hy{p}_G\left(\tau \right).$ Clearly, the mapping $\theta$ is injective. Next, we let ${\sigma }_1,{\sigma }_2$ be two elements in $Hy{p}_G\left(\tau \right)$. Then, by Lemma 3, we have $\theta \left({\sigma }_1{\circ }_G{\sigma }_2\right)=\overline{{\left({\sigma }_1{\circ }_G{\sigma }_2\right)}^{nd}}=\overline{{\sigma }_1^{nd}}{\circ }_G^{nd}\overline{{\sigma }_2^{nd}}=\theta \left({\sigma }_1\right){\circ }_G^{nd}\theta \left({\sigma }_2\right).$ This shows that $\theta$ is a homomorphism.  □

Corollary 1.

The left seminearring $(Hy{p}_G\left(\tau \right),{+}_G,{\circ }_G^{nd})$ can be embedded into the left seminearring $(Hy{p}_G^{nd}\left(\tau \right),{+}_G^{nd},{\circ }_G^{nd})$.

A significant consequence of Theorem 6 is that a mapping ${\sigma }_t$ in $Hy{p}_G\left(\tau \right)$ corresponds to the idempotent or a regular non-deterministic generalized hypersubstitution ${\sigma }_{\left\{t\right\}}^{nd}$ in $(Hy{p}_G^{nd}\left(\tau \right),{\circ }_G^{nd},{\sigma }_{id}).$

4. Representation of Menger Algebra with Infinitely Many Nullary Operations by n-Ary Functions

Firstly, we recall some preliminaries and background notions of n-ary functions, see [25,26,27]. Let $A^n$ be the n-th Cartesian product of a nonempty set A. Any mapping from $A^n$ to A is called a full n-ary function or an n-ary operation. The set of all such mapping is denoted by $T(A^n,A)$. One can consider the Menger’s composition on the set $T(A^n,A)$, i.e., an $(n+1)$-operation

$$\mathcal{O}:T{(A^n,A)}^{n+1}\to T(A^n,A)$$

defined by

$$\mathcal{O}(f,g_1,\dots ,g_n)(a_1,\dots ,a_n)=f(g_1(a_1,\dots ,a_n),\dots ,g_n(a_1,\dots ,a_n)),$$

where $f,g_1,\dots ,g_n\in T(A^n,A),a_1,\dots ,a_n\in A.$ The set $T(A^n,A)$ is said to be an algebra of full functions or algebra of operations if the composition of $(n+1)$ functions from this set is also in this set, i.e., closed with respect to Menger’s composition. We can remark here that the Menger’s composition can be reduced to the usual composition of functions if $n=1$.

A Menger algebra of all full n-ary functions or Menger algebra of all n-ary operations is a pair of the set $T(A^n,A)$ of all full n-ary functions defined on A and the Menger composition of full n-ary functions satisfying the superassociative law. Each subalgebra of this algebra will be called a Menger algebra of full n-ary functions or Menger algebra of n-ary operations.

For each term t of the algebra $(W_{\tau }\left(X\right),S^n)$, we associate the full n-ary function ${\lambda }_t:W_{\tau }{\left(X\right)}^n\to W_{\tau }\left(X\right)$ by putting

$${\lambda }_t(s_1,\dots ,s_n)=S^n(t,s_1,\dots ,s_n)$$

for all $s_1,\dots ,s_n\in W_{\tau }\left(X\right)$, where $S^n$ is an $(n+1)$-ary generalized superposition operation defined on $W_{\tau }\left(X\right)$. The full n-ary function ${\lambda }_t$ is an element of $T(W_{\tau }{\left(X\right)}^n,W_{\tau }\left(X\right))$, which is called an inner left translation of $W_{\tau }\left(X\right)$ corresponding to the term t of $W_{\tau }\left(X\right)$.

In order to prove our main theorem, the following lemmas are primarily essential.

Lemma 4.

Let $(W_{\tau }\left(X\right),S^n)$ be a Menger algebra. Then,

$${\lambda }_{S^n(t,s_1,\dots ,s_n)}=\mathcal{O}({\lambda }_t,{\lambda }_{s_1},\dots ,{\lambda }_{s_n})$$

for all $t,s_1,\dots ,s_n\in W_{\tau }\left(X\right)$, where $S^n$ and $\mathcal{O}$ are generalized superposition operation and Menger’s composition, respectively.

Proof. 

Let $t,s_1,\dots ,s_n,v_1,\dots ,v_n$ be arbitrary elements in $W_{\tau }\left(X\right)$. Then, we have

${\lambda }_{S^n(t,s_1,\dots ,s_n)}(v_1,\dots ,v_n)$	=	$S^n(S^n(t,s_1,\dots ,s_n),v_1,\dots ,v_n)$
	=	$S^n(t,S^n(s_1,v_1,\dots ,v_n),\dots ,S^n(s_n,v_1,\dots ,v_n))$
	=	${\lambda }_t(S^n(s_1,v_1,\dots ,v_n),\dots ,S^n(s_n,v_1,\dots ,v_n))$
	=	${\lambda }_t({\lambda }_{s_1}(v_1,\dots ,v_n),\dots ,{\lambda }_{s_n}(v_1,\dots ,v_n))$
	=	$\mathcal{O}({\lambda }_t,{\lambda }_{s_1},\dots ,{\lambda }_{s_n})(v_1,\dots ,v_n).$

The proof is completed.  □

Now, we let ${\mathsf{\Lambda }}^{\prime }=\{{\lambda }_t\mid t\in W_{\tau }\left(X\right)\}$. Our next aim is to show that $({\mathsf{\Lambda }}^{\prime },\mathcal{O})$ forms a Menger subalgebra of $(T(W_{\tau }{\left(X\right)}^n,W_{\tau }\left(X\right)),\mathcal{O})$.

Lemma 5.

The set ${\mathsf{\Lambda }}^{\prime }$ forms a subalgebra of $(T(W_{\tau }{\left(X\right)}^n,W_{\tau }\left(X\right)),\mathcal{O})$ and thus $({\mathsf{\Lambda }}^{\prime },\mathcal{O})$ is a Menger algebra of full n-ary functions.

Proof. 

Obviously, $\varnothing \ne {\mathsf{\Lambda }}^{\prime }\subseteq (T(W_{\tau }{\left(X\right)}^n,W_{\tau }\left(X\right)),\mathcal{O})$. Let ${\lambda }_t,{\lambda }_{s_1},\dots ,{\lambda }_{s_n}$ be arbitrary full n-ary functions in $T(W_{\tau }{\left(X\right)}^n,W_{\tau }\left(X\right))$. It follows immediately from Lemma 4 that the composition of such mappings again a full n-ary function.  □

We now establish the Cayley’s theorem of a Menger algebra with infinitely many nullary operations as follows:

Theorem 7.

Let $(W_{\tau }\left(X\right),S^n)$ be a Menger algebra with infinitely many nullary operations. Define a mapping $\psi :W_{\tau }\left(X\right)\to {\mathsf{\Lambda }}^{\prime }$ by

$$\psi \left(t\right)={\lambda }_t$$

for all $t\in W_{\tau }\left(X\right)$. Then, ψ is an isomorphism from $W_{\tau }\left(X\right)$ to ${\mathsf{\Lambda }}^{\prime }$ and so $W_{\tau }\left(X\right)\cong {\mathsf{\Lambda }}^{\prime }$.

Proof. 

Clearly, $\psi$ is surjective. By Lemma 4, we have $\psi \left(S^n(t,s_1,\dots ,s_n)\right)={\lambda }_{S^n(t,s_1,\dots ,s_n)}=\mathcal{O}({\lambda }_t,{\lambda }_{s_1},\dots ,{\lambda }_{s_n})=\mathcal{O}(\psi \left(t\right),\psi \left(s_1\right),\dots ,\psi \left(s_n\right))$ and thus $\psi$ is a homomorphism. Furthermore, $\varphi$ is injective. Indeed, suppose that ${\lambda }_t={\lambda }_s$. Then, we obtain ${\lambda }_t(v_1,\dots ,v_n)={\lambda }_s(v_1,\dots ,v_n)$. By the definition of generalized superposition $S^n$, we conclude that t and s are the same term. Hence, $\varphi$ is injective. Therefore, $\varphi$ is an isomorphism from $W_{\tau }\left(X\right)$ to ${\mathsf{\Lambda }}^{\prime }$.  □

Finally, an interesting concrete example is demonstrated by considering an indexed set I is singleton and setting the type ${\tau }_2^{\left|I\right|}$ with a binary operation symbol f and a natural number n equal to 1. This means that we have the algebra $(W_{{\tau }_2^1}\left(X\right),S^1)$ where $S^1:W_{{\tau }_2^1}\left(X\right)\times W_{{\tau }_2^1}\left(X\right)\to W_{{\tau }_2^1}\left(X\right)$. Moreover, the full n-ary function also reduces to the usual full transformation with one composition of functions.

Example 2.

Consider a semigroup $A=\{x_1,x_2,f(x_2,x_3),f(x_4,f(x_5,x_3))\}$ with respect to a binary operation $S^1$ which is defined by the following table:

$S^1$	$x_1$	$x_2$	$f(x_2,x_3)$	$f(x_4,f(x_5,x_3))$
$x_1$	$x_1$	$x_2$	$f(x_2,x_3)$	$f(x_4,f(x_5,x_3))$
$x_2$	$x_2$	$x_2$	$x_2$	$x_2$
$f(x_2,x_3)$	$f(x_2,x_3)$	$f(x_2,x_3)$	$f(x_2,x_3)$	$f(x_2,x_3)$
$f(x_4,f(x_5,x_3))$	$f(x_4,f(x_5,x_3))$	$f(x_4,f(x_5,x_3))$	$f(x_4,f(x_5,x_3))$	$f(x_4,f(x_5,x_3))$

It is observed that A is a semigroup containing an identity element $x_1$. We now illustrate that A is isomorphic to some sets of the full transformation semigroups. To do this, we first demonstrate the process to establish a full transformation by considering a mapping ${\lambda }_{x_1}:A\to A$ such that ${\lambda }_{x_1}\left(x_1\right)=S^1(x_1,x_1)=x_1$, ${\lambda }_{x_1}\left(x_2\right)=S^1(x_1,x_2)=x_2$, ${\lambda }_{x_1}\left(f(x_2,x_3)\right)=S^1(x_1,f(x_2,x_3))=f(x_2,x_3)$ and ${\lambda }_{x_1}\left(f(x_4,f(x_5,x_3))\right)=f(x_4,f(x_5,x_3))$. Thus, $x_1\mapsto {\lambda }_{x_1}=\left(\begin{array}{cccc}{x}_1& x_2& f(x_2,x_3)& f(x_4,f(x_5,x_3))\\ x_1& x_2& f(x_2,x_3)& f(x_4,f(x_5,x_3))\end{array}\right)$. Furthermore, a mapping ${\lambda }_{x_2}:A\to A$ is defined by ${\lambda }_{x_2}\left(x_1\right)=x_2$, ${\lambda }_{x_2}\left(x_2\right)=x_2$, ${\lambda }_{x_2}\left(f(x_2,x_3)\right)=x_2$ and ${\lambda }_{x_2}\left(f(x_4,f(x_5,x_3))\right)=x_2$. Thus, the full transformation which corresponding to a term $x_2$ in A is

$${\lambda }_{x_2}=\left(\begin{array}{cccc}{x}_1& x_2& f(x_2,x_3)& f(x_4,f(x_5,x_3))\\ x_2& x_2& x_2& x_2\end{array}\right)$$

and so $x_2\mapsto {\lambda }_{x_2}=\left(\begin{array}{cccc}{x}_1& x_2& f(x_2,x_3)& f(x_4,f(x_5,x_3))\\ x_2& x_2& x_2& x_2\end{array}\right)$. For other terms in A, we obtain

$$f(x_2,x_3)\mapsto {\lambda }_{f(x_2,x_3)}=\left(\begin{array}{cccc}{x}_1& x_2& f(x_2,x_3)& f(x_4,f(x_5,x_3))\\ f(x_2,x_3)& f(x_2,x_3)& f(x_2,x_3)& f(x_2,x_3)\end{array}\right),$$

$$\begin{gathered} f(x_4,f(x_5,x_3))\mapsto {\lambda }_{f(x_4,f(x_5,x_3))}= \\ \left(\begin{array}{cccc}{x}_1& x_2& f(x_2,x_3)& f(x_4,f(x_5,x_3))\\ f(x_4,f(x_5,x_3))& f(x_4,f(x_5,x_3))& f(x_4,f(x_5,x_3))& f(x_4,f(x_5,x_3))\end{array}\right). \end{gathered}$$

By Theorem 7, $A\cong \{{\lambda }_{x_1},{\lambda }_{x_2},{\lambda }_{f(x_2,x_3)},{\lambda }_{f(x_4,f(x_5,x_3))}\}$. Furthermore, the table for these representations is just like the original table with a term t renamed by ${\lambda }_t$, as seen in the following table:

$\mathcal{O}$	${\lambda }_{x_1}$	${\lambda }_{x_2}$	${\lambda }_{f(x_2,x_3)}$	${\lambda }_{f(x_4,f(x_5,x_3))}$
${\lambda }_{x_1}$	${\lambda }_{x_1}$	${\lambda }_{x_2}$	${\lambda }_{f(x_2,x_3)}$	${\lambda }_{f(x_4,f(x_5,x_3))}$
${\lambda }_{x_2}$	${\lambda }_{x_2}$	${\lambda }_{x_2}$	${\lambda }_{x_2}$	${\lambda }_{x_2}$
${\lambda }_{f(x_2,x_3)}$	${\lambda }_{f(x_2,x_3)}$	${\lambda }_{f(x_2,x_3)}$	${\lambda }_{f(x_2,x_3)}$	${\lambda }_{f(x_2,x_3)}$
${\lambda }_{f(x_4,f(x_5,x_3))}$	${\lambda }_{f(x_4,f(x_5,x_3))}$	${\lambda }_{f(x_4,f(x_5,x_3))}$	${\lambda }_{f(x_4,f(x_5,x_3))}$	${\lambda }_{f(x_4,f(x_5,x_3))}$

We can comment here that, if we put $W_{{\tau }_2^1}\left(X\right)\backslash \left\{x_1\right\}$, then this set is also an infinite subsemigroup of $(W_{{\tau }_2^1}\left(X\right),S^1)$ and then every term in this set is a left zero and idempotent. Hence, $W_{{\tau }_2^1}\left(X\right)\backslash \left\{x_1\right\}$ forms a left zero band. We also have that it is a right ideal of $(W_{{\tau }_2^1}\left(X\right),S^1)$ and thus $(W_{{\tau }_2^1}\left(X\right),S^1)$ is not a right simple semigroup.

5. Conclusions

The paper was established to study a potential connection between terms, tree languages, and full n-ary functions. We prove in Section 2 that there exists a monomorphism from the semigroup of terms to the semigroup of tree languages in a natural way by defining an image of a mapping to be a singleton of term. In Section 3, the most significant knowledge and some elementary results concerning a mapping which is called a non-deterministic generalized hypersubstitution are provided. We completely define a second binary operation for such mappings and construct a left seminearring. Some submomoids of non-deterministic generalized hypersubstitutions are given and interesting structural properties of them are studied. Other kinds of submonoids are challenging questions for study:

It is widely accepted that the representation by functions is one of the most important keys in the study of classical algebras that describes the relationship between the original algebras and the algebras of functions. For this reason, in the final section, we also make an attempt to establish an n-ary function corresponding to each term t. We also construct the Cayley’s theorems for a Menger algebra with infinitely many nullary operations. It observed that our main results are also noticeable foundations and practical applications in mathematical study, theoretical computer sciences, and various categories of sciences. For the exact applications of our works, semigroups and groups are algebras of type ${\tau }_2^1=\left(2\right)$ if I is a singleton. If an indexed set I has two elements, then our results can be applied to varieties of semirings, rings, or lattices, which are varieties of type ${\tau }_2^2=(2,2).$

Finally, we provide some open problems for future research works. Firstly, attempt to apply the idea of Menger hyperalgebra, which was introduced in [28] to terms and tree languages. Secondly, determine a relationship between hypersubstitutions for algebraic systems and Nd-hypersubstitutions for algebraic systems.