Tikhonov Regularization Terms for Accelerating Inertial Mann-Like Algorithm with Applications

Abstract

In this manuscript, we accelerate the modified inertial Mann-like algorithm by involving Tikhonov regularization terms. Strong convergence for fixed points of nonexpansive mappings in real Hilbert spaces was discussed utilizing the proposed algorithm. Accordingly, the strong convergence of a forward–backward algorithm involving Tikhonov regularization terms was derived, which counts as finding a solution to the monotone inclusion problem and the variational inequality problem. Ultimately, some numerical discussions are presented here to illustrate the effectiveness of our algorithm.

1. Introduction

Let ℶ be a real HS equipped with inner product $⟨.,.⟩$ and induced norm $∥.∥,$ and A be a non-empty CCS of a real HS ℶ. The mapping $P:A\to A$ is called, for all $\phi ,\Im \in A$,

• $L-$Lipschitzian if and only if $∥P\phi -P\Im ∥\le L∥\phi -\Im ∥,L>0;$
• NE if and only if $∥P\phi -P\Im ∥\le ∥\phi -\Im ∥.$

The set of FPs of the mapping P is denoted by $\Omega \left(P\right),$ that is, $\Omega \left(P\right)=\{\phi \in A:\phi =P\phi \}$. It is common in the science arena for iterations that Mann’s algorithm is one of many successful iteration schemes for approximating FPs of NEMs. The Mann algorithm is written as follows: Let ${\phi }_0$ be an arbitrary point in $\beth ,$ for all $n\ge 0,$

$${\phi }_{n+1}=(1-{\eta }_n){\phi }_n+{\eta }_{n}P{\phi }_n,$$

(1)

where $\left\{{\eta }_n\right\}$ is a sequence of non-negative real numbers in $(0,1).$ Researchers in this direction proved under the hypothesis $\Omega \left(P\right)\ne \varnothing$ and suitable stipulations forced on $\left\{{\eta }_n\right\},$ the sequence $\left\{{\phi }_n\right\}$ created by (1) converges weakly to an FP of P.

Approximating FP problems for NEMs has many vital applications. Many problems can be seen as FP problems of NEMs, such as convex optimization problems, image restoration problems, monotone variational inequalities, and convex feasibility [1,2,3]. A large number of the symmetrical iteration methods (in Mann-term) for FP problems of NEMs were presented in the literature; for example, see [4,5,6,7,8,9]. Therefore, the innovation of efficient and stable algorithm methods that involved the Mann algorithm attracted tremendous interest from researchers, for example, the forward–backward algorithm [10] and the Douglas–Rachford algorithm [11]. All these symmetric algorithms have a weak convergence, which is a disadvantage of the algorithms mentioned above. Despite this defect, they have more applications in infinite-dimensional spaces, such as quantum physics and image reconstruction. The need for strong convergence became desperate to save time and effort, and especially a weak convergence is disappointing. Several authors obtained strong convergence by putting solid restrictions on the involved mapping, such as in optimization, they considered the concept of strong convexity. In monotone inclusions, they considered strong monotonicity. As a result that there are many cases, this system cannot obtain strong convergence, so it was necessary to investigate new effective algorithms. Recently, several mathematicians were able to apply the strong convergence of algorithms, see [12,13,14,15].

In 2019, Bot et al. [16] proposed a new form for Mann’s algorithm to overcome the deficiency described before, and he formulated it as follows: Let ${\phi }_0$ be an arbitrary point in $\beth ,$ for all $n\ge 0,$

$${\phi }_{n+1}={\eta }_n^2{\phi }_n+{\eta }_n^1\left(P\left({\eta }_n^2{\phi }_n\right)-{\eta }_n^2{\phi }_n\right).$$

(2)

Under mild stipulations for $\left\{{\eta }_n^1\right\}$ and $\left\{{\eta }_n^2\right\},$ they proved that the iterative sequence $\left\{{\phi }_n\right\}$ by (2) is strongly convergent. In addition, they applied (2) to obtain the strong convergence of the forward–backward algorithm for MIPs. Sequence $\left\{{\eta }_n^1\right\}$ in scheme (2) plays an important role in accelerating convergence and is called Tikhonov regularization sequence. On the other hand, the Tikhonov method which generates a sequence $\left\{{\phi }_n\right\}$ by the rule

$${\phi }_n=J_{{\zeta }_n}^{P}u,\mathrm{for}\mathrm{all}n\in \mathbb{N},$$

where $\daleth ,J$ are defined in the next section, $u\in \daleth ,\mathrm{and}{\zeta }_n>0.$

Many theoretical and numerical results for studying strong convergence by Tikhonov regularization technique have been provided, for example, see [16,17,18,19,20,21].

Regularization terms intervene loosely in many applications about artificial regularization. To various gradient flows, the artificial regularization term has played an essential role in the energy stability analysis such as epitaxial thin film model either with or without slope selection, a second order energy stable BDF method for the epitaxial thin film equation with slope selection, and a third order exponential time differencing numerical scheme for no-slope-selection epitaxial thin film model. For more details about this topic, see [22,23,24,25,26,27,28].

Recently, new types of fast algorithms have emerged. One of these algorithms is called the inertial algorithm which was first proposed by Polyak [29]. He presented an inertial extrapolation technique for minimizing a smooth convex function. A common characteristic of inertial algorithms is that the next iteration depends on a combination of the previous two iterates. It should be noted that this slight change has significantly improved the effectiveness and performance of these algorithms. After the emergence of this idea, the authors made efforts to introduce other terms to the inertial algorithm with the aim of increasing the acceleration and studying more in-depth applications, such as inertial extragradient algorithms [9,30,31], inertial projection algorithms [15,32,33], inertial Mann algorithms [33,34], and inertial forward–backward splitting algorithms [35,36,37]. All of these algorithms have one symmetrical convergence form, which is stronger and faster than the inertial algorithms.

According to the above results, this manuscript aims to accelerate the inertial algorithm by introducing a modified inertial Mann-like algorithm. This algorithm is used here to study the strong convergence of FPs of NEMs in real HSs. The forward–backward terms are involved in studying the strong convergence for the minimal norm solution in zeros set under the symmetrical conditions. Finally, our algorithm’s performance and efficiency have been illustrated by some numerical comparisons with previous algorithms. We found that our algorithms converge faster, which indicates our method’s success.

2. Preliminaries

In this section, we shall introduce some previous symmetrical subsequences which greatly help in understanding our paper. Throughout this manuscript, the notions ⟶ and ⇒ denote strong convergence and multivalued mappings, respectively, $G\left(P\right)$ denotes the graph of the mapping P and A is a non-empty CCS in a real HS ℶ.

Lemma 1 ([38]).

Let $\kappa ,\omega$, and υ be points in a HS ℶ and $\rho \in (0,1)$. Then

$${∥\rho \kappa +(1-\rho )\omega -\upsilon ∥}^2\le \rho {∥\kappa -\upsilon ∥}^2+(1-\rho ){∥\omega -\upsilon ∥}^2-\rho (1-\rho ){∥\kappa -\omega ∥}^2.$$

Lemma 2 ([39]).

Let ℶ be a real HS. Then, for each $\kappa ,\omega \in \beth ,$

(i) ${∥\kappa -\omega ∥}^2\le {∥\kappa ∥}^2+{∥\omega ∥}^2-2⟨\kappa ,\omega ⟩$,

(ii) ${∥\kappa +\omega ∥}^2\le {∥\kappa ∥}^2-2⟨\omega ,\kappa +\omega ⟩,$

Definition 1.

Let ${\eta }^1\in (0,1)$ be fixed, we say that a mapping $V:\beth \to \beth$ is ${\eta }^1-$averaged if V is written as $V=(1-{\eta }^1)I+{\eta }^{1}P,$ where I is an identity mapping and $P:\beth \to \beth$ is an NEM.

It is easy to prove that ${\eta }^1-$averaged operators are also NE.

Definition 2.

Assume that $\Gamma :\beth \to \beth$ is a multi-valued operator and its graph described as $G(\Gamma )=\left\{\right(\phi ,n)\in \beth \times \beth :n\in \Gamma \phi \}.$ The operator Γ is called:

(1) 

monotone, if for all $(\phi ,n),(\Im ,m)\in G(\Gamma ),$$⟨\phi -\Im ,n-m⟩\ge 0;$

(2) 

MM, if it is monotone and its graph $G(\Gamma )$ is not a proper subset of one of any other monotone mapping;

(3) 

$\vartheta -ISM,$ if for all $\phi ,\Im \in \beth ,$ there is a constant $\vartheta >0$ so that $⟨\phi -\Im ,\Gamma \phi -\Gamma \Im ⟩\ge \vartheta {∥\Gamma \phi -\Gamma \Im ∥}^2.$

The resolvent of $\Gamma ,$$J_{\Gamma }:\beth \to \beth$ is described by $J_{\Gamma }={(I+\Gamma )}^{-1}$ and the reflected resolvent of $A,$$V_{\Gamma }:\beth \to \beth$ is defined by $V_{\Gamma }=2J_{\Gamma }-I.$ The mapping $J_{\Gamma }$ is single-valued, maximally monotone, and NE if $\Gamma$ is maximally monotone [1]. In addition, $0\in \left(\Gamma +\Xi \right)\left(\phi \right)$ iff $\phi =J_{\Gamma }(I-\tau \Xi )\left(\phi \right),$$\forall \tau >0.$ If $\Xi$ is $\vartheta -$ISM with $0<\tau <2\vartheta ,$ then $J_{\tau \Gamma }(I-\tau \Xi )$ is averaged.

We have to remember that, if the function $r:\beth \to (-\infty ,+\infty )$ is convex, proper, and lower-semicontinuous, then $\partial r:\beth \Rightarrow \beth$ is called the differentiable of r and it described by

$$\partial r\left(\phi \right)=\{t\in \beth :r(\Im )-r\left(\phi \right)\ge ⟨t,\Im -\phi ⟩,\forall \Im \in \beth \},$$

for $\phi \in \beth$ with $r\left(\phi \right)\ne +\infty .$ We define the proximal operator of r as

$$pro{x}_r:\beth \to \beth ,pro{x}_r\left(\phi \right)=arg\underset{\Im \in \beth }{min}\left\{\frac{1}{2}{∥\Im -\phi ∥}^2+r(\Im )\right\}.$$

It is worth mentioning that $pro{x}_r=J_{\partial r},$ i.e., the proximal operator of r, and the resolvent of $\partial r$ [1] are symmetric. The indicator function ${\delta }_A\left(\phi \right)$ of a non-empty closed and convex set $A\in \beth$ is given by

$${\delta }_A\left(\phi \right)=\left\{\begin{array}{cc}0,& \mathrm{if}\phi \in A,\\ +\infty ,& \mathrm{if}\phi \notin A.\end{array}\right.$$

By the theorem of Baillon-Haddad ([1], Corollary 18.16), $\nabla s:\beth \to \beth$ is a $\vartheta -$ISM operator provided that the function $s:\beth \to \mathbb{R}$ is Fréchet differentiable with $\frac{1}{\vartheta }-$Lipschitz gradient.

Lemma 3

(Demi-closedness property). Assume that A is a non-empty CCS of a real HS ℶ. Let $P:A\to \beth$ be an NEM and $\left\{{\phi }_n\right\}$ be a sequence in A and $\phi \in \beth$ so that ${\phi }_n$ converges weakly to φ and $P{\phi }_n-\phi ⟶0$ as $n\to +\infty$, then $\phi \in \Omega \left(P\right).$

Lemma 4 ([40])

Assume that $\left\{e_n\right\}$ is a sequence of non-negative real numbers so that

$$e_{n+1}\le (1-{\varpi }_n)e_n+q_n+v_n,n\ge 1,$$

where ${\varpi }_n\in (0,1)$ is a sequence and $q_n$ is a real sequence. Let ${\sum }_n^{\infty }{v}_n<\infty .$ Then the assumptions below hold:

(1) 

For some $\alpha \ge 0,$ if $q_n\le {\varpi }_n\alpha ,$ then the sequence $\left\{e_n\right\}$ is bounded;

(2) 

If ${\sum }_n^{\infty }{\varpi }_n=\infty$ and $lim{sup}_{n\to \infty }\frac{q_n}{{\varpi }_n}\le 0,$ then ${lim}_{n\to \infty }{e}_n=0.$

3. The Strong Convergence of a Modified Inertial Mann-Like Algorithm

In this part, we shall discuss the strong convergence for our proposed algorithm under mild conditions.

Theorem 1.

Let A be a CCS of a real HS ℶ and $P:A\to A$ be an NE mapping so that $\Omega \left(P\right)\ne \varnothing .$ In addition, suppose the hypotheses below are fulfilled:

(i) 

${lim}_{n\to +\infty }{\eta }_n^1=0={lim}_{n\to +\infty }{\eta }_n^2,$${\sum }_n^{\infty }{\eta }_n^1=\infty ,$${\sum }_n^{\infty }{\eta }_n^2=\infty ,$${\eta }_n^1,{\eta }_n^2$ with ${\eta }_n^1\ne {\eta }_n^2$ and ${\eta }_n^3\in [a,b]\subset (0,1],$

(ii) 

${lim}_{n\to +\infty }\frac{{\xi }_n}{{\eta }_n^1}∥{\phi }_n-{\phi }_{n-1}∥=0={lim}_{n\to +\infty }\frac{{\xi }_n}{{\rho }_n}∥{\phi }_n-{\phi }_{n-1}∥,$ where ${\rho }_n\in (0,1)$ and ${\rho }_n={\eta }_n^1-{\eta }_n^1{\eta }_n^3+{\eta }_n^2{\eta }_n^3.$

Set ${\phi }_0,{\phi }_1$ arbitrary. Define the sequence $\left\{{\phi }_n\right\}$ by the following iterative scheme:

$$\left\{\begin{array}{c}{\Lambda }_n={\phi }_n+{\xi }_n\left({\phi }_n-{\phi }_{n-1}\right),\hfill \\ {\Im }_n=(1-{\eta }_n^1){\Lambda }_n,\hfill \\ {\Re }_n=(1-{\eta }_n^2){\Lambda }_n,\hfill \\ {\phi }_{n+1}=(1-{\eta }_n^3){\Im }_n+{\eta }_n^{3}P{\Re }_n,n\ge 1.\hfill \end{array}\right.$$

(3)

Then the sequence $\left\{{\phi }_n\right\}$ defined by the algorithm (3) converges to $\Omega \left(P\right)$ in norm.

Proof. 

We split the proof into the following steps:

Step 1. Show that $\left\{{\phi }_n\right\}$ is bounded. Indeed, for any $\sigma \in \Omega \left(P\right),$ as P is NE and by the definition of $\left\{{\phi }_{n+1}\right\}$, we have

$$\begin{array}{ccc}\hfill ∥{\phi }_{n+1}-\sigma ∥& =& ∥(1-{\eta }_n^3){\Im }_n+{\eta }_n^{3}P{\Re }_n-\sigma ∥\hfill \\ & =& ∥(1-{\eta }_n^3)\left({\Im }_n-\sigma \right)+{\eta }_n^3\left(P{\Re }_n-\sigma \right)∥\hfill \\ & \le & (1-{\eta }_n^3)∥{\Im }_n-\sigma ∥+{\eta }_n^3∥{\Re }_n-\sigma ∥.\hfill \end{array}$$

(4)

From (3), we get

$$\begin{array}{ccc}\hfill ∥{\Im }_n-\sigma ∥& \le & (1-{\eta }_n^1)∥{\Lambda }_n-\sigma ∥+{\eta }_n^1∥\sigma ∥\hfill \\ & \le & (1-{\eta }_n^1)∥{\phi }_n-\sigma ∥+{\eta }_n^1∥\sigma ∥+(1-{\eta }_n^1){\xi }_n∥{\phi }_n-{\phi }_{n-1}∥.\hfill \end{array}$$

(5)

Similarly, we can obtain

$$∥{\Re }_n-\sigma ∥\le (1-{\eta }_n^2)∥{\phi }_n-\sigma ∥+{\eta }_n^2∥\sigma ∥+(1-{\eta }_n^2){\xi }_n∥{\phi }_n-{\phi }_{n-1}∥.$$

(6)

From (5) and (6) in (4), and using the hypothesis (ii), we get

$$\begin{array}{ccc}\hfill ∥{\phi }_{n+1}-\sigma ∥& \le & (1-{\eta }_n^3)\left[(1-{\eta }_n^1)∥{\phi }_n-\sigma ∥+{\eta }_n^1∥\sigma ∥+(1-{\eta }_n^1){\xi }_n∥{\phi }_n-{\phi }_{n-1}∥\right]\hfill \\ & & +{\eta }_n^3\left[(1-{\eta }_n^2)∥{\phi }_n-\sigma ∥+{\eta }_n^2∥\sigma ∥+(1-{\eta }_n^2){\xi }_n∥{\phi }_n-{\phi }_{n-1}∥\right]\hfill \\ & =& \left[(1-{\eta }_n^3)(1-{\eta }_n^1)+{\eta }_n^3(1-{\eta }_n^2)\right]∥{\phi }_n-\sigma ∥\hfill \\ & & +\left[{\eta }_n^1(1-{\eta }_n^3)+{\eta }_n^3{\eta }_n^2\right]∥\sigma ∥\hfill \\ & & +\left[\left(1-{\eta }_n^3)(1-{\eta }_n^1)+{\eta }_n^3(1-{\eta }_n^2\right)\right]{\xi }_n∥{\phi }_n-{\phi }_{n-1}∥\hfill \\ & =& (1-\left({\eta }_n^1-{\eta }_n^1{\eta }_n^3+{\eta }_n^2{\eta }_n^3\right))∥{\phi }_n-\sigma ∥+\left({\eta }_n^1-{\eta }_n^1{\eta }_n^3+{\eta }_n^2{\eta }_n^3\right)∥\sigma ∥\hfill \\ & & +(1-\left({\eta }_n^1-{\eta }_n^1{\eta }_n^3+{\eta }_n^2{\eta }_n^3\right)){\xi }_n∥{\phi }_n-{\phi }_{n-1}∥\hfill \\ & =& (1-{\rho }_n)∥{\phi }_n-\sigma ∥+{\rho }_n∥\sigma ∥+(1-{\rho }_n){\xi }_n∥{\phi }_n-{\phi }_{n-1}∥.\hfill \end{array}$$

(7)

By the fact that ${sup}_{n\ge 1}\frac{{\xi }_n}{{\rho }_n}∥{\phi }_n-{\phi }_{n-1}∥$ exists, consider

$$\Theta =2max\left\{∥\sigma ∥,\frac{(1-{\rho }_n){\xi }_n}{{\rho }_n}∥{\phi }_n-{\phi }_{n-1}∥\right\}.$$

Then, inequality (7) is reduced to

$$∥{\phi }_{n+1}-\sigma ∥\le (1-{\rho }_n)∥{\phi }_n-\sigma ∥+{\rho }_n\Theta .$$

By Lemma 4, we conclude that $\left\{{\phi }_n\right\}$ is bounded.

On the other side, by the definition of ${\Lambda }_n,$ we have

$${∥{\Lambda }_n-\sigma ∥}^2={∥{\phi }_n-\sigma ∥}^2+2{\xi }_n⟨{\phi }_n-{\phi }_{n-1},{\phi }_n-\sigma ⟩+{\xi }_n^2{∥{\phi }_n-{\phi }_{n-1}∥}^2.$$

(8)

Therefore, by the boundedness of $\left\{{\phi }_n\right\}$ and hypothesis (ii), we see that $\left\{{\Lambda }_n\right\}$ is bounded, and thus $\left\{{\Im }_n\right\}$ and $\left\{{\Re }_n\right\}$ are bounded too. From (3), one has

$$P{\Re }_n-{\Im }_n=\frac{1}{{\eta }_n^3}\left({\phi }_{n+1}-{\Im }_n\right).$$

(9)

and

$${∥{\Lambda }_n-{\phi }_{n+1}∥}^2={∥{\phi }_n-{\phi }_{n+1}∥}^2+2{\xi }_n⟨{\phi }_n-{\phi }_{n-1},{\phi }_n-{\phi }_{n+1}⟩+{\xi }_n^2{∥{\phi }_n-{\phi }_{n-1}∥}^2.$$

(10)

Using (4) and Lemma 1, 2 (i), we have

$$\begin{array}{ccc}\hfill {∥{\phi }_{n+1}-\sigma ∥}^2& =& {∥(1-{\eta }_n^3){\Im }_n+{\eta }_n^{3}P{\Re }_n-\sigma ∥}^2\hfill \\ & =& {\eta }_n^3{∥P{\Re }_n-\sigma ∥}^2+(1-{\eta }_n^3){∥{\Im }_n-\sigma ∥}^2-{\eta }_n^3(1-{\eta }_n^3){∥{\Im }_n-P{\Re }_n∥}^2\hfill \\ & =& {\eta }_n^3{∥P{\Re }_n-{\Im }_n-(\sigma -{\Im }_n)∥}^2+(1-{\eta }_n^3){∥{\Im }_n-\sigma ∥}^2-{\eta }_n^3(1-{\eta }_n^3){∥{\Im }_n-P{\Re }_n∥}^2\hfill \\ & \le & {\eta }_n^3{∥{\Im }_n-P{\Re }_n∥}^2+{\eta }_n^3{∥{\Im }_n-\sigma ∥}^2-2⟨P{\Re }_n-{\Im }_n,\sigma -{\Im }_n⟩\hfill \\ & & +(1-{\eta }_n^3){∥{\Im }_n-\sigma ∥}^2-{\eta }_n^3(1-{\eta }_n^3){∥{\Im }_n-P{\Re }_n∥}^2\hfill \\ & \le & {∥{\Im }_n-\sigma ∥}^2+{\left({\eta }_n^3\right)}^2{∥{\Im }_n-P{\Re }_n∥}^2-2⟨P{\Re }_n-{\Im }_n,\sigma -{\Im }_n⟩\hfill \\ & =& {∥{\Im }_n-\sigma ∥}^2+{∥{\phi }_{n+1}-{\Im }_n∥}^2-\frac{2}{{\eta }_n^3}⟨{\phi }_{n+1}-{\Im }_n,\sigma -{\Im }_n⟩.\hfill \end{array}$$

(11)

From Lemma 2, one gets

$$-2⟨{\phi }_{n+1}-{\Im }_n,\sigma -{\Im }_n⟩\le {∥{\phi }_{n+1}-\sigma ∥}^2-{∥{\Im }_n-\sigma ∥}^2.$$

(12)

Applying (12) in (11), one can write

$${∥{\phi }_{n+1}-\sigma ∥}^2\le {∥{\Im }_n-\sigma ∥}^2+{∥{\phi }_{n+1}-{\Im }_n∥}^2+\frac{1}{{\eta }_n^3}\left({∥{\phi }_{n+1}-\sigma ∥}^2-{∥{\Im }_n-\sigma ∥}^2\right),$$

this implies that

$$(1-\frac{1}{{\eta }_n^3}){∥{\phi }_{n+1}-\sigma ∥}^2\le (1-\frac{1}{{\eta }_n^3}){∥{\Im }_n-\sigma ∥}^2+{∥{\phi }_{n+1}-{\Im }_n∥}^2.$$

Setting $\frac{{\eta }_n^3}{{\eta }_n^3-1}=-k$, one can obtain

$${∥{\phi }_{n+1}-\sigma ∥}^2\le {∥{\Im }_n-\sigma ∥}^2-k{∥{\phi }_{n+1}-{\Im }_n∥}^2,$$

(13)

From (8), (10), and (13) and Lemma 2 (i), we have

$$\begin{array}{ccc}\hfill {∥{\phi }_{n+1}-\sigma ∥}^2& \le & {∥{\Im }_n-\sigma ∥}^2-k{∥{\Im }_n-{\phi }_{n+1}∥}^2\hfill \\ & \le & {∥{\Lambda }_n-\sigma -{\eta }_n^1{\Lambda }_n∥}^2-k{∥{\Lambda }_n-{\phi }_{n+1}-{\eta }_n^1{\Lambda }_n∥}^2\hfill \\ & =& {∥{\Lambda }_n-\sigma ∥}^2-2{\eta }_n^1⟨{\Lambda }_n,{\Lambda }_n-\sigma ⟩+{\left({\eta }_n^1\right)}^2{∥{\Lambda }_n∥}^2\hfill \\ & & -k{∥{\Lambda }_n-{\phi }_{n+1}∥}^2+2k{\eta }_n^1⟨{\Lambda }_n,{\Lambda }_n-{\phi }_{n+1}⟩-k{\left({\eta }_n^1\right)}^2{∥{\Lambda }_n∥}^2\hfill \\ & =& {∥{\Lambda }_n-\sigma ∥}^2-k{∥{\Lambda }_n-{\phi }_{n+1}∥}^2+{\eta }_n^1[-2⟨{\Lambda }_n,{\Lambda }_n-\sigma ⟩\hfill \\ & & +2k⟨{\Lambda }_n,{\Lambda }_n-{\phi }_{n+1}⟩+(1-k){\eta }_n^1{∥{\Lambda }_n∥}^2]\hfill \\ & =& {∥{\phi }_n-\sigma ∥}^2-k{∥{\phi }_n-{\phi }_{n+1}∥}^2\hfill \\ & & +2{\xi }_n⟨{\phi }_n-{\phi }_{n-1},{\phi }_n-\sigma ⟩+2k⟨{\phi }_n-{\phi }_{n-1},{\phi }_n-{\phi }_{n+1}⟩\hfill \\ & & +(1-k){\xi }_n^2{∥{\phi }_n-{\phi }_{n-1}∥}^2+{\eta }_n^1[-2⟨{\Lambda }_n,{\Lambda }_n-\sigma ⟩\hfill \\ & & +2k⟨{\Lambda }_n,{\Lambda }_n-{\phi }_{n+1}⟩+(1-k){\eta }_n^1{∥{\Lambda }_n∥}^2].\hfill \end{array}$$

(14)

Since $\left\{{\phi }_n\right\}$ and $\left\{{\Lambda }_n\right\}$ are bounded, then there is a constant ${\Theta }_1\ge 0$ so that

$$-2⟨{\Lambda }_n,{\Lambda }_n-\sigma ⟩+2k⟨{\Lambda }_n,{\Lambda }_n-{\phi }_{n+1}⟩+(1-k){\eta }_n^1{∥{\Lambda }_n∥}^2\le {\Theta }_1,\mathrm{for}\mathrm{all}n\ge 0.$$

Set

$${\Theta }_2=2{\xi }_n⟨{\phi }_n-{\phi }_{n-1},{\phi }_n-\sigma ⟩+2k⟨{\phi }_n-{\phi }_{n-1},{\phi }_n-{\phi }_{n+1}⟩+(1-k){\xi }_n^2{∥{\phi }_n-{\phi }_{n-1}∥}^2.$$

Then, the inequality (14) is reduced to

$${∥{\phi }_{n+1}-\sigma ∥}^2-{∥{\phi }_n-\sigma ∥}^2+k{∥{\phi }_n-{\phi }_{n+1}∥}^2\le {\eta }_n^1{\Theta }_1+{\Theta }_2.$$

(15)

Step 2. Prove that $\left\{{\phi }_n\right\}$ converges strongly to $\sigma .$ In order to reach it, we will discuss the two cases below:

Case 1. If the sequence $\left\{∥{\phi }_n-\sigma ∥\right\}$ is monotonically decreasing, then it is convergent. Therefore, we obtain

$${∥{\phi }_{n+1}-\sigma ∥}^2-{∥{\phi }_n-\sigma ∥}^2\to 0,\mathrm{as}n\to \infty ,$$

this implies with (15) and hypotheses (i) and (ii) that

$$∥{\phi }_n-{\phi }_{n+1}∥\to 0,\mathrm{as}n\to \infty .$$

(16)

On the other hand, it is easy to see that

$$∥{\Lambda }_n-{\phi }_{n+1}∥=∥{\phi }_n-{\phi }_{n+1}∥+{\xi }_n∥{\phi }_n-{\phi }_{n-1}∥\to 0,\mathrm{as}n\to \infty ,$$

(17)

and

$$∥{\Im }_n-{\Lambda }_n∥\le {\eta }_n^1∥{\Lambda }_n∥\to 0,\mathrm{as}n\to \infty ,$$

(18)

Similarly, one has

$$∥{\Re }_n-{\Lambda }_n∥\le {\eta }_n^2∥{\Lambda }_n∥\to 0,\mathrm{as}n\to \infty .$$

(19)

It follows from (17) and (18) and the triangle inequality that

$$∥{\Im }_n-{\phi }_{n+1}∥\le ∥{\Im }_n-{\Lambda }_n∥+∥{\Lambda }_n-{\phi }_{n+1}∥\to 0,\mathrm{as}n\to \infty .$$

(20)

By the same manner, using (17) and (19), one can obtain

$$∥{\Re }_n-{\phi }_{n+1}∥\le ∥{\Re }_n-{\Lambda }_n∥+∥{\Lambda }_n-{\phi }_{n+1}∥\to 0,\mathrm{as}n\to \infty .$$

(21)

Applying (16) and (20), we get

$$∥{\Im }_n-{\phi }_n∥\le ∥{\Im }_n-{\phi }_{n+1}∥+∥{\phi }_{n+1}-{\phi }_n∥\to 0,\mathrm{as}n\to \infty .$$

(22)

In addition, applying (16) and (21), we have

$$∥{\Re }_n-{\phi }_n∥\le ∥{\Re }_n-{\phi }_{n+1}∥+∥{\phi }_{n+1}-{\phi }_n∥\to 0,\mathrm{as}n\to \infty .$$

(23)

Going to Equation (9) and using (20), we can write

$$∥P{\Re }_n-{\Im }_n∥=\frac{1}{{\eta }_n^3}∥{\phi }_{n+1}-{\Im }_n∥\to 0,\mathrm{as}n\to \infty .$$

(24)

Combining (22)–(24), one sees that

$$\begin{array}{ccc}& & ∥{\phi }_n-P{\phi }_n∥\hfill \\ & \le & ∥{\phi }_n-{\Im }_n∥+∥{\Im }_n-P{\Re }_n∥+∥P{\Re }_n-P{\phi }_n∥\hfill \\ & \le & ∥{\phi }_n-{\Im }_n∥+∥{\Im }_n-P{\Re }_n∥+∥{\Re }_n-{\phi }_n∥\to 0,\mathrm{as}n\to \infty .\hfill \end{array}$$

(25)

Using the fact that $I-P$ is demi-closed, then $\left\{{\phi }_n\right\}$ converges weakly to an FP of $P.$

Still in our minds is proof that $\left\{{\phi }_n\right\}$ converges strongly to an FP of $P.$ In view of (14), we have

$$\begin{array}{ccc}& & {∥{\phi }_{n+1}-\sigma ∥}^2\hfill \\ & \le & {∥{\Im }_n-\sigma ∥}^2-k{∥{\Im }_n-{\phi }_{n+1}∥}^2\hfill \\ & =& {∥(1-{\eta }_n^1)({\Lambda }_n-\sigma )-{\eta }_n^1{\Lambda }_n∥}^2-k{∥{\Im }_n-{\phi }_{n+1}∥}^2\hfill \\ & \le & (1-{\eta }_n^1){∥{\Lambda }_n-\sigma ∥}^2-2{\eta }_n^1⟨{\Im }_n-\sigma ,\sigma ⟩-k{∥{\Im }_n-{\phi }_{n+1}∥}^2\hfill \\ & \le & (1-{\eta }_n^1){∥{\phi }_n-\sigma ∥}^2+2{\xi }_n⟨{\phi }_n-{\phi }_{n-1},{\phi }_n-\sigma ⟩\hfill \\ & & +{\left({\xi }_n\right)}^2{∥{\phi }_n-{\phi }_{n-1}∥}^2-2{\eta }_n^1⟨{\Im }_n-\sigma ,\sigma ⟩-k{∥{\Im }_n-{\phi }_{n+1}∥}^2.\hfill \end{array}$$

(26)

By hypotheses (i) and (ii), we deduce that

$$2{\xi }_n⟨{\phi }_n-{\phi }_{n-1},{\phi }_n-\sigma ⟩+{\left({\xi }_n\right)}^2{∥{\phi }_n-{\phi }_{n-1}∥}^2-2{\eta }_n^1⟨{\Im }_n-\sigma ,\sigma ⟩\to 0,\mathrm{as}n\to \infty .$$

(27)

Applying (20) and (27) in (26) after taking the limit as $n\to \infty$, we get

$${∥{\phi }_{n+1}-\sigma ∥}^2\le (1-{\eta }_n^1){∥{\phi }_n-\sigma ∥}^2.$$

Thus, by Lemma 4, we conclude that ${\phi }_n\to \sigma .$

Case 2. Assume that $\left\{∥{\phi }_n-\sigma ∥\right\}$ is not a monotonically decreasing sequence. Put ${\mho }_n=∥{\phi }_n-\sigma ∥.$ Suppose that $\chi \left(n\right):\mathbb{N}\to \mathbb{N}$ is a mapping defined by $\chi \left(n\right)=max\{\vartheta \in \mathbb{N}:\vartheta \le n,{\mho }_k\le {\mho }_{k+1}\}$ for all $n\ge n_0$ (for some large enough $n_0$). It is clear that $\chi \left(n\right)$ is a non-decreasing with $\chi \left(n\right)\to \infty$ as $n\to \infty$ and for all $n\ge n_0,$${\mho }_{\chi \left(n\right)}\le {\mho }_{\chi \left(n\right)+1}.$ By Applying (15), we have

$${∥{\phi }_{\chi \left(n\right)}-{\phi }_{\chi \left(n\right)+1}∥}^2\le \frac{{\eta }_{\chi \left(n\right)}^1{\Theta }_1+{\Theta }_2}{k}\to 0,\mathrm{as}n\to \infty ,$$

which leads to $∥{\phi }_{\chi \left(n\right)}-{\phi }_{\chi \left(n\right)+1}∥\to 0,$ as $n\to \infty .$ By the same manner as (17)–(27) in Case 1, we get directly that $\left\{{\phi }_{\chi \left(n\right)}\right\}$ converges weakly to $\sigma$ as $\chi \left(n\right)\to \infty .$ Using (26) for $n\ge n_0$, we get

$$\begin{array}{ccc}\hfill {∥{\phi }_{\chi \left(n\right)+1}-\sigma ∥}^2& \le & (1-{\eta }_n^1){∥{\phi }_{\chi \left(n\right)}-\sigma ∥}^2+2{\xi }_{\chi \left(n\right)}⟨{\phi }_{\chi \left(n\right)}-{\phi }_{\chi \left(n\right)-1},{\phi }_{\chi \left(n\right)}-\sigma ⟩\hfill \\ & & +{\left({\xi }_{\chi \left(n\right)}\right)}^2{∥{\phi }_{\chi \left(n\right)}-{\phi }_{\chi \left(n\right)-1}∥}^2-2{\eta }_{\chi \left(n\right)}^1⟨{\Im }_{\chi \left(n\right)}-\sigma ,\sigma ⟩-k{∥{\Im }_{\chi \left(n\right)}-{\phi }_{\chi \left(n\right)+1}∥}^2\hfill \\ & \le & (1-{\eta }_n^1){∥{\phi }_{\chi \left(n\right)}-\sigma ∥}^2+2{\xi }_{\chi \left(n\right)}⟨{\phi }_{\chi \left(n\right)}-{\phi }_{\chi \left(n\right)-1},{\phi }_{\chi \left(n\right)}-\sigma ⟩\hfill \\ & & +{\left({\xi }_{\chi \left(n\right)}\right)}^2{∥{\phi }_{\chi \left(n\right)}-{\phi }_{\chi \left(n\right)-1}∥}^2-2{\eta }_{\chi \left(n\right)}^1⟨{\Im }_{\chi \left(n\right)}-\sigma ,\sigma ⟩,\hfill \end{array}$$

in another form, we have

$$\begin{array}{ccc}\hfill 0& \le & {∥{\phi }_{\chi \left(n\right)+1}-\sigma ∥}^2-{∥{\phi }_{\chi \left(n\right)}-\sigma ∥}^2\hfill \\ & \le & {\eta }_{\chi \left(n\right)}^1\left[2⟨\sigma -{\Im }_{\chi \left(n\right)},\sigma ⟩-{∥{\phi }_{\chi \left(n\right)}-\sigma ∥}^2\right]+2{\xi }_{\chi \left(n\right)}⟨{\phi }_{\chi \left(n\right)}-{\phi }_{\chi \left(n\right)-1},{\phi }_{\chi \left(n\right)}-\sigma ⟩\hfill \\ & & +{\left({\xi }_{\chi \left(n\right)}\right)}^2{∥{\phi }_{\chi \left(n\right)}-{\phi }_{\chi \left(n\right)-1}∥}^2,\hfill \end{array}$$

which leads to

$$\begin{array}{ccc}\hfill {∥{\phi }_{\chi \left(n\right)}-\sigma ∥}^2& \le & 2⟨\sigma -{\Im }_{\chi \left(n\right)},\sigma ⟩+\frac{2{\xi }_{\chi \left(n\right)}}{{\eta }_{\chi \left(n\right)}^1}⟨{\phi }_{\chi \left(n\right)}-{\phi }_{\chi \left(n\right)-1},{\phi }_{\chi \left(n\right)}-\sigma ⟩\hfill \\ & & +\frac{{\left({\xi }_{\chi \left(n\right)}\right)}^2}{{\eta }_{\chi \left(n\right)}^1}{∥{\phi }_{\chi \left(n\right)}-{\phi }_{\chi \left(n\right)-1}∥}^2.\hfill \end{array}$$

(28)

Hence, by hypotheses (i), (ii), and (28), we can obtain

$$\underset{n\to \infty }{lim}∥{\phi }_{\chi \left(n\right)}-\sigma ∥=0.$$

Therefore, ${lim}_{n\to \infty }{\mho }_{\chi \left(n\right)}={lim}_{n\to \infty }{\mho }_{\chi \left(n\right)+1}=0.$ Further, for any $n\ge n_0,$ it can be easily obtained that ${\mho }_n\le {\mho }_{\chi \left(n\right)+1}$ if $n\ne \chi \left(n\right),$ that is $n>\chi \left(n\right),$ because ${\mho }_l\le {\mho }_{l+1}$ for $\chi \left(n\right)+1\le l\le n.$ Based on it, we find that for each $n\ge n_0$

$$0\le {\mho }_l\le max\{{\mho }_{\chi \left(n\right)},{\mho }_{\chi \left(n\right)+1}\}={\mho }_{\chi \left(n\right)+1}.$$

Consequently, we conclude that ${lim}_{n\to \infty }{\mho }_n=0,$ that is $\left\{{\phi }_n\right\}\to \sigma$ in norm. This finishes the proof. □

Remark 1.

We have discussions below about algorithm (3):

(1) 

If ${\xi }_n=0$, and ${\eta }_n^1={\eta }_n^2$ for each $n\ge 1$ in algorithm (3), then we get the exciting results of Bot et al. [16].

(2) 

For the Tikhonov regularization sequences $\left\{{\eta }_n^1\right\}$ and $\left\{{\eta }_n^2\right\}$, one can set ${\eta }_n^1={\eta }_n^2=\frac{1}{n+1},$ for any $n\ge 1$.

(3) 

Algorithm (3) is reduced to inertial Mann algorithm introduced by Maingé [34], if we take ${\eta }_n^1={\eta }_n^2=0.$

(4) 

The hypothesis (ii) of our theorem is easy to calculate and not complicated because the value $∥{\phi }_n-{\phi }_{n-1}∥$ is known before choosing ${\xi }_n$ so it plays an important role in the numerical discussions. For special options, the parameter ${\xi }_n$ in the proposed algorithm can be taken as:

$$0\le {\xi }_n\le \widehat{{\xi }_n},\widehat{{\xi }_n}=\left\{\begin{array}{cc}min\left\{\frac{{\xi }_n}{∥{\phi }_n-{\phi }_{n-1}∥},\frac{n-1}{n+\vartheta -1}\right\},& \mathrm{if}{\phi }_n\ne {\phi }_{n-1},\\ \frac{n-1}{n+\vartheta -1},& \mathrm{otherwise},\end{array}\right.$$

for some $\vartheta \ge 3$ and $\left\{{\xi }_n\right\}$ is a positive sequence so that ${lim}_{n\to +\infty }\frac{{\xi }_n}{{\eta }_n^1}=0={lim}_{n\to +\infty }\frac{{\xi }_n}{{\rho }_n}.$ This concept was introduced by Beck and Teboulle [41] for the inertial extrapolated step.

(5) 

If we set ${\eta }_n^1={\eta }_n^2$ in our algorithm, we have the results of Tan and Cho [42].

The result below is very important in the next section, where it has a prominent role in obtaining the strong convergence by the forward–backward method equipped with the Tikhonov regularization term.

Corollary 1.

Assume that A is a non-empty CCS of a real HS ℶ and $V:A\to A$ is an ${\eta }^1-$averaged mapping, where ${\eta }^1\in (0,1),$ with $\Omega \left(V\right)\ne \varnothing .$ Suppose that the assumptions below hold:

(C${}_1$)

${lim}_{n\to +\infty }{\eta }_n^1=0={lim}_{n\to +\infty }{\eta }_n^2,$${\sum }_n^{\infty }{\eta }_n^1=\infty ,$${\sum }_n^{\infty }{\eta }_n^2=\infty ,$${\eta }_n^1,{\eta }_n^2\in (0,1)$ with ${\eta }_n^1\ne {\eta }_n^2$ and ${\eta }_n^3\in [a,b]\subset (0,\frac{1}{{\eta }^1}],$

(C${}_2$)

${lim}_{n\to +\infty }\frac{{\xi }_n}{{\eta }_n^1}∥{\phi }_n-{\phi }_{n-1}∥=0={lim}_{n\to +\infty }\frac{{\xi }_n}{{\rho }_n}∥{\phi }_n-{\phi }_{n-1}∥,$ where ${\rho }_n\in (0,1)$ and ${\rho }_n={\eta }_n^1-{\eta }_n^1{\eta }_n^3+{\eta }_n^2{\eta }_n^3.$

Set ${\phi }_0,{\phi }_1$ arbitrary and define the sequence $\left\{{\phi }_n\right\}$ by:

$$\left\{\begin{array}{c}{\Lambda }_n={\phi }_n+{\xi }_n\left({\phi }_n-{\phi }_{n-1}\right),\hfill \\ {\Im }_n=(1-{\eta }_n^1){\Lambda }_n,\hfill \\ {\Re }_n=(1-{\eta }_n^2){\Lambda }_n,\hfill \\ {\phi }_{n+1}=(1-{\eta }_n^3){\Im }_n+{\eta }_n^{3}V{\Re }_n,n\ge 1.\hfill \end{array}\right.$$

(29)

Then the iterative sequence $\left\{{\phi }_n\right\}$ by (29) converges to an FP of V in norm.

Proof. 

Algorithm (29) is equivalent to algorithm (3) with the equation $V=(1-{\eta }_n^1)I+{\eta }_n^{1}P.$ As a result that $V:A\to A$ is an ${\eta }^1-$averaged mapping, then $P:\beth \to \beth$ is NE. Therefore, $\Omega \left(P\right)=\Omega \left(V\right)$ and the result follow immediately by Theorem 1. □

4. Applications

4.1. Solve Monotone Inclusion Problem

According to the general algorithm in Theorem 1, in this part, we will proposed a strongly convergent inertial forward–backward algorithm with Tikhonov regularization terms for solving the MIP below

$$\mathrm{Find}\phi \in \beth \mathrm{such}\mathrm{that}0\in \Gamma \phi +\Xi \phi$$

(30)

where $\Gamma :\beth ⟹\beth$ is an MM operator and $\Xi :\beth \to \beth$ is a $\vartheta -$ISM operator. MIP (30) has wonderful applications in linear inverse problem, machine learning, and image processing.

Theorem 2.

Let $\Gamma :\beth ⟹\beth$ be an MM operator and $\Xi :\beth \to \beth$ be an $\vartheta -$ISM operator so that $\Omega \left(\Gamma +\Xi \right)\ne \varnothing .$ Assume that $\tau \in (0,2\vartheta ]$. Let the assumptions below hold:

(MI${}_1$)

${lim}_{n\to +\infty }{\eta }_n^1=0={lim}_{n\to +\infty }{\eta }_n^2,$${\sum }_n^{\infty }{\eta }_n^1=\infty ,$${\sum }_n^{\infty }{\eta }_n^2=\infty ,$${\eta }_n^1,{\eta }_n^2\in (0,1)$ with ${\eta }_n^1\ne {\eta }_n^2$ and ${\eta }_n^3\in [a,b]\subset (0,\frac{4\vartheta -\tau }{2\vartheta }],$

(MI${}_2$)

${lim}_{n\to +\infty }\frac{{\xi }_n}{{\eta }_n^1}∥{\phi }_n-{\phi }_{n-1}∥=0={lim}_{n\to +\infty }\frac{{\xi }_n}{{\rho }_n}∥{\phi }_n-{\phi }_{n-1}∥,$ where ${\rho }_n\in (0,1)$ and ${\rho }_n={\eta }_n^1-{\eta }_n^1{\eta }_n^3+{\eta }_n^2{\eta }_n^3.$

Set ${\phi }_0,{\phi }_1$ arbitrary and define the sequence $\left\{{\phi }_n\right\}$ by the iterative scheme below:

$$\left\{\begin{array}{c}{\Lambda }_n={\phi }_n+{\xi }_n\left({\phi }_n-{\phi }_{n-1}\right),\hfill \\ {\Im }_n=(1-{\eta }_n^1){\Lambda }_n,\hfill \\ {\Re }_n=(1-{\eta }_n^2){\Lambda }_n,\hfill \\ {\phi }_{n+1}=(1-{\eta }_n^3){\Im }_n+{\eta }_n^3{J}_{\tau \Gamma }({\Re }_n-\tau \Xi \left({\Re }_n\right)),n\ge 1.\hfill \end{array}\right.$$

(31)

Then the sequence $\left\{{\phi }_n\right\}$ generated by (31) converges to ${\mho }_{{(\Gamma +\Xi )}^{-1}}\left(0\right)$ in norm.

Proof. 

Since the mapping $P:\beth ⟹\beth$ can be described by $P=J_{\tau \Gamma }\circ (I-\tau \Xi ),$ then algorithm (31) can be written as (3). To discuss the convergence, we consider two situations. The first one is $\tau \in (0,2\vartheta ].$ According to ([1], Remark 4.24(iii) and Corollary 23.8), $J_{\tau \Gamma }$ is $\frac{1}{2}-$ISM. Moreover, by means of ([1], Proposition 4.33), $I-\tau \Xi$ is $\frac{\tau }{2\vartheta }-$averaged. This implies from ([16], Proposition 6) that P is $\frac{2\vartheta }{4\vartheta -\tau }-$averaged. By noticing that $\Omega \left(P\right)={(\Gamma +\Xi )}^{-1}\left(0\right),$ then the desired result follows by Corollary 1. The second situation is $\tau =2\vartheta .$ Since $I-\tau \Xi$ is NE, then $P=J_{\tau \Gamma }\circ (I-\tau \Xi )$ is too. Therefore, the desired conclusion follows immediately by Theorem 1. □

Remark 2.

The applications below follow from Theorem 2:

• If ${\eta }_n^3=1,$${\eta }_n^1={\eta }_n^2$, and $\Xi =0,$ then the algorithm (31) turn into ${\phi }_{n+1}=J_{\tau \Gamma }\left((1-{\eta }_n^1){\Lambda }_n\right).$ This equation takes another form as,

  $${\Lambda }_n\in \frac{1}{1-{\eta }_n^1}{\phi }_{n+1}+\frac{\tau }{1-{\eta }_n^1}\Gamma {\phi }_{n+1}=\left(I+{\gamma }_{n}I+\frac{\tau }{1-{\eta }_n^1}\Gamma \right)\left({\phi }_{n+1}\right)$$
  where ${\gamma }_n=\frac{1}{1-{\eta }_n^1}-1>0$, ${lim}_{n\to +\infty }{\gamma }_n=0$, and the term ${\gamma }_{n}I$ is called the Tikhonov regularization. This term makes rapid convergence of iterative sequence $\left\{{\phi }_n\right\}$ the minimal norm solution. To more details about solving MIOs by Tikhonov-like methods, see [16,43,44].
• Suppose that the function $r:\beth \to (-\infty ,+\infty )$ is convex, proper, and lower-semicontinuous, and the function $s:\beth \to \mathbb{R}$ is a convex and Fréchet differentiable with $\frac{1}{\vartheta }-$Lipschitz continuous gradient so that $argmin(r+s)\ne \varnothing .$ Taking $\tau \in (0,2\vartheta ].$ For initial values ${\phi }_0,{\phi }_1\in \beth ,$ and $\left\{{\eta }_n^1\right\},$$\left\{{\eta }_n^2\right\},$$\left\{{\eta }_n^3\right\}$, and $\left\{{\xi }_n\right\}$ are real sequences verifying assumptions $\left(M{I}_1\right)$ and $\left(M{I}_2\right)$ of Theorem 2, the sequence $\left\{{\phi }_n\right\}$ created by the iterative scheme

  $$\left\{\begin{array}{c}{\Lambda }_n={\phi }_n+{\xi }_n\left({\phi }_n-{\phi }_{n-1}\right),\hfill \\ {\Im }_n=(1-{\eta }_n^1){\Lambda }_n,\hfill \\ {\Re }_n=(1-{\eta }_n^2){\Lambda }_n,\hfill \\ {\phi }_{n+1}=(1-{\eta }_n^3){\Im }_n+{\eta }_n^{3}pro{x}_{\tau r}({\Re }_n-\tau {\nabla }_s\left({\Re }_n\right)),n\ge 1,\hfill \end{array}\right.$$
  converges to ${\mho }_{argmin(r+s)}\left(0\right)$ in norm.

4.2. Solve Variational Inequality Problem

There are many applications to the variational inequality theory, and this is the reason why researchers working in this direction are constantly increasing. Among the developments involved in variational inequality techniques, contact problems in elasticity [45], economics equilibrium [46], transportation problems [47,48] and fluid flow through porous media [49]. Ideas explaining these formulas have led to the development of powerful new techniques for solving a wide class of linear and nonlinear problems.

In this part, we reformulate the algorithm (3) of Theorem 1 to find a solution to the VIP:

$$\mathrm{Find}\widehat{\phi }\in A\mathrm{such}\mathrm{that}⟨\Gamma \widehat{\phi },\Im -\widehat{\phi }⟩\ge 0,\Im \in A,$$

(32)

where $\Gamma :\beth \to \beth$ is a mapping and A is a non-empty CCS of $\beth .$ It is common that, for $\upsilon$, an arbitrary positive constant $\widehat{\phi }$ is a solution of (32) if and only if $\widehat{\phi }={\mho }_A(\widehat{\phi }-\upsilon \Gamma \widehat{\phi }).$

Theorem 3.

Suppose that $\Gamma :\beth \to \beth$ is a monotone and $L-$LC operator on a non-empty CCS A and $\upsilon =\frac{1}{L}.$ Put $P={\mho }_A(I-\upsilon \Gamma )$. Let the assumptions below be fulfilled:

(i) 

${lim}_{n\to +\infty }{\eta }_n^1=0={lim}_{n\to +\infty }{\eta }_n^2,$${\sum }_n^{\infty }{\eta }_n^1=\infty ,$${\sum }_n^{\infty }{\eta }_n^2=\infty ,$${\eta }_n^1,{\eta }_n^2,{\eta }_n^3\in (0,1)$ with ${\eta }_n^1\ne {\eta }_n^2$.

(ii) 

${lim}_{n\to +\infty }\frac{{\xi }_n}{{\eta }_n^1}∥{\phi }_n-{\phi }_{n-1}∥=0={lim}_{n\to +\infty }\frac{{\xi }_n}{{\rho }_n}∥{\phi }_n-{\phi }_{n-1}∥,$ where ${\rho }_n\in (0,1)$ and ${\rho }_n={\eta }_n^1-{\eta }_n^1{\eta }_n^3+{\eta }_n^2{\eta }_n^3.$

Set ${\phi }_0,{\phi }_1$ arbitrary, then the iterative sequence $\left\{{\phi }_n\right\}$ created by:

$$\left\{\begin{array}{c}{\Lambda }_n={\phi }_n+{\xi }_n\left({\phi }_n-{\phi }_{n-1}\right),\hfill \\ {\Im }_n=(1-{\eta }_n^1){\Lambda }_n,\hfill \\ {\Re }_n=(1-{\eta }_n^2){\Lambda }_n,\hfill \\ {\phi }_{n+1}=(1-{\eta }_n^3){\Im }_n+{\eta }_n^3{\mho }_A(I-\upsilon \Gamma ){\Re }_n,n\ge 1.\hfill \end{array}\right.$$

converges to ${\mho }_{\Omega \left(P\right)}\left(0\right)$ in norm.

Proof. 

Since $P={\mho }_A(I-\upsilon \Gamma )$ is NE, then the proof is finished by Theorem 1. □

5. Numerical Results

In this section, we include some experimental studies that appear in finite and infinite dimensional spaces to illustrate the computational efficiency of the suggested algorithm and to correlate them with certain previously reported algorithms. The MATLAB codes were run in MATLAB version 9.5 (R2018b) on a PC Intel(R) Core(TM)i5-6200 CPU @ 2.30 GHz 2.40 GHz, RAM 8.00 GB.

Example 1.

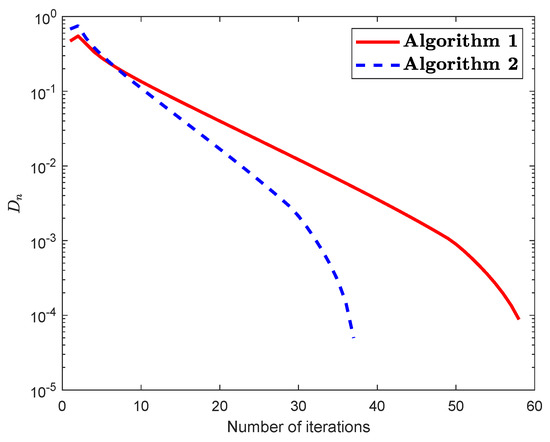
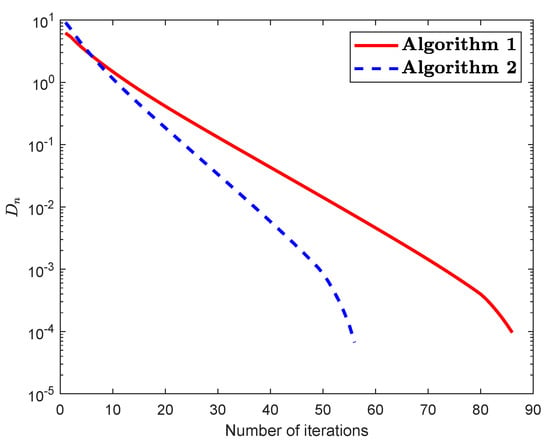
Consider that a fixed point problem taken from [50] in which the HS $\beth =\mathbb{R}$ through the usual real number space $\mathbb{R}$. A mapping $P:\beth \to \beth$ is defined by

$$P\left(\phi \right)={(5{\phi }^2-2\phi +48)}^{\frac{1}{3}},\forall \phi \in A,$$

where the set A is defined by $A:=\{\phi :0\le \phi \le 50\}.$ The control conditions for both algorithms are taken as follows:

• Algorithm (3) in [42] (shortly, Algorithm 1)

  $${\xi }_n=\frac{10}{{(n+1)}^2},\eta =4.00,{\beta }_n=0.90,{\alpha }_n=\frac{1}{100(n+2)}.$$
• Algorithm in (3) (shortly, Algorithm 2)

  $${\xi }_n=\frac{10}{{(n+1)}^2},\eta =4.00,{\eta }_n^3=0.90,{\eta }_n^1=\frac{1}{100(n+2)},2{\eta }_n^2=\frac{1}{100(n+2)}.$$

To illustrate the behaviour in this example see Table 1, Table 2, Table 3 and Table 4 and Figure 1 and Figure 2.

Table 1. Example 1: Numerical study of Algorithm 1 and ${\phi }_0={\phi }_1=10$.

	Algorithm 1
Iter $\left(\mathit{n}\right)$	Number of Iterations	Elapsed Time in Seconds
1	9.52906283555083	0.0003853
2	8.98011598373419	0.0004156
3	8.54688915734646	0.0004351
4	8.20841316725670	0.0004468
5	7.92926653937987	0.0004531
6	7.69282498118123	0.0004591
⋮	⋮	⋮
53	5.99022147329775	0.0007752
54	5.98986811411892	0.0007816
55	5.98960142820344	0.0007885
56	5.98940627063036	0.0007957
57	5.98926993349447	0.0008036
58	5.98918181370462	0.0008099
CPU time is seconds	0.001018

Table 2. Example 1: Numerical study of Algorithm 2 and ${\phi }_0={\phi }_1=10$.

	Algorithm 2
Iter $\left(\mathit{n}\right)$	Number of Iterations	Elapsed Time in Seconds
1	9.31859425332624	0.0023392
2	8.56685420324029	0.0032773
3	8.05137989020016	0.0041990
4	8.20841316725670	0.0042091
5	7.35921191232196	0.0042124
6	7.11497686074145	0.0042160
⋮	⋮	⋮
32	5.99074431688176	0.0044811
33	5.99000145749959	0.0044869
34	5.98951950276241	0.0044931
35	5.98922945392330	0.0044997
36	5.98907905077440	0.0045057
37	5.98902923939168	0.0045116
CPU time is seconds	0.004607

Table 3. Example 1: Numerical study of Algorithm 1 and ${\phi }_0={\phi }_1=50$.

	Algorithm 1
Iter $\left(\mathit{n}\right)$	Number of Iterations	Elapsed Time in Seconds
1	43.8258084339244	0.0039262
2	38.4664933517316	0.0044479
3	34.0650599167521	0.0051613
4	30.3707650173503	0.0055962
5	27.2384850931689	0.0105704
6	24.5651883090573	0.0123661
⋮	⋮	⋮
81	5.99300078418602	0.0129177
82	5.99272976847512	0.0129221
83	5.99251398870649	0.0129267
84	5.99234530749335	0.0129311
85	5.99221614282412	0.0129354
86	5.99211987429995	0.0129405
CPU time is seconds	0.012987

Table 4. Example 1: Numerical study of Algorithm 2 while ${\phi }_0={\phi }_1=50$.

	Algorithm 2
Iter $\left(\mathit{n}\right)$	Number of Iterations	Elapsed Time in Seconds
1	40.8637126508866	0.0012314
2	33.6942279764521	0.0017103
3	28.2476004881787	0.0023184
4	24.0192826082008	0.0029645
5	20.6928823067080	0.0062987
6	18.0487192661908	0.0090428
⋮	⋮	⋮
51	5.99321372817750	0.0094243
52	5.99275867152001	0.0094308
53	5.99244504784734	0.0094372
54	5.99223879898860	0.0094432
55	5.99211264487947	0.0094495
56	5.99204555921263	0.0094557
CPU time is seconds	0.009512

Figure 1. (For Example 1): Numerical illustration of Algorithm 1 and Algorithm 2 while ${\phi }_0={\phi }_1=10$.

Figure 2. (For Example 1): Numerical illustration of Algorithm 1 and Algorithm 2 while ${\phi }_0={\phi }_1=50$.

Example 2.

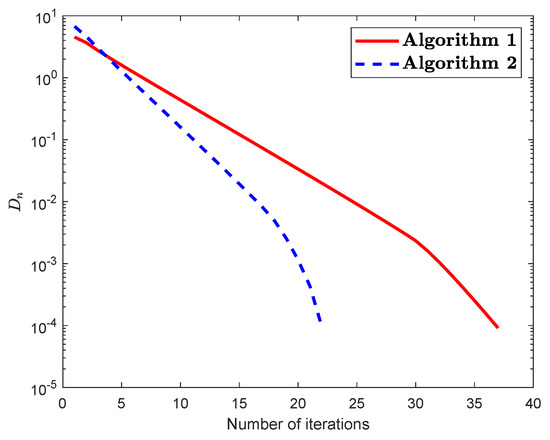
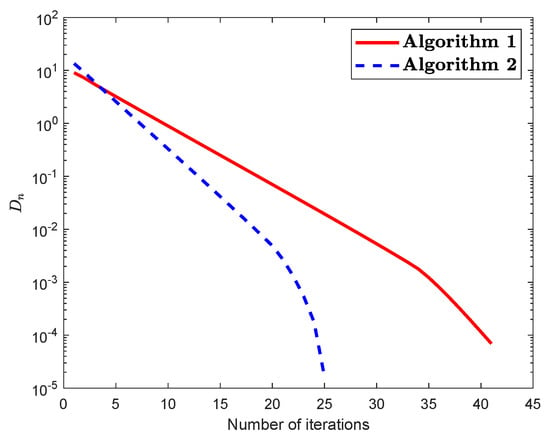
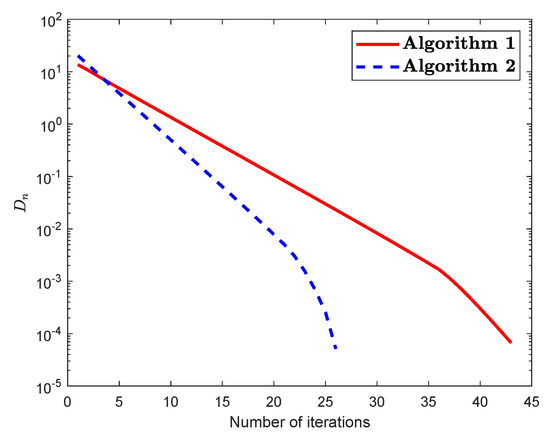
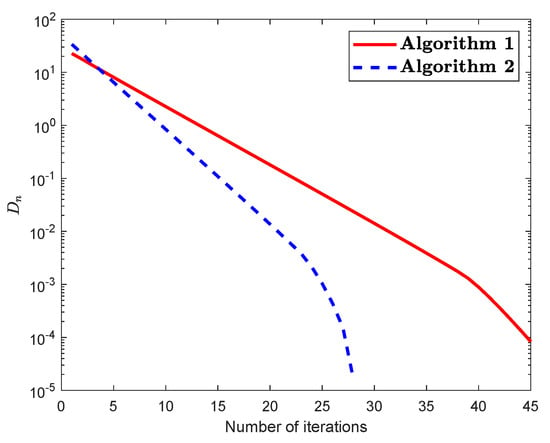
Let $P:A\to \beth$ be a mapping defined by

$$P\left(\phi \right)=max\{0,-\phi \}.$$

Then P is NE and has a unique fixed point $\phi =0.$ The set A is defined by $A:=\{\phi :-100\le \phi \le 100\}.$ The control condition for both algorithms are taken as follows:

• Algorithm 1

  $${\xi }_n=\frac{15}{{(n+1)}^2},\eta =3.00,{\beta }_n=0.85,{\alpha }_n=\frac{1}{10(n+2)}.$$
• Algorithm 2

  $${\xi }_n=\frac{15}{{(n+1)}^2},\eta =3.00,{\eta }_n^3=0.85,{\eta }_n^1=\frac{1}{10(n+2)},{\eta }_n^2=\frac{1}{20(n+2)}.$$

To illustrate the behaviour in this example see Figure 3, Figure 4, Figure 5 and Figure 6.

Figure 3. (For Example 2):Numerical illustration of Algorithm 1 and Algorithm 2 while ${\phi }_0={\phi }_1=20$.

Figure 4. (For Example 2): Numerical illustration of Algorithm 1 and Algorithm 2 while ${\phi }_0={\phi }_1=40$.

Figure 5. (For Example 2): Numerical illustration of Algorithm 1 and Algorithm 2 while ${\phi }_0={\phi }_1=60$.

Figure 6. (For Example 2): Numerical illustration of Algorithm 1 and Algorithm 2 while ${\phi }_0={\phi }_1=100$.

Example 3.

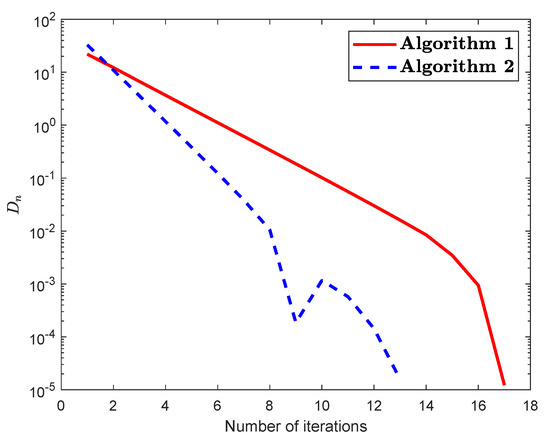
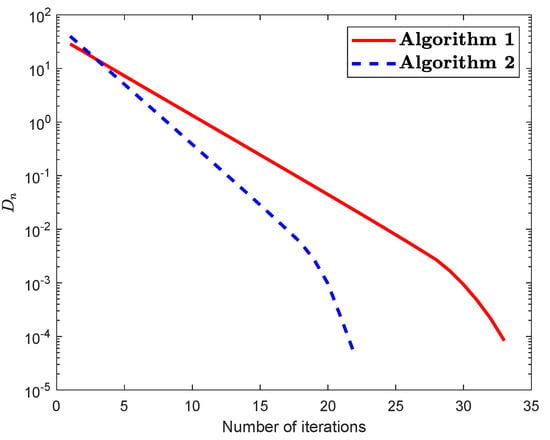
Let $P:\beth \to \beth$ be a mapping defined by

$$P\left(\phi \right)=-\phi +2,\forall \phi \in \mathbb{R}.$$

Then P is non-expansive and has a unique fixed point $\phi =0.$ The set A is defined by $A:=\{\phi :-100\le \phi \le 100\}.$ The control condition for both algorithms are taken as follows:

• Algorithm 1

  $${\xi }_n=\frac{30}{{(n+1)}^2},\eta =6.50,{\beta }_n=0.75,{\alpha }_n=\frac{1}{50(n+2)}.$$
• Algorithm 2

  $${\xi }_n=\frac{30}{{(n+1)}^2},\eta =6.50,{\eta }_n^3=0.75,{\eta }_n^1=\frac{1}{50(n+2)},{\eta }_n^2=\frac{1}{100(n+2)}.$$

To illustrate the behaviour in this example see Figure 7 and Figure 8.

Figure 7. (For Example 3):Numerical illustration of Algorithm 1 and Algorithm 2 while ${\phi }_0={\phi }_1=50$.

Figure 8. (For Example 3): Numerical illustration of Algorithm 1 and Algorithm 2 while ${\phi }_0={\phi }_1=100$.

Example 4.

Let $\mathcal{F}:A\subset \beth \to \beth$ be an operator and the variational inequality problem is defined in the following way:

$$\mathit{Find}{\phi }^{*}\in A\mathit{such}\mathit{that}⟨\mathcal{F}\left({\phi }^{*}\right),y-{\phi }^{*}⟩\ge 0,\forall y\in A.$$

Assume that $P:A\subset \beth \to \beth$ is a mapping defined by $P:=P_A(I-\lambda \mathcal{F})$ where $0<\lambda <\frac{2}{L}$ and L is the Lipschitz constant of the mapping $\mathcal{F}.$ Consider the constraint set A described by $A=\{\phi \in {\mathbb{R}}^4:1\le {\phi }_i\le 5,i=1,2,3,4\}$ and the mapping $P:{\mathbb{R}}^4\to {\mathbb{R}}^4$ evaluated by

$$\begin{array}{c}\hfill P\left(\phi \right)=\left(\begin{array}{c}{\phi }_1+{\phi }_2+{\phi }_3+{\phi }_4-4{\phi }_2{\phi }_3{\phi }_4\\ {\phi }_1+{\phi }_2+{\phi }_3+{\phi }_4-4{\phi }_1{\phi }_3{\phi }_4\\ {\phi }_1+{\phi }_2+{\phi }_3+{\phi }_4-4{\phi }_1{\phi }_2{\phi }_4\\ {\phi }_1+{\phi }_2+{\phi }_3+{\phi }_4-4{\phi }_1{\phi }_2{\phi }_3\end{array}\right).\end{array}$$

To illustrate the behaviour in this example see Table 5 and Table 6.

Table 5. Example 4: Numerical illustration of Algorithm 1 while ${\phi }_0={\phi }_1={(1,2,3,4)}^T$.

Iter $\left(\mathit{n}\right)$	${\mathit{\phi }}_1$	${\mathit{\phi }}_2$	${\mathit{\phi }}_3$	${\mathit{\phi }}_4$
1	7.88110105259549	11.1335921052147	11.6608026315329	11.4916973684078
2	2.72517069971347	5.52196307009909	5.91062617486984	5.78231681677249
3	2.74650358169779	5.23892462205654	5.43540972965547	5.37058363048288
4	2.79589652551700	5.10560097798145	5.20481731038818	5.17209179402342
5	2.84815300477526	5.04321208318383	5.09330195427214	5.07678246381620
6	2.90242325540275	5.01444727730850	5.03972755805987	5.03139070422338
7	2.95876979857588	5.00154113107122	5.01429541422714	5.01008946137975
⋮	⋮	⋮	⋮	⋮
94	4.99949159554096	4.99949159554096	4.99949159554096	4.99949159554096
95	4.99949420145518	4.99949420145518	4.99949420145518	4.99949420145518
96	4.99949678078979	4.99949678078979	4.99949678078979	4.99949678078979
97	4.99949933394941	4.99949933394941	4.99949933394941	4.99949933394941
98	4.99950186133047	4.99950186133047	4.99950186133047	4.99950186133047
CPU time is seconds	1.011633

Table 6. Example 4: Numerical illustration of Algorithm 2 while ${\phi }_0={\phi }_1={(1,2,3,4)}^T$.

Iter $\left(\mathit{n}\right)$	${\mathit{\phi }}_1$	${\mathit{\phi }}_2$	${\mathit{\phi }}_3$	${\mathit{\phi }}_4$
1	4.94814814709884	20.1659074073104	20.2289444443514	18.9075370362809
2	-8.0467085849302	12.4597307883609	12.5054021946827	11.3787988702116
3	1.03972935440247	4.90132095088790	4.89452802770933	4.98533018397129
4	1.11973537635742	4.89218078676053	4.88537889965809	4.95475431398367
5	1.20128523014071	4.89169908830941	4.88493057181313	4.94635475329384
6	1.27774539110779	4.89625929375273	4.88953484996449	4.94790178020963
7	1.34983811312425	4.90378394656115	4.89710336213719	4.95376528318611
8	1.41896397454886	4.91334870977828	4.90670981629961	4.96199173340817
⋮	⋮	⋮	⋮	⋮
44	4.99948911782781	4.99948911782781	4.99948911782781	4.99948911782781
45	4.99949261719944	4.99949261719944	4.99949261719944	4.99949261719944
46	4.99949606895811	4.99949606895811	4.99949606895811	4.99949606895811
47	4.99949947406902	4.99949947406902	4.99949947406902	4.99949947406902
48	4.99950283347142	4.99950283347142	4.99950283347142	4.99950283347142
CPU time is seconds	0.7115419

• Algorithm 1

  $${\xi }_n=\frac{10}{{(n+1)}^2},\eta =4.00,{\beta }_n=0.90,{\alpha }_n=\frac{1}{100(n+2)}.$$
• Algorithm 2

  $${\xi }_n=\frac{10}{{(n+1)}^2},\eta =4.00,{\eta }_n^3=0.90,{\eta }_n^1=\frac{1}{100(n+2)},{\eta }_n^2=\frac{1}{200(n+2)}.$$

6. Conclusions

In the subject of algorithms, the effectiveness of the algorithm is measured by two main factors. The first is reaching the desired point with the fewest iterations possible, and the second factor is the time. When the taken time to obtain strong convergence is short, results are good. There is no doubt that the paper [42] addressed many algorithms and proved, under symmetrical conditions, that its algorithm accelerates better than the previous one. Based on previous tables and pictures, we were able to verify that our algorithm converges faster than the algorithm from [42], so it converges faster than all the algorithms included in the paper [42]. Additionally, the numerical results (tables and images) show that our algorithm needs fewer iterations in a short time to achieve the desired goal, and this is what makes our method successful in obtaining strong convergence to the fixed point from its symmetrical one in the previous literature.