A Cooperative Partner Selection Study of Military-Civilian Scientific and Technological Collaborative Innovation Based on Interval-Valued Intuitionistic Fuzzy Set
Abstract
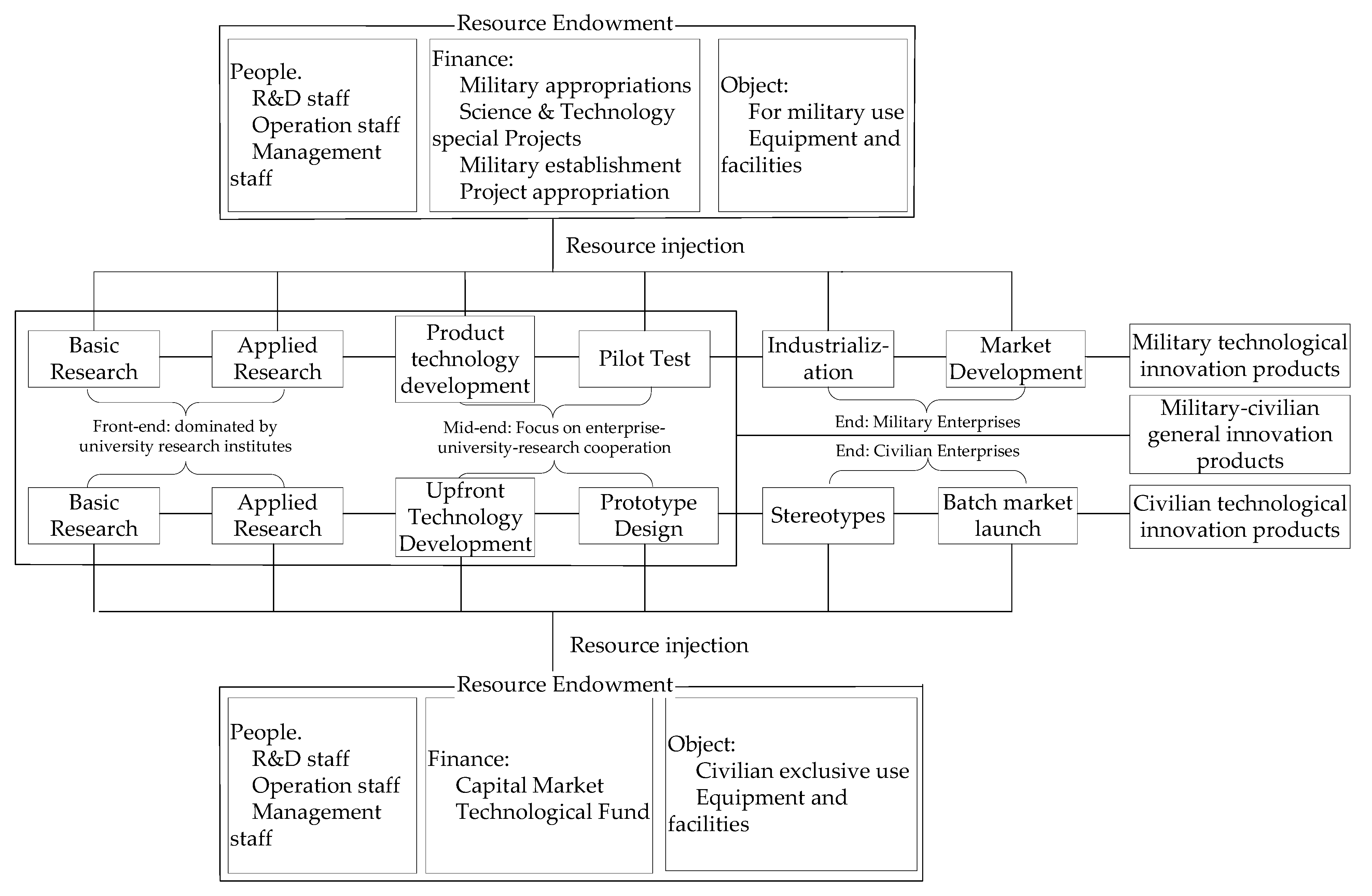
1. Introduction
2. Literature Review
3. Preliminaries
- (1)
- (2)
- (3)
- (4)
- (1)
- IF, then; IF, then.
- (2)
- IF, then when, ; when, ; when, .
4. Index Selection
4.1. Top-Level Design
4.2. Main Characteristics
4.3. Technical Characteristics
4.4. Interaction between Cooperative Entities
5. Model Building
5.1. Determination of Index Weights
5.1.1. Improvement of Scoring Function Based on Accuracy Function and Interval Length
- I.
- II.
- III
- I.
- If, then
- II.
- If, then
- III.
- If, then
5.1.2. Entropy Weighting Theory to Determine Index Weights
5.2. Considering Matrix Assembly and Transformation of Decision Makers’ Risk Attitudes
5.2.1. Assembly of Expert Evaluation Matrix
5.2.2. Matrix Transformation Based on Hesitancy Distribution
5.2.3. Decision-Making Process Based on Grey Correlation Analysis and the TOPSIS Method
6. Numerical Examples
7. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shang, Q.M. “The pillars of a great power” shows “China power”. Outlook 2017, 18, 4. [Google Scholar]
- Zhao, H.Z.; Shu, H.F. The Guardian of Science in National Affairs—On the “Big Science” of the United States. Sci. Sci. Manag. S T 1994, 15, 40–44. [Google Scholar]
- Jinping, X. Secure a Decisive Victory in Building a Moderately Prosperous Society in All Respects and Strive for the Great Success of Socialism with Chinese Characteristics for a New Era. Engl. Ed. Qiushi J. 2018, 10, 34. [Google Scholar]
- Yi, B.Y.; Huang, S.L.; Lei, E.Q. The way how DARPA takes the leadership in national defense science and technology innovation. Sci. Technol. Rev. 2018, 36, 33–36. [Google Scholar]
- Lv, H.J.; Gan, Z.X. Civil-Military Integration and Dual-Use Policy Implications in the Evolution Process of National Innovation System in America and Japan. China Soft Sci. 2005, 6, 43–46. [Google Scholar]
- Osborn, A. Russia Returns to Commercial Airline Market: Consolidation Key to Wider Strategy. Wash. Post 2007, 6, 26. [Google Scholar]
- Li, L.; Xie, J.; Wang, R.; Su, J.; Sindakis, S. The Partner Selection Modes for Knowledge-Based Innovation Networks: A Multiagent Simulation. IEEE Access 2019, 7, 140969–140979. [Google Scholar] [CrossRef]
- Sun, F.; Liu, S.; Zhu, X.; Men, B. Research and progress of Beidou satellite navigation system. Sci. China Inf. Sci. 2012, 55, 2899–2907. [Google Scholar] [CrossRef]
- Mai, Q.; Chen, X.; An, S. Integrity, complexity and system integration of major aerospace engineering: The practice of Beidou satellite engineering. Manag. World 2019, 35, 196–204. [Google Scholar]
- Zhou, Y.; Zhou, D.M.; Ding, Y.W.; Ruoyu, L. Research on the path evolution and driving factors of military-civilian integration technology transfer—“Zhong Wu-Tech” 2004–2017 case study. Manag. Rev. 2020, 32, 323–336. [Google Scholar]
- Fang, W.; Xiao, L.M.; Yang, B. An empirical study of influencing factors on civil-involved military knowledge transfer: A perspective of civil-military integration collaborative innovation. Stud. Sci. Sci. 2019, 39, 664–678. [Google Scholar]
- Kulve, H.T.; Smit, W.A. Civilian-military cooperation strategies in developing new technologies. Res. Policy 2003, 32, 955–970. [Google Scholar] [CrossRef]
- Zhao, L.M.; Sun, J.H.; Zhang, H.B. Technology sharing behavior in civil-military integration collaborative innovation system based on differential game. J. Ind. Eng. Eng. Manag. 2017, 31, 183–191. [Google Scholar]
- Fang, W.; Wang, C. The Cooperative Stability Evolutionary Game Analysis of the Military-Civilian Collaborative Innovation for China’s Satellite Industry. Math. Probl. Eng. 2019, 3. [Google Scholar] [CrossRef]
- Zhao, Z.B.; Han, C.Q.; Wang, L.Q. Collaborative innovation network of defence-related science and technology industry alliance: Structure and evolution. J. Public Manag. 2019, 16, 156–167. [Google Scholar]
- Wang, P.P.; Chen, B. Study on technical efficiency and its antecedents of civilian-military integrated firms. Bus. Rev. 2019, 31, 70–82. [Google Scholar]
- Lavallee, T.M. Civil-Military Integration: The Politics of Outsourcing National Security. Bull. Sci. Technol. Soc. 2010, 30, 10–13. [Google Scholar] [CrossRef]
- Lv, B.; Qi, X.G. Research on partner combination selection of the supply chain collaborative product innovation based on product innovative resources. Comput. Ind. Eng. 2019, 128, 245–253. [Google Scholar] [CrossRef]
- Nikghadam, S.; Sadigh, B.L.; Ozbayoglu, A.M.; Unver, H.O.; Kilic, S.E. A survey of partner selection methodologies for virtual enterprises and development of a goal programming–based approach. Int. J. Adv. Manuf. Technol. 2016, 85, 1713–1734. [Google Scholar] [CrossRef]
- Han, Y.; Chen, G.H. Research of knowledge sharing partner selection in cluster enterprises based on invisible contract. Chin. J. Manag. Sci. 2018, 26, 179–185. [Google Scholar]
- Zhu, Q.; Yang, Y.; He, Q.S.; Qu, S.Y. Research on the selection of innovation allies in internet + projects based on ELECTRE-Ⅰ method. China Soft Sci. 2016, 4, 143–149. [Google Scholar]
- Xiao, J.; Niu, Y.; Chen, P.; Leung, S.C.; Xing, F. An improved gravitational search algorithm for green partner selection in virtual enterprises. Neurocomputing 2016, 217, 103–109. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Atanassov, K.T.; Gargov, G. Interval-valued intuitionistic fuzzy sets. Fuzzy Sets Syst. 1989, 31, 343–349. [Google Scholar] [CrossRef]
- Fu, X.L.; Ouyang, T.X.; Yang, Z.L.; Liu, S. A product ranking method combining the features opinion pairs mining and interval-valued Pythagorean fuzzy sets. Appl. Soft Comput. 2020, 97, 106803. [Google Scholar] [CrossRef]
- Chen, X.H.; Zhao, C.C.; Yang, L. A group decision-making model based on interval-valued intuitionistic fuzzy numbers and its application on social network. Syst. Eng. Theory Pract. 2017, 37, 1842–1852. [Google Scholar]
- Hu, K.; Tan, Q.; Zang, T.; Wang, S. Assessing technology portfolios of clean energy-driven desalination-irrigation systems with interval-valued intuitionistic fuzzy sets. Renew. Sustain. Energy Rev. 2020, 132, 109950. [Google Scholar] [CrossRef]
- Narayanamoorthy, S.; Geetha, S.; Rakkiyappan, R.; Joo, Y.H. Interval-valued intuitionistic hesitant fuzzy entropy based VIKOR method for industrial robots selection. Expert Syst. Appl. 2019, 121, 28–37. [Google Scholar] [CrossRef]
- Gong, R.Z.; Ma, L.Y. A new score function and accuracy function of interval-valued intuitionistic fuzzy number and its application. Syst. Eng. Theory Pract. 2019, 39, 463–475. [Google Scholar]
- Gao, J.W.; Liu, H.H.; Gu, Y.D. Interval-valued intuitionistic fuzzy multi-criteria decision-making method based on prospect thoery. Syst. Eng. Theory Pract. 2014, 34, 3175–3181. [Google Scholar]
- Chen, S.M.; Huang, Z.C. Multiattribute decision making based on interval-valued intuitionistic fuzzy values and linear programming methodology. Inf. Sci. Inf. Sci. 2017, 381, 341–351. [Google Scholar] [CrossRef]
- Zhou, H.; Ma, X.; Zhou, L.; Chen, H.; Ding, W. A Novel Approach to Group Decision-Making with Interval-Valued Intuitionistic Fuzzy Preference Relations via Shapley Value. Int. J. Fuzzy Syst. 2018, 20, 1172–1187. [Google Scholar] [CrossRef]
- Xu, Z.S. Methods for aggregating interval-valued intuitionistic fuzzy information and their application to decision making. Control Decis. 2007, 22, 215–219. [Google Scholar]
- Zhao, F.X. Distances between Interval-Valued Intuitionistic Fuzzy Sets. Micro Electron. Comput. 2010, 27, 188–192. [Google Scholar]
- You, G.R.; Zhao, L.B. Integrated Development of Civil-Military Science and Technology: Theory and Practice; Nation Defense Industry Press: Beijing, China, 2017. [Google Scholar]
- Shen, H.Y.; Zheng, X.P. The establishment and empirical study on the evaluation system of scientific and technological innovation ability from the perspective of military-civilian integration. Reform Econ. Syst. 2019, 214, 140–146. [Google Scholar]
- Tian, Q.F.; Zhang, T.; Zhang, S.; Miao, D.D. Research on elements fusion mechanism of dual-use science and technology collaborative innovation. Sci. Technol. Prog. Policy 2020, 37, 136–145. [Google Scholar]
- Jiang, L.; Yang, P.P.; Zhang, Q.P. Research on the influence mechanism of civil-military fusion innovation for UAV. Sci. Sci. Manag. S T 2018, 39, 96–111. [Google Scholar]
- Chen, X.H.; Zhou, K. Analysis of regional innovation efficiency and the influencing factors in civil-military integration in China—An analysis based on random frontier panel data model. Shanghai J. Econ. 2019, 9, 69–79. [Google Scholar]
- Yin, J.; Tan, Q.M. A research on the evaluation of the degree of civil-military integration and its optimization measures. Sci. Res. Manag. 2020, 41, 90–97. [Google Scholar]
- Hansen, L.P.; Sargent, T. Robustness; Princeton University Press: New York, NY, USA, 2008. [Google Scholar]
- Nicholson, W.; Snyder, C. Microeconomic Theory Basic Principles and Extensions, 12th ed.; Cengage Learning: Boston, MA, USA, 2017; pp. 212–221. [Google Scholar]
| First-Level Indicators | Second-Level Indicators | Authors | Index Description |
|---|---|---|---|
| Top-level Design | Civil-Military integration policy, technology policy, and operating mechanism | You and Zhao [35], Shen and Zheng [36], Tian, et al. [37] | Standards and rules formulated to meet the Chinese strategic needs and realize civil-military integration. |
| Main characteristics | Civil-Military integration willingness | Fang, el al. [3], Tian, et al. [37] | The concept and intention of the innovation entities to participate in civil-military integration. |
| Organizational structure (unit nature) | Wang and Chen [16], Jiang, el al. [38] | The division of labor and cooperation system of the innovation entities in terms of management system, department setting, function planning, and normal operation. | |
| Technical char-acteristics | Technological innovation level | Kulve and Smit [12], Wang and Chen [16], Tian, el al. [37], Chen and Zhou [39] | The core technology and innovation capabilities of the innovation entities, including the degree of generality and matching that meet the requirements of civil-military integration. |
| Technology transfer capability | Zhou, el al. [10], Tian et al. [37], Yin and Tan [40] | The ability of technology to transfer and diffuse among different innovation entities. | |
| Interaction between cooperative entities | Collaborative configuration of elements | You and Zhao [35], Shen and Zheng [36] | The interaction of various innovative entities through the coordinative configuration of platforms. |
| Benefit distribution model | Fang and Wang [14] | The interest relationship between the entities is manifested in the distribution of revenue and the ownership of technological intellectual property rights. |
| [0.62, 0.71], [0.13, 0.21] | [0.51, 0.73], [0.16, 0.21] | [0.59, 0.86], [0.06, 0.10] | [0.16, 0.46], [0.41, 0.53] | [0.14, 0.28], [0.47, 0.66] | [0.25, 0.45], [0.46, 0.53] | [0.63, 0.96], [0.02, 0.04] | ||
| [0.50, 0.83], [0.11, 0.15] | [0.45, 0.66], [0.12, 0.23] | [0.66, 0.72], [0.14, 0.21] | [0.21, 0.36], [0.46, 0.58] | [0.31, 0.51], [0.14, 0.31] | [0.51, 0.57], [0.21, 0.31] | [0.12, 0.46], [0.23, 0.43] | ||
| [0.72, 0.82], [0.05, 0.16] | [0.41, 0.81], [0.11, 0.18] | [0.36, 0.51], [0.26, 0.36] | [0.11, 0.38], [0.56, 0.60] | [0.13, 0.56], [0.26, 0.43] | [0.16, 0.56], [0.21, 0.42] | [0.55, 0.90], [0.02, 0.05] | ||
| [0.59, 0.85], [0.07, 0.12] | [0.62, 0.78], [0.14, 0.20] | [0.41, 0.76], [0.11, 0.18] | [0.21, 0.33], [0.44, 0.57] | [0.21, 0.54], [0.07, 0.36] | [0.26, 0.46], [0.14, 0.21] | [0.40, 0.75], [0.10, 0.15] | ||
| [0.73, 0.89], [0.06, 0.09] | [0.43, 0.55], [0.27, 0.38] | [0.36, 0.61], [0.03, 0.11] | [0.08, 0.21], [0.31, 0.56] | [0.20, 0.42], [0.36, 0.56] | [0.51, 0.81], [0.12, 0.18] | [0.34, 0.55], [0.22, 0.45] | ||
| [0.40, 0.72], [0.10, 0.15] | [0.10, 0.42], [0.33, 0.58] | [0.13, 0.25], [0.54, 0.70] | [0.12, 0.34], [0.40, 0.60] | [0.74, 0.85], [0.10, 0.15] | [0.13, 0.58], [0.27, 0.42] | [0.46, 0.67], [0.15, 0.25] | ||
| [0.55, 0.65], [0.07, 0.15] | [0.37, 0.39], [0.51, 0.61] | [0.57, 0.90], [0.02, 0.05] | [0.05, 0.36], [0.17, 0.42] | [0.35, 0.60], [0.10, 0.25] | [0.16, 0.32], [0.27, 0.47] | [0.26, 0.31], [0.12, 0.16] | ||
| [0.43, 0.88], [0.06, 0.12] | [0.41, 0.75], [0.08, 0.15] | [0.35, 0.47], [0.12, 0.48] | [0.12, 0.45], [0.26, 0.50] | [0.20, 0.52], [0.15, 0.25] | [0.41, 0.66], [0.13, 0.22] | [0.35, 0.45], [0.16, 0.25] | ||
| [0.70, 0.88], [0.05, 0.12] | [0.10, 0.42], [0.43, 0.65] | [0.25, 0.46], [0.13, 0.15] | [0.20, 0.34], [0.10, 0.15] | [0.09, 0.14], [0.36, 0.42] | [0.44, 0.71], [0.15, 0.27] | [0.10, 0.35], [0.55, 0.61] | ||
| [0.30, 0.54], [0.10, 0.15] | [0.34, 0.54], [0.22, 0.42] | [0.60, 0.81], [0.02, 0.10] | [0.40, 0.81], [0.06, 0.16] | [0.74, 0.92], [0.01, 0.06] | [0.13, 0.25], [0.35, 0.50] | [0.26, 0.34], [0.51, 0.52] | ||
| [0.41, 0.66], [0.21, 0.31] | [0.45, 0.72], [0.06, 0.14] | [0.74, 0.83], [0.01, 0.02] | [0.11, 0.46], [0.25, 0.29] | [0.21, 0.36], [0.05, 0.27] | [0.21, 0.25], [0.41, 0.43] | [0.72, 0.82], [0.03, 0.12] | ||
| [0.16, 0.56], [0.30, 0.37] | [0.28, 0.45], [0.12, 0.33] | [0.35, 0.42], [0.12, 0.21] | [0.36, 0.55], [0.24, 0.35] | [0.11, 0.23], [0.35, 0.42] | [0.33, 0.46], [0.12, 0.19] | [0.21, 0.44], [0.05, 0.26] | ||
| [0.66, 0.71], [0.20, 0.26] | [0.46, 0.81], [0.15, 0.19] | [0.22, 0.48], [0.41, 0.45] | [0.50, 0.61], [0.11, 0.14] | [0.41, 0.65], [0.11, 0.16] | [0.21, 0.56], [0.05, 0.25] | [0.16, 0.22], [0.47, 0.65] | ||
| [0.51, 0.62], [0.11, 0.13] | [0.52, 0.63], [0.03, 0.13] | [0.66, 0.71], [0.03, 0.05] | [0.11, 0.32], [0.35, 0.46] | [0.35, 0.50], [0.13, 0.30] | [0.13, 0.42], [0.38, 0.49] | [0.55, 0.65], [0.23, 0.31] | ||
| [0.30, 0.42], [0.04, 0.09] | [0.26, 0.46], [0.12, 0.15] | [0.42, 0.57], [0.23, 0.31] | [0.51, 0.73], [0.02, 0.20] | [0.52, 0.61], [0.22, 0.30] | [0.35, 0.50], [0.25, 0.32] | [0.20, 0.58], [0.10, 0.32] | ||
| [0.42, 0.61], [0.12, 0.15] | [0.51, 0.76], [0.03, 0.20] | [0.42, 0.60], [0.12, 0.33] | [0.15, 0.22], [0.20, 0.38] | [0.31, 0.52], [0.11, 0.25] | [0.70, 0.72], [0.12, 0.18] | [0.42, 0.61], [0.25, 0.33] | ||
| [0.38, 0.55], [0.11, 0.23] | [0.26, 0.51], [0.11, 0.14] | [0.52, 0.70], [0.01, 0.23] | [0.20, 0.45], [0.40, 0.41] | [0.45, 0.50], [0.22, 0.23] | [0.24, 0.30], [0.40, 0.61] | [0.15, 0.21], [0.43, 0.51] | ||
| [0.61, 0.72], [0.02, 0.05] | [0.72, 0.92], [0.01, 0.06] | [0.56, 0.70], [0.21, 0.26] | [0.13, 0.30], [0.26, 0.42] | [0.43, 0.52], [0.21, 0.27] | [0.52, 0.60], [0.08, 0.12] | [0.09, 0.12], [0.45, 0.66] | ||
| [0.12, 0.31], [0.36, 0.40] | [0.40, 0.61], [0.12, 0.28] | [0.21, 0.54], [0.37, 0.39] | [0.50, 0.71], [0.26, 0.38] | [0.20, 0.30], [0.24, 0.27] | [0.44, 0.49], [0.21, 0.24] | [0.42, 0.53], [0.33, 0.35] | ||
| [0.22, 0.57], [0.02, 0.25] | [0.57, 0.66], [0.13, 0.15] | [0.50, 0.57], [0.31, 0.40] | [0.15, 0.24], [0.55, 0.62] | [0.34, 0.51], [0.21, 0.26] | [0.26, 0.35], [0.15, 0.20] | [0.16, 0.23], [0.34, 0.39] | ||
| [0.42, 0.78], [0.12, 0.20] | [0.39, 0.53], [0.25, 0.30] | [0.42, 0.55], [0.05, 0.21] | [0.13, 0.32], [0.34, 0.38] | [0.32, 0.36], [0.30, 0.39] | [0.22, 0.35], [0.31, 0.39] | [0.45, 0.48], [0.21, 0.25] | ||
| [0.30, 0.36], [0.02, 0.11] | [0.50, 0.57], [0.20, 0.31] | [0.35, 0.42], [0.22, 0.30] | [0.42, 0.46], [0.31, 0.35] | [0.52, 0.69], [0.21, 0.30] | [0.52, 0.67], [0.21, 0.30] | [0.38, 0.58], [0.10, 0.24] | ||
| [0.42, 0.55], [0.35, 0.37] | [0.36, 0.38], [0.15, 0.20] | [0.17, 0.28], [0.32, 0.40] | [0.22, 0.32], [0.38, 0.45] | [0.41, 0.46], [0.20, 0.25] | [0.41, 0.48], [0.20, 0.25] | [0.60, 0.78], [0.15, 0.18] | ||
| [0.12, 0.46], [0.30, 0.32] | [0.22, 0.48], [0.31, 0.44] | [0.71, 0.85], [0.03, 0.07] | [0.26, 0.37], [0.05, 0.10] | [0.57, 0.60], [0.06, 0.14] | [0.57, 0.60], [0.06, 0.15] | [0.51, 0.71], [0.10, 0.21] | ||
| [0.11, 0.14], [0.37, 0.40] | [0.42, 0.63], [0.20, 0.21] | [0.55, 0.62], [0.07, 0.14] | [0.43, 0.56], [0.09, 0.12] | [0.80, 0.91], [0.02, 0.06] | [0.80, 0.91], [0.02, 0.06] | [0.22, 0.35], [0.40, 0.43] |
| Indicators Weight | |||||||
|---|---|---|---|---|---|---|---|
| 0.126 | 0.129 | 0.133 | 0.149 | 0.158 | 0.148 | 0.157 | |
| 0.107 | 0.144 | 0.161 | 0.144 | 0.160 | 0.145 | 0.139 | |
| 0.127 | 0.124 | 0.140 | 0.152 | 0.148 | 0.134 | 0.175 | |
| 0.132 | 0.115 | 0.113 | 0.166 | 0.112 | 0.135 | 0.226 | |
| 0.146 | 0.111 | 0.136 | 0.234 | 0.124 | 0.127 | 0.122 |
| Decision Maker’s Risk Attitude | Degree of Comprehensive Closeness | Ranking of Candidate Partners | |
|---|---|---|---|
| risk-seeking attitude | 0.8 | ||
| risk-neutral attitude | 0.5 | ||
| risk-averse attitude | 0.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Zhang, J. A Cooperative Partner Selection Study of Military-Civilian Scientific and Technological Collaborative Innovation Based on Interval-Valued Intuitionistic Fuzzy Set. Symmetry 2021, 13, 553. https://doi.org/10.3390/sym13040553
Li B, Zhang J. A Cooperative Partner Selection Study of Military-Civilian Scientific and Technological Collaborative Innovation Based on Interval-Valued Intuitionistic Fuzzy Set. Symmetry. 2021; 13(4):553. https://doi.org/10.3390/sym13040553
Chicago/Turabian StyleLi, Bing, and Jihai Zhang. 2021. "A Cooperative Partner Selection Study of Military-Civilian Scientific and Technological Collaborative Innovation Based on Interval-Valued Intuitionistic Fuzzy Set" Symmetry 13, no. 4: 553. https://doi.org/10.3390/sym13040553
APA StyleLi, B., & Zhang, J. (2021). A Cooperative Partner Selection Study of Military-Civilian Scientific and Technological Collaborative Innovation Based on Interval-Valued Intuitionistic Fuzzy Set. Symmetry, 13(4), 553. https://doi.org/10.3390/sym13040553






