Abstract
Clustering is more popular than the expert knowledge approach in Interval Fuzzy Type-2 membership function construction because it can construct membership function automatically with less time consumption. Most research proposed a two-fuzzifier fuzzy C-Means clustering method to construct Interval Fuzzy Type-2 membership function which mainly focused on producing Gaussian membership function. The other two important membership functions, triangular and trapezoidal, are constructed using the grid partitioning method. However, the method suffers a drawback of not being able to represent actual data composition in the underlying dataset. Some research proposed triangular and trapezoidal membership functions construction using readily formed Fuzzy Type-1 membership functions, which means it remains unclear how the membership functions are heuristically constructed using fuzzy C-Means outputs. The triangular and trapezoidal membership functions are important because previous works have shown that they may produce superior performance than Gaussian membership function in some applications. Therefore, this paper presents a structured literature review on generating triangular and trapezoidal Interval Fuzzy Type-2 membership functions using fuzzy C-Means. Initially, 110 related manuscripts were collected from Web of Science, Scopus, and Google Scholar. These manuscripts went through the identification, screening, eligibility, and inclusion processes, and as a result, 21 manuscripts were reviewed and discussed in this paper. To ensure that the review also covers the important components of fuzzy logic, this paper also reviews and discusses another 49 manuscripts on fuzzy calculation and operation. Furthermore, this paper also discusses the contributions of the conducted review to the body of knowledge, future research directions and challenges, with the aim to motivate the future works of constructing the methods to generate Interval Fuzzy Type-2 triangular and trapezoidal membership functions using fuzzy C-Means. The methods imply flexibility in choosing membership function type, hence increasing the effectiveness of fuzzy applications through leveraging the advantages that each of the three membership function types could provide.
1. Introduction
The innate nature of information, by default, is tied to the concept of uncertainty. The factor for this uncertainty is information insufficiency which may be in the form of incomplete, unreliable, ambiguous, fragmented, or a combination of these forms [1,2]. Attempting to formalize this uncertainty led to the introduction of fuzzy set theory which proposes that elements of a set have a degree of association in a subset [3]. Mathematically, rather than being either 0 or 1 in truth value, it can be subjectively belong to a set, for instance µA(y) = 0.6. This means that the degree of membership of y in fuzzy set A is 0.6, and this kind of structure is known as Fuzzy type-1 (FT1) [4]. However, it is shown that even though the membership degree is within the 0 and 1 range, the value is still considered a crisp value—which can represent a limited amount of uncertainties and fuzziness. It limits the capability of FT1 to address complex uncertainty problems and has become the main argument in the research community. This has led to the introduction of Fuzzy type-2 (FT2) set whereby a membership degree is also represented in the form of fuzzy value. This is made possible because FT2 contains a third dimension known as the footprint of uncertainty (FOU) that provides more degrees of freedom, hence making it capable of handling complex uncertainties present in a system. For instance, the previous FT1 set may be represented in FT2 as µ(y) = [0.5, 0.7] whereby the membership degree is in the range of 0.5–0.7. This range represents FOU, while 0.5 and 0.7 are, respectively, known as Lower MF (LMF) and Upper MF (UMF).
Despites having superior capability than FT1 in handling nonlinearities and uncertainties, FT2′s main drawback is its high computational cost, resulting from its third dimension computation. Another fuzzy set, which is an extension of FT2 known as Interval Fuzzy type-2 (IT2) was then introduced. In IT2, the third dimension of FT2 is ignored, and left only with the FOU [5]. This means that all characteristics of FT2 remain in IT2, except that the third dimension value is set to the same value for all data points. In other words, IT2 is the extension of FT1 but having a better capability to produce accurate and precise computations, with good computational cost. Concern about FT2 and IT2, and their applications have become central issues in fuzzy and uncertainty domains, and as a result many studies in recent years have focused on these two methods. Figure 1 shows the number of publications related to FT2 and IT2 has been growing since 2010 (numbers for 2020 are by November 2020). The graph in Figure 1 contains data from the three major databases, namely Web of Science, Scopus, and Google Scholar. This paper focuses on the review of IT2 method.
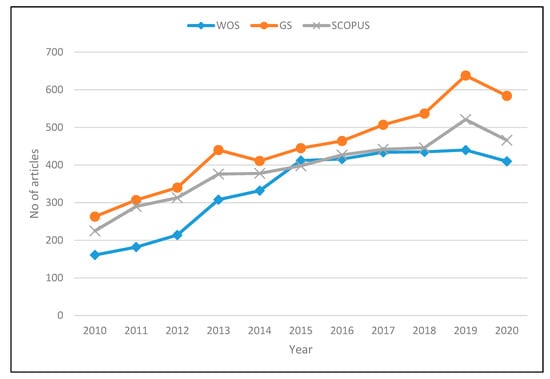
Figure 1.
Number of publications related to FT2 and IT2 in major databases (2010–2020).
Application of fuzzy logic can be found as fuzzy inference system (FIS) as shown in Figure 2. One of the components of an FIS is fuzzifier, where inputs are compared against membership function (MF) to obtain membership degree [6]. The membership degree will go through a fuzzy rules inference engine for further processing of decision making. There are three main types of MF—Gaussian, triangular, and trapezoidal. Table 1 presents the examples of implementation of MFs, which proves that each of the three MF types is relevant. Table 1 also shows that each of the MF types are able to provide good and, in some cases, better solutions, than the other MFs.
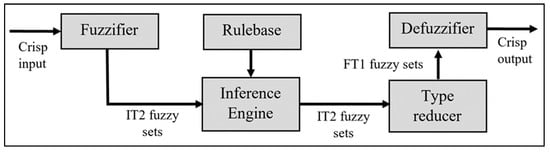
Figure 2.
IT2 fuzzy inference system.

Table 1.
Example of Gaussian, triangular, and trapezoidal MFs implementation.
MF can be constructed by either one of two methods; expert knowledge or data-centric generation [13]. The construction through expert knowledge suffers from loss of accuracy due to subjective opinions among individuals or conflict between experts [14]. It is also time consuming [1] and may not always available [6]. For example, MF construction using arbitrary partitioning by expert opinion is exposed to risk of loss of accuracy due to bias by the expert because human semantics and knowledge are limited to what they know and have experienced [15]. Hence, it is not suitable for FIS solutions that require MFs to be adaptively constructed based on recent data or the systems that require rapid, frequent and dynamic MF construction.
Therefore, most research has been focusing on the data-centric approach because it allows automatic MF construction by learning through historical trends. One of the common methods of data-centric MF construction is a clustering algorithm such as Fuzzy C-means (FCM). The importance of FCM in the construction of MF has been demonstrated by its application in various fields such as classification [16], IT2 improvement [17], and forecasting [18]. FCM clusters the underlying datasets, and its outputs are used to generate MFs. However, the limitation of FCM is that it only produces Gaussian MF [5,19]. It does not produce triangular and trapezoidal MFs, which have been used in numerous research such as antenna positioning fuzzy controller [15], crime prevention analysis [20], gesture monitoring [21], fuzzy cognitive map [22,23], and fuzzy PI/PD controller [24]. These two MF types are important because they may produce superior performance in some FIS implementations as discussed previously and shown in Table 1. For instance, a study conducted by Ali et al. (2015) [25], which aimed at investigating the effectiveness of each of the three MF types in an antenna azimuth controller system, concluded that triangular and trapezoidal MFs respond better than Gaussian due to the nature of antenna signal reception having an effective window by using the two MF types. This shows the significance of non-Gaussian MFs in certain FIS use cases.
Most of previous works have focused only on generating Gaussian IT2 MF using FCM or applying the Gaussian IT2 MF generated by FCM in their solutions. There remains a need to conduct a study to enhance FCM-based IT2 MF generation method so that it will have the capability to produce triangular and trapezoidal MFs. The method implies flexibility in choosing MF type, hence increasing the effectiveness of FIS through leveraging the advantages that each of the three MF types could provide.
The objective of this paper is to present a structured literature review to motivate the future works of constructing IT2 triangular and trapezoidal MFs with FCM. In this paper, 21 manuscripts are reviewed, which were collected from the three main databases, namely Scopus, Web of Science, and Google Scholar. To ensure that the review also includes important components of fuzzy logic, this paper also reviews and discusses another 49 manuscripts on fuzzy calculation and operation, which were also gathered from the three main databases mentioned above. This paper also discusses the contributions of the conducted review to the body of knowledge, and future research directions and challenges. This paper is organized as follows; Section 2 presents the background of the related methods whereby it begins with the review on existing works on IT2 MF constructions, followed by IT2, fuzzy MFs and FCM. Section 3 presents the discussion on the reviewed literature and their contributions and limitations. Section 4 discusses the challenges and future research works. Section 5 summarizes the outcomes of this paper.
2. Background
2.1. Existing Works on the Construction of IT2 MF
The construction of IT2 MF requires the formation of its FOU. At the moment:
- The blurring method is applied on the readily constructed FT1 MF as shown in Figure 3 [5]. The original FT1 MF in Figure 3a is blurred to the left and right which produces the shape as shown in Figure 3b. Then, the blurred MF is improved so that the FOU of IT2 MF is properly formed as shown in Figure 3c. To relate this construction of IT2 MF with FCM, the original FT1 MF in Figure 3a can be constructed using the outputs of FCM and a heuristic method. As discussed above, this approach only produces Gaussian FT1 MF, hence imposing a blurring method on it will generate Gaussian IT2 MF. Existing research proposed that the triangular and trapezoidal MFs construction is carried out using the grid partitioning method. Although the grid partitioning method can fulfill those objectives, its generated MFs lack representation of the actual composition of the underlying data set because the width of all clusters is equally distributed or spread out. Hence, an alternative approach on how to construct triangular and trapezoidal IT2 MFs from FCM should be investigated.
 Figure 3. IT2 MF generation from the blurring method [5].
Figure 3. IT2 MF generation from the blurring method [5]. - Another possible method to form the MF FOU is through adaptive network-based fuzzy inference system (ANFIS). Unfortunately, applying ANFIS directly to IT2 FIS is not possible, and optimization of FT1 needs to be performed in order to generate the MF [26]. Moreover, the MF type produced is Gaussian type [26]. Hence, there remains a need for a study to extend the capability of FCM in generating more than a single type of MF.
- Most research proposed a double fuzzifier FCM method to form IT2 FOU [7,27]. This was achieved by applying FCM clustering using two different fuzzifier values upon a single data set [28]. This means that an MF constructed with one fuzzifier value will represent the LMF and another MF constructed with another fuzzifier value will generate the UMF of an FOU. However, this method is also based on FCM, hence it generates Gaussian IT2 MF type only.
2.2. Interval Fuzzy Type-2
FT2 was introduced in 1975 with the motivation to enhance FT1 that is still bound to crisp membership degree value, thus raises concern that FT1 is not capable of handling higher complexity of uncertainties [29,30,31]. The factor that differentiates FT2 from FT1 is the inclusion of FOU. FOU defines FT2 by adding another dimension of fuzziness to the MF. The added dimension results in the membership degree of a variable being represented in a fuzzy value (range) form instead of a crisp degree as in FT1. Figure 4 shows the difference between FT1 and FT2 MFs whereby FT1 MF is represented by a single line. In contrast, FT2 MF is represented by two lines known as UMF and LMF. The shaded area between these two lines is FOU. The FOU can be constructed by several means such as histogram [32], double clustering [7,27,33], and double center shift [13].
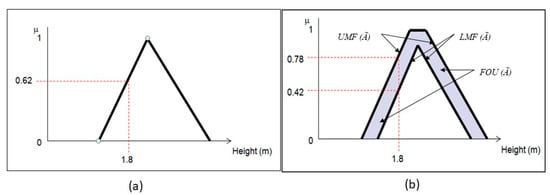
Figure 4.
The difference between (a) FT1 MF and (b) FT2 MF.
As mentioned above, IT2 was then introduced to provide an alternative to FT2 because the computational complexity of FT2 can significantly be reduced by IT2. One of the factors that simplifies IT2 from FT2 is that its fuzziness only concerns within its FOU (two dimensions) instead of the full three dimensions within FT2. The difference is visualized in Figure 5, whereby in the third dimension of FT2, all data points are assigned with varying membership degrees. In contrast, the third dimension of IT2 is represented by the rectangle-looking shape shown in Figure 5b, which means all data points are assigned with an equal value of membership degree (normally the value is set to 1).
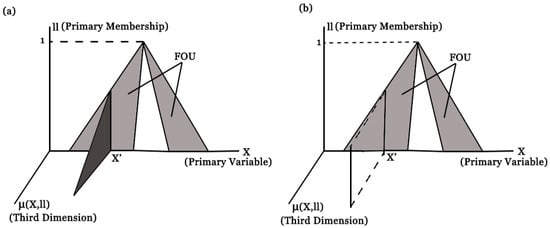
Figure 5.
(a) FT2 and (b) IT2.
An FT1 fuzzy set F can be described as follows; assuming X is the universe with collections of x objects, a fuzzy set F is defined as the following:
The notation µF(x) in Equation (1) is an MF, which contains the membership degree of each element in X. The value of membership degree is within the range of 0 and 1.
Taking the same scenario where X is the universe with collections of x objects, the MF of IT2 sets takes the following form:
In Equation (2), X and Jx denote the primary and secondary domains, respectively. The notation µ(x, u) denotes the secondary MF, in which all values are set to 1 for . As mentioned above, in FT2, these values vary instead of all being equal to 1. Therefore, IT2 function shown in Equation (2) can be redefined as FT2 as the following:
2.3. Fuzzy Membership Function
An MF is a function that specifies the degree of an input function that belongs to a set. It can also be defined as a curve that determines how each point in the input space is mapped to a membership degree between 0 and 1. The concept of MF was first introduced by Zadeh (1965) [34].
As discussed above, MFs can be generated by two means: expert knowledge and data-centric generation [1]. Expert knowledge-based MF depends on a group of experts determining certain intervals of a set to partition and thus construct a function [35]. However, expert knowledge-based MFs are open to several weaknesses, namely loss of accuracy due to bias [1] and a high increase in fuzzy rules for higher-dimension problems [36]. In some cases, conflicts of opinions may arise in the group of experts and thus will take a longer time to agree upon decisions [37].
Another method to derive MF is through data-centric approaches. Examples of data-centric MF generation method are grid partitioning and fuzzy clustering. Grid partitioning is where the input space of the function is distributed evenly between curves (clusters). This is shown in Figure 6 whereby all curves are distributed evenly in the input space for all three types of MFs i.e., triangular, Gaussian, and trapezoidal. This characteristic has made grid partitioning-based MF suffer from the problem of not giving the actual representation of the underlying data especially if the data groupings are dissimilar in terms of volume.
Figure 6.
Triangular, Gaussian, and trapezoidal MFs generated from grid partitioning.
The alternative of the grid partitioning method is the clustering approach; an unsupervised learning whereby data points are closely grouped together in clusters according to metrics specified [38]. Examples of clustering include FCM [39] and possibilistic C-Means [19]. As mentioned in the previous section, although FCM offers advantages over other methods, it has a limitation in a way that it naturally forms a Gaussian MF [19]. Hence, it does not leverage on the advantages that the other two MFs, triangular and trapezoidal MFs, may offer [26]. Triangular and trapezoidal, together with Gaussian, are the most used MFs [11] and none of them can be declared as the best shape for all types of FIS solutions. The selection of the best shapes of MFs usually depends on the problem, type of data, and the experimental results [11,40]. This has become the main motivation of our study, which is to investigate the method to construct triangular and trapezoidal MFs from FCM.
As shown in Figure 7, a triangular MF is defined by a lower and upper limit, l and u, and a center value, m, where l < m < u [41]. Figure 8, on the other hand, shows trapezoidal MF, which is defined by a lower limit l, an upper limit u, a lower support limit m, and an upper support limit n, where l < m < n < u [41,42]. Hence, a triangular MF is specified by three parameters, l, c, and u as in Figure 7, while a trapezoidal MF is specified by four parameters, l, a, b, and u as in Figure 8.
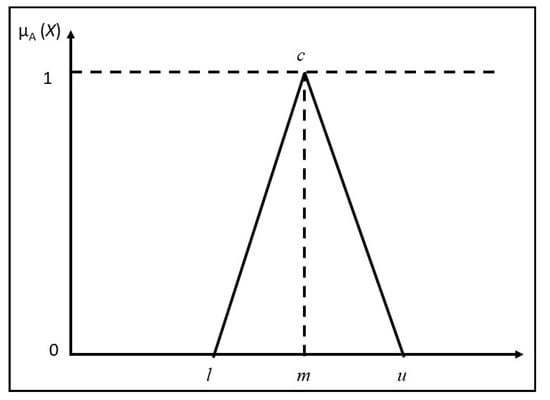
Figure 7.
Triangular MF.
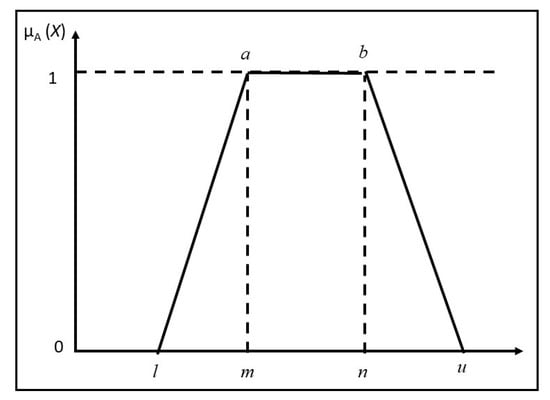
Figure 8.
Trapezoidal MF.
2.4. Fuzzy C-Means
FCM was introduced by Dunn (1973) [14], and then improved by Bezdek et al. (1984) [39]. FCM has been utilized in substantial number of studies such as in image processing and pattern recognition [15]. It is an optimization-based method whereby it executes the algorithm and improves the objective function repeatedly until the threshold is reached. Based on the number of clusters predefined by the user, FCM assigns each data point with a membership degree for each of the clusters [20].
In the process to cluster a set of data points, FCM iteratively executes three processes until it reaches a goal to produce the minimum objective function. The processes are as the following:
Process 1: Assume there are n data points represented by {X1, X2, …, Xn} and c number of clusters. Firstly, FCM guesses the center of each cluster, ci, i = 1, 2, …, c. Next, FCM computes and assigns each data point with a membership degree for each cluster [43]. This is computed based on Equation (4), and the generated membership degrees are stored in matrix U.
The notation dij = ||ci – xj|| is the Euclidean distance from jth data point to the ith cluster center, while m is the fuzzy weighting exponent [43].
Process 2: FCM computes the objective function, which is defined in Equation (5).
This objective function determines the termination of FCM processes; a condition when its value reaches the threshold i.e., the minimum value.
Process 3: If the objective function does not reach the threshold value yet, FCM resumes its execution with computing the new value of the center of each cluster. This newly generated set of cluster centers will overwrite the previous set of guessed values. The computation is based on Equation (6).
As mentioned above, FCM repeats the execution of processes 1 to 3 until the objective function reaches its threshold value. In each repetition, the value of the objective function is minimized, and the value of each cluster center is optimized. Hence, the final sets of cluster centers and membership degrees produced by FCM represent the optimum clustering state of the underlying data set.
FCM has been proposed in numerous works. Egrioglu et al. (2013) [44] argued that the dynamic and uncertain scenario such as in stock market index forecasting should be carried out using fuzzy forecasting rather than using conventional hard computation. Hence, they proposed time series forecasting based on FCM and neural network. FCM was used because it removed the need of subjective measure for length of interval determination, which is important for forecasting performance. On the other hand, Zhao et al. (2014) [45] argued that the use of FCM in image segmentation is needed as compared to its counterpart, namely hard computing. This is because FCM can retain more image information by introducing fuzziness for the image pixel belongingness. They also found that FCM is the most representative clustering algorithm, which has become the reason for adoption in many image segmentations works. Furthermore, Babaei et al. (2016) [46] introduced soft constraints for improving university timetable systems so that they can satisfy lecturers by allowing them to set their priorities. This required data clustering implementation, and they applied FCM that showed the ability to produce good results.
Another alternative for fuzzy data clustering is through subtractive clustering method. Yazdani-Chamzini et al. (2013) [47] showed that Takagi–Sugeno FIS developed based on subtractive clustering was used for road header prediction. The clustering method was utilized in the study for the purpose of constructing the fuzzy rules of the FIS. Like FCM, the subtractive clustering has also been implemented to solve image segmentation problems. This was shown in Dhanachandra et al. (2015) [48], whereby subtractive clustering was used to generate the cluster centers that were then used in K-Means algorithm to segment the images. Generally, subtractive clustering method is applied in Takagi–Sugeno FIS. However, it can also be used in Mamdani FIS. An example of the utilization of subtractive clustering in Mamdani-based FIS was shown in Chu et al. (2015) [49].
Overall, all these reviewed studies show that data clustering methods have generated considerable research interest. The studies also show that constructing MF from data clustering is preferred over expert knowledge-based MF construction because it is faster and less prone to subjectivity and uncertainties.
3. Materials and Methods
3.1. Methodology
The structured literature review was conducted by following four stages—identification, screening, eligibility, and inclusion. These stages are described as the following:
3.1.1. Identification (Pi)
The manuscripts were gathered from the three main databases—Thompson Reuters Web of Science, SCOPUS, and Google Scholar for all previous years until 2020. The review began with framing the question for review so that the searching for literature became specific, and the problems to be addressed can be firmed up. Hence, the review was done only upon the literature related to triangular and trapezoidal fuzzy MF construction using FCM or clustering method. The literature was searched using the keywords “clustering AND triangular membership function”, “c-means AND triangular membership function”, “clustering AND trapezoidal membership function”, and “c-means AND trapezoidal membership function”. From this search 104 manuscriptswere collected, hence Pi1 = 104.
We carried out another search through random search, such as using other keywords, referring from the listed references in the collected manuscripts, etc. This was to ensure that we could conduct a more thorough review, and hence six more manuscripts were collected, Pi2 = 6. Hence, the total number of manuscripts collected from this stage, Pi, was Pi = Pi1 + Pi2 = 110 manuscripts.
3.1.2. Screening (Ps)
In this stage, firstly, the collected manuscripts were filtered in order to remove duplication. This resulted in 16 manuscripts being removed, hence the number of remaining manuscripts were Ps1 = 94. Next, we assessed the collected 94 manuscripts by reviewing their title and abstract. As mentioned above, the manuscripts were excluded from being reviewed if they did not meet the selection criteria: (1) the manuscripts must describe the triangular MF construction using clustering or FCM method, and (2) the manuscripts must describe the trapezoidal MF construction using clustering or FCM method. The result from this screening was that the number of excluded manuscripts was Ps2 = 73. Among the reasons for the exclusion of the manuscripts were the topic that does not focus on FCM or clustering in MF construction, and the use of nonfuzzy solution such as Neural Network and bio-inspired algorithms. Therefore, the number of manuscripts was reduced in this stage, Ps = Ps1 – Ps2 = 21 manuscripts.
3.1.3. Eligibility (Pe) and Included (Pn)
In this stage, the 21 manuscripts from the screening stage were assessed for eligibility. From the review that we conducted on these manuscripts, all of them were eligible to be included for synthesis and analysis, Pe = 21 manuscripts.
Overall, a total of 21 manuscripts were further reviewed, synthesized, and analyzed in the included stage. Hence, Pn = 21 manuscripts. The results of this review are presented in the following section of this paper.
3.2. Results
Shukla and Muhuri (2019) [50] proposed IT2 implementation to cluster big data in modeling gene expression. They generated FOU for the IT2 implementation with the aim to account for all possible uncertainties that occurred in the big dataset of gene expression. In the model, a novel algorithm was proposed for the generation of IT2 MF. This involved the generation of primary MF to represent gene expression data containing different types of uncertainty. There were several sources of noise producing uncertainty in the dataset, hence one primary MF was generated to represent one type of uncertainty. All these primary MFs were then combined to form the FOU of the IT2 MF. Specifically, the IT2 MF was developed based on a heuristic approach. They firstly determined the two extreme points of a trapezoidal MF by uniformly distributing the uncertainty values. These two values were taken as a and d of the trapezoidal MF as formulated in Equation (6). Then, based on these two values, the values of b and c as in Equation (6) were determined randomly between the interval [a, b] and [c, d]. As a result, a type-1 trapezoidal MF was formed. IT2 MF was generated by “moving” the type-1 MF to the left and right using random scaling factors between 0 and 1. For example, the type-1 MF was scaled 70% to the left and 50% to the right. This eventually generated the IT2 trapezoidal MF. The similar processes were also applied to generate triangular MF based on Equation (4). Overall, the work did not focus on generating IT2 MF from FCM clustering as reviewed and discussed in the present paper. Instead, the work proposed the heuristic approach and random scaling to the right and left in order to generate the IT2 MF. FCM was proposed in the work only to carry out cluster analysis, which intended to evaluate the generated IT2 MF.
Cao et al. (2013) [51] described the proposed fuzzy MF formation method using clustering analysis. Firstly, the data were clustered using an improved density-based clustering algorithm. Then, another clustering was conducted that formed intervals of the data. These intervals were used to form the a, b, and c values of triangular MF based on Equation (4). The a and c values were the values located at the leftmost and rightmost of the clusters, respectively. The value of b was the projected centroid of cluster. The proposed method was based on shared nearest neighbor similarity and density based spatial clustering of application with noise (DBSCAN). However, this work did not base on MF generation using FCM. Furthermore, the work also did not cover on the generation of IT2 MF.
Lv et al. (2017) [52] presented their work on fuzzy modeling of gas pipeline pressure, by proposing a multiobjective clustering based MFs generation. The method involved the formation of a single MF based on three objectives namely accuracy, complexity, and interpretability. This means that the dataset was clustered using density clustering based on local density and relative distance of the data points. Next, due to the complexity and nonlinear relationships of industrial data they used, three objectives were evaluated upon the clustering outcomes. Firstly, the model accuracy was evaluated based on root mean squared error (RMSE). The second objective was to evaluate the model’s complexity. This was carried out by measuring the number of fuzzy sets and fuzzy rules imposed in the model. The third objective was model’s interpretability whereby the model was measured based on the average coverage of the samples used. Overall, the work did not involve FCM in generating the MF. Furthermore, the work only focused on type-1 MF generation instead of IT2 MF.
Bulutsuz et al. (2015) [53] proposed a fuzzy model for predicting dynamic measurement errors of coordinate measuring machines (CMM). The work proposed the use of Mamdani FIS, and the generation of MF based on the mapping of the input parameters’ values into the MF plot. There were six input parameters used in the work, namely probe diameter, probe velocity, measurement angle (x direction), measurement angle (y angle), probed point number, and approach distance to probe. All these six input parameters contained eight levels of values categorized as A–H. Hence, the MFs of each input parameters contained eight clusters, whereby each cluster covered the range of values defined in its category (A–H). The work, however, did not investigate the construction of IT2 MF from FCM in their method.
Kowalczyk and Pelikant (2007) [54] investigated the implementation of automatic MF generation based on grouping algorithms. They applied the model to enhance the traditional SQL language for database queries by allowing the keeping of ambiguous and imprecise data. The MF was generated based on K-Means and Mountain clustering methods, by which the gathered information from databases were clustered accordingly to generate trapezoidal MF. Kumar et al. (2008) [55], on the other hand, proposed Kohonen-like self-organizing neural network known as unsupervised discrete clustering technique (UDCT) and supervised discrete clustering technique (SDCT) to produce a nonuniform-yet-normal and not-necessarily-convex fuzzy sets. The data were firstly clustered based on unsupervised or supervised clustering method. The clustering results were plotted in a graph, whereby the values of a, b, and c of Equation (4) were identified for all clusters. The data points were assigned with a membership degree; the points near the cluster centroid will be assigned with membership degree of close to 1, while the points near the cluster edges will be assigned with membership degree of close to 0. The membership degree values of all the data points were used to plot the graph to form the MF. Overall, these works did not focus on FCM-based generation of IT2 MF as discussed in the present paper.
Heng and Jie (2012) [56] determined the method of piecewise liner MF based on interval density cluster. In this work, the MF was generated by utilizing density clustering based on interval method. The clustering will determine the cluster centers. Then, the values of MF that touched the graph floor (membership degree 0) were determined according to the vicinity principle. For example, assuming that there are three clusters, c1 – c3, in the triangular MF where c1 is adjacent to c2, and c3 is adjacent to c2. Based on Equation (4) and the vicinity principle, a value of c2 is equal to b value of c1, and a value of c3 is equal to b value of c2. Through these steps, a type-1 MF will be generated. This work, however, did not enhance FCM algorithm in generating triangular and trapezoidal IT2 MFs as being focused on by the present paper. The work also did not focus on generating IT2 MF.
Rubio and Castillo (2013) [7] extended the FCM algorithm with the objectives to enhance the algorithm’s capability in performing fuzzy clustering as well as handling problems with higher degree of uncertainties. The proposed algorithm is the fundamental of IT2FCM, which is used to generate IT2 MFs from FCM. This was done by carrying out FCM upon the dataset with different fuzzifying values, m. These values are the parameters of FCM, and in the work conducted by Rubio and Castillo (2013) [7], the range of values used were [1.5, 2.5]. The multiple MFs produced by FCM through different m values became the components to construct the FOU of the IT2 MFs. Since the proposed algorithm was based on FCM, hence only Gaussian MF was produced. There were no findings towards generating non-Gaussian MFs from that of FCM algorithm.
Alemu (2018) [57] proposed a fuzzy model for chaotic time series prediction. Fuzzy time series predictor development consisted of three steps, namely (1) defining universe of discourse and partitioning interval, (2) defining fuzzy sets and fuzzifying time series, (3) constructing the prediction model. The universe of discourse, U, was defined from the minimum, maximum, and standard deviation of training data. From this U, the training data was partitioned into k interval and the linguistic variables were then determined. There are several methods that can be used to perform the interval partitioning. Alemu (2018) [57] proposed that the task is performed by using FCM. The generated linguistic variables and intervals were represented by triangular, modified triangular, or trapezoidal MF. The optimum shape of MF was then determined by linearly searching the width of the upper base of trapezoidal MF. The best shape was the one that yielded the smallest mean squared error during training. This linear searching of the width of trapezoidal MF was carried out until the minimum (i.e., 0) and maximum values. If the width is 0, the trapezoidal MF will become a triangular MF. Then the fuzzy rules and prediction model were defined and constructed. Overall, the work utilized FCM to perform interval partitioning and determine the linguistic variables. There was no formulation of triangular and trapezoidal IT2 MFs from FCM as being discussed in the present paper.
Moewes and Kruse (2013) [58] proposed evolutionary fuzzy rules for ordinal binary classification. The main work was about using Rough Set Approach and applying K-means clustering to generate the fuzzy rules. The work did not investigate the IT2 trapezoidal and triangular MFs generation through FCM. Jang (1993) [6] proposed parameterized MFs that were generated from clustered raw data. Heuristic approximation was introduced in the study to estimate triangular and trapezoidal MFs from raw data. However, the study did not involve IT2 MF generation and FCM. Chen et al. (2017) [36] investigated stability analysis of polynomial fuzzy-model-based (PFMB) control systems whereby two sets of MFs were generated for both polynomial fuzzy model and polynomial fuzzy controller. General-formed MFs were introduced for nonlinear FIS, which were not generated through data clustering. The work also did not focus on IT2 MF generation.
Khayatzadeh and Yelten (2018) [59] proposed a circuit to generate multiple MFs, which were Gaussian, trapezoidal, triangular, S-shaped, and Z-shaped MFs. The generator was circuit-based and did not depend on data, which would be suitable for a simple control system. The work also did not focus on IT2 MF generation. Ruanpeng et al. (2017) [60] produced a system which detected movements of humans and dogs by using Mamdani inference system with automated generation of MFs. The system produced recognition rate of 93.97% but with misclassification due to missing segmentation. It was limited to type-1 Gaussian MF and not based on FCM.
Viattchenin et al. (2013) [61] constructed MF based on data through possibilistic heuristic approach. Their work was based on their earlier research on the possibilistic heuristic method [62]. The results of the work showed that the generated MF can be applied in FIS and was able to produce correct outputs. However, in their work, they only focused on constructing Gaussian MF. Furthermore, the work only produced type-1 MF instead of IT2 MF.
The work by Bhatt et al. (2012) [63] described the importance of generating MF from data clustering method since the raw outputs from the clustering process were hardly useful to the users. In constructing the MF from FCM outputs, they argued that there were limitations in the convex hull method for estimating trapezoidal membership functions from the clustered raw data. These limitations gave effects to the MF in terms of either becoming highly overlapped or highly separated. Hence, they proposed heuristic approach whereby the outputs from FCM method, namely membership degrees and clusters’ centers were used in estimating the trapezoidal and triangular MFs. Overall, the work only investigated the construction of two types of FT1 MF, instead of IT2 MFs. In another perspective, it can be summarized that heuristically, formulating IT2 MFs from FT1 MFs will involve some investigations on how to place the double clusters’ centers in Gaussian and trapezoidal MFs, and the new x-axis points for triangular MF. Furthermore, the range of UMF and LMF in the MF do affect the performance of FIS. Hence their effective range should be examined so that the performance of FIS is not disregarded.
Liao (2017) [64] introduced an extended version of IT2 MF, based on minimum and maximum MFs of FT1. It produces extended Gaussian, triangular, and trapezoidal MFs. Their method was based on their earlier work known as fuzzy C-Means Variant (FCMV) [65]. The FCMV determined the centers of each clusters in the MF and membership degrees of all points in each cluster. Using heuristic methods, trapezoidal, triangular, and Gaussian IT2 MFs were generated. Unfortunately, not all of the resultant shapes were smooth and followed the correct shapes. Moreover, the proposed method lacks efficiency and accurate defuzzification results, which requires further enhancements [64].
Koduru et al. (2020) [66] proposed triangular MF in brain images segmentation. The fundamental concept of their work was the implementation of intuitionistic fuzzy set in determining the early regions of brain tissue. This was achieved by applying the triangular MF, at the initial stage, to identify the initial clusters and regions and help in controlling the number of iterations used in segmentation. The regions produced by the triangular MF were then used to find the centroid values that were required to execute intuitionistic FCM. Their method successfully determined the brain tissues and produced significant results in terms of accuracy and computational time. However, the work only focused on using triangular MF for the initial stage of the method by which it generated the parameters required for FCM. Using those parameters, FCM continued the image segmentation processes. The work did not investigate the IT2 MF generation from FCM.
Mahdipour et al. (2013) [67] proposed a vector form of FCM (VFCM), a method that can apply FCM on noncrisp numbers, with less complexity and reduced resources needed for calculation. This was achieved through simplification processes of FCM. In evaluating the generation of noncrisp numbers (i.e., fuzzy numbers), they performed the simulations upon fuzzy numbers representation such as trapezoidal fuzzy set. Hence, the work did not investigate the generation of IT2 MF generation from FCM to construct non-Gaussian MF type.
Rajendran (2019) [68] proposed FCM based scheduler for assigning weights to local PI controllers. The main purpose was to achieve control of the nonlinear process in a wide operating range. The parameters of the local controller were determined based on optimum fuzzy MF generated using FCM. The work emphasized the significant role of the number and shape of MF in fuzzy clustering. The work also concluded that the proposed method improved the existing method in a way that it generated MF by considering several characteristics and parameters through FCM clustering, instead of using fixed triangular MF. The method utilized FCM to determine the number of clusters for the MF. Using the information, the MF was then constructed based on projection technique, whereby the values of the controller gain and integral time parameters were varied. Based on that process, all the required parameter values to construct triangular and trapezoidal MFs can be approximated. Although the proposed approach produced multiple MF types, its application on the noncontroller data remains unclear. The approach involved varying parameters’ values and setting the minimum and maximum operating limits for each cluster in order to approximate MF parameters. Other types of data may not have the same premises as the controller data to allow for the approach to be implemented. Furthermore, the work only utilized FCM in determining the number of clusters in the MF. More explorations can be carried out such as the FCM outputs themselves can be used to approximate the MF parameters.
Amsini and Rani (2020) [69] investigated breast cancer image enhancement, using type-2 triangular intuitionistic fuzzy MF. Contrast Limited Adaptive Histogram Equalization (CLAHE) method was used in the first place to decrease noise, hence producing a better result. CLAHE carried out its processes based on predefined clip limit value, which was generated by using type-2 intuitionistic triangular fuzzy MF. The process then continued with the segmentation by using FCM. Overall, the work did not focus on IT2 MF generation using FCM.
Overall, the reviewed manuscripts can be summarized in Table 2.

Table 2.
Summary of the reviewed manuscripts.
3.3. Fuzzy Calculation and Operation
To ensure that our review also covers the important components of fuzzy logic, namely its calculation and operation, we extended the manuscript gathering by searching using the keywords “fuzzy calculation” and “fuzzy operation”. As mentioned before, this search was also conducted from the three main databases—Thompson Reuters Web of Science, SCOPUS, and Google Scholar for all previous years until 2020. As a result, 49 manuscripts were gathered, and the review is presented in Section 3.3.1 and Section 3.3.2.
3.3.1. Fuzzy Calculation
Shi et al. (2014) [70] investigated the problem of transformers that are in the loss fault period, with the aim to produce a more accurate assessment model. They combined the implementation of the fault tree model and fuzzy calculation in their proposed model. The fault tree model contained the probability importance and the weighting of each event. Meanwhile, the fuzzy model functioned as the module to determine the operational status of the transformers in bottom events (loss period). The fuzzy model was constructed based on Gaussian MF type, whereby they were generated using statistical and probability calculations, as well as opinions from experts. Yu and Xiang (2014) [71] proposed an approach to reduce the issues of subjectivity, time consuming, and errors in X-ray radiographs evaluation, which is based on human experiences (clinician). Their work investigated the classification of cervical spondylosis (CS) using fuzzy calculation. The main idea was to produce an approach that can give evaluation upon any given CS based on diagnosis from a number of orthopedic experts, rather than from a single expert. In their work, the fuzzy model was based on data from literature as well as the statistical analysis.
Ghazinoory et al. (2010) [72] applied the concept of fuzzy calculation to improve portfolio analysis for a strategic decision making model. Their proposed solution was based on fuzzy set theory, which took into account the limitations and problems of classic portfolio analysis approach. This covered internal and external factors which were evaluated in linguistic terms and in terms of fuzzy triangular numbers. The novelty of their work lies in the combination of industry attractiveness–business strength matrix with the α-cuts of fuzzy triangular numbers. Vostroknutov and Kaneda (2018) [73] presented an approach that allows the computational capabilities of modern CASIO CG-50 graphical calculators to solve complex mathematical problems. This was done using the aggregation of numerical values of a complex of indicators based on fuzzy inferences. They proposed the calculation of MFs values, the numerical values of linguistic variables, as well as the state of the object in relation to the sets’ parameters.
Encheva (2014) [74] proposed the implementation of fuzzy calculation in cooperative decision making, which involves a huge number of conditional attributes and alternative solutions. The proposed solution was able to select options automatically. The solution also has the capability to evaluate nonbinary options, i.e., other than “yes” and “no” or 1 and 0. Hamidreza et al. (2011) [75] proposed the use of fuzzy calculation in evaluating qualitative alternatives for civil engineering scope of jobs. In their work, the qualitative alternatives provided by the referees were categorized into nine linguistic variables. These linguistic variables became the clusters implemented in their triangular-based MFs. Wei et al. (2009) [76] proposed a solution utilizing computer software and fuzzy calculation to establish fingerprint for controlling food products’ stability. The implementation of fuzzy calculation was in combining the qualitative and quantitative data in order to reflect the entire samplings’ chemical components and their distributions. However, detailed implementation of fuzzy calculation was not presented in the paper.
Degrauwe et al. (2006) [77] proposed an improvement on fuzzy calculation to resolve the issue of the same function being maximized and minimized with different bounds for a repeated number of times. They introduced the Gradual _-level Decreasing (GαD) algorithm that overcame the issue, which could be seen in the implementation applied on a damage detection problem of a reinforced concrete (RC) beam by a FEM. Na et al. (2010) [78] investigated the mix of consumption motivation type theory, fuzzy modeling, and emotion of online review texts to establish fuzzy corpus. The work presented the generation of fuzzy rules and antecedents for their solution to carry out the product recommendation tasks. Wang and Wei (2020) [79] proposed an approach for evaluating financial development based on convergence and spillover factors. In this work, they proposed the implementation of ARMA-GARCH and fuzzy calculation, that was able to verify several financial risks. However, their work did not involve FCM and non-Gaussian MF constructions.
Ramos et al. (2009) [80] investigated the use of data mining techniques in predicting the probability of failure of electrical equipment. In the work, the case study was using highly uncertain data, which required the use of fuzzy calculation and monte carlo simulation. The implementation of MFs and fuzzy rules was however not discussed in detail in the paper. Yu et al. (2015) [81] studied gynecological chronic pelvic pain (CPP), whereby they proposed an approach with accurate diagnosis results. In their solution, fuzzy logic based on fuzzy matrix calculation was used. The generation of membership degrees was done using weighting approach rather than FCM.
3.3.2. Fuzzy Operation
Yang et al. (2019) [82] studied the operation of just-in-time (JIT) production based on processing and assembly scheduling. The operation time factor is highly uncertain; hence, it is represented by fuzzy numbers. In this work, they proposed triangular fuzzy numbers to represent operation time, while trapezoidal fuzzy numbers were used to represent delivery time. They also proposed the implementation of a genetic algorithm in the event that the complexity of the problem occurs. Bocewicz et al. (2019), Bocewicz et al. (2015), Wojcik et al. (2015), and Nielsen et al. (2016) [83,84,85,86] proposed a Grid-like Material Transportation Network (GMTN) that allows heterogeneous means of transportation (Automated Guided Vehicles (AGVs), hoists, lifts, etc.) to interact with each other. The main contribution of their work was in terms of solving a constraint satisfaction problem addressing AGVs fleet match-up scheduling subject to GMTN as well as fuzzy operation time constraints. In this work, the operations execution time are represented by imprecise (fuzzy) data.
Chen and Wang (2017) [87] utilized the fuzzy operation time approach for scheduling the process of weighing and handling of cement vehicles entering the plant. The fuzzy operation time was needed due to the fact that there existed occurrence of operation time of uncertain vehicles. Cheng and Huang (2006) [88] described the issue of uncertainty in the operation time involved in supply-chain management (SCM). This had made time estimation a daunting task. Eventually, this may have an impact on the SCM process since the market is vigorous and requires quick response to customers’ requests. Therefore, this work proposed triangular fuzzy numbers (TFNs) to represent these uncertain variables and an order-fulfillment analysis model of a supply-chain system in an uncertain environment.
Reiser et al. (2016) [89] presented the quantum processes that provide a parallel model for fuzzy connectives. The calculations involved in quantum states can be simultaneously performed by the superposition of membership and nonmembership degrees of each element of intuitionistic fuzzy sets. They proposed an approach to interpret Atanassov’s intuitionistic fuzzy logic through quantum computing. They presented the involvement of various fuzzy operations such as negation, conjunction, etc., in the proposed approach. Ledeneva (2020) [90] presented the analysis of additive generators in the form of linear fractional functions. The work was mainly focusing on proposing a new family of dual triangular norms and conorms, rather than the FCM-based generation of MF.
Han et al. (2019) [91] proposed cellular neural networks with stochastic pertubations and fuzzy operations model. This was constructed using semidiscretization technique of differential equations. The model has the capability to generate a more accurate characterization for continuous-time models as compared to the Euler scheme. In their work, fuzzy theory was implemented as a result of most real world applications involving dealing with uncertain problems. The fuzzy operations, such as MIN, MAX, etc., were applied in the model to complement the capability of neural networks. Meanwhile, Hu et al. (2018) [92] proposed distance measures as factors to enhance and extend the capability of the complex fuzzy set. In their work, they applied the proposed measures in several applications in order to evaluate their effectiveness. Zernov and Mladov (2017) [93] introduced the associative methods for fuzzy operations implementation, through multiple disjunction and conjunction associative. The methods also comprised 2-argument fuzzy disjunction and conjunction, as well as fuzzy negation. The methods were applied in modeling associative operations in 3D associative information storage and processing devices.
Okmen and Oztas (2014) [94] dealt with uncertainty problems in construction project activities. One of the examples was the duration of uncertainty due to variations in project risks. Hence, they proposed the fuzzy set for representing the project duration parameter, while fuzzy operations were utilized for network calculations in Critical Path Method (CPM). They applied triangular and trapezoidal MFs in their fuzzy sets, and as for the fuzzy operations some operations involved such as min, max, etc., to calculate project lead/lag time. Pietraszek (2013) [95] introduced a novel formalism to perform fuzzy operations on correlated assessments. The work allowed fuzzy values to be represented by membership sequence pattern or scalar MF, while binary vector can be used to describe fuzzy operations. Having these characteristics, fuzzy values and variables can have identity, which is required for operations involving correlations. Zhu et al. (2013) [96] presented an approach for centrifugal compressors safety evaluation. The evaluation process involves subjective experts’ experience and knowledge, hence a fuzzy-based solution was required to deal with this kind of linguistic values-based properties. The input for the fuzzy model were the compressors’ failure identification using failure mode and effects analysis (FMEA) method. From these inputs, an expert-failure model was established. This was then used to construct a fuzzy matrix using weightage index of fuzzy analytic hierarchy process (AHP).
Yoon and Choi (2013) [97] investigated fuzzy least squares estimation of the fuzzy linear regression model. The focus was on models with fuzzy input-output data, containing an error structure. The proposed fuzzy least squares estimators for regression parameters were based on a suitable metric. In determining the estimators, they used a notion of triangular fuzzy matrices whose elements are given as triangular fuzzy numbers, and also provided some operations among all triangular fuzzy matrices. Simple computational examples of this applications are given. Wang and Jeong (2012) [98] proposed a novel deinterlacing algorithm based on adaptive bilateral filter with local intensity histogram screening and generalized fuzzy operation. Adaptive bilateral filter with local intensity histogram screening can effectively prevent producing noise magnification or over-sharpening artifacts. Generalized fuzzy operation can enhance image local contrast and prevent involving noise. Experimental results demonstrate the proposed algorithm outperforms the mostly popular algorithms.
Zhang et al. (2012) [99] proposed a mathematical morphology for digital image blind forensic. The proposed solution was aimed at enhancing the technique for distinguishing splice post-retouching images. The solution analyzed image edges and utilized homomorphic filtering enhance artificially fuzzy operation boundaries. It removed the interference of natural fuzzy, and then detected the image edge of counterfeit tamper. Huang and Huang (2011) [100], in their work, introduced an algorithm to adjust the output brightness of a light emitting diode (LED) so that it could light along with improvement of brightness. The MFs of the fuzzy model comprised sampling brightness in working area, brightness in variation, and value of brightness adjustment. Saneifard (2011) [101] focused on defuzzification problem on parametric interval approximation of fuzzy numbers. The work introduced a novel ranking method to resolve the problem and used the interval as a crisp approximation for a fuzzy quantity, which is able to rank various fuzzy numbers. Gal et al. (2010) [102] proposed a new triangular t-norm and t-conorm, whereby the fuzzy operations and the standard negation were combined to resolve practical problems. The algorithm was based on triangular norms for a fuzzy flip-flop-based neuron, and fuzzy J-K and D flip-flop-based neurons using algebraic connectives. Maturo (2009) [103] applied fuzzy numbers in humanistic/social science systems, leveraging its capability in dealing with indeterministics. The work considered the possible alternatives in the system’s operations based on fuzzy extension principle. Rudas et al. (2008) [104] investigated parametric operations of fuzzy systems in the context of hardware implementation. The proposed method involved parametric classes of fuzzy conjunctions and disjunctions through generators and basic operations. They implemented a few generators of parametric fuzzy operations in the research.
Xu and Xiao (2008) [105] focused on enhancing the assembly line balancing problem (ALBP), which normally works under uniform and certain conditions. However, in some cases the assembly lines comprise fuzzy operation times and drifting operations, which require a fuzzy model to be built. In their work, fuzzy simulation was integrated with genetic algorithm (GA) to achieve the problem of the above-mentioned problem. Cai et al. (2008) [106] argued that parametric fuzzy conjunction and disjunction operations are not suitable for hardware implementation due to the fact that they utilize product and computing powers of operations. Hence, they introduced a new approach of generation of nonassociative conjunctions fuzzy operations in this study. Batyrshin et al. (2007) [107] also studied fuzzy operations in hardware implementation, whereby they argued that in most cases only basic operations such as min, max, etc., are used. Other more complicated fuzzy operations are normally left out. Hence, their work proposed fuzzy parametric conjunction and disjunction operations in digital hardware implementation. In other related works, Su and Guo (2005) [108] investigated fuzzy operation’s properties with equality constraints, Koprinkova-Hristova (2004) [109] studied fuzzy operations’ parameters influence on fuzzy control systems as well as the MF shapes, Tang et al. (2004) [110] proposed a fuzzy operation based on association for data in a multisensor array with severe errors, Turken et al. (2002) [111] studied the practicality of nonassociativity operations with regards to conjunctive normal form and disjunctive normal form, and Li and Rao (2001) [112] presented conjunctive and disjunctive operations based on vague sets.
Older works on fuzzy operations include a study on fuzzy operations and their effects in engineering [113], comparison look-ahead for fast fuzzy operations [114,115], fuzzy inclusion and equality between fuzzy subsets [116], fuzzy numbers for design varaibles [117], and computing fuzzy operations in high speed and high precision using binary positive-digit number arithmetic operation [118].
Overall, the reviewed manuscripts on fuzzy calculation and operation can be summarized in Table 3.

Table 3.
Summary of the reviewed manuscripts on fuzzy calculation and operation.
3.4. Contributions and Limitations of the Existing Works
The main contributions from the works on triangular and trapezoidal IT2 MFs generation from FCM are listed in Table 4.

Table 4.
Contributions of the studies in this structured literature review.
The previous works such as Bhatt et al. (2012) [63] and their extended work presented in Swathi et al. (2015) [119] had placed a good fundamental on the issue of IT2 MF construction from FCM. Their method was based on approximation and heuristic, whereby the output of FCM i.e., membership degrees of each data point in matrix U were used to approximate the triangular and trapezoidal. Other works, Liao et al. (2003) [65], and the extended work presented in Liao (2017) [64] showed that IT2 MFs can be constructed through their enhanced version of FCM known as FCMV. They showed in their work that triangular and trapezoidal IT2 MFs were generated using FCMV outputs and heuristic methods. Unfortunately, the methods proposed by these works do not always guarantee the correct triangular and trapezoidal shapes in their results. This limitation may also affect the accuracy and precision of the generated results. Hence, there remains a need for a method that is able to produce correct triangular and trapezoidal shapes regardless of the type of the underlying dataset.
4. Challenges and Future Research
As discussed in the previous section, some limitations still exist in the current methods, hence, alternative approaches are necessary. Some of the further research can be highlighted as follows:
- Introducing a method that can heuristically produce the correct triangular and trapezoidal shapes given any types of data. The improvement in terms of accuracy or precision, for example, can be further explored.
- The existing method of developing IT2 MF from FCM is based on double fuzzifiers approach. There remains a need for exploring the development of IT2 MF from FCM using other methods such as different mean values [13,64].
- Optimizing IT2 FIS results through the application of optimization algorithms in MF generation processes. The existing works mainly focused on finding the effective range of LMF and UMF based on fuzzier values of FCM.
- Exploring the application of the triangular and trapezoidal IT2 MFs in various applications such as prediction, classification, multiattribute decision making system, and case-based reasoning system.
- Investigating the IT2 MFs generated by FCM being applied in the general fuzzy Type-2 FIS. The performance effects in various general fuzzy Type-2 applications can be further explored.
Future research works come with challenges. Some of the challenges are as the following:
- FCM faces the challenges in managing different uncertainties associated with data and getting trapped in local optima and fails to find optimal cluster centers when dealing with large data. Qaiyum et al. (2019) [120] described this challenge and proposed an optimized Interval Type-2 Fuzzy C-Means (IT2FCM) using Ant Colony-based Optimization (ACO). Therefore, while exploring the construction of triangular and trapezoidal IT2 MF using FCM, the optimization issue needs to be of concern too.
- Despite its simplicity and effectiveness in clustering, FCM suffers from being sensitive to initial values and susceptible to noise. Many studies proposed the utilization of bio-inspired algorithms such as particle swarm optimization (PSO) Dhanachandra and Chanu (2020) [121] to tackle the issues. The study on IT2 FIS developed with trapezoidal and triangular MF-based FCM may require further consideration in terms of noise reduction, in order to ensure the results are accurate and acceptable.
- FCM is thought to have a slight defect when dealing with large datasets [122]. Hence, exploring the construction and application of IT2 triangular and trapezoidal MF based on FCM will be a challenging issue when dealing with large datasets.
5. Conclusions
FCM is used to construct the MF for FIS due to its superior capability over the expert knowledge-based approach in terms of time consumption and subjectivity in making decisions. Despite these advantages, most of the existing works only showed the utilization of FCM in produce Gaussian MF. The construction of the other two popular MFs, namely triangular and trapezoidal, remains unclear. As shown in this paper, the triangular and trapezoidal MFs are also able to produce superior results over the Gaussian MF in certain applications. Other than that, there is also limited literature that investigates the construction of these three types of MFs using FCM in order to develop an IT2 application. Hence, we conducted a structured literature review on these two scopes of FCM-based FIS, and this paper presented and discussed the review results.
Although there were some papers presenting the proposed methods related to the triangular and trapezoidal IT2 MF construction using FCM, some limitations still exist. Hence, this paper presented some future works and their challenges. It is important to note that these research scopes imply the development of a useful method that has flexibility in choosing MF type, hence increasing the effectiveness of FIS through leveraging the advantages that each of the three MF types could provide. It also implies the more robust fuzzy method through IT2, which is not only faster and better at dealing with uncertainty than FT1, but it will also have the capability of choosing the best MF type in solving the problems.
Author Contributions
Conducted the review, analyzed the results and drafted the manuscript, S.H.K. Planning, supervision of the work, and editing/reviewing of the manuscript, M.H.H. Provided the funding for the work, M.H.H. Planning and supervision of the work, M.A.H. Review and analyzed partial of the results, M.H.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research is an ongoing research supported by Fundamental Research Grant Scheme (FRGS/1/2018/ICT02/UTP/02/1); a grant funded by the Ministry of Higher Education, Malaysia.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Guillaume, S. Designing fuzzy inference systems from data: An interpretability-oriented review. IEEE Trans. Fuzzy Syst. 2001, 9, 426–443. [Google Scholar] [CrossRef]
- Bolos, M.I.; Bradea, I.A.; Delcea, C. The Development of a Fuzzy Logic System in a Stochastic Environment with Normal Distribution Variables for Cash Flow Deficit Detection in Corporate Loan Policy. Symmetry 2019, 11, 548. [Google Scholar] [CrossRef]
- Ma, X.; Liu, Q.; Zhan, J. A survey of decision making methods based on certain hybrid soft set models. Artif. Intell. Rev. 2017, 47, 507–530. [Google Scholar] [CrossRef]
- Mohd Adnan, M.R.H.; Sarkheyli, A.; Mohd Zain, A.; Haron, H. Fuzzy logic for modeling machining process: A review. Artif. Intell. Rev. 2015, 43, 345–379. [Google Scholar] [CrossRef]
- Castillo, O.; Melin, P. Design of Intelligent Systems with Interval Type-2 Fuzzy Logic. In Handbook of Granular Computing; Springer: Berlin, Germany, 2008; pp. 575–601. [Google Scholar]
- Jang, J.-R. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man, Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Rubio, E.; Castillo, O. Interval type-2 fuzzy clustering for membership function generation. In Proceedings of the 2013 IEEE Workshop on Hybrid Intelligent Models and Applications (HIMA), Singapore, 16–19 April 2013; pp. 13–18. [Google Scholar]
- Rodríguez-Sánchez, J.E.; Orozco-del-Castillo, M.G.; Rodríguez-Castellanos, A.; Ávila-Carrera, R.; Valle-Molina, C. A fuzzy inference system applied to estimate the error in the recovery of the Green’s function by means of seismic noise correlations. J. Geophys. Eng. 2018, 15, 2110–2123. [Google Scholar] [CrossRef]
- Ahmad, K.A.; Abdullah, S.L.S.; Mahmod, O.; A Bakar, M. Induction of Membership Function and Fuzzy Rules for Harumanis Classification. J. Fundam. Appl. Sci. 2018, 10, 1202–1215. [Google Scholar]
- Ghani, U.; Bajwa, I.; Ashfaq, A. A Fuzzy Logic Based Intelligent System for Measuring Customer Loyalty and Decision Making. Symmetry 2018, 10, 761. [Google Scholar] [CrossRef]
- Pancardo, P.; Hernández-Nolasco, J.A.; Acosta-Escalante, F. A Fuzzy Logic-Based Personalized Method to Classify Perceived Exertion in Workplaces Using a Wearable Heart Rate Sensor. Mob. Inf. Syst. 2018, 2018, 1–17. [Google Scholar] [CrossRef]
- Subbotin, I. Trapezoidal Fuzzy Logic Model for Learning Assessment. 2014. Available online: https://www.researchgate.net/publication/263582488_Trapezoidal_Fuzzy_Logic_Model_for_Learning_Assessment (accessed on 17 November 2020).
- Hasan, M.H.; Jaafar, J.; Hassan, M.F. Fuzzy C-Means and two clusters’ centers method for generating interval type-2 membership function. In Proceedings of the 2016 3rd International Conference on Computer and Information Sciences (ICCOINS), Kuala Lumpur, Malaysia, 15–17 August 2016; pp. 627–632. [Google Scholar]
- Dunn, J.C. A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact Well-Separated Clusters. J. Cybern. 1973, 3, 32–57. [Google Scholar] [CrossRef]
- Kalist, V.; Ganesan, P.; Sathish, B.S.; Jenitha, J.M.M.; Basha.shaik, K. Possiblistic-Fuzzy C-Means Clustering Approach for the Segmentation of Satellite Images in HSL Color Space. Procedia Comput. Sci. 2015, 57, 49–56. [Google Scholar] [CrossRef]
- Sridevi, P. Identification of suitable membership and kernel function for FCM based FSVM classifier model. Clust. Comput. 2018, 22, 11965–11974. [Google Scholar] [CrossRef]
- Rhee, F.; Choi, B.-I. Interval Type-2 Fuzzy Membership Function Generation Methods for Representing Sample Data. In Studies in Fuzziness and Soft Computing; Springer: Berlin, Germany, 2013; Volume 301, pp. 165–184. [Google Scholar]
- Faustino, C.P.; Novaes, C.P.; Pinheiro, C.A.M.; Carpinteiro, O.A. Improving the performance of fuzzy rules-based forecasters through application of FCM algorithm. Artif. Intell. Rev. 2012, 41, 287–300. [Google Scholar] [CrossRef]
- Krishnapuram, R.; Keller, J.M. A possibilistic approach to clustering. IEEE Trans. Fuzzy Syst. 1993, 1, 98–110. [Google Scholar] [CrossRef]
- Wang, L.; Wang, J. Feature Weighting Fuzzy Clustering Integrating Rough Sets and Shadowed Sets. Int. J. Pattern Recognit. Artif. Intell. 2012, 26, 26. [Google Scholar] [CrossRef]
- Saha, S.; Pal, M.; Konar, A. Triangular membership function based real-time gesture monitoring system for physical disorder detection. Comput. Vis. Sci. 2019, 22, 1–14. [Google Scholar] [CrossRef]
- Felix, G.; Nápoles, G.; Falcon, R.; Froelich, W.; Vanhoof, K.; Bello, R. A review on methods and software for fuzzy cognitive maps. Artif. Intell. Rev. 2019, 52, 1707–1737. [Google Scholar] [CrossRef]
- Liu, F.; Peng, Y.; Chen, Z.; Shi, Y. Modeling of Characteristics on Artificial Intelligence IQ Test: A Fuzzy Cognitive Map-Based Dynamic Scenario Analysis. Int. J. Comput. Commun. Control. 2019, 14, 653–669. [Google Scholar] [CrossRef]
- Raj, R.; Mohan, B.M. General structure of Interval Type-2 fuzzy PI/PD controller of Takagi–Sugeno type. Eng. Appl. Artif. Intell. 2020, 87, 103273. [Google Scholar] [CrossRef]
- Ali, O.A.M.; Ali, A.Y.; Sumait, B.S. Comparison between the Effects of Different Types of Membership Functions on Fuzzy Logic Controller Performance. Int. J. Emerg. Eng. Res. Technol. 2015, 3, 76–83. [Google Scholar]
- Umoh, U.; Udoh, S.; Isong, E.; Asuquo, R.; Nyoho, E. PSO Optimized Interval Type-2 Fuzzy Design for Elections Results Prediction. Int. J. Fuzzy Log. Syst. 2019, 9, 1–19. [Google Scholar] [CrossRef]
- Mai, D.S.; Ngo, L.T. Interval Type-2 Fuzzy C-Means Clustering with Spatial Information for Land-Cover Classification. In Proceedings of the Asian Conference on Intelligent Information and Database Systems 2015, Dong Hoi City, Vietnam, 19–21 March 2018; pp. 387–397. [Google Scholar]
- Choi, B.-I.; Rhee, F.C.-H. Interval type-2 fuzzy membership function generation methods for pattern recognition. Inf. Sci. 2009, 179, 2102–2122. [Google Scholar] [CrossRef]
- Mendel, J.M. x Type-2 Fuzzy Sets and Systems: A Retrospective. Inform. Spektrum 2015, 38, 523–532. [Google Scholar] [CrossRef]
- Zhang, Z. Trapezoidal interval type-2 fuzzy aggregation operators and their application to multiple attribute group decision making. Neural Comput. Appl. 2016, 29, 1039–1054. [Google Scholar] [CrossRef]
- Dan, S.; Kar, M.B.; Majumder, S.; Roy, B.; Kar, S.; Pamucar, D. Intuitionistic Type-2 Fuzzy Set and Its Properties. Symmetry 2019, 11, 808. [Google Scholar] [CrossRef]
- Memon, K.H. A histogram approach for determining fuzzifier values of interval type-2 fuzzy c-means. Expert Syst. Appl. 2018, 91, 27–35. [Google Scholar] [CrossRef]
- Melin, P.; Castillo, O. A review on type-2 fuzzy logic applications in clustering, classification and pattern recognition. Appl. Soft Comput. 2014, 21, 568–577. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Casillas, J.; Moreno, D. Analyzing Strengths and Weaknesses of Fuzzy Association Rules Algorithms; Universidad de Granada: Granada, Spain, 2011; Available online: http://repositorio.conicit.go.cr:8080/xmlui/bitstream/handle/123456789/89/paper_Daniel_Moreno_vFinal%20%2812-12-2011%29.pdf?sequence=1&isAllowed=y (accessed on 17 November 2020).
- Chen, C.; John, R.; Twycross, J.; Garibaldi, J.M. Type-1 and interval type-2 ANFIS: A comparison. In Proceedings of the 2017 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Naples, Italy, 9–12 July 2017; pp. 1–6. [Google Scholar]
- Wu, K.-L. Analysis of parameter selections for fuzzy c-means. Pattern Recognit. 2012, 45, 407–415. [Google Scholar] [CrossRef]
- Garima, G.H.; Singh, P.K. Clustering techniques in data mining: A comparison. In Proceedings of the 2015 2nd International Conference on Computing for Sustainable Global Development (INDIACom), New Delhi, India, 11–13 March 2015; pp. 410–415. [Google Scholar]
- Bezdek, J.C.; Ehrlich, R.; Full, W. FCM: The fuzzy c-means clustering algorithm. Comput. Geosci. 1984, 10, 191–203. [Google Scholar] [CrossRef]
- Sadollah, A. Introductory Chapter: Which Membership Function is Appropriate in Fuzzy System? In Fuzzy Logic Based in Optimization Methods and Control Systems and Its Applications; Sadollah, A., Ed.; IntechOpen, 2018; Available online: https://www.researchgate.net/publication/328643706_Introductory_Chapter_Which_Membership_Function_is_Appropriate_in_Fuzzy_System (accessed on 17 November 2020).
- Reyna Vargas, M.E. Fuzzy Analytical Hierarchy Process Approach for Multicriteria Decision-Making with an Application to developing an ‘Urban Greenness Index’; University of Toronto: Toronto, ON, Canada, 2018; Available online: https://www.semanticscholar.org/paper/Fuzzy-Analytical-Hierarchy-Process-Approach-for-an-Vargas-Elvia/e2b9376e5b2f222a6dd5cc9a5b1095fb4bf4879e (accessed on 17 November 2020).
- Kreinovich, V.; Kosheleva, O.; Shahbazova, S. Why Triangular and Trapezoid Membership Functions: A Simple Explanation. Recent Dev. Fuzzy Log. Fuzzy Sets 2020, 25–31. [Google Scholar] [CrossRef]
- Guldemır, H.; Sengur, A. Comparison of clustering algorithms for analog modulation classification. Expert Syst. Appl. 2006, 30, 642–649. [Google Scholar] [CrossRef]
- Egrioglu, E.; Aladag, C.H.; Yolcu, U. Fuzzy time series forecasting with a novel hybrid approach combining fuzzy c-means and neural networks. Expert Syst. Appl. 2013, 40, 854–857. [Google Scholar] [CrossRef]
- Zhao, F.; Fan, J.; Liu, H. Optimal-selection-based suppressed fuzzy c-means clustering algorithm with self-tuning non local spatial information for image segmentation. Expert Syst. Appl. 2014, 41, 4083–4093. [Google Scholar] [CrossRef]
- Babaei, H.; Karimpour, J.; Oroji, H. Using fuzzy c-means clustering algorithm for common lecturers timetabling among departments. In Proceedings of the 2016 6th International Conference on Computer and Knowledge Engineering (ICCKE), Mashhad, Iran, 26–27 October 2016; pp. 243–250. [Google Scholar]
- Yazdani-Chamzini, A.; Razani, M.; Yakhchali, S.H.; Zavadskas, E.K.; Turskis, Z. Developing a fuzzy model based on subtractive clustering for road header performance prediction. Autom. Constr. 2013, 35, 111–120. [Google Scholar] [CrossRef]
- Dhanachandra, N.; Manglem, K.; Chanu, Y.J. Image Segmentation Using K -means Clustering Algorithm and Subtractive Clustering Algorithm. Procedia Comput. Sci. 2015, 54, 764–771. [Google Scholar] [CrossRef]
- Chu, F.; Ma, X.; Wang, F.; Jia, R. Novel robust approach for constructing Mamdani-type fuzzy system based on PRM and subtractive clustering algorithm. J. Central South Univ. 2015, 22, 2620–2628. [Google Scholar] [CrossRef]
- Shukla, A.K.; Muhuri, P.K. Big-data clustering with interval type-2 fuzzy uncertainty modeling in gene expression datasets. Eng. Appl. Artif. Intell. 2019, 77, 268–282. [Google Scholar] [CrossRef]
- Cao, H.; Jia, L.; Si, G.; Zhang, Y. A Clustering-analysis-based membership functions formation method for fuzzy controller of ball mill pulverizing system. J. Process. Control. 2013, 23, 34–43. [Google Scholar] [CrossRef]
- Lv, Z.; Zhao, J.; Liu, Y.; Wang, W.; Han, M. A multi-objective clustering-based membership functions formation method for fuzzy modeling of gas pipeline pressure. IFAC-PapersOnLine 2017, 50, 12823–12828. [Google Scholar] [CrossRef]
- Bulutsuz, A.G.; Yetilmezsoy, K.; Durakbasa, N. Application of fuzzy logic methodology for predicting dynamic measurement errors related to process parameters of coordinate measuring machines. IFAC-PapersOnLine 2017, 50, 12823–12828. [Google Scholar] [CrossRef]
- Kowalczyk, A.; Pelikant, A. Implementation of automatically generated membership functions based on grouping algorithms. In Proceedings of the EUROCON 2007—The International Conference on “Computer as a Tool”, Warsaw, Poland, 9–12 September 2007; pp. 835–840. [Google Scholar]
- Kumar, A.; Quek, C.; Cho, S. DCT-Yager FNN: A Novel Yager-Based Fuzzy Neural Network With the Discrete Clustering Technique. IEEE Trans. Neural Netw. 2008, 19, 625–644. [Google Scholar]
- Heng, Z.; Jie, W. Determination Method of Piecewise Linear Membership Function Based on the Interval Density Cluster. In Proceedings of the 2012 International Conference on Industrial Control and Electronics Engineering, Xi’an, China, 23–25 August 2012; pp. 1134–1137. [Google Scholar]
- Alemu, M.N. A fuzzy model for chaotic time series prediction. Int. J. Innov. Comput. Inf. Control. 2018, 14, 1767–1786. [Google Scholar]
- Moewes, C.; Kruse, R. Evolutionary Fuzzy Rules for Ordinal Binary Classification with Monotonicity Constraints. Stud. Fuzziness Soft Comput. 2013, 291, 105–112. [Google Scholar]
- Khayatzadeh, R.; Yelten, M.B. A Novel Multiple Membership Function Generator for Fuzzy Logic Systems. In Proceedings of the 2018 15th International Conference on Synthesis, Modeling, Analysis and Simulation Methods and Applications to Circuit Design (SMACD), Prague, Czech, 2–5 July 2018; pp. 101–104. [Google Scholar]
- Ruanpeng, C.; Auephanwiriyakul, S.; Theera-Umpon, N. Human and dog movement recognition using fuzzy inference system with automatically generated membership functions. In Proceedings of the 2017 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Naples, Italy, 9–12 July 2017; pp. 1–5. [Google Scholar]
- Viattchenin, D. A Heuristic Approach to Possibilistic Clustering for Fuzzy Data. J. Inf. Organ. Sci. 2008, 32, 149–163. [Google Scholar]
- Viattchenin, D.; Tati, R.; Damaratski, A. Designing Gaussian Membership Functions for Fuzzy Classifier Generated by Heuristic Possibilistic Clustering. J. Inf. Organ. Sci. 2013, 37, 127–139. [Google Scholar]
- Bhatt, R.B.; Narayanan, S.J.; Paramasivam, I.; Khalid, M. Approximating fuzzy membership functions from clustered raw data. In Proceedings of the 2012 Annual IEEE India Conference (INDICON), Kerala, India, 7–9 December 2012; pp. 487–492. [Google Scholar]
- Liao, T.W. A procedure for the generation of interval type-2 membership functions from data. Appl. Soft Comput. 2017, 52, 925–936. [Google Scholar] [CrossRef]
- Liao, T.W.; Celmins, A.K.; Hammell, R.J. A fuzzy c-means variant for the generation of fuzzy term sets. Fuzzy Sets Syst. 2003, 135, 241–257. [Google Scholar] [CrossRef]
- Koduru, G.K.; Nageswararao, K.; Namburu, A. T1 Weighted MR Brain Image Segmentation with Triangular Intuitionistic Fuzzy Set. Int. J. Innov. Technol. Explor. Eng. 2020, 9, 762–768. [Google Scholar]
- Mahdipour, H.; Khademi, M.; Sadoghi Yazdi, H. Vector fuzzy C-means. J. Intell. Fuzzy Syst. 2013, 24, 363–381. [Google Scholar]
- Rajendran, V. FCM Scheduled Multiple Model Controller for the Simulated Model of Spherical Tank Process. In Proceedings of the 2019 IEEE International Conference on Electrical, Computer and Communication Technologies (ICECCT), Coimbatore, India, 20–22 February 2019; pp. 1–6. [Google Scholar]
- Amsini, P.; Rani, R.U. Enhanced Type 2 Triangular Intuitionistic Fuzzy C Means Clustering Algorithm for Breast Cancer Histopathology Images. In Proceedings of the 2020 Fourth International Conference on Computing Methodologies and Communication (ICCMC), 11–13 March 2020; pp. 589–594. Available online: https://ieeexplore.ieee.org/document/9076454 (accessed on 17 November 2020).
- Shi, H.F.; Li, T.; Zhang, C. The Transformer Condition Assessment Model is Based on The Fuzzy Calculation. In Proceedings of the 3rd International Conference on Computer Science and Service System, Bangkok, Thailand, 13–15 June 2014; pp. 224–228. [Google Scholar]
- Yu, X.H.; Xiang, L.B. Classifying Cervical Spondylosis Based on Fuzzy Calculation. Abstr. Appl. Anal. 2014, 2014, 1–7. [Google Scholar] [CrossRef]
- Ghazinoory, S.; Esmail Zadeh, A.; Kheirkhah, A.S. Application of fuzzy calculations for improving portfolio matrices. Inf. Sci. 2010, 180, 1582–1590. [Google Scholar] [CrossRef]
- Vostroknutov, I.; Kaneda, Y. The possibilities of using modern casio cg-50 graphing calculators for volumetric and complex calculations, including fuzzy calculations. In Advances in Intelligent Systems and Computing; Springer: Berlin, Germany, 2018; pp. 702–708. [Google Scholar]
- Encheva, S. Selecting processes supported by fuzzy calculations. In Lecture Notes in Electrical Engineering; Springer: Berlin, Germany, 2014; pp. 39–43. [Google Scholar]
- Ghazinoory, S.; Esmail Zadeh, A.; Kheirkhah, A.S. Development of new evaluation methods for qualitative alternatives, using fuzzy calculations. Eur. J. Sci. Res. 2011, 51, 305–314. [Google Scholar]
- Wei, X.; Zhang, H.; Wang, W.; Mo, H.; Li, B. Fingerprint chromatogram and fuzzy calculation for quality control of shenrong tonic wine. In Proceedings of the 5th International Conference on Natural Computation, Sendai, Japan, 12–13 December 2009; pp. 519–522. [Google Scholar]
- Degrauwe, D.; Arman, E.O.; Reynders, E.; De Roeck, G.; Lombaert, G. An efficient fuzzy calculation algorithm with application to finite element model updating. In Proceedings of the International Conference on Noise and Vibration Engineering, Heverlee, The Netherlands, 18–20 September 2006; pp. 4105–4116. [Google Scholar]
- Na, R.S.; Liu, Y.; Li, Y. Semantic Fuzzy Calculation and Product Recommendation Based on Online Reviews. J. Guangxi Norm. Univ. 2010, 1. Available online: https://en.cnki.com.cn/Article_en/CJFDTotal-GXSF201001038.htm (accessed on 17 November 2020).
- Wang, C.; Wei, Y. Simulation of financial risk spillover effect based on ARMA-GARCH and fuzzy calculation model. J. Intell. Fuzzy Syst. 2020, 1–12. [Google Scholar] [CrossRef]
- Ramos, S.; Khodr, H.M.; Azevedo, F.; Vale, Z. Power systems reliability calculation based on fuzzy data mining. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26-30 July 2009; pp. 1–7. [Google Scholar]
- Yu, X.; Meng, W.; Xiang, L. Comprehensive evaluation chronic pelvic pain based on fuzzy matrix calculation. Neurocomputing 2016, 173, 2097–2101. [Google Scholar] [CrossRef]
- Yang, M.S.; Ba, L.; Zheng, H.Y.; Liu, Y.; Wang, X.F.; He, J.Z.; Li, Y. An integrated system for scheduling of processing and assembly operations with fuzzy operation time and fuzzy delivery time. Adv. Prod. Eng. Manag. 2019, 14, 367–378. [Google Scholar] [CrossRef]
- Bocewicz, G.; Banaszak, Z.; Nielsen, I. Multimodal processes prototyping subject to grid-like network and fuzzy operation time constraints. Ann. Oper. Res. 2017, 273, 561–585. [Google Scholar] [CrossRef]
- Bocewicz, G.; Banaszak, Z.; Nielsen, I. Multimodal processes prototyping subject to fuzzy operation time constraints. IFAC-PapersOnLine 2015, 48, 2103–2108. [Google Scholar] [CrossRef]
- Nielsen, I.; Wójcik, R.; Bocewicz, G. Multimodal processes optimization subject to fuzzy operation time constraints: Declarative modeling approach. Front. Inf. Technol. Electron. Eng. 2016, 17, 338–347. [Google Scholar] [CrossRef]
- Wójcik, R.; Nielsen, I.; Bocewicz, G.; Banaszak, Z. Multimodal Processes Optimization Subject to Fuzzy Operation Time Constraints. In Proceedings of the 12th International Conference. Advances in Intelligent Systems and Computing, Seville, Spain, 13–15 May 2019; p. 373. [Google Scholar]
- Chen, D.-J.; Wang, P. Research on Weighing Strategy of Vehicle Entering Plant Based on Fuzzy Operation Time. In Proceedings of the 2017 International Conference on Applied Mechanics and Mechanical Automation (AMMA 2017), Phuket, Thailand, 6–7 August 2017; pp. 132–138. [Google Scholar]
- Chen, C.-T.; Huang, S.-F. Order-fulfillment ability analysis in the supply-chain system with fuzzy operation times. Int. J. Prod. Econ. 2006, 101, 185–193. [Google Scholar] [CrossRef]
- Reiser, R.; Lemke, A.; Avila, A.; Vieira, J.; Pilla, M.; Bois, A.D. Interpretations on Quantum Fuzzy Computing: Intuitionistic Fuzzy Operations×Quantum Operators. Electron. Notes Theor. Comput. Sci. 2016, 324, 135–150. [Google Scholar] [CrossRef]
- Ledeneva, T. Additive generators of fuzzy operations in the form of linear fractional functions. Fuzzy Sets Syst. 2020, 386, 1–24. [Google Scholar] [CrossRef]
- Han, S.; Liu, G.; Zhang, T. Mean almost periodicity and moment exponential stability of semi-discrete random cellular neural networks with fuzzy operations. PLoS ONE 2019, 14, e0220861. [Google Scholar] [CrossRef] [PubMed]
- Bo, H.; Lvqing, B.; Songsong, D.; Sizhao, L. Distances of Complex Fuzzy Sets and Continuity of Complex Fuzzy Operations. J. Intell. Fuzzy Syst. 2018, 35, 2247–2255. [Google Scholar]
- Zernov, M.M.; Mladov, V.V. Associative methods of fuzzy operations implementation. In Proceedings of the 2017 Second Russia and Pacific Conference on Computer Technology and Applications (RPC), Vladivostok, Russia, 25–29 September 2017; pp. 199–204. [Google Scholar]
- Ökmen, Ö.; Öztaş, A. A CPM-based scheduling method for construction projects with fuzzy sets and fuzzy operations. J. S. Afr. Inst. Civ. Eng. 2014, 56, 2–8. [Google Scholar]
- Pietraszek, J. The modified sequential-binary approach for fuzzy operations on correlated assessments. In Proceedings of the 12th International Conference on Artificial Intelligence and Soft Computing, Zakopane, Poland, 9–13 June 2013. [Google Scholar]
- Zhu, X.-P.; Zhang, L.-B.; Liang, W.; Shi, G.-N. A quantitative comprehensive safety evaluation method for centrifugal compressors using FMEA-fuzzy operations. In Proceedings of the 2nd International Symposium on Instrumentation and Measurement, Sensor Network and Automation, Toronto, ON, Canada, 23–24 December 2013. [Google Scholar]
- Yoon, J.H.; Choi, S.H. Fuzzy Least Squares Estimation with New Fuzzy Operations. In Advances in Intelligent Systems and Computing; Kruse, R., Berthold, M., Moewes, C., Gil, M., Grzegorzewski, P., Hryniewicz, O., Eds.; Synergies of Soft Computing and Statistics for Intelligent Data Analysis; Springer: Berlin/Heidelberg, Germany, 2013; p. 190. [Google Scholar]
- Wang, A.; Jeong, J. ShiAdaptive bilateral filter with local intensity histogram combine generalized fuzzy operation (GFO) for intra-frame deinterlacing. In Proceedings of the 2012 International Conference on Systems and Informatics, Jiaxing, China, 18–20 December 2012. [Google Scholar]
- Zhang, L.; Duan, W.; Guo, H. Fuzzy Operation Forensics Research Based on Mathematical Morphology. In Lecture Notes in Electrical Engineering; Zhu, R., Ma, Y., Eds.; Information Engineering and Applications; Springer: London, UK, 2012; p. 154. [Google Scholar]
- Huang, S.; Huang, Y. Monitor and control the desk-top illumination based on fuzzy operation. In Proceedings of the 2011 International Conference on Machine Learning and Cybernetics, Guilin, China, 10–13 July 2011; pp. 248–253. [Google Scholar]
- Saneifard, R. A new algorithm for selecting equip system based on fuzzy operations. Int. J. Phys. Sci. 2011, 6, 3279–3287. [Google Scholar]
- Gál, L.; Lovassy, R.; Kóczy, L.T. Function approximation performance of Fuzzy Neural Networks based on frequently used fuzzy operations and a pair of new trigonometric norms. In Proceedings of the International Conference on Fuzzy Systems, Barcelona, Spain, 18–23 July 2010; pp. 1–8. [Google Scholar]
- Maturo, A. Alternative fuzzy operations and applications to social sciences. Int. J. Intell. Syst. 2009. [Google Scholar] [CrossRef]
- Rudas, I.J.; Batyrshin, I.Z.; Zavala, A.H.; Nieto, O.C.; Horváth, L.; Vargas, L.V. Generators of Fuzzy Operations for Hardware Implementation of Fuzzy Systems. In MICAI 2008: Advances in Artificial Intelligence. MICAI 2008. Lecture Notes in Computer Science; Gelbukh, A., Morales, E.F., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; p. 5317. [Google Scholar]
- Xu, W.; Xiao, T. Mixed model assembly line balancing problem with fuzzy operation times and drifting operations. In Proceedings of the 2008 Winter Simulation Conference, Miami, FL, USA, 7–10 December 2008; pp. 1752–1760. [Google Scholar]
- Cai, S.; Chen, X.; Wang, Q.; Yin, M. FPGA Implementation of Generalized Fuzzy Operations. In Proceedings of the 2008 Fifth International Conference on Fuzzy Systems and Knowledge Discovery, Shandong, China, 18–20 October 2008; pp. 560–564. [Google Scholar]
- Batyrshin, I.; Zavala, A.; Camacho, O.; Vargas, L. Generalized Fuzzy Operations for Digital Hardware Implementation. In Proceedings of the Mexican International Conference on Artificial Intelligence, Aguascalientes, Mexico, 4–10 November 2007; pp. 9–18. [Google Scholar]
- Su, Z.-X.; Guo, S.-C. Fuzzy operation with equality constraint. J. Liaoning Tech. Univ. 2005, 24, 299–302. [Google Scholar]
- Koprinkova-Hristova, P.D. Fuzzy operations’ parameters versus membership functions’ parameters influence on fuzzy control systems properties. In Proceedings of the 2004 2nd International IEEE Conference on ‘Intelligent Systems’, Varna, Bulgaria, 22–24 June 2004; pp. 219–224. [Google Scholar]
- Tang, L.; Xie, W.-X.; Huang, J.; Huang, J.-X. Fuzzy operation based multitarget-multisensor tracking algorithm. Xi Tong Gong Cheng Yu Dian Zi Ji Shu/Syst. Eng. Electron. 2004, 26, 1573–1577. [Google Scholar]
- Turksen, I.B.; Esper, A.; Patel, K.; Starks, S.A.; Kreinovich, V. Selecting a fuzzy logic operation from the DNF-CNF interval: How practical are the resulting operations? In Proceedings of the 2002 Annual Meeting of the North American Fuzzy Information Processing Society Proceedings, New Orleans, LA, USA, 27–29 June 2002; pp. 28–33. [Google Scholar]
- Li, F.; Rao, Y. Weighted fuzzy operations based on Vague sets. Huazhong Ligong Daxue Xuebao/J. Huazhong Univ. Sci. Technol. 2001, 29, 12–14. [Google Scholar]
- Czogala, E.; Kowalczyk, R. Investigation of selected fuzzy operations and implications for engineering. In Proceedings of the IEEE 5th International Fuzzy Systems, New Orleans, LA, USA, 11 September 1996; pp. 879–885. Available online: https://ieeexplore.ieee.org/abstract/document/552295 (accessed on 17 November 2020).
- Han, J.; Singh, S. Fast digital fuzzy operation units using comparison look-ahead. In Proceedings of the 33rd Midwest Symposium on Circuits and Systems, Calgary, AB, Canada, 12–15 August 1990; pp. 870–873. [Google Scholar]
- Han, J.; Singh, S. Comparison look-ahead and design of fast fuzzy operation units. In Proceedings of the Twentieth International Symposium on Multiple-Valued Logic, Charlotte, NC, USA, 23–25 May 1990; pp. 121–125. [Google Scholar]
- Wygralak, M. Fuzzy inclusion and fuzzy equality of two fuzzy subsets, fuzzy operations for fuzzy subsets. Fuzzy Sets Syst. 1983, 10, 157–168. [Google Scholar] [CrossRef]
- Arakawa, M.; Yamakawa, H.; Ishikawa, H. Robust design using fuzzy numbers (consideration of correlation of design variables in fuzzy operation). In Proceedings of theDETC2000: ASME 2000 Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Anaheim, CA, USA, 18–21 August 2000. [Google Scholar]
- Tabata, T.; Ueno, F.; Eguchi, K.; Zhu, H. CMOS-Based Fuzzy Operation Circuit Using Binary-Coded Redundantly-Represented Positive-Digit Numbers. In Proceedings of the IEEK Conference, The Institute of Electronics and Information Engineers, Atlanta, GA, USA, 2000; Available online: https://www.koreascience.or.kr/article/CFKO200011921291336.page (accessed on 17 November 2020).
- Swathi, J.N.; Bhatt, R.; Paramasivam, I.; Khalid, M. A study on the approximation of clustered data to parameterized family of Fuzzy membership functions for the induction of Fuzzy Decision Trees. Cybern. Inf. Technol. 2015, 15, 75–96. [Google Scholar]
- Qaiyum, S.; Izzatdin, A.; Jaafar, J.; Kai, A. Ant Colony Optimization of Interval Type-2 Fuzzy C-Means with Subtractive Clustering and Multi-Round Sampling for Large Data. Int. J. Adv. Comput. Sci. Appl. 2019, 10, 10. [Google Scholar] [CrossRef]
- Dhanachandra, N.; Chanu, Y.J. An image segmentation approach based on fuzzy c-means and dynamic particle swarm optimization algorithm. Multimedia Tools Appl. 2020, 79, 18839–18858. [Google Scholar] [CrossRef]
- Venkat, R.; Reddy, K.S. Dealing Big Data using Fuzzy C-Means (FCM) Clustering and Optimizing with Gravitational Search Algorithm (GSA). In Proceedings of the 2019 3rd International Conference on Trends in Electronics and Informatics (ICOEI), Tirunelveli, India, 23–25 April 2019; pp. 465–467. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).