An Improved Whale Optimization Algorithm with Random Evolution and Special Reinforcement Dual-Operation Strategy Collaboration
Abstract
1. Introduction
2. Whale Optimization Algorithm (WOA)
2.1. Encircling Prey
2.2. Bubble Net Attacking Method
2.3. Searching for Prey
3. Random Evolutionary Whale Optimization Algorithm (REWOA)
3.1. Random Evolutionary
3.2. Special Reinforcement
3.3. Main Procedure of the REWOA
3.4. Complexity Analysis
4. Experimental Results and Discussion
4.1. Evaluation of Exploitation Capability
4.2. Evaluation of Exploration Capability
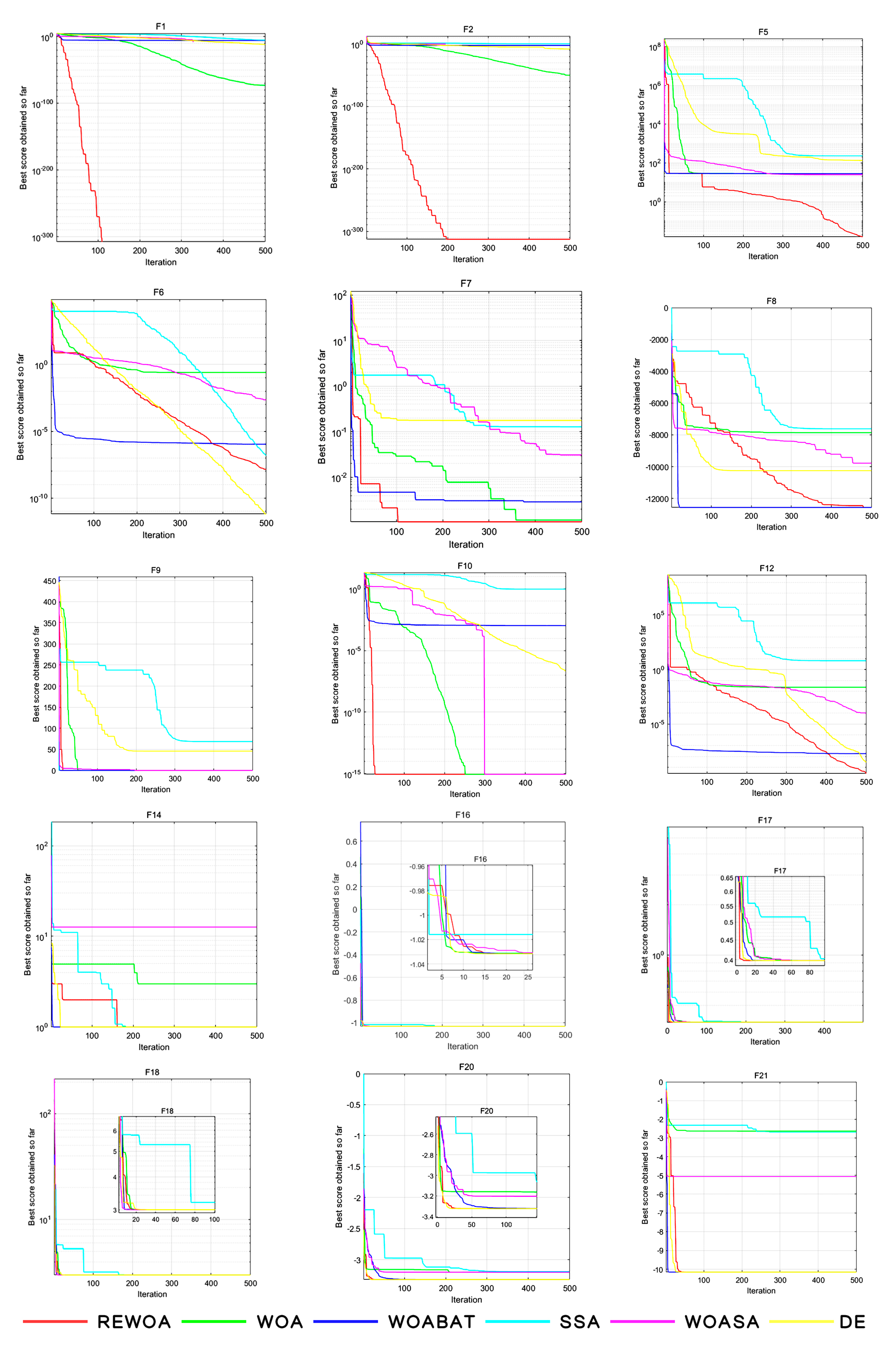
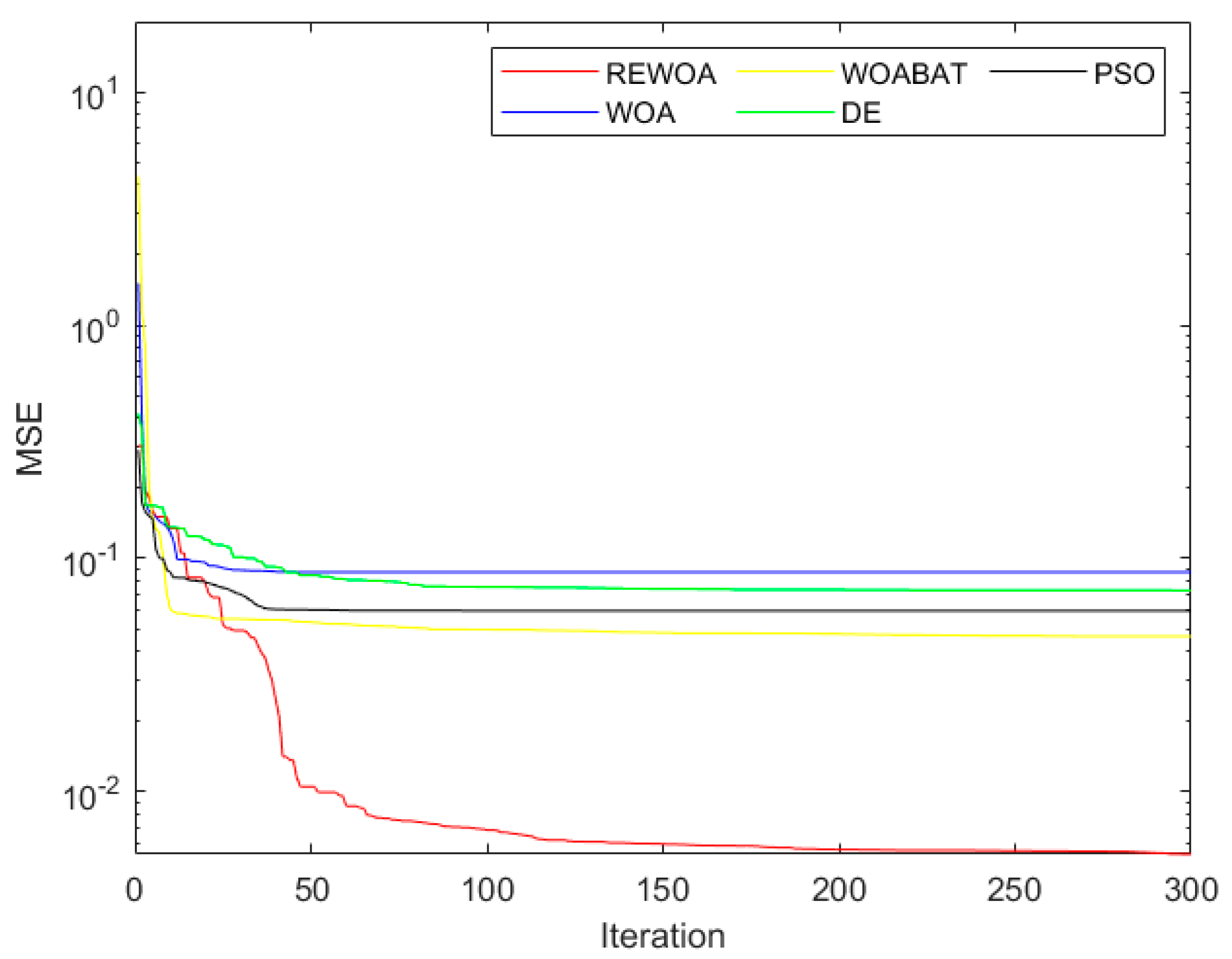
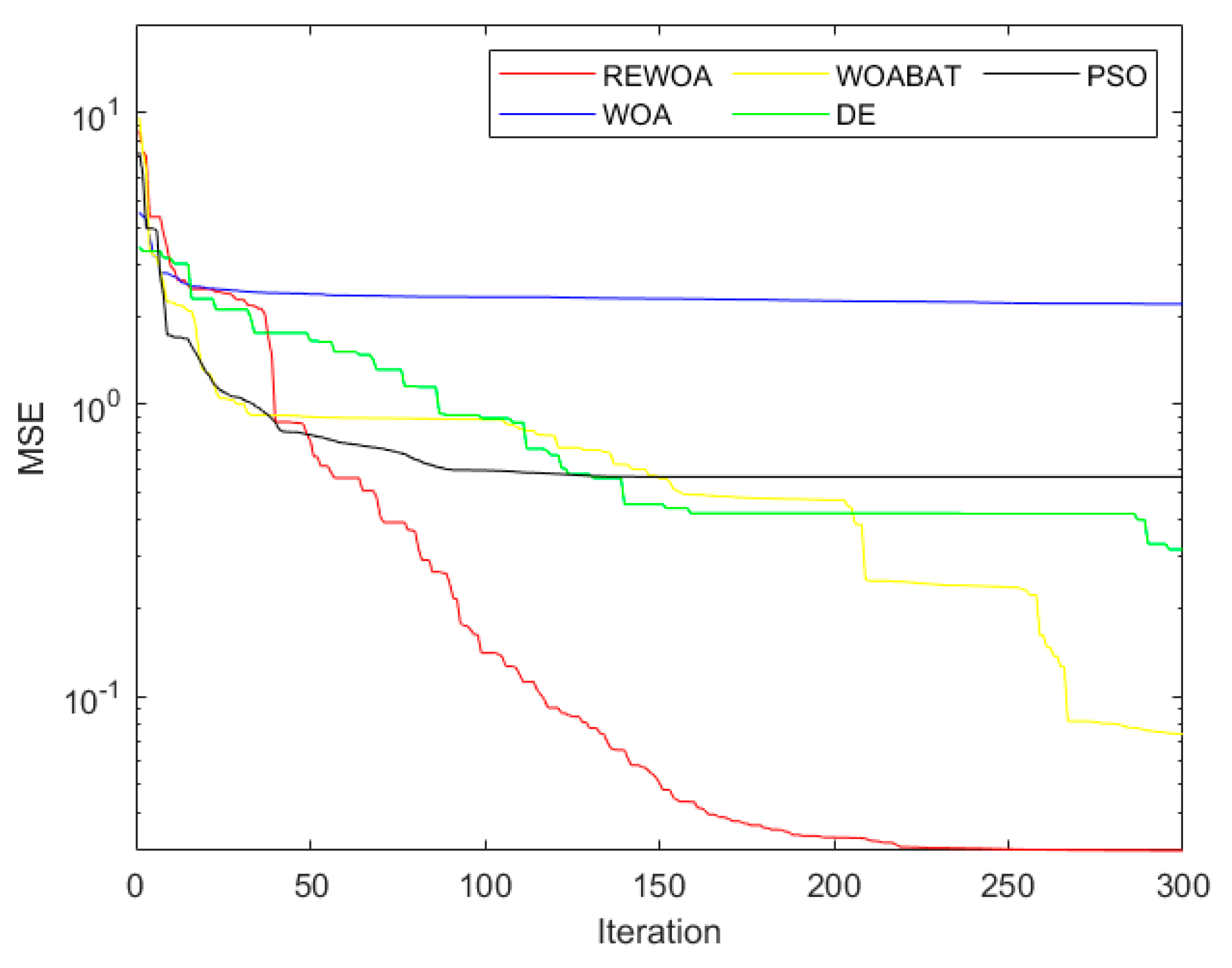
4.3. Analysis of Convergence Behavior
5. Hammerstein Model Identification Using REWOA
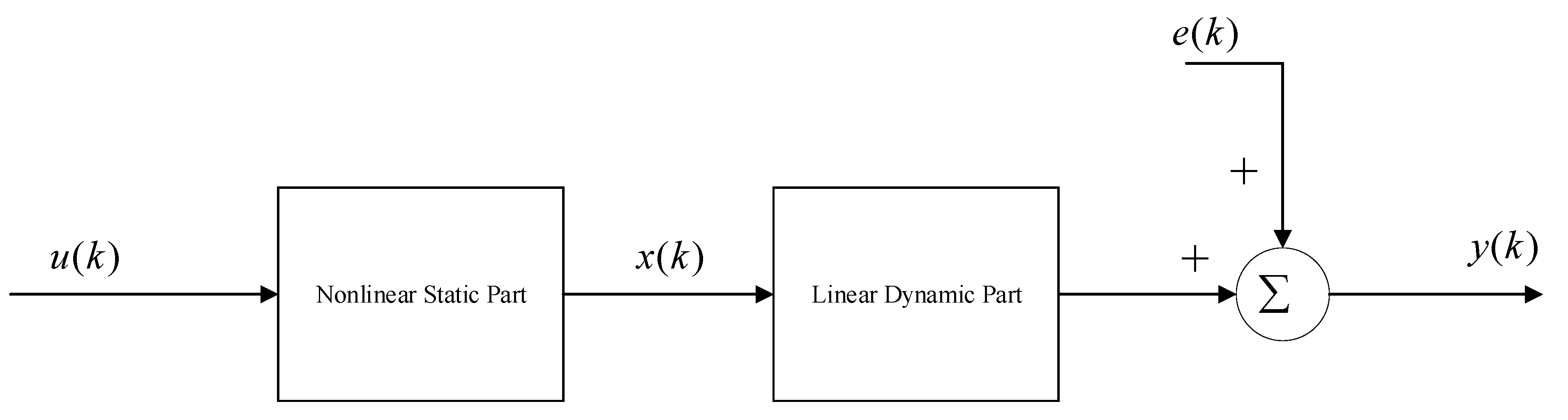
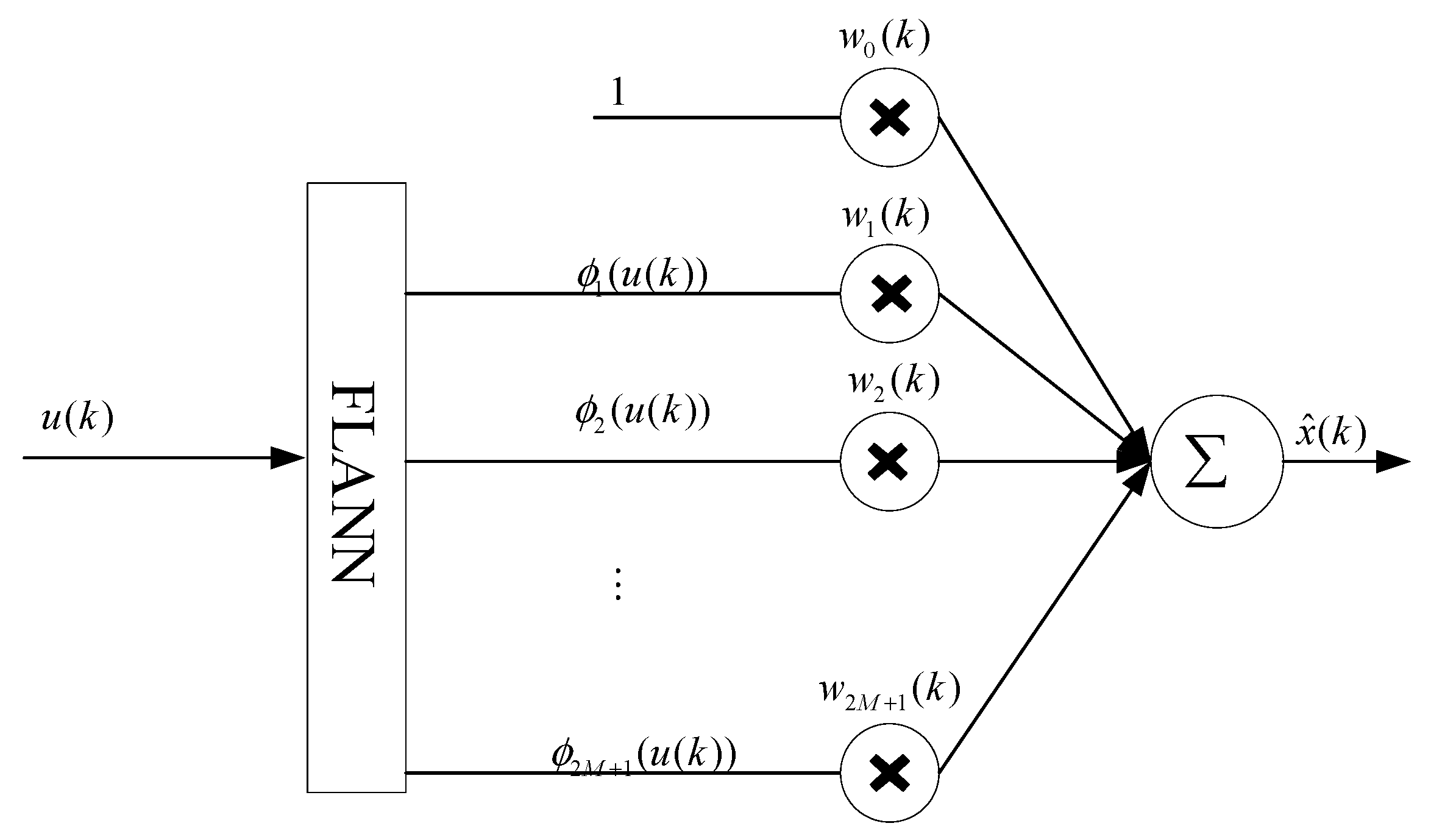
5.1. Hammertein Model
- (a)
- Two-term Gaussian mixture distribution
- (b)
- The t-distribution
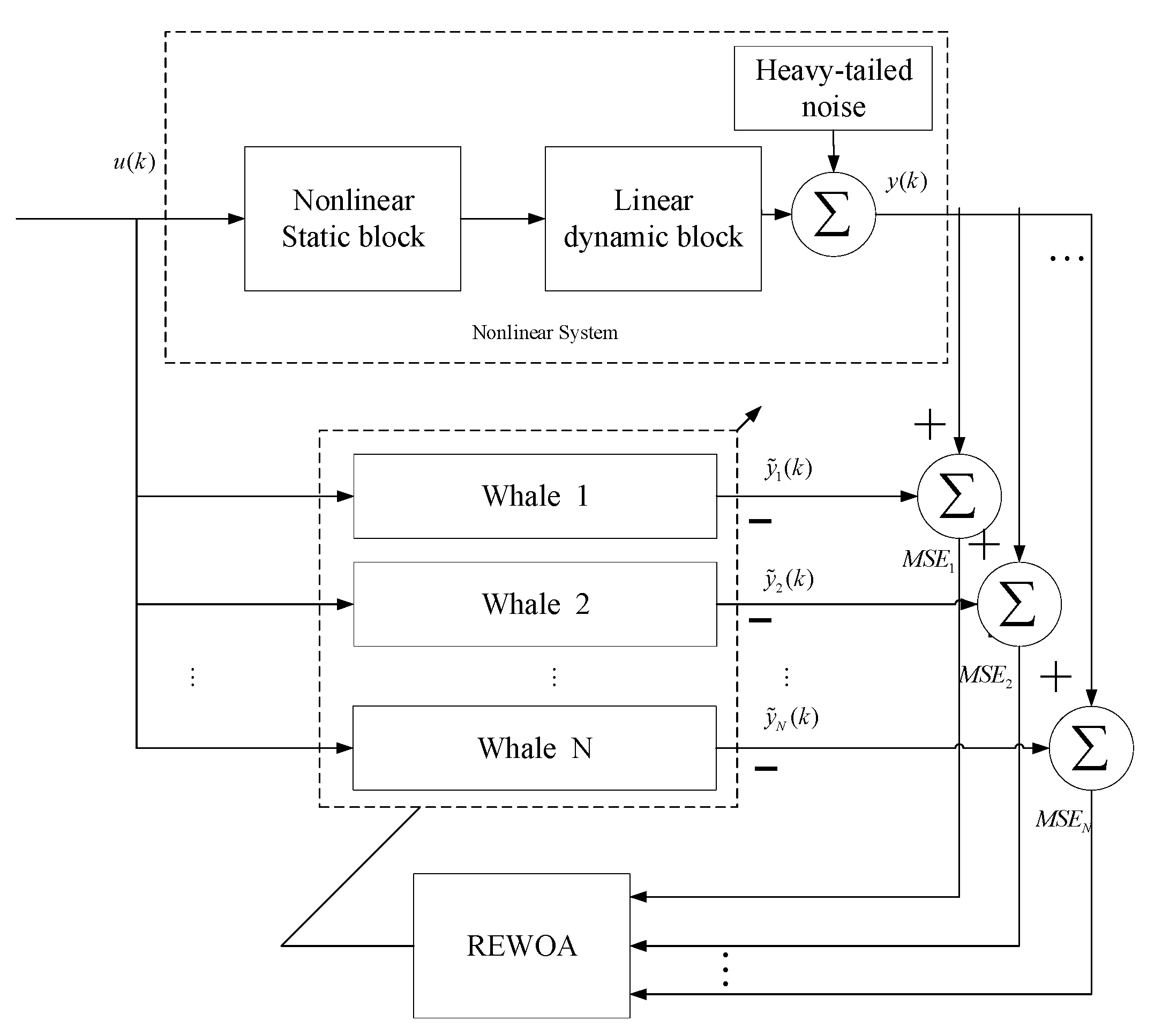
5.2. The Identification Proceduce
- Step1: Obtain the input sample data and output sample data of the system;
- Step2: Calculate the output of the model according to the weight vector of the auxiliary model;
- Step3: Initialization of positions and parameters;
- Step4: Minimize the fitness value using REWOA to get the best solution in the current iteration;
- Step5: Check whether the identification result is satisfied or not. If satisfied, then stop the algorithm and get the best solutions; if not, go back to step 4 and set .
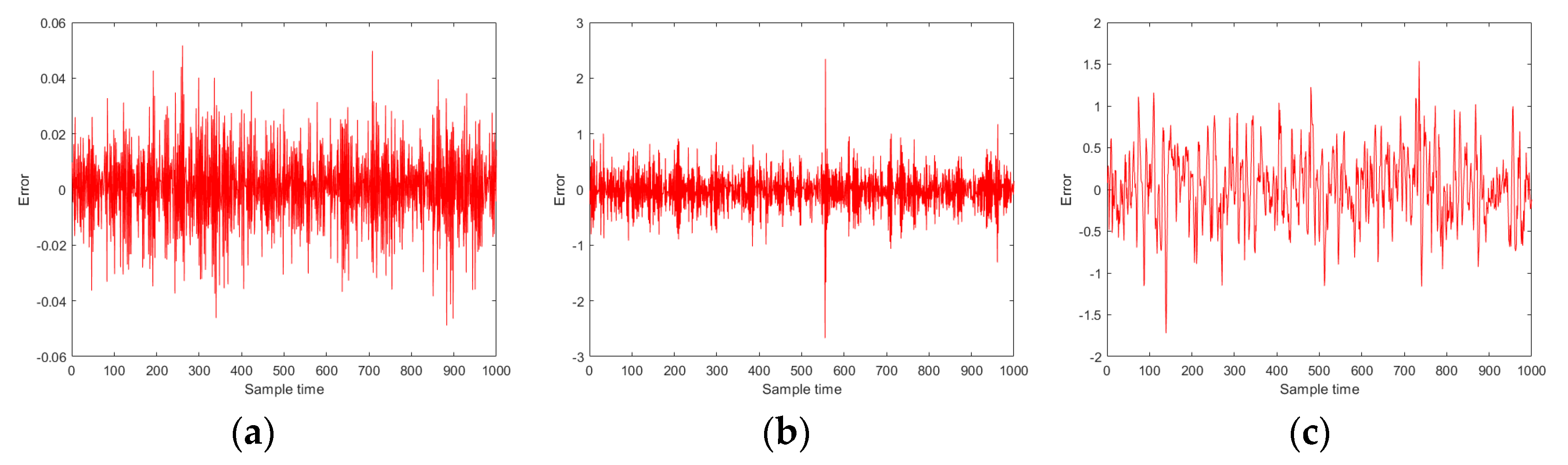
5.3. Simulation Study
- Experiment 1
- Experiment 2
- Experiment 3
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Greiner, R. PALO: A probabilistic hill-climbing algorithm. Artif. Intell. 1996, 84, 177–208. [Google Scholar] [CrossRef]
- Solis, F.J.; Wets, R.J.B. Minimization by Random Search Techniques. Math. Oper. Res. 1981, 6, 19–30. [Google Scholar] [CrossRef]
- Ouyang, W.; Zhang, B. Newton’s method for fully parameterized generalized equations. Optimization 2018, 67, 2061–2080. [Google Scholar] [CrossRef]
- Jamil, M. Levy Flights and Global Optimization. In Swarm Intelligence and Bio-Inspired Computation: Theory and Applications; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.S.; Talatahari, S.; Alavi, A.H. Metaheuristic Algorithms in Modeling and Optimization. Metaheuristic Appl. Struct. Infrastruct. 2013, 1–24. [Google Scholar] [CrossRef]
- Yang, X.-S. Nature-Inspired Metaheuristic Algorithms; Luniver Press, Middlesex University: London, UK, 2010. [Google Scholar]
- Yang, X.S. Firefly Algorithm, Levy Flights and Global Optimization. In Research and Development in Intelligent Systems XXVI; Springer: London, UK, 2010. [Google Scholar]
- Holland, J.H. Genetic Algorithms. Sci. Am. 1992, 267, 66–72. [Google Scholar] [CrossRef]
- Simon, D. Biogeography-Based Optimization. IEEE Trans. Evol. Comput. 2009, 12, 702–713. [Google Scholar] [CrossRef]
- Das, S.; Suganthan, P.N. Differential Evolution: A Survey of the State-of-the-Art. IEEE Trans. Evol. Comput. 2011, 15, 4–31. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stützle, T. Ant Colony Optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. On the performance of artificial bee colony (ABC) algorithm. Appl. Soft Comput. 2007, 8, 687–697. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Alavi, A.H. Krill herd: A new bio-inspired optimization algorithm. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4831–4845. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, G.G.; Deb, S.; Lu, M.; Zhao, X.J. Solving 0–1 knapsack problem by a novel binary monarch butterfly optimization. Neural Comput. Appl. 2017, 28, 1619–1634. [Google Scholar] [CrossRef]
- Wang, G.; Deb, S.; Coelho, L. Earthworm optimization algorithm: A bio-inspired metaheuristic algorithm for global optimization problems. Intern. J. Bio-Inspir. Comput. 2018. [Google Scholar] [CrossRef]
- Wang, G.G.; Deb, S.; Coelho, L.D.S. Elephant Herding Optimization. In Proceedings of the 2015 3rd International Symposium on Computational and Business Intelligence (ISCBI 2015), Bali, Indonesia, 7–9 December 2015; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Li, S.; Chen, H.; Wang, M.; Heidari, A.A.; Mirjalili, S. Slime mould algorithm: A new method for stochastic optimization. Future Gener. Comput. Syst. 2020, 111, 300–323. [Google Scholar] [CrossRef]
- Wang, G.G. Moth search algorithm: A bio-inspired metaheuristic algorithm for global optimization problems. Futur. Gener. Comput. Syst. 2020, 111, 300–323. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp swarm algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Wu, G.; Mallipeddi, R.; Suganthan, P.N.; Wang, R.; Chen, H. Differential evolution with multi-population based ensemble of mutation strategies. Inf. Sci. Int. J. 2016, 329, 329–345. [Google Scholar] [CrossRef]
- Qin, A.K.; Huang, V.L.; Suganthan, P.N. Differential Evolution Algorithm With Strategy Adaptation for Global Numerical Optimization. IEEE Trans. Evol. Comput. 2009, 13, 398–417. [Google Scholar] [CrossRef]
- Olorunda, O.; Engelbrecht, A.P. Measuring Exploration/Exploitation in Particle Swarms using Swarm Diversity. In Proceedings of the 2008 IEEE Congress on Evolutionary Computation (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–6 June 2008; pp. 1128–1134. [Google Scholar]
- Alba, E.; Dorronsoro, B. The exploration/exploitation tradeoff in dynamic cellular genetic algorithms. IEEE Trans. Evol. Comput. 2005, 9, 126–142. [Google Scholar] [CrossRef]
- Lin, L.; Gen, M. Auto-tuning strategy for evolutionary algorithms: Balancing between exploration and exploitation. Soft Comput. 2009, 13, 157–168. [Google Scholar] [CrossRef]
- Heidari, A.A.; Aljarah, I.; Faris, H.; Chen, H.; Luo, J.; Mirjalili, S. An enhanced associative learning-based exploratory whale optimizer for global optimization. Neural Comput. Appl. 2019, 32, 5185–5211. [Google Scholar] [CrossRef]
- Liu, S.H.; Mernik, M.; Hrnčič, D.; Črepinšek, M. A parameter control method of evolutionary algorithms using exploration and exploitation measures with a practical application for fitting Sovova’s mass transfer model. Appl. Soft Comput. 2013, 13, 3792–3805. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Vesselinov, V.V.; Harp, D.R. Adaptive hybrid optimization strategy for calibration and parameter estimation of physical process models. Comput. Geosci. 2012, 49, 10–20. [Google Scholar] [CrossRef]
- Li, L.-L.; Wang, L.; Liu, L.-H. An effective hybrid PSOSA strategy for optimization and its application to parameter estimation. Appl. Math. Comput. 2006, 179, 135–146. [Google Scholar] [CrossRef]
- Dzemyda, G.; Senkienė, E.; Valevicienė, J. Simulated annealing for parameter grouping. Informatica 1990, 1, 20–39. [Google Scholar]
- Mo, W.; Guan, S.G.; Puthusserypady, S.K. A Novel Hybrid Algorithm for Function Optimization: Particle Swarm Assisted Incremental Evolution Strategy. Stud. Comput. Intell. 2007, 75, 101–125. [Google Scholar] [CrossRef]
- Ghanem, W.A.; Jantan, A.B. Hybridizing artificial bee colony with monarch butterfly optimization for numerical optimization problems. Neural Comput. Appl. 2018, 30, 163–181. [Google Scholar] [CrossRef]
- Javaid, N.; Ullah, I.; Zarin, S.S.; Kamal, M.; Omoniwa, B.; Mateen, A. Differential-evolution-earthworm hybrid meta-heuristic optimization technique for home energy management system in smart grid. In Proceedings of the 12-th International Conference on Innovative Mobile and Internet Services in Ubiquitous Computing (IMIS-2018), Matsue, Japan, 4–6 July 2018; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Prakash, D.; Lakshminarayana, C. Optimal siting of capacitors in radial distribution network using Whale Optimization Algorithm. Alex. Eng. J. 2017, 56, 499–509. [Google Scholar] [CrossRef]
- Kumar, C.S.; Rao, R.S.; Cherukuri, S.K.; Rayapudi, S.R. A Novel Global MPP Tracking of Photovoltaic System based on Whale Optimization Algorithm. Int. J. Renew. Energy Dev. 2016, 5, 225. [Google Scholar] [CrossRef]
- Miao, Y.; Zhao, M.; Makis, V.; Lin, J. Optimal swarm decomposition with whale optimization algorithm for weak feature extraction from multicomponent modulation signal. Mech. Syst. Signal Process. 2019, 122, 673–691. [Google Scholar] [CrossRef]
- Petrović, M.; Miljković, Z.; Jokić, A. A novel methodology for optimal single mobile robot scheduling using whale optimization algorithm. Appl. Soft Comput. 2019, 81, 105520. [Google Scholar] [CrossRef]
- Aljarah, I.; Faris, H.; Mirjalili, S. Optimizing connection weights in neural networks using the whale optimization algorithm. Soft Comput. 2018, 22, 1–15. [Google Scholar] [CrossRef]
- Bhatt, U.R.; Dhakad, A.; Chouhan, N.; Upadhyay, R. Fiber wireless (FiWi) access network: ONU placement and reduction in average communication distance using whale optimization algorithm. Heliyon 2019, 5, e01311. [Google Scholar] [CrossRef]
- Mohammed, H.M.; Umar, S.U.; Rashid, T.A. A Systematic and Meta-Analysis Survey of Whale Optimization Algorithm. Comput. Intell. Neuroence 2019. [Google Scholar] [CrossRef]
- Bozorgi, S.M.; Yazdani, S. IWOA: An improved whale optimization algorithm for optimization problems. J. Comput. Des. Eng. 2019, 6, 243–259. [Google Scholar]
- Singh, A. Laplacian whale optimization algorithm. Int. J. Syst. Assur. Eng. Manag. 2019, 10, 713–730. [Google Scholar] [CrossRef]
- Sayed, G.I.; Darwish, A.; Hassanien, A.E. A New Chaotic Whale Optimization Algorithm for Features Selection. J. Classif. 2018, 35, 300–344. [Google Scholar] [CrossRef]
- Fan, Q.; Chen, Z.; Zhang, W.; Fang, X. ESSAWOA: Enhanced Whale Optimization Algorithm integrated with Salp Swarm Algorithm for global optimization. Eng. Comput. 2020, 1–18. [Google Scholar] [CrossRef]
- Yan, Z.; Zhang, J.; Tang, J. Modified whale optimization algorithm for underwater image matching in a UUV vision system. Multimed. Tools Appl. 2021, 80, 187–213. [Google Scholar] [CrossRef]
- Salgotra, R.; Singh, U.; Saha, S. On Some Improved Versions of Whale Optimization Algorithm. Arab. J. Sci. Eng. 2019, 44, 9653–9691. [Google Scholar] [CrossRef]
- Elghamrawy, S.M.; Hassanien, A.E. GWOA: A hybrid genetic whale optimization algorithm for combating attacks in cognitive radio network. J. Ambient. Intell. Hum. Comput. 2018, 10, 4345–4360. [Google Scholar] [CrossRef]
- Mafarja, M.M.; Mirjalili, S. Hybrid Whale Optimization Algorithm with simulated annealing for feature selection. Neurocomputing 2017, 260, 302–312. [Google Scholar] [CrossRef]
- Barthelemy, P.; Bertolotti, J.; Wiersma, D.S. A Levy flight for light. Nature 2008, 453, 495–498. [Google Scholar] [CrossRef]
- Yanming, D.; Huihui, X.; Fang, L. Flower pollination algorithm with new pollination methods. Comput. Eng. Appl. 2018, 54, 94–108. [Google Scholar]
- Papadimitriou, F. The Probabilistic Basis of Spatial Complexity. In Spatial Complexity, Theory, Mathematical Methods and Applications; Springer: Cham, Switzerland; Metro Manila, Philippines, 2020. [Google Scholar]
- Gutowski, M. Lévy flights as an underlying mechanism for global optimization algorithms. 2001, arXiv:math-ph/0106003. Available online: https://arxiv.org/abs/math-ph/0106003 (accessed on 30 January 2021).
- Kung, F.-C.; Shih, D.-H. Analysis and identification of Hammerstein model non-linear delay systems using block-pulse function expansions. Int. J. Control 2007, 43, 139–147. [Google Scholar] [CrossRef]
- Kumar, T.A.; Deergha Rao, K. A new m-estimator based robust multiuser detection in flat-fading non-gaussian channels. IEEE Trans. Commun. 2009, 57, 1908–1913. [Google Scholar] [CrossRef]




| No. | Formula | Dim | Range | |
|---|---|---|---|---|
| F1 | 30 | [−100, 100] | 0 | |
| F2 | 30 | [−10, 10] | 0 | |
| F3 | 30 | [−100, 100] | 0 | |
| F4 | 30 | [−100, 100] | 0 | |
| F5 | 30 | [−30, 30] | 0 | |
| F6 | 30 | [−100, 100] | 0 | |
| F7 | 30 | [−1.28, 1.28] | 0 | |
| F8 | 30 | [−500, 500] | −12,569.49 | |
| F9 | 30 | [−5.12, 5.12] | 0 | |
| F10 | 30 | [−32, 32] | 0 | |
| F11 | 30 | [−600, 600] | 0 | |
| F12 | 30 | [−50, 50] | 0 | |
| F13 | 30 | [−50, 50] | 0 | |
| F14 | 2 | [−65, 65] | 1 | |
| F15 | 4 | [−5, 5] | 0.0003 | |
| F16 | 2 | [−5, 5] | −1.0316 | |
| F17 | 2 | [−5, 5] | 0.398 | |
| F18 | 2 | [−2, 2] | 3 | |
| F19 | 3 | [1, 3] | −3.86 | |
| F20 | 6 | [0, 1] | −3.32 | |
| F21 | 4 | [0, 10] | −10.1532 | |
| F22 | 4 | [0, 10] | −10.4028 | |
| F23 | 4 | [0, 10] | −10.5363 |
| Method | Control Parameter | Value |
|---|---|---|
| REWOA | Convergence factor | [1, 2] |
| Mutation probability | 0.2 | |
| Crossover probability | [0, 0.5] | |
| Adaptive weight | [0, 1] | |
| WOA [21] | Convergence factor | [0, 2] |
| Probability coefficient | 0.5 | |
| WOABAT [43] | Convergence factor | [0, 2] |
| Probability coefficient | 0.5 | |
| Pulse rate | 0.5 | |
| Sound loudness | 0.5 | |
| SSA [22] | Probability coefficient | 0.5 |
| WOASAT [51] | Reduction rate | 0.99 |
| Initial temp | 0.1 | |
| Maximum Number of Iterations | 30 | |
| Convergence factor | [0, 2] | |
| Probability coefficient | 0.5 | |
| DE [10] | Mutation operator | 0.5 |
| Crossover probability | 0.3 |
| Function | Metric | REWOA | WOA | WOABAT | SSA | WOASAT | DE |
|---|---|---|---|---|---|---|---|
| F1 | avg | 4.2 × 10−322 | 3.67 × 10−73 | 1.57 × 10−06 | 1.60 × 10−07 | 0 | 3.44 × 10−15 |
| std | 0 | 1.12 × 10−72 | 7.11 × 10−07 | 2.24 × 10−07 | 0 | 1.04 × 10−14 | |
| F2 | avg | 2.60 × 10−213 | 5.57 × 10−52 | 7.33 × 10−03 | 2.34 | 0 | 2.10 × 10−09 |
| std | 0 | 1.82 × 10−51 | 1.39 × 10−03 | 1.49 | 0 | 3.82 × 10−09 | |
| F3 | avg | 0 | 4.21 × 104 | 9.56 × 10−06 | 1.53 × 103 | 7.93 × 10−01 | 4.07 × 103 |
| std | 0 | 1.48 × 104 | 2.17 × 10−06 | 7.48 × 102 | 5.00 × 10−01 | 1.99 × 103 | |
| F4 | avg | 5.65 × 10−151 | 49.6 | 1.01 × 10−03 | 11.4 | 8.04 × 10−01 | 8.30 |
| std | 2.79 × 10−150 | 29.4 | 8.71 × 10−05 | 3.93 | 3.92 × 10−01 | 3.90 | |
| F5 | avg | 2.64 | 27.9 | 6.58 | 3.40 × 102 | 29.6 | 62.1 |
| std | 7.88 | 4.88 × 10−01 | 11.9 | 4.59 × 102 | 19.0 | 51.9 | |
| F6 | avg | 2.01 × 10−08 | 3.64 × 10−01 | 1.71 × 10−06 | 2.72 × 10−07 | 1.28 × 10−03 | 6.90 × 10−14 |
| std | 3.94 × 10−08 | 2.20 × 10−01 | 8.14 × 10−07 | 3.02 × 10−07 | 7.99 × 10−04 | 1.56 × 10−13 | |
| F7 | avg | 1.47 × 10−03 | 2.92 × 10−03 | 4.85 × 10−04 | 1.74 × 10−01 | 5.99 × 10−02 | 2.76 × 10−01 |
| std | 1.26 × 10−03 | 3.34 × 10−03 | 8.45 × 10−04 | 5.91 × 10−02 | 3.59 × 10−02 | 2.61 × 10−01 | |
| 3 | 0 | 1 | 0 | 2 | 1 | ||
| 4 | 0 | 0 | 0 | 0 | 0 | ||
| Function | Metric | REWOA | WOA | WOABAT | SSA | WOASAT | DE |
|---|---|---|---|---|---|---|---|
| F8 | avg | −1.25 × 104 | −1.03 × 104 | −1.22 × 104 | −7.60 × 103 | −9.97 × 103 | −1.03 × 104 |
| std | 58.7 | 2.05 × 103 | 1.07 × 103 | 8.92 × 102 | 1.65 × 103 | 6.42 × 102 | |
| F9 | avg | 0 | 5.68 × 10−15 | 5.97 | 53.4 | 0 | 32.0 |
| std | 0 | 2.25 × 10−14 | 11.9 | 18.8 | 0 | 12.6 | |
| F10 | avg | 8.88 × 10−16 | 4.44 × 10−15 | 9.36 × 10−04 | 2.55 | 8.88 × 10−16 | 2.27 |
| std | 0 | 2.59 × 10−15 | 2.11 × 10−04 | 5.52 × 10−01 | 0.00 × 10+00 | 1.96 | |
| F11 | avg | 0 | 5.87 × 10−03 | 8.55 × 10−08 | 1.87 × 10−02 | 0.00 × 10+00 | 2.43 × 10−02 |
| std | 0 | 3.16 × 10−02 | 3.79 × 10−08 | 1.69 × 10−02 | 0.00 × 10+00 | 2.39 × 10−02 | |
| F12 | avg | 3.18 × 10−09 | 2.61 × 10−02 | 1.32 × 10−08 | 6.55 × 10+00 | 1.81 × 10−04 | 7.60 × 10−01 |
| std | 1.40 × 10−08 | 2.93 × 10−02 | 5.60 × 10−09 | 3.38 | 1.76 × 10−04 | 1.41 | |
| F13 | avg | 2.17 × 10−03 | 4.97 × 10−01 | 2.22 × 10−07 | 18.5 | 1.35 × 10−32 | 5.15 × 10−01 |
| std | 5.11 × 10−03 | 2.42 × 10−01 | 1.03 × 10−07 | 14.8 | 5.47 × 10−48 | 8.97 × 10−01 | |
| 5 | 0 | 0 | 0 | 4 | 0 | ||
| 0 | 2 | 2 | 0 | 0 | 0 | ||
| Function | Metric | REWOA | WOA | WOABAT | SSA | WOASAT | DE |
|---|---|---|---|---|---|---|---|
| F14 | avg | 1.32 | 3.22 | 1.78 | 1.16 | 8.14 | 2.51 |
| std | 1.75 | 3.47 | 2.50 | 4.50 × 10−01 | 5.09 | 2.26 | |
| F15 | avg | 5.37 × 10−04 | 8.27 × 10−04 | 4.03 × 10−04 | 2.96 × 10−03 | 5.51 × 10−04 | 3.86 × 10−03 |
| std | 1.67 × 10−04 | 5.57 × 10−04 | 3.56 × 10−04 | 1.11 × 10−02 | 3.59 × 10−04 | 7.39 × 10−03 | |
| F16 | avg | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 |
| std | 6.08 × 10−16 | 1.42 × 10−09 | 5.53 × 10−16 | 1.86 × 10−14 | 1.15 × 10−10 | 6.21 × 10−16 | |
| F17 | avg | 3.98 × 10−01 | 3.98 × 10−01 | 3.98 × 10−01 | 3.98 × 10−01 | 3.98 × 10−01 | 3.98 × 10−01 |
| std | 0 | 8.08 × 10−06 | 2.12 × 10−15 | 1.11 × 10−14 | 8.79 × 10−09 | 0 | |
| F18 | avg | 3.90 | 3.00 | 12.0 | 3.00 | 3.00 | 5.70 |
| std | 4.85 | 4.82 × 10−04 | 12.7 | 1.79 × 10−13 | 2.21 × 10−08 | 8.10 | |
| F19 | avg | −3.86 | −3.85 | −3.86 | −3.86 | −3.81 | −3.86 |
| std | 2.55 × 10−15 | 1.29 × 10−02 | 1.97 × 10−03 | 9.36 × 10−11 | 1.93 × 10−01 | 2.65 × 10−15 | |
| F20 | avg | −3.26 | −3.23 | −3.29 | −3.21 | −3.26 | −3.27 |
| std | 5.94 × 10−02 | 9.53 × 10−02 | 5.06 × 10−02 | 5.70 × 10−02 | 5.93 × 10−02 | 5.93 × 10−02 | |
| F21 | avg | −7.38 | −8.52 | −9.48 | −7.96 | −5.40 | −5.56 |
| std | 3.07 | 2.48 | 1.72 | 2.74 | 1.27 | 3.17 | |
| F22 | avg | −8.55 | −8.05 | −9.17 | −8.38 | −5.09 | −5.29 |
| std | 2.86 | 3.20 | 2.24 | 3.15 | 2.26 × 10−07 | 3.17 | |
| F23 | avg | −8.66 | −7.11 | −10.0 | −8.42 | −5.31 | −6.34 |
| std | 3.19 | 3.51 | 1.61 | 3.30 | 9.71 × 10−01 | 3.52 | |
| 4 | 2 | 6 | 4 | 2 | 4 | ||
| 4 | 1 | 1 | 0 | 1 | 0 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, Q.; Xu, Z.; Cai, W. An Improved Whale Optimization Algorithm with Random Evolution and Special Reinforcement Dual-Operation Strategy Collaboration. Symmetry 2021, 13, 238. https://doi.org/10.3390/sym13020238
Jin Q, Xu Z, Cai W. An Improved Whale Optimization Algorithm with Random Evolution and Special Reinforcement Dual-Operation Strategy Collaboration. Symmetry. 2021; 13(2):238. https://doi.org/10.3390/sym13020238
Chicago/Turabian StyleJin, Qibing, Zhonghua Xu, and Wu Cai. 2021. "An Improved Whale Optimization Algorithm with Random Evolution and Special Reinforcement Dual-Operation Strategy Collaboration" Symmetry 13, no. 2: 238. https://doi.org/10.3390/sym13020238
APA StyleJin, Q., Xu, Z., & Cai, W. (2021). An Improved Whale Optimization Algorithm with Random Evolution and Special Reinforcement Dual-Operation Strategy Collaboration. Symmetry, 13(2), 238. https://doi.org/10.3390/sym13020238







