Abstract
The modified second Zagreb index, symmetric difference index, inverse symmetric index, and augmented Zagreb index are among the molecular descriptors which have good correlations with some physicochemical properties (such as formation heat, total surface area, etc.) of chemical compounds. By a random cyclooctane chain, we mean a molecular graph of a saturated hydrocarbon containing at least two rings such that all rings are cyclooctane, every ring is joint with at most two other rings through a single bond, and exactly two rings are joint with one other ring. In this article, our main purpose is to determine the expected values of the aforementioned molecular descriptors of random cyclooctane chains explicitly. We also make comparisons in the form of explicit formulae and numerical tables consisting of the expected values of the considered descriptors of random cyclooctane chains. Moreover, we outline the graphical profiles of these comparisons among the mentioned descriptors.
Keywords:
modified Zagreb index; symmetric difference index; inverse symmetric index; augmented Zagreb index; random cyclooctane chain; cycloalkane; expected values; comparisons; graphical representation MSC:
05C09; 05C92; 05C90
1. Introduction
Chemical graph theory is a branch of mathematics which deals with the mathematical modeling of graphs that is also an essential branch of theoretical chemistry. Initial chemical research introduced the theory of chemical graphs. Chemists have confirmed that the physicochemical properties of a compound have been associated with molecular arrangement, with results derived from an enormous number of investigational data. Furthermore, the researchers considered the same topological index based on various chemical properties and applied it to QSR/QSPR learning. Generally, the features of a compound derived by chemical experiments are not very authentic. However, theoretical calculations assume a vital role in many extraordinary cases. There are numerous topological indices in the literature of chemical graph theory. The first of its kind is the Wiener index [1]. After that, the most important topological index is the class of the Zagreb indices and its variants [2]. The family of Adriatic indices was introduced in [3,4,5,6]. An especially interesting subclass of these descriptors consists of 148 discrete Adriatic indices. The so-called inverse sum indeg index (ISI) was defined in [4] as a significant predictor of the total surface area of octane isomers. A graph consists of some points (nodes) and lines (edges). Suppose is a graph of order n with vertex set and edge set E. Let be the node of a graph. Then, the degree of a node is the number of edges incident to that vertex and is denoted by . If an edge connects a vertex of degree i and a vertex of degree j in , then we call it an -edge. Let denote the number of -edges in the graph .
Significant efforts have been made to give an explicit formula for the topological indices for a special family of graphs or chemical graphs; see for example the recent papers [7,8].
2. Materials and Methods
A cyclooctane chain is when every node of a cyclooctane system is in an octagon. We obtain a cyclooctane chain by composing an edge joining octagons. Figure 1 shows the unique for , and Figure 2 shows four chains for . We termed , , , and by local adjustment of the cyclooctane chains (see Figure 3). Therefore, can be attained by stepwise addition of a terminal octagon. A random selection is made at each step from one of the four probable structures:
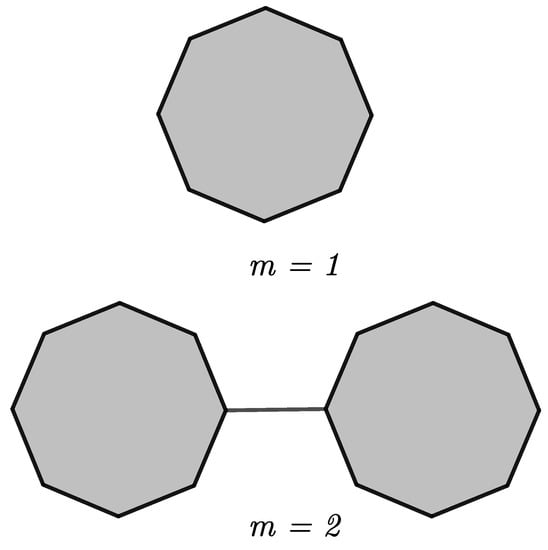
Figure 1.
The cyclooctane chains for .
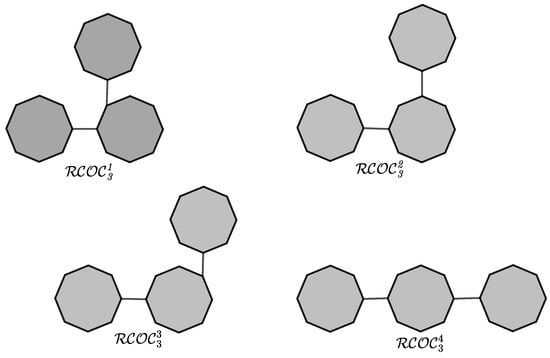
Figure 2.
The four types of cyclooctane chains for .
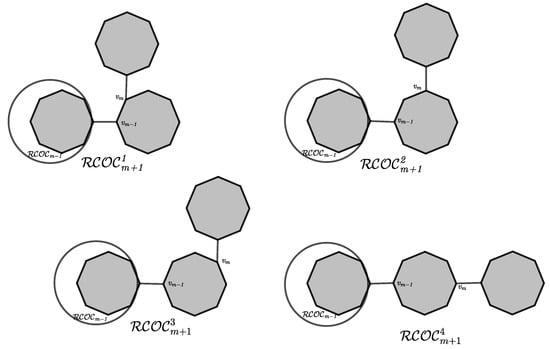
Figure 3.
The four types of local arrangements in cyclooctane for .
- (i)
- with probability ,
- (ii)
- with probability ,
- (iii)
- with probability , or
- (iv)
- with probability
A process is a zeroth-order Markov process if the probabilities are unvarying in step parameter and steady. Several papers are concentrated about random arrangement of graphs. For more details, see [9,10,11,12,13,14,15]. The comparison and inequalities among some indices for molecular graphs have been derived in [16,17]. Around one decade before, the coindex versions of these Zagreb indices were introduced. First, two extremum Zagreb indices and coindices of chemical trees were considered in [18]. In degree-based topological indices, many indices depend on the vertex degree of the molecular graph. Some degree-based topological indices are described for pentagonal chains [19]. Bond incident degree (BID) indices for some nanostructures [20,21], tree-like polyphenylene systems, spiro hexagonal systems and polyphenylene dendrimer nanostars [22] are bounds for the general sum-connectivity index of composite graphs [23]. Some vertex-degree-based topological indices are of cacti [24,25]. The Wiener indices of random benzenoid chain was considered by Gutman et al. [26,27]. In 2012, random polyphenyl chains were studied by Yang and Zhang [28].
A number of papers are attentive regarding the random arrangement of topological indices [29]. Cyclooctanes are a kind of saturated hydrocarbons. For many years, chemists have paid a lot of attention to their derivatives [30,31,32,33]. These derivatives are seen and used in drug synthesis, combustion kinetics, organic synthesis, etc. For example, the osmium-catalysed bis-dihydroxylation of 1,5-cyclooctadiene has utilized cyclooctane tetrol [33]. Alamdari et al. [30] considered the combination of some cyclooctane-based quinoxaline pyrazines. These molecular-like graphs [34,35] are geometric graphs (finite two-connected) bounded by a quadrangles of side length one and a regular octagon.
Note that a class of polycyclic conjugated hydrocarbons with tree-like octagonal systems is represented in [34]. Some mathematicians were attracted by octagonal graphs [36]. The numbers of isomers in tree-like octagonal graphs were expressed by Brunvoll et al. [34]. Yang and Zhao [35] studied the relationship among the numbers in a class of Hosoya index of the caterpillar trees and octagonal graphs.
In this work, we study the expected values of the modified Zagreb, symmetric difference, inverse symmetric, and augmented Zagreb indices in random cyclooctane chain. Furthermore, we give analytic proofs for comparison, along with numerical and graphical profiles of these indices in a random cyclooctane chain.
Here, let us examine the modified Zagreb index, symmetric difference index, inverse symmetric index, and augmented Zagreb index in the chain with m octagons. Consider to be the cyclooctane chain obtained from , as shown in Figure 3. It is easy to see from the structure of the chain that it contains only , , and -types of edges. Therefore, to calculate these indices for the chain , we need to determine only its edges of types , and . Hence, from Equations (1)–(4), one can write as:
3. Results
Notice that is a random cyclooctane chain due to its local arrangements. Therefore, , , and are the random variables. Now, we will calculate the expected values of these indices in , and denote these as , , , , respectively.
Theorem 1.
Let and a random cyclooctane chain . Then
Proof.
Since is correct, then for , there are 4 types of probabilities (see Figure 3).
Theorem 2.
Let and a random cyclooctane chain . Then
Proof.
Since is correct, then for , there are 4 types of probabilities (see Figure 3).
Theorem 3.
Let and a random cyclooctane chain . Then
Proof.
Theorem 4.
Let and a random cyclooctane chain . Then
Proof.
Since is correct, then for , there are 4 types of probabilities (see Figure 3). Thus, from (8), we get the following:
However, thus, applying the operator E on (15), we obtain
and by the recurrence relation (16) using initial conditions, we get
□
We now turn our attention to the special cyclooctane chains and , as shown in Figure 4. These chains can also be obtained as and . Then, we can easily calculate these indices for these four special chains by using Theorems 1–4.
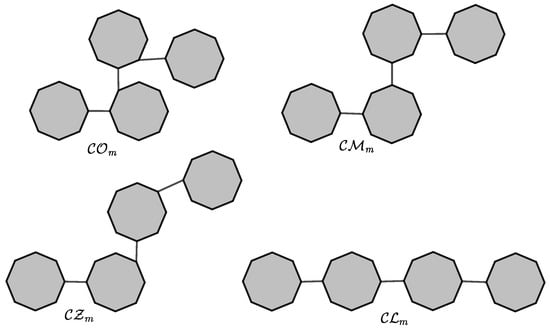
Figure 4.
Four special cyclooctain chains with m octagons.
Corollary 1.
For , we have the following:
- 1.
- .;
- ;
- ;
- .
- 2.
- ;
- .;
- ;
- .
4. Discussion and Conclusions
In this section, we are going to provide an expository comparison between the expected values for the modified Zagreb, symmetric difference, inverse symmetric, and augmented Zagreb indices for arbitrary cyclooctane chains with the same probabilities. At that point, the comparison between the expected values of these indices for diverse values of the probability is given in Table 1, Table 2, Table 3 and Table 4. The augmented Zagreb index is continuously more noteworthy than the other three indices, specifically the modified Zagreb, symmetric difference, and inverse symmetric indices. The graphical profile of the comparison between two indices is given in Figure 5, which recommends that the augmented Zagreb index is always greater than the symmetric difference index. From Figure 6, one can see that the symmetric difference index is continuously greater than the inverse symmetric index, and Figure 7 proposes that the inverse symmetric index is continuously more prominent than the modified Zagreb index. The graphical profile of the comparison between all four indices is given in Figure 8, which suggests that the augmented Zagreb index is always greater than the other indices.

Table 1.
Expected values of indices for .

Table 2.
Expected values of indices for .

Table 3.
Expected values of indices for .

Table 4.
Expected values of indices for .
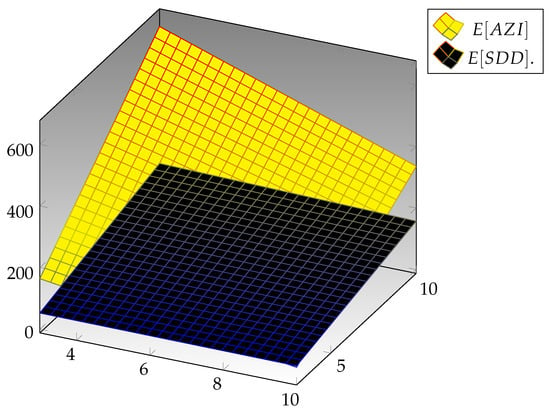
Figure 5.
Difference between and .
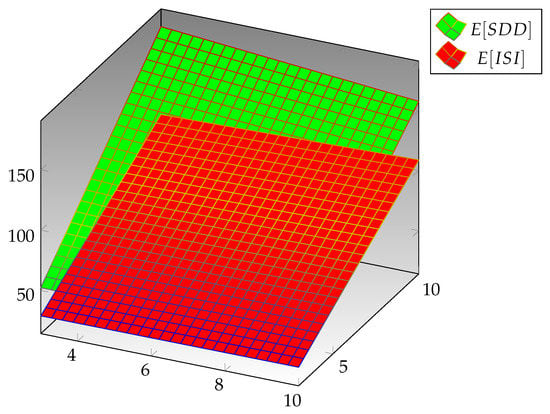
Figure 6.
Difference between and .
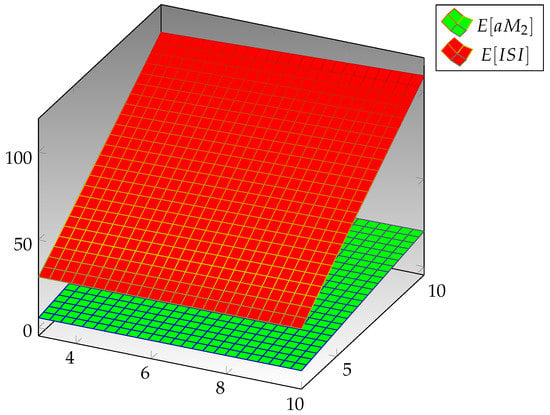
Figure 7.
Difference between and .
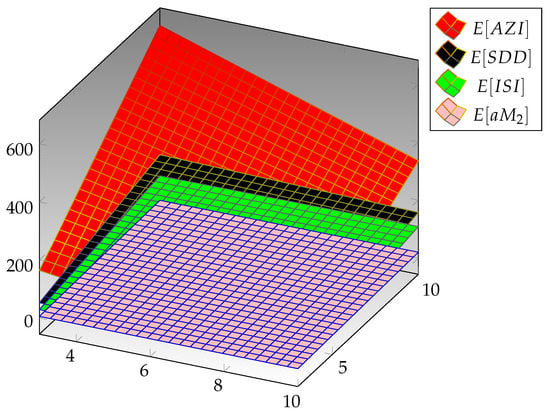
Figure 8.
Difference between , , and, .
Theorem 5.
If , then
Proof.
It is true for . Now, let us solve it for ; by using Theorems 1 and 3, we have
□
Theorem 6.
If , then
Proof.
It is true for . Now, let us solve it for ; by using Theorems 2 and 3, we have
□
Theorem 7.
If , then
Proof.
It is true for . Now, let us solve it for ; by using Theorems 3 and 4, we have
□
Theorem 8.
If , then
Proof.
We may prove this result with the help of Theorems 5–7. □
In this work, we study the expected values of the modified Zagreb, symmetric difference, inverse symmetric, and augmented Zagreb indices in a random cyclooctane chain. Furthermore, we give analytic proofs for comparisons, along with numerical and graphical profiles of these indices in random cyclooctane chains. More precisely, the numerical tables and graphical profiles suggest that the augmented Zagreb index is continuously more noteworthy than the other three indices, specifically the modified Zagreb, symmetric difference, and inverse symmetric indices.
Author Contributions
Conceptualization, Z.R.; methodology, Z.R.; validation, Z.R.; investigation, Z.R. and M.I.; resources, M.I. and Z.R.; writing—original draft preparation, Z.R.; writing—review and editing, Z.R. and M.I.; supervision, Z.R.; funding acquisition, M.I. and Z.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Muhammad Imran has been supported during the work on this paper by the University program of Advanced Research (UPAR) and UAEU-AUA grants of United Arab Emirates University (UAEU) via Grant No. G00003271 and Grant No. G00003461. Zahid Raza has been supported during the work on this paper by the University of Sharjah under Projects and and MASEP Research Group.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wiener, H. Structure determination of paraffin boiling points. J. Am. Chem. Soc. 1947, 69, 17–20. [Google Scholar] [CrossRef] [PubMed]
- Gutman, I.; Das, K. The first Zagreb index 30 years after. MATCH Commun. Math. Comput. Chem. 2004, 50, 83–92. [Google Scholar]
- Furtula, B.; Graovac, A.; Vukicevic, D. Augmented Zagreb index. J. Math. Chem. 2010, 48, 370–380. [Google Scholar] [CrossRef]
- Vukicevic, D.; Gasperov, M. Bond additive modeling 1 Adriatic indices. Croat. Chem. Acta 2010, 83, 243–260. [Google Scholar]
- Vukicevic, D. Bond additive modeling 2. Mathematical properties of max-min rodeg index. Croat. Chem. Acta 2010, 83, 261–273. [Google Scholar]
- Milicevi, A.; Nikoli, S.; Trinajsti, N. On reformulated Zagreb indices. Mol. Divers. 2004, 8, 393–399. [Google Scholar] [CrossRef] [PubMed]
- Koam, A.N.A.; Ahmad, A.; Nadeem, M.F. Comparative study of valency-based topological descriptor for hexagon star network. Comput. Syst. Sci. Eng. 2021, 36, 293–306. [Google Scholar] [CrossRef]
- Ahmad, A.; Hasni, R.; Elahi, K.; Asim, M.A. Polynomials of Degree-based Indices for Swapped Networks Modeled by Optical Transpose Interconnection System. IEEE Access 2020, 8, 214293–214299. [Google Scholar] [CrossRef]
- Ranjini, P.S.; Lokesha, V.; Usha, A. Relation between phenylene and hexagonal squeeze using harmonic index. Int. J. Graph Theory 2013, 1, 116–121. [Google Scholar]
- Wei, S.; Ke, X.; Hao, G. Comparing the excepted values of atom-bond connectivity and geometric arithmetic indices in random spiro chains. J. Inequal. Appl. 2018, 2018, 45. [Google Scholar] [CrossRef]
- Huang, G.; Kuang, M.; Deng, H. The expected values of Kirchhoff indices in the random polyphenyl and spiro chains. Ars Math. Contemp. 2018, 9, 197–207. [Google Scholar] [CrossRef]
- Jahanbani, A. The Expected Values of the First Zagreb and Randic Indices in Random Polyphenyl Chains. Polycycl. Aromat. Compd. 2020, 1–10. [Google Scholar] [CrossRef]
- Raza, Z. The expected values of arithmetic bond connectivity and geometric indices in random phenylene chains. Heliyon 2020, 6, e04479. [Google Scholar] [CrossRef]
- Raza, Z. The harmonic and second Zagreb indices in random polyphenyl and spiro chains. Polycycl. Aromat. Compd. 2020, 1–10. [Google Scholar] [CrossRef]
- Raza, Z. The expected values of some indices in random phenylene chains. Eur. Phys. J. Plus 2021, 136, 1–15. [Google Scholar] [CrossRef]
- Das, K.C.; Trinajstic, N. Comparison between first geometric arithmetic index and atom-bond connectivity index. Chem. Phys. Lett. 2010, 497, 149–151. [Google Scholar] [CrossRef]
- Shao, Z.; Jiang, H.; Raza, Z. Inequalities among topological descripter. Kragujev. J. Math. 2023, 47, 661–672. [Google Scholar]
- Du, Z.; Ali, A.; Rafee, R.; Raza, Z.; Jamil, M.K. On the first two extremum Zagreb indices and coindices of chemical trees. Int. J. Quantum Chem. 2021, 121, e26547. [Google Scholar] [CrossRef]
- Ali, A.; Raza, Z.; Bhatti, A.A. Extremal pentagonal chains with respect to degree-based topological indices. Can. J. Chem. 2016, 94, 870–876. [Google Scholar] [CrossRef]
- Ali, A.; Raza, Z.; Bhatti, A.A. Bond incident degree (BID) indices for some nanostructures. Optoelectron. Adv. Mater.-Rapid Commun. 2016, 10, 108–112. [Google Scholar]
- Ali, A.; Raza, Z.; Bhatti, A.A. Bond incident degree (BID) indices of polyomino chains: A unified approach. Appl. Math. Comput. 2016, 287, 28–37. [Google Scholar] [CrossRef]
- Ali, A.; Bhatti, A.A.; Raza, Z. Topological study of tree-like polyphenylene systems, spiro hexagonal systems and polyphenylene dendrimer nanostars. Quantum Matter 2016, 5, 534–538. [Google Scholar] [CrossRef]
- Akhter, S.; Imran, M.; Raza, Z. Bounds for the general sum-connectivity index of composite graphs. J. Inequal. Appl. 2017, 2017, 1–12. [Google Scholar] [CrossRef]
- Akhter, S.; Imran, M.; Raza, Z. On the general sum-connectivity index and general Randic index of cacti. J. Inequal. Appl. 2016, 2016, 1–9. [Google Scholar] [CrossRef]
- Ali, A.; Raza, Z.; Bhatti, A.A. Some vertex-degree-based topological indices of cacti. Ars Comb. 2019, 144, 195–206. [Google Scholar]
- Gutmana, I.; Kairtvic, T. Wiener indices and molecular surfaces. Z. Naturforschung A 1995, 50, 669–671. [Google Scholar] [CrossRef][Green Version]
- Gutman, I.; Kennedy, J.W.; Quintas, L.V. Wiener numbers of random benzenoid chains. Chem. Phys. Lett. 1990, 173, 403–408. [Google Scholar] [CrossRef]
- Yang, W.; Zhang, F. Wiener index in random polyphenyl chains. Match-Commun. Math. Comput. Chem. 2012, 68, 371. [Google Scholar]
- Raza, Z. Zagreb Connection Indices for Some Benzenoid Systems. Polycycl. Aromat. Compd. 2020, 1–14. [Google Scholar] [CrossRef]
- Alamdari, M.H.; Helliwell, M.; Baradarani, M.M.; Jouleb, J.A. Synthesis of some cyclooctane-based pyrazines and quinoxalines. Arkivoc 2008, 14, 166–179. [Google Scholar] [CrossRef]
- Ali, K.A.; Hosni, H.M.; Ragab, E.A.; Elas-Moez, S.I.A. Synthesis and antimicrobial evaluation of some new cyclooctanones and cyclooctane-based heterocycles. Arch. Pharm. 2012, 345, 231–239. [Google Scholar] [CrossRef] [PubMed]
- Bharadwaj, R.K. Conformational properties of cyclooctane: A molecular dynamics simulation study. Mol. Phys. 2000, 98, 211–218. [Google Scholar] [CrossRef]
- Salamci, E.; Ustabaay, R.; Aoruh, U.; Yavuz, M.; Vazquez-Lopez, E.M. Cyclooctane-1, 2, 5, 6-tetrayl tetraacetate. Acta Crystallogr. Sect. E Struct. Rep. Online 2006, 62, 02401–02402. [Google Scholar] [CrossRef]
- Brunvoll, J.; Cyvin, S.J.; Cyvin, B.N. Enumeration of tree-like octagonal systems. J. Math. Chem. 1997, 21, 193–196. [Google Scholar] [CrossRef]
- Yang, X.; Zhao, B. Kekulic Structures of Octagonal Chains and the Hosoya Index of Caterpillar Trees. J. Xinjiang Univ. (Nat. Sci. Ed.) 2013, 3, 1–5. [Google Scholar]
- Destainville, N.; Mosseri, R.; Bailly, F. Fixed-boundary octagonal random tilings: A combinatorial approach. J. Stat. Phys. 2001, 102, 147–190. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).