Traveling Wave Solutions to the Nonlinear Evolution Equation Using Expansion Method and Addendum to Kudryashov’s Method

Abstract

The inspection of wave motion and propagation of diffusion, convection, dispersion, and dissipation is a key research area in mathematics, physics, engineering, and real-time application fields. This article addresses the generalized dimensional Hirota–Maccari equation by using two different methods: the $exp(-\phi (\zeta \left)\right)$ expansion method and Addendum to Kudryashov’s method to obtain the optical traveling wave solutions. By utilizing suitable transformations, the nonlinear pdes are transformed into odes. The traveling wave solutions are expressed in terms of rational functions. For certain parameter values, the obtained optical solutions are described graphically with the aid of Maple 15 software.

1. Introduction

The study of the traveling wave solutions plays a significant role in understanding and describing the characters of nonlinear problems in physical science. The elements of physical systems usually operate on multiple time scales [1]. Although closed form descriptions for nonlinear partial differential equations (nlpdes) of physical significance exist, we cannot obtain these forms explicitly. Such problems occur especially in various realistic problems in physical systems. In this scenario, we aim to investigate exact physically significant solutions, which are so important and useful due to their very wide application of nlpdes in fluid mechanics, fluid dynamics, quantum mechanics, bio-science, physics, chemistry, and other areas of engineering.

Modeling of wave motion has attracted many researchers due to its crucial role in ocean, coastal, naval and marine engineering. In addition, waves are considered to be the major source of environmental actions on beaches or floating structures for most geographical areas. Most problems of practical interest create physical phenomena in nature that are often nonlinear and can be described by fractional differential equations. For example, heat conduction systems, nonlinear chaotic systems, plasma waves, and diffusion processes are modeled by fractional mathematics and equations [2,3,4]. Therefore, numerous investigations have been conducted to develop new methods to solve such equations. For example, Choucha et al. [5] investigated problems of a nonlinear viscoelastic wave equation in the presence of distributed delay, strong damping and source terms. By considering suitable conditions, they obtained a blow-up result of solutions. The improved sub-equation method has been used by Zhong et al. [6] to obtain exact solutions for a wide range of nonlinear problems of fractional equations. By converting nonlinear problems of fractional and integer order equations with the modified Riemann–Liouville derivative into Riccati equations, they obtained exact solutions, including wave solutions, soliton solutions, and complex solutions. Simbanefayi et al. [7] obtained traveling wave solutions for the Korteweg–de Vries–Benjamin–Bona–Mahony equation using Lie symmetry and Jacobi elliptic function expansion methods. The main objective of the Lie symmetry method is to transform the governing equations to a simpler equation while maintaining the invariance of the original equation. Others have previously used different methods to find the traveling wave solutions for nonlinear evolution equations (nees) (see, for example, [8,9,10,11,12,13,14,15,16,17,18,19,20]).

Over the past few years, many researchers have explored several direct methods to solve nonlinear evolution equations. One of the popular examples of such methods is the Kudryashov method, which typically only performs the calculation without the need for the form of a specific function. Examples of Kudryashov methods include the extended Kudryashov method [21], the generalized Kudryashov method [22], and the new extended generalized Kudryashov method [23]. The generalized Kudryashov method by Kaplan et al. [22] does usefully apply to the nonlinear Jaulent–Miodek hierarchy and $(2+1)$-dimensional Calogero–Bogoyavlenskii–Schiff equation. This method has successfully provided exact solutions to the nonlinear evolution equations. The Addendum to Kudryashov’s method is also among the Kudryashov methods and was introduced by [24]. This method is the general form of previous Kudryashov methods because the trial equation is proposed as the general form of the trial equations in other Kudryashov methods.

In this article, we construct the exact significant solutions for different types of cases of the $exp(-\phi (\zeta \left)\right)$-expansion method and akm. Both methods are used as powerful mathematical tools for constructing traveling wave solutions of nonlinear partial differential equations (see, for example, [20,21,22,23,24,25,26]).

For the purposes of discussion, we consider the nonlinear $(2+1)$ dimensional Hirota–Maccari equation [27]. Let x and y be the independent spatial variables and t be the time variable. Consider the complex and the real scalar fields $u=u(x,y,t)$ and $v=v(x,y,t)$, respectively, satisfying the $(2+1)$-dimensional Hirota–Maccari equation

$$\begin{array}{cc}\hfill i{u}_t+u_{xy}+i{u}_{xxx}+uv-i{\left|u\right|}^2{u}_x& =0,\hfill \\ \hfill 3v_x+{\left({\left|u\right|}^2\right)}_y& =0.\hfill \end{array}$$

(1)

Assuming that $x=y$, then the system (1) reduces to the $(1+1)$-dimensional Hirota equation [28].

In the last two decades, scientists have explored the Hirota–Maccari system using several approaches to efficiently compute and predict exact solutions. The approach by Painlevé has been applied successfully to construct the general solutions of certain nonlinear second-order equations [27]. Other methods that have been introduced include a new unified algebraic method [29], Weierstrass elliptic function expansion method [30] and extended trial method [31].

Here, we focus attention on using the expansion method and akm to predict and derive exact solutions of the Hirota–Maccari system. This paper is organized as follows. Section 2 presents the methodology of the $exp(-\phi (\zeta \left)\right)$-expansion method. Section 3 discusses the Hirota–Maccari equation. In addition, numerical computations are carried out by Maple to present the behavior of the optical traveling wave solution through figures. Section 4 addresses the $(2+1)$-dimensional Hirota–Maccari equation by using Addendum to Kudryashov’s method (akm) to find the straddled solitary wave solution and the singular soliton solution and presents them in graphs.

2. Methodology of the Expansion Method

This section presents the procedure of the $exp(-\phi (\zeta \left)\right)$-expansion method. In the first step, we consider a nonlinear partial differential equation in the following form:

$$F\left(u,u_t,u_x,u_{tt},u_{xx},u_{xt},\cdots \right)=0,$$

(2)

where $u=u(x,t)$ represents an unknown function, and F is a polynomial function in $u(x,t)$ and its partial derivatives. We define an appropriate traveling wave transformation as follows,

$$u(x,t)=u\left(\zeta \right),\zeta =x-ct,$$

(3)

where c is the velocity of a traveling wave. By utilizing this appropriate traveling wave transformation (3), the nonlinear partial differential Equation (2) reduces to the ordinary differential equation (ode):

$$Q(u,u^{{}^{\prime }},u^{{}^{″}},\cdots )=0,$$

(4)

in which Q is a polynomial in $u\left(\zeta \right)$ and its total derivatives such that ${}^{{}^{{}^{\prime }}}=\frac{d}{d\zeta }.$

We seek traveling wave solutions for a large class of Equation (4) in the following form:

$$u\left(\zeta \right)=\sum _{i=0}^N{a}_i{\left[exp(-\phi (\zeta \left)\right)\right]}^i,i=0,\cdots ,N.$$

(5)

where $a_i$ are arbitrary constants, N is a positive integer, and $\phi \left(\zeta \right)$ is the elementary function that satisfies the following ode:

$${\phi }^{{}^{\prime }}=exp(-\phi \left(\zeta \right))+\mu exp\left(\phi \left(\zeta \right)\right)+\lambda ,$$

(6)

where $\lambda$ and $\mu$ are arbitrary constants. By taking the transformation $\mathrm{\Psi }=exp\left(\phi \right)$, the nonlinear ode (6) can be written in the following form

$${\mathrm{\Psi }}^{{}^{\prime }}=\mu {(\mathrm{\Psi }+\lambda /2\mu )}^2+1-{\lambda }^2/\left(4\mu \right).$$

(7)

The above Equation (7) is the generalized Riccati first ode’s. By taking this transformation $\eta =\mathrm{\Psi }+\lambda /\left(2\mu \right)$, the generalized Riccati first ode’s (7) reduces to the following form

$${\eta }^{{}^{\prime }}=\mu {\eta }^2+\frac{4\mu -{\lambda }^2}{4\mu },$$

(8)

which can be solved by applying a separation of variables to obtain the following solutions:

• First, when ${\lambda }^2-4\mu >0,$ and $\mu \ne 0,$ we have the hyperbolic function solutions:

  $$\begin{array}{cc}\hfill \mathrm{\Psi }=exp\left(\phi \right)& =\frac{-\sqrt{{\lambda }^2-4\mu }tanh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}(\zeta +E)\right)-\lambda }{2\mu }\hfill \\ \hfill \phi \left(\zeta \right)& =ln\left[\frac{-\sqrt{{\lambda }^2-4\mu }tanh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}(\zeta +E)\right)-\lambda }{2\mu }\right],\hfill \end{array}$$

  (9)

  or

  $$\begin{array}{cc}\hfill \mathrm{\Psi }=exp\left(\phi \right)& =\frac{-\sqrt{{\lambda }^2-4\mu }coth\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}(\zeta +E)\right)-\lambda }{2\mu },\hfill \\ \hfill \phi \left(\zeta \right)& =ln\left[\frac{-\sqrt{{\lambda }^2-4\mu }coth\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}(\zeta +E)\right)-\lambda }{2\mu }\right],\hfill \end{array}$$

  (10)

  where E is the integration constant.
• Second, when $\lambda >0,$ and $\mu =0,$ we have solutions as:

  $$\begin{array}{cc}\hfill \mathrm{\Psi }=exp\left(\phi \right)& =\frac{1}{-\lambda }\left(exp(-\lambda (\zeta +E\left)\right)-1\right)\hfill \\ \hfill \phi \left(\zeta \right)& =-ln\left[\frac{-\lambda }{exp(-\lambda (\zeta +E\left)\right)-1}\right].\hfill \end{array}$$

  (11)
• Third, when ${\lambda }^2-4\mu <0,$ we obtain the periodic solutions as:

  $$\begin{array}{cc}\hfill \mathrm{\Psi }=exp\left(\phi \right)& =\frac{\sqrt{4\mu -{\lambda }^2}tan\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}(\zeta +E)\right)-\lambda }{2\mu }\hfill \\ \hfill \phi \left(\zeta \right)& =ln\left[\frac{\sqrt{4\mu -{\lambda }^2}tan\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}(\zeta +E)\right)-\lambda }{2\mu }\right],\hfill \end{array}$$

  (12)

  or

  $$\begin{array}{cc}\hfill \mathrm{\Psi }=exp\left(\phi \right)& =\frac{\sqrt{4\mu -{\lambda }^2}cot\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}(\zeta +E)\right)-\lambda }{2\mu }\hfill \\ \hfill \phi \left(\zeta \right)& =ln\left[\frac{\sqrt{4\mu -{\lambda }^2}cot\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}(\zeta +E)\right)-\lambda }{2\mu }\right].\hfill \end{array}$$

  (13)
• Fourth, when ${\lambda }^2-4\mu =0,$ we obtain the solution as:

  $$\begin{array}{cc}\hfill \mathrm{\Psi }=exp\left(\phi \right)& =\frac{2(\lambda \zeta +\lambda E+2)}{{\lambda }^2(\zeta +E)}\hfill \\ \hfill \phi \left(\zeta \right)& =ln\left[\frac{2(\lambda \zeta +\lambda E+2)}{{\lambda }^2(\zeta +E)}\right].\hfill \end{array}$$

  (14)
• Fifth, when $\mu =\lambda =0,$ we obtain the solution as:

  $$\begin{array}{cc}\hfill \mathrm{\Psi }=exp\left(\phi \right)& =\zeta +E,\hfill \\ \hfill \phi \left(\zeta \right)& =ln(\zeta +E).\hfill \end{array}$$

  (15)

Substituting Equation (5) into Equation (4) and using ode (6), the left-hand side is transferred to a polynomial in $exp(-\phi (\zeta \left)\right).$ By equating the coefficient of this polynomial to zero, we obtain a system of algebraic equations that describes the model equations for $a_N,\cdots ,c,\lambda ,$ and $\mu .$ These algebraic system of equations are solved by means of the Maple software. Substituting the values of the parameters $a_N,\cdots ,c,\lambda ,\mu ,$ and the general solution of Equation (6) into Equation (5), we obtain the desired traveling wave solutions, as shown in Equation (2).

3. Application

The proposed method in the previous section is implemented successfully to the Hirota–Maccari system (1) to obtain explicit and exact traveling wave solutions. The traveling wave solutions of the Hirota–Maccari system (1) are expressed in the form [32]

$$u(x,y,t)=U\left(\zeta \right)e^{-i(px+qy+kt)},v(x,y,t)=V\left(\zeta \right),$$

(16)

where U and V are real functions,$\zeta =x+y+ct$ and c is the wave velocity, p is the frequency of the wave, while q and k are arbitrary constants. Using the traveling wave transformation (16) empowers us to transform the Hirota–Maccari system (1) into the following system of odes:

$$\begin{array}{cc}\hfill 3(1-3p)U^{″}+3(p^3-pq-k)U+(3p-1)U^3& =0,\hfill \\ \hfill V& =-U^2/3,\hfill \end{array}$$

(17)

where $p\ne 1/3.$ By explicitly taking advantage of the homogeneous balance method [33], we balance the nonlinear term $U^3$ and the highest order derivative $U^{″}$ in Equation (17) to obtain the balance constant $N=1.$ Therefore, the solution of Equation (17) takes the following form:

$$U\left(\zeta \right)=a_0+a_{1}exp(-\phi ),$$

(18)

where $a_0,a_1$ are non-zero constants. Elementary algebra gives $U^{″}$ and $U^3$ as:

$$U^{″}=a_1\left[2exp(-3\phi )+2\mu exp(-\phi )+{\lambda }^{2}exp(-\phi )+3\lambda exp(-2\phi )+\mu \lambda \right],$$

(19)

and

$$U^{{}^3}=a_0^3+3a_0^2{a}_{1}exp(-\phi )+3a_1^2{a}_{0}exp(-2\phi )+a_1^{3}exp(-3\phi ).$$

(20)

Substitute Equations (18)–(20) into Equation (17) and collect all terms with the same power of $exp(-i\phi )$, for $(i=0,1,2,3).$ Then, setting the coefficients of $exp(-i\phi )$, for $(i=0,1,2,3)$ to zero, yields:

$$\begin{array}{cc}\hfill exp(-3\phi ):& 6a_1(1-3p)+a_1^3(3p-1)=0,\hfill \\ \hfill exp(-2\phi ):& 6a_1\lambda (1-3p)+3a_1^2{a}_0(3p-1)=0,\hfill \\ \hfill exp\left(0\phi \right):& 3\mu \lambda a_1(1-3p)+3a_0(p^3-pq-k)+a_0^3(3p-1)=0,\hfill \\ \hfill exp(-\phi ):& 6a_1\mu (1-3p)+3a_1{\lambda }^2(1-3p)+3a_1(p^3-pq-k)+3a_0^2{a}_1(3p-1)=0.\hfill \end{array}$$

(21)

Solving the above algebraic equations gives the values of the constants $a_0,a_1$, and $\mu$ as:

$$a_0=\pm \sqrt{\frac{3}{2}}\lambda ,a_1=\pm \sqrt{6},\mu =\frac{{\lambda }^2}{4}-\left(\frac{p^3-pq-k}{6(1-3p)}\right).$$

(22)

Therefore, substituting these constants into the solution (18), we obtain

$$U\left(\zeta \right)=\pm \sqrt{\frac{3}{2}}\lambda \pm \sqrt{6}exp[-\phi \left(\zeta \right)].$$

(23)

To obtain the optical traveling wave solutions for the Hirota–Maccari system, we substitute Equations (9)–(15) into Equation (23) to obtain the following five optical traveling wave solutions:

• Case 1: when ${\lambda }^2-4\mu =\frac{4(p^3-pq-k)}{6(1-3p)}>0,$ and $\mu \ne 0,$ the complex and the real scalar fields can be expressed respectively as:

  $$u_{11}(x,y,t)=\pm \sqrt{6}{e}^{i(px+qy+kt)}\left[\frac{\lambda }{2}-\frac{2\mu }{\sqrt{\frac{4(p^3-pq-k)}{6(1-3p)}}tanh\left(\frac{1}{2}\sqrt{\frac{4(p^3-pq-k)}{6(1-3p)}}(\zeta +E)\right)+\lambda }\right],$$

  (24a)

  $$v_{11}(x,y,t)=-2{\left[\frac{\lambda }{2}-\frac{2\mu }{\sqrt{\frac{4(p^3-pq-k)}{6(1-3p)}}tanh\left(\frac{1}{2}\sqrt{\frac{4(p^3-pq-k)}{6(1-3p)}}(\zeta +E)\right)+\lambda }\right]}^2,$$

  (24b)

  and

  $$u_{12}(x,y,t)=\pm \sqrt{6}{e}^{i(px+qy+kt)}\left[\frac{\lambda }{2}-\frac{2\mu }{\sqrt{\frac{4(p^3-pq-k)}{6(1-3p)}}coth\left(\frac{1}{2}\sqrt{\frac{4(p^3-pq-k)}{6(1-3p)}}(\zeta +E)\right)+\lambda }\right],$$

  (25a)

  $$v_{12}(x,y,t)=-2{\left[\frac{\lambda }{2}-\frac{2\mu }{\sqrt{\frac{4(p^3-pq-k)}{6(1-3p)}}coth\left(\frac{1}{2}\sqrt{\frac{4(p^3-pq-k)}{6(1-3p)}}(\zeta +E)\right)+\lambda }\right]}^2.$$

  (25b)
  For special values of parameters, Figure 1 represents the real part (Figure 1a) and imaginary part (Figure 1b) of (24a) and its projections (Figure 1c) and (Figure 1d), respectively, while the exact solution (24b) and its projections are shown in Figure 2.
  

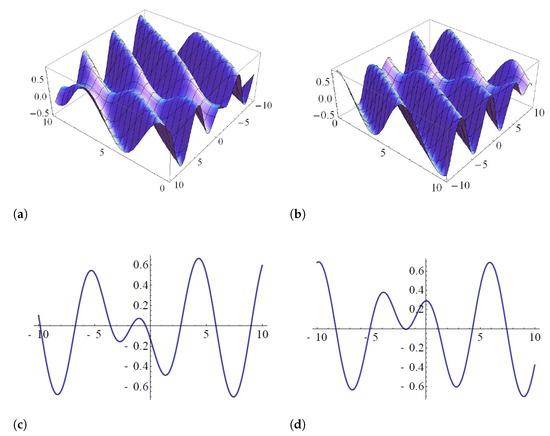  Figure 1. Periodic wave solution of the real part (a) and imaginary part (b) of (24a) and its projections (c,d), respectively, when $\lambda =3,\mu =26/12,y=2,$ and $c=p=q=k=E=1$.
  

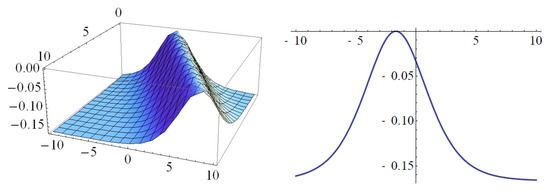  Figure 2. Bright wave solution (24b) (left) and its projections (right), when $\lambda =3,\mu =26/12,y=2,$ and $c=p=q=k=E=1$.
• Case 2: when ${\lambda }^2=\frac{4(p^3-pq-k)}{6(1-3p)}>0,$$\mu =0,$ and $\lambda \ne 0$ the complex and the real scalar fields can be expressed, respectively, as:

  $$u_{22}(x,y,t)=\pm \sqrt{6}\sqrt{\frac{p^3-pq-k}{6(1-3p)}}\left[1+\frac{2}{exp[2\sqrt{\frac{p^3-pq-k}{6(1-3p)}}\zeta +E]-1}\right].e^{i(px+qy+kt)},$$

  (26a)

  $$v_{22}(x,y,t)=-2\sqrt{\frac{p^3-pq-k}{6(1-3p)}}{\left[1+\frac{2}{exp[2\sqrt{\frac{p^3-pq-k}{6(1-3p)}}\zeta +E]-1}\right]}^2.$$

  (26b)
  For special values of parameters, Figure 3 represents the real part (Figure 3a) and imaginary part (Figure 3b) of (26a) and its projections (Figure 3c) and (Figure 3d), respectively, while the exact solution (26b) and its projections are shown in Figure 4.
  

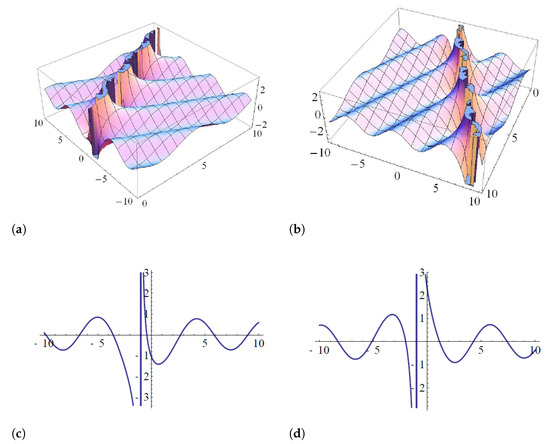  Figure 3. The singular solitary wave solution of the real part (a) and imaginary part (b) to (26a) and its projections (c,d), respectively, when $\lambda =1/\sqrt{3},\mu =0,y=2,$ and $c=p=q=k=E=1$.
  

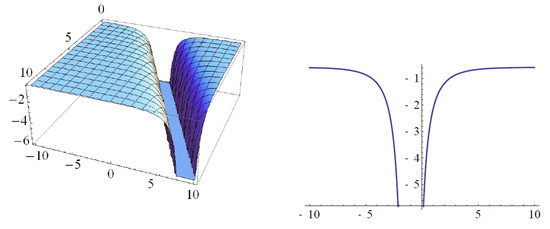  Figure 4. The singular Kink wave solution (26b) (left) and its projections (right), when $\lambda =1/\sqrt{3},\mu =0,y=2,$ and $c=p=q=k=E=1$.
• Case 3: when ${\lambda }^2-4\mu =\frac{4(p^3-pq-k)}{6(1-3p)}<0,$ and $\mu \ne 0,$ the complex and the real scalar fields can be expressed respectively as:

  $$u_{33}(x,y,t)=\pm \sqrt{6}\left[\frac{\lambda }{2}+\frac{2\mu }{\sqrt{-\frac{4(p^3-pq-k)}{6(1-3p)}}tan\left(\frac{1}{2}\sqrt{-\frac{4(p^3-pq-k)}{6(1-3p)}}(\zeta +E)\right)-\lambda }\right].e^{i(px+qy+kt)}$$

  (27a)

  $$v_{33}(x,y,t)=-2{\left[\frac{\lambda }{2}+\frac{2\mu }{\sqrt{-\frac{4(p^3-pq-k)}{6(1-3p)}}tan\left(\frac{1}{2}\sqrt{-\frac{4(p^3-pq-k)}{6(1-3p)}}(\zeta +E)\right)-\lambda }\right]}^2$$

  (27b)
  Figure 5 represents the real part (Figure 5a) and imaginary part (Figure 5b) of (27a) and its projections (Figure 5c) and (Figure 5d), respectively, while the exact solution (27b) and its projections are shown in Figure 6, for special values of parameters.
  

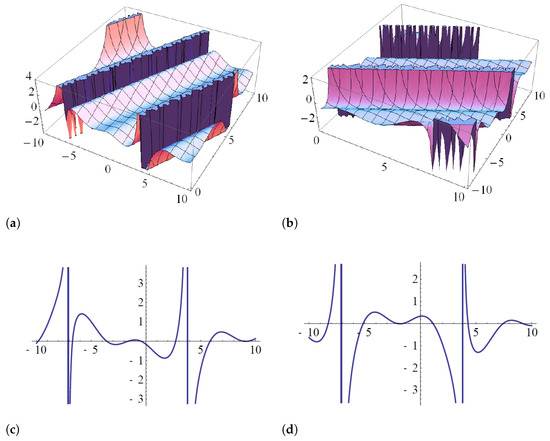  Figure 5. The periodic wave solution of the real part (a) and imaginary part (b) to (27b) and its projections (c,d), respectively, when $\lambda =3,\mu =7/3,y=2,c=p=q=E=1,$ and $k=-1$.
  

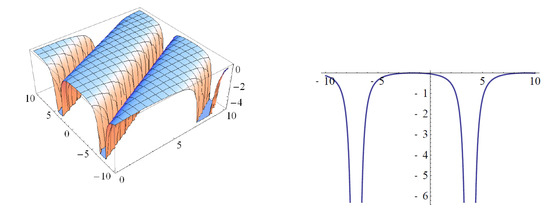  Figure 6. The singular Kink solution of (27a) (left) and its projections (right), when $\lambda =3,\mu =7/3,y=2,c=p=q=E=1,$ and $k=-1$.
• Case 4: when ${\lambda }^2-4\mu =\frac{4(p^3-pq-k)}{6(1-3p)}=0,$$\mu \ne 0,$ and $\lambda \ne 0,$ the complex and the real scalar fields can be expressed, respectively, as:

  $$u_{44}(x,y,t)=\pm \sqrt{6}\left[\sqrt{\frac{6\mu (1-3p)+p^3-pq-k}{6(1-3p)}}+\frac{(2\sqrt{\frac{6\mu (1-3p)+p^3-pq-k}{6(1-3p)}}(\zeta +E)+2)}{2\frac{6\mu (1-3p)+p^3-pq-k}{6(1-3p)}(\zeta +E)}\right].e^{i(px+qy+kt)}$$

  (28a)

  $$v_{44}(x,y,t)=-2{\left[\sqrt{\frac{6\mu (1-3p)+p^3-pq-k}{6(1-3p)}}+\frac{(2\sqrt{\frac{6\mu (1-3p)+p^3-pq-k}{6(1-3p)}}(\zeta +E)+2)}{2\frac{6\mu (1-3p)+p^3-pq-k}{6(1-3p)}(\zeta +E)}\right]}^2.$$

  (28b)
• Case 5: when ${\lambda }^2=\frac{4(p^3-pq-k)}{6(1-3p)}=0,$$\mu =0,$ and $\lambda =0,$ the complex and the real scalar fields can be expressed, respectively, as:

  $$u_{55}(x,y,t)=\frac{\pm \sqrt{6}}{(\zeta +E)}.e^{i(px+qy+p^{3}t-pqt)},$$

  (29a)

  $$v_{55}(x,y,t)=\frac{-2}{{(\zeta +E)}^2}.$$

  (29b)
  Figure 7 represents the singular Kink wave solution of the real part (Figure 7a) and imaginary part (Figure 7b) of (29a) and its projections (Figure 7c) and (Figure 7d), respectively, while the singular Kink wave solution (29b) and its projections are shown in Figure 8, for special values of parameters.
  

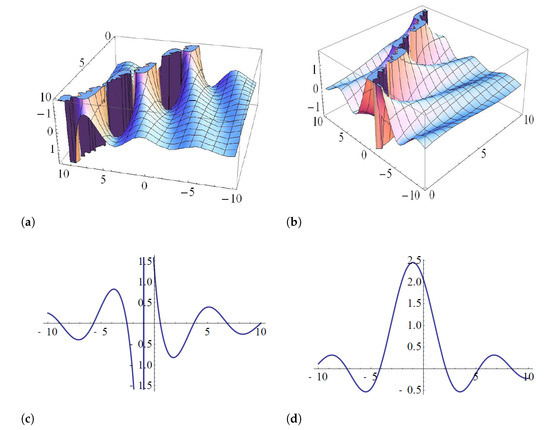  Figure 7. The singular Kink solution of the real part (a) and imaginary part (b) to (29a) and its projections (c,d), respectively, when $\lambda =\mu =0,y=2,c=p=E=1,$ and $q=k=1/2$.
  

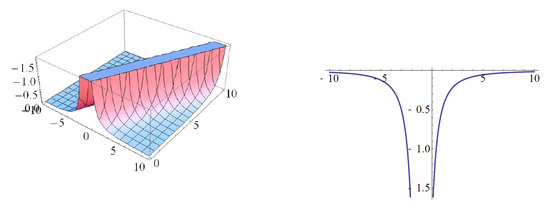  Figure 8. The singular Kink solution of (29b) (left) and its projections (right), when $\lambda =\mu =0,y=2,c=p=E=1,$ and $q=k=1/2$.

4. Addendum to Kudryashov’s Method (AKM) for $(2+1)$-Dimensional Hirota–Maccari Equation

For nonlinear evolution equations (nlees), Kudryashov [34] introduced a new approach to find highly dispersive optical solitons. This method is intended to be used to perform the calculation without the need for the form of a specific function. Inspired by the work of Kudryashov [34], Zayed et al. [24] recently introduced the Addendum to Kudryashov’s method akm. One aim of this section is to apply this method to find the straddled solitary wave solutions and the singular soliton solutions of the $(2+1)$-dimensional Hirota–Maccari equation.

For convenience, we start by presenting the main steps of the akm as follows:

• Step 1: Assuming that (17) has a solution in the following form

  $$\varphi \left(\xi \right)=\sum _{g=0}^N{\sigma }_g{\left[R\left(\xi \right)\right]}^g,$$

  (30)

  where ${\sigma }_g\ne 0$ for $(g=0,1,2,\cdots ,N)$ are constants can be determined, and $R\left(\xi \right)$ satisfies the node so that

  $$R^{{}^{\prime }2}\left(\xi \right)=R^2\left(\xi \right)[1-\chi R^{2T}\left(\xi \right)]{\left[lnK\right]}^2,0<K\ne 1,$$

  (31)

  where $\chi$ is an arbitrary constant. We can verify that Equation (31) can be written in the form:

  $$R\left(\xi \right)={\left[\frac{4A}{4A^2{exp}_K\left(T\xi \right)+\chi {exp}_K(-T\xi )}\right]}^{1/T},$$

  (32)

  where A represents a non- zero real number, T is a natural number, and ${exp}_K\left(T\xi \right)=K^{T\xi }$.
• Step 2: The relation between N and T can be calculated as follows: Setting $D\left[\varphi \right(\xi \left)\right]=N$ then $D\left[{\varphi }^{{}^{\prime }}\left(\xi \right)\right]=N+T$, $D\left[{\varphi }^{{}^{\prime \prime }}\left(\xi \right)\right]=N+2T$, hence $D\left[{\varphi }^{\left(r\right)}\left(\xi \right)\right]=N+rT$ and $D\left[{\varphi }^{\left(r\right)}\left(\xi \right){\varphi }^s\left(\xi \right)\right]=(s+1)N+Tr.$
• Step 3: Substituting Equations (30) and (31) into Equation (17), then setting the coefficients of ${\left[R\left(\xi \right)\right]}^f{\left[R^{{}^{\prime }}\left(\xi \right)\right]}^i,$ for $(f=0,1,2,\cdots ,i=0,1)$ to zero, we obtain a system of equations in ${\sigma }_g$ for $(g=0,1,2,\cdots ,N).$ To evaluate the values of ${\sigma }_g$ for $(g=0,1,2,\cdots ,N)$ and c, we must solve this system of equations. Consequently, we will obtain the analytical solutions of Equation (17).

Here we apply the akm in the class of nonlinear pde. Balancing $U^{{}^{″}}$ and $U^3,$ in Equation (17), we obtain

$$N+2T=3N\Rightarrow N=T.$$

(33)

In the following, we present two cases to find the straddled solitary wave solutions and the singular soliton solutions of Equation (17):

• Case 1. Setting $T=1,$ hence $N=1.$ Then, we deduce from Equation (33) that

  $$U\left(\xi \right)={\sigma }_0+{\sigma }_{1}R\left(\xi \right),$$

  (34)

  where ${\sigma }_0,$ and ${\sigma }_1$ are constants and ${\sigma }_1\ne 0.$ Substituting Equations (34) and (31) into Equation (17) and collecting all the transactions of this term ${\left[R\left(\xi \right)\right]}^l{\left[R^{{}^{\prime }}\left(\xi \right)\right]}^f,$ for ($l=0,1,2,\cdots ,12,$ and $f=0,1$), and setting them to zero, leads to a system of equations that can be solved to obtain:

  $${\sigma }_0=0,{\sigma }_1=ln\left(K\right)\sqrt{-6\chi },$$

  (35)

  and

  $$k=-3p{ln}^2\left(K\right)+p^3+{ln}^2\left(K\right)-pq,$$

  (36)

  provided $\chi <0.$ Substituting Equations (35) and (32) into Equation (34), and calculating the straddled solitary solution of Equation (17) gives:

  $$u(x,y,t)=\left\{\frac{4Aln\left(K\right)\sqrt{-6\chi }}{4A^2{exp}_K\left[\zeta \right]+\chi {exp}_K[-\zeta ]}\right\}{e}^{i-(px+qy+kt)},$$

  (37)

  and

  $$v(x,y,t)=-\frac{1}{3}{\left\{\frac{4Aln\left(K\right)\sqrt{-6\chi }}{4A^2{exp}_K\left[\zeta \right]+\chi {exp}_K[-\zeta ]}\right\}}^3,$$

  (38)

  provide $\chi <0.$ In particular, setting $\chi =-4A^2$ in Equation (38), we obtain the singular soliton solution to Equation (17) as

  $$u(x,y,t)=\left\{ln\left(K\right)\sqrt{6}\csc \mathrm{h}[\zeta lnK]\right\}{e}^{i-(px+qy+kt)},$$

  (39)

  and

  $$v(x,y,t)=-\frac{1}{3}{\left\{ln\left(K\right)\sqrt{6}\csc \mathrm{h}[\zeta lnK]\right\}}^3.$$

  (40)
• Case 2. Setting $T=2,$ hence $N=2.$ Then, we deduce from Equation (30) that Equation (17) has solutions in following form:

  $$U\left(\xi \right)={\sigma }_0+{\sigma }_{1}R\left(\xi \right)+{\sigma }_2{R}^2\left(\xi \right),$$

  (41)

  where ${\sigma }_0,{\sigma }_1$, and ${\sigma }_2$ are constants, and ${\sigma }_2\ne 0.$ Substituting Equations (41) and (12) into Equation (17) and collecting all the transactions of this term ${\left[R\left(\xi \right)\right]}^l{\left[R^{{}^{\prime }}\left(\xi \right)\right]}^f,$ for ($l=0,1,2,\cdots ,20,$ and $f=0,1$), and setting them to zero, we obtain a system of equations that can be solved to obtain the following results:

  $${\sigma }_0={\sigma }_1=0,{\sigma }_2=2ln\left(K\right)\sqrt{-6\chi },$$

  (42)

  and

  $$k=-12p{ln}^2\left(K\right)+p^3+4{ln}^2\left(K\right)-pq,$$

  (43)

  provided $\chi <0.$ Substituting Equations (42) and (43) into Equation (41), and calculating the straddled solitary solution of Equation (17) leads to

  $$u(x,y,t)=\left\{\frac{8Aln\left(K\right)\sqrt{-6\chi }}{4A^2{exp}_K\left[2\zeta \right]+\chi {exp}_K\left[2\zeta \right]}\right\}{e}^{i-(px+qy+kt)},$$

  (44)

  and

  $$v(x,y,t)=-\frac{1}{3}{\left\{\frac{8Aln\left(K\right)\sqrt{-6\chi }}{4A^2{exp}_K\left[2\zeta \right]+\chi {exp}_K\left[2\zeta \right]}\right\}}^3,$$

  (45)

  providing $\chi <0.$ In particular, setting $\chi =-4A^2$ in Equation (38), we obtain the singular soliton solution to Equation (17) as

  $$u(x,y,t)=\left\{2ln\left(K\right)\sqrt{6}\csc \mathrm{h}[2\zeta lnK]\right\}{e}^{i-(px+qy+kt)},$$

  (46)

  and

  $$v(x,y,t)=-\frac{1}{3}{\left\{2ln\left(K\right)\sqrt{6}\csc \mathrm{h}[2\zeta lnK]\right\}}^3.$$

  (47)
  Note that by choosing different values for the parameters T and N, we can obtain several solitary wave solutions of Equation (17).

Figure 9 shows the straddled solitary solution (37) when the velocity of the soliton is $c=4$ and the frequency is $A=3$ when $y=2.$ Figure 9c,d shows the straddled solitary solution, which is a singular solution at $x=2.5$. In addition, Figure 10 shows the straddled solitary solution (38), and Figure 10c,d shows the singular solutions at $x=2$.

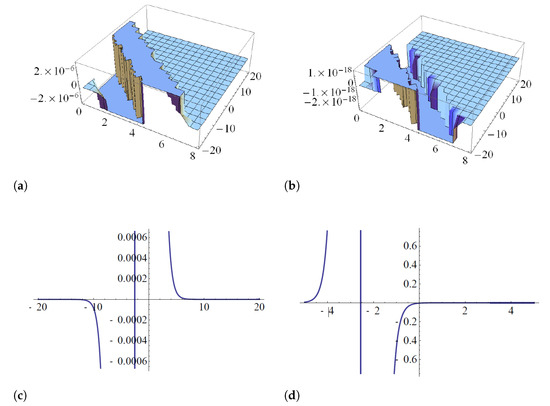
Figure 9. The solutions (37) (a,b) and its projection when $K=5,A=3,y=2,$ and $c=4$. (c,d) shows the straddled solitary solution, which is a singular solution at $x=2.5$.

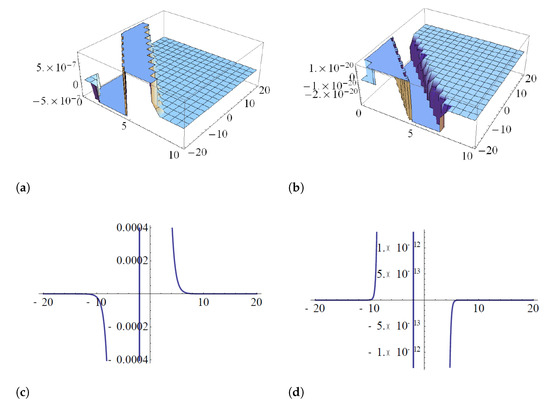
Figure 10. The solutions (38) (a,b) and its projection when $K=5,A=3,y=2,$ and $c=4.$ (c,d) shows the singular solutions at $x=2$.

5. Conclusions

The search for exact solutions for nees has attracted the attention of many scientists in physics and mathematics. In this paper, I investigate the optical traveling wave solutions to a nonlinear evolution equation in mathematical physics, namely for the $(2+1)$-dimensional Hirota–Maccari equation by means of the expansion method. Additionally, by following the method of the Addendum to Kudryashov’s method akm, introduced by Zayed et al. [24], Section 4 analogously derives the straddled solitary wave solution and the singular soliton solution of the $(2+1)$-dimensional Hirota–Maccari Equation (1), which is presented with the support of graphs. The resulting solutions indicate that the proposed approach promises to empower us to address a wide class of nonlinear evolution equations arising in mathematical physics. The optical wave solutions obtained in this paper is just one important example of solutions that can have the potential to empower systematic analysis and understanding of the nonlinear evolution equation in many fields used widely in engineering and science.