Abstract
Many scientific papers are devoted to solving multi-criteria problems. Researchers solve these problems, usually using methods that find discrete solutions and with the collaboration of domain experts. In both symmetrical and asymmetrical problems, the challenge is when new decision-making variants emerge. Unfortunately, discreet identification of preferences makes it impossible to determine the preferences for new alternatives. In this work, we propose a new approach to identifying a multi-criteria decision model to address this challenge. Our proposal is based on stochastic optimization techniques and the characteristic objects method (COMET). An extensive work comparing the use of hill-climbing, simulated annealing, and particle swarm optimization algorithms are presented in this paper. The paper also contains preliminary studies on initial conditions. Finally, our approach has been demonstrated using a simple numerical example.
1. Introduction
Optimization is one of the instruments used to solve various types of decision-making problems [1,2]. Formally, optimization is a method of determining the best solution from a defined quality criterion [3,4,5]. Moreover, optimization is also a part of operational research, which focuses on determining the method and solving defined problems connected to making the right decisions. In optimization, one can identify single and multi-criteria optimizations [6,7,8]. Multi-criteria optimizations exist where optimal decisions must be made in the presence of compromises between conflicting objectives [9,10].
Deterministic and stochastic methods are the main groups of optimization techniques used in decision-making problems. In the optimization process, deterministic methods use mathematical formulas, while stochastic methods also use random processes for this purpose [11]. The deterministic techniques find local extremes more frequently, which often makes it impossible to find global extremes. On the other hand, the stochastic methods have techniques to avoid falling into local extremes [12,13]. In the deterministic approach, fewer objective function evaluations are needed to reach a solution than in the stochastic approach. Deterministic methods can find global extremes through a close search and have no stochastic elements [14]. There are two approaches in stochastic methods: the global approach and the local approach [15]. The global approach is based on evaluating functions at several random points [16]. In the local approach, the selection of points is directed to get a candidate for the global extremity using local searches.
Solving decision-making problems using stochastic methods does not guarantee success, but they can solve severe and different problems [17,18]. Furthermore, stochastic techniques are easy to implement for problems complex to evaluate the "black box" function [19]. The mathematical structure of the problem under investigation is more important in understanding the deterministic approach than the stochastic approach. However, deterministic methods are effective in local search.
Random global search algorithms are methods that take into account randomly selected neighboring states. Simple structure and little resistance to the irregularity of the objective function behavior make the global random search algorithms very attractive. Global random search algorithms can also be associated with the metaheuristic term, because they do not directly solve any problem, but provide a way to create a suitable algorithm for it [20].
The algorithm that moves between possible solutions in search of the right solution is called the metaheuristics algorithm [19,21]. Metaheuristic algorithms, such as evolutionary algorithms (EA) or genetic algorithm (GA), can be adapted to meet the most realistic optimization problems in terms of expected solution quality and calculation time [22].
The examples of global random search algorithms are the hill-climbing algorithm, simulated annealing, and particle swarm optimization [23]. The hill-climbing algorithm works by selecting a random state from the neighborhood and comparing it with the current state [24,25]. If the state from the neighborhood turns out to be better, it becomes the current state. This step is performed in a loop until the stop condition is reached.
The simulated annealing is a method based on simulated annealing of solids [26,27]. It uses the Boltzmann coefficient, which during the optimization process can assume a worse state than the current one, in order not to fall into local extremes if the value of a random variable from a uniform distribution [0, 1] is smaller than it [28,29]. Updating the current state is the same as in the hill-climbing algorithm.
Particle swarm optimization is based on finding a solution using unique points in spaces, described through feature vectors [17,30]. Particles have parameters such as position, velocity, and direction of movement. The particles also remember their best solution found, which is known as a local solution. The best solution from the whole swarm is a global solution [31,32].
The stochastic methods, such as hill-climbing algorithm, simulated annealing and particle swarm optimization can be used in continuous and discrete space. However, they are not able to provide a global solution. Unlike simulated annealing and particle swarm optimization, the hill-climbing algorithm has no mechanisms to protect it from falling into local extremes. However, in contrast, it is characterized by lower memory requirements and more frequent acceptance of solutions. The PSO method is more probable and useful in finding global extremes compared to the hill-climbing algorithm. Also, particle swarm optimization is capable of performing parallel calculations, but setting PSO parameters is a big challenge [33]. The simulated annealing method works very well in discrete spaces, while the iteration time it takes to find an extremity is extensive compared to other stochastic methods.
The methods mentioned above will be used in the problem of searching for optimal values of preferences of objects characteristic for given sets of decision variants, i.e., those for which the objective function will reach the lowest value. The characteristic objects are defined in Section 2.2. This problem occurs when we want to calculate the preference of decision-making variants, with unknown preferences of characteristic objects and known calculated by the model preferences of decision-making variants [34,35,36]. The objective function in this problem is defined as the absolute difference of the sums of the preferences of the reference decision variants with the calculated ones. The preference of decision variants is calculated using the COMET method. Although the RAFSI method is also resistant to rank reversal, our study was conducted based on COMET modeling, which seems to be more proper according to the identification of the continuous space of the problem [37].
The COMET method is a new method designed to solve decision-making problems. Among the methods of multi-criteria decision making, the characteristic object technique has a unique property, i.e., resistance to the paradox of reversal of ranking order [38,39]. This property results from the fact that the assessment of decision variants is based on characteristic object assessments, which are independent of the set of assessed alternatives. The advantage of the COMET method is also the ease of identification of linear and non-linear decision-making functions.
The novelties and contributions are presented as follows. The paper presents an innovative approach, which consists of building a decision-making model based on already evaluated alternatives and stochastic optimization techniques. Multi-Criteria Decision-Analysis (MCDA) methods use an approach in which an expert in a given field defines the model, and then the decision variants are evaluated [40,41,42]. The method proposed in the paper allows building a proper decision-making model without the need to interfere with the process. With this approach, we can assess a set of alternatives with the help of already assessed alternatives. The alternatives we have in our possession enable us to estimate the expert’s model. Additionally, the model built with such an approach can be further exploited. The suggested method can be useful when an expert in a given field is not available.
For this purpose, stochastic methods have been used, which allow one to approximate the evaluation of the expert model. The defined model, with the help of stochastic techniques, can evaluate the given alternatives similar to the unknown decision model. Additionally, stochastic algorithms are easy to implement and adapt, so the proposed approach can be tested on more metaheuristic methods. The paper uses such methods as the hill-climbing algorithm, simulated annealing method, and particle swarm optimization. The effectiveness of stochastic techniques has been compared to estimate which one works best with different input data.
The rest of the paper is organized as follows. In Section 2 there are definitions. Section 2.2 presents the COMET method. The selected stochastic methods, i.e., the climbing algorithm, the simulated annealing method, and optimization by means of a particle swarm are presented in Section 2.3, Section 2.4 and Section 2.5. The selected similarity coefficients are presented in Section 2.6. Section 3 shows the research carried out. It consists of Section 3.1 on the effects of the initial conditions, Section 3.2 showing the distribution of fitness functions, and Section 3.3 which presents the application of the proposed approach. Section 4 contains conclusions.
2. Preliminaries
2.1. Fuzzy Set Theory
Fuzzy Set Theory is used in many scientific fields and could be especially useful for solving MCDA problems [43,44,45]. Here we present some definitions and basic concepts of the Fuzzy Set Theory which are necessary to understand the COMET method [46,47].
Definition 1.
The fuzzy set A in a certain non-empty space of solutions X is defined as follows in Equation (1).
where
is a membership function of the fuzzy set A. This function indicates the degree of the membership of the element in the set A.means full membership,means partial membership andmeans no membership at all.
Definition 2.
Definition 3.
The support of a TFN—subset of the A set in which all elements have a non-zero membership value in the A set of Equation (6).
Definition 4.
The core of a TFN is a singleton with membership value 1 shown in Equation (7).
Definition 5.
The fuzzy rule—it is based on the,, andlogical connectives, which are used in the reasoning process.
Definition 6.
The rule base—it includes logical rules defining the relations in the system.
Definition 7.
2.2. The Comet Method
Many MCDM methods exhibit the rank reversal phenomenon. To see the above point more clearly, suppose that we have set of three alternatives A, B, and C. Suppose that the best variant is A, followed by B, which is followed by C. Next, we suppose that an even worse element replace B, say alternative D. When the new set of variants are ranked collectively and by considering that the criteria have equal weights as before. Sometimes, it turns out that under some decision-making techniques, the best choice may be changed now, and this is known as a rank reversal. It is only of the types of rank reversals. However, the Characteristic Objects Method (COMET) is completely free of this problem [48]. In previous works, the accuracy of the COMET method was verified [43]. The formal notation of the COMET method should be briefly recalled [46,47,49]:
Step 1. The expert defines the dimensionality of the problem by choosing r criteria, . Then, a set of fuzzy numbers is selected for each criterion , e.g., Equation (16):
where are the ordinals of the fuzzy numbers for all criteria.
Step 2. The characteristic objects () are determined with the method of the Cartesian product of the triangular fuzzy numbers’ cores of all the criteria Equation (17):
As a result, an ordered set of all is obtained Equation (18):
where t is the count of s and is equal to Equation (19):
Step 3. The expert identifies the Matrix of Expert Judgment () by pairwise comparison of the s. The MEJ matrix is shown as Equation (20):
where is the result of comparing and by the expert. The function denotes the subjective judgment of the selected expert. It depends entirely on the knowledge and experience of the expert. The expert’s preferences are presented in the following Equation (21):
After the MEJ matrix is prepared, a vertical vector of the Summed Judgments () is obtained as follows Equation (22):
Finally, the values of preference are estimated for each . As a result, a vector P is determined, where the i-th row contains the approximate value of preference for .
Step 4. Each and its preference value is changed to a fuzzy rule by using the following Equation (23):
In this way, a complete fuzzy rule base is obtained.
Step 5. Each decision variant is shown as a set of crisp numbers, e.g., . This set corresponds to the criteria . The preference of the i-th alternative is calculated by using Mamdani’s fuzzy inference method. The constant rule base guarantees that the received results are unambiguous. The whole process of the COMET method is presented in Figure 1.

Figure 1.
The flow chart of the COMET procedure [44].
2.3. Hill-Climbing
Hill-Climbing (HC) is a mathematical method used for optimization purposes, which belongs to the field of local search methods. HC technique starts with generating an initial state, i.e., an initial solution. Local ekstremum is searched in the neighborhood of the current state, where the first accepted value of the current state is the initial state value. Solution c is called local optimization, where the N(c) neighborhood does not have a better solution, and it is not the best solution in the whole set of solutions [50]. In optimizing with a hill-climbing algorithm it is not possible to determine whether the local extreme found is a global one. The process of optimization using a hill-climbing algorithm can be presented as follows:
Step 1.Initialization of the hill-climbing algorithm. Randomly create one candidate solution , depending on the length .
Step 2.Evaluation. Create a fitness function to evaluate the current solution. The first generation is as follows:
Step 3.Mutation. Mutate the current solution one by one and evaluate the new solution .
Step 4.Selection. If the value of the fitness function for the new solution is better than for the current solution, replace as follows:
Step 5.Termination. When there is no improvement in fitness function after a few generations
The pseudocode of the hill-climbing method is presented by using the Algorithm 1.
| Algorithm 1: Hill-climbing [51]. |
 |
2.4. Simulated Annealing
Simulated annealing is a stochastic method that has a mechanism to avoid getting stuck in local extremes. The mechanism for further searching the global extremes allows you to accept a worse solution to get out of the local extremes and explore the entire problem area [52]. The simulated annealing method is presented as Algorithm 2 and may look like this:
Step 1.Initialization of the simulated annealing method. Select the initial temperature value and randomly create one feasible candidate solution . Select a parameter and the maximum number of iterations L. Let the iteration counter be initiated as and a further counter .
Step 2.Evaluation. Create a fitness function to evaluate the current solution. The first generation is as follows:
Step 3.Mutation. Randomly choose a new solution in the neighborhood of the current solution
Step 4.Selection. If the value of the fitness function for the new solution is better than for the current solution, replace as follows:
Otherwise, calculate the difference between the value of the fitness function of the new solution and the current solution, followed by the probability density function as follows:
Generate a random number z uniformly distributed in [0,1]. If , then the new solution becomes the current solution .
Step 5.Increasing the temperature If , the iteration counter is increased and the counter is reset . A new temperature value is calculated following the Equation (29).
Otherwise and return to the mutation.
Step 6.Termination If and one of the stop criteria is satisfied, terminate the algorithm and return the current solution .
| Algorithm 2: Simulated annealing. |
 |
2.5. Particle Swarm Optimization
Particle swarm optimization is a metaheuristic technique that was designed in 1995 by Kennedy and Eberhart [53]. The original idea of PSO was to simulate a simplified social system. PSO is a population-based method in which individuals are called particles and a population is called a swarm. Each particle in the swarm is a possible solution to a given optimization problem. All individuals in the swarm move towards their own best solution and towards the best global solution in the swarm [54,55]. The overall performance of the particle swarm optimization can be presented as follows:
Step 1.Initialization of the PSO method. Set population size S. Choose cognitive and social coefficients. Then initiate the swarm and randomly select the position and velocity for each particle in the swarm. Set the maximum number of iterations and initialize the iteration counter .
Step 2.Evaluation. In the first generation, for each particle from the swarm, the position becomes its best position . Select the particle that has the best position in the swarm from the whole population and assigns it the best position in the swarm .
Step 3.Mutation. For each particle, some vectors are randomized from a uniform distribution as follows:
The particle velocity and the position of the particle are then updated. This is explained by Equation (31).
Step 4.Selection. Compare the evaluation of the position of the particle and the evaluation of its best position. The evaluation is provided by the fitness function. If it is better, the position of the particle becomes the best position of the particle. Compare it with an evaluation of the best position in the swarm. Replace the best position in the swarm when the evaluation of the best position of the particle is better.
Step 5.Termination The algorithm terminates when the iteration counter reaches a higher value than the number of maximum iterations. One iteration cycle starts from mutation to selection.
The pseudocode of the particle swarm optimization is presented by using the Algorithm 3.
| Algorithm 3: Particle swarm optimization. |
 |
2.6. Similarity Coefficient
The similarity coefficients of the rankings allow us to compare the two indicated order. It is important to choose such coefficients that work well in the decision-making field. The paper uses three such coefficients, i.e., Spearman correlation coefficient Equation (32), Spearman weighted correlation coefficient Equation (33) and WS similarity coefficients Equation (34) [56].
3. Results and Discussion of The Research
The goal of the experiment is to compare the quality of three stochastic methods in searching for optimal preference values of characteristic objects at different initial states. The initial state in the study determines the initial preference values of characteristic objects. The selected methods for the experiment are the hill-climbing algorithm, the simulated annealing method, and particle swarm optimization. Several particles in the PSO method have been set to 20, while parameters , , have been given values of 0.5, 0.3, and 0.9, respectively. The maximum number of iterations in each method has been set to 1000. Preference of characteristic objects has been determined using a set of alternatives. A set of alternatives determined the preference of characteristic objects.
The optimization process consisted in obtaining the smallest difference in the absolute value of the sum of alternatives preferences calculated with reference alternatives. The calculated alternatives are those whose preference values were calculated using a model defined using characteristic objects whose preference is a candidate for the solution. For this purpose, the objective function has been defined by Equation (35).
where means calculated alternatives and means reference alternatives.
The experiment was conducted for 200 sets of decision variants consisting of 5, 10, 15, 20, 25 alternatives. The preference of decision variants forming the set intended for the optimization process was selected randomly or calculated using a generated random vector. The criteria by which characteristic objects were defined took static values [0, 0.5, 1] and dynamic values depending on the set of alternatives. In Equation (36) this is given.
The study was conducted with four initial state variants. The characteristic objects assumed a preference value equal to 0, 0.5, 1, or a random value.
3.1. Impact of the Initial Conditions
Figure 2 presents heat maps with nuclear density estimators for a hill-climbing algorithm for a static variant of criteria with a non-existent model, i.e., one in which the preferences of the alternatives were selected randomly. The charts show the solutions found about the number of iterations for the given number of alternatives in the set and the initial state variants.

Figure 2.
The value of the target function depending on the number of iterations, the number of alternatives, and initial conditions (method: HC; criteria variant: static; model: not existing).
For an increasing number of alternatives for characteristic objects assuming the value of preference 0 at the beginning, one can see an increase in the value of found solutions. The accuracy of the five alternatives in the set is high because the concentration of the smallest found values of the fitness function is close to the value of 0. The largest number of solutions found was between 300 and 500 iterations. With more alternatives, the number of iterations in which solutions have been found slightly increases. However, the values of the solutions were found to increase significantly. For the ten alternatives, the highest concentration of the smallest found fitness values oscillates between [1, 1.5]. For fifteen alternatives [2, 2.35], twenty alternatives [2.9, 3.1], and for twenty five alternatives [4.5, 5].
The initial state in which the preference of characteristic objects is set to 0.5 does not reach as large values in the range of the number of iterations needed to find a solution as in the initial state for the value 0. This range is [175, 280]. The clusters of solutions found about their costs are slightly different from the initial state for the value 0.
In the initial state, where characteristic objects take preference values equal to 1, the distribution of found solutions is much larger than in the case where the initial state value is 0.5. The most massive clusters of found solutions occur between iterations 390 and 500.
For a randomly selected preference value of the characteristic objects, the number of iterations needed to find a solution is much smaller than when the initial state takes a preference value of 0 or 1. However, compared with the initial state where the characteristic objects take a preference value of 0.5, the initial state with a random value is worse due to the density nuclear estimator. It shows that the method needed more iteration when estimating some of the smallest fitness function values.
Thermal maps, together with nuclear density estimators for a hill-climbing algorithm for a dynamic variant of criteria with a non-existent model, are presented using Figure 3. Solutions found about the number of iterations for the given number of alternatives in the set and variants of the initial state are presented in the charts.
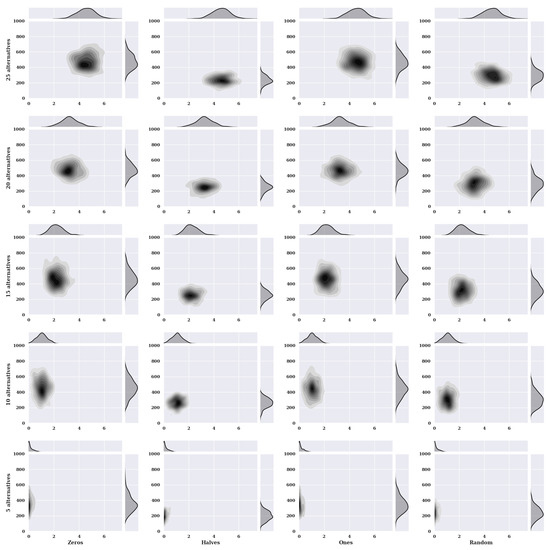
Figure 3.
The value of the target function depending on the number of iterations, the number of alternatives, and initial conditions (method: HC; criteria variant: dynamic; model: not existing).
For characteristic objects taking at the beginning the value of preference 0 for an increasing number of alternatives, you can see an increase in the value of found solutions. For a set consisting of five alternatives, the concentration of the smallest found values of the fitness function is close to 0, which means that the accuracy is high. However, as the number of alternatives increases, the accuracy decreases. For the ten alternatives, the highest concentration of the smallest found fitness values is in the range [1.5, 1.6]. For fifteen alternatives [1.9, 2.2], twenty alternatives [3.1] and for twenty five alternatives [4.1, 4.9]. Most of the solutions found for 10, 15, 20, 25 alternatives were between 400 and 500 iterations. The exception is a set consisting of five alternatives in which most of the solutions were found before the 400 iterations. With more alternatives, the number of iterations in which solutions were found slightly increases. The value of the solutions found increases significantly.
The initial state where the preference of the characteristic objects is set to 0.5 does not reach as high values in the range of the number of iterations needed to find a solution as the preference of the characteristic objects is 0. This range is approximately [190, 280]. The clusters of solutions found about their values differ slightly from the initial state for 0.
In the initial state where the characteristic objects take values of 1, the distribution of solutions found is higher than for the initial state value of 0.5. The most significant clusters of solutions found occur between iterations 400 and 500. Compared with the initial state where the characteristic objects take a preference value of 0, the differences are slight.
The number of iterations needed to find a solution for a randomly selected preference value of the characteristic objects is much smaller than when the initial state takes a preference value of 0 or 1. However, compared with the initial state where the characteristic objects take a preference value of 0.5, the initial state with a random value is worse due to the nuclear density estimator. It shows that the method needed more iteration when estimating some of the smallest fitness function values.
Figure 4 shows thermal maps together with nuclear density estimators for a hill-climbing algorithm for a static variant of criteria with an existing model. A current model means a model in which the preferences of alternatives have been calculated using a randomly selected vector . The individual charts show the solutions found concerning iteration numbers for the given alternatives and initial state variants.

Figure 4.
The value of the target function depending on the number of iterations, the number of alternatives, and initial conditions (method: HC; criteria variant: static; model: existing).
For a start preference of characteristic objects of 0, the change in the value of found solutions with an increase in the number of alternatives is not substantial. The hill-climbing algorithm usually finds a solution between 400 and 600 iterations. However, the solutions found are in the range [0, 0.2], which indicates very high accuracy.
However, a better solution seems to be the starting value of the preference of characteristic objects of 0.5. This variant needs less iteration than finding solutions, and their cost is lower.
However, this cannot be said about the variant where the characteristic objects take a preference value of 1. The distribution of the values of the solutions found is much greater than in the case of the start preference value of 0. An example of this is ten alternatives where the cloud is more extensive when the start state has a value of 1 than when it takes the amount of 0.
In the initial state, where characteristic objects take random preference values, the number of iterations needed to find a solution is much smaller than for the initial state values of 0 and 1. However, the costs of solutions are much higher than for the initial state with a value of 0.5. The increase in the number of iterations compared to the number of alternatives is not so large.
Figure 5 shows thermal maps together with nuclear density estimators for a hill-climbing algorithm for a dynamic variant of criteria with an existing model. The individual charts show the solutions found concerning iteration numbers for the given alternatives and initial state variants.

Figure 5.
The value of the target function depending on the number of iterations, the number of alternatives, and initial conditions (method: HC; criteria variant: dynamic; model: existing).
In the case of a starting preference of characteristic objects of 0, the change in the value of found solutions decreases with the number of alternatives. The hill-climbing algorithm usually finds a solution between 400 and 600 iterations. Solutions found for five alternatives are in the range [0, 0.05], for ten and fifteen [0, 0.2], for twenty and twenty-five [0, 0.1], which indicates very high accuracy.
However, the starting value of the characteristic object preference of 0.5 seems to be a better solution. This option needs less iteration than finding solutions, and its cost is lower.
The variant in which the characteristic objects take the initial preference value of 1 needs more iterations to find solutions than for the start value of 0.5. The distribution of found solutions is much higher than for the start value of 0. An example is ten alternatives where the cloud is more extensive when the start state has the benefit of 1 than when it takes the amount of 0.
In the initial state where the characteristic objects take random preference values, the number of iterations needed to find a solution is much smaller than for the initial state values of 0 and 1. However, the costs of solutions are much higher than for the initial state with a value of 0.5. The increase in the number of iterations compared to the number of alternatives is not so large.
Figure 6 presents thermal maps with density nuclear estimators for simulated annealing method for a static variant of criteria with a non-existent model. The charts show the solutions found about the number of iterations for the given number of alternatives in the set and the initial state variants.

Figure 6.
The value of the target function depending on the number of iterations, the number of alternatives, and initial conditions (method: SA; criteria variant: static; model: not existing).
For an increasing number of alternatives for characteristic objects assuming the value of preference 0 at the beginning, one can see an increase in the value of found solutions. The accuracy of the five alternatives in the set is high because the concentration of the smallest found values of the fitness function is close to 0. Most of the solutions were found in 1000 iterations. With more alternatives, the number of iterations in which solutions were found slightly decreases. However, the values of the solutions were found to increase significantly. For the ten alternatives, the largest concentration of the smallest found fitness values is in the range [2, 3.1]. For fifteen alternatives [3, 4.1], twenty alternatives [4.05, 5.9], and for twenty-five alternatives [5.8, 6.2].
The initial state where the preference of the characteristic objects is set to 0.5 reaches as high values in the range of the number of iterations needed to find a solution as for the initial state for value 0. The clusters of found solution values differ significantly from the initial state for value 0 because they are smaller.
In the initial state, where characteristic objects take preference values equal to 1, the distribution of solutions found is much larger than in the case where the initial state value is 0.5. However, the number of iterations needed to find an answer is the same.
For a randomly selected preference value of the characteristic objects, the values of the solutions found are much smaller than when the initial state takes the value 0 or 1. However, compared with the initial state where the characteristic objects take the preference value 0.5, the initial state with a random value is worse due to the nuclear density estimator. It shows that the method has found smaller fitness function values.
Thermal maps, together with nuclear density estimators for the simulated annealing method for a dynamic variant of criteria with a non-existent model, are presented using Figure 7. The solutions found about the number of iterations for the given number of alternatives in the set and variants of the initial state are presented in the charts.

Figure 7.
The value of the target function depending on the number of iterations, the number of alternatives, and initial conditions (method: SA; criteria variant: dynamic; model: not existing).
For characteristic objects assuming at the beginning, the value of preference 0 for an increasing number of alternatives, an increase in the amount of found solutions can be observed. For a set consisting of five choices, the concentration of the smallest found importance of the fitness function is close to 0, which means that the accuracy is high. However, as the number of alternatives increases, the efficiency decreases. For the ten alternatives, the highest concentration of the smallest found fitness values is in the range [2, 3], for the fifteen options [3.8, 4], for twenty alternatives [4.1, 5.8], and the twenty-five alternatives [5.95, 6.8]. The most significant number of solutions found for all the considered number of other options was between 980 and 1000 iterations. With a more substantial amount of alternatives, the number of iterations in which solutions were found slightly decreases.
The initial state in which the preference of characteristic objects is set to 0.5 does not need as large numbers of iterations to find a solution as in the case of the preference of characteristic objects of 0. The values of found solutions for a given amount of alternatives are increasing, but they are not as large as for the initial state with value 0.
In the initial state, where characteristic objects take preference values equal to 1, the distribution of found solutions is higher than in the case where the value of the initial state is 0.5. A large concentration of found solutions occurs between the iteration 985 and 1000. Compared to the initial state where characteristic objects take preference values equal to 0, the differences are insignificant.
The iteration numbers needed to find a solution for a randomly selected preference value of the characteristic objects are approximately the same as when the initial state takes the value 0, 0.5, or 1. However, the values of the solutions found are much smaller than when the initial state takes the value 0 or 1. Compared to the initial state where the characteristic objects take the preference value 0.5, the initial state with a random value is worse due to the nuclear density estimator. It shows that the method has found smaller fitness function values.
Figure 8 shows thermal maps together with nuclear density estimators for the simulated annealing method for a static variant of criteria with an existing model. Individual charts show solutions found against iteration numbers for given alternatives and initial state variants.

Figure 8.
The value of the target function depending on the number of iterations, the number of alternatives, and initial conditions (method: SA; criteria variant: static; model: existing).
For a starting preference of characteristic objects of 0, the value of found solutions increases with the number of alternatives. The simulated annealing method usually finds solutions between 990 and 1000 iterations. The accuracy is high for five alternatives because the solution values found are less than 1. However, the efficiency decreases as the number of alternatives increases, e.g., for 25 alternatives numbers, several solutions reach amounts greater than 4.
A better solution seems to be the starting value of the characteristic object preference of 0.5. The increase of the smallest found values of the fitness function is not as big as in the case of a starting state with a value of 0. The accuracy is also very high because, for all considered numbers of alternatives, most of the solution values are in the range [0, 1].
This cannot be said about the variant, where the characteristic objects take the preference value of 1. The distribution of the found solution values is much larger than in the case of the starter preference value of 0.5. An example is the 25 alternatives, where the solution values are in the range [2.1, 4] in case the starter state takes the amount of 1, while for the starter state with the cost of 0.5 they are in the range [0, 1].
The number of iterations needed to find a solution for a randomly selected preference value of the characteristic objects is approximately the same as when the initial state takes the amount 0, 0.5, or 1. However, the amounts of solutions found are much smaller than when the initial state takes the value 0 or 1. Compared to the initial state where the characteristic objects take the preference value 0.5, the initial state with a random value is worse due to the nuclear density estimator. It shows that the method has found smaller fitness function values.
Figure 9 shows thermal maps together with nuclear density estimators for the simulated annealing method for a dynamic variant of criteria with an existing model. Individual charts show solutions for a given number of alternatives and initial parameters.

Figure 9.
The value of the target function depending on the number of iterations, the number of alternatives, and initial conditions (method: SA; criteria variant: dynamic; model: existing).
For a starting preference of characteristic objects of 0, the values of found solutions increase with the number of alternatives. The simulated annealing method usually gets final solutions between 900 and 1000 iterations. Solutions found for five alternatives are in the range [0.2, 1.4], for ten [0.8, 2.1], for fifteen [1.85, 2.8], for twenty and twenty-five [2.2, 3.4]. This indicates a decrease in accuracy as the number of alternatives increases.
A better solution seems to be the starting value of characteristic objects’ preferences amounting to 0.5. This variant, with the increase in the number of alternatives, needs less iteration to find solutions, and its value is lower compared to the initial state with the amount of 0. A variant in which the characteristic objects take an initial preference value of 1 needs more iterations to find solutions than for a start value of 0.5. The distribution of the costs of solutions found is the same as for a start value of 0.
In the initial state where the characteristic objects take random preference values, the number of iterations needed to find a solution is much smaller than for the initial state values of 0 and 1. However, the costs of solutions are much higher than for the initial state of 0.5. The increase of iterations compared to the number of alternatives is not significant.
Figure 10 shows thermal maps with nuclear density estimators for particle swarm optimization for the static variant of criteria with the non-existent model. The charts show the solutions found about the number of iterations for the given number of alternatives in the set and the initial state variants.
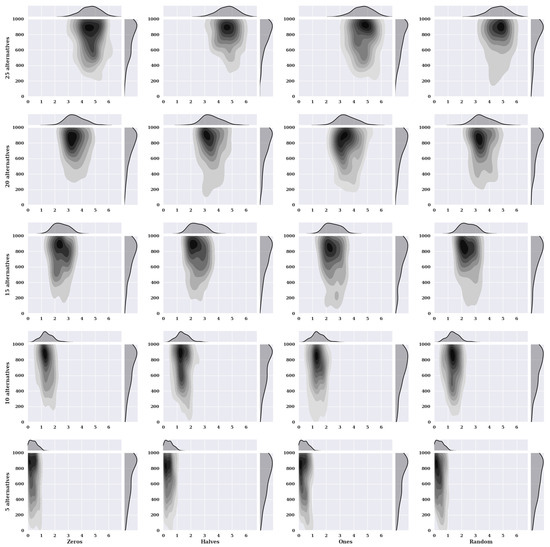
Figure 10.
The value of the target function depending on the number of iterations, the number of alternatives, and initial conditions (method: PSO; criteria variant: static; model: not existing).
For the increasing number of alternatives for characteristic objects assuming the value of preference 0 at the beginning, one can see an increase in the value of found solutions. The accuracy of the five alternatives in the set is high because the concentration of the smallest found values of the fitness function is in the range [0, 1]. The number of iterations increases with the number of alternatives in the set and the value of the solutions found. For the ten alternatives, the largest concentration of the smallest found fitness values is in the range [1, 1.9]. For fifteen alternatives [2, 3.15], twenty alternatives [2.95, 4], and for twenty five alternatives [4, 5.4].
The initial state where the preference of the characteristic objects is set to 0.5 reaches as high values in the range of the number of iterations needed to find a solution as for the initial state for value 0. The clusters of found solution values differ significantly from the initial state for value 0 because the solution values are smaller.
In the initial state, where characteristic objects take preference values equal to 1, the distribution of solutions found is slightly different from the case where the initial state value is 0.5. However, the number of iterations needed to find a solution, as the number of alternatives increases is smaller.
For a randomly selected preference value of characteristic objects, the number of iterations needed to find solutions and the costs of solutions increase with the number of alternatives. An example is a graph for twenty-five alternatives where a minority of solutions were found in 400 iterations, which cannot be said about the chart for five alternatives.
Thermal maps, together with nuclear density estimators for particle swarm optimization for a dynamic variant of criteria with a non-existent model, are presented in Figure 11. Solutions found about the number of iterations for the given number of alternatives in the set and variants of the initial state are presented on the charts.

Figure 11.
The value of the target function depending on the number of iterations, the number of alternatives, and initial conditions (method: PSO; criteria variant: dynamic; model: not existing).
For characteristic objects assuming at the beginning, the value of preference 0 for an increasing number of alternatives, an increase in the value of found solutions can be observed. For a set consisting of five alternatives, the concentration of the smallest found values of the fitness function is close to 0, which means that the accuracy is high. However, as the number of alternatives increases, the accuracy decreases. For the ten alternatives, the highest concentration of the smallest fitness values found is in the range [1, 1.4].For the fifteen alternatives [1.9, 2.9], twenty alternatives [3.1, 3.85] and for the twenty-five alternatives [4.05, 5.1]. The largest number of solutions found for all the considered number of alternatives was between 800 and 1000 iterations. With a larger number of alternatives, the number of iterations in which solutions have been found increases.
The initial state in which the preference of characteristic objects is set to 0.5 for ten alternatives needs smaller numbers of iterations to find a solution than the initial state of 0.
In other cases, there are no statistically significant differences.
Figure 12 shows thermal maps together with nuclear density estimators for particle swarm optimization for a static variant of criteria with an existing model. The individual charts show the solutions found for iteration numbers for the given alternatives and initial state variants.

Figure 12.
The value of the target function depending on the number of iterations, the number of alternatives, and initial conditions (method: PSO; criteria variant: static; model: existing).
For a starting preference of characteristic objects of 0, the values of found solutions increase with the number of alternatives. Particle swarm optimization usually finds solutions between 600 and 1000 iterations. The accuracy is very high for all considered alternatives numbers because all solution values are less than 1.
A variant where the start value of the characteristic object preference is 0.5 performs worse for five alternatives than the start value of 0. The number of iterations that this variant achieves for the solution values found is much higher.
The variants in which the characteristic objects take the initial preference value of 1 and random are missing statistically significant differences.
Figure 13 shows thermal maps together with nuclear density estimators for particle swarm optimization for a dynamic variant of criteria with an existing model. The individual charts show the solutions found for iteration numbers for the given alternatives and initial state variants.

Figure 13.
The value of the target function depending on the number of iterations, number of alternatives and initial conditions (method: PSO; criteria variant: dynamic; model: existing).
For a starting preference of characteristic objects of 0, the values of found solutions increase with the number of alternatives. Particle swarm optimization usually finds solutions between 600 and 1000 iterations. Solutions found for five alternatives are in the range [0, 0.05], for ten [0.15, 0.21], for fifteen [0.22, 0.38], for twenty [0.33, 0.42] and twenty-five [0.4, 0.6]. This indicates a small decrease in accuracy as the number of alternatives increases.
A better solution seems to be the starting value of characteristic objects’ preferences amounting to 0.5. In the case of sets consisting of 5 and 20 alternatives, the distribution of the found smallest values of the fitness function indicates lower values obtained than in the case of the initial state in which the characteristic objects’ preferences are 0. The variant that obtained the lowest values of solutions for 25 alternatives is the initial state with a value of 1. The highest concentration of solutions is close to 0.4, where for the initial state with a value of 0 and 0.5, the highest level was with an amount of solution 0.5.
For the initial state in which characteristic objects take a random preference value, there are no differences that would be statistically significant.
3.2. Fitness Function Distribution
Figure 14 shows violin charts for a hill-climbing algorithm for a non-existent model. The graphs show variants of criteria and variants of initial states.
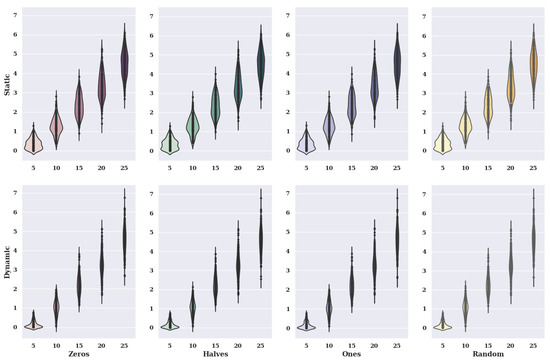
Figure 14.
Visualization of the value of solutions in relation to the number of alternatives to criteria and initial state variants (method: HC; model: not existing).
In the case of the charts for the initial state, in which the preferences of characteristic objects took the value of 0, the static value of criteria has smaller values of solutions than the dynamic value. Therefore, the size of the violin for a static case is much larger with small values of solutions. It is worth mentioning, however, that the data distribution for the five alternatives in the set for the dynamic case indicates that most of the smallest values of the fitness function obtained take values smaller than 0.2, which is a much better result than for the static variant.
For the initial state, where the preference of the characteristic objects took the value 0.5, 1, and random, the same relationship between the static values of the criteria and the dynamic values of the criteria occurs as for the initial state with the value 0.
Figure 15 shows fiddle charts for the hill-climbing algorithm for an existing model. The charts show variants of criteria and variants of initial states.
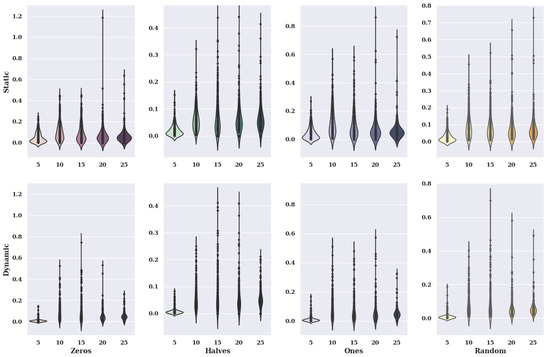
Figure 15.
Visualization of the value of solutions in relation to the number of alternatives to criteria and initial state variants (method: HC; model: existing).
In the case of the charts for the initial state, in which the preferences of characteristic objects took the value of 0, the static value of criteria has smaller values of solutions than the dynamic value. Therefore, the size of the violin for a static case is much larger with small values of solutions. It is worth mentioning, however, that the data distribution for the five alternatives in the set for the dynamic case indicates that most of the smallest values of the fitness function obtained take values smaller than 0.1, which is a much better result than for the static variant. However, the static variant has higher maximum found values for twenty and twenty-five alternatives than the dynamic variant.
For the initial state, where the preference of the characteristic objects takes the value of 0.5, the values of the solutions are lower than for the initial state, where the criteria are chosen statically, the accuracy is very high. In contrast, for the dynamic criteria variant, it is much lower. Many solutions in the static variant were found in the range [0, 0.1], which cannot be said for the dynamic variant. On the other hand, the static variant of criteria has much higher maximum values of solutions found for all the considered number of alternatives than the dynamic variant.
For initial state values equal to 1, the static variant of criteria takes smaller values of solutions than the static variant. The distribution of solutions found is similar for the distribution of the initial state variant with a value of 0. However, the found values of solutions are more significant than for the initial state in which the characteristic objects take preference values of 0.5.
In the case of graphs for the initial state where the preference of the characteristic objects took a random value, the static value of the criteria has smaller values of solutions than the dynamic value. The accuracy decreases with the increase of the number of alternatives in the set in the case of the static criteria variant.
Figure 16 shows violin charts for the simulated annealing method for a non-existent model. The charts show variants of criteria and variants of initial states.
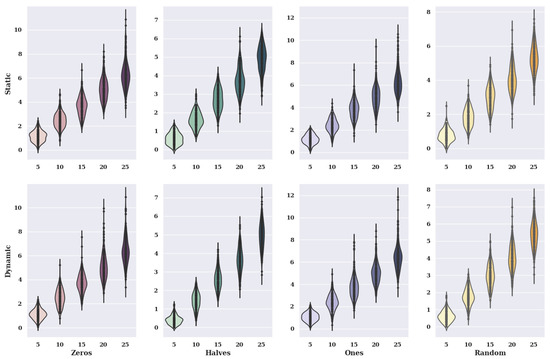
Figure 16.
Visualization of the value of solutions in relation to the number of alternatives to criteria and initial state variants (method: SA; model: not existing).
In the case of charts for the initial state, in which the preferences of characteristic objects took the value of 0, the static value of criteria has smaller values of solutions than the dynamic value. Therefore, the size of the violin for a static case is much larger with small values of solutions.
For the initial state, where the preference of the characteristic objects has taken the value of 0.5, the values of the solutions are smaller than when the initial state takes the value of 0. When the criteria are chosen statically, the accuracy is very high, while for the dynamic criteria variant, it is much lower. Moreover, the dynamic criteria variant has much higher maximum solution values found for 5, 15, and 25 alternatives than the static variant. For an initial state value of 1, the static variant of criteria has similar distributions of solution values as the dynamic variant due to its violin appearance. However, the most significant solution values found vary considerably.
In the case of the graphs for the initial state, in which the preferences of characteristic objects took a random value, there are no statistically significant differences between the static variant and the dynamic variant of the criteria.
Figure 17 shows violin charts for the simulated annealing method for an existing model. The graphs show variants of criteria and options of initial states.
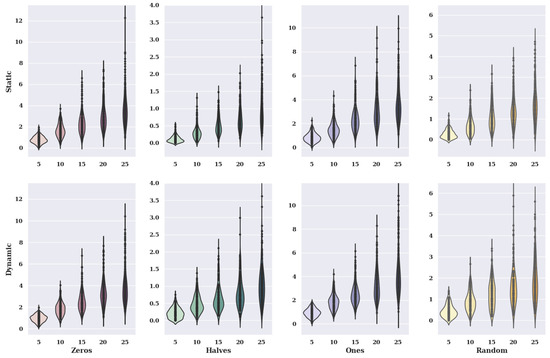
Figure 17.
Visualization of the value of solutions in relation to the number of alternatives to criteria and initial state variants (method: SA; model: existing).
In the case of the charts for the initial state, in which the preferences of characteristic objects took the value 0, the static value of criteria has similar amounts of solutions as the dynamic value. The accuracy in both variants of criteria selection decreases with the increase in the number of alternatives.
For the initial state where the preference of the characteristic objects has assumed the value of 0.5, the amounts of the solutions are smaller than when the initial state assumes the cost of 0. This is indicated by the size of the violin, which is significantly higher when the initial value of the preference of the characteristic objects is 0.5. When criteria are selected dynamically, the accuracy is very high, while for the variant of static criteria, it is significantly lower. However, the dynamic criteria option has much higher maximum solution values found for 5, 10, 15, and 25 alternatives than the static variant.
For an initial state value of 1, the static variant of criteria has similar distributions of solution values as the dynamic variant due to its violin appearance. However, the most significant solution values found vary considerably.
In the case of the graphs for the initial state, in which the preference of characteristic objects took a random value, the static variant of the criteria is characterized by small benefits of solutions. Higher amounts of solutions assume the dynamic variant. The static variant is more accurate than the dynamic option.
Figure 18 shows violin charts for particle swarm optimization for a non-existent model. The graphs show variants of criteria and options of initial states.
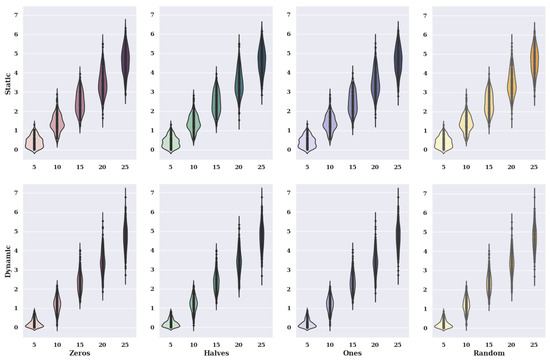
Figure 18.
Visualization of the value of solutions in relation to the number of alternatives to criteria and initial state variants (method: PSO; model: nonexistent).
In the case of charts for the initial state, in which the preference of characteristic objects took the value 0, the static value of criteria has smaller amounts of solutions than the dynamic value. Therefore, the size of the violin for a static case is much larger with small values of solutions.
For the initial state, where the preference of the characteristic objects has assumed the value of 0.5, the costs of solutions are similar to those of 0. When criteria are chosen statically, the accuracy decreases as the number of alternatives increases. In addition, the dynamic variant of criteria has much higher maximum solution values found for 15 and 25 alternatives than the static option.
For an initial state value of 1 fiddle size for solutions found are similar to those where the initial state is 0.5. The accuracy for static criteria is higher than for dynamic criteria. The smallest and largest solution values found are significantly different for dynamic and static criteria.
For a random initial state value, the distribution of solutions found is similar to when the initial state is 0.5 and 1. For five alternatives, the static variant has significantly higher amounts of solutions than the dynamic option. For ten, fifteen, twenty, and twenty-five choices, the static variant has higher accuracy than the static variant.
Figure 19 shows violin charts for particle swarm optimization for the existing model. The graphs show variants of criteria and options of initial states.
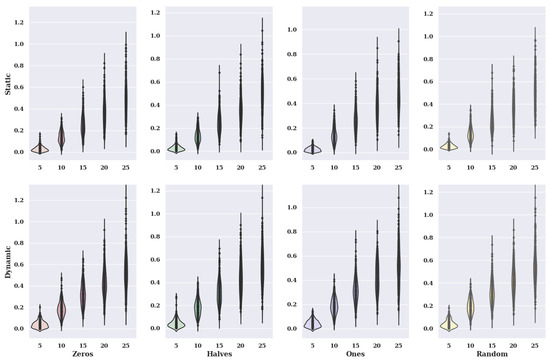
Figure 19.
Visualization of the value of solutions in relation to the number of alternatives to criteria and initial state variants (method: PSO; model: existing).
In the case of diagrams for the initial state, where the preference of characteristic objects took the value 0, the static value of criteria has smaller amounts of solutions than the dynamic value. For 5 and 10 alternatives, the accuracy of static criteria is higher than for dynamic criteria. However, where there are 15, 20 and 25 alternatives in a set, the accuracy for static criteria is lower than for dynamic criteria.
For an initial state where the preference of the characteristic objects has taken the value 0.5, the benefits of the solutions are more significant than when the initial state takes the amount 0. The accuracy decreases as the number of alternatives for each criterion selection variant increases. The dynamic variant of criteria has significantly higher maximum solution values found for 15, 20, and 25 options than the static option.
For an initial state value of 1, the static values of the criteria have smaller solution values than the static variant of the criteria. The accuracy for static criteria is higher than for dynamic criteria. The smallest and largest solution values found are significantly different for dynamic and static criteria.
For a random initial state value, the distribution of solutions found differs slightly from a 0 initial state. For all alternatives considered, the dynamic variant has significantly higher amounts of solutions than the static option. The accuracy of the static variant is much higher than for the dynamic variant.
3.3. Use of the Proposed Approach
A study was carried out to demonstrate the operation of the proposed approach. For dynamic and static criteria with an existing model, twenty alternatives were drawn. The preference for characteristic objects was set to 0.5 as the initial state, as this approach is more productive according to the previously presented surveys.
To calculate the similarity coefficient of final rankings between the reference ranking and the one obtained using stochastic methods, the alternatives were divided into a training set and a test set. The division of the set of alternatives was partial, i.e., the first half was a teaching set and the second a test set.
The static criteria were set to [0, 0.5, 0], while the dynamic ones were calculated with the use of the teaching set according to the Formula (36). A randomly generated vector evaluated the alternatives constituting the teaching and test set.
Then, the teaching set was used to determine the preferences of characteristic objects using selected stochastic methods. The defined model evaluated the alternatives from the test set using the calculated preferences of characteristic objects.
Training set of 10 alternatives for a static variant of the criteria are presented in Table 1. The preference was calculated using a randomly generated vector. The generated points served as input for HC, SA and PSO techniques. On their basis, decision models were identified using each method.

Table 1.
Summary of ten alternatives from the training set (criteria variant: static; model: existing; start state: 0.5).
Table 2 presents alternatives included in the test set and their preferences as well as rankings for a static variant of the criteria. The simulated annealing method performed slightly worse than the hill-climbing algorithm and particle swarm optimization. The lowest value of fitness function obtained by it is much higher than the other two methods. The particle swarm optimization method did very well because the ranking of the assessed alternatives is approximate to a reference ranking. The same is true for the hill-climbing algorithm, whose preferences are very similar to those of the reference model.

Table 2.
Summary of ten alternatives from the test set for selected stochastic methods (criteria variant: static; model: existing; start state: 0.5).
Spearman’s correlation coefficients for a static variant of the criteria between the reference ranking and calculated by stochastic methods are 0.9879 (HC), 0.9152 (SA), 0.9636 (PSO). The high accuracy of the methods used can be seen here, however, the simulated annealing method differs significantly from the PSO and HC methods. The strongest correlation between the reference ranking and the calculated one has a hill-climbing algorithm.
Spearman’s weighted correlation coefficients for a static variant of the criteria for stochastic methods are as follows: 0.9835 (HC), 0.9096 (SA), 0.9736 (PSO). Similarly to Spearman’s correlation coefficients, the weighted coefficients show that the strongest correlation is with the hill-climbing algorithm and the weakest with the simulated overhang method. However, the difference between the coefficient for PSO and HC methods is much smaller than for Spearman’s correlation coefficient.
correlation coefficients calculated for the preference of a reference testing set and the preference calculated using stochastic methods for a static variant of the criteria are as follows: 0.9717 (HC), 0.9143 (SA), 0.9919 (PSO). The most substantial relation between the reference ranking and the calculated one is particle swarm optimization. In the case of and coefficient, the most correlated method was the HC method. Moreover, a much higher difference in the ws factor between the PSO method and the hill-climbing algorithm can be seen here than in the case of the Spearman weighted factor. On the other hand, the correlation of the simulated annealing method, as in the case of the rest of correlation coefficients, is the weakest of the methods considered.
Table 3 shows a training set of 10 alternatives and their preference for a dynamic variant of criteria. The preference was calculated using a randomly generated vector. The generated points served as input for HC, SA, and PSO techniques. On their basis, decision models were identified using each method.

Table 3.
Summary of ten alternatives from the training set (criteria variant: dynamic; model: existing; start state: 0.5).
Table 4 shows the alternatives included in the test set and their preferences, as well as rankings for the dynamic variant of criteria. The simulated annealing method has fared worse than the hill-climbing algorithm and particle swarm optimization. The lowest value of fitness function obtained by it is much higher than the other two methods. The particle swarm optimization method did very well because the ranking of the assessed alternatives is the same as the reference ranking. The same is true for the hill-climbing algorithm, whose preferences are very similar to those of the reference model.

Table 4.
Summary of ten alternatives from the test set for selected stochastic methods (criteria variant: dynamic; model: existing; start state: 0.5).
The obtained Spearman correlation coefficients between the reference ranking and the one calculated by stochastic methods for the dynamic variant of criteria are 1.0 (HC), 0.9273 (SA), 1.0 (PSO). The accuracy of HC and PSO methods is very high, whereas the simulated expression method has much lower accuracy.
Spearman’s weighted correlation coefficients for stochastic methods for the dynamic variant of criteria are as follows: 1.0 (HC), 0.9537 (SA), 1.0 (PSO). As with Spearman’s correlation coefficients, the weighted coefficients show that the strongest correlation occurs with the hill-climbing algorithm and particle swarm optimization, and the weakest with the simulated overhang method.
correlation coefficients calculated for the preference of the reference testing set and the preference calculated using stochastic methods for the dynamic variant of the criteria are as follows: 1.0 (HC), 0.9885(SA), 1.0 (PSO). The PSO and HC methods have the most substantial relationship between the reference ranking and the calculated one. However, the correlation of the simulated annealing method, as in the case of the rest of the correlation coefficients, is the weakest of the methods considered.
4. Conclusions and Future Research Directions
In this paper, we consider a new approach to the identification of a multi-criteria decision-making model, based on the stochastic optimization technologies. The research carried out has shown that the proposed approach has a very high accuracy for an initial state of 0.5 and the models existing for the two criterion variants under consideration, i.e., static and dynamic. The novelties and contributions are presented as follows. The paper presents an innovative approach, which consists of building a decision-making model based on already evaluated alternatives and stochastic optimization techniques.
The hill-climbing algorithm is best suited for an initial state with a value of 0.5, which is the most accurate for all the tested variants of criteria with existing and non-existent models. The state with a random value is slightly worse and has lower accuracy. On the other hand, the initial states with a value of 0 and 1 have the lowest accuracy of the tested states. Moreover, the state with a value of 0.5 and random needs fewer iterations than the initial state with 0 and 1.
The simulated annealing method is best suited for finding solutions when the start state is 0.5. At this state, the method finds the smallest values of solutions. Initial states with a value of 0 and 1, which are less accurate than those for 0.5 and random states, are much worse. The random value of the starting preference of characteristic objects is characterized by a quite high accuracy, but not higher than when the starting preference is 0.5. It is worth mentioning that with the increase in the number of alternatives to the SA method, the number of iterations needed to find a solution at a random initial state and equal to 0.5 for the existing model decreases. However, solutions found with fewer iterations have a much higher value than those found with more iterations.
Particle swarm optimization with an existing model for dynamic and static criteria values is best performed when the initial state is 1. It has higher accuracy than a random initial state value, 0 or 0.5. Also, it does not need as many iterations as the rest of the initial state values. For a model that does not exist for dynamic criterion values, the starting value of the preference of characteristic objects equal to 0.5 works best. The accuracy of the rest of the initial states is lower than that of the model, but for the number of iterations, the initial states differ slightly. With static values of criteria and a non-existent model, the starting states of 0 and 1 perform best. Their accuracy is slightly higher than when the start preference of the characteristic objects takes a random value or equal to 0.5.
Compared to the HC technique, the SA technique needs more iteration to find a solution, and the solutions found have much more value. On the other hand, in the hill-climbing algorithm, the decrease in the number of iterations with an increase in the number of alternatives does not occur as in the case of the simulated annealing method.
The PSO method, unlike the SA method, needs much smaller numbers of iterations to find a solution, whilst the PSO method needs more iterations compared to the HC method. The number of iterations in particle swarm optimization relative to an increase in the number of alternatives is increasing as in the case of a hill-climbing algorithm.
The correlation coefficients used in the example show that the HC and PSO methods are best suited for identifying a multi-criteria model. On the other hand, the SA method has a worse correlation than them, so that the obtained rankings are far from the ranking of the reference model. The main limitations are that we have researched only the simple case where characteristic objects are constant. We should determine the algorithm of obtained optimal characteristic values. Additionally, empirical case studies should be continued.
The directions for further research should focus on the parameters of the stochastic methods considered to obtain the best possible value of solutions and the smallest possible number of iterations. The issue of iteration numbers in the simulated annealing method should also be looked at because it obtained very high values compared to the hill-climbing algorithm and particle swarm optimization. Furthermore, some tests should be carried out for a more significant number of criteria and their values. The number of sets of decision variants tested should also be more significant to make the results more accurate. Other stochastic methods should also be tested for smaller solution values and fewer iterations.
Author Contributions
Conceptualization, W.S.; methodology, B.K. and W.S.; software, B.K.; validation, B.K. and W.S.; formal analysis, W.S.; investigation, B.K.; resources, B.K.; data curation, B.K.; writing—original draft preparation, B.K. and W.S.; writing—review and editing, B.K. and W.S.; visualization, B.K. and W.S.; supervision, W.S.; project administration, W.S.; funding acquisition, W.S. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by the National Science Centre, Decision No. UMO-2016/23/N/HS4/01931.
Acknowledgments
The authors would like to thank the editor and the anonymous reviewers, whose insightful comments and constructive suggestions helped us to significantly improve the quality of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| EA | Evolutionary Algorithms |
| GA | Genetic Algorithm |
| HC | Hill-Climbing |
| SA | Simulated Annealing |
| PSO | Particle Swarm Optimization |
| MCDA | Multi-Criteria Decision-Analysis |
| COMET | Characteristic Objects METhod |
| MEJ | Matrix of Expert Judgment |
| SJ | vector of the Summed Judgments |
References
- Stojčić, M.; Pamučar, D.; Mahmutagić, E.; Stević, Ž. Development of an ANFIS Model for the Optimization of a Queuing System in Warehouses. Information 2018, 9, 240. [Google Scholar] [CrossRef]
- Jovanović, A.D.; Pamučar, D.S.; Pejčić-Tarle, S. Green vehicle routing in urban zones—A neuro-fuzzy approach. Expert Syst. Appl. 2014, 41, 3189–3203. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S. Numerical Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Törn, A.; Žilinskas, A. Global Optimization; Springer: Berlin/Heidelberg, Germany, 1989; Volume 350. [Google Scholar]
- Sauer, M. Operations Research Kompakt; De Gruyter: Berlin, Germany, 2020. [Google Scholar]
- Ehrgott, M. Multicriteria Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005; Volume 491. [Google Scholar]
- Miettinen, K. Nonlinear Multiobjective Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 12. [Google Scholar]
- Ćirović, G.; Pamučar, D.; Božanić, D. Green logistic vehicle routing problem: Routing light delivery vehicles in urban areas using a neuro-fuzzy model. Expert Syst. Appl. 2014, 41, 4245–4258. [Google Scholar] [CrossRef]
- Muravev, D.; Hu, H.; Zhou, H.; Pamucar, D. Location Optimization of CR Express International Logistics Centers. Symmetry 2020, 12, 143. [Google Scholar] [CrossRef]
- Softić, E.; Radičević, V.; Subotić, M.; Stević, Ž.; Talić, Z.; Pamučar, D. Sustainability of the Optimum Pavement Model of Reclaimed Asphalt from a Used Pavement Structure. Sustainability 2020, 12, 1912. [Google Scholar] [CrossRef]
- Horst, R.; Pardalos, P.M. Handbook of Global Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 2. [Google Scholar]
- Floudas, C.A. Deterministic Global Optimization: Theory, Methods and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 37. [Google Scholar]
- Leyffer, S. Deterministic Methods for Mixed Integer Nonlinear Programming. Ph.D. Thesis, University of Dundee, Dundee, Scotland, 1993. [Google Scholar]
- Lin, M.H.; Tsai, J.F.; Yu, C.S. A review of deterministic optimization methods in engineering and management. Math. Probl. Eng. 2012, 2012. [Google Scholar] [CrossRef]
- Boender, C.G.E.; Romeijn, H.E. Stochastic methods. In Handbook of Global Optimization; Springer: Berlin/Heidelberg, Germany, 1995; pp. 829–869. [Google Scholar]
- Kan, A.R.; Timmer, G. Stochastic methods for global optimization. Am. J. Math. Manag. Sci. 1984, 4, 7–40. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S.; Fong, S.; He, X.; Zhao, Y.X. From swarm intelligence to metaheuristics: Nature-inspired optimization algorithms. Computer 2016, 49, 52–59. [Google Scholar] [CrossRef]
- Erten, H.I.; Deveci, H.; Artem, H.S. Stochastic Optimization Methods. In Designing Engineering Structures Using Stochastic Optimization Methods; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Zabinsky, Z.B. Random search algorithms. Wiley Encyclopedia of Operations Research and Management Science; John Wiley and Sons Ltd.: Hoboken, NJ, USA, 2010. [Google Scholar]
- Zhigljavsky, A.; Zilinskas, A. Stochastic Global Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007; Volume 9. [Google Scholar]
- Kaveh, A. Advances in Metaheuristic Algorithms for Optimal Design of Structures; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Sörensen, K.; Glover, F. Metaheuristics. Encycl. Oper. Res. Manag. Sci. 2013, 62, 960–970. [Google Scholar]
- Lones, M.A. Metaheuristics in nature-inspired algorithms. In Proceedings of the Companion Publication of the 2014 Annual Conference on Genetic and Evolutionary Computation, Vancouver, BC, Canada, 12–16 July 2014; pp. 1419–1422. [Google Scholar]
- Selman, B.; Gomes, C.P. Hill-climbing search. Encycl. Cogn. Sci. 2006, 81, 82. [Google Scholar]
- Kvasnicka, V.; Pelikán, M.; Pospichal, J. Hill climbing with learning (an abstraction of genetic algorithm). In Neural Network World, 6; Citeseer: Slovak Technical University, Bratislava, Slovakia, 1995. [Google Scholar]
- Van Laarhoven, P.J.; Aarts, E.H. Simulated annealing. In Simulated Annealing: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 1987; pp. 7–15. [Google Scholar]
- Lukovac, V.; Pamučar, D.; Popović, M.; Đorović, B. Portfolio model for analyzing human resources: An approach based on neuro-fuzzy modeling and the simulated annealing algorithm. Expert Syst. Appl. 2017, 90, 318–331. [Google Scholar] [CrossRef]
- Dowsland, K.A.; Thompson, J. Simulated annealing. In Handbook of Natural Computing; Springer: Berlin/Heidelberg, Germany, 2012; pp. 1623–1655. [Google Scholar]
- Bertsimas, D.; Tsitsiklis, J. Simulated annealing. Stat. Sci. 1993, 8, 10–15. [Google Scholar] [CrossRef]
- Sahoo, R.K.; Ojha, D.; Dash, S. Nature Inspired Metaheuristic Algorithms—A Comparative Review. Int. J. Dev. Res. 2016, 6, 8427–8432. [Google Scholar]
- Yang, X.S. Nature-Inspired Metaheuristic Algorithms; Luniver Press: London, UK, 2010. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Abdmouleh, Z.; Gastli, A.; Ben-Brahim, L.; Haouari, M.; Al-Emadi, N.A. Review of optimization techniques applied for the integration of distributed generation from renewable energy sources. Renew. Energy 2017, 113, 266–280. [Google Scholar] [CrossRef]
- Więckowski, J.; Kizielewicz, B.; Kołodziejczyk, J. Application of Hill Climbing Algorithm in Determining the Characteristic Objects Preferences Based on the Reference Set of Alternatives. In Proceedings of the International Conference on Intelligent Decision Technologies, Split, Croatia, 17–19 June 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 341–351. [Google Scholar]
- Więckowski, J.; Kizielewicz, B.; Kołodziejczyk, J. The Search of the Optimal Preference Values of the Characteristic Objects by Using Particle Swarm Optimization in the Uncertain Environment. In Proceedings of the International Conference on Intelligent Decision Technologies, Split, Croatia, 17–19 June 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 353–363. [Google Scholar]
- Więckowski, J.; Kizielewicz, B.; Kołodziejczyk, J. Finding an Approximate Global Optimum of Characteristic Objects Preferences by Using Simulated Annealing. In Proceedings of the International Conference on Intelligent Decision Technologies, Split, Croatia, 17–19 June 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 365–375. [Google Scholar]
- Žižović, M.; Pamučar, D.; Albijanić, M.; Chatterjee, P.; Pribićević, I. Eliminating Rank Reversal Problem Using a New Multi-Attribute Model—The RAFSI Method. Mathematics 2020, 8, 1015. [Google Scholar] [CrossRef]
- Faizi, S.; Sałabun, W.; Ullah, S.; Rashid, T.; Więckowski, J. A New Method to Support Decision-Making in an Uncertain Environment Based on Normalized Interval-Valued Triangular Fuzzy Numbers and COMET Technique. Symmetry 2020, 12, 516. [Google Scholar] [CrossRef]
- Palczewski, K.; Sałabun, W. Identification of the football teams assessment model using the COMET method. Procedia Comput. Sci. 2019, 159, 2491–2501. [Google Scholar] [CrossRef]
- Podvezko, V. The comparative analysis of MCDA methods SAW and COPRAS. Eng. Econ. 2011, 22, 134–146. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z. Multiple criteria decision making (MCDM) methods in economics: An overview. Technol. Econ. Dev. Econ. 2011, 17, 397–427. [Google Scholar] [CrossRef]
- Wątróbski, J.; Jankowski, J.; Ziemba, P.; Karczmarczyk, A.; Zioło, M. Generalised framework for multi-criteria method selection. Omega 2019, 86, 107–124. [Google Scholar] [CrossRef]
- Sałabun, W.; Piegat, A. Comparative analysis of MCDM methods for the assessment of mortality in patients with acute coronary syndrome. Artif. Intell. Rev. 2017, 48, 557–571. [Google Scholar] [CrossRef]
- Sałabun, W.; Palczewski, K.; Wątróbski, J. Multicriteria approach to sustainable transport evaluation under incomplete knowledge: Electric Bikes Case Study. Sustainability 2019, 11, 3314. [Google Scholar] [CrossRef]
- Si, A.; Das, S.; Kar, S. An approach to rank picture fuzzy numbers for decision making problems. Decis. Mak. Appl. Manag. Eng. 2019, 2, 54–64. [Google Scholar] [CrossRef]
- Faizi, S.; Sałabun, W.; Rashid, T.; Wątróbski, J.; Zafar, S. Group decision-making for hesitant fuzzy sets based on characteristic objects method. Symmetry 2017, 9, 136. [Google Scholar] [CrossRef]
- Faizi, S.; Rashid, T.; Sałabun, W.; Zafar, S.; Wątróbski, J. Decision making with uncertainty using hesitant fuzzy sets. Int. J. Fuzzy Syst. 2018, 20, 93–103. [Google Scholar] [CrossRef]
- Jankowski, J.; Sałabun, W.; Wątróbski, J. Identification of a multi-criteria assessment model of relation between editorial and commercial content in web systems. In Multimedia and Network Information Systems; Springer: Berlin/Heidelberg, Germany, 2017; pp. 295–305. [Google Scholar]
- Piegat, A.; Sałabun, W. Identification of a multicriteria decision-making model using the characteristic objects method. Appl. Comput. Intell. Soft Comput. 2014, 2014. [Google Scholar] [CrossRef]
- Sha, Z.C.; Huang, Z.T.; Zhou, Y.Y.; Wang, F.H. Blind spreading sequence estimation based on hill-climbing algorithm. In Proceedings of the 2012 IEEE 11th International Conference on Signal Processing, Beijing, China, 21–25 October 2012; IEEE: Piscataway, NJ, USA, 2012; Volume 2, pp. 1299–1302. [Google Scholar]
- Shehab, M.; Khader, A.T.; Al-Betar, M.A.; Abualigah, L.M. Hybridizing cuckoo search algorithm with hill climbing for numerical optimization problems. In Proceedings of the 2017 8th International Conference on Information Technology (ICIT), Amman, Jordan, 17 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 36–43. [Google Scholar]
- Arora, J.S. 15—Discrete Variable Optimum Design Concepts and Methods. In Introduction to Optimum Design, 2nd ed.; Arora, J.S., Ed.; Academic Press: San Diego, CA, USA, 2004; pp. 513–530. [Google Scholar] [CrossRef]
- Trelea, I.C. The particle swarm optimization algorithm: Convergence analysis and parameter selection. Inf. Process. Lett. 2003, 85, 317–325. [Google Scholar] [CrossRef]
- Van den Bergh, F.; Engelbrecht, A.P. A cooperative approach to particle swarm optimization. IEEE Trans. Evol. Comput. 2004, 8, 225–239. [Google Scholar] [CrossRef]
- Ganguly, S. Multi-objective distributed generation penetration planning with load model using particle swarm optimization. Decis. Mak. Appl. Manag. Eng. 2020, 3, 30–42. [Google Scholar] [CrossRef]
- Sałabun, W.; Urbaniak, K. A new coefficient of rankings similarity in decision-making problems. In International Conference on Computational Science; Springer: Cham, Switzerland, 2020. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).