Clustering Stock Performance Considering Investor Preferences Using a Fuzzy Inference System

Abstract

The fact that many stocks are traded in the marketplace makes the selection process of choosing the right stocks for investment crucial and challenging. In the literature on stock selection, cluster analysis-based methods have usually been used to group and to determine the best stock for investment. Many established cluster analysis-based methods often cluster stocks under consideration using the average of the variables, where stocks with similar scores are concluded as having the same performances. Nevertheless, the performance results obtained do not reflect the actual performance of the stocks. Depending only on the average score of each variable is inefficient, as market situations usually involve uncertain extreme values. Moreover, when grouping stock performance, the established clustering methods assume that investors’ selection preferences are single and unclear, when actually, in reality, investors’ selection preferences vary; some investors are pessimistic, while others may be more optimistic. Due to this issue, this paper presents a novel fuzzy clustering method using a fuzzy inference system to flexibly assess the consistent evaluations given to stock performance that differentiate between pessimistic and optimistic investors that are symmetrical in nature. All variables considered in this study were defined in terms of linguistic inputs, where the consensus among them was aggregated using rule bases. These rule bases provide assistance in obtaining the linguistic output, which is the actual performance of the stock. Next, each stock under consideration was ranked using the proposed novel stock selection strategy based on investors’ confidence levels and preferences. The proposed method was then applied to a case study of 30 Syariah stocks listed on the Malaysian stock exchange, where the results obtained were empirically validated with established cluster analysis-based methods.

1. Introduction

Stocks traded on the financial market are often observed as unpredictable and unstable. This is due to the uncertain fluctuations of the daily prices of stocks, which leads to hesitance in the process of selecting the right stocks to invest in [1,2,3]. Dubious investors’ selection preferences due to the hefty identification of the well-balanced interaction between risks and returns also contribute toward indefinite stock selection [1]. In making investment decisions regarding stock selection, investors usually aim to select stocks when both the risks and the returns are consistent, such that the prior is low and the latter is high [1,4]. Stocks providing high returns and low risks are ranked as profitable investments by investors [3,4].

In the literature of modern portfolio theory, the initial stock selection approach developed for investment focuses on clustering stocks based on risk tolerance and return expectations [3,5,6,7,8]. When employing this approach, risk is measured using variance, while asset return data are assumed to be normally distributed. However, this is misleading, as the risk measures obtained are not consistent with investors’ preferences and the assumption made on the asset return data is invalid for a real market scenario, which are actually left or right-skewed [2,9]. Thus, methods based on cluster analysis are presented as alternative stock selection approaches that aim at clustering multiple best stocks simultaneously, otherwise known as the optimal portfolio [1,10]. The established clustering analysis-based methods, such as k-means and hierarchical, generally cluster stocks based on the averages of variables involved, where stocks with similar average scores are presumed as having the same performances [4]. Among the advantages of using these methods in stock clustering are the reduced time taken to develop the optimal portfolio given many diverse stocks, the important investment-related information made available to investors, and the minimal risk level obtained on the optimal portfolio [7,8,11].

In the past two decades, clustering equities (i.e., stock and mutual funds) have received global attention from researchers utilizing numerous clustering techniques to study their local market situations [4,6,10,11,12,13]. A survey conducted by Chen and Huang [4] on Taiwan’s mutual funds used the k-means clustering method. In the evaluation, the funds were measured based on the return rates, standard deviation, turnover rate, and Treynor index, where the results obtained were clustered into four clustering performance groups—namely, inferior, stable, good, and aggressive. Among the four clustering performance groups, the researchers considered good and aggressive performances as the best group of funds for investment. Similarly, Kiliçman and Sivalingam [3] used 38 funds to examine the performance of the Malaysian stock market using the return rate, Treynor index, and variance. Employing the same method used by Chen and Huang [4], Mirnoori and Shariati [7] studied 39 funds and formed three clusters designated as inferior, good, and aggressive. Although these clustering methods have distinct procedures for obtaining the best stock or optimal portfolio, both achieve equivalent clustering results for investment [4]. Nevertheless, the performance results obtained by known established methods do not reflect the actual performance of stocks. Actual stock performance depends on its market situations, which are volatile in nature, by taking the outcome using average scores of each variable, although this is deemed to be insufficient when there exist extreme values of returns and risks [14,15,16]. In addition, the average score tends to be influenced by outliers [17,18].

In the literature, k-means clustering is the most applied clustering method [4,10]. A study on the Indian stock market by Nanda et al. [10] carried out analysis based on three distinct clustering methods, namely, k-means, self-organizing maps (SOMs), and fuzzy c-means clustering, that were applied to the Markowitz model to generate an efficient portfolio. The results show that k-means clustering is the best clustering method, as it produced 12 clusters. Instead of using the k-means clustering method, Tekin and Gümüş [6] used the hierarchical clustering method to evaluate the stock performance in Borsa Istanbul. The variables considered were the price per earnings ratio, the market value per book value ratio, the dividend yield, the return on assets, the return on equity, the change in sales and equity, the return on average, the returns, and the risks, producing 12 clusters. Meanwhile, Alqaryouti et al. [11] studied the Abu Dhabi stocks using the k-means and k-medoids clustering methods, testing 61 stocks and forming four distinct clusters.

K-means clustering is favored among researchers; however, the clustering results of this method depend on the initial value assigned, and this value needs to be predetermined, which is a disadvantage of this method [17,18]. This leads to inconsistency in forming clusters, depending on the situation. Another limitation is that the method is sensitive to outliers [17,18]. Other research [12,19] of cluster stocks was based on the individual stock performance, by comparing the values of the variables considered for each stock one by one. The main reason for evaluating stock performance individually is to consider their effects on fundraising by non-professional investors [19]. In [12], the authors evaluated the performance of 10 sectorial stock indices individually, using the Sharpe, Treynor, Jensen alpha, adjusted Sharpe, adjusted Jensen, and Sortino indices. Unfortunately, it is time consuming to analyze stocks one at a time, and thus, this concept is unsuitable for large data sets.

Apart from the variables that are related to stocks, investors’ preferences toward risk-taking have also been considered as one of the most important factors for evaluating stock performance. Shams and Rezvani [20] investigated investors’ risk aversion and risk taking by ranking the performance of investment companies using three loss aversion indices and comparing the results against the Treynor index. The result shows that the loss aversion behavior of investment companies is influenced by the outcome of previous performances. In [21], multiple hybrid methods were developed by combining SOM and k-means cluster stocks, the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) to rank stocks, and the genetic algorithm to establish different classes of investors with respect to their risk-taking levels.

The established clustering methods in the literature consider several options to ensure that the stocks preferred by investors are good and the best to invest in. Among investors’ preferences studied are stocks that have high return rates, low standard deviation and high Treynor index values [3,4], low standard deviations, moderate return rates, moderate turnover ratios, and moderate Sortino index values [7], or high return rates, high Sharpe index values, high appraisal ratios, high Sortino index values, low standard deviations, and downside risks [8]. However, investors’ preferences considered by these methods are ambiguous, since such evaluation focuses only on one unknown investor’s selection preference when clustering stock performance. These evaluations are inconsistent with investors’ genuine preferences, which can be either pessimistic or optimistic in nature; thus, clustering methods are unable to track the true performance of stocks [2,22]. The inefficiencies of the established clustering methods justify the motivation for this study.

As indicated above, the established clustering methods neglect to take into consideration the importance of diverse investors’ preferences when selecting stocks, and thus are inefficient in accurately clustering stocks. This study extends the works of [4,6] by proposing a novel fuzzy clustering method that has the capability to distinctively express investors’ vague preferences which establish clustering methods cannot capture. Furthermore, investors’ diverse preferences, which can be distinguished in various forms, such as pessimistic or optimistic, enhance and complement fuzzy inference systems for developing specific stock selection strategies for different types of investors. A fuzzy inference system was utilized in this study, as it possesses great capability for considering vague decision-makers’ preferences, as well as the uncertainty in the decision-making environment [23,24]. In this proposed method, the variables considered were defined as the linguistic inputs, while stock performance was defined as the linguistic output. All defined linguistic inputs were then aggregated using fuzzy rule bases that were developed in accordance with established investors’ preferences on stock clustering. In this case, rule base development is important to achieve rational interaction between the variables and the performances of stocks that are defined linguistically based on investors’ preferences [23,24]. As for the output, the proposed method produces two distinct views of investors’ preferences, which are pessimistic and optimistic, with each view consisting of multiple levels of investors’ preferences differentiated based on confidence levels and the frequency of stock performance. The novel differentiation process in this study is the first of its kind to be developed with the objective of assisting investors in selecting the best stock to invest, given their preferences. For efficiency purposes, the results obtained from the analysis of this proposed method were compared against the established clustering methods.

The rest of the paper is structured as follows. Section 2 explains the development of the novel proposed fuzzy clustering method. Section 3 presents a case study on clustering 30 Syariah-compliant stocks in Malaysia for the year 2011, and then validation of the results is provided in Section 4. The discussion and conclusion are presented in Section 5 and Section 6, respectively.

2. Research Formulation

As mentioned in the introduction section, previous works on clustering were unable to handle outliers, providing inconsistent numbers of clusters and neglecting investor’s preferences. Taking into consideration the limitations of previous studies, in this study, a novel fuzzy clustering method that is capable of distinctively expressing vague investors’ preferences is presented. Furthermore, investors’ diverse preferences, which can be distinguished in various forms, such as pessimistic or optimistic, enhance and complement fuzzy inference systems for developing specific stock selection strategies for different types of investors.

The development of the novel proposed fuzzy clustering method using a fuzzy inference system involved four steps. The first step was data collection and the identification of the inputs and outputs, as well as normalization. In this step, the inputs were variables related to the stocks—namely, return rates, standard deviations and Treynor index values—while stock performance served as the output. All inputs and outputs were then normalized to ensure that the data were in generic forms. In the second step, the results obtained from the normalization process were transformed into triangular fuzzy numbers—this process is known as fuzzification. All normalized inputs and outputs defined were in the form of linguistics terms described as triangular fuzzy numbers. For step 3, processes such as fuzzy rule base, fuzzy inference system, and defuzzification were performed. Fuzzy rule bases were developed based on the results of [3,4,7,8] and characterized by IF THEN rules. These rule bases were then aggregated in the fuzzy inference system, and the products were converted into crisp values that represent stock performance. This conversion process is known as defuzzification. The defuzzification process covers the limitation of outliers and inconsistent numbers of clusters. In step 4, the results obtained from defuzzification were projected according to confidence levels, where the confidence levels represent the actual levels of investors’ preferences. This step covered the limitation of neglecting investors’ preferences. For the purpose of distinguishing each stock based on its performance and on investors’ confidence levels, this study presents a unique stock selection strategy, whereby the best stocks are ranked based on investors’ preference priority. A flowchart on the development of the novel proposed fuzzy clustering method is given in Figure 1. The steps involved in the development of the novel proposed fuzzy clustering method are described below.

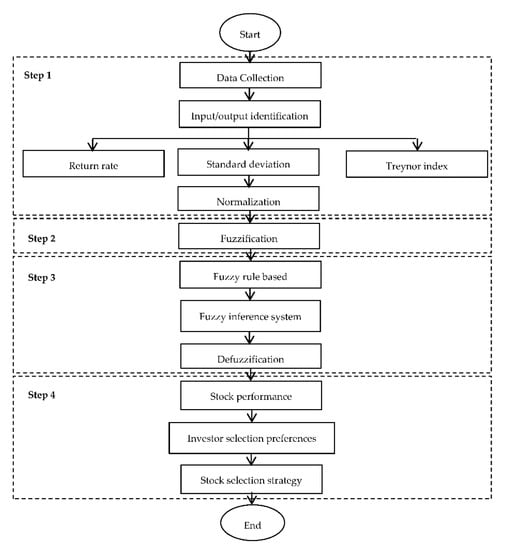
Figure 1. Flowchart of the novel proposed fuzzy clustering method.

2.1. Step 1: Data Collection, Input and Output Identification, and Normalization

This study started with data collection, where information related to the input and output variables was identified. The inputs were return rates, standard deviations, and Treynor index values, while the output was the stock performance. Based on [4,12,25,26], a definition for each input variable is given, as follows.

Definition 1.

Return rates,$R_t$: The return rate,$R_t$, is the return gained from investment. A high value of$R_t$indicates a high profit gain, and thus positive stock performance is a good sign for investors. As Chen and Huang [4] demonstrated,$R_t$is defined based on the concept of net asset value (NAV), where the definition of$R_t$is given as follows:

$$R_t=\frac{NA{V}_t-NA{V}_{t-1}}{NA{V}_{t-1}}\times 100\%$$

(1)

where$R_t$is the return rate for stock t,$NA{V}_t$is the net asset value for the current transaction, and$NA{V}_{t-1}$is the net asset value of the previous transaction.

Definition 2.

Standard Deviation,$S_t$: Standard deviation,$S_t$, measures the volatility of returns denoted as the investment risk level [4,25]. The standard deviation,$S_t$, can be calculated using Equation (2), shown as follows:

$$S_t=\sqrt{\frac{{\displaystyle \sum _{t=1}^n{\left(R_{ti}-{\overline{R}}_t\right)}^2}}{n-1}}$$

(2)

where$R_{ti}$is the rate return of stock t on the ith day, and${\overline{R}}_t$is the average return rate for n period of time.

Definition 3.

Treynor Index,$T_t$: The Treynor index,$T_t$, is a measure of the excess return earned per unit of systematic risk [4]. The Treynor index was chosen in this study as it examines the stock portfolio against the market as a whole and is highly sensitive to market risk [12,26]. A high value of$T_t$denotes a high return per market risk [4]. The Treynor index is given by Equation (3), as follows:

$$T_t=\frac{{\overline{R}}_t-{\overline{R}}_{rf}}{\beta }.$$

(3)

where$\beta$is the systematic risk or the market risk, and${\overline{R}}_{rf}$is the daily average risk-free rate for a week.

As mentioned earlier, step 1 of the novel proposed fuzzy clustering method involved the normalization process. In this case, all of the values obtained from the inputs were normalized using the following definition.

Definition 4.

Normalization,${{\varpi }^{\prime }}_i$: Let${\varpi }_i^{\prime }$be the normalization of input variables [9] with$i={R^{\prime }}_t,{S^{\prime }}_t \mathrm{and} {T^{\prime }}_t$, and${\varpi }_i^{\prime }$is given as

$${\varpi }_i^{\prime }=\frac{{\varpi }_i-Min\left({\varpi }_{i,j}\right)}{Ma{x}_j\left({\varpi }_{i,j}\right)-Min\left({\varpi }_{i,j}\right)}$$

(4)

where$Mi{n}_i\left({\varpi }_{i,j}\right)$and$Ma{x}_i\left({\varpi }_{i,j}\right)$is the minimum and maximum$i$with$j=1,2,3\cdots n$respectively.

With respect to all inputs defined above, all variables were normalized using Equation (4), as shown in Equations (5)–(7):

$$R_t\to {R^{\prime }}_t$$

(5)

$$S_t\to {S^{\prime }}_t$$

(6)

$${T^{\prime }}_t\to {T^{\prime }}_t$$

(7)

where ${R^{\prime }}_t$, ${S^{\prime }}_t$ and ${T^{\prime }}_t$ are the values of normalization for the return rates, standard deviations, and Treynor index values, respectively.

2.2. Step 2: Fuzzification

The results obtained from the normalization process in step 1 were then transformed into linguistic triangular fuzzy numbers shown by Equations (8)–(10).

$${R^{\prime }}_t\to R_t^{\ast }=\left(a_{R_t^{\ast }},b_{R_t^{\ast }},c_{R_t^{\ast }};1\right)$$

(8)

$${S^{\prime }}_t\to S_t^{\ast }=\left(a_{S_t^{\ast }},b_{S_t^{\ast }},c_{S_t^{\ast }};1\right)$$

(9)

$${T^{\prime }}_t\to T_t^{\ast }=\left(a_{T_t^{\ast }},b_{T_t^{\ast }},c_{T_t^{\ast }};1\right)$$

(10)

where $R_t^{\ast }$, $S_t^{\ast }$, and $T_t^{\ast }$ are the linguistic triangular fuzzy numbers for the return rates, standard deviations and Treynor index values, respectively. Figure 2 shows the generic linguistic triangular fuzzy numbers for $R_t^{\ast }$.

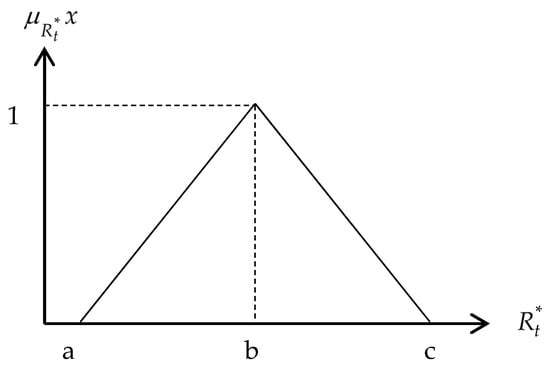
Figure 2. Triangular fuzzy number.

Where $a$ and $c$ are the minimum and maximum values, respectively, while $b$ is the modal value of the triangular fuzzy numbers [27,28].

2.3. Step 3: Fuzzy Rule Base, Fuzzy Inference System, and Defuzzification

In this step, rule bases in the form of linguistic terms were developed based on established stock performance decisions [23,24,29,30,31]. All inputs in step 2 were aggregated using the rule bases developed in this step and the output obtained represent the performance of the stocks. It is worth noting that the output produced underwent defuzzification where the linguistic triangular fuzzy numbers were transformed into crisp values. The interaction between the inputs, fuzzy rule bases, and outputs are generically given as follows:

• IF$R_t^{\ast }$is ….AND$S_t^{\ast }$is ….AND$T_t^{\ast }$is …. THEN …. Performance.

2.4. Step 4: Stock Performance, Investor Selection Preferences and Stock Selection Strategy

The stock performance obtained from the defuzzification process in step 3 was expressed as a single value; this value represents investors’ evaluation of the stocks. The evaluation was then projected onto the height of the linguistics triangular fuzzy numbers, where the two confidence levels were obtained. The confidence level represents the selection preferences of two types of investors, namely, pessimistic and optimistic investors. To distinguish the stocks in accordance to investors’ preference priority, a stock selection strategy was developed, and is displayed using Equation (11):

$$\mathrm{Investors}’ \mathrm{preferences} \mathrm{priority}, P=\left({\displaystyle \sum _{k=1}^4{w}_k{b}_k}\right)\cdot {\overline{c}}_l$$

(11)

where $w_k$ is the weight of the performance, $b_k$ is the number of performances obtained for the stock, $k$ is the stock performance, and ${\overline{c}}_l$ is the average of the confidence levels for stock performance.

3. Clustering Malaysia’s Stock Market

According to [32], in studies to develop a model, selecting perfect data for model illustration is not a key factor; it is sufficient to use a sample of real data to illustrate the realistic scenario of investment. As a small economy, Malaysia is vulnerable to global and regional developments, and in Malaysia a stock market crash led to economic downturn. The global downturn of the 2007 financial crisis hit Malaysia hard, and the market took about 3 years to recover to its pre-crisis level. In this study, data of the year 2011 were considered when the stock market started to recover [33] to observe investors’ preferences towards stocks selection that were not affected by the crisis. Generally, the proposed fuzzy clustering method can be applied to any data set, as carried out by [3,34] by employing a small sample and a shorter time frame for evaluating stock performance. Thus, consistent with previous studies where the objective was to present a novel clustering method, the capability of this novel method was demonstrated by employing real data of 30 stocks listed on Bursa Malaysia. These 30 stocks are listed under the Syariah category of consumer products and services sector, a dominant sector observed by the masses [35,36]. The details of the processes involved in the application of the proposed model are given below.

3.1. Step 1: Data Collection, Input/Output Identification and Normalization

In this study, data of 30 Syariah compliant companies listed under the consumer products and services sector from 3rd January 2011 to 30th December 2011 were collected. The data of the 30 stocks considered comprised stock prices, return rates, $R_t$, standard deviations, $S_t$, and Treynor index values, $T_t$, as the input variables, while stock performance served as the output for this investigation. The companies’ stock prices were derived from DataStream, while the Syariah and Kuala Lumpur Composite Index (KLCI) indices are from Bursa Malaysia. Table 1 shows part of the variables evaluated for Aeon Co (M) Bhd, one of the 30 stocks examined.

Table 1. The evaluation variables for Aeon Co (M) Bhd.

Date	Stock Price	${\mathit{R}}_{\mathit{t}}$	${\mathit{S}}_{\mathit{t}}$	${\mathit{T}}_{\mathit{t}}$
18/3/11	1.45	−0.74	0.95	−15.51
25/3/11	1.49	0.65	0.89	12.75
1/4/11	1.47	−0.29	1.00	−7.07
8/4/11	1.50	0.37	0.62	3.59
15/4/11	1.55	0.72	2.15	10.73
22/4/11	1.57	0.29	3.11	2.14
29/4/11	1.49	−1.05	2.76	−25.27
6/5/11	1.50	0.18	0.60	−0.09
13/5/11	1.55	0.67	1.77	9.99
20/5/11	1.59	0.54	0.44	7.28
27/5/11	1.61	0.25	0.44	1.44
3/6/11	1.61	0.00	0.35	−3.66
10/6/11	1.70	1.04	0.94	17.46
17/6/11	1.96	2.91	3.33	55.71
24/6/11	1.78	−1.83	2.56	−40.99

Using the values from Equation (4), each variable was normalized, as displayed in Table 2.

Table 2. Normalization values of the variables for Aeon Co (M) Bhd.

Date	${{\mathit{R}}^{\prime }}_{\mathit{t}}$	${{\mathit{S}}^{\prime }}_{\mathit{t}}$	${{\mathit{T}}^{\prime }}_{\mathit{t}}$
18/3/11	0.23	0.28	0.26
25/3/11	0.52	0.27	0.56
1/4/11	0.32	0.30	0.35
8/4/11	0.46	0.19	0.46
15/4/11	0.54	0.65	0.53
22/4/11	0.45	0.93	0.45
29/4/11	0.16	0.83	0.16
6/5/11	0.42	0.18	0.42
13/5/11	0.53	0.53	0.53
20/5/11	0.50	0.13	0.50
27/5/11	0.44	0.13	0.44
3/6/11	0.39	0.11	0.39
10/6/11	0.60	0.28	0.60
17/6/11	1.00	1.00	1.00
24/6/11	0.00	0.77	0.00

3.2. Step 2: Fuzzification

The normalization results obtained in step 1 were transformed into linguistic triangular fuzzy numbers, where they were defined in linguistic terms as very high, high, moderate, low, and very low for the input variables, while for outputs, the linguistic terms were inferior, stable, good, and aggressive. Table 3 and Table 4 describe the linguistic terms and their respective triangular fuzzy numbers for the inputs and outputs, respectively.

Table 3. Linguistic terms and triangular fuzzy numbers for the inputs.

Linguistic Terms	Triangular Fuzzy Number
Very low	[0, 0, 0.2511]
Low	[0, 0.2511, 0.5]
Moderate	[0.2511, 0.5, 0.7511]
High	[0.5, 0.7511, 1]
Very high	[0.7511, 1, 1]

Table 4. Linguistic terms and triangular fuzzy numbers for the output variables.

Performance	Triangular Fuzzy Number
Inferior	[0, 0, 0.3333]
Stable	[0, 0.3333, 0.6667]
Good	[0.3333, 0.6667, 1]
Aggressive	[0.6667, 1, 1]

3.3. Step 3: Fuzzy Rule Base, Fuzzy Inference System, and Defuzzification

In this step, fuzzy rule bases were developed to aggregate the inputs considered. These rule bases were obtained based on the results achieved from past known works [3,4,7,8]. In total, there were 125 rule bases developed, utilizing the five linguistics terms for the input variables and the four linguistic terms for the output variables defined in step 2. Some of the rules generated for Aeon Co (M) Bhd are given below.

• IF${R^{\prime }}_t$is very lowAND${S^{\prime }}_t$is lowAND${T^{\prime }}_t$is highTHENinferior stock performance.
• IF${R^{\prime }}_t$is highAND${S^{\prime }}_t$is highAND${T^{\prime }}_t$is very highTHENaggressive stocks performance.
• IF${R^{\prime }}_t$is highAND${S^{\prime }}_t$is lowAND${T^{\prime }}_t$is very highTHENgood stocks performance.
• IF${R^{\prime }}_t$is moderateAND${S^{\prime }}_t$is moderateAND${T^{\prime }}_t$is highTHENstable stocks performance.

3.4. Step 4: Stock Performance, Investor Selection Preferences, and Stock Selection Strategy

The results of the stock performance acquired in step 3 are presented in the form of a single value. Table 5 gives the results for the stock performance and the confidence levels with respect to the pessimistic and optimistic investors for Aeon Co (M) Bhd.

Table 5. Results of the stock performance and investors’ confidence levels for Aeon Co (M) Bhd.

Performance	Pessimistic	Confidence Level	Optimistic	Confidence Level
0.332	Inferior	0.004	Stable	0.996
0.426	Good	0.279	Stable	0.721
0.422	Good	0.267	Stable	0.733
0.428	Good	0.285	Stable	0.715
0.418	Good	0.255	Stable	0.745
0.242	Inferior	0.274	Stable	0.726
0.119	Stable	0.357	Inferior	0.643
0.442	Good	0.327	Stable	0.673
0.39	Good	0.171	Stable	0.829
0.495	Good	0.486	Stable	0.514
0.495	Good	0.486	Stable	0.514
0.516	Stable	0.451	Good	0.549
0.473	Good	0.420	Stable	0.580
0.892	Good	0.324	Aggressive	0.676
0.109	Stable	0.327	Inferior	0.673

To determine the overall performance of a specific stock given by different types of investors, the performance frequency for the stocks was evaluated. Table 6 shows part of the performance evaluation for 10 stocks.

Table 6. The performance evaluation for 10 stocks.

Stocks/Investor Preferences	Pessimistic				Optimistic
	I	S	G	A	I	S	G	A
Aeon Co (M) Bhd	5	13	34	0	3	40	8	1
Asia Brands Bhd	4	12	35	1	1	31	20	0
CAM Resources Bhd	1	18	33	0	2	32	18	0
CWG Holdings Bhd	2	30	17	3	3	20	29	0
Classic Century Bhd	1	20	29	2	1	25	26	0
AHB Holdings Bhd	17	9	26	0	2	42	7	1
Asia File Corporation Bhd	5	16	31	0	1	27	23	1
Euro Holdings Bhd	6	9	37	0	2	45	5	0
Emico Holdings Bhd	41	5	6	0	1	50	0	1
Eurospan Holdings Bhd	0	19	32	1	1	31	20	0

Note: I, inferior; S, stable, G, good; A, aggressive.

Based on Table 6, the performance that emerges most frequently indicates the actual performance of the stock. In this case, Aeon Co (M) is considered to have good performance from the point of view of pessimistic investors, while optimistic investors classify the stock performance as stable. Table 7 provides the results of the stock performance for all 30 stocks evaluated, as well as the confidence level average based on both pessimistic and optimistic investors.

Table 7. Performance evaluation results for the 30 stocks and the confidence levels of the investors.

Stocks/Investor Preferences	Pessimistic		Optimistic
	Performance	CL	Performance	CL
Asia Brands Bhd	Good	0.281	Stable	0.756
Aeon Co (M) Bhd	Good	0.305	Stable	0.740
CAM Resources Bhd	Good	0.300	Stable	0.780
CWG Holdings Bhd	Stable	0.163	Good	0.880
Classic Century Bhd	Good	0.305	Good	0.799
AHB Holdings Bhd	Good	0.503	Stable	0.813
Asia File Corporation Bhd	Good	0.503	Stable	0.764
Euro Holdings Bhd	Good	0.309	Stable	0.744
Emico Holdings Bhd	Inferior	0.062	Stable	0.918
Eurospan Holdings Bhd	Good	0.366	Stable	0.655
Federal International Holdings	Inferior	0.078	Stable	0.892
Poh Huat Resources Holdings Bhd	Good	0.261	Stable	0.779
Paragon Union Bhd	Good	0.309	Stable	0.769
Ni Hsin Resources Bhd	Good	0.366	Stable	0.737
Khind Holdings Bhd	Good	0.298	Stable	0.762
SWS Capital Bhd	Good	0.320	Stable	0.709
Sand Nisko Capital Bhd	Good	0.254	Stable	0.817
SHH Resources Holdings Bhd	Good	0.439	Stable	0.576
Latitude Tree Holdings Bhd	Good	0.389	Stable	0.775
Milux Corporation Bhd	Stable	0.185	Good	0.859
Homeritz Corporation Bhd	Stable	0.446	Stable	0.748
Yoong Onn Corporation Bhd	Good	0.306	Stable	0.737
Lee Swee Kiat Group Bhd	Good	0.327	Stable	0.775
Tafi Industries Bhd	Stable	0.426	Good	0.669
Parkson Holdings Bhd	Good	0.324	Stable	0.711
Lii Hen Resources Bhd	Good	0.597	Good	0.811
Syf Resources Bhd	Good	0.282	Stable	0.811
Jaycorp Bhd	Good	0.255	Stable	0.753
Kamdar Group (M) Bhd	Good	0.260	Stable	0.795
Cheetah Holdings Bhd	Good	0.433	Stable	0.726

Note: CL, confidence level.

The same technique was applied to evaluate market performance, and consistent results between the market and stock performances were obtained. Such evaluation is important to ensure that stocks and markets are coherent. Table 8 and Table 9 display the market performance evaluation for Syariah and KLCI.

Table 8. The market performance evaluation.

Market/Investor Preferences	Pessimistic				Optimistic
	I	S	G	A	I	S	G	A
Syariah Index	3	15	33	1	1	25	25	1
KLCI Index	4	12	35	1	1	31	20	0

Note: I, inferior, S, stable, G good and A indicates aggressive.

Table 9. The performance of the market index.

Market Indices	Pessimistic		Optimistic
	Performance	Confidence Level	Performance	Confidence Level
Syariah Index	Good	0.432	Stable/Good	0.718/0.811
KLCI Index	Good	0.457	Stable	0.771

Stock Selection Strategy

There are various ways to select stock in the market. However, this study introduces a novel stock selection strategy based on investors’ confidence levels and preferences of stocks. The strategy aims to provide investors with a unique stock priority evaluation, so that high priority stocks from the available pool of stocks will be selected first for investment. This is computed by assigning each performance a value, such that 0.1 refers to inferior performance, 0.2 stable, 0.3 good and 0.4 aggressive. Thus, the proposed strategy based on the novel stock priority evaluation for Aeon Co (M) Bhd was calculated using Equation (11).

$$P=\left(\left(5\times 0.1\right)+\left(13\times 0.2\right)+\left(34\times 0.3\right)+\left(0\times 0.4\right)\right)\times 0.305=4.0565$$

Table 10 shows the stock priority evaluation and the ranking for the 30 stocks analyzed in this study.

Table 10. Stock ranking-based performance weightage.

Stocks/Investor Preferences	Pessimistic			Optimistic
	Performance	Weightage	Rank	Performance	Weightage	Rank
Asia Brands Bhd	Good	13.7	8	Stable	12.3	11
Aeon Co (M) Bhd	Good	13.3	12.5	Stable	11.1	22.5
CAM Resources Bhd	Good	13.6	9.5	Stable	12	14
CWG Holdings Bhd	Stable	12.5	25	Good	13	4
Classic Century Bhd	Good	13.6	9.5	Good	12.9	5
AHB Holdings Bhd	Good	11.3	24	Stable	11.1	22.5
Asia File Corporation Bhd	Good	13	16.5	Stable	12.8	6
Euro Holdings Bhd	Good	13.5	11	Stable	10.7	25.5
Emico Holdings Bhd	Inferior	6.9	30	Stable	10.5	27.5
Eurospan Holdings Bhd	Good	13.8	6.5	Stable	12.3	11
Federal International Holdings	Inferior	8	29	Stable	10.3	28
Poh Huat Resources Holdings Bhd	Good	12.6	21	Stable	11.8	15.5
Paragon Union Bhd	Good	13.3	12.5	Stable	11.7	17
Ni Hsin Resources Bhd	Good	12.8	19	Stable	12.7	7.5
Khind Holdings Bhd	Good	13	16.5	Stable	10.5	27.5
SWS Capital Bhd	Good	14.3	2	Stable	11.2	21
Sand Nisko Capital Bhd	Good	12.3	22	Stable	10.8	24
SHH Resources Holdings Bhd	Good	14.5	1	Stable	11	23
Latitude Tree Holdings Bhd	Good	13.1	14.5	Stable	12.3	11
Milux Corporation Bhd	Stable	12	26	Good	13.8	1
Homeritz Corporation Bhd	Stable	11.8	28	Stable	12.7	7.5
Yoong Onn Corporation Bhd	Good	14.2	3	Stable	11.4	19.5
Lee Swee Kiat Group Bhd	Good	11.7	23	Stable	12.4	9
Tafi Industries Bhd	Stable	11.4	27	Good	13.2	2
Parkson Holdings Bhd	Good	14.1	4	Stable	11.4	19.5
Lii Hen Resources Bhd	Good	13.1	14.5	Good	13.1	3
Syf Resources Bhd	Good	12.8	19	Stable	10.7	25.5
Jaycorp Bhd	Good	13.8	6.5	Stable	11.6	18
Kamdar Group (M) Bhd	Good	12.8	19	Stable	11.8	15.5
Cheetah Holdings Bhd	Good	14	5	Stable	12.2	13

The distinct selection made based on different investors’ preferences can be observed in Table 10. As shown, pessimistic investors select the stock of SHH Resources Holding Bhd, while optimistic investors choose the Milux Corporation Bhd stock to invest in.

4. Validation of the Results

For validation purposes, a comparative analysis between the novel proposed fuzzy clustering, k-means clustering, and hierarchical clustering methods is presented. The validation focused on obtaining the correlation between the actual stock performance rankings, the novel proposed fuzzy clustering method, the k-means method, and the hierarchical clustering method. Table 11 summarizes the stock performance evaluations for the k-means, hierarchical, and novel proposed fuzzy clustering methods.

Table 11. Comparison results of the k-means, hierarchical, and novel proposed fuzzy clustering methods.

Stocks/Performance	K-Means	Hierarchical	Novel Proposed Fuzzy Clustering Method
			Pessimistic	Weightage	Optimistic	Weightage
Asia Brands Bhd	Good	Good	Good	3.8497	Stable	9.2988
Aeon Co (M) Bhd	Good	Good	Good	4.0565	Stable	8.214
CAM Resources Bhd	Good	Good	Good	4.08	Stable	9.36
Classic Century Bhd	Stable	Good	Good	5.8072	Good	10.3071
AHB Holdings Bhd	Good	Good	Good	3.4465	Stable	9.0243
Asia File Corporation Bhd	Stable	Stable	Good	6.89	Stable	9.7792
Euro Holdings Bhd	Good	Good	Good	4.1715	Stable	7.9608
Eurospan Holdings Bhd	Stable	Stable	Good	5.0508	Stable	8.0565
Paragon Union Bhd	Good	Stable	Good	4.1097	Stable	8.9973
SWS Capital Bhd	Good	Good	Good	4.576	Stable	7.9408
Sand Nisko Capital Bhd	Good	Stable	Good	3.1242	Stable	8.8236
Latitude Tree Holdings Bhd	Good	Good	Good	5.0959	Stable	9.5325
Yoong Onn Corporation Bhd	Good	Stable	Good	4.3452	Stable	8.4018
Tafi Industries Bhd	Stable	Good	Stable	4.8564	Good	8.8308
Parkson Holdings Bhd	Stable	Stable	Good	4.5684	Stable	8.1054
Lii Hen Resources Bhd	Good	Good	Good	7.8207	Good	10.6241
Jaycorp Bhd	Good	Good	Good	3.519	Stable	8.7348
Kamdar Group (M) Bhd	Good	Good	Good	3.328	Stable	9.381

Table 11 provides the ranking order decided by the different methods, namely, k-means, hierarchical clustering, and the novel proposed fuzzy clustering. This ranking order was then validated against the actual ranking performance using Spearman’s rank coefficient of correlation [37]. Table 12 describes the rankings and Spearman’s rank coefficient of correlation scores for the k-means, hierarchical clustering, and novel proposed fuzzy clustering methods.

Table 12. Stock ranking and Spearman’s rank coefficient of correlation scores for all clustering methods under consideration.

Stocks	Actual	K-Means	Hierarchical	A Novel Proposed Method
				Pessimistic	Optimistic
Asia Brands Bhd	14	7	6.5	14	7
Aeon Co (M) Bhd	13	7	6.5	13	14
CAM Resources Bhd	6	7	6.5	12	6
Classic Century Bhd	2	16	6.5	3	2
AHB Holdings Bhd	10	7	6.5	16	8
Asia File Corporation Bhd	3	16	15.5	2	3
Euro Holdings Bhd	18	7	6.5	10	17
Eurospan Holdings Bhd	11	16	15.5	5	16
Paragon Union Bhd	7	7	15.5	11	9
SWS Capital Bhd	15	7	6.5	7	18
Sand Nisko Capital Bhd	16	7	15.5	18	11
Latitude Tree Holdings Bhd	4	7	6.5	4	4
Yoong Onn Corporation Bhd	9	7	15.5	9	13
Tafi Industries Bhd	5	16	6.5	6	10
Parkson Holdings Bhd	8	16	15.5	8	15
Lii Hen Resources Bhd	1	7	6.5	1	1
Jaycorp Bhd	17	7	6.5	15	12
Kamdar Group (M) Bhd	12	7	6.5	17	5
Correlation		−14.55%	10.99%	70.28%	70.90%

Based on the result shown in Table 12, the novel proposed fuzzy clustering method outperforms the other established methods, providing higher correlation values for both pessimistic investors, at 70.28%, and optimistic investors, at 70.90%.

5. Discussion

As projected in Section 4, this study successfully extended the established clustering methods [4,6] by developing a novel fuzzy clustering method using a fuzzy inference system. The novel fuzzy clustering method is capable of determining stock performance based on investor preferences, as well as ranking stock based on priority. As shown in Table 5, four performance evaluations, namely, inferior, stable, good, and aggressive, were formed. As exhibited in this study, inferior performance consists of stocks that are unstable and in poor condition, yielding high risk and low return gains. Investment in this performance classification is deemed to be unworthy. The classification of stable performance for stocks consists of stocks that are still considered to be high risk and to have low return gains, but the performance is slightly better than that of inferior performance. Moreover, stable performance also consists of stocks that have moderate return rates and risk levels, but are unable to provide profit for shorter investment periods. Good performance stocks are the best stocks for investment, since the risk is low and the return rate is high, indicating that investors’ chances of losing are low and that they are able to secure high returns in investments. Finally, the aggressive performance classification consists of stocks that provide higher returns but with higher risk. This stock classification is for investors who are not intimidated by high investment risk to gain high profit returns. Stocks with a lack of investor preference are classified as inferior and stable, rather than good or aggressive. Therefore, it is suggested that investors invest in stocks classified as having good and aggressive performance.

Unlike established past works that only considered a single investors’ selection preferences, which cannot be justified, the proposed novel fuzzy clustering method is able to distinguish investors’ preferences based on stock performance. Real investors’ selection preferences can be either pessimistic or optimistic, as shown by the results obtained using the novel fuzzy clustering method. The types of investors are represented based on confidence levels, with a low value indicating pessimistic investors, while a high value denotes optimistic investors, as shown in Table 5 and Table 7. Even though investors express different preferences toward performance evaluation, the results of overall stock performance show that some stocks are given the same performance evaluation by both optimistic and pessimistic investors. This implies that investors’ preferences are an important element to consider when selecting appropriate stocks.

The stock performance presented using the novel fuzzy clustering method is in the form of a numerical value. This numerical value shows the strength of the stock performance, which can be used to rank stocks based on priority, and which established works were unable to do. Typically, most established works used more than one method to sort and rank stocks based on priority, as was done by [20,21]. Providentially, this study used only one method to determine stock performance, to cluster stock performance, to rank stocks based on priority, as well as to determine and rank priority stocks based on investor preferences.

In step 4, stocks based on priority were applied to search for the best stocks to invest in. At this stage, the stocks were rank based on the priority of the stock performance, as shown in Table 10. Such ranking was done for both pessimistic and optimistic investors. The performance of the proposed method was validated against established works, and was actual rank using Spearman’s rank coefficient of correlation. The results show that the proposed novel fuzzy clustering method is superior compared to the k-means and hierarchical clustering methods.

6. Conclusions

This paper presents a novel fuzzy clustering method for stock selection based on investors’ selection preferences. The novel proposed method provides precise and unambiguous investors’ selection preferences compared to established methods with regard to different types of investors, such as pessimistic and optimistic investors’ views. Moreover, unlike established methods, the novel investors’ selection strategy developed in this study ensures that high-priority stocks are chosen as the best stock and selected first for investment by employing the proposed stock priority method. The efficiency of the proposed method was illustrated and validated by clustering 30 Syariah stocks listed in Bursa Malaysia. This study successfully applied the novel fuzzy clustering method to the problem of stock selection based on investors’ preferences so as to assist investors in their investment choices. The results obtained from the validation justify this novel fuzzy clustering method, as it provided higher efficiency by achieving consistent ranking correlations against the actual results, unlike the established clustering methods. Although the novel clustering method obtained consistent results in terms of the actual stock performances, the ranking correlation values were not adequately sufficient, and thus, better computations will be needed to increase the level of accuracy. In addition, the novel fuzzy clustering method considers only the uncertain component of pessimistic and optimistic investors’ behaviors; for better results, the reliability, hesitancy, and bipolarity components may need to be embedded into stock selection. In the future, the authors aim to explore stock selection procedures in relation to investors’ reliability, hesitancy, and bipolarity.