Exact Likelihood Inference for an Exponential Parameter under Generalized Adaptive Progressive Hybrid Censoring
Abstract
1. Introduction
2. Model Description and Inference
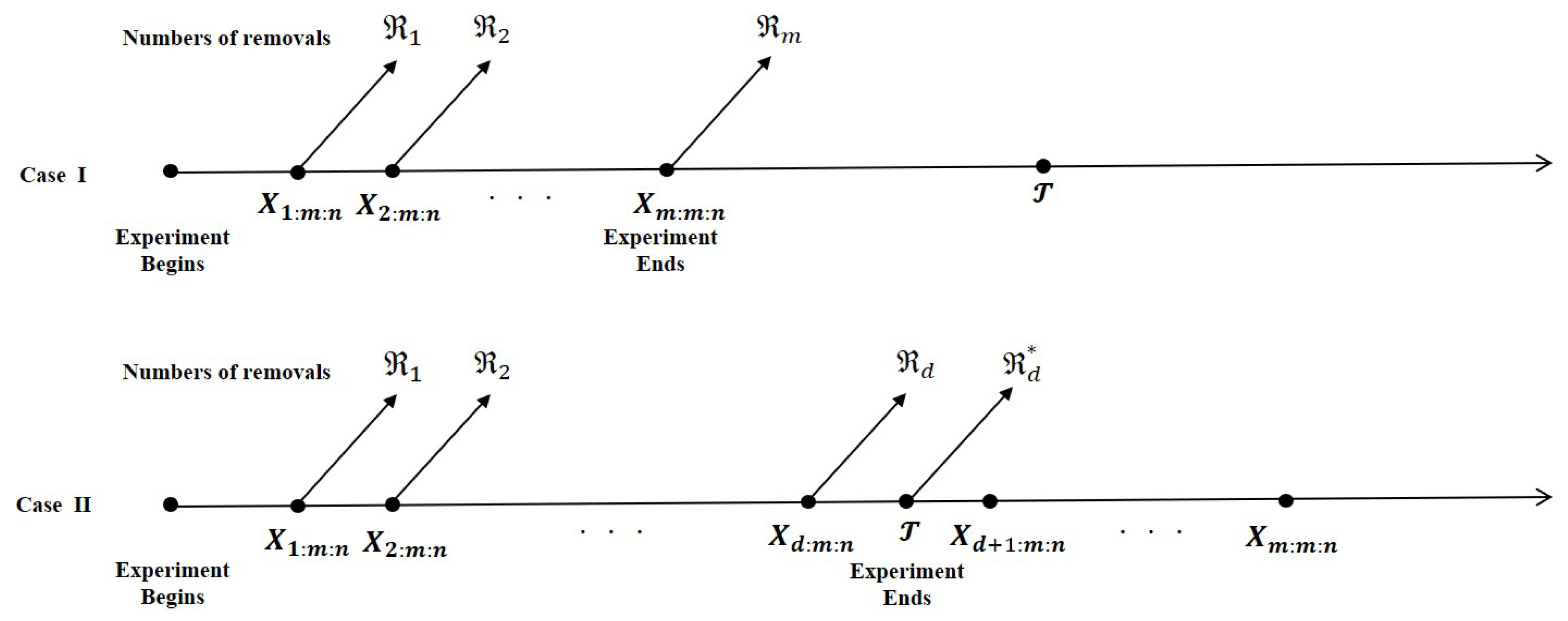
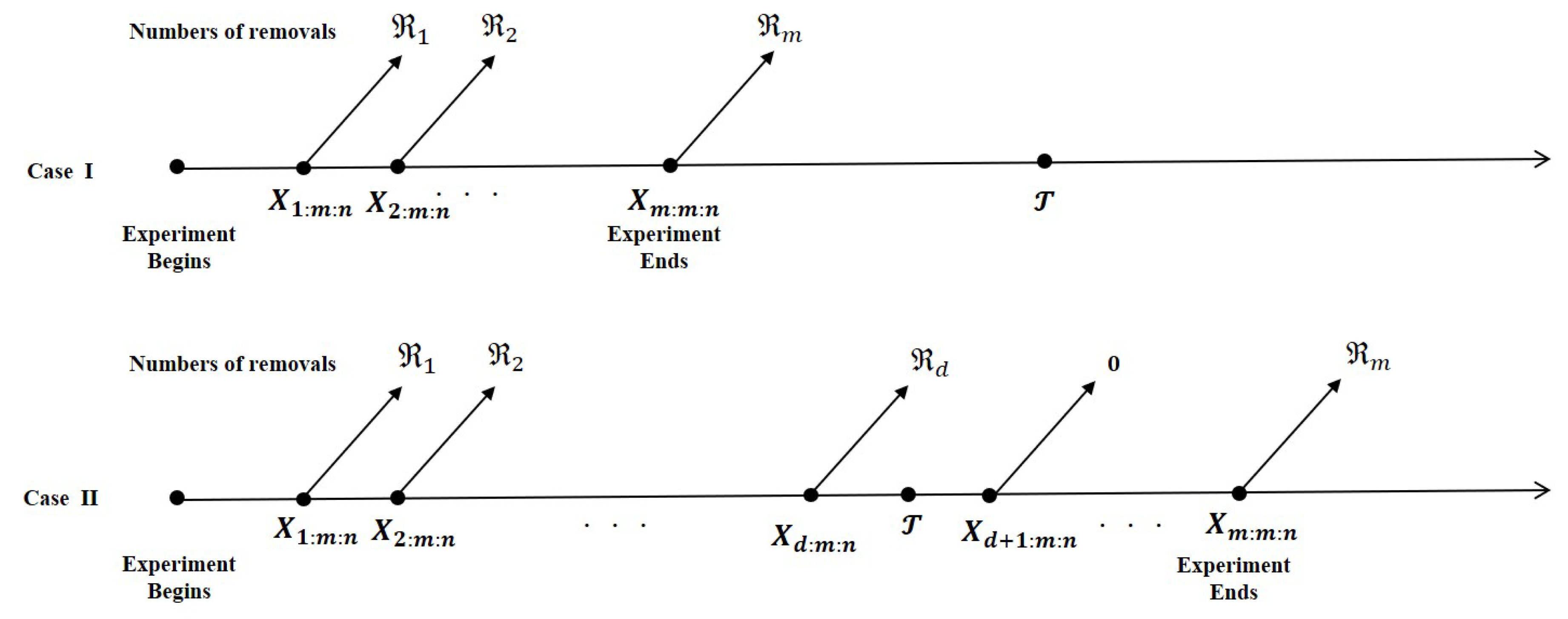
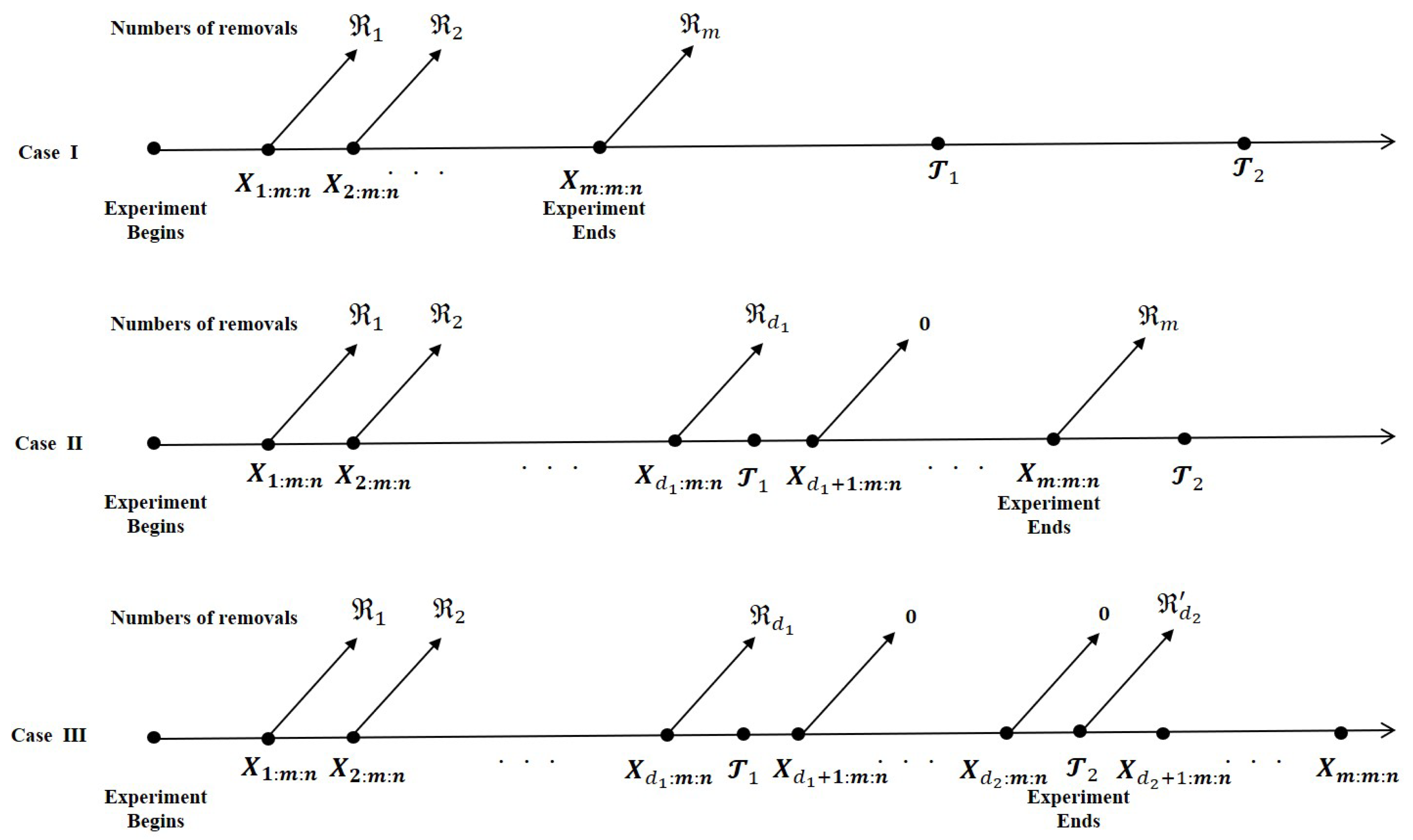
2.1. Model Description
2.2. MLE
2.3. Exact Inference for MLE
- (a)
- The conditional joint density (ConJD) of given , iswhere for .
- (b)
- For and , the ConJD of given and , is
- (c)
- For , the ConJD of given , is
3. Real Data Analysis and Simulation Results
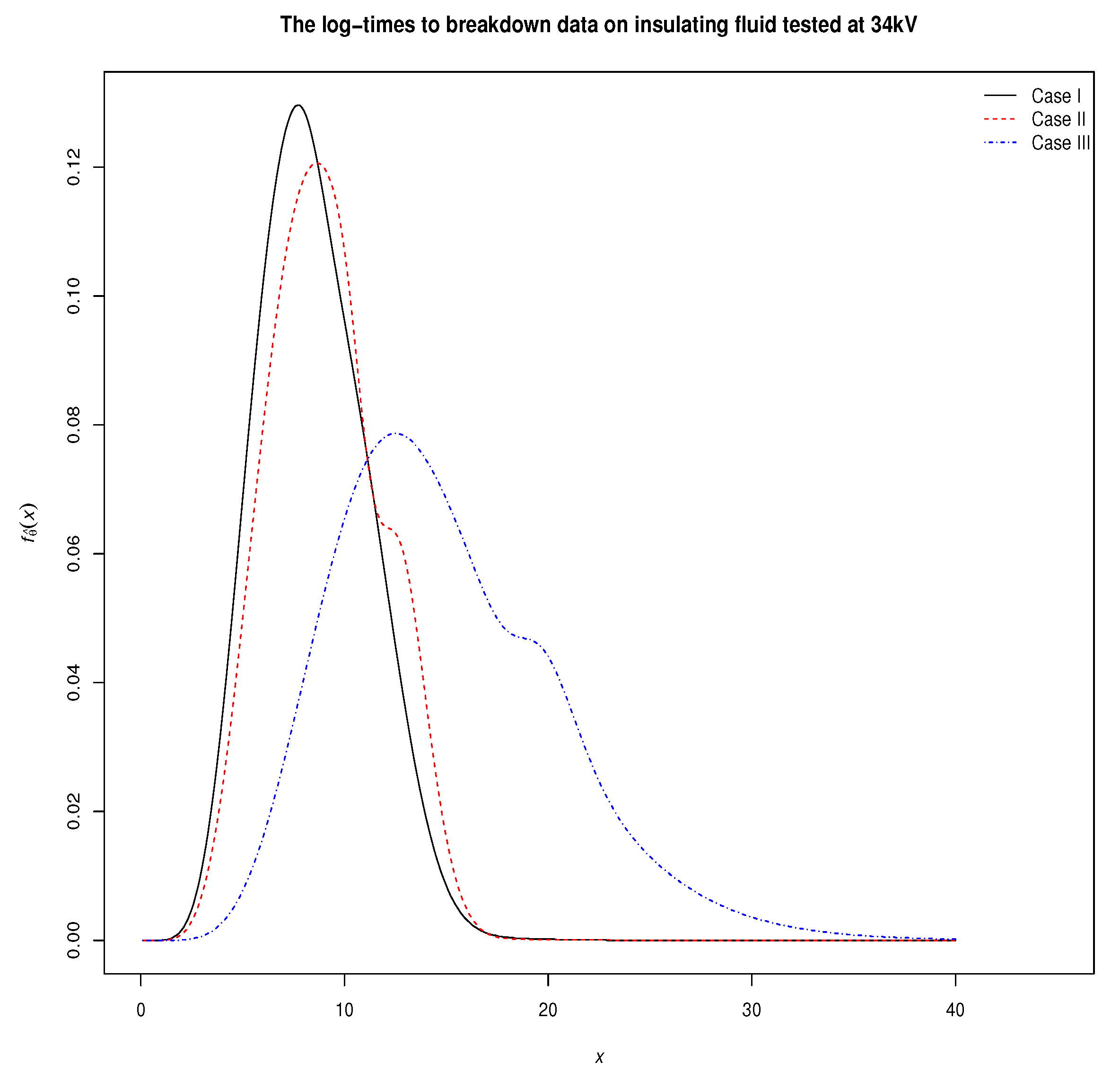
3.1. Real Data Analysis
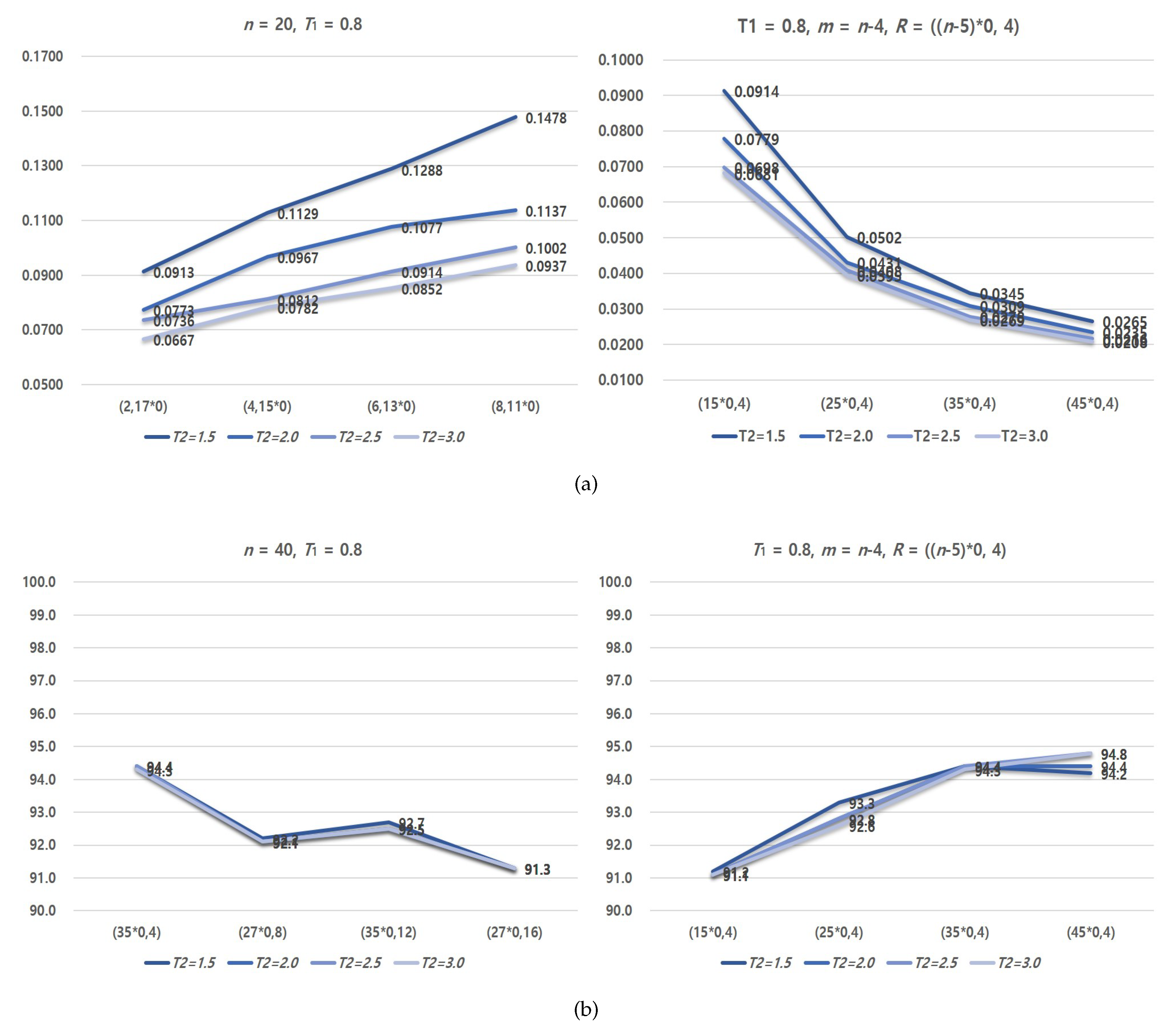
3.2. Simulation Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proof of Theorem 1
Appendix B. Proof of Theorem 2
Appendix C. Proof of Theorem 3
References
- Balakrishnan, N.; Aggarwala, R. Progressive Censoring: Theory, Methods and Applications; Birkhauser: Boston, MA, USA, 2000. [Google Scholar]
- Herd, R.G. Estimation of the Parameters of a Population from a Multi-Censored Sample. Ph.D. Thesis, Iowa State College, Ames, IA, USA, 1956. [Google Scholar]
- Górny, J.; Cramer, E. A volume based approach to establish B-spline based expressions for density functions and its application to progressive hybrid censoring. J. Korean Stat. Soc. 2019, 48, 340–355. [Google Scholar]
- Goyal, T.; Rai, P.K.; Maurya, S.K. Bayesian estimation for GDUS exponential distribution under type-I progressive hybrid censoring. Ann. Data Sci. 2020, 7, 307–345. [Google Scholar] [CrossRef]
- Sen, T.; Singh, S.; Tripathi, Y.M. Statistical inference for Lognormal distribution with type-I progressive hybrid censored data. Am. J. Math. Manag. Sci. 2019, 38, 70–95. [Google Scholar] [CrossRef]
- Xie, Y.; Gui, W. Statistical inference of the lifetime performance index with the log-logistic distribution based on progressive first-failure-censored data. Symmetry 2020, 12, 937. [Google Scholar] [CrossRef]
- Kundu, D.; Joarder, A. Analysis of type II progressively hybrid censored data. Comput. Stat. Data Anal. 2006, 50, 2509–2528. [Google Scholar] [CrossRef]
- Childs, A.; Chandrasekar, B.; Balakrishnan, N. Exact likelihood inference for an exponential parameter under progressive hybrid schemes. In Statistical Models and Methods for Biomedical and Technical Systems; Vonta, F., Huber-Carol, C., Limnios, N., Nikulin, M.S., Eds.; Birkhauser: Boston, MA, USA, 2007; pp. 319–330. [Google Scholar]
- Ng, H.K.T.; Kundu, D.; Chan, P.S. Statistical analysis of exponential lifetimes under an adaptive type-II progressively censoring scheme. Nav. Res. Logist. 2010, 56, 687–698. [Google Scholar] [CrossRef]
- Ashour, S.K.; Nassar, M. Inference for Weibull distribution under adaptive type-I progressive hybrid censored competing risks data. Commun. Stat. Theory Methods 2017, 46, 4756–4773. [Google Scholar] [CrossRef]
- Nassar, M.; Abo-Kasem, O.E. Estimation of the inverse Weibull parameters under adaptive type-II progressive hybrid censoring scheme. J. Comput. Appl. Math. 2017, 315, 228–239. [Google Scholar] [CrossRef]
- Sobhi, M.M.A.; Soliman, A.A. Estimation for the exponentiated Weibull model with adaptive type-II progressive censored schemes. Appl. Math. Model. 2016, 40, 1180–1192. [Google Scholar] [CrossRef]
- Xu, B.; Gui, W. Entropy estimation of inverse Weibull distribution under adaptive type-II progressive hybrid censoring schemes. Symmetry 2019, 11, 1463. [Google Scholar]
- Yan, Z.; Wang, N. Statistical analysis based on adaptive progressive hybrid censored sample from alpha power generalized exponential distribution. IEEE Access 2020, 8, 54691–54697. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Childs, A.; Chandrasekar, B. An efficient computational method for moments of order statistics under progressive censoring. Stat. Probab. Lett. 2002, 60, 359–365. [Google Scholar] [CrossRef]
- Viveros, R.; Balakrishnan, N. Interval estimation of parameters of life from progressively censored data. Technometrics 1994, 36, 84–91. [Google Scholar] [CrossRef]
| i | 1 | 2 | 3 | 4 |
| 0.18999 | 0.77997 | 0.95993 | 1.30996 | |
| 0 | 0 | 3 | 0 | |
| i | 5 | 6 | 7 | 8 |
| 2.77986 | 4.84962 | 6.49999 | 7.35000 | |
| 3 | 0 | 0 | 5 |
| C.I for | |||||
|---|---|---|---|---|---|
| Case | MSE | SE. | |||
| Case I | 9.08855 | 14.9261 | 3.6217 | (4.99597, 20.96100) | (5.48302, 18.17892) |
| Case II | 10.80235 | 23.2914 | 4.5846 | (5.98840, 25.00965) | (6.56902, 21.69869) |
| Case III | 11.89555 | 45.7945 | 6.6352 | (9.88020, 41.89090) | (10.85072, 36.28145) |
| MSE (Bias) | |||||||
|---|---|---|---|---|---|---|---|
| 20 | 0.8 | 18 | (17*0,2) † | 0.0807 (0.0353) | 0.0725 (0.0228) | 0.0650 (0.0154) | 0.0613 (0.0109) |
| (2,17*0) ‡ | 0.0913 (0.0399) | 0.0773 (0.0274) | 0.0736 (0.0200) | 0.0667 (0.0165) | |||
| (1,16*0,1) | 0.0900 (0.4210) | 0.0751 (0.0242) | 0.0669 (0.0176) | 0.0641 (0.0145) | |||
| 16 | (15*0,4) | 0.0914 (0.0286) | 0.0779 (0.0165) | 0.0698 (0.0081) | 0.0681 (0.0070) | ||
| (4,15*0) | 0.1129 (0.0379) | 0.0967 (0.2810) | 0.0812 (0.0198) | 0.0782 (0.0185) | |||
| (2,14*0,2) | 0.1005 (0.0355) | 0.0841 (0.0231) | 0.0774 (0.0168) | 0.0710 (0.0101) | |||
| 14 | (13*0,6) | 0.0863 (0.0188) | 0.0765 (0.0101) | 0.0754 (0.0094) | 0.0752 (0.0094) | ||
| (6,13*0) | 0.1288 (0.0522) | 0.1077 (0.0377) | 0.0914 (0.0267) | 0.0852 (0.0207) | |||
| (3,12*0,3) | 0.1101 (0.0420) | 0.0857 (0.0191) | 0.0790 (0.0123) | 0.0769 (0.0100) | |||
| 12 | (11*0,8) | 0.0856 (0.0133) | 0.0826 (0.0115) | 0.0826 (0.0115) | 0.0826 (0.0115) | ||
| (8,11*0) | 0.1478 (0.0542) | 0.1137 (0.0319) | 0.1002 (0.0270) | 0.0937 (0.0236) | |||
| (4,10*0,4) | 0.1051 (0.0311) | 0.0897 (0.0171) | 0.0839 (0.0121) | 0.0830 (0.0117) | |||
| 30 | 0.8 | 26 | (25*0,4) | 0.0502 (0.0168) | 0.0431 (0.0075) | 0.0408 (0.0023) | 0.0395 (0.0007) |
| (4,55*0) | 0.0613 (0.0256) | 0.0498 (0.0140) | 0.0451 (0.0090) | 0.0426 (0.0059) | |||
| (2,24*0,2) | 0.0551 (0.0223) | 0.0464 (0.0129) | 0.0428 (0.0067) | 0.0408 (0.0030) | |||
| 24 | (23*0,6) | 0.0503 (0.0140) | 0.0446 (0.0050) | 0.0426 (0.0022) | 0.0423 (0.0020) | ||
| (6,23*0) | 0.0658 (0.0247) | 0.0531 (0.0123) | 0.0490 (0.0081) | 0.0463 (0.0061) | |||
| (3,22*0,3) | 0.0553 (0.0194) | 0.0483 (0.0094) | 0.0449 (0.0057) | 0.0429 (0.0029) | |||
| 22 | (21*0,8) | 0.0498 (0.0115) | 0.0444 (0.0040) | 0.0438 (0.0036) | 0.0437 (0.0036) | ||
| (8,21*0) | 0.0682 (0.0326) | 0.0569 (0.0222) | 0.0530 (0.0167) | 0.0488 (0.0116) | |||
| (4,20*0,4) | 0.0554 (0.0245) | 0.0491 (0.0120) | 0.0456 (0.0055) | 0.0442 (0.0039) | |||
| 20 | (19*0,10) | 0.0548 (0.0060) | 0.0512 (0.0036) | 0.0511 (0.0036) | 0.0511 (0.0036) | ||
| (10,19*0) | 0.0824 (0.0344) | 0.0684 (0.0214) | 0.0606 (0.0128) | 0.0572 (0.0108) | |||
| (5,18*0,5) | 0.0649 (0.0205) | 0.0558 (0.0077) | 0.0522 (0.0042) | 0.0513 (0.0037) | |||
| 40 | 0.8 | 36 | (35*0,4) | 0.0345 (0.0124) | 0.0309 (0.0056) | 0.0278 (−0.0007) | 0.0269 (−0.0031) |
| (4,35*0) | 0.0371 (0.0149) | 0.0340 (0.0085) | 0.0317 (0.0057) | 0.0294 (0.0014) | |||
| (2,34*0,2) | 0.0359 (0.0122) | 0.0325 (0.0085) | 0.0295 (0.0025) | 0.0279 (−0.0006) | |||
| 32 | (27*0,8) | 0.0368 (0.0073) | 0.0341 (0.0000) | 0.0323 (−0.0023) | 0.0323 (−0.0023) | ||
| (8,27*0) | 0.0438 (0.0132) | 0.0389 (0.0095) | 0.0360 (0.0051) | 0.0349 (0.0033) | |||
| (4,26*0,4) | 0.0392 (0.0121) | 0.0348 (0.0038) | 0.0343 (0.0007) | 0.0331 (−0.0013) | |||
| 28 | (35*0,12) | 0.0382 (0.0027) | 0.0358 (−0.0002) | 0.0356 (−0.0003) | 0.0356 (−0.0003) | ||
| (12,35*0) | 0.0511 (0.0165) | 0.0436 (0.0099) | 0.0420 (0.0088) | 0.0401 (0.0069) | |||
| (6,34*0,6) | 0.0435 (0.0129) | 0.0388 (0.0042) | 0.0363 (0.0004) | 0.0356 (−0.0003) | |||
| 24 | (27*0,16) | 0.0424 (0.0021) | 0.0423 (0.0020) | 0.0423 (0.0020) | 0.0423 (0.0020) | ||
| (16,27*0) | 0.0650 (0.0247) | 0.0525 (0.0119) | 0.0488 (0.0079) | 0.0462 (0.0059) | |||
| (8,26*0,8) | 0.0485 (0.0102) | 0.0430 (0.0026) | 0.0424 (0.0021) | 0.0423 (0.0020) | |||
| 50 | 0.8 | 46 | (45*0,4) | 0.0265 (0.0070) | 0.0235 (0.0031) | 0.0216 (−0.0010) | 0.0208 (−0.0030) |
| (4,45*0) | 0.0293 (0.0085) | 0.0258 (0.0049) | 0.0236 (0.0011) | 0.0225 (−0.0005) | |||
| (2,44*0,2) | 0.0275 (0.0069) | 0.0243 (0.0040) | 0.0224 (0.0003) | 0.0215 (−0.0015) | |||
| 42 | (41*0,8) | 0.0280 (0.0082) | 0.0256 (0.0017) | 0.0234 (−0.0025) | 0.0234 (−0.0026) | ||
| (8,41*0) | 0.0324 (0.0094) | 0.0288 (0.0042) | 0.0272 (0.0033) | 0.0263 (0.0030) | |||
| (4,40*0,4) | 0.0301 (0.0087) | 0.0265 (0.0043) | 0.0254 (0.0016) | 0.0240 (−0.0015) | |||
| 38 | (37*0,12) | 0.0305 (0.0021) | 0.0275 (−0.0033) | 0.0272 (−0.0035) | 0.0272 (−0.0035) | ||
| (12,37*0) | 0.0410 (0.0144) | 0.0345 (0.0063) | 0.0312 (0.0015) | 0.0296 (0.0004) | |||
| (6,36*0,6) | 0.0340 (0.0089) | 0.0298 (0.0017) | 0.0282 (−0.0023) | 0.0273 (−0.0035) | |||
| 34 | (33*0,16) | 0.0295 (−0.0019) | 0.0286 (−0.0029) | 0.0286 (−0.0029) | 0.0286 (−0.0029) | ||
| (16,33*0) | 0.0396 (0.0048) | 0.0341 (0.0012) | 0.0323 (0.0007) | 0.0311 (0.0000) | |||
| (8,32*0,8) | 0.0326 (0.0036) | 0.0292 (−0.0024) | 0.0287 (−0.0030) | 0.0287 (−0.0030) | |||
| 60 | 0.8 | 54 | (53*0,6) | 0.0217 (0.0041) | 0.0191 (−0.0001) | 0.0180 (−0.0048) | 0.0177 (−0.0058) |
| (6,53*0) | 0.0249 (0.0069) | 0.0210 (0.0013) | 0.0194 (−0.0018) | 0.0188 (−0.0026) | |||
| (3,52*0,3) | 0.0228 (0.0052) | 0.0198 (0.0008) | 0.0187 (−0.0017) | 0.0180 (−0.0051) | |||
| 48 | (47*0,12) | 0.0231 (0.0016) | 0.0213 (−0.0035) | 0.0207 (−0.0044) | 0.0207 (−0.0044) | ||
| (12,47*0) | 0.0296 (0.0088) | 0.0246 (0.0027) | 0.0232 (−0.0011) | 0.0219 (−0.0030) | |||
| (6,46*0,6) | 0.0245 (0.0048) | 0.0225 (−0.0003) | 0.0216 (−0.0026) | 0.0210 (−0.0040) | |||
| 42 | (41*0,18) | 0.0244 (−0.0011) | 0.0234 (−0.0026) | 0.0234 (−0.0026) | 0.0234 (−0.0026) | ||
| (18,41*0) | 0.0323 (0.0094) | 0.0288 (0.0043) | 0.0271 (0.0034) | 0.0263 (0.0030) | |||
| (9,40*0,9) | 0.0276 (0.0077) | 0.0250 (0.0002) | 0.0235 (−0.0025) | 0.0234 (−0.0026) | |||
| 36 | (35*0,24) | 0.0267 (−0.0035) | 0.0267 (−0.0035) | 0.0267 (−0.0035) | 0.0267 (−0.0035) | ||
| (24,35*0) | 0.0368 (0.0145) | 0.0337 (0.0085) | 0.0317 (0.0056) | 0.0295 (0.0013) | |||
| (12,34*0,12) | 0.0297 (0.0020) | 0.0268 (−0.0034) | 0.0267 (−0.0035) | 0.0267 (−0.0035) | |||
| Coverage Percentage (Confidence Length) | |||||||
|---|---|---|---|---|---|---|---|
| 20 | 0.8 | 18 | (17*0,2) † | 94.8 (1.0548) | 94.5 (0.9846) | 94.4 (0.9525) | 94.4 (0.9385) |
| (2,17*0) ‡ | 93.8 (1.1183) | 94.0 (1.0371) | 94.3 (0.9945) | 94.4 (0.9709) | |||
| (1,16*0,1) | 94.3 (1.0925) | 94.8 (1.0069) | 94.4 (0.9688) | 94.4 (0.9509) | |||
| 16 | (15*0,4) | 93.2 (1.0608) | 93.1 (1.0083) | 93.1 (0.9894) | 93.1 (0.9869) | ||
| (4,15*0) | 93.8 (1.1865) | 94.0 (1.1043) | 93.5 (1.0559) | 93.2 (1.0340) | |||
| (2,14*0,2) | 93.5 (1.1170) | 93.1 (1.0427) | 93.1 (1.0112) | 93.1 (0.9938) | |||
| 14 | (13*0,6) | 93.5 (1.0837) | 93.4 (1.0595) | 93.3 (1.0577) | 93.3 (1.0575) | ||
| (6,13*0) | 93.5 (1.2875) | 93.1 (1.1916) | 93.4 (1.1359) | 93.4 (1.1056) | |||
| (3,12*0,3) | 93.5 (1.1650) | 93.5 (1.0862) | 93.5 (1.0647) | 93.3 (1.0591) | |||
| 12 | (11*0,8) | 93.8 (1.1490) | 93.8 (1.1446) | 93.8 (1.1446) | 93.8 (1.1446) | ||
| (8,11*0) | 93.8 (1.3988) | 94.2 (1.2792) | 94.0 (1.2301) | 94.0 (1.2006) | |||
| (4,10*0,4) | 93.8 (1.2077) | 93.8 (1.1580) | 93.8 (1.1460) | 93.8 (1.4490) | |||
| 30 | 0.8 | 26 | (25*0,4) | 94.3 (0.8377) | 94.8 (0.7898) | 94.8 (0.7737) | 94.6 (0.7699) |
| (4,55*0) | 94.6 (0.9104) | 94.0 (0.8461) | 94.7 (0.8145) | 94.8 (0.7965) | |||
| (2,24*0,2) | 93.9 (0.8728) | 94.0 (0.8157) | 93.8 (0.7879) | 93.8 (0.7757) | |||
| 24 | (23*0,6) | 93.6 (0.8418) | 93.4 (0.8086) | 93.5 (0.8023) | 93.3 (0.8018) | ||
| (6,23*0) | 94.1 (0.9456) | 94.1 (0.8784) | 94.1 (0.8470) | 93.8 (0.8295) | |||
| (3,22*0,3) | 94.1 (0.8855) | 93.6 (0.8313) | 93.4 (0.8116) | 93.4 (0.8038) | |||
| 22 | (21*0,8) | 93.4 (0.8574) | 93.3 (0.8398) | 93.2 (0.8388) | 93.2 (0.8387) | ||
| (8,21*0) | 93.8 (0.9978) | 93.1 (0.9292) | 93.9 (0.8936) | 94.4 (0.8713) | |||
| (4,20*0,4) | 93.4 (0.9100) | 93.5 (0.8589) | 93.3 (0.8425) | 93.3 (0.8394) | |||
| 20 | (19*0,10) | 93.9 (0.8855) | 93.9 (0.8799) | 93.9 (0.8797) | 93.9 (0.8797) | ||
| (10,19*0) | 93.4 (1.0503) | 93.2 (0.9745) | 93.1 (0.9331) | 93.0 (0.9138) | |||
| (5,18*0,5) | 93.0 (0.9320) | 93.8 (0.8898) | 93.9 (0.8811) | 93.9 (0.8799) | |||
| 40 | 0.8 | 36 | (35*0,4) | 94.4 (0.7193) | 94.4 (0.6765) | 94.4 (0.6573) | 94.3 (0.6520) |
| (4,35*0) | 94.5 (0.7607) | 94.3 (0.7134) | 94.5 (0.6890) | 94.1 (0.6726) | |||
| (2,34*0,2) | 94.3 (0.7376) | 94.2 (0.6947) | 94.3 (0.6694) | 94.3 (0.6580) | |||
| 32 | (27*0,8) | 94.2 (0.7208) | 94.1 (0.6956) | 94.1 (0.6914) | 94.1 (0.6914) | ||
| (8,27*0) | 94.7 (0.8049) | 94.5 (0.7580) | 94.3 (0.7305) | 94.6 (0.7158) | |||
| (4,26*0,4) | 94.5 (0.7583) | 94.4 (0.7134) | 94.1 (0.6979) | 94.9 (0.6929) | |||
| 28 | (35*0,12) | 94.7 (0.7466) | 94.5 (0.7408) | 94.5 (0.7406) | 94.5 (0.7406) | ||
| (12,35*0) | 94.0 (0.8650) | 94.6 (0.8108) | 94.9 (0.7851) | 94.5 (0.7688) | |||
| (6,34*0,6) | 94.7 (0.7854) | 94.7 (0.7501) | 94.5 (0.7418) | 94.5 (0.7406) | |||
| 24 | (27*0,16) | 93.3 (0.8020) | 93.3 (0.8017) | 93.3 (0.8017) | 93.3 (0.8017) | ||
| (16,27*0) | 93.1 (0.9444) | 93.1 (0.8773) | 93.1 (0.8464) | 93.8 (0.8291) | |||
| (8,26*0,8) | 93.6 (0.8227) | 93.4 (0.8031) | 93.3 (0.8019) | 93.3 (0.8017) | |||
| 50 | 0.8 | 46 | (45*0,4) | 94.2 (0.6377) | 94.4 (0.6011) | 94.8 (0.5834) | 94.8 (0.5773) |
| (4,45*0) | 94.0 (0.6664) | 94.5 (0.6278) | 94.5 (0.6056) | 94.5 (0.5937) | |||
| (2,44*0,2) | 94.9 (0.6507) | 95.0 (0.6137) | 94.7 (0.5927) | 94.7 (0.5827) | |||
| 42 | (41*0,8) | 94.8 (0.6403) | 94.8 (0.6107) | 94.7 (0.6035) | 94.8 (0.6033) | ||
| (8,41*0) | 94.5 (0.6984) | 94.1 (0.6565) | 94.9 (0.6360) | 94.1 (0.6245) | |||
| (4,40*0,4) | 94.8 (0.6668) | 94.8 (0.6284) | 94.9 (0.6117) | 94.8 (0.6050) | |||
| 38 | (37*0,12) | 94.6 (0.6461) | 94.8 (0.6340) | 94.8 (0.6337) | 94.8 (0.6337) | ||
| (12,37*0) | 94.9 (0.7398) | 94.9 (0.6919) | 94.5 (0.6666) | 94.4 (0.6541) | |||
| (6,36*0,6) | 94.8 (0.6824) | 94.7 (0.6462) | 94.6 (0.6356) | 94.8 (0.6337) | |||
| 34 | (33*0,16) | 94.7 (0.6719) | 94.7 (0.6703) | 94.7 (0.6703) | 94.7 (0.6703) | ||
| (16,33*0) | 94.4 (0.7715) | 94.3 (0.7272) | 94.6 (0.7050) | 94.2 (0.6920) | |||
| (8,32*0,8) | 94.7 (0.6880) | 94.7 (0.6712) | 94.7 (0.6702) | 94.7 (0.6702) | |||
| 60 | 0.8 | 54 | (53*0,6) | 94.8 (0.5796) | 94.9 (0.5469) | 94.3 (0.5332) | 94.2 (0.5306) |
| (6,53*0) | 94.4 (0.6136) | 94.9 (0.5763) | 94.9 (0.5567) | 94.5 (0.5465) | |||
| (3,52*0,3) | 95.2 (0.5956) | 95.2 (0.5606) | 94.9 (0.5429) | 94.2 (0.5337) | |||
| 48 | (47*0,12) | 94.1 (0.5814) | 94.2 (0.5646) | 94.2 (0.5633) | 94.2 (0.5633) | ||
| (12,47*0) | 94.5 (0.6523) | 94.1 (0.6123) | 94.9 (0.5909) | 94.5 (0.5792) | |||
| (6,46*0,6) | 94.3 (0.6114) | 94.0 (0.5776) | 94.1 (0.5664) | 94.2 (0.5637) | |||
| 42 | (41*0,18) | 94.9 (0.6055) | 94.8 (0.6033) | 94.8 (0.6033) | 94.8 (0.6033) | ||
| (18,41*0) | 94.5 (0.6981) | 94.1 (0.6564) | 94.9 (0.6359) | 94.1 (0.6244) | |||
| (9,40*0,9) | 94.7 (0.6343) | 94.9 (0.6078) | 94.8 (0.6034) | 94.8 (0.6033) | |||
| 36 | (35*0,24) | 94.3 (0.6510) | 94.3 (0.6510) | 94.3 (0.6510) | 94.3 (0.6510) | ||
| (24,35*0) | 94.5 (0.7592) | 94.3 (0.7129) | 94.4 (0.6886) | 94.0 (0.6725) | |||
| (12,34*0,12) | 94.3 (0.6621) | 94.3 (0.6513) | 94.3 (0.6510) | 94.3 (0.6510) | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.; Lee, K. Exact Likelihood Inference for an Exponential Parameter under Generalized Adaptive Progressive Hybrid Censoring. Symmetry 2020, 12, 1149. https://doi.org/10.3390/sym12071149
Lee H, Lee K. Exact Likelihood Inference for an Exponential Parameter under Generalized Adaptive Progressive Hybrid Censoring. Symmetry. 2020; 12(7):1149. https://doi.org/10.3390/sym12071149
Chicago/Turabian StyleLee, Hyojin, and Kyeongjun Lee. 2020. "Exact Likelihood Inference for an Exponential Parameter under Generalized Adaptive Progressive Hybrid Censoring" Symmetry 12, no. 7: 1149. https://doi.org/10.3390/sym12071149
APA StyleLee, H., & Lee, K. (2020). Exact Likelihood Inference for an Exponential Parameter under Generalized Adaptive Progressive Hybrid Censoring. Symmetry, 12(7), 1149. https://doi.org/10.3390/sym12071149





