Energy Efficiency and User Capacity Optimization of Cognitive MIMO Systems Via the SCMA-Based Nonorthogonal Time Slot Allocation

Abstract

This paper investigates the energy-efficient communications and user capacity in the cognitive multiple input multiple output (MIMO) symmetric system of underlay mode. The advantage of the improved energy efficiency provided by the orthogonal slot allocation for time division multiple access (TDMA) has a side effect of restricting the number of users accessing the system. To tackle the above problem, this paper proposes a nonorthogonal time resource allocation method with sparse code multiple access (SCMA), which allows one to convert the orthogonal slot units of TDMA into non-orthogonal shared slot units for multiple secondary users (SUs). The method of adding virtual users is adopted, wherein each SU is treated as multiple SUs who occupy a shared unit, to facilitate the packet access. Finally, the greedy algorithm is applied to optimize the time slot allocation of unoccupied shared slot units. The simulation results show that SCMA-based nonorthogonal slot allocation can reduce not only the energy consumption by nearly 40%, but also the average power interference from SUs to primary users by nearly 2 dB if their number is relatively high. Moreover, in the case of satisfying the rate requirement of the users, the system user capacity increased by more than 50%.

1. Introduction

The state-of-the-art wireless communication system should have adequate characteristics of continuous wide area coverage, hot spot area, high capacity, low energy consumption, and mass connection [1]. The latter two issues, given the increased energy consumption and limited spectrum supply/demand, are quite urgent. Low power consumption is the key to reducing carbon emissions, extending battery life, and promoting “green communications” for wireless devices [2,3,4]. Numerous studies have been performed with the aim of more comprehensive use of spectrum resources, improving the spectrum utilization efficiency, reducing power/energy consumption, and overall improvement of the energy efficiency (EE). This paper addresses the issues of energy efficiency and user capacity in a cognitive wireless network with multiple antennas and a sharing time slot. Nowadays, many research efforts are dedicated to the cognitive radio (CR), which is a new type of radio with adaptive spectrum awareness that is centered on spectrum sensing and intelligent learning capabilities. CR enables secondary users (SUs) to adaptively occupy the local spectrum of primary authorized users (PUs) available immediately [2,3]. In recent years, the diverse applications of CR technology have also received more and more attention. For example, CR will be a brand-new field for the tactile Internet, and it is expected to improve the overall quality of the network [5]. In addition, CR has certain guiding significance for the data decision of internet of multimedia things (IoMT) [6].The multiple input multiple output (MIMO) approach is used to ensure the coexistence of SUs and PUs in the space domain, and to avoid adverse interference to the primary user links [7,8]. Among the popular technologies of the fifth generation (5G) mobile communication, the sparse code multiple access (SCMA) technology can provide strong support for slot sharing [9,10]. Therefore, the cognitive MIMO radio network can provide support for more users to access resources in the same time by combining SCMA technology.

SCMA is one of the nonorthogonal multiple access (NOMA) technologies, which was developed on the base of the code division multiple access (CDMA) technology of low-density signature (referred to as LDS-CDMA), which is a kind of physical layer potential air interface technology. In particular, the LDS-CDMA has been put forward to solve the problem of the system overload during mass connection [11,12,13]. In recent years, the LDS-CDMA technology was further developed into the high-performance SCMA, which joins the high dimensional and sparse spread spectra together so that the bit streams are directly mapped to predetermined codewords in the multidimensional complex domain. Due to the sparsity of spread spectrum code, no serious interference between users can occur, and the receiver can use the message passing algorithm (MPA) with a low complexity [14,15,16,17,18]. The structure is a spread spectrum on orthogonal frequency division multiplexing(OFDM) subcarriers and is detected by MPA. The SCMA sharing time-frequency resource units based on factor diagrams provide the theoretical support for time-sharing of time division multiple access (TDMA).

In recent years, the combination of CR and NOMA can further effectively improve energy efficiency, and spectrum utilization has been widely concerned [19,20,21,22,23,24]. But, its user capacity is limited, and there is even some interference from secondary systems. Therefore, many studies consider using MIMO technology to assist CR-NOMA networks to further improve energy efficiency while increasing the number of users’ access. Among many CR-MIMO technologies assisted by NOMA technology, SCMA technology has not been reported. Moreover, most of the research focuses on resource allocation and codebook design to study the utilization of energy efficiency, and few papers focus on non-orthogonal slot allocation to improve energy efficiency.

Inspired by the above research, this paper will further explore and analyze the energy consumption and user capacity of the secondary user in the cognitive MIMO system under the underlay model. The space division multiplexing of MIMO technology can ensure that multiple data streams are simultaneously transmitted to the base station (BS), which can achieve better EE than the transmit diversity approach, which is used to diminish the effects of fading by transmitting the same information from two different antenna models. It is known that the nonconvex problem of energy consumption in the system with multiple users can be reduced to the convex problem of time resource allocation optimization. Within the framework of the TDMA approach, the continuous time is split into discrete orthogonal slots, which allows one to avoid the interference between users, but limits the number of users in the MIMO-CR system. In order to override this obstacle, we propose to use the nonorthogonal slot access scheme and time resource allocation optimization based on SCMA. This will not only minimize the interference between users but also yield better EE than the orthogonal slot access and reduce the average interference power from the SUs to the PUs links when the system is accessed by a larger number of users. Considering the practical application, this study discusses the statistical channel state information (CSI) model, wherein the rate requirements of SUs and interference threshold are used to ensure the quality of service (QoS) of SUs and PUs, respectively. The interference power constraints are used to ensure with a high probability that the interference of SUs to PUs is below the threshold value. By meeting the minimum time slot requirements of each user, the system user capacity can be greatly enhanced.

Notation: Throughout the paper, we use bold uppercase and lowercase letters to denote matrices and vectors, respectively. For a square matrix A, tr (A), rank(A), A^T, A* and A^H denote its trace, rank, transpose, conjugate and conjugate transpose, respectively. ${ℂ}^{N\times M}$ denotes the space of $N\times M$ complex matrices. $|·|$ denotes the absolute value of a scalar, and $A\succcurlyeq 0$ means A is a Hermitian positive semidefinite matrix. $E\{·\}$ represents the statistical expectation and $I_m$ stands for the $m\times m$ identity. $x\sim cN(u,{\sigma }^2)$ indicates that the variable $x$ follows the complex normal distribution with mean $u$ and variance ${\sigma }^2$. $\lceil x\rceil$ denotes the ceiling of $x$. $Fix\left(x\right)$ and $\mathrm{mod}\left(x\right)$ represent the integer part and remainder part of $x$, respectively.

2. Related Works

Recently, SCMA technology has been discovered to be a NOMA technology with great potential because of its excellent advantages of improving spectrum efficiency. In the literature, most studies have focused on combining NOMA technology with CR technology to improve EE and user access [19,20,21,22,23,24]. In Reference [19], a CR-NOMA network with wireless information and power transmission (SWIPT) is considered under the nonlinear energy collection model to improve EE and spectrum efficiency (SE). In Reference [20], robust beamforming and power split control are jointly designed to optimize the transmission power minimization and energy harvesting maximization in the MISO-NOMA CR-aided SWIPT system. Reference [21] studied the optimization problem to maximize EE in the CR-NOMA system, which was proposed in two modes of the overlay network and underlying network. Reference [22] has designed a new secure CR-NOMA transmission strategy that pairs the PUs and SUs according to the channel gain to improve the performance of the secondary system. In Reference [23], a fair-aware joint power allocation and SU allocation problem based on downlink cognitive NOMA networks is studied, in which an alternative optimization scheme is adopted to enhance the system capacity. Reference [24] studied the robust resource allocation and sub-channel allocation to maximize the total EE of SUs from the perspective of EE-robustness trade-offs in the multi-user cognitive NOMA network.

Although NOMA-SU allocation technology is an effective method, it can enhance the resource utilization efficiency in the power domain and spectrum domain to support the cognitive NOMA network [23]. However, it is difficult to guarantee that EE can be improved while accessing more users and reducing interference. Therefore, we consider introducing MIMO technology into the CR system to improve its performance. In the literature, most of the research on energy efficiency and user capacity of MIMO-assisted CR networks can be divided into two categories: the traditional CR-MIMO network [25,26,27,28,29,30,31,32,33,34,35] and the network combining CR-MIMO with NOMA (CR-MIMO-NOMA) Technology [36,37,38,39,40,41].

In the traditional CR-MIMO network, spectrum sensing and energy harvesting technology have been the main research directions in recent years [30,31,32,33,34,35], while the EE and user capacity were mainly studied in earlier years [25,26,27,28,29]. The problems of EE optimization of a MIMO-CR system with multiple secondary receivers for the cases of single and multiple data streams was addressed in References [25], respectively. In the latter case, a higher EE was achieved, as compared to the former one. In Reference [27], the problems of distributed and centralized energy efficiency optimization in CR-MIMO networks with interfering channels are proposed. Under the constraints of power and interference, the energy efficiency of the MIMO spectrum sharing cognitive radio system is studied in Reference [28]. In Reference [29], a method of antenna selection for a spatial multiplexing CR-MIMO system based on a linear receiver, and a cross-layer EE measurement method based on user capacity are proposed.

In recent years, more and more attention has been paid to the EE and user capacity of CR-MIMO-NOMA networks. In Reference [36], a CR-MIMO network inspired by NOMA was investigated, and a joint antenna selection (AS) algorithm with high computational efficiency was proposed to maximize the signal-to-noise ratio (SNR) of secondary users while satisfying the QoS of PUs. Reference [37] proposes a downlink cascading transmit zero-force beamforming (ZFBF) technology to ensure communication security in the CR-MIMO-NOMA network. In Reference [38], a new AS algorithm is proposed based on the maximum channel gain, on the premise of meeting the service quality requirements of the primary user, to maximize the reachable rate of the secondary user. Reference [39] proposes a framework for simultaneous spectral efficiency design using CR, MIMO and NOMA technologies in the downlink, and calculates the sum rate of secondary users. In Reference [40], a new design scheme is proposed to study the problem of coordinated beamforming and power allocation based on interference alignment (IA) in CR-MIMO-NOMA downlink networks. In Reference [41], it is proven that the spectrum efficiency and EE of MIMO-NOMA in the CR network are better than those of an orthogonal multiple access CR network based on MIMO-OMA by using the blindly combined energy detection (BCED).

In the literature, SCMA-assisted CR-MIMO network research has not been reported, and few papers focus on non-orthogonal slot allocation to improve energy efficiency. In this paper, we further explore and analyze the SCMA-based time slot allocation scheme to optimize the energy consumption and user capacity of secondary users in the CR-MIMO system. Table 1 provides a summary of the related work.

Table 1. Summary of related work. Energy efficient (EE); User capacity (UC); Energy harvesting (EH); Spectrum efficiency (SE); Cognitive radio (CR); Multiple input multiple output (MIMO); Nonorthogonal multiple access (NOMA).

Reference		Objective	Method	Advantages	Limitations
CR - NOMA	[19]	EE; SE	weighted Tchebycheff	The efficiency of EH is higher than that of the linear model.	The decoding rate of users is affected.
	[20]	Power; EH	one-dimensional search	The system performance is improved.	The interference generated by multiple cells is not considered.
	[21]	EE	Dinkelbach method	The tradeoff between EE and sub-slot is realized.	The UC has not been improved.
	[22]	Power; security	power allocation and transmit rate control	Reduce interference and improve security.	The increase of the number of secondary users will reduce the security performance.
	[23]	UC	successive convex approximation	Total throughput increased.	Energy consumption increased
	[24]	EE	successive convex approximation	The algorithm has good robustness and EE.	System complexity and interference is not considered.
CR - MIMO	[25]	EE	matrix eigenvalue-eigenvector computation	It reduces energy consumption and interference.	The optimization problem under imperfect channel state information (CSI) is not considered.
	[26]	EE	water-filling and greedy algorithm	Both perfect CSI and imperfect CSI optimization are considered.	Secondary users will not only interfere with the primary users, but also interfere with each other.
	[27]	EE	Dinkelbach’s method.	Network energy consumption is reduced.	Fairness may be lost.
	[28]	EE	singular value decomposition; water-filling	Optimal power allocation improves performance.	The interference threshold has a significant effect on EE.
	[29]	EE	iterative cross-layer algorithm	Cross-layer scheme improves UC and EE.	High computational complexity.
CR - MIMO - NOMA	[36]	EE	subset-based joint antenna selection	Improve the signal-to-noise ratio of secondary users.	The impact of interference was not considered.
	[37]	UC	zero-forcing-beamforming	Improve the overall security level of the system and access users.	There are certain restrictions on the number of base station antennas.
	[38]	UC	maximum-channel- gain-based antenna selection	Near optimal performance can be achieved while reducing complexity.	Only when one user is closer to the base station than another user can a better complexity saving be achieved.
	[39]	UC	Shannon channel capacity formula	The proposed scheme is superior to CR-NOMA in terms of data rate.	General channel is not considered.
	[40]	UC	Interference alignment -based coordinated beamforming	Eliminate interference and increase system sum-rate.	The number of user antennas affects the system and rate.
	[41]	SE; UC	Bblindly combined energy detection	It provides better SE.	EE is not considered.
proposed scheme		EE; UC	water-filling and greedy algorithm	Improve EE, reduce interference and increase the number of user access.	Interference between secondary users is not considered.

3. System Model

Consider a MIMO-CR network containing K SUs and J transmitter–receiver pairs. Let S_k and P_j denote the kth secondary user and jth pair of primary transmitter–receiver links, respectively. In the underlay model, the primary links are potentially active and always protected. The primary network consists of J transmitter–receiver pairs, while the secondary one is a single cellular network, in which all SUs have the uplinks via TDMA to the secondary base station (BS), and the SCMA-based non-orthogonal strategy is used for slot allocation. The secondary BS is located at the center of the secondary system, and can evaluate the channel matrix $H_{BS,S_k}$ of $S_k$, and feed it back to $S_k$ through an independent control channel. Therefore, the information on both $S_k$ and the secondary BS is fed into the channel matrix of $S_k$. The uplink transmission of SUs is synchronized by the secondary BS, which allows SUs to make transmissions in orthogonal slots without interference. The coexistence of PUs and SUs in the CR networks implies their mutual interference. When the bandwidth exceeds the bandwidth of the transmitted signal, the gain of the frequency flat fading channel is constant and has a linear phase response, which is applied so that the channel matrix within the prescribed bandwidth is unchanged. Moreover, in the case of a block fading channel application, the channel matrix will not change within a TDMA frame and, thus, needs no correlation between frames. For example, consider two pairs of PUs links with a distance of 10 meters between transceivers. The SUs are randomly distributed in a 200*200m area, and the minimum separation distance from the PUs link is set to 35 m. The case of 35 SUs in the MIMO-CR network is depicted in Figure 1.

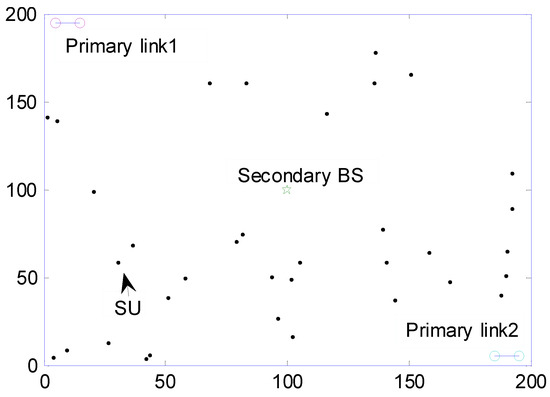
Figure 1. A random MIMO-CR network.

In MIMO-CR symmetric networks, both PUs and SUs can transmit multiple data streams via multiple antennas. The list of related notations is provided in Table 2.

Table 2. List of related notations.

Symbol	Definition
Sk	The kth secondary user
Pj	The jth pair of primary transmitter–receiver links
$M_{S_k}$	The number of transmitting antennas of $S_k$
$M_{P_j}$	The number of transmitting antennas of $P_j$
$N_{P_j}$	The number of receiver antennas of $P_j$
$N_{BS}$	The number of receiver antennas of secondary base station (BS)
$H_{BS,S_k}\in {ℂ}^{N_{BS}\times M_{S_k}}$	The channel matrix from $S_k$ to the secondary BS
$H_{P_j,S_k}\in {ℂ}^{N_{P_j}\times M_{S_k}}$	The channel matrix from $S_k$ to the receiver of $P_j$
$H_{BS,P_j}\in {ℂ}^{N_{BS}\times M_{P_j}}$	The channel matrix from the transmitter of $P_j$ to the secondary BS
$D_{S_k}$	The number of data streams of $S_k$
$D_{P_j}$	the number of data streams of $P_j$
$x_{S_k}$	The data flow matrix transmitted by $S_k$
$x_{P_j}$	The data flow matrix transmitted by $P_j$
$Q_{S_k}$	The Hermitian positive semidefinite covariance matrix of $x_{S_k}$, whose eigenvalues are non-negative
$Q_{P_j}$	The Hermitian positive semidefinite covariance matrix of $x_{P_j}$, whose eigenvalues are non-negative

The SCMA technology opens new horizons in the time-frequency resource sharing. Assuming an uplink SCMA system with $K$ users and $N$ resources ($K>N$), the users share orthogonal time-frequency resources and transmit data to the same BS. The overloading factor is defined as $\lambda =K/N$. The ${\log }_2{}^Q$ bits of $K$ users are directly mapped to the $N$ shared orthogonal time-frequency resources through each individual codebook. The receiver with a low-complexity MPA multiuser detector can recover the transmitted bit data for each user. The uplink MIMO-CR SCMA system model with $K=6,N=4$ is shown in Figure 2, where $n\sim cN(0,{\sigma }^{2}I)$ denotes the Gaussian noise.

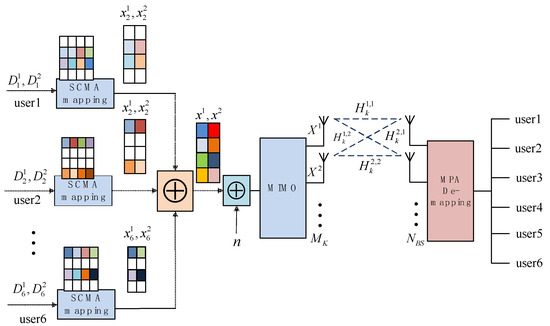
Figure 2. Uplink MIMO-CR sparse code multiple access (SCMA) system model (K = 6, N = 4).

SCMA encoding can use the factor diagram matrix $F=\left(f_1,f_2,\dots ,f_k\right)$ to represent. The variable node (VN) V_k connects to the function node (FN) F_n only if $F_{n,k}=1$, otherwise, $F_{n,k}=0$. When the VNs represent the SUs, and the FNs represent the time slot, the corresponding relation between the SCMA factor graph and matrix F is shown in Figure 3. $F=\left\{F_{T_n,S_k}\right\}$, where $F_{T_n,S_k}=1$ if secondary user $s_k$ occupies time slot $T_n$, otherwise $F_{T_n,S_k}=0$. As seen in Figure 2and Figure 3, using the SCMA principle, we can share the TDMA orthogonal slot by the packet sharing to access more SUs. Therefore, in the same SUs conditions, when a frame is ended, the slot allocation strategy of SCMA-based non-orthogonal slot sharing provides more time being eventually assigned to each SU.

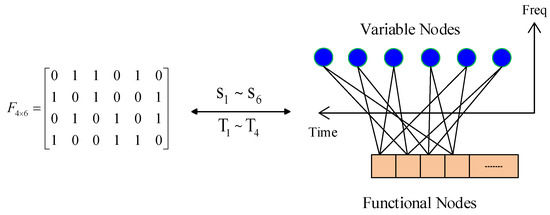
Figure 3. The relation between matrix F and factor graph.

The received vector of $S_k$ at the secondary BS is derived as follows:

$$\begin{array}{ll}{y}_{B{S}_k}=& H_{BS,S_k}{F}_{T_n,S_k}{x}_{S_k}+n_{BS},\\ & k=1,\cdots ,K,n=1,\cdots ,N\end{array},$$

(1)

where $n_{BS}$ is additive Gauss white noise with the noise power spectral density $N_0/2$.

The user capacity of $S_k$ is defined as the maximum mutual information between the transmitter and receiver signals, as follows:

$$\begin{array}{l}{R}_{S_k}^{}=\max I(F_{T_n,S_k}{x}_{S_k};y_{B{S}_k}|H_{BS,S_k})\\ \hspace{1em} =\max h(y_{B{S}_k}|H_{BS,S_k})-h(n_{BS})\\ \hspace{1em} \le \log \left[{(\pi e)}^N\det ({\sigma }_n{{\rm I}}_N+H_{BS,S_k}{F}_{T_n,S_k}{Q}_{S_k}{H}_{BS,S_k})\right]\\ \hspace{1em}\hspace{1em}\hspace{1em}-K\log [\pi e{\sigma }_n]\\ \hspace{1em} =\log \left[\det ({{\rm I}}_N+\frac{1}{{\sigma }_n}{H}_{BS,S_k}{F}_{T_n,S_k}{Q}_{S_k}{H}_{BS,S_k})\right]\end{array},$$

(2)

where $Q_{S_k}$ is the covariance matrix of $x_{S_k}$ and is given by:

$$Q_{S_k}=\left[\begin{array}{cccc}E\left(x_{s_1}{x}_{s_1}^H\right)& E\left(x_1{x}_2^H\right)& \cdots & E\left(x_1{x}_{s_K}^H\right)\\ ⋮& ⋮& \ddots & ⋮\\ E\left(x_{s_k}{x}_1^H\right)& E\left(x_{s_k}{x}_2^H\right)& \cdots & E\left(x_{s_K}{x}_{s_K}^H\right)\end{array}\right],$$

(3)

where eachV $E\left(x_{s_k}{x}_{s_k}^H\right)$ is given by:

$$\begin{array}{l}E\left(x_{s_i}{x}_{s_j}^H\right)=\\ \left[\begin{array}{cccc}E\left(x_{s_1,s_i}{x}_{s_1,s_j}^{*}\right)& E\left(x_{s_1,s_i}{x}_{s_2,s_j}^{*}\right)& \cdots & E\left(x_{s_1,s_i}{x}_{s_K,s_j}^{*}\right)\\ ⋮& ⋮& \ddots & ⋮\\ E\left(x_{s_K,s_i}{x}_{s_1,s_j}^{*}\right)& E\left(x_{s_K,s_i}{x}_{s_2,s_j}^{*}\right)& \cdots & E\left(x_{s_K,s_i}{x}_{s_K,s_j}^{*}\right)\end{array}\right]\end{array},$$

(4)

If the secondary BS fails to eliminate the interference from the PUs links, which is regarded as noise, then the interference-plus-noise covariance matrix is derived as:

$$C_{S_k}={\displaystyle \sum _{j=1}^J{H}_{BS,P_j}{Q}_{P_j}{H}_{BS,P_j}^H+N_{0}w{I}_{N_{BS}}},$$

(5)

where w is defined as the bandwidth of the secondary network. $Q_{P_j}$ is the covariance matrix of $x_{p_j}$, which are Hermitian positive semidefinite matrices. According to Shannon’s formula, which interrelates and links the information rate with SNR and bandwidth in the MIMO link, the achievable transmission rate $r_{S_k}$ of $S_k$ can be depicted as:

$$\begin{array}{rr}{r}_{S_k}=w\log [\det (I+\frac{H_{BS,S_k}{F}_{T_n,S_k}{Q}_{S_k}{H}_{BS,S_k}^H}{C_{S_k}^{}})],& \\ k=1,\cdots ,K,n=1,\cdots ,& N\end{array},$$

(6)

where $r_{S_k}$ is the instantaneous transmission rate of $S_k$, expressed in the natural units of information (nats) per second. The total transmission power of $S_k$ in all antennas is $P_{S_k}=tr\left(F_{T_n,S_k}E\left(x_{s_k}{x}_{s_k}^H\right)\right)=tr\left(F_{T_n,S_k}{Q}_{S_k}\right)$, while the total power of interference from $S_k$ to $P_j$ is calculated as:

$$\begin{array}{ll}{q}_{P_j,S_k}=& tr(H_{P_j,S_k}{F}_{T_n,S_k}{Q}_{S_k}{H}_{P_j,S_k}^H),\\ & k=1,\cdots ,K;j=1,\cdots ,J;n=1,\cdots ,N\end{array},$$

(7)

4. Problem Formulation and Optimization

In this section, we first introduce the problem construction of SCMA-based nonorthogonal slot allocation in the cognitive MIMO system, and turn the energy efficiency problem into a mathematical formula. On this basis, the problem is further optimized by combining the statistical CSI and the numerical characteristics of time slot integer.

4.1. Problem Formulation

The system aims at optimizing the total power consumption of SU by allocating an appropriate transmission time for each SU. This would not only minimize the power of interference from SUs to PUs links, but also ensure an adequate QoS of each SU. In the statistical CSI, a power constraint is set for each SU to protect the PUs with the maximum possible QoS. To ensure QoS of each SU, the requirements on the transmission rate $R_{S_k}$ (in nats/second) of $S_k$ should be satisfied. Here, $R_{S_k}$ is the number of nats required for the transmission in each frame by $S_k$. In order to simplify, the length of the TDMA timeframe in the secondary network is normalized to unity. When transmitting data, each $S_k$ occupies a time period of $t_{s_k}\left(0<t_{s_k}<1\right)$, and the maximum transmission power of $S_k$ is set to $p_{S_k,\max }$. Thus, the problem formulation can be reduced to the following formulas:

$$\begin{array}{l}\underset{t_{S_k},Q_{S_k},F_{T_n,S_k}}{{\displaystyle \min }}{\displaystyle \sum _{n=1}^N}{\displaystyle \sum _{k=1}^K{t}_{S_k}tr(F_{T_n,S_k}{Q}_{S_k})}\\ s.t.C1:t_{S_k}w\log [\det (I+\frac{H_{BS,S_k}{F}_{T_n,S_k}{Q}_{S_k}{H}_{BS,S}^H}{C_{S_k}^{}})]\ge R_{S_k},\forall k,n\\ \hspace{1em} C2:{\displaystyle \sum _{k=1}^K{t}_{S_k}}\le 1,\\ \hspace{1em} C3:\frac{1}{j}tr(H_{P_j,S_k}{F}_{T_n,S_k}{Q}_{S_k}{H}_{P_j,S_k}^H)\le {\varphi }_{P_j},\forall k,j,n\\ \hspace{1em} C4:tr(F_{T_n,S_k}{Q}_{S_k})\le P_{S_k,\max },\forall k,n\\ \hspace{1em} C5:{\displaystyle \sum _{k=1}^K{F}_{T_n,S_k}}\le d_f,\forall n\\ \hspace{1em} C6:{\displaystyle \sum _{n=1}^N{F}_{T_n,S_k}}\le d_v,\forall k\\ \hspace{1em} C7:F_{T_n,S_k}\in \left\{0,1\right\},\forall k,n\\ \hspace{1em} C8:t_{S_k}\ge 0,\forall k,\\ \hspace{1em} C9:Q_{S_k}\succcurlyeq 0,\forall k.\end{array}.$$

(8)

Equation (8) is used to minimize the total energy consumption of the entire network. C1 guarantees the rate requirement for each SU. C2 indicates that the total time allocated for all SUs does not exceed the frame length. C3 implies that each primary receiver suffers interference below the interference threshold ${\varphi }_{P_j}$. C4 indicates that the maximum transmittance of $S_k$ is not more than $p_{S_k,\max }$. C5 limits the maximum number of multiplexed signals in each slot, and $d_f$ represents the maximum number of users that can be multiplexed in each slot. C6 guarantees that each user occupies $d_v$ time slots, thus ensuring the sparsity of SCMA. C8 means that the time allocated by each SU is non-negative. C9 ensures that the covariance matrix $Q_{S_k}$ of $S_k$ is a semidefinite matrix.

4.2. Problem Optimization

For this mathematical model, the objective function and C1 fall into the scope of nonconvex problems, while the model realization implies solving a nondeterministic polynomial (N-P) problem. The direct solution to the N-P problem is usually difficult. Given $F_{T_n,S_k}$ in general, in the statistical CSI, the channel matrix $H_{P_j,S_k}$ has zero mean and a variance of ${\beta }_{P_j,S_k}$, where ${\beta }_{P_j,S_k}$ denotes the path loss from $S_k$ to the jth primary receiver [42]. Numerous wireless applications are known to accept occasional outages without affecting the QoS. Let ${\delta }_{P_j}$ denote the outage probability. This probability should be very small, to ensure a high probability of satisfying the interference constraint of primary users. The C3 is then replaced by

$$\underset{H_{P_j,S_k}}{\mathrm{Pr}}\left\{\mathrm{tr}\left(H_{P_j,S_k}{F}_{T_n,S_k}{Q}_{S_k}{H}_{P_j,S_k}^H\right)\le {\varphi }_{P_j}\right\}\ge 1-{\delta }_{P_j},\forall k,j,n,$$

(9)

where the probability is taken over $H_{P_j,S_k}$. We assume that ${\beta }_{P_j,S_k}$ is known to $S_k$. Given the Rayleigh distribution of the channels, an exponential distribution with the parameter $1/{\beta }_{p_j,S_k}tr\left(F_{T_n,S_k}{Q}_{S_k}\right)$ can be obtained from Reference [43]. Equation (9) can be rewritten as:

$$\underset{{}_{H_{P_j,S_k}}}{\mathrm{Pr}}\{tr\left(H_{P_j,S_k}{F}_{T_n,S_k}{Q}_{S_k}{H}_{P_j,S_k}^H\right)\le {\varphi }_{P_j}\}=1-\exp \left(-\frac{{\varphi }_{p_j}}{{\beta }_{P_j,S_k}tr\left(F_{T_n,S_k}{Q}_{S_k}\right)}\right).$$

(10)

Thus, the outage probability constraint (9) is equivalent to

$$tr\left(F_{T_n,S_k}{Q}_{S_k}\right)\le \frac{-\varphi p_j}{{\beta }_{P_j,S_k}\log {\delta }_{P_j}},\forall k,j,n.$$

(11)

In addition, we can combine Formula (11) with constraint C4 in Equation (8), which has the same form and can be reconstructed as

$$tr\left(F_{T_n,S_k}{Q}_{S_k}\right)\le {\rho }_{S_k},\forall k,n,$$

(12)

where ${\rho }_{S_k}$ is satisfied as

$${\rho }_{S_k}=\min \left\{\frac{-{\varphi }_{P_1}}{{\beta }_{P_1,S_k}\log {\delta }_{P_1}},\cdots ,\frac{-{\varphi }_{P_J}}{{\beta }_{P_J,S_k}\log {\delta }_{P_J}},p_{S_k,\max }\right\}.$$

(13)

Given $F_{T_n,S_k}$, the maximum instantaneous rate $r_{S_k,\max }$ of $S_k$ (in nats per second) is limited by its maximum transmission power and the interference caused to the primary user. The maximum instantaneous rate of each SU is expressed as follows [26]:

$$\begin{array}{l}\underset{{}_{Q_{S_k}}}{\max }w\log [\det (I+\frac{H_{BS,S_k}{F}_{T_n,S_k}{Q}_{S_k}{H}_{BS,S_k}^H}{C_{S_k}^{}})]\\ s.t.\mathrm{C}1:tr(F_{T_n,S_k}{Q}_{S_k})\le {\rho }_{S_k},\\ \hspace{1em} \mathrm{C}2:Q_{S_k}\succcurlyeq 0.\end{array},$$

(14)

Equation (14) can be solved via the standard “water-filling (WF)” algorithm [44,45]. The minimum time resource $t_{S_k,\min }$, which is needed by each $S_k$ to satisfy the rate requirement, is calculated as

$$t_{S_k,\min }=\frac{R_{S_k}}{r_{S_k,\max }}.$$

(15)

Given any feasible time allocation $\left(t_{S_1},\cdots ,t_{S_K}\right)$, Equation (8) reduces separate transmit covariance matrix optimization problems to K, one for each $S_k$:

$$\begin{array}{l}\underset{{}_{Q_{S_k}}}{\min }tr\left(Q_{S_k}\right)\\ s.t.\mathrm{C}1:w\log [\det (I+\frac{H_{BS,S_k}{F}_{T_n,S_k}{Q}_{S_k}{H}_{BS,S_k}^H}{C_{S_k}^{}})]\ge \frac{R_{S_k}}{t_{S_k}}\\ \hspace{1em} C2:tr(F_{T_n,S_k}{Q}_{S_k})\le {\rho }_{S_k},\\ \hspace{1em} \mathrm{C}3:Q_{S_k}\succcurlyeq 0\end{array}.$$

(16)

.

Let $A_{S_k}=H_{BS,S_k}{C}_{S_k}^{-1}{H}_{BS,S_k}^H$ and $W_{S_k}=rank\left(A_{S_k}\right)$, $A_{S_k}$ is an $M_{S_k}\times M_{S_k}$ Hermitian positive semidefinite matrix, and all the non-negative eigenvalues of $A_{S_k}$ are ${\lambda }_{S_k,1}\ge {\lambda }_{S_k,2}\ge \cdots \ge {\lambda }_{S_K,W_{S_k}}$. When the CSI is known at the transmitter (and at the receiver), then $H_{BS,S_k}$ is known in (16) and we optimize the capacity over $Q_{S_k}$ subject to the power constraint $tr(F_{T_n,S_k}{Q}_{S_k})\le {\rho }_{S_k}$. According to the principle of the WF algorithm [45], if $t_{S_k}\ge t_{S_k,\min }$ is satisfied, then the resulting capacity is given by

$$C_{WF}=r_{S_k,\max }={\displaystyle \sum _{i=1}^{W_{S_k}}\log }{\left({\lambda }_{S_{k,i}}{\mu }_{S_k}\right)}^{+}=\frac{R_{S_k}}{w{t}_{S_k}},$$

(17)

where ${(x)}^{+}=\max \{0,x\}$, and the ${\mu }_{S_k}$ is chosen to satisfy

$${\rho }_{S_k}={\displaystyle \sum _{i=1}^{W_{S_k}}{\left({\mu }_{S_k}-{\lambda }_{S_{k,i}}^{-1}\right)}^{+}}.$$

(18)

The WF is adopted to tackle the power limitation of $S_k$. Equation (8) can be re-arranged for the case of a convex problem of the time allocation optimization. Therefore, the energy consumption for $S_k$ is a function of $t_{S_k}$, which can be computed as [43]:

$$E_{S_k}(t_{S_k})=t_{S_k}\left(D_{S_k}^{\ast }(t_{S_k}){\mu }_{{}_{S_k}}^{*}-{\displaystyle \sum _{i=1}^{D_{S_k}^{\ast }(t_{S_k})}\frac{1}{{\lambda }_{S_k,i}}}\right),$$

(19)

where ${\mu }_{{}_{S_k}}^{*}={\left(\frac{\exp (\frac{R_{S_k}}{w{t}_{S_k}})}{{\displaystyle \sum _{i=1}^{D_{S_k}^{\ast }(t_{S_k})}{\lambda }_{S_k,i}}}\right)}^{\frac{1}{D_{S_k}^{\ast }(t_{S_k})}}$ is the optimal “water level” which is a function of $t_{S_k}$. Where $D_{S_k}^{*}\left(t_{S_k}\right)$ is the optimal number of data streams. The optimal number of data streams and the optimal energy consumption of each $S_k$ are dependent on its time resource allocation, which can be written as

$$D_{S_k}^{\ast }(t_{S_k})=\{\begin{array}{c}{w}_{S_k},0\le t_{S_k}\le {\tau }_{S_k}(w_{S_k}-1)\\ m_{S_k},{\tau }_{S_k}(m_{S_k})\le t_{S_k}\le {\tau }_{S_k}(m_{S_k}-1)\\ 1,t_{S_k}\ge {\tau }_{S_k}(1)\end{array},$$

(20)

and,

$${\tau }_{S_k}(m_{S_k})=\frac{R_{S_k}}{w\left(\left({\displaystyle \sum _{i=1}^{m_{S_k}}\log {\lambda }_{S_k,i}}\right)-m_{S_k}\log {\lambda }_{S_k,(m_{S_k}+1)}\right)},$$

(21)

where ${\tau }_{S_k}$ is a reduction function of $m_{S_k}$, and $m_{S_k}\in \left\{1,\cdots ,\left(W_{S_k}-1\right)\right\}$.

It is noteworthy that $E_{S_k}\left(t_{S_k}\right)$ takes different forms at various intervals of $t_{S_k}$, because $D_{S_k}^{\ast }(t_{S_k})$ is a step-wise function of $t_{S_k}$. It follows from Equation (8) that $E_{S_k}\left(t_{S_k}\right)$ is a continuous function. In addition, the optimal energy consumption $E_{S_k}\left(t_{S_k}\right)$ of $S_k$ is a first-order differentiable, strictly convex function. Therefore, the mathematical model of Equation (8) is finally transformed into the following form:

$$\begin{array}{l}\underset{t_{S_k}}{{\displaystyle \min }}{\displaystyle \sum _{k=1}^K{E}_{S_k}(t_{S_k})}\\ s.t.\mathrm{C}1:{\displaystyle \sum _{k=1}^K{t}_{S_k}=1,}\\ \hspace{1em} \mathrm{C}2:t_{S_k}\ge t_{S_k,\min },\forall k\end{array}.$$

(22)

It follows from (22) that the non-convex problem of the energy consumption in the secondary system can be reduced to the convex problem of time allocation optimization.

In this network, each frame is subdivided into many time slots, which participate in the allocation as the smallest unit of time. Under the normal conditions, the time resource allocated by each $S_k$ is an integer multiple of the time slot. Assume that a normalized time cycle has T slots so that the time resource optimization problem among the SUs is given by

$$\begin{array}{l}\underset{t_{S_k}}{\min }{\displaystyle \sum _{k=1}^K{E}_{S_k}(t_{S_k})}\\ s.t.\mathrm{C}1:{\displaystyle \sum _{k=1}^K{t}_{S_k}}=T,\\ \hspace{1em} \mathrm{C}2:t_{S_k}=\left\{t_{S_k,\min }^{(I)},(t_{S_k,\min }^{(I)}+1),\cdots ,T\right\},\forall k\end{array},$$

(23)

where $t_{S_k,\min }^{(I)}=\lceil t_{S_k,\min }T\rceil$ is the minimum number of time slots for each $S_k$. Equation (23) corresponds to an integer convex optimization problem, if and only if the following conditions are satisfied:

$${\displaystyle \sum _{k=1}^K{t}_{S_k,\min }^{(I)}}\le T.$$

(24)

In the TDMA-based orthogonal slot allocation network, a simple greedy algorithm can be used to solve Equation (23) [26,46]. Assuming the number of allocated time slots of $S_k$ is increased from $t_{S_k}-1$ to $t_{S_k}$, the energy consumption variation ${\Delta }_k\left(t_{S_k}\right)$ can be defined as:

$$\begin{array}{c}{\Delta }_k\left(t_{S_k}\right)=E_{S_k}\left(t_{S_k}\right)-E_{S_k}\left(t_{S_k}-1\right),\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{t}_{S_k}=\left\{t_{S_k,\min }^{(I)},\left(t_{S_k,\min }^{(I)}+1\right),\cdots ,T\right\}\end{array}.$$

(25)

In the greedy algorithm, starting from the minimum slots’ allocation $t_{\min }^{(I)}=\left(t_{S_1,\min }^{(I)},\cdots ,t_{S_K,\min }^{(I)}\right)$, one time slot is allocated at a time. A time slot is added to the $S_k$, which has the minimum ${\Delta }_k\left(t_{S_k}\right)$ among all the SUs.

5. SCMA-Based Non-Orthogonal Slot Allocation

The monotonicity of the $E_{S_k}\left(t_{S_k}\right)$ function implies that the more time each $S_k$ is allocated, the less energy it consumes. The TDMA-based orthogonal slot allocation avoids the interference between SUs but also limits the number of users accessing the network. The NOMA concept, which has been introduced by the International Mobile Telecommunications for 2020 (IMT-2020) (5G) Promotion Group in China in 2013 for the next generation of wireless communication, can realize sharing of time-frequency resources, which does not make the user’s access strictly orthogonal, but excludes any serious interference between users [47]. Within the framework of the NOMA concept, the SCMA technology is lucrative air interface technology [42]. Using the same time-frequency resource, SCMA can achieve 150%, 200%, or even higher equipment connection [9]. The nonconvex problem of the total energy consumption of the multi-user system can be transformed into the convex problem of time allocation optimization. Note that Equation (23) is a piecewise function of $t_{S_k}$, and although the function is continuous and the first-order is differentiable, unfortunately, its second order is not. Therefore, only the first-order optimization method is available. In order to optimize the time slot allocation, a nonorthogonal slot allocation strategy based on SCMA is proposed, which can realize the sharing of TDMA time slots and achieve the overload rates of 150%, 200%, 250% or even higher under the same time slot resource so that the SUs cause no serious interference. In the following subsection, the implementation process is described in detail.

5.1. Time Slot Grouping

The obtained relation between the SCMA factor graph and matrix F implies that the time slot can deal with more SUs data through sharing, for example, with overload rates of 150%, 200% and so on. Due to slot sharing, the SCMA-based nonorthogonal slot allocation requires different slot allocation strategies than the TDMA-based approach. The implementation of non-orthogonal slot allocation is based on a sharing time slot as a unit, which is referred to as shared slot unit. Therefore, it is necessary to group the total time slots within a frame. Each successive N time slot is subdivided into groups, with no overlaps among groups, which means that the relation between groups is orthogonal, while N time slots in each group are nonorthogonal. The total number of groups obtained is calculated as:

$$T_N=\frac{T}{N},$$

(26)

where $T_N$ is the number of shared slot units after grouping.

5.2. A Method of Virtually Adding Users

After grouping, each group starts accessing SUs, which need access with SCMA technology and to satisfy the minimum time requirements of each SU. The minimum slots $n_{S_k}=t_{S_k,\min }^{\left(I\right)}$ of $S_k$ are required to be extended to the shared slot. If $n_{S_k}=1$, it is directly extended to one shared time slot unit. But, for $n_{S_k}>1$, the data of $S_k$ would need to be extended to more than one shared unit, which is quite problematic when J SUs are assigned to one shared unit. For simplicity, we adopted a method of virtually adding users. In other words, each $S_k$ is treated as $n_{S_k}$ SUs that occupy a shared unit, where $s_k=[s_{k,1},\cdots ,s_{k,i},\cdots s_{k,n_{S_k}}]$ to facilitate the packet access. The virtualization process of $S_k$ is depicted in Figure 4. The total number, $L$, of SUs obtained in the secondary system at this time is calculated as:

$$L={\displaystyle \sum _{k=1}^K{t}_{S_k,\min }^{(I)}}={\displaystyle \sum _{k=1}^K{\displaystyle \sum _{i=1}^{n_{S_k}}{t}_{S_{k,i},\min }^{(I)}}}.$$

(27)

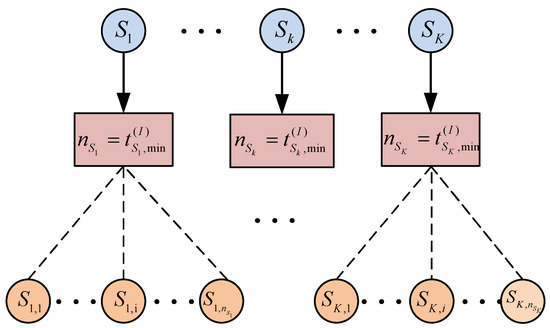
Figure 4. The virtualization process of $S_k$.

Now, the minimum time slot needed for each SU is 1.

The virtualization process of $S_k$ does not affect the true $S_k$, which is not required for the data mapping into several shared slot units. The access of each SU to shared slot units is easily organized. We assume that a shared time slot unit can be accessed by J SUs so that the grouping of L SUs is required. The group principle is as follows:

$$\begin{array}{l}{L}_{\tau }=fix(\frac{L}{J});m=\mathrm{mod}(L,J),\\ \{\begin{array}{c}{L}_{\tau ,\min }=L_{\tau },m=0,\\ L_{\tau ,\min }=L_{\tau }+1,m\ne 0,\end{array}\end{array}.$$

(28)

The integer part and remainder of $L/J$ is obtained by fix (.) and mod (.), respectively. $L_{\tau ,\min }$ is the minimum time required to meet the rate requirements of all SUs. The formula shows that when the number of the remaining users in the last group is insufficient, a shared time slot unit should be allocated to the remaining users. If $L_{\tau ,\min }<T_N$, the remaining shared time slots need to be allocated to SUs of some groups with some guidelines. Insofar as J SUs can share a shared time slot, the transmission energy consumption of each $S_{k,i}$ should be taken into account to ensure that the shared slot provides a more accurate allocation for all members of a group.

In this section, the greedy algorithm is used to allocate the surplus shared slot units with the average energy difference value (D-value) of all members of a group. Assume the shared time slot unit from $L_{t,1}$ to $L_{t,n}$ at the time of $L_{\tau ,\min }$, whereas $L_{t,i}$ has accessed $J_{t,i}$ SUs. Let ${\Delta }_{L_{t,i}}\left(t_{L_{t,i}}\right)$ denote the average energy D-value among all SUs in $L_{t,i}$, which can be written as:

$$\begin{array}{ll}{\Delta }_{L_{t,i}}\left(t_{L_{t,i}}\right)=\{{\displaystyle \sum _{j_{t,i}=1}^{J_{t,i}}}& \left[E_{S_{k,i}}^{J_{t,i}}\left({t^{\prime }}_{S_k}\right)-E_{S_{K,i}}^{J_{t,i}}\left({t^{\prime }}_{S_k}-1\right)\right]\}/J_{t,i}\\ & {t^{\prime }}_{S_k}\in N\times \left\{t_{S_{k,i},\min }^{(I)},(t_{S_{k,i},\min }^{(I)}+1),\cdots ,T_N\right\}\end{array}.$$

(29)

After the allocation is started, the shared time slot unit is allocated from the minimum period $t_{S_{k,i},\min }^{(I)}=\left(t_{S_{1,1},\min }^{(I)},\cdots ,t_{S_{K,n_{S_K}},\min }^{(I)}\right)$, and at the same time, one shared time slot will be allocated each time. A shared time slot is allocated to the members of $L_{t,i}$, which have the minimum ${\Delta }_{L_{t,i}}\left(t_{L_{t,i}}\right)$ among all $L_{\tau ,\min }$. The algorithm will stop after allocating all TN shared time slots. The process is shown in Figure 5.

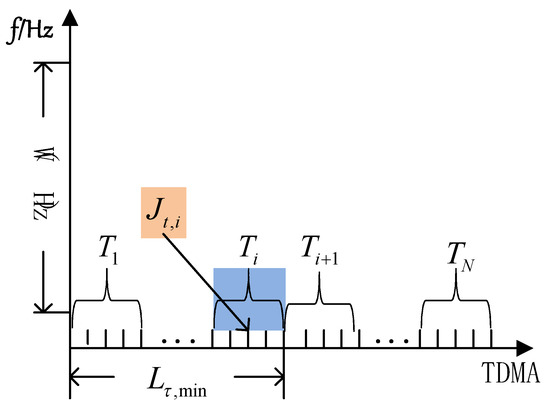
Figure 5. Division of time slot and access of SUs.

In Figure 5, W is bandwidth, and the band frame used in this study is 20 MHz. Also, the SCMA principle is realized by the sparse spread spectrum and combined with the codebook design. It is known that the data of each $S_k$ after spreading causes the data to increase. Therefore, the non-orthogonal slot sharing of SCMA, $r_{S_k},$ must be substituted by the data rate $r{\prime }_{S_k}$ after spreading. Since SCMA uses the sparse spread spectrum, the value $r{\prime }_{S_k}=2r_{S_{k }}$ is used to calculate $E_{S_{k,i}}^{j_{t,i}}\left({t\prime }_{S_k}\right)$ by using Equation (6). The flowchart for the SCMA-based nonorthogonal slot allocation optimization scheme is shown in Figure 6.

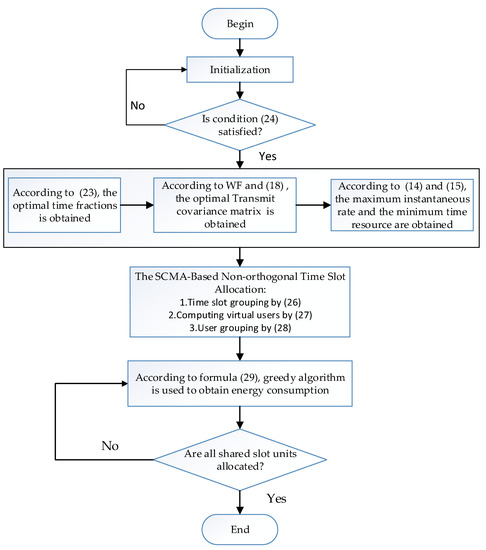
Figure 6. The flowchart for the SCMA-based nonorthogonal slot allocation optimization scheme.

6. Numerical Results

To verify the performance of the proposed method regarding energy consumption, interference caused by the secondary system to the PUs links system and its user capacity, the simulation system is set up. Two pairs of PU links with a distance of 10 m are established between the transceivers. It is assumed that each node in the MIMO-CR network has four antennas. The parameters of the system are summarized in Table 3.

Table 3. Simulation parameters.

Parameter	Value
Frame length	20 ms
Each frame	200 time slots
Carrier frequency	1 GHz
Bandwidth	20 MHZ
Cell	200*200 m
Noise power density (N0)	−178 dBm/Hz
Interference power threshold (${\varphi }_{P_j}/\left(N0\ast w\right)$)	25 dB
Outage probability (${\delta }_{P_j}$)	0.01
Maximum transmitting power of PUs	20 dBm
Maximum transmitting power of SUs	27.5 dBm
Rate requirement of SU	32 kbps
Channel model	Rayleigh fading channel
SCMA overload factor	1.5\2.0\2.5
Number of transceiver antennas	4
Minimum distance between BS and SUs	10 m

6.1. Energy Consumption

Figure 7 shows the cumulative distribution function (CDF) of the average energy consumption of the MIMO-CR system. The SCMA-based nonorthogonal time allocation scheme is compared with the slot allocation schemes of “MIMO and max-rate” and “MIMO and OMA”, respectively. In the “MIMO and max-rate” scheme, each SU uses the minimum time resource and the transmission covariance matrix solved by Formula (14) with the maximum achievable rate. In addition, in the “MIMO and OMA” scheme proposed in Reference [25], the orthogonal slot allocation scheme is adopted for MIMO-CR system. The number of SUs is set to 35, the overload rate of SCMA is 150%, and the distance between secondary user and secondary BS is not less than 10 m, as shown in Figure 1. Compared with MIMO and max-rate and MIMO and OMA, this algorithm can significantly reduce the energy consumption of the MIMO-CR system. This is because the SCMA-based nonorthogonal time allocation scheme makes use of its sparse feature. After slot allocation, each SU gets more time than the orthogonal slot allocation strategy.

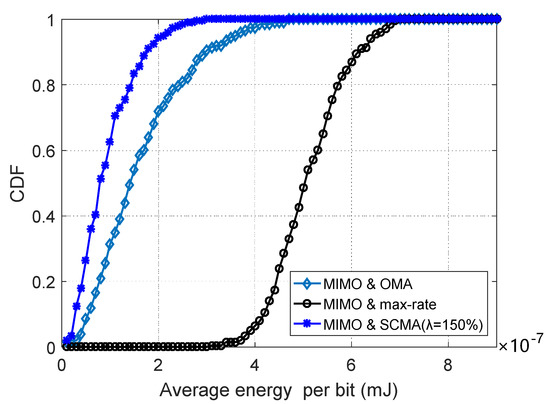
Figure 7. The cumulative distribution function (CDF) of the three schemes.

The relationship between the average energy consumption per bit of the system and the minimum distance between the SUs and secondary BS is shown in Figure 8. In this scheme, the number of SUs is set to 35, and the overload rate is 150%. The location relationship and minimum distance between the secondary BS and SUs are shown in Figure 9. The average energy consumption per bit of the three schemes increases with the distance between the secondary BS and the SUs, because in order to ensure the QoS of the user, the transmission power needs to be increased. “MIMO and OMA” and “MIMO and max-rate” algorithms mainly use the orthogonal slot allocation scheme and refer to the user’s channel gain for allocation. The CSI is mainly determined by the reference distance and path loss. Therefore, with the increasing space distance between the SUs and the BS, the channel state will become worse and the energy consumption will be more and more. The SCMA-based nonorthogonal time allocation scheme algorithm proposed in this paper is less affected by distance and can achieve greater energy savings.

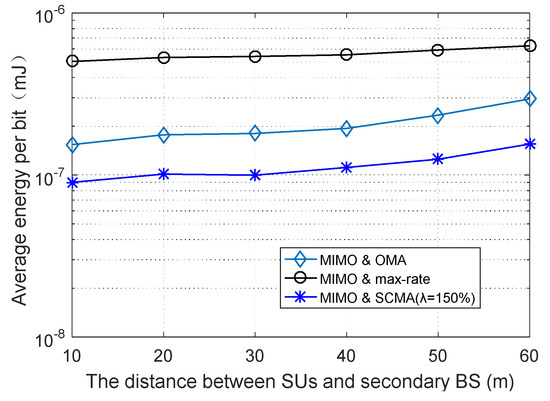
Figure 8. The average energy consumption per bit versus the minimum distance between the SUs and secondary BS.

Figure 9. The minimum distance between the SUs and secondary BS.

The energy consumption per bit of SUs is shown in Figure 10. In this study, the “MIMO and max-rate”, “MIMO and optimum time” and the “SCMA and optimum time” schemes for the overload rates of 150%, 200% and 250% are simulated and compared. In the “MIMO and optimal time”, each SU optimizes its time allocation with multiple data streams [26]. As illustrated in Figure 10, the average energy consumption per bit of all the optimal time allocations is lower than that of the “MIMO and max-rate”. When the number of SUs in the system is small, the energy consumption in the proposed SCMA-based nonorthogonal time allocation scheme is higher than that of the orthogonal one. This can be attributed to the fact that the data rate of SUs is increased after the sparse spread spectrum. However, for a larger number of SUs, the application of SCMA nonorthogonal slot allocation has certain advantages in the energy efficiency, and with an increase in the SCMA overload rate (λ = 250%), the energy efficiency improvement becomes more pronounced, saving nearly 40% of energy consumption. The reason is that when the time slot allocation is completed via the nonorthogonal slot sharing allocation strategy, each SU obtains more time than in the case of the orthogonal slot allocation, which promotes the data rate increase after sparse spreading. With the development trend of future wireless communications, the secondary system will access more SUs. Therefore, the use of the SCMA nonorthogonal slot sharing allocation strategy has some advantages in reducing power consumption and improving energy efficiency.

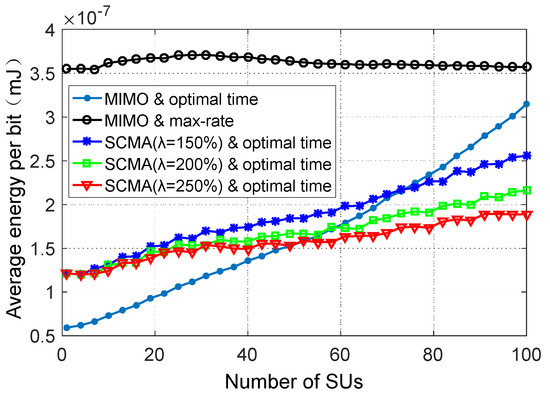
Figure 10. The average energy consumption per bit versus the number of SUs.

6.2. User Capacity

Figure 11 shows the user capacity of the secondary system with the time slots from T = 4 to T = 100, which is measured by the maximum number of SUs accessed by the system if and only if it satisfies the need of each SU in the time slots (referred to as “the min-time slots scheme”). Thus, ${{\displaystyle \sum }}_{k=1}^K{t}_{S_k,\min }^{\left(I\right)}=T$. In Figure 11, the number of SUs of the secondary system is increased with the number of time slots. The SU capacity with the SCMA-based nonorthogonal slot access has some advantages over that provided by the orthogonal slot access scheme. For example, when the overload rate is 150%, the user capacity of nonorthogonal slot access is 50% higher than that of the orthogonal slot access with T = 100. As the overload rate increases, the number of SUs rapidly increases. Therefore, the SCMA-based nonorthogonal slot access is an effective way to improve the secondary system’s user capacity.

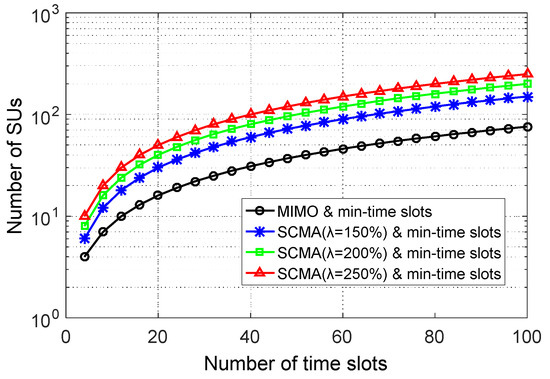
Figure 11. The number of SUs versus the number of time slots.

6.3. Interference

Figure 12 demonstrates the average interference power from SUs to PUs links, which is based on the interference noise ratio (INR) as the main standard. As seen in Figure 12, the average INR in the “MIMO and max-rate” scheme is less than the required 25 dB, because the transmitting power of the SU needs to meet its interference constraint at two PUs links. When the excess time slots are allocated rationally, the INR is less than that of the “MIMO and max-rate” scheme. In other words, the interference to the PUs links is reduced. When the number of SUs is small, the average INR in the proposed SCMA-based nonorthogonal time allocation scheme is higher than that in the case of the orthogonal slot allocation. This occurs because the sparse spread spectrum leads to an increase in the data rate of SUs. However, for a larger number of SUs, the SCMA-based nonorthogonal slot allocation has certain advantages in reducing the interference, advantages which become more pronounced at the higher SCMA overload rates. Moreover, one can observe that the interference power in the “SCMA and optimal time” scheme increases slower than in the “MIMO and optimal time”.

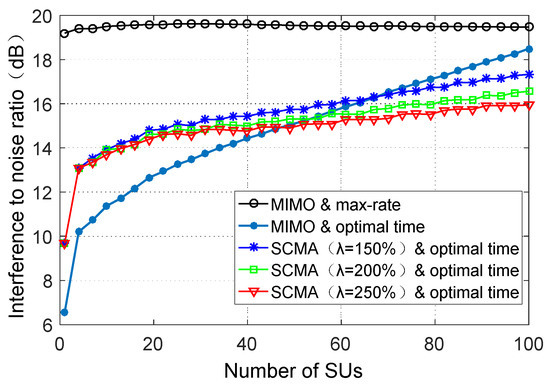
Figure 12. Average interference power at PUs links versus the number of SUs.

Figure 13 shows the average INR from the SUs to the PUs links in the “min-time slots” scheme versus the number of SUs. The time slot number is 100, which satisfies the minimum slot needs of each SU without considering the excess slot allocation problem of SUs. As seen in Figure 13, the interference is less than 25 dB for both orthogonal and nonorthogonal access slot allocation schemes, because SU must satisfy the interference threshold for any kind of access. However, the INR of the SCMA-based nonorthogonal slot access scheme is higher than that of the orthogonal one. The average energy difference value (D-value) is about 2 dB. It can also be seen that the average INR of SCMA for the overload rates of 150% and 200% are nearly identical. Thus, the magnitude of the overload rate has a feeble effect on the average interference power of the PUs links.

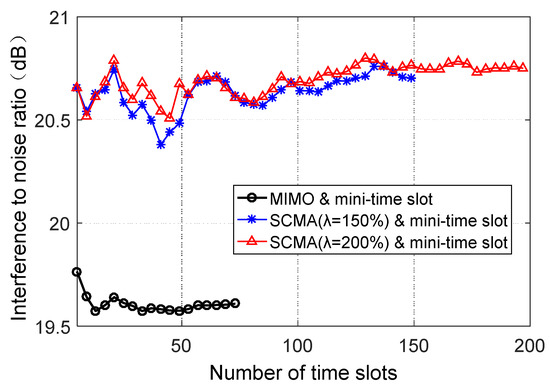
Figure 13. Average interference power at PUs links versus the number of SUs, if and only if the min-time slot requirement is satisfied.

7. Discussion and Conclusions

In this paper, the nonconvex problem of energy consumption in MIMO-CR networks under the underlay model was reduced to the convex problem of time allocation optimization, which was implemented via the TDMA technology. The greedy algorithm was adopted to solve the latter problem, while the SCMA-based nonorthogonal optimization method was used to optimize the slot allocation. By attaining the maximum transmission rate of each SU, the minimum time needed by each SU to transmit data can be obtained. Under the requirement of the minimum time slot of SUs, the total energy consumption of SUs can be improved by optimizing time slot allocation. The SCMA-based nonorthogonal slot allocation requires time slot grouping and user packet access. In this paper, the method of adding virtual SUs was adopted to simplify the packet access. The average energy D-value of all SUs among the same shared time slot was determined as the allocation criterion. The simulation results obtained show that for a larger number of SUs, the SCMA-based nonorthogonal slot allocation has lower energy consumption and the interference to the PUs links than the orthogonal slot allocation. With an increase in the SCMA overload rate, these advantages become more pronounced. It is noteworthy that the maximum number of SUs (i.e., the spectrum) of the secondary system was substantially improved without exceeding the interference threshold, which makes the proposed slot allocation scheme quite lucrative for further large-scale implementation.

The scheme provided in this paper is helpful for the following further research: (1) This paper considers the statistical CSI between users, so we will expand to a more general channel and CSI for further research. (2) With the increase of data stream and the complexity of high-dimensional modulation, the interference between SUs will be a topic that must be considered. Therefore, we will further trade-off between multiplexing and interference cancellation.