Abstract
This paper investigates the energy-efficient communications and user capacity in the cognitive multiple input multiple output (MIMO) symmetric system of underlay mode. The advantage of the improved energy efficiency provided by the orthogonal slot allocation for time division multiple access (TDMA) has a side effect of restricting the number of users accessing the system. To tackle the above problem, this paper proposes a nonorthogonal time resource allocation method with sparse code multiple access (SCMA), which allows one to convert the orthogonal slot units of TDMA into non-orthogonal shared slot units for multiple secondary users (SUs). The method of adding virtual users is adopted, wherein each SU is treated as multiple SUs who occupy a shared unit, to facilitate the packet access. Finally, the greedy algorithm is applied to optimize the time slot allocation of unoccupied shared slot units. The simulation results show that SCMA-based nonorthogonal slot allocation can reduce not only the energy consumption by nearly 40%, but also the average power interference from SUs to primary users by nearly 2 dB if their number is relatively high. Moreover, in the case of satisfying the rate requirement of the users, the system user capacity increased by more than 50%.
1. Introduction
The state-of-the-art wireless communication system should have adequate characteristics of continuous wide area coverage, hot spot area, high capacity, low energy consumption, and mass connection [1]. The latter two issues, given the increased energy consumption and limited spectrum supply/demand, are quite urgent. Low power consumption is the key to reducing carbon emissions, extending battery life, and promoting “green communications” for wireless devices [2,3,4]. Numerous studies have been performed with the aim of more comprehensive use of spectrum resources, improving the spectrum utilization efficiency, reducing power/energy consumption, and overall improvement of the energy efficiency (EE). This paper addresses the issues of energy efficiency and user capacity in a cognitive wireless network with multiple antennas and a sharing time slot. Nowadays, many research efforts are dedicated to the cognitive radio (CR), which is a new type of radio with adaptive spectrum awareness that is centered on spectrum sensing and intelligent learning capabilities. CR enables secondary users (SUs) to adaptively occupy the local spectrum of primary authorized users (PUs) available immediately [2,3]. In recent years, the diverse applications of CR technology have also received more and more attention. For example, CR will be a brand-new field for the tactile Internet, and it is expected to improve the overall quality of the network [5]. In addition, CR has certain guiding significance for the data decision of internet of multimedia things (IoMT) [6].The multiple input multiple output (MIMO) approach is used to ensure the coexistence of SUs and PUs in the space domain, and to avoid adverse interference to the primary user links [7,8]. Among the popular technologies of the fifth generation (5G) mobile communication, the sparse code multiple access (SCMA) technology can provide strong support for slot sharing [9,10]. Therefore, the cognitive MIMO radio network can provide support for more users to access resources in the same time by combining SCMA technology.
SCMA is one of the nonorthogonal multiple access (NOMA) technologies, which was developed on the base of the code division multiple access (CDMA) technology of low-density signature (referred to as LDS-CDMA), which is a kind of physical layer potential air interface technology. In particular, the LDS-CDMA has been put forward to solve the problem of the system overload during mass connection [11,12,13]. In recent years, the LDS-CDMA technology was further developed into the high-performance SCMA, which joins the high dimensional and sparse spread spectra together so that the bit streams are directly mapped to predetermined codewords in the multidimensional complex domain. Due to the sparsity of spread spectrum code, no serious interference between users can occur, and the receiver can use the message passing algorithm (MPA) with a low complexity [14,15,16,17,18]. The structure is a spread spectrum on orthogonal frequency division multiplexing(OFDM) subcarriers and is detected by MPA. The SCMA sharing time-frequency resource units based on factor diagrams provide the theoretical support for time-sharing of time division multiple access (TDMA).
In recent years, the combination of CR and NOMA can further effectively improve energy efficiency, and spectrum utilization has been widely concerned [19,20,21,22,23,24]. But, its user capacity is limited, and there is even some interference from secondary systems. Therefore, many studies consider using MIMO technology to assist CR-NOMA networks to further improve energy efficiency while increasing the number of users’ access. Among many CR-MIMO technologies assisted by NOMA technology, SCMA technology has not been reported. Moreover, most of the research focuses on resource allocation and codebook design to study the utilization of energy efficiency, and few papers focus on non-orthogonal slot allocation to improve energy efficiency.
Inspired by the above research, this paper will further explore and analyze the energy consumption and user capacity of the secondary user in the cognitive MIMO system under the underlay model. The space division multiplexing of MIMO technology can ensure that multiple data streams are simultaneously transmitted to the base station (BS), which can achieve better EE than the transmit diversity approach, which is used to diminish the effects of fading by transmitting the same information from two different antenna models. It is known that the nonconvex problem of energy consumption in the system with multiple users can be reduced to the convex problem of time resource allocation optimization. Within the framework of the TDMA approach, the continuous time is split into discrete orthogonal slots, which allows one to avoid the interference between users, but limits the number of users in the MIMO-CR system. In order to override this obstacle, we propose to use the nonorthogonal slot access scheme and time resource allocation optimization based on SCMA. This will not only minimize the interference between users but also yield better EE than the orthogonal slot access and reduce the average interference power from the SUs to the PUs links when the system is accessed by a larger number of users. Considering the practical application, this study discusses the statistical channel state information (CSI) model, wherein the rate requirements of SUs and interference threshold are used to ensure the quality of service (QoS) of SUs and PUs, respectively. The interference power constraints are used to ensure with a high probability that the interference of SUs to PUs is below the threshold value. By meeting the minimum time slot requirements of each user, the system user capacity can be greatly enhanced.
Notation: Throughout the paper, we use bold uppercase and lowercase letters to denote matrices and vectors, respectively. For a square matrix A, tr (A), rank(A), AT, A* and AH denote its trace, rank, transpose, conjugate and conjugate transpose, respectively. denotes the space of complex matrices. denotes the absolute value of a scalar, and means A is a Hermitian positive semidefinite matrix. represents the statistical expectation and stands for the identity. indicates that the variable follows the complex normal distribution with mean and variance . denotes the ceiling of . and represent the integer part and remainder part of , respectively.
2. Related Works
Recently, SCMA technology has been discovered to be a NOMA technology with great potential because of its excellent advantages of improving spectrum efficiency. In the literature, most studies have focused on combining NOMA technology with CR technology to improve EE and user access [19,20,21,22,23,24]. In Reference [19], a CR-NOMA network with wireless information and power transmission (SWIPT) is considered under the nonlinear energy collection model to improve EE and spectrum efficiency (SE). In Reference [20], robust beamforming and power split control are jointly designed to optimize the transmission power minimization and energy harvesting maximization in the MISO-NOMA CR-aided SWIPT system. Reference [21] studied the optimization problem to maximize EE in the CR-NOMA system, which was proposed in two modes of the overlay network and underlying network. Reference [22] has designed a new secure CR-NOMA transmission strategy that pairs the PUs and SUs according to the channel gain to improve the performance of the secondary system. In Reference [23], a fair-aware joint power allocation and SU allocation problem based on downlink cognitive NOMA networks is studied, in which an alternative optimization scheme is adopted to enhance the system capacity. Reference [24] studied the robust resource allocation and sub-channel allocation to maximize the total EE of SUs from the perspective of EE-robustness trade-offs in the multi-user cognitive NOMA network.
Although NOMA-SU allocation technology is an effective method, it can enhance the resource utilization efficiency in the power domain and spectrum domain to support the cognitive NOMA network [23]. However, it is difficult to guarantee that EE can be improved while accessing more users and reducing interference. Therefore, we consider introducing MIMO technology into the CR system to improve its performance. In the literature, most of the research on energy efficiency and user capacity of MIMO-assisted CR networks can be divided into two categories: the traditional CR-MIMO network [25,26,27,28,29,30,31,32,33,34,35] and the network combining CR-MIMO with NOMA (CR-MIMO-NOMA) Technology [36,37,38,39,40,41].
In the traditional CR-MIMO network, spectrum sensing and energy harvesting technology have been the main research directions in recent years [30,31,32,33,34,35], while the EE and user capacity were mainly studied in earlier years [25,26,27,28,29]. The problems of EE optimization of a MIMO-CR system with multiple secondary receivers for the cases of single and multiple data streams was addressed in References [25], respectively. In the latter case, a higher EE was achieved, as compared to the former one. In Reference [27], the problems of distributed and centralized energy efficiency optimization in CR-MIMO networks with interfering channels are proposed. Under the constraints of power and interference, the energy efficiency of the MIMO spectrum sharing cognitive radio system is studied in Reference [28]. In Reference [29], a method of antenna selection for a spatial multiplexing CR-MIMO system based on a linear receiver, and a cross-layer EE measurement method based on user capacity are proposed.
In recent years, more and more attention has been paid to the EE and user capacity of CR-MIMO-NOMA networks. In Reference [36], a CR-MIMO network inspired by NOMA was investigated, and a joint antenna selection (AS) algorithm with high computational efficiency was proposed to maximize the signal-to-noise ratio (SNR) of secondary users while satisfying the QoS of PUs. Reference [37] proposes a downlink cascading transmit zero-force beamforming (ZFBF) technology to ensure communication security in the CR-MIMO-NOMA network. In Reference [38], a new AS algorithm is proposed based on the maximum channel gain, on the premise of meeting the service quality requirements of the primary user, to maximize the reachable rate of the secondary user. Reference [39] proposes a framework for simultaneous spectral efficiency design using CR, MIMO and NOMA technologies in the downlink, and calculates the sum rate of secondary users. In Reference [40], a new design scheme is proposed to study the problem of coordinated beamforming and power allocation based on interference alignment (IA) in CR-MIMO-NOMA downlink networks. In Reference [41], it is proven that the spectrum efficiency and EE of MIMO-NOMA in the CR network are better than those of an orthogonal multiple access CR network based on MIMO-OMA by using the blindly combined energy detection (BCED).
In the literature, SCMA-assisted CR-MIMO network research has not been reported, and few papers focus on non-orthogonal slot allocation to improve energy efficiency. In this paper, we further explore and analyze the SCMA-based time slot allocation scheme to optimize the energy consumption and user capacity of secondary users in the CR-MIMO system. Table 1 provides a summary of the related work.

Table 1.
Summary of related work. Energy efficient (EE); User capacity (UC); Energy harvesting (EH); Spectrum efficiency (SE); Cognitive radio (CR); Multiple input multiple output (MIMO); Nonorthogonal multiple access (NOMA).
3. System Model
Consider a MIMO-CR network containing K SUs and J transmitter–receiver pairs. Let Sk and Pj denote the kth secondary user and jth pair of primary transmitter–receiver links, respectively. In the underlay model, the primary links are potentially active and always protected. The primary network consists of J transmitter–receiver pairs, while the secondary one is a single cellular network, in which all SUs have the uplinks via TDMA to the secondary base station (BS), and the SCMA-based non-orthogonal strategy is used for slot allocation. The secondary BS is located at the center of the secondary system, and can evaluate the channel matrix of , and feed it back to through an independent control channel. Therefore, the information on both and the secondary BS is fed into the channel matrix of . The uplink transmission of SUs is synchronized by the secondary BS, which allows SUs to make transmissions in orthogonal slots without interference. The coexistence of PUs and SUs in the CR networks implies their mutual interference. When the bandwidth exceeds the bandwidth of the transmitted signal, the gain of the frequency flat fading channel is constant and has a linear phase response, which is applied so that the channel matrix within the prescribed bandwidth is unchanged. Moreover, in the case of a block fading channel application, the channel matrix will not change within a TDMA frame and, thus, needs no correlation between frames. For example, consider two pairs of PUs links with a distance of 10 meters between transceivers. The SUs are randomly distributed in a 200*200m area, and the minimum separation distance from the PUs link is set to 35 m. The case of 35 SUs in the MIMO-CR network is depicted in Figure 1.
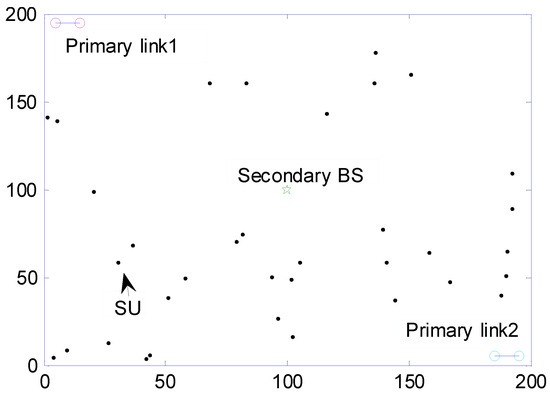
Figure 1.
A random MIMO-CR network.
In MIMO-CR symmetric networks, both PUs and SUs can transmit multiple data streams via multiple antennas. The list of related notations is provided in Table 2.

Table 2.
List of related notations.
The SCMA technology opens new horizons in the time-frequency resource sharing. Assuming an uplink SCMA system with users and resources (), the users share orthogonal time-frequency resources and transmit data to the same BS. The overloading factor is defined as . The bits of users are directly mapped to the shared orthogonal time-frequency resources through each individual codebook. The receiver with a low-complexity MPA multiuser detector can recover the transmitted bit data for each user. The uplink MIMO-CR SCMA system model with is shown in Figure 2, where denotes the Gaussian noise.
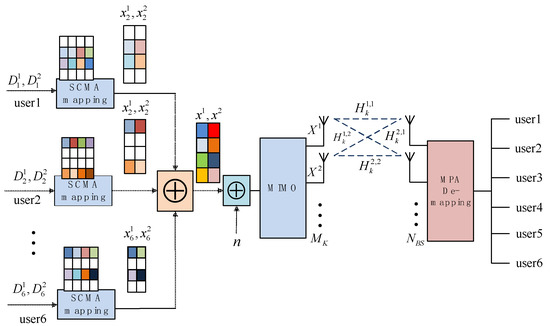
Figure 2.
Uplink MIMO-CR sparse code multiple access (SCMA) system model (K = 6, N = 4).
SCMA encoding can use the factor diagram matrix to represent. The variable node (VN) Vk connects to the function node (FN) Fn only if , otherwise, . When the VNs represent the SUs, and the FNs represent the time slot, the corresponding relation between the SCMA factor graph and matrix F is shown in Figure 3. , where if secondary user occupies time slot , otherwise . As seen in Figure 2and Figure 3, using the SCMA principle, we can share the TDMA orthogonal slot by the packet sharing to access more SUs. Therefore, in the same SUs conditions, when a frame is ended, the slot allocation strategy of SCMA-based non-orthogonal slot sharing provides more time being eventually assigned to each SU.
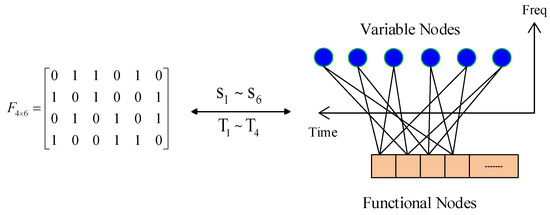
Figure 3.
The relation between matrix F and factor graph.
The received vector of at the secondary BS is derived as follows:
where is additive Gauss white noise with the noise power spectral density .
The user capacity of is defined as the maximum mutual information between the transmitter and receiver signals, as follows:
where is the covariance matrix of and is given by:
where eachV is given by:
If the secondary BS fails to eliminate the interference from the PUs links, which is regarded as noise, then the interference-plus-noise covariance matrix is derived as:
where w is defined as the bandwidth of the secondary network. is the covariance matrix of , which are Hermitian positive semidefinite matrices. According to Shannon’s formula, which interrelates and links the information rate with SNR and bandwidth in the MIMO link, the achievable transmission rate of can be depicted as:
where is the instantaneous transmission rate of , expressed in the natural units of information (nats) per second. The total transmission power of in all antennas is , while the total power of interference from to is calculated as:
4. Problem Formulation and Optimization
In this section, we first introduce the problem construction of SCMA-based nonorthogonal slot allocation in the cognitive MIMO system, and turn the energy efficiency problem into a mathematical formula. On this basis, the problem is further optimized by combining the statistical CSI and the numerical characteristics of time slot integer.
4.1. Problem Formulation
The system aims at optimizing the total power consumption of SU by allocating an appropriate transmission time for each SU. This would not only minimize the power of interference from SUs to PUs links, but also ensure an adequate QoS of each SU. In the statistical CSI, a power constraint is set for each SU to protect the PUs with the maximum possible QoS. To ensure QoS of each SU, the requirements on the transmission rate (in nats/second) of should be satisfied. Here, is the number of nats required for the transmission in each frame by . In order to simplify, the length of the TDMA timeframe in the secondary network is normalized to unity. When transmitting data, each occupies a time period of , and the maximum transmission power of is set to . Thus, the problem formulation can be reduced to the following formulas:
Equation (8) is used to minimize the total energy consumption of the entire network. C1 guarantees the rate requirement for each SU. C2 indicates that the total time allocated for all SUs does not exceed the frame length. C3 implies that each primary receiver suffers interference below the interference threshold . C4 indicates that the maximum transmittance of is not more than . C5 limits the maximum number of multiplexed signals in each slot, and represents the maximum number of users that can be multiplexed in each slot. C6 guarantees that each user occupies time slots, thus ensuring the sparsity of SCMA. C8 means that the time allocated by each SU is non-negative. C9 ensures that the covariance matrix of is a semidefinite matrix.
4.2. Problem Optimization
For this mathematical model, the objective function and C1 fall into the scope of nonconvex problems, while the model realization implies solving a nondeterministic polynomial (N-P) problem. The direct solution to the N-P problem is usually difficult. Given in general, in the statistical CSI, the channel matrix has zero mean and a variance of , where denotes the path loss from to the jth primary receiver [42]. Numerous wireless applications are known to accept occasional outages without affecting the QoS. Let denote the outage probability. This probability should be very small, to ensure a high probability of satisfying the interference constraint of primary users. The C3 is then replaced by
where the probability is taken over . We assume that is known to . Given the Rayleigh distribution of the channels, an exponential distribution with the parameter can be obtained from Reference [43]. Equation (9) can be rewritten as:
Thus, the outage probability constraint (9) is equivalent to
In addition, we can combine Formula (11) with constraint C4 in Equation (8), which has the same form and can be reconstructed as
where is satisfied as
Given , the maximum instantaneous rate of (in nats per second) is limited by its maximum transmission power and the interference caused to the primary user. The maximum instantaneous rate of each SU is expressed as follows [26]:
Equation (14) can be solved via the standard “water-filling (WF)” algorithm [44,45]. The minimum time resource , which is needed by each to satisfy the rate requirement, is calculated as
Given any feasible time allocation , Equation (8) reduces separate transmit covariance matrix optimization problems to K, one for each :
.
Let and , is an Hermitian positive semidefinite matrix, and all the non-negative eigenvalues of are . When the CSI is known at the transmitter (and at the receiver), then is known in (16) and we optimize the capacity over subject to the power constraint . According to the principle of the WF algorithm [45], if is satisfied, then the resulting capacity is given by
where , and the is chosen to satisfy
The WF is adopted to tackle the power limitation of . Equation (8) can be re-arranged for the case of a convex problem of the time allocation optimization. Therefore, the energy consumption for is a function of , which can be computed as [43]:
where is the optimal “water level” which is a function of . Where is the optimal number of data streams. The optimal number of data streams and the optimal energy consumption of each are dependent on its time resource allocation, which can be written as
and,
where is a reduction function of , and .
It is noteworthy that takes different forms at various intervals of , because is a step-wise function of . It follows from Equation (8) that is a continuous function. In addition, the optimal energy consumption of is a first-order differentiable, strictly convex function. Therefore, the mathematical model of Equation (8) is finally transformed into the following form:
It follows from (22) that the non-convex problem of the energy consumption in the secondary system can be reduced to the convex problem of time allocation optimization.
In this network, each frame is subdivided into many time slots, which participate in the allocation as the smallest unit of time. Under the normal conditions, the time resource allocated by each is an integer multiple of the time slot. Assume that a normalized time cycle has T slots so that the time resource optimization problem among the SUs is given by
where is the minimum number of time slots for each . Equation (23) corresponds to an integer convex optimization problem, if and only if the following conditions are satisfied:
In the TDMA-based orthogonal slot allocation network, a simple greedy algorithm can be used to solve Equation (23) [26,46]. Assuming the number of allocated time slots of is increased from to , the energy consumption variation can be defined as:
In the greedy algorithm, starting from the minimum slots’ allocation , one time slot is allocated at a time. A time slot is added to the , which has the minimum among all the SUs.
5. SCMA-Based Non-Orthogonal Slot Allocation
The monotonicity of the function implies that the more time each is allocated, the less energy it consumes. The TDMA-based orthogonal slot allocation avoids the interference between SUs but also limits the number of users accessing the network. The NOMA concept, which has been introduced by the International Mobile Telecommunications for 2020 (IMT-2020) (5G) Promotion Group in China in 2013 for the next generation of wireless communication, can realize sharing of time-frequency resources, which does not make the user’s access strictly orthogonal, but excludes any serious interference between users [47]. Within the framework of the NOMA concept, the SCMA technology is lucrative air interface technology [42]. Using the same time-frequency resource, SCMA can achieve 150%, 200%, or even higher equipment connection [9]. The nonconvex problem of the total energy consumption of the multi-user system can be transformed into the convex problem of time allocation optimization. Note that Equation (23) is a piecewise function of , and although the function is continuous and the first-order is differentiable, unfortunately, its second order is not. Therefore, only the first-order optimization method is available. In order to optimize the time slot allocation, a nonorthogonal slot allocation strategy based on SCMA is proposed, which can realize the sharing of TDMA time slots and achieve the overload rates of 150%, 200%, 250% or even higher under the same time slot resource so that the SUs cause no serious interference. In the following subsection, the implementation process is described in detail.
5.1. Time Slot Grouping
The obtained relation between the SCMA factor graph and matrix F implies that the time slot can deal with more SUs data through sharing, for example, with overload rates of 150%, 200% and so on. Due to slot sharing, the SCMA-based nonorthogonal slot allocation requires different slot allocation strategies than the TDMA-based approach. The implementation of non-orthogonal slot allocation is based on a sharing time slot as a unit, which is referred to as shared slot unit. Therefore, it is necessary to group the total time slots within a frame. Each successive N time slot is subdivided into groups, with no overlaps among groups, which means that the relation between groups is orthogonal, while N time slots in each group are nonorthogonal. The total number of groups obtained is calculated as:
where is the number of shared slot units after grouping.
5.2. A Method of Virtually Adding Users
After grouping, each group starts accessing SUs, which need access with SCMA technology and to satisfy the minimum time requirements of each SU. The minimum slots of are required to be extended to the shared slot. If , it is directly extended to one shared time slot unit. But, for , the data of would need to be extended to more than one shared unit, which is quite problematic when J SUs are assigned to one shared unit. For simplicity, we adopted a method of virtually adding users. In other words, each is treated as SUs that occupy a shared unit, where to facilitate the packet access. The virtualization process of is depicted in Figure 4. The total number, , of SUs obtained in the secondary system at this time is calculated as:
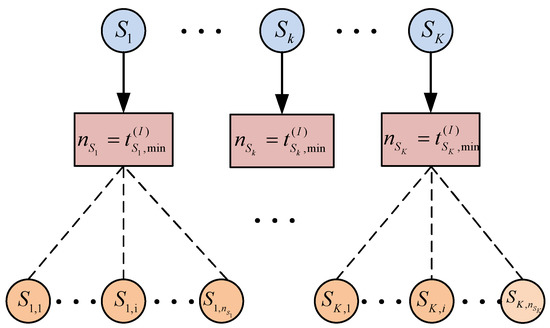
Figure 4.
The virtualization process of .
Now, the minimum time slot needed for each SU is 1.
The virtualization process of does not affect the true , which is not required for the data mapping into several shared slot units. The access of each SU to shared slot units is easily organized. We assume that a shared time slot unit can be accessed by J SUs so that the grouping of L SUs is required. The group principle is as follows:
The integer part and remainder of is obtained by fix (.) and mod (.), respectively. is the minimum time required to meet the rate requirements of all SUs. The formula shows that when the number of the remaining users in the last group is insufficient, a shared time slot unit should be allocated to the remaining users. If , the remaining shared time slots need to be allocated to SUs of some groups with some guidelines. Insofar as J SUs can share a shared time slot, the transmission energy consumption of each should be taken into account to ensure that the shared slot provides a more accurate allocation for all members of a group.
In this section, the greedy algorithm is used to allocate the surplus shared slot units with the average energy difference value (D-value) of all members of a group. Assume the shared time slot unit from to at the time of , whereas has accessed SUs. Let denote the average energy D-value among all SUs in , which can be written as:
After the allocation is started, the shared time slot unit is allocated from the minimum period , and at the same time, one shared time slot will be allocated each time. A shared time slot is allocated to the members of , which have the minimum among all . The algorithm will stop after allocating all TN shared time slots. The process is shown in Figure 5.
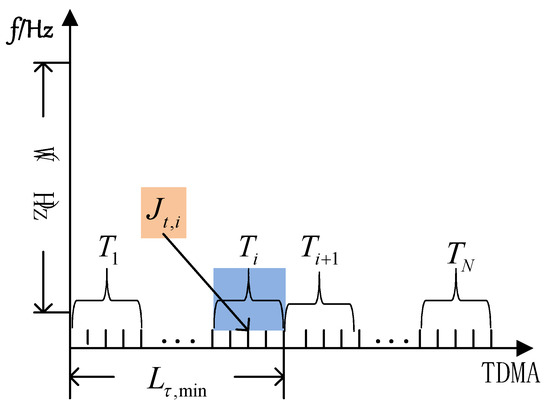
Figure 5.
Division of time slot and access of SUs.
In Figure 5, W is bandwidth, and the band frame used in this study is 20 MHz. Also, the SCMA principle is realized by the sparse spread spectrum and combined with the codebook design. It is known that the data of each after spreading causes the data to increase. Therefore, the non-orthogonal slot sharing of SCMA, must be substituted by the data rate after spreading. Since SCMA uses the sparse spread spectrum, the value is used to calculate by using Equation (6). The flowchart for the SCMA-based nonorthogonal slot allocation optimization scheme is shown in Figure 6.
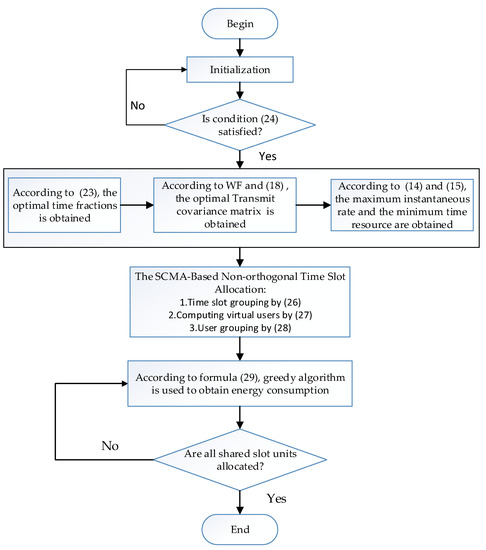
Figure 6.
The flowchart for the SCMA-based nonorthogonal slot allocation optimization scheme.
6. Numerical Results
To verify the performance of the proposed method regarding energy consumption, interference caused by the secondary system to the PUs links system and its user capacity, the simulation system is set up. Two pairs of PU links with a distance of 10 m are established between the transceivers. It is assumed that each node in the MIMO-CR network has four antennas. The parameters of the system are summarized in Table 3.

Table 3.
Simulation parameters.
6.1. Energy Consumption
Figure 7 shows the cumulative distribution function (CDF) of the average energy consumption of the MIMO-CR system. The SCMA-based nonorthogonal time allocation scheme is compared with the slot allocation schemes of “MIMO and max-rate” and “MIMO and OMA”, respectively. In the “MIMO and max-rate” scheme, each SU uses the minimum time resource and the transmission covariance matrix solved by Formula (14) with the maximum achievable rate. In addition, in the “MIMO and OMA” scheme proposed in Reference [25], the orthogonal slot allocation scheme is adopted for MIMO-CR system. The number of SUs is set to 35, the overload rate of SCMA is 150%, and the distance between secondary user and secondary BS is not less than 10 m, as shown in Figure 1. Compared with MIMO and max-rate and MIMO and OMA, this algorithm can significantly reduce the energy consumption of the MIMO-CR system. This is because the SCMA-based nonorthogonal time allocation scheme makes use of its sparse feature. After slot allocation, each SU gets more time than the orthogonal slot allocation strategy.
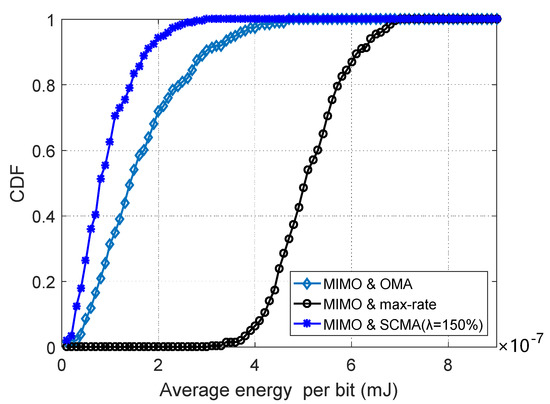
Figure 7.
The cumulative distribution function (CDF) of the three schemes.
The relationship between the average energy consumption per bit of the system and the minimum distance between the SUs and secondary BS is shown in Figure 8. In this scheme, the number of SUs is set to 35, and the overload rate is 150%. The location relationship and minimum distance between the secondary BS and SUs are shown in Figure 9. The average energy consumption per bit of the three schemes increases with the distance between the secondary BS and the SUs, because in order to ensure the QoS of the user, the transmission power needs to be increased. “MIMO and OMA” and “MIMO and max-rate” algorithms mainly use the orthogonal slot allocation scheme and refer to the user’s channel gain for allocation. The CSI is mainly determined by the reference distance and path loss. Therefore, with the increasing space distance between the SUs and the BS, the channel state will become worse and the energy consumption will be more and more. The SCMA-based nonorthogonal time allocation scheme algorithm proposed in this paper is less affected by distance and can achieve greater energy savings.
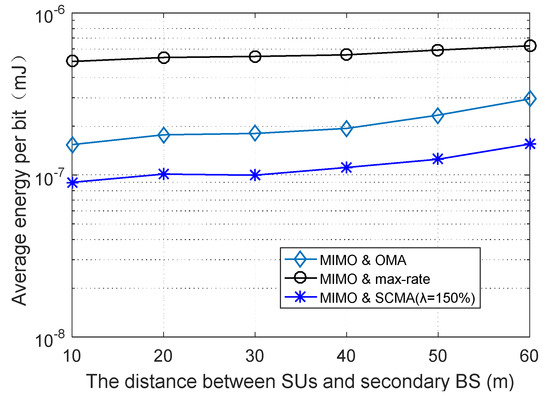
Figure 8.
The average energy consumption per bit versus the minimum distance between the SUs and secondary BS.
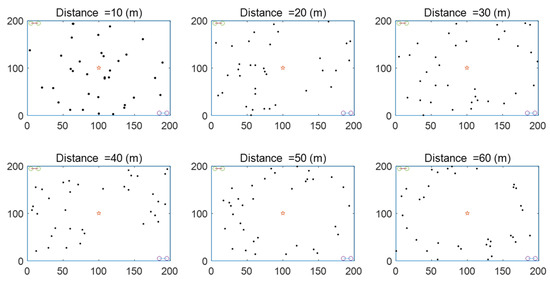
Figure 9.
The minimum distance between the SUs and secondary BS.
The energy consumption per bit of SUs is shown in Figure 10. In this study, the “MIMO and max-rate”, “MIMO and optimum time” and the “SCMA and optimum time” schemes for the overload rates of 150%, 200% and 250% are simulated and compared. In the “MIMO and optimal time”, each SU optimizes its time allocation with multiple data streams [26]. As illustrated in Figure 10, the average energy consumption per bit of all the optimal time allocations is lower than that of the “MIMO and max-rate”. When the number of SUs in the system is small, the energy consumption in the proposed SCMA-based nonorthogonal time allocation scheme is higher than that of the orthogonal one. This can be attributed to the fact that the data rate of SUs is increased after the sparse spread spectrum. However, for a larger number of SUs, the application of SCMA nonorthogonal slot allocation has certain advantages in the energy efficiency, and with an increase in the SCMA overload rate (λ = 250%), the energy efficiency improvement becomes more pronounced, saving nearly 40% of energy consumption. The reason is that when the time slot allocation is completed via the nonorthogonal slot sharing allocation strategy, each SU obtains more time than in the case of the orthogonal slot allocation, which promotes the data rate increase after sparse spreading. With the development trend of future wireless communications, the secondary system will access more SUs. Therefore, the use of the SCMA nonorthogonal slot sharing allocation strategy has some advantages in reducing power consumption and improving energy efficiency.
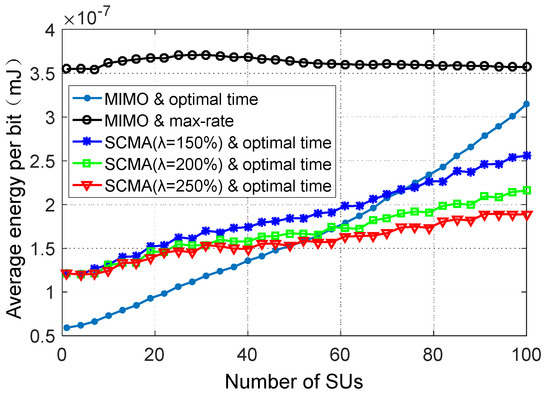
Figure 10.
The average energy consumption per bit versus the number of SUs.
6.2. User Capacity
Figure 11 shows the user capacity of the secondary system with the time slots from T = 4 to T = 100, which is measured by the maximum number of SUs accessed by the system if and only if it satisfies the need of each SU in the time slots (referred to as “the min-time slots scheme”). Thus, . In Figure 11, the number of SUs of the secondary system is increased with the number of time slots. The SU capacity with the SCMA-based nonorthogonal slot access has some advantages over that provided by the orthogonal slot access scheme. For example, when the overload rate is 150%, the user capacity of nonorthogonal slot access is 50% higher than that of the orthogonal slot access with T = 100. As the overload rate increases, the number of SUs rapidly increases. Therefore, the SCMA-based nonorthogonal slot access is an effective way to improve the secondary system’s user capacity.
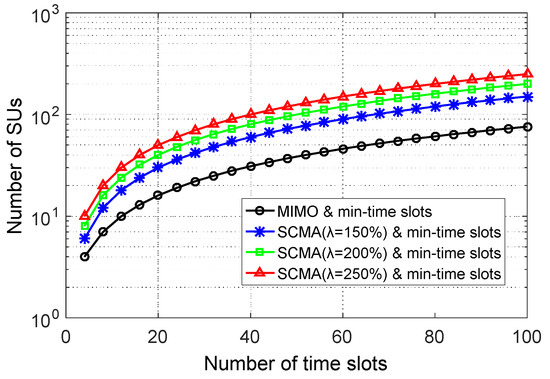
Figure 11.
The number of SUs versus the number of time slots.
6.3. Interference
Figure 12 demonstrates the average interference power from SUs to PUs links, which is based on the interference noise ratio (INR) as the main standard. As seen in Figure 12, the average INR in the “MIMO and max-rate” scheme is less than the required 25 dB, because the transmitting power of the SU needs to meet its interference constraint at two PUs links. When the excess time slots are allocated rationally, the INR is less than that of the “MIMO and max-rate” scheme. In other words, the interference to the PUs links is reduced. When the number of SUs is small, the average INR in the proposed SCMA-based nonorthogonal time allocation scheme is higher than that in the case of the orthogonal slot allocation. This occurs because the sparse spread spectrum leads to an increase in the data rate of SUs. However, for a larger number of SUs, the SCMA-based nonorthogonal slot allocation has certain advantages in reducing the interference, advantages which become more pronounced at the higher SCMA overload rates. Moreover, one can observe that the interference power in the “SCMA and optimal time” scheme increases slower than in the “MIMO and optimal time”.
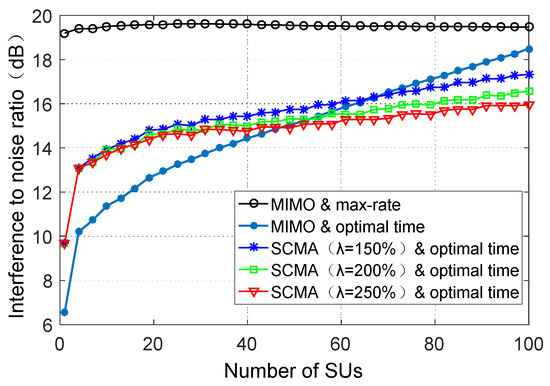
Figure 12.
Average interference power at PUs links versus the number of SUs.
Figure 13 shows the average INR from the SUs to the PUs links in the “min-time slots” scheme versus the number of SUs. The time slot number is 100, which satisfies the minimum slot needs of each SU without considering the excess slot allocation problem of SUs. As seen in Figure 13, the interference is less than 25 dB for both orthogonal and nonorthogonal access slot allocation schemes, because SU must satisfy the interference threshold for any kind of access. However, the INR of the SCMA-based nonorthogonal slot access scheme is higher than that of the orthogonal one. The average energy difference value (D-value) is about 2 dB. It can also be seen that the average INR of SCMA for the overload rates of 150% and 200% are nearly identical. Thus, the magnitude of the overload rate has a feeble effect on the average interference power of the PUs links.
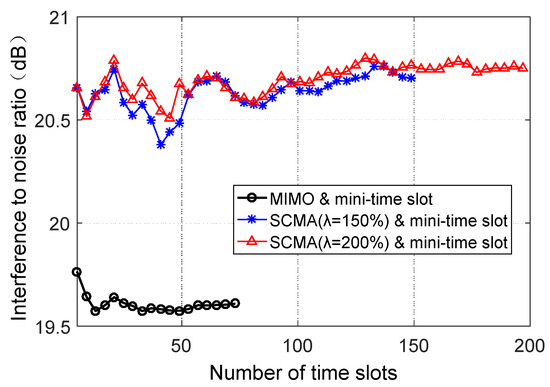
Figure 13.
Average interference power at PUs links versus the number of SUs, if and only if the min-time slot requirement is satisfied.
7. Discussion and Conclusions
In this paper, the nonconvex problem of energy consumption in MIMO-CR networks under the underlay model was reduced to the convex problem of time allocation optimization, which was implemented via the TDMA technology. The greedy algorithm was adopted to solve the latter problem, while the SCMA-based nonorthogonal optimization method was used to optimize the slot allocation. By attaining the maximum transmission rate of each SU, the minimum time needed by each SU to transmit data can be obtained. Under the requirement of the minimum time slot of SUs, the total energy consumption of SUs can be improved by optimizing time slot allocation. The SCMA-based nonorthogonal slot allocation requires time slot grouping and user packet access. In this paper, the method of adding virtual SUs was adopted to simplify the packet access. The average energy D-value of all SUs among the same shared time slot was determined as the allocation criterion. The simulation results obtained show that for a larger number of SUs, the SCMA-based nonorthogonal slot allocation has lower energy consumption and the interference to the PUs links than the orthogonal slot allocation. With an increase in the SCMA overload rate, these advantages become more pronounced. It is noteworthy that the maximum number of SUs (i.e., the spectrum) of the secondary system was substantially improved without exceeding the interference threshold, which makes the proposed slot allocation scheme quite lucrative for further large-scale implementation.
The scheme provided in this paper is helpful for the following further research: (1) This paper considers the statistical CSI between users, so we will expand to a more general channel and CSI for further research. (2) With the increase of data stream and the complexity of high-dimensional modulation, the interference between SUs will be a topic that must be considered. Therefore, we will further trade-off between multiplexing and interference cancellation.
Author Contributions
Conceptualization, P.Z. and W.G.; methodology, P.Z., Y.Z., G.Z. and M.G.; software, P.Z. and Y.Z.; validation, P.Z. and W.G.; formal analysis, P.Z. and G.Z.; investigation, P.Z., Y.Z. and G.Z.; resources, W.G.; data curation, P.Z. and Y.Z.; writing—original draft preparation, P.Z. and W.G.; writing—review and editing, P.Z., Y.Z., M.G. and W.G.; visualization, P.Z.; supervision, W.G.; project administration, W.G.; funding acquisition, W.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Natural Science Foundation of Xinjiang Uygur Autonomous Region of China under Grant 2018D01C033 and in part by Key Program of Scientific Research Plan of Universities in Xinjiang Uygur Autonomous Region of China under Grant XJEDU2020I003.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Thompson, J.; Ge, X.H.; Wu, H.C.; Irmer, R.; Jiang, H.; Fettweis, G.; Alamouti, S. 5g Wireless Communication Systems: Prospects and Challenges Part 2. IEEE Commun. Mag. 2014, 52, 24–25. [Google Scholar] [CrossRef]
- Liu, J.Q.; Ding, H.C.; Cai, Y.; Yue, H.; Fang, Y.G.; Chen, S.G. An Energy-Efficient Strategy for Secondary Users in Cooperative Cognitive Radio Networks for Green Communications. IEEE J. Sel. Areas Commun. 2016, 34, 3195–3207. [Google Scholar] [CrossRef]
- Kumar, N. A Study on Green Energy Powered Cognitive Radio Network for Communication Network Architecture of Smart Grid. In Proceedings of the 2018 3rd International Innovative Applications of Computational Intelligence on Power, Energy and Controls with Their Impact on Humanity (CIPECH), Ghaziabad, India, 1–2 November 2018; pp. 3–7. [Google Scholar]
- Gandotra, P.; Jha, R.K.; Jain, S. Prolonging User Battery Lifetime using Green Communication in Spectrum Sharing Networks. IEEE Commun. Lett. 2018, 22, 1490–1493. [Google Scholar] [CrossRef]
- Yu, H.; Afzal, M.K.; Zikria, Y.B.; Rachedi, A.; Fitzek, F.H.P. Tactile Internet: Technologies, test platforms, trials, and applications. Future Gener. Comput. Syst. 2020, 106, 685–688. [Google Scholar] [CrossRef]
- Zikria, Y.B.; Afzal, M.K.; Kim, S.W. Internet of Multimedia Things (IoMT): Opportunities, Challenges and Solutions. Sensors 2020, 20, 2334. [Google Scholar] [CrossRef] [PubMed]
- Liang, Y.C.; Chen, K.C.; Li, G.Y.; Mahonen, P. Cognitive Radio Networking and Communications: An Overview. IEEE Trans. Veh. Technol. 2011, 60, 3386–3407. [Google Scholar] [CrossRef]
- Mamiya, T.; Fujimoto, M. MIMO Cognitive Radio Considering Interference. In Proceedings of the 2018 IEEE International Workshop on Electromagnetics: Applications and Student Innovation Competition (iWEM), Vancouver, BC, Canada, 29–31 August 2018; pp. 1–2. [Google Scholar]
- Nikopour, H.; Baligh, H. Sparse code multiple access. In Proceedings of the 2013 IEEE 24th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), London, UK, 8–11 September 2013. [Google Scholar]
- Abebe, A.T.; Kang, C.G. Grant-Free Uplink Transmission With Multi-Codebook-Based Sparse Code Multiple Access (MC-SCMA). IEEE Access 2019, 7, 169853–169864. [Google Scholar] [CrossRef]
- Van De Beek, J.; Popovic, B.M. Multiple Access with Low-Density Signatures. In Proceedings of the GLOBECOM 2009-2009 IEEE Global Telecommunications Conference, Honolulu, HI, USA, 30 Novemver–4 December 2009; pp. 1–6. [Google Scholar]
- Razavi, R.; Hoshyar, R.; Imran, M.A.; Wang, Y. Information Theoretic Analysis of LDS Scheme. IEEE Commun. Lett. 2011, 15, 798–800. [Google Scholar] [CrossRef]
- Hoshyar, R.; Wathan, F.P.; Tafazolli, R. Novel Low-Density Signature for Synchronous CDMA Systems Over AWGN Channel. IEEE Trans. Signal Process. 2008, 56, 1616–1626. [Google Scholar] [CrossRef]
- Yang, D.; Dong, B.; Zhi, C.; Gao, P.; Fang, J. Joint Sparse Graph-Detector Design for Downlink MIMO-SCMA Systems. IEEE Wirel. Commun. Lett. 2017, 6, 14–17. [Google Scholar]
- Kurniawan, D.; Arifianto, M.S.; Kurniawan, A. Low Complexity MIMO-SCMA Detector. In Proceedings of the 2019 IEEE 5th International Conference on Wireless and Telematics (ICWT), Yogyakarta, Indonesia, 25–26 July 2019; pp. 1–5. [Google Scholar]
- Sun, W.; Su, Y.; Ueng, Y.; Yang, C. An LDPC-Coded SCMA Receiver With Multi-User Iterative Detection and Decoding. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 3571–3584. [Google Scholar] [CrossRef]
- Taherzadeh, M.; Nikopour, H.; Bayesteh, A.; Baligh, H. SCMA Codebook Design. In Proceedings of the 2014 IEEE 80th Vehicular Technology Conference (VTC2014-Fall), Vancouver, BC, Canada, 14–17 September 2014. [Google Scholar]
- Dai, J.; Niu, K.; Lin, J. Iterative Gaussian-Approximated Message Passing Receiver for MIMO-SCMA System. IEEE J. Sel. Top. Signal Process. 2019, 13, 753–765. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, Y.; Zhou, F.; Chu, Z.; Wu, Y.; Yuan, F. Multi-Objective Resource Allocation in a NOMA Cognitive Radio Network With a Practical Non-Linear Energy Harvesting Model. IEEE Access 2018, 6, 12973–12982. [Google Scholar] [CrossRef]
- Sun, H.; Zhou, F.; Hu, R.Q.; Hanzo, L. Robust Beamforming Design in a NOMA Cognitive Radio Network Relying on SWIPT. IEEE J. Sel. Areas Commun. 2019, 37, 142–155. [Google Scholar] [CrossRef]
- Wang, X.; Na, Z.; Lam, K.; Liu, X.; Gao, Z.; Li, F.; Wang, L. Energy Efficiency Optimization for NOMA-Based Cognitive Radio With Energy Harvesting. IEEE Access 2019, 7, 139172–139180. [Google Scholar] [CrossRef]
- Xiang, Z.; Yang, W.; Pan, G.; Cai, Y.; Song, Y. Physical Layer Security in Cognitive Radio Inspired NOMA Network. IEEE J. Sel. Top. Signal Process. 2019, 13, 700–714. [Google Scholar] [CrossRef]
- Xu, L.; Xing, H.; Deng, Y.; Nallanathan, A.; Zhuansun, C. Fairness-Aware Throughput Maximization for Underlaying Cognitive NOMA Networks. IEEE Syst. J. 2020, in press. [Google Scholar] [CrossRef]
- Xu, Y.; Hu, R.Q.; Li, G. Robust Energy-efficient Maximization for Cognitive NOMA Networks under Channel Uncertainties. IEEE Internet Things J. 2020, 1, in press. [Google Scholar] [CrossRef]
- Fu, L.; Zhang, Y.J.A.; Huang, J. Energy Efficient Transmissions in MIMO Cognitive Radio Networks. IEEE J. Sel. Areas Commun. 2013, 31, 2420–2431. [Google Scholar]
- Fu, L.; Johansson, M.; Bengtsson, M. Energy Efficient Transmissions in Cognitive MIMO Systems With Multiple Data Streams. IEEE Trans. Wirel. Commun. 2015, 14, 5171–5184. [Google Scholar] [CrossRef]
- Zhang, X.; Li, H. Energy efficiency optimization for MIMO cognitive radio network. In Proceedings of the 2015 IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 7713–7718. [Google Scholar]
- Sboui, L.; Rezki, Z.; Sultan, A.; Alouini, M. Energy-Efficient Power Allocation for Cognitive MIMO Channels. In Proceedings of the 2016 IEEE 84th Vehicular Technology Conference (VTC-Fall), Montréal, QC, Canada, 18–21 September 2016; pp. 1–6. [Google Scholar]
- Okumu, E.M.; Dlodlo, M.E. Optimal and sub-optimal iterative cross-layer energy efficient schemes for CR MIMO systems with antenna selection. In Proceedings of the IEEE EUROCON 2017-17th International Conference on Smart Technologies, Ohrid, Macedonia, 6–8 July 2017; pp. 62–67. [Google Scholar]
- Miridakis, N.I.; Tsiftsis, T.A.; Alexandropoulos, G.C. MIMO Underlay Cognitive Radio: Optimized Power Allocation, Effective Number of Transmit Antennas and Harvest-Transmit Tradeoff. IEEE Trans. Green Commun. Netw. 2018, 2, 1101–1114. [Google Scholar] [CrossRef]
- Wu, F.; Xiao, L.; Yang, D.; Cuthbert, L.; Liu, X. Transceiver design and power allocation for SWIPT in MIMO cognitive radio systems. Symmetry 2018, 10, 647. [Google Scholar] [CrossRef]
- Yuan, Y.; Ding, Z. Outage Constrained Secrecy Rate Maximization Design With SWIPT in MIMO-CR Systems. IEEE Trans. Veh. Technol. 2018, 67, 5475–5480. [Google Scholar] [CrossRef]
- Maurya, S.; Bansal, M.; Trivedi, A. Joint source and relay precoder design for energy-efficient MIMO-cognitive relay networks. IET Commun. 2019, 13, 2226–2234. [Google Scholar] [CrossRef]
- Patil, V.; Singhal, C. Throughput Improvement in Hybrid MIMO Cognitive Radio Using Simultaneous Narrowband and Wideband System. In Proceedings of the 2019 11th International Conference on Communication Systems & Networks (COMSNETS), Bangalore, India, 7–11 January 2019; pp. 285–290. [Google Scholar]
- Song, C.; Lee, H.; Lee, K. Optimal Precoder Designs for Sum-Utility Maximization in SWIPT-Enabled Multi-User MIMO Cognitive Radio Networks. IEEE Syst. J. 2019, 13, 2332–2343. [Google Scholar] [CrossRef]
- Yu, Y.; Chen, H.; Li, Y.; Ding, Z.; Zhuo, L. Antenna Selection in MIMO Cognitive Radio-Inspired NOMA Systems. IEEE Commun. Lett. 2017, 21, 2658–2661. [Google Scholar] [CrossRef]
- Nandan, N.; Majhi, S.; Wu, H. Secure Beamforming for MIMO-NOMA-Based Cognitive Radio Network. IEEE Commun. Lett. 2018, 22, 1708–1711. [Google Scholar] [CrossRef]
- Yu, Y.; Chen, H.; Li, Y.; Ding, Z.; Song, L.; Vucetic, B. Antenna Selection for MIMO Nonorthogonal Multiple Access Systems. IEEE Trans. Veh. Technol. 2018, 67, 3158–3171. [Google Scholar] [CrossRef]
- Thakur, P.; Singh, G. Sum-Rate Analysis of MIMO Based CR-NOMA Communication System. In Proceedings of the 2019 Fifth International Conference on Image Information Processing (ICIIP), Shimla, India, 15–17 November 2019; pp. 414–419. [Google Scholar]
- Xiao, Y.S.; Tsang, D.H.K. Interference Alignment Beamforming and Power Allocation for Cognitive MIMO-NOMA Downlink Networks. In Proceedings of the 2019 IEEE Wireless Communications and Networking Conference (WCNC), Marrakesh, Morocco, 15–18 April 2019; pp. 1–6. [Google Scholar]
- Yasrab, T.; Gurugopinath, S. Spectral Efficiency of MIMO-NOMA Cognitive Radios with Energy-Based Spectrum Sensing. In Proceedings of the 2019 IEEE International Conference on Distributed Computing, VLSI, Electrical Circuits and Robotics (DISCOVER), Manipal, India, 11–12 August 2019; pp. 1–6. [Google Scholar]
- Wang, B.; Wang, K.; Lu, Z.; Xie, T.; Quan, J. Comparison study of non-orthogonal multiple access schemes for 5G. In Proceedings of the 2015 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting, Ghent, Belgium, 17–19 June 2015; pp. 1–5. [Google Scholar]
- Rappaport, T.S. Wireless Communications–Principles and Practice; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1996; Volume 2. [Google Scholar]
- Telatar, E. Capacity of Multi-antenna Gaussian Channels. Eur. Trans. Telecommun. 1999, 10, 585–595. [Google Scholar] [CrossRef]
- Gesbert, D.; Shafi, M.; Da-shan, S.; Smith, P.J.; Naguib, A. From theory to practice: An overview of MIMO space-time coded wireless systems. IEEE J. Sel. Areas Commun. 2003, 21, 281–302. [Google Scholar] [CrossRef]
- Ibaraki, T.; Katoh, N. Resource Allocation Problems: Algorithmic Approaches; MIT Press: Cambridge, MA, USA, 1988. [Google Scholar]
- Baghani, M.; Parsaeefard, S.; Derakhshani, M.; Saad, W. Dynamic Non-Orthogonal Multiple Access and Orthogonal Multiple Access in 5G Wireless Networks. IEEE Trans. Commun. 2019, 67, 6360–6373. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).