Abstract
An exact analytical expression for the effective angle is determined for an arbitrary energy value of a radiating particle. An effective angle of instantaneous power is defined for synchrotron radiation in the framework of classical electrodynamics. This definition explicitly contains the most symmetric distribution of half the total of the instantaneous power of synchrotron radiation. Two exact analytical expressions for the effective angle are considered for the arbitrary energy values of a radiating particle, and the second expression brings to light the exact asymptotics of the effective angle in the ultrarelativistic limit.
1. Introduction
Theoretical research into the angular distribution of synchrotron radiation power was sufficiently well developed already in the pioneering works on this subject [1,2,3,4,5,6,7,8,9,10]. However, in most of these works, time-average angular distributions, which are currently being observed in experiment, were paid the most attention.
In particular, the first works on the classical theory [1,2,3,4,5,6] for the time-average synchrotron radiation investigated the issue of an effective angular span of radiation. Since the actual experiment involves relativistic electrons, it was crucial to understand how their average radiation is distributed in space. The structure of the radiation diagrams showed unambiguously that the radiation power of relativistic electrons, on average, in time, is concentrated in the plane of the particles’ orbits. Later on (see, for instance, [11,12]), precise effective angles were determined for all the polarizations of radiation power.
There are much less publications on theoretical research into the instantaneous angular distribution of synchrotron radiation power (see, for instance, [7,8,9,10]). In classical theory, diagrams of angular distribution for instantaneous radiation have been constructed; however, the issue of an exact analytical expression for the effective angle still remains unsolved. There are only a few works (for instance, [7,9,10]) dealing with a qualitative ultrarelativistic approximation.
The present article determines, in the framework of classical theory, the effective angle of instantaneous power for synchrotron radiation and investigates a precise analytical expression for this quantity.
2. Spatial Structure of Angular Distribution for Instantaneous Power of Synchrotron Radiation
The spatial structure of angular distribution for instantaneous synchrotron radiation (SR) power can be specified using the following coordinates (the same coordinates have also been suggested in other works, see, for instance, [1]). The origin of such a coordinate system is chosen as the location of a radiating charge. We direct the x-axis along the electron velocity, with the y-axis directed toward the center of a circular trajectory, and the z-axis chosen so that the coordinate system is a right-handed one (when the charge moves in a constant and uniform magnetic field, the z-axis is parallel to the external magnetic field). The radius of the circular orbit containing the radiating particle is denoted by and is oriented along the y-axis of the coordinate system. The angle between the x-axis and the vector is denoted by , whereas the angle between the y-axis and the projection of the vector onto the plane is denoted by . The vector is directed from the origin of the coordinate system to a certain observation point of SR power. The coordinate system is exemplified by Figure 1.
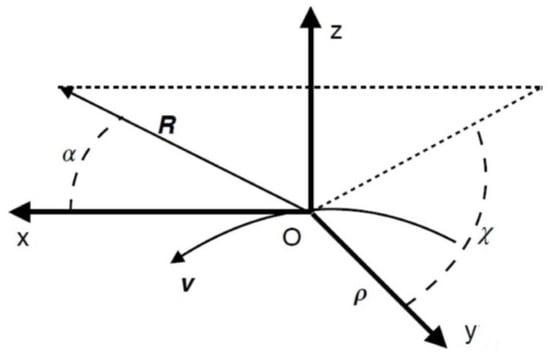
Figure 1.
Coordinate system.
Under these assumptions, the instantaneous angular distribution of SR power in the wave zone has the following form [6,7,8,9,10]:
The following notation has been used: e is the radiating charge value; c is the speed of light; is the velocity of the radiating particle ; is the cyclotron frequency; is the particle rest mass; H is the magnetic field strength. The orbit radius of the radiating particle depends on the velocity and the cyclotron frequency via the following relation:
It is precisely the expression (1) (see also [6,7,8,9,10]) that is responsible for instantaneous angular distribution in the relativistic case to be mainly concentrated in a narrow cone with a central axis identical in direction with the instantaneous particle velocity v. The angular span of the cone is .
Angular integration in (1),
produces the following well-known expression [6,7,8,9,10] for the SR total radiated power:
3. Effective Distribution Angle for Instantaneous Synchrotron Radiation Power
Consider the part of SR instantaneous power that is concentrated inside a cone whose central axis is directed along the instantaneous velocity of the particle (namely, the x-axis), and whose angular span is . From (2), it follows that an expression for can be obtained by integrating over in the limits and by integrating over in the limits ,
where a dimensionless function has been introduced in (4),
Let us point out an essential feature of the function . Due to integration over , the function ceases to depend on the details of angular distribution and is determined only by the total instantaneous SR power, which testifies to a distribution symmetry of the instantaneous SR power inside the selected cone.
The integral over in (5) is taken in a manifest form:
where the function introduced in (6) reads as follows:
We define the SR effective angle as such an angle that meets the condition . This condition, with account taken of (3) and (4), implies an equation for the value :
By solving this equation (for instance, numerically), we determine the function . The definition introduced here must conform to the qualitative condition that should make the value tend to zero: .
Equation (8) admits an essential simplification. Let us present the function as follows:
where the function to be determined is the value . Substituting the expression (9) into (8) and taking (7) into account, we establish a defining equation for :
With respect to the function , Equation (10) is a forth-degree polynomial, whose coefficients are certain polynomials of that do not exceed the fifth degree. Equation (10) differs from (8) by the domain of solutions; the point is not a singular point for (10), whereas it is a singular one for (8). Consequently, Equation (10) allows one to define the function in the closed interval . Let us proceed to determine the exact values and of this function.
By setting the value in (10), we find the following:
By setting the value in (10), we find the following:
It is easy to see that Equation (12) can be presented as follows:
Thereby, we encounter only one root of (12) that is physically meaningful:
The Equation (10) could also be solved for other values of by using a complex combination of expressions containing cubic and square roots of polynomials with respect to ; however, it is much easier to determine a numerical value for each specific by using Equation (10) directly.
With account taken of (9), one readily finds the following:
Thereby, the Equation (14) allows one to use a given value in order to find the effective angle .
Let us recast the expression (14) in the following form:
Comparison of (14) and (15) leads to an expression for :
From (16), we find, due to (11) and (13), that the function is limited in the closed interval and takes the following exact values at the endpoints:
Using the expression (15) at (which corresponds to ), we find, due to (17), the following exact asymptotic expression:
which is in agreement with the known qualitative data.
Non-relativistically (which corresponds to ), one encounters the obvious result .
In conclusion, we present some tables and plots of the functions under consideration (see Table 1 and Figure 2), and we also indicate their common feature of a monotonous decrease in time along with an increase in the argument .

Table 1.
Values of , , .
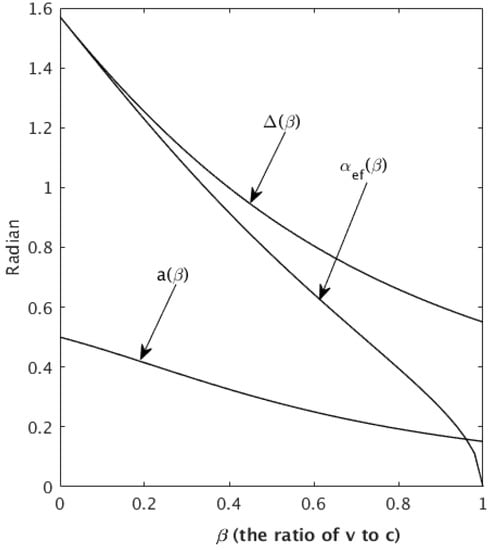
Figure 2.
Functions , , .
We have therefore achieved exact analytical expressions for the effective angle of instantaneous SR.
Author Contributions
Conceptualization, V.B.; formal analysis, V.B., A.K. and A.P.; software, A.K. and A.P.; writing—original draft preparation, V.B.; writing—review and editing, V.B. and A.P. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported in part by RFBR Grant No. 18-02-00149 and by the Program of Tomsk State University Competitiveness Improvement among the World’s Leading Research and Educational Centers.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Schott, G.A. Electron Theory of Matter and on Radiation. Philos. Mag. 1907, 13, 189–213. [Google Scholar] [CrossRef][Green Version]
- Schott, G.A. Uber die Strahlung von Electronengruppen. Ann. Phys. 1907, 24, 635–661. [Google Scholar] [CrossRef]
- Schott, G.A. Electromagnetic Radiation; Cambridge University Press: Cambridge, UK, 1912. [Google Scholar]
- Arzimovich, L.A.; Pomeranchuk, I. The Radiation of Fast Electrons in the Magnetic Field. J. Phys. USSR 1945, 91, 267–276. [Google Scholar]
- Arzimovich, L.A.; Pomeranchuk, I. The Radiation of Fast Electrons in the Magnetic Field. Zhurn. Exsp. Teor. Fiz. 1946, 16, 379–389. [Google Scholar]
- Vladimirski, V.V. Influence of the terrestial magnetic field on large Auger showers. Zhurn. Exsp. Teor. Fiz. 1948, 18, 392–401. [Google Scholar]
- Schwinger, J. On the Classical Radiation of Accelerated Electrons. Phys. Rev. 1949, 75, 1912. [Google Scholar] [CrossRef]
- Ivanenko, D.D.; Sokolov, A.A. On the theory of the ’luiinous’ electron. Dokl. Akad. Nauk SSSR 1948, 59, 1551–1554. [Google Scholar]
- Tomboulian, D.; Hartman, P. Spectral and Angular Distribution of Ultraviolet Radiation from the 300-Mev Cornell Synchrotron. Phys. Rev. 1956, 102, 1423–1447. [Google Scholar]
- Bagrov, V.G. Angular Distribution of Radiation from a Charge in an External Field in Accordance with Classical Theory. Optica Spektr. 1965, 18, 541–544. [Google Scholar]
- Bagrov, V.G.; Dolzhin, M.V.; Tlyachev, V.B.; Jarovoi, A.T. Evolution of the Angular Distribution of Circularly Polarized Synchrotron Radiation with Charge Energy. Rus. Phys. J. 2004, 47, 414–423. [Google Scholar] [CrossRef]
- Bagrov, V.G.; Gitman, D.M.; Tlyachev, V.B.; Jarovoi, A.T. New Theoretical Results in Synchrotron Radiation. Nucl. Instrum. Methods B 2005, 240, 638–645. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).