Abstract
The present study utilizes the generalized thermoelasticity theory, with one thermal relaxation time (TR), to examine the thermoelastic problem of a functionally graded thin slim strip (TSS). The authors heated the plane surface bounding using a non-Gaussian laser beam with a pulse length of ps. The material characteristics varied continually based on exponential functions. Moreover, the equations governing the generalized thermoelasticity for a functionally graded material (FGM) are recognized. The problem’s ideal solution was primarily obtained in the Laplace transform (LT) space. The LTs were converted numerically because of the considerable importance of the response in the transient state. For a hypothetical substance, the numerical procedures calculating the displacement, stress, temperature and strain were given. The analogous problem solution to an isotropic homogeneous material was provided by defining the parameter of non-homogeneity adequately. The obtained results were displayed using graphs to illustrate the extent to which non-homogeneity affected displacement, stress, temperature and strain. A comparison was been made between the present study and those previously obtained by others, when the new parameters vanish to show the impact of the non-homogeneity, TSS and laser parameters on the phenomenon. The results obtained indicate a significant strong impact of FGM, TSS and laser parameters.
1. Introduction
Functionally graded materials (FGMs) are defined as the diverse and advanced materials whose thermal and elastic characteristics differ slowly and continually between surfaces, resulting in the reduction of thermal stress (TS). Therefore, they are extremely helpful in nuclear, aviation and space technology applications. Their applications extend to other fields, such as geophysics, plasma physics, magnetic storage and structural elements, as well as the measurement of thermoelasticity.
Because of the need for resistant materials in the extreme temperatures involved in a lot engineering applications as thermal barrier coatings and engine parts, many efforts have been exerted in their development. For example, FGMs were introduced as one of these materials in the late 1980s in Japan. Their macroscopic material characteristics always differ, distinguishing them from laminated composite materials whose sudden shift of material properties across layer interfaces results in significant interlinear stresses that cause damage. Both FGMs and laminated composite materials combine the favorable constituent stages of properties to achieve superior efficiency.
Ye et al. [1] proposed the perfect thermoelastic axisymmetric solution problem of the heated functionally graded uniformly transversely isotropic cylindrical shell. They argued that the elastic modulus and the coefficient of linear expansion of temperature differ with the product of the variable radial coordinate of the power form. Utilizing a finite difference technique, El-Naggar et al. [2] investigated the temperature transient stress in an orthotropic nonhomogeneous rotating hollow cylinder. Wang and Mai [3] examined the one-dimensional transient TS in heterogeneous materials, e.g., spheres and plates, by employing the finite element method (FEM). Ootao and Tanigawa [4] investigated a transient thermoelasti functionally graded hollow cylinder one-dimensional problem, in which thermoelastic and thermal constants differed with the power product form of a variable of the radial coordinate. Shao et al. [5] worked out a thermomechanical problem in an FGM circular hollow cylinder, in which the material characteristics are independent of temperature and often differ radially.
Because of the applications of broad pulsed laser technology in processing material and nondestructive characterization and detection, exciting the thermoelastic waves in solids using a pulsed laser is of considerable interest. If a solid is illuminated and has a laser pulse, the temperature rises. Accordingly, thermal expansion is induced, and a thermoelastic wave is created. In ultrashort pulsed laser heating, two considered effects become significant. One of them is the non-Fourier effect in thermal conduction, which is a modification Fourier’s law of thermal conduction to justify the effect of TR time in the collision phase of the energy carrier. Moreover, considering the non-Fourier effect removes the uncertainty of the infinite propagation speed of thermal signals. The other effect is the stress wave dissipation because of the combination of temperature and strain rate. As a result, the stress wave associated with the mechanical energy is converted into the material’s thermal energy.
Thermoelasticity refers to different phenomena related to the interaction that occurs within a body between deformation and heat exchange. The classical uncoupled thermoelasticity theory describes two processes that are not consistent with physical observations. First, no elastic terms are included in its thermal conduction equation. Second, the thermal equation is a parabolic form that predicts the infinite propagation speed of thermal waves. Biot [6] developed the principle of coupled thermoelasticity CTE to address the first shortcoming. In this theory, the equations governing thermoelasticity are paired in order to resolve the classical theory’s first paradox. Nevertheless, the second shortcoming is common in these theories because the thermal equation is still parabolic for the coupled theory.
Because of the development of pulsed lasers, particle accelerators and rapid burst nuclear reactors, etc., that can supply heat pulses with increasing rapidity, the theory of generalized thermoelasticity has attracted considerable attention. The development of the second sound effect has been revisited. Two different generalized thermoelasticity models are often utilized. They were developed by Lord and Shulman (L–S) [7], and Green and Lindsay (G–L) [8]. While L–S theory proposes one relaxation time, so that Fourier’s law of thermal conduction is modified, G–L theory suggests a thermoelastic theory with two thermal relaxation times, and results in modifying the equations of motion and energy.
Researchers have tried to resolve thermoelastic wave problems, taking into account the non-Fourier effect. However, they neglected the temperature strain rate coupling effect. Kao [9] studied the non-Fourier effect on the thermoelastic wave in a half-space. McDonald [10] examined the significance of thermal diffusion for generating thermoelastic waves in the metals created by Gaussian laser beams heating a surface. Furthermore, Enguehard and Bertrand [11] explored the laser pulse’s influence and the optical penetration depth duration on longitudinal acoustic waves caused by absorption of a volumetric laser beam.
With the action of a thermal shock—for example, an ultra-short laser pulse—the thermal processes are very rapid, which is interesting from the thermoelasticity standpoint, and requires coupled temperature and deformation fields analysis. This means that the very rapid movements of the temperature shock induce the elements’ structure, causing and reducing the rise of inertial forces, and the rise of the vibrations is very significant. The expansions in oscillatory movements and the rapid changeable contractions generate changes temperature in the susceptible material, owing to diffusion due to heat conduction (Trajkovski and Cukic [12]).
Gaussian beams have a profile of Gaussian intensity at any location along the axis of the beam, which only causes variation on the radius beam. A Gaussian beam remains Gaussian after passing simple optical elements (e.g., lenses without optical aberrations). Gaussian beams are the lowest-order of distribution of a self-consistent field in optical resonators, provided that there are no intracavity elements causing distortions on the beam. For that reason, the output beams of many lasers are Gaussian. Single mode fibers have beam profiles which are usually close to Gaussian beams. There are Hermite–Gaussian types, so-called higher-order modes. These have more complicated field patterns and exhibit the parameter product of a larger beam; in cases with a less than perfect fit, the Gaussian approximation is popular due to the relatively simple rules for the calculation of beam propagation. Pulsed lasers are an important source of thermal effects, which give a high density in small time periods, which in turn has great importance in many areas, especially economic ones. The so-called ultra-short laser generally emits radiations that have a pulse duration ranging from nanoseconds to femtoseconds. In the case of laser heating with very short pulses, the high-intensity energy flux and the very short duration laser beam cause situations where there may be very large temperature gradients, or a very high heating velocity may occur on the material surface [13].
Al-Huniti et al. [14] investigated the dynamic reactions of a copper rod under the wave form thermal conduction model, because of a moving heat source. Employing the LT, the temperature was directly obtained from the thermal conductivity equation. Abouelregal [15] used the dual-phase-lag heat transfer model in an isotropic solid sphere. To solve the problem encountered, he maintained the boundary of the sphere at a stable heat flux and limited surface displacement. Youssef and Al-Felali [16] examined the stress fields and temperature-induced effects in an elastic half-space concerning the classical and generalized CTE. They used a non-Gaussian laser beam to heat the bounding plane surface. Abo-Dahab and Abouelregal [17] discussed the micro-beam resonators’ vibrations caused by a harmonically variable heat. Elsherbeny et al. [18] investigated thermoelastic analysis for an infinite rigid cylinder with variable thermal conductivity caused by harmonically distributed heat. Marin et al. [19] discussed the problems for micropolar porous bodies considering the mixed initial-boundary value. Riaz et al. [20] and Bhatti et al. [21] investigated Hall’s numerical study’s current impact, and heat transfer on peristaltic propulsion of particle-fluid suspension with compliant wall properties. Abo-Dahab and Abouelregal [22] investigated a problem in two dimensional thermoelasticity half-space with a microstructure under a uniform thermal shock. Abbas [23] investigated the effects of a moving heat source and relaxation times on a generalized two-temperature thermoelastic material. Abbas and Abo-Dahab [24] discussed a thermal shock numerical solution problem of generalized magneto-thermoelasticity with variable thermal conductivity for an infinitely long annular cylinder.
In the present paper, the authors provide a generalization solution to the thermoelastic wave in a TSS caused by pulsed laser heating. They studied the non-Fourier effect in thermal conduction, the temperature-strain coupling effect, and the volumetric loss from laser beam energy. In Section 2, the authors derived this generalization solution to the thermoelastic wave produced by pulsed laser heating. Moreover, they obtained the numerical figures of temperature, stress, displacement and strain of a hypothetical material. Accordingly, they performed calculations and validated the findings in Section 4. The results obtained indicate a significant strong impact of FGM, TSS and laser parameters.
2. Formulation of the Problem and Governing Equations
All equations of field, represented by L-S theory [7], may be formulated as follows:
This is known as the constitutive relation, where is the tensor of stress, is the displacement tensor, is the Kronecker delta function, , is the thermal expansion, is relaxation time, and is the resonator’s temperature increment, in which is the temperature distribution, is the environment temperature, and coefficients are the Lamé constants for the material that can be represented by
where expresses the Young’s modulus and stands for the Poisson’s ratio.
The equation of motion, in which is the body force component and , takes the form
and
This forms the thermal conduction theory. stands for the thermal conductivity, is the specific heat per unit mass, is relaxation time, is the body temperature and is the source of heat. When , Equations reduce to CTE.
The thermoelastic characteristics in FGM layers often change in the direction of thickness. The study of the variation of the elastic properties generally concerns polynomial and/or exponential functions applied directly to the engineering constants, e.g., Shear Moduli, Young’s Moduli , Bulk Moduli and/or Poisson ratio , or directly to stiffness. Poisson’s ratio of FGM has a limited number of variations. We argue that is a constant, as is the thermal expansion coefficient . Under the functionally graded solid, , , , and are not constant anymore. That is, they depend on space. Therefore, we substitute , , , for in the following
where , , , and are constants and is a dimensionless function of space variable .
After that, the corresponding Equations – are given, as follows:
3. Theoretical Analysis
In the present study, the problem of a thermoelastic functionally graded TSS at a reference temperature is considered. The strip is uniformly irradiated (the bounding plane ) using a non-Gaussian laser pulse with the profile of time. The coordinate is selected point on the inside of the goal and arises from the surface. We presume that the medium is not influenced by any body forces, and all state functions are equal to zero. Presume that the longitudinal scale along the x-axis is larger than those in the other two orthogonal directions of the x-axis. Therefore, TSS’s dynamic problem may be viewed as one-dimensional.
The displacement vector and thermal field are presented as follows:
Hence, the governing Equations in a one-dimensional plane are shown as follows:
where
3.1. The Non-Gaussian Laser Pulse
The initial distribution of temperature in the TSS is , i.e., . From , the upper surface of the TSS is the uniformly heated by laser pulse, with a temporal non-Gaussian profile in the following form [12,25,26]:
where is a time characteristic of the laser pulse and is the laser intensity, defined as the cumulative energy transmitted by a laser pulse for unit cross-section of the TSS. In addition to the Gaussian shape of the profile of intensity, a Gaussian beam has the profile of a transverse phase, which can be described with a polynomial, at most a second order. A linear variation of phase in one direction describes a tilt, and a quadratic variation of phase is associated with the beam divergence or convergence. There are also multimode beams with a profile of Gaussian intensity, but complicated phase patterns, and these are not Gaussian beams. It was reported in [12] that the laser intensity maxima decreases when arises.
Following [24,25,26], the transfer of thermal conduction in the beam may be formulated as a problem of one-dimension, assuming an energy source near to the surface, namely
where is the absorptive depth of the energy heating and is the irradiated surface absorptivity.
When considered on the surface of the medium, if the laser pulse is , the source of energy takes the following form:
3.2. Nondimensionalization
The afore-mentioned governing equations may be formulated in a nondimensional form using these nondimensional parameters:
where is the speed of the longituidinal plane wave and is the thermal viscosity.
Deleting the primes, Equations (7)–(9) take the following non-dimensional form:
where
3.3. The Solution to the Problem Considering LT Domain
We presumed the strip to be primarily at rest. It has a reference of temperature , and the velocity temperature vanishes. The initial conditions IC are supposed to be
Applying the LT, Equations are defined using the following formula:
Therefore, we get the following differential equations system:
where
3.4. Exponential Variation of Nonhomogeneity
In this problem, we assume that
where is a dimensionless nonhomogeneity parameter.
Later, the resultant equation decreases to
where
Eliminating and between the Equations and , we get
where
The solutions to Equations and are
where are the parameters that depend on and are obtained considering the boundary conditions, and
where are the origins of this characteristic
Using the solutions of and , we get the TS and the strain , in the forms
To obtain the value of , we apply to the bounding plane the boundary conditions, as follows:
where L is the total length.
After applying LT, it gives
After employing the aforementioned boundary conditions, we get the following equations:
Equations (35)(38) are expressed with matrixes as:
where
and
The exact solution of the former linear equation system results in the unknown parameters and .
Accordingly, the problem solution in the LT domain is completed.
3.5. Inversion of the LTs
To solve the problem in the defined physical domain, we use a numerical inversion approach based on a Fourier series expansion [27]. The inverse of the LT is approximated using the relation
where is a large integer sufficiently representing the terms number in a truncated infinite Fourier series.
The parameter should be selected as
where is a persecuted positive small number, which coordinates with the desired degree of precision. As a free positive parameter, is greater than the all singular real parts of .
The authors employed two methods to decrease the total error. First, they made use of the Korrecktur method to minimize the discretization error. After that, they utilized the algorithm to reduce the error of truncation and hasten convergence, as shown in Honig and Hirdes [27]. By selecting a constant large enough, the error of discretization can be made arbitrarily small. In the present numerical computations, the chosen values of and are selected based on the optimizing criteria discussed in [28].
4. Numerical Example and Discussion
To resolve the thermal displacement, stress, temperature and strain in the spatial–temporal domain, we applied the inversion formula of Laplace to the Equations , , and , respectively. We did so numerically by employing a method based on the aforementioned Fourier series expansion.
We provide some numerical results based on the theoretical results concluded in the former sections. We consider a copper material with material constants as shown in Table 1.

Table 1.
Physical constants of the copper material [23].
We did numerical calculations of the temperature, displacement, strain and components of stress along the x- direction. We carried out the computations for one time, i.e., and the laser intensity (i.e., L0 = 1011 J.m−2). Therefore, we adopted the Mathematica programming language for all numerical calculations.
Firstly, we can say that the very rapid speed of the thermal processes of a thermal shock, for example an ultra-short laser pulse, is interesting from a thermoelasticity standpoint, requiring coupled temperature and deformation fields analysis. This means that very rapid movements of the temperature shock induce the elements of structure, thus causing and reducing the rise of very significant inertial forces, and, thereby, the rise of vibrations. The expansions in oscillatory movements and the rapid changeable contractions generate temperature changes in the material susceptible to diffusion, owing to the heat conduction (Trajkovski and Cukic [12]).
We performed the numerical calculation for two different cases. The first of them examined how the dimensionless temperatures, displacement, strain and stress vary with different values of the parameter of nonhomogeneity when the relaxation time remains constant; N is the material graded parameter or the nonhomogeneity parameter. The mechanical and thermal properties of FGMs are assumed usually to have the same functions of certain space coordinates. In our work, the properties of FGM material are assumed to vary in x-direction, and are described in terms of exponential functions along the strip length. On the other hand, the nonhomogeneity parameter significantly affect the thermo-mechanical stress fields around the crack tip, and give a negative or zero or positive value due to the material nature; moreover, the crack compressesed, unaffected or extended with the effect of nonhomogeneity.
The second examined how the dimensionless temperature, stresses and displacement vary with different values of the relaxation time when the nonhomogeneity parameter remains constant.
Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 show the numerical evaluation of the thermoelastic displacement, temperature distribution and stress variation.

Figure 1.
Effect of nonhomogeneity parameter on the temperature .
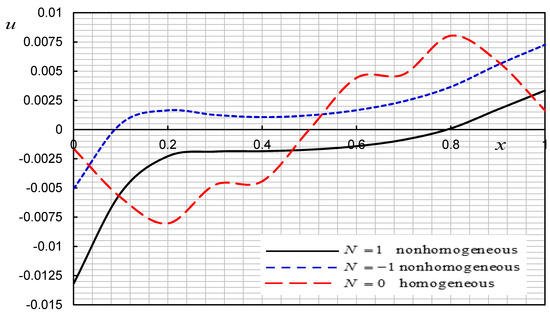
Figure 2.
Effect of nonhomogeneity parameter on the displacement .

Figure 3.
Effect of nonhomogeneity parameter on the thermal stress .
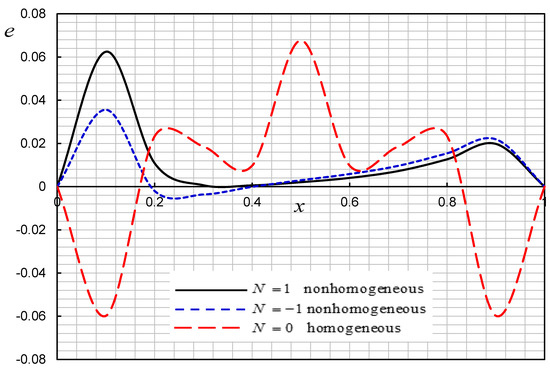
Figure 4.
Effect of nonhomogeneity parameter on the strain .

Figure 5.
Effect of relaxation time on the temperature .
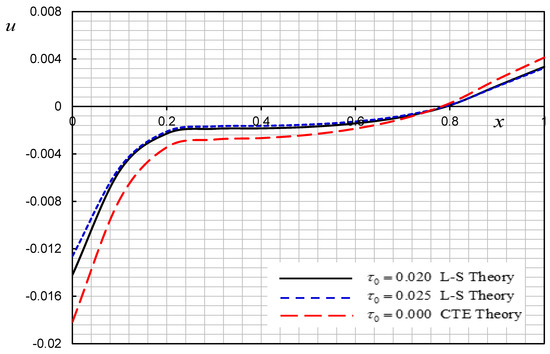
Figure 6.
Effect of relaxation time on the displacement .
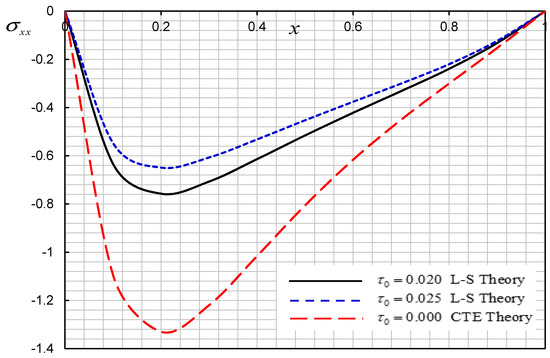
Figure 7.
Effect of relaxation time on the thermal stress .
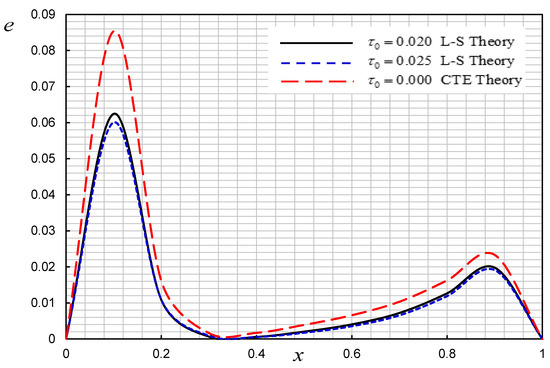
Figure 8.
Effect of relaxation time on the strain .
For the first case, we take three different values of the parameter of nonhomogeneity , and (homogeneous case), while the constant relaxation time .
Figure 1, Figure 2, Figure 3 and Figure 4 illustrate that the parameter significantly affects all fields. The results coincide with those mentioned in [25,26]. From Figure 1 and Figure 2, it can be found that the temperature and displacement distributions decrease as the nonhomogeneity parameter values increase. Figure 3 shows that, as the value of the parameter of non-homogeneity decreases, the peak of TS decreases. In Figure 4, the strain at both ends of the TSS is always zero, which matches the described boundary condition. We note that this matches the mechanical boundary condition. The displacement distributions, temperature and the absolute values of TS reach the maximum value at a certain distance. Then, they gradually decrease to zero, suggesting that the equation satisfied by the L–S model predicts propagation by a finite speed of the thermal signal.
In the second case, we consider different values of relaxation time while the constant nonhomogeneity parameter is . Figure 5, Figure 6, Figure 7 and Figure 8 illustrate the displacement, stress, temperature, and strain distributions for different three values of the parameters . We found that relaxation time parameter significantly affects all fields.
For a comparison of the results of the two models of thermoelasticity, the L-S model and CTE model , the displacements, temperature, and stresses are shown in Figure 5, Figure 6, Figure 7 and Figure 8. The figures show that the CTE model differs from the L–S theory.
Numerical results show that the effect of thermal relaxation causes the results of the non-Fourier heat conduction model to reach peak values later than those in the Fourier model, in agreement with [29].
It is clear that the effects of non-homogeneity, TSS and laser parameters are significant in the phenomenon of a thermoelastic on a TSS non-Gaussian laser beam.
Finally, the Gaussian beam and non-Gaussian beam provide an excellent and applicable example of important concepts relating to laser modes, beam radius and time diffraction limits. A change in the beam radius definition from aperture to focal plane also alters the mode content of the beam, resulting in inconsistent measures. The mode content of a given beam can change depending upon the experimenters’ choice of definition of radius beam. The content of a given beam mode is determined by the priori choice definition of beam radius [30].
5. Conclusions
The generalization theory of thermoelastic, with tr, assuming the L–S theory, was adopted to examine the problem of thermoelastic in an isotropic functionally graded TSS, where the surface of plane bounding is heated by a pulsed non-Gaussian laser beam. The material characteristics vary exponentially with distance. The generalized coupled thermoelastic governing equations were worked out. Employing the LT and the numerical inversion of the Laplace technique, the basic governing equations were solved. The numerical calculations were carried out for the studied variables, and the findings were illustrated graphically. By discussing the results, concluding remarks can be made:
- 1-
- The nonhomogeneity parameter significantly influences the solutions of displacement, temperature, stress and strain.
- 2-
- The impact of relaxation time has a considerable role in all distributions.
- 3-
- The Non-Gaussian laser pulse significantly affects all of the physical quantities (temperature, displacement, stress and strain).
- 4-
- The coupled thermoelasticity theory can be extracted as a special case.
- 5-
- The finite propagation speeds are manifested in all of the displayed graphs. This is expected because of the traveling of a thermal wave with a finite speed.
Author Contributions
Conceptualization, S.M.A.-D., A.E.A. and M.M.; methodology, S.M.A.-D. and M.M.; software, A.E.A.; validation, S.M.A.-D., A.E.A. and M.M.; formal analysis, A.E.A. and M.M.; investigation, S.M.A.-D.; resources, A.E.A.; data curation, S.M.A.-D. and A.E.A.; writing—original draft preparation, S.M.A.-D., A.E.A. and M.M.; writing—review and editing, S.M.A.-D. and A.E.A.; visualization, A.E.A.; supervision, M.M.; project administration, S.M.A.-D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ye, G.R.; Chen, W.Q.; Cai, J.B. A uniformly heated functionally graded cylindrical shell with transverse isotropy. Mech. Res. Commun. 2001, 28, 535–542. [Google Scholar] [CrossRef]
- El-Naggar, A.M.; Abd-Alla, A.M.; Fahmy, M.A.; Ahmed, S.M. Thermal stresses in a rotating non-homogeneous orthotropic hollow cylinder. Heat Mass Transf. 2002, 39, 41–46. [Google Scholar] [CrossRef]
- Wang, B.L.; Mai, Y.W. Transient one-dimensional heat conduction problems solved by finite element. Int. J. Mech. Sci. 2005, 47, 303–317. [Google Scholar] [CrossRef]
- Ootao, Y.; Tanigawa, Y. Transient thermoelastic analysis for a functionally graded hollow cylinder. J. Therm. Stresses 2006, 29, 1031–1046. [Google Scholar] [CrossRef]
- Shao, Z.S.; Wang, T.J.; Ang, K.K. Transient thermo-mechanical analysis of functionally graded hollow circular cylinders. J. Therm. Stresses 2007, 30, 81–104. [Google Scholar] [CrossRef]
- Biot, M.A. Thermoelasticity and irreversible thermodynamics. J. Appl. Phys. 1956, 27, 240–253. [Google Scholar] [CrossRef]
- Lord, H.; Shulman, Y. A generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solid 1967, 15, 299–309. [Google Scholar] [CrossRef]
- Green, A.E.; Lindsay, K.A. Thermoelasticity. J. Elast. 1972, 2, 1–7. [Google Scholar] [CrossRef]
- Kao, T.T. On Thermally Induced Non-Fourier Stress Waves in a Semi-Infinite Medium. AIAA J. 1976, 14, 818–820. [Google Scholar] [CrossRef]
- McDonald, F.A. On the Precursor in Laser-Generated Ultrasound Waveforms in Metals. Appl. Phys. Lett. 1990, 56, 230–232. [Google Scholar] [CrossRef]
- Enguehard, F.; Bertrand, L. Effects of Optical Penetration and Laser Pulse Duration on Laser Generated Longitudinal Acoustic Waves. Appl. Phys. Lett. 1997, 82, 1532–1538. [Google Scholar] [CrossRef]
- Trajkovski, D.; Cukic, R. A coupled problem of thermoelastic vibrations of a circular plate with exact boundary conditions. Mech. Res. Commun. 1999, 26, 217–224. [Google Scholar] [CrossRef]
- Sun, Y.; Fang, D.; Saka, M.; Soh, A.K. Laser-induced vibrations of micro-beams under different boundary conditions. Int. J. Solids Struct. 2008, 45, 1993–2013. [Google Scholar] [CrossRef]
- Al-Huniti, N.S.; Al-Nimr, M.A.; Naji, M. Dynamic response of rod due to a moving heat source under the hyperbolic heat conduction model. J. Sound Vib. 2001, 242, 629–640. [Google Scholar] [CrossRef]
- Abouelergal, E. Generalized thermoelasticity in an infinite nonhomogeneous solid having a spherical cavity using DPL model. Appl. Math. 2011, 2, 271–282. [Google Scholar]
- Youssef, H.M.; Al-Felali, A.S. Generalized Thermoelasticity Problem of Material Subjected to Thermal Loading Due to Laser Pulse. Applied Math. 2012, 3, 142–146. [Google Scholar] [CrossRef]
- Abo-Dahab, S.M.; Abouelregal, A.E. Investigation of the vibration of micro-beam resonators induced by a harmonically varying heat. J. Comput. Theor. Nanosci. 2015, 12, 924–933. [Google Scholar] [CrossRef]
- Elsherbeny, K.Z.; Abouelregal, A.E.; Abo-Dahab, S.M.; Rashid, A.F. Thermoelastic analysis for an infinite solid cylinder due to harmonically varying heat with thermal conductivity variable. J. Comput. Theor. Nanosci. 2016, 13, 4493–4500. [Google Scholar] [CrossRef]
- Marin, M.; Craciun, E.M.; Pop, N. Considerations on mixed initial-boundary value problems for micropolar porous bodies. Dyn. Syst. Appl. 2016, 25, 175–196. [Google Scholar]
- Riaz, A.; Ellahi, R.; Bhatti, M.M.; Marin, M. Study of heat and mass transfer in the Eyring–Powell model of fluid propagating peristaltically through a rectangular compliant channel. Heat Transf. Res. 2019, 50, 1539–1560. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Ellahi, R.; Zeeshan, A.; Marin, M. Numerical study of heat transfer and Hall current impact on peristaltic propulsion of particle-fluid suspension with compliant wall properties. Mod. Phys. Lett. B 2019, 33, 1950439. [Google Scholar] [CrossRef]
- Abo-Dahab, S.M.; Abouelregal, A.E. On a two-dimensional problem in thermoelasticity half-space with microstructure subjected to a uniform thermal shock. Phys. Waves Phemomena 2019, 27, 56–66. [Google Scholar] [CrossRef]
- Abbas, I.A. The effects of relaxation times and a moving heat source on a two-temperature generalized thermoelastic thin slim strip. Can. J. Phys. 2015, 93, 585–590. [Google Scholar] [CrossRef]
- Abbas, I.A.; Abo-Dahab, S.M. On the numerical solution of thermal shock problem for generalized magneto-thermoelasticity for an infinitely long annular cylinder with variable thermal conductivity. J. Comput. Theor. Nanosci. 2014, 11, 607–618. [Google Scholar] [CrossRef]
- Othman, M.I.; Abouelregal, A.E. The effect of pulsed laser radiation on a thermoviscoelastic semi-infinite solid under two-temperature theory. Arch. Thermodyn. 2017, 38, 77–99. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Zenkour, A.M. A generalized thermoelastic medium subjected to pulsed laser heating via a two-temperature model. J. Theor. Appl. Mech. 2019, 57, 631–639. [Google Scholar] [CrossRef]
- Honig, G.; Hirdes, U. A method for the numerical inversion of the Laplace transform. J. Comput. Appl. Math. 1984, 10, 113–132. [Google Scholar] [CrossRef]
- Fotuhi, A.R.; Fariborz, S.J. Anti-plane analysis of a functionally graded strip with multiple cracks. Int. J. Solids Struct. 2006, 43, 1239–1252. [Google Scholar] [CrossRef][Green Version]
- Zhou, Y.T.; Zhang, C.; Zhong, Z.; Wang, L. Transient thermo-electro-elastic contact analysis of a sliding punch acting on a functionally graded piezoelectric strip under non-Fourier heat conduction. Eur. J. Mech. A Solids 2019, 73, 90–100. [Google Scholar] [CrossRef]
- Ross, T.S. An analysis of a non-Gaussian, Gaussian laser beam. In Proceedings: Laser Beam Control and Applications; Laser Beam Control and Applications: San Jose, CA, USA, 2006; Volume 6101, p. 610111. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).