Abstract
We study the dilute and ultracold unitary Bose gas, characterized by a universal equation of state due to the diverging s-wave scattering length, under a transverse harmonic confinement. From the hydrodynamic equations of superfluids we derive an effective one-dimensional nonpolynomial Schrödinger equation (1D NPSE) for the axial wavefunction which, however, also takes into account the transverse wavefunction. By solving the 1D NPSE we obtain meaningful analytical formulas for the dark (gray and black) solitons of the bosonic system.
1. Introduction
The possibility of tuning the interaction between atoms near Feshbach resonances [1] almost at will, by precision control of external magnetic fields, is allowing the experimenters to explore the physics of ultracold gases in a wide range of values of the coupling constant characterized by the s-wave scattering length. The possibility to control the scattering length via Feshbach resonances makes ultracold atomic gases an excellent setting for studies of strongly correlated behavior. In particular it made possible to observe first a Fermi gas [2,3,4,5,6] and then also a Bose gas at unitarity [7,8,9,10], that is the limit in which the s-wave scattering length is infinitely large. In this so-called unitary regime, the interactions are as strong as allowed by quantum mechanics, and the physics cannot explicitly depend on the scattering length, leading to the possibility of new types of universal behavior [11]. In the case of a Bose gas, the presence of three body recombination processes [12] complicates the experimental realization of the unitary limit, which can be held for a limited amount of time. Nevertheless, the peculiar properties of a unitary gas, which behaves in a universal manner and exhibits scale invariance, encourage us to study the physics of such systems more in depth.
In this paper we investigate solitonic configurations of the unitary Bose gas. More specifically, we analyze axial and transverse density profiles of dark solitons in bosonic alkali-metal atoms at unitarity under the action of a transverse harmonic confinement. A dark soliton is a self-bound solitary wave, whose existence is made possible by the interplay between the repulsive interaction and the presence of a phase gradient. A dark soliton is characterized by a local decrease in density with respect to a uniform background. The depth of the dark soliton crucially depends on the phase of the complex field which describes the Bose gas.
The realizability of black and gray solitons in ultracold gases is well documented in the weak-coupling limit [13,14] and in a unitary Fermi gas [15]. Moreover, the properties of black solitons have been theoretically investigated for superfluid fermions also in the BCS-BEC crossover [16,17,18,19]. It is then a natural question to ask, whether black and gray solitons can be realized also in the case of Bose gases at unitarity, and what their specific properties are. It is important to stress that dark (black and gray) solitons of the unitary Bose gas have not yet been observed experimentally nor theoretically analyzed. Our theoretical paper can help experimental groups because we are giving analytical and semi-analytical formulas for density profiles, widths, and velocities of these dark solitons. All these quantities are universal because, contrary to the dark solitons of weakly-interacting bosonic gases, they do not depend on the s-wave scattering length.
We first derive the equations which govern the dynamics of these systems. The resulting equation is a nonlinear Schrödinger equation for a complex order parameter of the bosonic system [20]. Then, we find the solutions which are in the form of dark solitons, specifically as stationary objects in a moving frame.
Mimicking the experimental practice of confining ultracold gases in the minimum of a potential, we study the case in which the Bose gas is placed in a harmonic potential with cylindrical symmetry, which is an approximation to a more realistic cigar shaped potential [13,15]. A Gaussian variational approach, whose effectiveness in similar cases has already been proved [21,22,23,24,25,26], is then deployed to obtain an effective one-dimensional nonpolynomial Schrödinger equation (1D NPSE) for the axial wavefunction. The relevance of using the 1D NPSE in the study of solitons is due to the fact that the obtained solutions are a reliable generalization of familiar strictly one-dimensional results. These generalized solutions take properly into account that the transverse width of the cigar-shaped bosonic cloud depends on the axial coordinate.
In particular, we focus on the case of weak transverse confinement, in which more naive attempts to reduce the dimensionality of the problem fail. We integrate analytically the 1D NPSE thanks to the presence of a constant of motion, leaving behind a solution in terms of an integral, which we finally evaluate by means of numerical techniques. We are then able to find the axial density profile, transverse width and phase of the bosonic system. Moreover, we find the relation between density at the minimum and velocity of the soliton. While doing so, we also find that the theory actually depends on just one free parameter. Finally, we comment on the limits of the weak-coupling approximation.
2. From Euler Equations to Nonlinear Schrödinger Equation
Euler equations describe the dynamics of a non-viscous and irrotational fluid, such as a superfluid Bose gas at zero temperature [27]. In presence of an external potential , these equations are given by
The equation of state of the unitary Bose gas at zero temperature, namely the bulk pressure P as a function of the number density n, is given by
where n is the number density of atoms and , with u a universal and adimensional (positive) coefficient [7,28]. Notice that , where is the bulk chemical potential and is the bulk internal energy. In general, in the absence of external confinement, that is, , if the uniform atomic gas is very dilute and at zero temperature, there are only two length scales: the mean distance between atoms and the s-wave scattering length of the inter-atomic interaction. For the unitary gas the scattering length diverges and consequently the remaining length scale is . In addition, in the Hamiltonian of the many-body problem always appears the ratio . Thus, from dimensional analysis it follows that the energy scales as and the pressure as . The unknown quantity in our problem with the unitary Bose gas is the universal coefficient u. However, the value of has been derived in many ways [28,29,30,31,32] and, depending on the procedure, values in the range have been reported.
We shall now derive a nonlinear Schrödinger equation (NLSE) with a nonlinearity exponent [20], starting from Equations (1) and (2) and adding a term, which will account for quantum effects. This is done via the mapping
where is a scalar field. Equation (5) is indeed fully justified by the fact the fluid is irrotational, that is, .
Let us integrate Equation (7) and multiply both sides by
The integration constant C appeared, but we shall see that it is not going to affect the dynamics. In order to get a mathematically sound Schrödinger equation, instead of the nasty Guerra-Pusterla Schrödinger equation [33,34,35] given by (8), we add the term on the right hand side of Equation (8). Indeed, adopting the same procedure for the weakly-interacting Bose gas, where the scattering length is small and , one obtains the Gross-Pitaevskii equation, whose validity for weak coupling is well established [36,37]. In other words, this additional term implies a quantum correction, explicitly dependent on in the Euler equations.
We can express the system of real equations as a single complex equation by adding Equation (6) multiplied by to Equation (8). Then we multiply every term by , to get
Finally, by defining
the last equation can be written as a nonlinear Schrödinger equation (NLSE)
C results in a potential energy offset. It can be removed by substituting . It is important to stress that Equation (10) implies that the scalar field is an angle and the circulation of the velocity field is quantized.
3. Nonpolynomial Schrödinger Equation
Let us suppose that the confining potential is harmonic in the plane with cylindrical symmetry along the z axis
Thus, we are assuming that there is no confinement along the z axis but there is instead a harmonic trap of frequency in the two other directions. We consider the following variational ansatz for
where the variational parameters are the axial wavefunction and the width of the transverse Gaussian wavefunction. The choice of a Gaussian function in the plane is justified by the presence of a harmonic potential in the plane. In fact, when the nonlinear term of the Schrödinger equation is negligible, the ground state wavefunction of the problem in the plane is indeed a Gaussian, where with the characteristic length of the transverse harmonic confinement.
By plugging Equation (15) into the action in Equation (12) we obtain
under the approximation of neglecting the space derivative of . In the case of weakly-interacting bosons, which are very well described in three dimensions by the Gross-Pitaevskii equation (i.e., the 3D Schrödinger equation with cubic nonlinearity) this approximation has also been found to be quite good when depends strongly but monotonically on z [21,26].
Minimizing the action with respect to with the constraint (13), we obtain
and by doing the same with respect to
where . We shall refer to Equation (17) endowed with (18) as the nonpolynomial Schrödinger equation [21,22,23,24,25,26].
Let us rewrite the equations in terms of adimensional quantities. We can do that with the substitutions
Remember that in this equation is adimensional—it is in units of the characteristic length of the transverse harmonic confinement. In Equation (20) one can identify two regimes: a regime of strong transverse confinement where and consequently the system is effectively mean-field one-dimensional, but also a regime of weak transverse confinement where . Thus, the regime of weak transverse confinement is obtained by neglecting the first addend on the right hand side of Equation (20), supposing that . This gives rise to
which plugged back in Equation (19) yields the following equation for
In the same approximation we can neglect the term , and obtain
where we defined
Finally, let us also express in terms of
It will prove useful to study also the limit of strong confinement, that is instead given by :
4. Dark Solitons in the 1D NPSE
A soliton is a solution to Equation (23) of the form
where and are real functions, and v is the velocity of the soliton. Once we substitute (28) in (23) we obtain the equations for f and
Upon inspection of Equation (30), we find that the right hand side should depend only on , so is only function of . Let us assume the following
4.1. Phase
Let us solve Equation (33) in order to obtain in terms of f. We can rewrite it as
for . After integration with respect to we have
where D is an integration constant. If we assume that
and we get . The expression for we are looking for is then
valid for .
4.2. Modulus
The total energy K is then a conserved quantity for all
and energy balance gives us the following first order equation
which is satisfied by the two branches
This equation can be put in the integral form with the separation of variables, giving
where, since the integral is positive, we have chosen the + sign when and the − sign otherwise. Therefore, has even parity with respect to reflections around , and we just need to study the case .
We now have to find the values of the parameters . This can be done by choosing boundary conditions for f.
4.3. Black Solitons
Let us find an odd parity solution (which features a node in the origin for the density n) with a positive horizontal asymptote at . We set , and since f is even, the phase will account for the change of sign. Then, the following boundary conditions are needed
This is possible only if in order to get rid of the term in Equation (45) which diverges as . The condition applied to Equation (41) gives
while applied to (45) gives
Equation (47) then becomes
It is possible to get rid of with the rescaling
and the parameter
while does not change: . We obtain
Plots of the numerical integration of Equation (54) are shown in Figure 1, for three values of . Accordingly with those integrations, also is computed and shown in the plot.
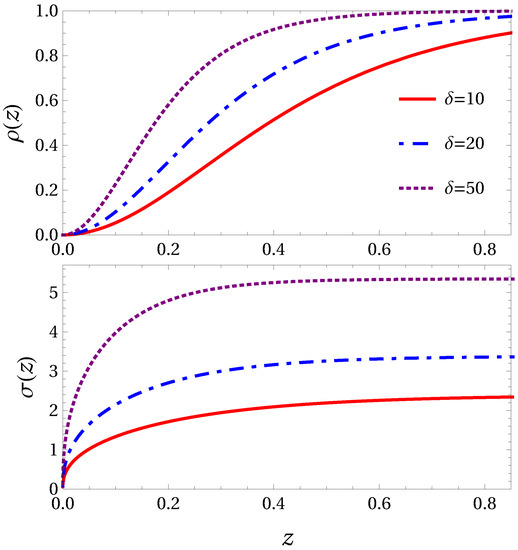
Figure 1.
Black soliton. Normalized axial density profile and transverse width profile vs. axial coordinate z, for three values of the parameter , with given by Equation (24) and the bulk value of the soliton wavefunction.
We may define and , so that the theory has no free parameters. This way there is only one plot to make, but we want to explicitly show in the plots the effects of changing the interaction, so for the moment we are keeping z and .
4.4. Gray Solitons
Let us find an even parity solution with a positive horizontal asymptote. We set once again, and require the following boundary conditions
The condition applied to Equation (41) gives
applied to Equation (45) gives
while by equating K inside Equation (45) evaluated at 0 and at ∞, applying we get a relation between and
Equation (47) then becomes
Also in this case we can get rid of in the same way as before, obtaining
where of course and is the speed of sound, that is, the propagation velocity of an infinitesimal perturbation in the fluid density.
Now the theory has two free parameters, namely and , while v is given in terms of them. In order to be more concise, we now define , and
so that we are left with a theory that depends only on (or ). The scaled velocity ranges from 0 (black soliton) to 1 (sound wave).
Plots of the numerical integration of Equation (61) are shown in Figure 2, for three values of . Accordingly with those integrations, is also computed and shown in the plot.
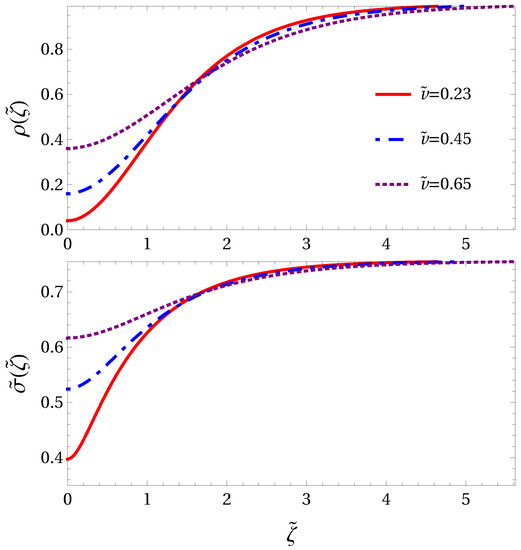
Figure 2.
Gray soliton. Upper panel: Scaled axial density profile vs. scaled comoving axial coordinate . Lower panel: Scaled transverse width vs. . Notice that , with given by Equation (24) and the bulk value of the soliton wavefunction. is the velocity rescaled by the sound velocity .
4.5. Phase
In the case of the black soliton, Equation (38) becomes . Since we want the solution to be odd, we choose
In the general case, we can now compute h and substitute inside Equation (38) to obtain . Let us express also in terms of :
it follows that
therefore
Last equation upon integration yields . A plot of the numerical integration of Equation (66) is shown in Figure 3 for four values of , including , which is the black soliton case.
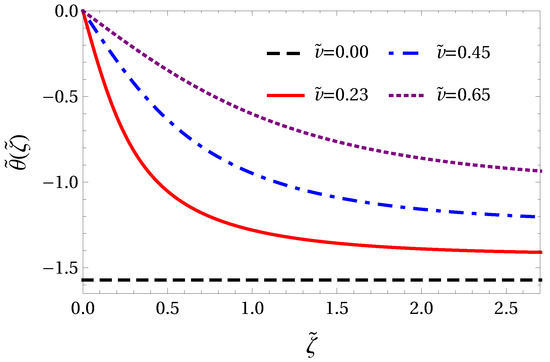
Figure 3.
Scaled phase of gray () and black () solitons vs. the scaled comoving axial coordinate .
5. Weak vs. Strong Transverse Confinement
In the previous sections we have mainly investigated the regime of weak transverse confinement where . See the discussion of Equation (20). Let us now briefly analyze some properties of the regime of strong transverse confinement where . In this case the system is truly one dimensional and the equations are much simpler.
By performing computations which are very close to the ones we have already shown in the weak confinement case, one can derive from (26) that in the case of a black soliton the following relation holds
where . Instead, for a gray soliton we obtain
where . In dimensional units, taking into account Equation (18), denoting the minimal axial density of the dark soliton and the bulk axial density of the dark soliton, one finds that under the condition the dark soliton is surely in the strictly 1D regime of strong transverse confinement at any point of the axial coordinate. Instead, under the condition the dark soliton is surely in the 3D regime of weak transverse confinement at any point of the axial coordinate. Clearly, in the case of the black soliton, where , near the minimum the bosonic cloud cannot be in the regime of weak transverse confinement.
It is important to stress that the comparison of our theoretical results with future experiments is constrained not only by the short lifetime of unitary bosonic gas due to fast three-body recombinations but also by the lifetime due to the snake instability [16,17,18,19]. A dark soliton, that is not strictly 1D, has a snaking transverse oscillation which breaks the axial symmetry and eventually destroys the soliton. Since the NPSE preserves axial symmetry, it is not suitable for investigating snaking oscillations and the dynamics of the dissolving dark soliton. However, it is possible to write a triaxial NPSE by using two transverse width and in the ansatz of Equation (15); see Reference [38] for details in the case of weakly-interacting bosons.
6. Conclusions
We have derived the dynamical equations that govern the motion of a unitary Bose gas at zero temperature. Using these equations, we have studied dark solitons in a unitary Bose gas, confined in a cylindrically symmetric potential. We have reduced the dimensionality of the 3D nonlinear Schrödinger problem by means of the 1D nonpolynomial Schrödinger equation approach, which also takes dynamically into account the transverse width. We have solved the equations employing for the most analytical techniques, in order to find axial density, transverse width, phase and velocity of both black and gray solitons, in the weak and strong confinement regimes. We have found that the weak confinement approximation breaks down in the case of a black soliton.
Our theoretical predictions could be tested experimentally employing Bose gases of alkali-metal atoms at ultra-low temperatures, whose scattering length can be tuned by means of Feshbach resonance techniques to reach the unitary limit. Despite the difficulties which presently limit the time during which such systems can be observed due to three-body losses but also to the snake instability, we are confident that the recent developments in the experimental techniques are going to allow in the future to put our predictions at test.
Author Contributions
Conceptualization, L.S.; Investigation, L.S. and M.C.; analytical calculations, M.C.; software M.C.; writing–original draft preparation, M.C.; writing–review and editing, L.S. and M.C.; supervision, L.S.; funding acquisition, L.S. All authors have read and agreed to the published version of the manuscript.
Funding
Partial support from the BIRD project “Time-dependent density functional theory of quantum atomic mixtures” of the University of Padova.
Acknowledgments
L.S. thanks Alberto Cappellaro and Andrea Tononi for useful discussions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Inouye, S.; Andrews, M.R.; Stenger, J.; Miesner, H.-J.; Stamper-Kurn, D.M.; Ketterle, W. Observation of Feshbach resonances in a Bose-Einstein condensate. Nature 1998, 392, 151–154. [Google Scholar] [CrossRef]
- O’Hara, K.M.; Hemmer, S.L.; Gehm, M.E.; Granade, S.R.; Thomas, J.E. Observation of a Strongly Interacting Degenerate Fermi Gas of Atoms. Science 2002, 298, 2179–2182. [Google Scholar] [CrossRef] [PubMed]
- Regal, C.A.; Ticknor, C.; Bohn, J.L.; Jin, D.S. Creation of ultracold molecules from a Fermi gas of atoms. Nature 2003, 424, 47–50. [Google Scholar] [CrossRef] [PubMed]
- Strecker, K.E.; Partridge, G.B.; Hulet, R.G. Conversion of an Atomic Fermi Gas to a Long-Lived Molecular Bose Gas. Phys. Rev. Lett. 2003, 91, 080406. [Google Scholar] [CrossRef] [PubMed]
- Jochim, S.; Bartenstein, M.; Altmeyer, A.; Hendl, G.; Riedl, S.; Chin, C.; Hecker Denschlag, J.; Grimm, R. Bose-Einstein Condensation of Molecules. Science 2003, 302, 2101–2103. [Google Scholar] [CrossRef] [PubMed]
- Gehm, M.E.; Hemmer, S.L.; Granade, R.S.; O’Hara, K.M.; Thomas, J.E. Mechanical stability of a strongly interacting Fermi gas of atoms. Phys. Rev. A 2003, 68, 011401. [Google Scholar] [CrossRef]
- Li, W.; Ho, T.-L. Bose Gases near Unitarity. Phys. Rev. Lett. 2012, 108, 195301. [Google Scholar] [CrossRef]
- Rem, B.S.; Grier, A.T.; Ferrier-Barbut, I.; Eismann, U.; Langen, T.; Navon, N.; Khaykovich, L.; Werner, F.; Petrov, D.S.; Chevy, F.; et al. Lifetime of the Bose Gas with Resonant Interactions. Phys. Rev. Lett. 2013, 110, 163202. [Google Scholar] [CrossRef]
- Makotyn, P.; Klauss, C.E.; Goldberger, D.L.; Cornell, E.A.; Jin, D.S. Universal dynamics of a degenerate unitary Bose gas. Nat. Phys. 2014, 10, 116–119. [Google Scholar] [CrossRef]
- Fletcher, R.J.; Gaunt, A.L.; Navon, N.; Smith, R.P.; Hadzibabic, Z. Stability of a Unitary Bose Gas. Phys. Rev. Lett. 2013, 111, 125303. [Google Scholar] [CrossRef]
- Giorgini, S.; Pitaevskii, L.P.; Stringari, S. Theory of ultracold atomic Fermi gases. Rev. Mod. Phys. 2008, 80, 1215. [Google Scholar] [CrossRef]
- Roberts, J.L.; Claussen, N.R.; Cornish, S.L.; Wieman, C.E. Magnetic Field Dependence of Ultracold Inelastic Collisions near a Feshbach Resonance. Phys. Rev. Lett. 2000, 85, 728. [Google Scholar] [CrossRef] [PubMed]
- Burger, S.; Bongs, K.; Dettmer, S.; Ertmer, W.; Sengstock, K.; Sanpera, A.; Shlyapnikov, G.V.; Lewenstein, M. Dark Solitons in Bose-Einstein Condensates. Phys. Rev. Lett. 1999, 83, 5198. [Google Scholar] [CrossRef]
- Denschlag, J.; Simsarian, J.E.; Feder, D.L.; Clark, C.W.; Collins, L.A.; Cubizolles, J.; Deng, L.; Hagley, E.W.; Helmerson, K.; Reinhardt, W.P.; et al. Generating Solitons by Phase Engineering of a Bose-Einstein Condensate. Science 2000, 287, 97–101. [Google Scholar] [CrossRef] [PubMed]
- Ku, M.J.H.; Mukherjee, B.; Yefsah, T.; Zwierlein, M.W. Cascade of Solitonic Excitations in a Superfluid Fermi gas: From Planar Solitons to Vortex Rings and Lines. Phys. Rev. Lett. 2016, 116, 045304. [Google Scholar] [CrossRef] [PubMed]
- Antezza, M.; Dalfovo, F.; Pitaevskii, L.P.; Stringari, S. Dark solitons in a superfluid Fermi gas. Phys. Rev. A 2007, 76, 043610. [Google Scholar] [CrossRef]
- Cetoli, A.; Brand, J.; Scott, R.G.; Dalfovo, F.; Pitaevskii, L.P. Snake instability of dark solitons in fermionic superfluids. Phys. Rev. A 2013, 88, 043639. [Google Scholar] [CrossRef]
- Lombardi, G.; Van Alphen, W.; Klimin, S.N.; Tempere, J. Soliton core filling in superfluid Fermi gases with spin-imbalance. Phys. Rev. A 2017, 96, 033609. [Google Scholar] [CrossRef]
- Van Alphen, W.; Lombardi, G.; Klimin, S.N.; Tempere, J. Dark soliton collisions in superfluid Fermi gases. New J. Phys. 2018, 20, 053052. [Google Scholar] [CrossRef]
- Adhikari, S.K.; Salasnich, L. Nonlinear Schrödinger equation for a superfluid Bose gas from weak coupling to unitarity: Study of vortices. Phys. Rev. A 2008, 77, 033618. [Google Scholar] [CrossRef]
- Salasnich, L.; Parola, A.; Reatto, L. Effective wave equations for the dynamics of cigar-shaped and disk-shaped Bose condensates. Phys. Rev. A 2002, 65, 043614. [Google Scholar] [CrossRef]
- Salasnich, L.; Parola, A.; Reatto, L. Transition from three dimensions to one dimension in Bose gases at zero temperature. Phys. Rev. A 2004, 70, 013606. [Google Scholar] [CrossRef]
- Salasnich, L.; Parola, A.; Reatto, L. Quasi-one-dimensional bosons in three-dimensional traps: From strong-coupling to weak-coupling regime. Phys. Rev. A 2005, 72, 025602. [Google Scholar] [CrossRef]
- Salasnich, L.; Malomed, B.A. Vector solitons in nearly one-dimensional Bose-Einstein condensates. Phys. Rev. A 2006, 74, 053610. [Google Scholar] [CrossRef]
- Salasnich, L.; Cetoli, A.; Malomed, B.A.; Toigo, F.; Reatto, L. Bose-Einstein condensates under a spatially modulated transverse confinement. Phys. Rev. A 2007, 76, 013623. [Google Scholar] [CrossRef]
- Salasnich, L.; Malomed, B.A.; Toigo, F. Matter-wave vortices in cigar-shaped and toroidal waveguides. Phys. Rev. A 2007, 76, 063614. [Google Scholar] [CrossRef]
- Pitaevskii, L.P.; Stringari, S. Bose-Einstein Condensation; Oxford Univ. Press: Oxford, UK, 2003. [Google Scholar]
- Rossi, M.; Salasnich, L.; Ancilotto, F.; Toigo, F. Monte Carlo simulations of the unitary Bose gas. Phys. Rev. A 2014, 89, 041602. [Google Scholar] [CrossRef]
- Cowell, S.; Heiselberg, H.; Mazets, I.; Morales, J.; Pandharipande, V.R.; Pethick, C.J. Cold Bose Gases with Large Scattering Lengths. Phys. Rev. Lett. 2002, 88, 210403. [Google Scholar] [CrossRef]
- Song, J.L.; Zhou, F. Ground State Properties of Cold Bosonic Atoms at Large Scattering Lengths. Phys. Rev. Lett. 2009, 103, 025302. [Google Scholar] [CrossRef]
- Lee, Y.-L.; Lee, Y.-W. Universality and stability for a dilute Bose gas with a Feshbach resonance. Phys. Rev. A 2010, 81, 063613. [Google Scholar] [CrossRef]
- Diederix, J.M.; van Heijst, T.C.F.; Stoof, H.T.C. Universality and stability for a dilute Bose gas with a Feshbach resonance. Phys. Rev. A 2011, 84, 033618. [Google Scholar] [CrossRef]
- Guerra, F.; Pusterla, M. A nonlinear schrödinger equation and its relativistic generalization from basic principles. Lett. Nuovo Cim. 1982, 34, 351–356. [Google Scholar] [CrossRef]
- Salasnich, L.; Toigo, F. Extended Thomas-Fermi density functional for the unitary Fermi gas. Phys. Rev. A 2008, 78, 053626. [Google Scholar] [CrossRef]
- Salasnich, L. Hydrodynamics of Bose and Fermi superfluids at zero temperature: The superfluid nonlinear Schrödinger equation. Laser Phys. 2009, 19, 642–646. [Google Scholar] [CrossRef]
- Gross, E.P. Structure of a quantized vortex in boson systems. Nuovo Cim. 1961, 20, 454–477. [Google Scholar] [CrossRef]
- Pitaevskii, L.P. Vortex lines in an imperfect Bose gas. Sov. Phys. JETP 1961, 13, 451–454. [Google Scholar]
- Salasnich, L. Generalized nonpolynomial Schrödinger equations for matter waves under anisotropic transverse confinement. J. Phys. A: Math. Theor. 2009, 42, 335205. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).