New Fixed Point Results via (θ,ψ)_R-Weak Contractions with an Application

Abstract

In this paper, inspired by Jleli and Samet (Journal of Inequalities and Applications 38 (2014) 1–8), we introduce two new classes of auxiliary functions and utilize the same to define ${(\theta ,\psi )}_{\mathcal{R}}$-weak contractions. Utilizing ${(\theta ,\psi )}_{\mathcal{R}}$-weak contractions, we prove some fixed point theorems in the setting of relational metric spaces. We employ some examples to substantiate the utility of our newly proven results. Finally, we apply one of our newly proven results to ensure the existence and uniqueness of the solution of a Volterra-type integral equation.

1. Introduction

Fixed point theory remains a very important and popular tool in pure, as well as applied mathematics, especially in the existence and uniqueness theories. It contains classical results to establish the existence and uniqueness theorems in ordinary differential equations, partial differential equations, integral equations, random differential equations, matrix equations, functional equations, iterated function systems, variational inequalities, etc. The Banach contraction principle [1] is one of the pivotal results of fixed point theory, which asserts that every contraction mapping defined on a complete metric space $(E,d)$ to itself always admits a unique fixed point. This principle is a very effective and popular tool for guaranteeing the existence and uniqueness of the solution of certain problems arising within and beyond mathematics. This principle has been generalized and extended in several directions. For this kind of work, one may recall Boyd and Wong [2], Matkowski [3], Ciric [4], Ran and Reurings [5], Jleli and Samet [6], and Imdad et al. [7], among others. As the Banach contraction principle and its extensions are existence and uniqueness results, they are very effectively utilized in several kinds of applications in the entire domain of mathematical and physical sciences, which also includes economics. One of the well-known extensions of the Banach contraction principle is due to Jleli and Samet [6], which is known as $\theta$-contractions (or $JS$-contractions). In order to define $\theta$-contractions, Jleli and Samet [6], in 2014, introduced a new class of auxiliary functions as given below.

Definition 1.

Let $\theta :(0,\infty )\to (1,\infty )$ be a function satisfying the following conditions:

$({\Theta }_1)$

θ is nondecreasing,

$({\Theta }_2)$

for any $\{{\alpha }_n\}\subseteq (0,\infty ),\underset{n\to \infty }{lim}{\alpha }_n=0$ iff $\underset{n\to \infty }{lim}\theta ({\alpha }_n)=1$,

$({\Theta }_3)$

there exists $l\in (0,\infty ]$ and $0<r<1$ satisfying $\underset{\alpha \to 0^{+}}{lim}\frac{\theta (\alpha )-1}{{\alpha }^r}=l$,

$({\Theta }_4)$

θ is continuous.

Jleli and Samet [6] proved the following result:

Theorem 1.

[6] Let $(E,d)$ be a complete generalized metric space and $f:E\to E$. Assume that there exist θ satisfying ${\Theta }_1,{\Theta }_2,{\Theta }_3$, and $\lambda \in (0,1)$ such that:

$$d\left(f(a),f(b)\right)>0\Rightarrow \theta (d\left(f(a),f(b)\right))\le {(\theta (d(a,b)))}^{\lambda },foralla,b\in E.$$

(1)

Then, f has a unique fixed point.

The mapping f in Theorem 1 is called $\theta$-contraction (or $JS$-contraction).

In 2015, Hussain et al. [8] extended Theorem 1 for some new contraction mappings in which the authors used the condition $({\Theta }_4)$ instead of $({\Theta }_3)$. Imdad et al. [7] relaxed the condition $({\Theta }_1)$ and called such mappings weak $\theta$-contractions.

On the other hand, there is yet another way to improve the Banach contraction principle utilizing various types of binary relations. In 2004, Ran and Reurings [5] proved a fixed point result in metric space equipped with a partial order relation, which was further generalized by Nieto and Rodríguez-López in [9,10]. In the same quest, in 2015, Alam and Imdad [11] generalized the Banach contraction to a complete relational metric space.

The study of this paper goes in four directions, which can be described as follows:

• to introduce the notion of ${(\theta ,\psi )}_{\mathcal{R}}$-weak contraction;
• to prove our results in the setting of relational metric spaces;
• to adopt some examples substantiating the utility of our proven results;
• to utilize our newly proven results and establish an existence and uniqueness result for the solution of a Volterra-type integral equation.

2. Preliminaries

In this manuscript, the set of all fixed points of $f:E\to E$ is denoted as $Fix(f).$ For simplicity, sometimes we write $fa$ instead of $f(a)$.

Our main results involve relation theoretic concepts. Therefore, we recall some preliminaries of the same.

Definition 2.

[12] Let E be a nonempty set. A subset $\mathcal{R}$ of $E^2$ is said to be a binary relation on E. For $a,b\in E$ with $(a,b)\in \mathcal{R}$, we say that “a is related to b” or “a relates to b under $\mathcal{R}$”. Sometimes, we write $a\mathcal{R}b$ instead of $(a,b)\in \mathcal{R}$. If $(a,b)\notin \mathcal{R}$, we say “a is not related to b” or “a does not relate to b under $\mathcal{R}$”. If $a\mathcal{R}b,b\mathcal{R}c$ implies $a\mathcal{R}c$, then $\mathcal{R}$ is called transitive.

In this paper, $\mathcal{R}$ denotes a nonempty binary relation defined on a nonempty set E. For brevity, we only use “binary relation” instead of “nonempty binary relation”.

Definition 3.

[11]

• A binary relation $\mathcal{R}$ on E is said to be f-closed if, for any $a,b\in E$,

  $$(a,b)\in \mathcal{R}\Rightarrow \left(f(a),f(b)\right)\in \mathcal{R}.$$
• A sequence $\{a_n\}\subseteq E$ is called $\mathcal{R}$-preserving if $(a_n,a_{n+1})\in \mathcal{R}\forall n\in \mathbb{N}$.

Definition 4.

A sequence $\{a_n\}\subseteq E$ is called an $\mathcal{R}$-preserving Cauchy sequence if it is a Cauchy sequence and $(a_n,a_{n+1})\in \mathcal{R}\forall n\in \mathbb{N}$.

Definition 5.

[11,13] Let $(E,d)$ be a metric space and $\mathcal{R}$ a binary relation on E.

• $\mathcal{R}$ is called d-self-closed if, for any $\mathcal{R}$-preserving sequence $\{a_n\}$ converging to a, there exists a subsequence $\{a_{n_k}\}\subseteq \{a_n\}$ with $(a_{n_k},a)\in \mathcal{R}$.
• $(E,d)$ is called $\mathcal{R}$-complete if every $\mathcal{R}$-preserving Cauchy sequence in E converges in E.
• A mapping $f:E\to E$ is called $\mathcal{R}$-continuous at $a\in E$ if for any $\mathcal{R}$-preserving sequence $\{a_n\}$ converging to a, we have $f{a}_n\to fa$. Moreover, f is $\mathcal{R}$-continuous on E if it is $\mathcal{R}$-continuous at each point of E.

We need the following lemma in the sequel.

Lemma 1.

[14] Let $(E,d)$ be a metric space and $\{a_n\}\subseteq E$ such that $\underset{n\to \infty }{lim}d(a_n,a_{n+1})=0$. If $\{a_n\}$ is not Cauchy, then there exist $ϵ>0$ and two subsequences $\{a_{n_k}\}$ and $\{a_{m_k}\}$ of $\{a_n\}$ with $n_k\ge m_k>k$ such that:

$$\begin{array}{lll}\underset{n\to \infty }{lim}d(a_{m_k},a_{n_k})& =& \underset{n\to \infty }{lim}d(a_{m_k},a_{n_k+1})=\underset{n\to \infty }{lim}d(a_{m_k-1},a_{n_k+1})\\ & =& \underset{n\to \infty }{lim}d(a_{m_k+1},a_{n_k+1})=ϵ.\end{array}$$

3. Main Results

Firstly, we introduce the following two classes of auxiliary functions, which are relatively larger than the class of the auxiliary functions covered under Definition 1.

Definition 6.

Let Θ be the collection of all $\theta :(0,\infty )\to (1,\infty )$ that satisfy the following conditions:

$({\Theta }_2)$

for every sequence $\{a_n\}\subseteq (0,\infty ),\underset{n\to \infty }{lim}{a}_n=0$ iff $\underset{n\to \infty }{lim}\theta (a_n)=1$,

$({\Theta }_3^{\prime })$

θ is lower semicontinuous.

The following examples of the functions $\theta :(0,\infty )\to (1,\infty )$ belong to the class of $\Theta$:

Example 1.

$\theta (a)=\left\{\begin{array}{c}{e}^{\frac{a}{2}}ifa\le 1\\ e^{a}ifa>1\end{array}\right.$,

Example 2.

$\theta (a)=\left\{\begin{array}{c}a+1ifa\le 1\\ a+2ifa>1\end{array}\right.$,

Example 3.

$\theta (a)=\left\{\begin{array}{c}{e}^{\frac{a}{2}+sina}ifa\le 2\pi \\ e^{\frac{a}{2}+cosa}ifa>2\pi \end{array}\right.$,

Example 4.

$\theta (a)=\left\{\begin{array}{c}{a}^2+1ifa\le 2\\ a^{3}ifa>2\end{array}\right.$.

Next, we introduce yet another class of auxiliary functions:

Definition 7.

Let Ψ be the collection of all $\psi :(0,\infty )\to (1,\infty )$ that satisfy the following conditions:

$({\mathsf{\Psi }}_2)$

for every sequence $\{a_n\}\subseteq (0,\infty ),\underset{n\to \infty }{lim}{a}_n=0$ iff $\underset{n\to \infty }{lim}\psi (a_n)=1$,

$({\mathsf{\Psi }}_3^{\prime })$

ψ is right upper semicontinuous.

The following mappings $\psi :(0,\infty )\to (1,\infty )$ belong to the class $\mathsf{\Psi }$:

Example 5.

$\psi (a)=\left\{\begin{array}{c}{e}^a+1ifa<2\\ a^{4}ifa\ge 2\end{array}\right.$,

Example 6.

$\psi (a)=\left\{\begin{array}{c}\sqrt{a}+1ifa<1\\ a+2ifa\ge 1\end{array}\right.$,

Example 7.

$\psi (a)=\left\{\begin{array}{c}{e}^{\frac{a}{2}+acosa}ifa<\pi \\ e^{\frac{a}{2}+sina}ifa\ge \pi \end{array}\right.$,

Example 8.

$\psi (a)=\left\{\begin{array}{c}{a}^2+1ifa<2\\ e^{2}ifa\ge 2\end{array}\right.$.

In what follows, we write $M(a,b)=max\{d(a,b),d(a,f(a)),d(b,f(b)),\frac{d(a,f(b))+d(b,f(a))}{2}\}$.

Finally, we introduce the concept of ${(\theta ,\psi )}_{\mathcal{R}}$-weak contractions as follows:

Definition 8.

Let $(E,d)$ be a metric space, $\mathcal{R}$ a binary relation on E, and $f:E\to E$. Then, f is called a ${(\theta ,\psi )}_{\mathcal{R}}$-weak contraction if there exist $\lambda \in (0,1),\theta \in \Theta$ and $\psi \in \mathsf{\Psi }$ with $\theta (t)\ge \psi (t)$ ($\forall t>0$) such that:

$$\theta (d\left(f(a),f(b)\right))\le {(\psi (M(a,b)))}^{\lambda },$$

$\forall a,b\in E$ with $a\mathcal{R}b$ and $f(a)\ne f(b)$.

Now, we state and prove our first main result as follows:

Theorem 2.

Let $(E,d)$ be a metric space endowed with a transitive binary relation $\mathcal{R}$ and $f:E\to E$. Assume that:

(i) 

E is $\mathcal{R}$-complete,

(ii) 

there exists $a_0\in E$ such that $a_0\mathcal{R}f(a_0)$,

(iii) 

$\mathcal{R}$ is f-closed,

(iv) 

f is ${(\theta ,\psi )}_{\mathcal{R}}$-weak contraction and

(v) 

f is $\mathcal{R}$-continuous.

Then, f has a fixed point.

Proof. 

In view of $(ii)$, there is $a_0\in E$ such that $a_0\mathcal{R}f{a}_0$. Consider the sequence $\{a_n\}$ of Picard iterates of f based at $a_0$, i.e.,

$$a_n=f^n{a}_0\forall n\in {\mathbb{N}}_0.$$

(2)

If $a_{n+1}=a_n$, for some $n\in {\mathbb{N}}_0$, then $f{a}_n=a_n$, i.e., $a_n$ is a fixed point of f, and there is nothing to prove. Now, assume that $a_n\ne a_{n+1},$ for all $n\in {\mathbb{N}}_0$. We claim that the sequence {$a_n$} is $\mathcal{R}$-preserving. Due to Condition $(ii)$ and (2), we have $a_0\mathcal{R}f{a}_0$ and $a_1=f{a}_0$; hence, $a_0\mathcal{R}{a}_1$. Suppose $a_n\mathcal{R}{a}_{n+1}$, for some $n\in \mathbb{N}$. As $\mathcal{R}$ is f-closed, we have $f{a}_n\mathcal{R}f{a}_{n+1}$, i.e., $a_{n+1}\mathcal{R}{a}_{n+2}$. Hence, by mathematical induction, we conclude that $\{a_n\}$ is $\mathcal{R}$-preserving and $f{a}_n\ne f{a}_{n+1}$, for all $n\in {\mathbb{N}}_0$.

In view of the contraction condition (2), we have:

$$\theta (d(a_n,a_{n+1}))=\theta (d(f{a}_{n-1},f{a}_n))\le (\psi {(M(a_{n-1},a_n))}^{\lambda },$$

where $M(a_{n-1},a_n)$:

$$\begin{array}{ll}=& max\{d(a_{n-1},a_n),d(a_{n-1},f{a}_{n-1}),d(a_n,f{a}_n),\frac{d(a_n,f{a}_{n-1})+d(a_{n-1},f{a}_n)}{2}\}\\ =& max\{d(a_{n-1},a_n),d(a_{n-1},a_n),d(a_n,a_{n+1}),\frac{d(a_n,a_n)+d(a_{n-1},a_{n+1})}{2}\}\\ =& max\{d(a_{n-1},a_n),d(a_n,a_{n+1})\},\end{array}$$

as $d(a_{n-1},a_{n+1})\le d(a_{n-1},a_n)+d(a_n,a_{n+1})$ and $max\{x,y,\frac{z}{2}\}=max\{x,y\}$ whenever $x,y,z\ge 0$ and $z\le x+y$.

If $M(a_{n-1},a_n)$=$d(a_n,a_{n+1})$, then,

$$\theta (d(a_n,a_{n+1}))\le \psi {((d(a_n,a_{n+1})))}^{\lambda }<\psi (d(a_n,a_{n+1}))\le \theta (d(a_n,a_{n+1})),$$

a contradiction. Hence,

$$M(a_{n-1},a_n)=d(a_{n-1},a_n),$$

so that:

$$\theta (d(a_n,a_{n+1}))\le {(\psi (d(a_{n-1},a_n)))}^{\lambda }\le {(\theta (d(a_{n-1},a_n)))}^{\lambda },$$

as $\theta (t)\ge \psi (t)\forall t>0$. Finally, we have:

$$1<\theta (d(a_n,a_{n+1}))\le {(\theta (d(a_{n-1},a_n)))}^{\lambda }\le \cdots \le (\theta {(d(a_0,a_1))}^{{\lambda }^n}.$$

Now, letting $n\to \infty$, we obtain:

$$1\le \underset{n\to \infty }{lim}\theta (d(a_n,a_{n+1}))\le 1,\mathrm{so}\mathrm{that}\underset{n\to \infty }{lim}\theta (d(a_n,a_{n+1}))=1.$$

Making use of $({\Theta }_2)$, we get:

$$\underset{n\to \infty }{lim}d(a_n,a_{n+1})=0.$$

Now, we proceed to prove that $\{a_n\}$ is Cauchy. Let on the contrary $\{a_n\}$ not be Cauchy. From Lemma 1, one can infer that there exist an $ϵ>0$ and $\{m_k\},\{n_k\}\subseteq \mathbb{N}$ with $n_k\ge m_k>k$ such that:

$$\{d(a_{m_k},a_{n_k})\},\{d(a_{m_k},a_{n_k+1})\},\{d(a_{m_k-1},a_{n_k})\},\{d(a_{m_k-1},a_{n_k+1})\},\{d(a_{m_k+1},a_{n_k+1})\}$$

(3)

tend to $ϵ$ when $k\to \infty$.

As $\mathcal{R}$ is transitive, so $a_{m_k+1}\mathcal{R}{a}_{n_k+1}$, for all $k\in \mathbb{N}$. Furthermore, for sufficiently large $k_0,f{a}_{m_k}\ne f{a}_{n_k}$, for all $k\ge k_0$ (as $d(a_{m_k+1},a_{n_k+1})\to ϵ$). Therefore, we have:

$$\theta (d(a_{n_k+1},a_{m_k+1}))=\theta (d(f{a}_{n_k},f{a}_{m_k}))\le (\psi {(M(a_{n_k},a_{m_k}))}^{\lambda },$$

(4)

so that:

$$\underset{k\to \infty }{lim\; inf}\theta (d(a_{n_k+1},a_{m_k+1}))\le \underset{k\to \infty }{lim\; inf}{(\psi (M(a_{n_k},a_{m_k})))}^{\lambda }\le \underset{k\to \infty }{lim\; sup}{(\psi (M(a_{n_k},a_{m_k})))}^{\lambda },$$

wherein $M(a_{n_k},a_{m_k})$:

$$\begin{array}{lll}& =& max\{d(a_{n_k},a_{m_k}),d(a_{n_k},f{a}_{n_k}),d(a_{m_k},f{a}_{m_k}),\frac{d(a_{n_k},f{a}_{m_k})+d(a_{m_k},f{a}_{n_k})}{2}\}\\ & =& max\{d(a_{n_k},a_{m_k}),d(a_{n_k},a_{n_k+1}),d(a_{m_k},a_{m_k+1}),\frac{d(a_{n_k},a_{m_k+1})+d(a_{m_k},a_{n_k+1})}{2}\}.\end{array}$$

Observe that:

$d(a_{n_k},a_{m_k+1})+d(a_{m_k},a_{n_k+1})\le d(a_{n_k},a_{m_k})+d(a_{m_k},a_{m_k+1})+d(a_{m_k},a_{n_k})+d(a_{n_k},a_{n_k+1})$.

Now, as $\underset{n\to \infty }{lim}d(a_n,a_{n+1})=0$, and $d(a_{n_k},a_{m_k})\to ϵ$, so due to Lemma 1, we have:

$$\underset{k\to \infty }{lim}M(a_{m_k},a_{n_k})=ϵ.$$

(5)

On using (3), (4), and (5), we get:

$$\theta (ϵ)\le \underset{k\to \infty }{lim\; inf}\theta (d(a_{n_k+1},a_{m_k+1}))\le \underset{k\to \infty }{lim\; sup}{(\psi (M(a_{n_k},a_{m_k})))}^{\lambda }\le {(\psi (ϵ))}^{\lambda }<\psi (ϵ)\le \theta (ϵ),$$

a contradiction. Thus, $\{a_n\}$ is Cauchy. As $\{a_n\}$ is $\mathcal{R}$-preserving Cauchy in E, which is $\mathcal{R}$-complete, therefore, there is some $a\in E$ such that:

$$\underset{n\to \infty }{lim}{a}_n=a.$$

As f is $\mathcal{R}$-continuous, we obtain:

$$f{a}_n\to fa\mathrm{and},\mathrm{as}n\to \infty ,$$

i.e., $a_{n+1}\to fa$ as $n\to \infty$. Now, using the uniqueness of the limit, we have $fa=a$. Hence, f has a fixed point in E. This ends the proof. □

Next, we adopt the following example, which exhibits the utility of Theorem 2.

Example 9.

Let $E={\mathbb{R}}^{+}$ and d be the usual metric defined by $d(a,b)=|a-b|$, $\forall a,b\in E$. Define $\{{\alpha }_n\}$ as:

$${\alpha }_n=\frac{n(n+1)(n+2)(n+3)}{4},foralln\in \mathbb{N},$$

whose first few terms are 6, 30, 90, 210, and so on. Define a binary relation $\mathcal{R}$ on E as:

$$\mathcal{R}=\{(1,1),(1,{\alpha }_i),({\alpha }_i,{\alpha }_j):i,j\in \mathbb{N},i<j\}.$$

Define f on E by:

$$f(x)=\left\{\begin{array}{l}x,if0\le x<1,\\ 1,if1\le x<6,\\ 1+\frac{5}{24}(x-6),if{\alpha }_1\le x<{\alpha }_2,\\ {\alpha }_{i-1}+\frac{{\alpha }_i-{\alpha }_{i-1}}{{\alpha }_{i+1}-{\alpha }_i}(x-{\alpha }_i),if{\alpha }_i\le x<{\alpha }_{i+1}.\end{array}\right.$$

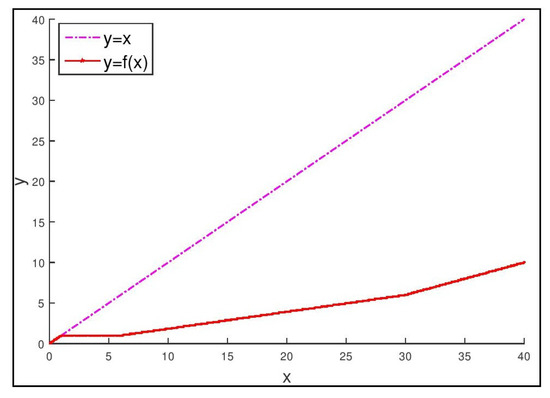
The mapping f is continuous (see Figure 1).

Figure 1. Graph of $y=x$ and $y=fx$ in Example 9.

To show that $\mathcal{R}$ is f-closed, consider the following three different cases.

Case I: Let $(a,b)=(1,1)\in \mathcal{R}$, then $\left(f(a),f(b)\right)=(1,1)\in \mathcal{R}$.

Case II: When $(a,b)=(1,{\alpha }_i)\in \mathcal{R}$, then $\left(f(a),f(b)\right)=(1,1)$ or $(1,{\alpha }_i)$, i.e., $fa\mathcal{R}fb$.

Case III: When $(a,b)=({\alpha }_i,{\alpha }_j),i<j$, then $\left(f(a),f(b)\right)=(1,{\alpha }_{j-1})$ or $({\alpha }_{i-1},{\alpha }_{j-1})$ and, hence, $fa\mathcal{R}fb$. Thus, $\mathcal{R}$ is f-closed.

Now, to show that f is a ${(\theta ,\psi )}_{\mathcal{R}}$-weak contraction mapping, we define $\theta ,\psi :{\mathbb{R}}^{+}\to \mathbb{R}$ as follows:

$$\theta (t)=e^{e^{{\gamma }_1(t)}},\psi (t)=e^{e^{{\gamma }_2(t)}},$$

where ${\gamma }_1,{\gamma }_2:{\mathbb{R}}^{+}\to \mathbb{R}$ are given by:

$${\gamma }_1(t)=\left\{\begin{array}{c}\frac{-1}{t}+\frac{t}{2},t\le 10,\\ \frac{-1}{t}+t,t>10,\end{array}\right.and\text{:}{\gamma }_2(t)=\left\{\begin{array}{c}\frac{-1}{t}+\frac{t}{3},t<25,\\ \frac{-4}{t}+t,t\ge 25.\end{array}\right.$$

We have to show that there exists some $\lambda \in (0,1)$ such that:

$$\begin{array}{lll}\hfill \theta (d\left(f(a),f(b)\right))& \le & {(\psi (M(a,b)))}^{\lambda }\\ \hfill i.e.,e^{e^{{\gamma }_1(d\left(f(a),f(b)\right))}}& \le & {(e^{e^{{\gamma }_2(M(a,b))}})}^{\lambda }=e^{\lambda e^{{\gamma }_2(M(a,b))}}\\ \hfill or,e^{{\gamma }_1(d\left(f(a),f(b)\right))}& \le & \lambda e^{{\gamma }_2(M(a,b))}\\ \hfill or,{\gamma }_1(d\left(f(a),f(b)\right))& \le & ln(\lambda )+{\gamma }_2(M(a,b))\end{array}$$

(6)

We do not need to consider the cases $(1,1),(1,{\alpha }_1)\in \mathcal{R}$ as $fa=fb$. Now, we distinguish the following four cases.

Case I: If $a=1$ and $b={\alpha }_2=30,$ then $d(a,b)=29,d\left(f(a),f(b)\right)=5$,

$$\begin{array}{lll}\mathit{where}M(a,b)& =& max\{d(a,b),d(a,fa),d(b,fb),\frac{d(a,fb)+d(b,fa)}{2}\}\\ & =& max\{29,0,24,\frac{5+29}{2}\}=29,\end{array}$$

so that:

$$\begin{array}{lll}\hfill 4+{\gamma }_1(d\left(f(a),f(b)\right))& =& 4+{\gamma }_1(5)=10-\frac{1}{5}+\frac{5}{2}\\ & \le & -\frac{4}{29}+29={\gamma }_2(29)\\ \hfill i.e.,4+{\gamma }_1(d\left(f(a),f(b)\right))& =& {\gamma }_2(M(a,b)).\end{array}$$

Case II: If $a=1$ and $b={\alpha }_i,i>2$, then $d(a,b)\ge 89,d\left(f(a),f(b)\right)\ge 29$

$$\begin{array}{lll}\hfill \mathit{wherein}M(a,b)& =& max\{d(a,b),d(a,fa),d(b,fb),\frac{d(a,fb)+d(b,fa)}{2}\}\\ & \ge & max\{89,0,60,\frac{29+89}{2}\}=89,\end{array}$$

so that:

$$\begin{array}{lll}\hfill 4(d\left(f(a),f(b)\right))-M(a,b)& <& 4(d\left(f(a),f(b)\right))\\ & <& M(a,b)d\left(f(a),f(b)\right)\\ & <& M(a,b)(d\left(f(a),f(b)\right))(M(a,b)-d\left(f(a),f(b)\right)-4)\\ \hfill \mathit{yielding}\mathit{thereby}\frac{4}{M(a,b)}-\frac{1}{d\left(f(a),f(b)\right)}& <& M(a,b)-d\left(f(a),f(b)\right)-4\\ \hfill or,4+d\left(f(a),f(b)\right)-\frac{1}{d\left(f(a),f(b)\right)}& <& -\frac{4}{M(a,b)}+M(a,b)\\ \hfill i.e.,4+{\gamma }_1(d\left(f(a),f(b)\right))& \le & {\gamma }_2(M(a,b).\end{array}$$

Case III: If $a={\alpha }_1=6$ and $b={\alpha }_2=30$, then $d(a,b)=24,d\left(f(a),f(b)\right)=(1,6)=5$:

$$\begin{array}{lll}\hfill \mathit{where}M(a,b)& =& max\{d(a,b),d(a,fa),d(b,fb),\frac{d(a,fb)+d(b,fa)}{2}\}\\ & =& max\{24,5,24,\frac{0+29}{2}\}=24,\end{array}$$

so that:

$$\begin{array}{lll}\hfill 4+{\gamma }_1(d\left(f(a),f(b)\right))& =& 4+{\gamma }_1(5)\\ & =& 4-\frac{1}{5}+\frac{5}{2}\\ & \le & -\frac{1}{24}+\frac{24}{3}\\ & =& -\frac{1}{M(a,b)}+\frac{M(a,b)}{3}\\ \hfill i.e.,4+{\gamma }_1(d\left(f(a),f(b)\right))& =& {\gamma }_2(M(a,b)).\end{array}$$

Case IV: If $a={\alpha }_i$ and $b={\alpha }_j,(i,j)\ne (1,2)$, then $d(a,b)\ge 60,d\left(f(a),f(b)\right)\ge 24$:

$$\begin{array}{lll}\mathit{where}M(a,b)& =& max\{d(a,b),d(a,fa),d(b,fb),\frac{d(a,fb)+d(b,fa)}{2}\}\\ & \ge & max\{24,5,24,\frac{0+29}{2}\}=24,\end{array}$$

so that:

$$\begin{array}{lll}\hfill 4(d\left(f(a),f(b)\right))-M(a,b)& <& 4(d\left(f(a),f(b)\right))\\ & <& M(a,b)d\left(f(a),f(b)\right)\\ & <& M(a,b)(d\left(f(a),f(b)\right))(M(a,b)-d\left(f(a),f(b)\right)-4)\\ \hfill \mathit{yielding}\mathit{thereby}\frac{4}{M(a,b)}-\frac{1}{d\left(f(a),f(b)\right)}& <& M(a,b)-d\left(f(a),f(b)\right)-4\\ \hfill or,4+d\left(f(a),f(b)\right)-\frac{1}{d\left(f(a),f(b)\right)}& <& \frac{4}{M(a,b)}+M(a,b)\\ \hfill i.e.,4+{\gamma }_1(d\left(f(a),f(b)\right))& \le & {\gamma }_2(M(a,b).\end{array}$$

Therefore, in all four cases, we have:

$${\gamma }_1(d\left(f(a),f(b)\right))\le -4+{\gamma }_2(M(a,b)\forall a,b\in Ewhenevera\mathcal{R}bandd\left(f(a),f(b)\right)>0$$

Thus, the condition (6) is satisfied if we take $\lambda =\frac{1}{e^4}\in (0,1)$. Therefore, we have furnished a $\lambda \in (0,1)$ such that $\theta (d\left(f(a),f(b)\right))\le {(\psi (M(a,b)))}^{\lambda }$, for all $a,b\in E$ with $a\mathcal{R}b$, i.e., f is a ${(\theta ,\psi )}_{\mathcal{R}}$-weak contraction mapping on X. Observe that the remaining assumptions of Theorem 2 are also fulfilled. Thus, f possesses a fixed point in E. Observe that f has infinitely many fixed points; in fact, $Fix(f)=[0,1]$ (see Figure 1).

The pre-existing results in this direction, say the results of Jleli and Samet [6], Hussain et al. [8], and Imdad et al. [7], cannot be applied in this example as these results require the contraction condition to hold on the whole space. However, in this example, the contraction condition holds for those $a,b\in E$, which are related under the binary relation $\mathcal{R}$.

Now, we prove an analog of Theorem 2 using the d-self-closedness property.

Theorem 3.

The conclusion of Theorem 2 holds true if Assumption (v) is replaced by:

$(v^{\prime })$$\mathcal{R}$ is d-self-closed.

Proof. 

On the lines of the proof of Theorem 2, we can show that $\{a_n\}$ is an $\mathcal{R}$-preserving Cauchy sequence converging to $a\in E$. Our aim is to show that $a=fa$. Suppose on the contrary that $d(a,fa)>0$. In view of the condition ($v^{\prime }$), there exists a subsequence $\{a_{n_k}\}\subseteq \{a_n\}$ with $a_{n_k}\mathcal{R}a$, for all $k\in \mathbb{N}$. Now, as $a_n\to a$ and $a\ne fa$, for sufficiently large $k_0$, we have $f{a}_{n_k}\ne fa$, for all $k\ge k_0$. Hence, we have (for all $k\ge k_0$):

$$\theta (d(a_{n_k+1},fa))\le (\psi {(M(a_{n_k+1},a))}^{\lambda },$$

(7)

where $M(a_{n_k+1},a)=$:

$$max\{d(a_{n_k+1},a),d(a_{n_k+1},f{a}_{n_k+1}),d(a,fa),\frac{d(a,f{a}_{n_k+1})+d(a_{n_k+1},fa)}{2}\}.$$

As:

$$\frac{d(a,f{a}_{n_k+1})+d(a_{n_k+1},fa)}{2}\le \frac{d(a,f{a}_{n_k+1})+d(a_{n_k+1},a)+d(a,fa)}{2}$$

and the sequence $\{a_n\}$ converges to a with $d(a,fa)>0$, we have (for all $k\ge k_0$):

$$d(a_{n_k+1},a)<d(a,fa),d(a_{n_k+1},f{a}_{n_k+1})=d(a_{n_k+1},a_{n_k+2})<d(a,fa),$$

$$d(a,f{a}_{n_k+1})+d(a_{n_k+1},a)=d(a,a_{n_k+2})+d(a_{n_k+1},a)<\frac{d(a,fa)}{2},$$

so that (for all $k\ge k_0$):

$$M(a_{n_k+1},a)=d(a,fa).$$

Hence, (7) reduces to:

$$\theta (d(a_{n_k+1},fa))\le {(\psi (d(a,fa)))}^{\lambda }, \mathrm{for} \mathrm{all} k\ge k_0,$$

implying thereby:

$$\underset{n\to \infty }{lim\; inf}\theta (d(a_{n_k+1},fa))\le \underset{n\to \infty }{lim\; inf}({(\psi (d(a,fa)))}^{\lambda }={(\psi (d(a,fa)))}^{\lambda }.$$

As $\theta$ is lower semicontinuous, $\underset{n\to \infty }{lim\; inf}\theta (d(a_{n_k+1},fa))\ge \theta (d(a,fa))$, which gives rise to the following:

$$\theta (d(a,fa))\le {(\psi (d(a,fa)))}^{\lambda }<\psi (d(a,fa))\le \theta (d(a,fa)).$$

This is a contradiction. Hence, the assumption $d(a,fa)\ne 0$ is wrong. Therefore, we must have $d(a,fa)=0$, i.e., a is a fixed point of f. This completes the proof. □

Next, we prove the following corresponding uniqueness result.

Theorem 4.

If we assume in addition to the assumptions of Theorem 2 (or Theorem 3) that $Fix(f)$ is complete or $Fix(f)$ is ${\mathcal{R}}^S$-connected, then f has a unique fixed point in E.

Proof. 

In view of Theorem 2 (or 3), we have $Fix(f)$ is nonempty. Assume that $Fix(f)$ is complete, and let $a,b$ be two different points in $Fix(f)$. Therefore, $a\mathcal{R}b$ or $b\mathcal{R}a$, i.e., $[a,b]\in \mathcal{R}$ or $a{\mathcal{R}}^{S}b$. As $a=fa,b=fb$ and $a\ne b$, we have $d\left(f(a),f(b)\right)>0$. Hence, using the contraction condition $(iv)$, we get:

$$\theta (d(a,b))=\theta (d\left(f(a),f(b)\right))\le {(\theta (d(a,b)))}^{\lambda },\mathrm{for}\mathrm{some}\lambda \in (0,1).$$

This is a contradiction as $\theta (d(a,b))>0$. Hence, our assumption that $a\ne b$ is wrong. Therefore, f has a unique fixed point in E.

Now, if $Fix(f)$ is ${\mathcal{R}}^S$-connected and $a,b\in Fix(f)$, then there exist $a_1,a_2...,a_{n-1}$ in $Fix(f)$ such that $a_i{\mathcal{R}}^S{a}_{i+1},$ for all $i:0\le i\le n-1$ where $a_0=a\mathrm{and}{a}_n=b$. Now, as $a_i{\mathcal{R}}^S{a}_{i+1}$ and $a_i,a_{i+1}\in Fix(f),$ for all $i:0\le i\le n-1;$ from the earlier part of the theorem, we have $a_i=a_{i+1}$, for all i. Therefore, $a=b$, $i.e.$, the fixed point of f is unique. This concludes the proof. □

Now, to substantiate the utility of Theorems 3 and 4, we furnish the following example:

Example 10.

Let $E=(-1,3]$ and d be the usual metric on E. Define $\mathcal{R}$ on E as:

$$\mathcal{R}=\{(0,0),(0,1),(1,0),(1,1),(0,3),(1,3)\}.$$

Then, $\mathcal{R}$ is transitive. Now, define $f:E\to E$ by:

$$f(t)=\left\{\begin{array}{l}0,if-1<t\le 1,\\ 1,if1<t\le 3.\end{array}\right.$$

We observe that the following holds:

• E is $\mathcal{R}$-complete, as for any $\mathcal{R}$-preserving Cauchy sequence $\{a_n\}$ in E, there exists $K\in \mathbb{N}$ such that $a_n=1$, $\forall n\ge K$ or $a_n=0$, $\forall n\ge K$, i.e., $\{a_n\}$ converges to zero or one;
• $0\in E$ and $0\mathcal{R}f0$;
• $\mathcal{R}$ is f-closed;

Now, we show that f is a ${(\theta ,\psi )}_{\mathcal{R}}$-weak contraction. Take $\theta \in \Theta ,\psi \in \mathsf{\Psi }$ as the following:

$$\theta (t)=e^{e^{{\gamma }_1(t)}},\psi (t)=e^{e^{{\gamma }_2(t)}},$$

where ${\gamma }_1,{\gamma }_2:{\mathbb{R}}^{+}\to \mathbb{R}$ are given by:

$${\gamma }_1(t)=\left\{\begin{array}{c}\frac{-1}{t}+\frac{t}{2},t\le 10,\\ \frac{-1}{t}+t,t>10,\end{array}\right.and{\gamma }_2(t)=\left\{\begin{array}{c}\frac{-1}{t}+\frac{t}{3},t<25,\\ \frac{-4}{t}+t,t\ge 25.\end{array}\right.$$

We have to show that there exists $\lambda \in (0,1)$ such that:

$$\begin{array}{lll}\hfill \theta (d\left(f(a),f(b)\right))& \le & {(\psi (M(a,b)))}^{\lambda }\\ \hfill i.e.,e^{e^{{\gamma }_1(d\left(f(a),f(b)\right))}}& \le & {(e^{e^{{\gamma }_2(M(a,b))}})}^{\lambda }=e^{k{e}^{{\gamma }_2(M(a,b))}}\\ \hfill or,e^{{\gamma }_1(d\left(f(a),f(b)\right))}& \le & k{e}^{{\gamma }_2(M(a,b))}\\ \hfill or,{\gamma }_1(d\left(f(a),f(b)\right))& \le & ln(\lambda )+{\gamma }_2(M(a,b)).\end{array}$$

Observe that $d\left(f(a),f(b)\right)>0$ implies that $(a,b)\in \{(0,3),(1,3)\}$. Therefore, we consider only the two cases $(0,3)$ and $(1,3)$.

Case I: Let $(a,b)=(0,3)$. Then:

$$d\left(f(a),f(b)\right)=d(0,1)=1<3=d(0,3)=d(a,b)\le M(a,b).$$

Observe that,

$$\frac{1}{2}+{\gamma }_1(1)=0\le \frac{2}{3}=-\frac{1}{3}+1={\gamma }_2(3).$$

Case II: If $(a,b)=(1,3)$, then:

$$d\left(f(a),f(b)\right)=d(0,1)=1<2=d(1,3)=d(a,b)\le M(a,b).$$

As:

$$\frac{1}{2}+{\gamma }_1(1)=0\le \frac{1}{6}=-\frac{1}{2}+\frac{2}{3}={\gamma }_2(2),$$

Therefore, for $\lambda =e^{-\frac{1}{2}}\in (0,1)$, we have:

$${\gamma }_1(d\left(f(a),f(b)\right))\le ln(\lambda )+{\gamma }_2(M(a,b)),$$

or:

$$\theta (d\left(f(a),f(b)\right))\le {(\psi (M(a,b)))}^{\lambda },$$

for all $a,b\in E$ with $a\mathcal{R}b$ and $fa\ne fb$. Hence, the Condition $(iv)$ is satisfied.

Next, in order to verify $(v^{\prime })$, observe that for any $\mathcal{R}$-preserving sequence $\{a_n\}$ converging to some $a\in E$, there is some $K\in \mathbb{N}$ such that either $a_n=0$, for all $n\ge K$ or $a_n=1$, for all $n\ge K$. Hence, ${\{a_{K+i}\}}_{i\in {\mathbb{N}}_0}$ is a subsequence of $\{a_n\}$ such that $a_{K+i}\mathcal{R}a$ for each $i\in {\mathbb{N}}_0$.

Therefore, all the assumptions of Theorem 3 are satisfied. Hence, f has a fixed point in E. We can see that zero is the fixed point of f. Furthermore, $Fix(f)=\{0\}$, which is complete as $(0,0)\in \mathcal{R}$. Thus, Theorem 4 ensures the uniqueness of the fixed point of f.

4. Applications

In this section, we apply Theorem 4 to ensure the existence and uniqueness of the solution for the following integral equation:

$$a(s)={\int }_0^{s}G(s,v,a(v))dv+g(s),s\in [0,1],$$

(8)

where G is a continuous function from $[0,1]\times [0,1]\times [0,1]$ to [0, 1] and g is a continuous function from [0, 1] to [0, 1].

Consider the Banach space $(E,\parallel .\parallel )$ of all continuous functions $a:[0,1]\to [0,1]$ equipped with the norm:

$$\parallel a\parallel =\underset{t\in [0,1]}{max}|a(t)|.$$

Define a metric d on E by:

$$d(a,b)=\underset{t\in [0,1]}{max}|a(t)-b(t)|.$$

Then, $(E,d)$ is a complete metric space.

Now, we state and prove our first result in this section as follows:

Theorem 5.

If G is nondecreasing in the third variable and there exists $M>0$ such that:

$$|G(s,v,a(v)-G(s,v,b(v))|\le |a(v)-b(v)|e^{-\frac{1}{1+M(a,b)}-M}$$

for all $s,v\in [0,1]anda,b\in E$ such that $a\le b$, then the existence of a lower solution of the integral Equation (8) ensures the existence of a unique solution of the same.

Proof. 

Define a self-mapping $f:E\to E$ by:

$$(fa)(s)={\int }_0^{s}G(s,v,a(v))dv+g(s)\forall a\in E.$$

Define $\mathcal{R}$ on E by:

$$\mathcal{R}=\{(a,b)\in E\times E:a(s)\le b(s)\forall s\in [0,1]\}.$$

For any $(a,b)\in \mathcal{R}$, we have:

$$\begin{array}{lll}(fa)(s)& =& {\int }_0^{s}G(s,v,a(v))dv+g(s)\\ & \le & {\int }_0^{s}G(s,v,b(v))dv+g(s)\\ & =& (fb)(s).\end{array}$$

Therefore, $\mathcal{R}$ is f-closed. In the hypotheses, we assumed the existence of a lower solution of (8), i.e., there is some $a_0\in E$ such that the following holds:

$$a_0(s)\le {\int }_0^{s}k(s,v,a_0(v))dv+g(s).$$

Therefore, $a_0\in E$ is such that $a_0(s)\le (f{a}_0)(s)$ for each $s\in [0,1]$. Hence, $a_0\mathcal{R}f{a}_0$. Now, for any $a,b\in E$ such that $a\mathcal{R}b$, we have:

$$\begin{array}{lll}\hfill |f(a(s))-f(b(s))|& =& |{\int }_0^s(G(s,v,a(v))-G(s,y,b(v))dv|\\ & \le & {\int }_0^s|(G(s,v,a(v))-G(s,y,b(v))|dv\\ & \le & {\int }_0^s|a(v)-b(v)|e^{-\frac{1}{1+M(a,b)}-M}dv\\ & \le & e^{-\frac{1}{1+M(a,b)}-M}\underset{v\in [0,1]}{sup}|a(v)-b(v)|{\int }_0^{s}dv\\ & =& d(a,b)e^{-\frac{1}{1+M(a,b)}-M}{\int }_0^{s}dv\\ & =& d(a,b)e^{-\frac{1}{1+M(a,b)}-M}s.\\ \hfill \mathrm{Taking}\mathrm{the}\mathrm{maximum}\mathrm{over}\mathrm{both}\mathrm{sides},\mathrm{we}\mathrm{get}\text{:}& & \\ \hfill d\left(f(a),f(b)\right)& \le & d(a,b)e^{-\frac{1}{1+M(a,b)}-M}\\ & \le & M(a,b)e^{-\frac{1}{1+M(a,b)}-M}\\ \hfill \Rightarrow e^{d\left(f(a),f(b)\right)}& \le & e^{M(a,b)e^{-\frac{1}{1+M(a,b)}}{e}^{-M}}\\ & =& {\left(e^{M(a,b)e^{-\frac{1}{1+M(a,b)}}}\right)}^{e^{-M}}.\end{array}$$

Consider $\theta (t)=e^t,\psi (t)=e^{t{e}^{-\frac{1}{1+t}}},\lambda =e^{-M}\in (0,1)$; then, f becomes a ${(\theta ,\psi )}_{\mathcal{R}}$-weak contraction. Now, for any $\mathcal{R}$-preserving sequence $\{a_n\}$ in E converging to $a\in E$, we have:

$$a_0(t)\le a_1(t)\le a_2(t)\le \cdots \le a_n(t)\le a_{n+1}(t)\le \cdots ,\forall t\in [0,1].$$

Thus, $a_n(t)\le a(t)$ for all $t\in [0,1]$. Therefore, $\mathcal{R}$ is d-self-closed in E. Hence, using Theorem 2, we conclude that f has a fixed point, i.e., there is some $a\in E$ such that:

$$a(s)={\int }_0^{s}G(s,v,a(v))dv+g(s).$$

Now, for any $a,b\in Fix(f),c:=max\{a,b\}\in E$ and $c\in Fix(f)$. Furthermore, $a\le c,b\le c$, i.e., $a\mathcal{R}c$ and $b\mathcal{R}c$. Therefore, $Fix(f)$ is ${\mathcal{R}}^S$ connected. Hence, Theorem 4 ensures the uniqueness of the solution of the integral Equation (8). This accomplishes the proof. □

Next, we provide the following theorem in the presence of an upper solution.

Theorem 6.

If G is nondecreasing in the third variable and $M>0$ such that:

$$|G(s,v,a(v)-G(s,v,b(v))|\le |a(v)-b(v)|e^{-\frac{1}{1+M(a,b)}-M}$$

for all $s,v\in [0,1]\mathrm{and}a,b\in E$ such that $a\le b$, then the existence of an upper solution of the integral Equation (8) ensures the existence of a unique solution of the same.

Proof. 

In this case, we define the binary relation $\mathcal{R}$ as follows:

$$\mathcal{R}=\{(a,b)\in E\times E:a(s)\ge b(s)\forall s\in [0,1]\}.$$

Now, following the same steps as Theorem 5 one can see that all the hypotheses of Theorem 4 hold true. Therefore, the existence and uniqueness of the solution of the integral equation (8) are ensured (due to Theorem 4). □