Abstract
The hospital location selection problem is one of the most important decisions in the healthcare sector in big cities due to population growth and the possibility of a high number of daily referred patients. A poor location selection process can lead to many issues for the health workforce and patients, and it can result in many unnecessary costs for the healthcare systems. The COVID-19 outbreak had a noticeable effect on people’s lives and the service quality of hospitals during recent months. The hospital location selection problem for infected patients with COVID-19 turned out to be one of the most significant and complicated decisions with many uncertain involved parameters for healthcare sectors in countries with high cases. In this study, a gray-based decision support framework using criteria importance through inter-criteria correlation (CRITIC) and combined compromise solution (CoCoSo) methods is proposed for location selection of a temporary hospital for COVID-19 patients. A case study is performed for Istanbul using the proposed decision-making framework.
1. Introduction
Human beings have always been faced with a diversity of disasters for thousands of years. Some examples of natural disasters include earthquakes, floods, volcanic eruptions, tornados, and the outbreak of diseases [1]. There are different definitions of outbreak disease, and the highest level is a pandemic which involves the worldwide spread of a new disease. Recently, the world faced a big threat highlighting a direct relationship with the mortality rate of human beings. The coronavirus disease (COVID-19) is caused by the SARS-CoV-2 virus [2]. Throughout history, humans experienced different pandemics such as Spanish flu, HIV, SARS, and now COVID-19. With the growth of medical science, technology, and science, the number of deaths was decreased considerably in comparison with the Spanish flu disaster. This could be a consequence of proper decision-making and rapid reaction. The coronavirus originated from Wuhan, Hubei province, China [3] and was reported to the World Health Organization at the last day of 2019 [4]. The spread of COVID-19 was incredibly fast, such that the outbreak was declared a pandemic late January 2020. Almost all countries are affected by the virus with effects on every aspect of people’s lifestyle, in terms of social, economic, and other factors.
Due to fast spread of COVID-19, countries faced many limitations in their resources and capacities in order to treat the infected patients. Hospitals became one of the most dangerous locations for patients that are diagnosed with other diseases, since infected patients with COVID-19 increase the risk of virus outbreak even inside the hospitals. The information on high-ranked countries in terms of dead bodies shows that healthcare facilities play the most important role in saving peoples’ life. For example, Germany managed the circumstance better than other countries with almost the same number of infected people with the help of a high number of hospitals and hospitality facilities in comparison with Spain or Italy. With a high level of quantitative human resources and facilities, taking care of the patient’s situation will be better and it will increase the probability of saving patients. Therefore, healthcare policy-makers are proposing some recommendations toward building new temporary hospitals for COVID-19-infected patients. The establishment of hospitals includes many costs for governments and other stakeholders; thus, important decisions should be taken before each step. Although COVID-19 is a very dangerous and fast-spreading virus, decision-makers cannot only focus on medical capacities when they are planning to establish an exclusive hospital. Ignoring other involved factors may lead to other costs that may have an effect on patients and their process of getting cured. Therefore, location selection for a new a hospital is not only affected by only one factor or only medical-related factors. In other words, multiple location factors are also involved in the process of selecting a suitable location for hospitals. These factors integrate most technical, economic, environmental, and social aspects into the decision-making process in order to select the most appropriate location. COVID-19 increased the importance of the social, economic, and environmental aspects of the location selection process for a hospital during the current critical time. Therefore, decision-makers require reliable and robust decision-making tools which enable them to make decisions during the uncertain period that we are all in.
Multi-criteria decision-making (MCDM) methods are some of the frequently utilized decision-making tools that are well designed for complicated problems that involve multiple criteria with a need to prioritize the alternatives. MCDM methods enable decision-makers to evaluate number of alternatives with various data that are available such as crisp, fuzzy, interval, rough, etc. The criteria importance through inter-criteria correlation (CRITIC) approach is one of the well-known MCDM methods, which is designed to determine the importance of criteria for an MCDM problem [5]. Unlike other MCDM methods that are focused on a weight determination process, the CRITIC method does not require separate pairwise comparisons for the criteria, since it uses the initial decision matrix that is constructed for the comparison of the alternatives. As one of the recently introduced powerful MCDM methods, the combined compromise solution (CoCoSo) method [6] is an MCDM method that enables decision-makers to prioritize the alternatives under multiple criteria. In this paper, we present a decision support framework to address the temporary hospital location selection problem under a gray uncertainty environment. A case study is performed for Istanbul which is one of the top cities in terms of the number of infected COVID-19 cases.
The remainder of the paper is organized as follows: in Section 2, a literature review of the applications of MCDM methods for the location selection problem is presented. In Section 3, the steps of the integrated decision-making framework are given. In Section 4, we perform a real-life case study in order to show the feasibility and applicability of the proposed methodology for the temporary hospital location selection problem in Istanbul, Turkey. Finally, we present conclusions in Section 5.
2. Literature Review
Location selection is always an important issue in decision-making science. Business owners, managers, and decision-makers are always faced with this issue in different circumstances, with an effect on tangible profits or losses. As choosing an appropriate location is a part of decision-making science, multi-criteria decision-making (MCDM) was discussed in many previous studies. These studies can be classified using different themes as follows: construction, energy, and production, with some subsets. As there are many articles which discussed site selection with MCDM methodologies, this study presents the most significant studies in each theme.
Firstly, we present the prior studies that used MCDM techniques in order to select the best choice in a construction theme. Hashemkhani Zolfani et al. [7] implemented a hybrid multi-attribute decision-making (MADM) methodology called SWARA–WASPAS, in order to find a suitable location for a shopping mall with foresight perspective. This hybrid model was presented for the first time in this article. The SWARA technique was used to prioritize criteria and the weighted aggregated sum product assessment (WASPAS) method was applied to assess the alternatives. Moreover, Ijadi Maghsoodi et al. [8] propounded BWM–CODAS for site selection in terms of a mega-structure project involving a shopping mall in Iran.
Finding the best place for constructing a forest road was considered in [9]. The article presented the site selection of a forest road among three places in an expanded forested region in Iran. AHP was implemented to calculate the importance of criteria; then, COPRAS-G methodology was applied to evaluate places in order to find the best location. Rezaeiniya et al. and Haghnazar Kouchaksaraei et al. [10,11] presented hybrid models to find the best location for a greenhouse. Rezaeiniya et al. [10] studied the importance of finding an appropriate site for a greenhouse by using the ANP method to weight the criteria and applying COPRAS-G to rate the selected places. In addition, presented the SWARA–COPRAS hybrid model to find a suitable location for a glasshouse. With this description, choosing an optimum place for a glasshouse is a significant decision because it needs an incredibly large area and must have financial feasibility. SWARA was applied to weight and COPRAS was applied to rate the important places. Two new methodologies were applied to find a proper location for waste disposal systems in previous studies [12,13]. Kahraman et al. [12] proposed an intuitionistic fuzzy EDAS method to evaluate solid waste disposal site alternatives. Moreover, Krylovas et al. [13] applied the KEMIRA-M method find the best place for constructing a non-hazardous waste incineration plant in Lithuania. The KEMIRA-M methodology is based on searching solutions of an optimization problem.
The site selection of professional workplaces was also discussed in prior studies [14,15]. While considering environmental risk, Suder & Kahraman [15] proposed the fuzzy TOPSIS method to find the most suitable location for a faculty university in Turkey. Rock or soil structure, remoteness to health facilities, transportation availability, and transportation costs were prioritized as having high to low importance, respectively. Computer workstation selection was achieved with hesitant fuzzy linguistic term sets (HFLTS) by using AHP and TOPSIS in [14], where a new fuzzy quality function was deployed in order to solve a real industrial application.
This study focuses on Istanbul in Turkey as a case study in order to determine the optimum location for a temporary hospital for infected people. Some previous studies discussed the same topic such as [16], who proposed a mixed integer linear programming method to select the location of temporary shelter sites in terms of unpredictable earthquakes in Istanbul, Turkey. A cause-and-effect model for the location of temporary shelters in disaster operations management was proposed by [17]. Furthermore, an MCDM method called DEMATEL was presented in a fuzzy environment with 14 different criteria. Iqbal et al. [18] studied the effectiveness of natural disaster management using stochastic model and Mont Carlo simulation. Then, in order to check the sampled numbers from a random space, they proposed a statistical model to check for relief supply location and distribution related to the healthcare system in natural disaster management.
Another subject that was discussed in the MCDM framework was finding the best residential place, which was proposed [19,20]. Neighborhood selection was presented for a newcomer in Chile by (Hashemkhani Zolfani et al. 2020). BWM and revised MAIRCA were applied to investigate which neighborhoods were appropriate, and the approach was compared with three other MADM methods: MABAC, VIKOR, and CODAS. Karasan et al. [20] proposed the hesitant fuzzy CODAS method to find the optimum location for a construction site and implemented a sensitivity analysis to stabilize the ranking result. Hotel site selection was proposed by [21], where BWM–WASPAS methodologies were presented with a sustainable perspective.
The last part of the construction theme is related to healthcare system site selection. Lin & Tsai [22] developed an integrated model consisting of ANP and TOPSIS to determine the best ranking for hospital selection. A case study was performed in China for foreign investment. Furthermore, Senvar et al. [23] considered hesitant fuzzy sets and TOPSIS to locate the best site for constructing a hospital in Istanbul. Establishing a well-organized and distributed network of a hospital in order to deliver healthcare services to patients was considered and discussed in the study. In addition, Kutlu Gündoǧdu et al. [24] presented a new hesitant fuzzy EDAS with TOPSIS method to find the best place for an organ transplantation hospital. This novel model is an extension of classical EDAS which considers the hesitancies of decision-makers. The last study in the construction theme and healthcare subset applied the flexible and interactive tradeoff (FITradeoff) method in order to evaluate healthcare facility stakeholders in order to select an optimum site for a hospital in Milan, Italy.
Secondly, we introduce publications which discussed site selection using MCDM methodologies in the energy theme. Currently, renewable energies have a high priority in the energy industry; thus, site selection of new energy resources were investigated by different researchers from different countries all around the world. The number of energy site selection publications is too extensive to cover in this literature review; thus, we refer only to some of them. Vafaeipour et al. [25] prioritized regions for solar power plants in Iran by applying a hybrid model SWARA–WASPAS. Many criteria such as environmental, economic, technical, social, and risk factors were considered in 25 cities by using a GIS map of the country. Moreover, Marques-Perez et al. [26] studied photovoltaic power plant site selection by applying PROMETHEE and AHP methods with a GIS-based approach in Spain. Furthermore, Ekmekçioglu et al. [27] proposed a SWOT analysis model and then developed this model by applying fuzzy TOPSIS and fuzzy AHP methods to find an optimum location for nuclear power plants in Istanbul. Another renewable energy which is a hot issue in energy science is wind energy. Moradi et al. [28] implemented the AHP methodology to determine an appropriate location for a wind farm. Structural, topological, and ecological criteria were discussed based upon an ArcGIS map.
Finally, the last theme in our classification, i.e., production, introduces previous studies that discussed site selection by applying MCDM methods in the manufacturing industry. Athawale et al. [29] proposed the PROMETHEE II method to achieve facility location selection in the manufacturing industry. This application is faced with complex problems, and the best decision can result in better economic benefits by increasing productivity and qualified network distribution. Logistic center site selection was brought up as a complex decision problem in [30], which was solved with a multi hybrid model. As a first step, communities were compared using DEA to find beneficial alternatives. In the next step, a model was constructed to assess the performance of efficient communities with the R-FUCOM method and they were prioritized with R-COCOSO. The discussed literature is presented in Table 1, containing study subjects and methodologies.

Table 1.
Application of multi-criteria decision-making (MCDM) in location selection.
After reviewing different studies on site selection with MCDM techniques, it was concluded that the MCDM framework can enable better decision-making, especially in disaster situations. However, there were not many studies which worked on hospital locations in a pandemic or disaster circumstance with multi-criteria decision-making. This issue motivated us to implement hybrid MADAM techniques to find an optimum location in Turkey during the coronavirus pandemic in 2020. This fact shows the novelty of this study which can be used as a guide for future studies.
3. Methodology
The procedure of the proposed integrated decision support framework is presented in this section. Gray-based CRITIC and CoCoSo methods are applied to determine the importance of criteria and to prioritize the location alternatives, respectively.
3.1. Criteria Importance through Inter-Criteria Correlation (CRITIC)
In MCDM problems, the identification of criteria and the determination of their weights are very important processes, since weights of criteria can significantly affect the final output of the decision-making framework. The CRITIC method [5] is one of the frequently used MCDM methods to obtain the importance of criteria. In this method, the objective importance of the criteria is obtained by applying the contrast intensity of each criterion, which is considered as the standard deviation, while conflicts between criteria are considered as the correlation coefficient between criteria. Steps of the CRITIC method for an MCDM problem with m alternatives and n criteria are presented below.
Step 1. The decision-maker constructs the initial decision matrix.
The elements () of the decision matrix (X) represent the performance value of the i-th alternative on the j-th criterion.
Step 2. Equations (2) and (3) normalize the initial decision matrix considering the benefit and cost criteria.
Step 3. A symmetric linear correlation matrix (mij) is calculated by the decision-maker.
Step 4. In order to obtain the objective importance of a criterion, the standard deviation and the correlation of each criterion with other criteria are calculated. With this information, the importance of each criterion can be determined via Equation (4).
where Cj is the amount of information contained in the criterion j and is calculated using Equation (5).
In Equation (5), σ is the standard deviation of the j-th criterion. In fact, the CRITIC method assigns higher weights to criteria with higher values of σ and lower correlation with the other criteria. A higher value of Cj denotes a higher amount of information included in a specific criterion; therefore, it is assigned a higher weight value.
3.2. Gray Numbers
In this section, we provide the fundamental principles and functions of gray numbers and their integration with the recently developed CoCoSo method [6].
The exact value of a gray number is uncertain; however, we know that it is within a range or a closed interval. Gray numbers can be continuous gray numbers within an interval. On the other hand, values from a finite number or a set of numbers are labeled as discrete gray numbers. A combined approach for both continuous and discrete gray numbers provided a new definition for gray numbers [33,34].
Definition 1.
Suppose that is a gray value. If and , then is known as an interval gray number, where and are the upper and lower bounds of and .
Definition 2.
Assume that and are two interval gray numbers, and , . The arithmetic operations are defined as follows [34,35]:
Definition 3.
For a gray number , if , then is called an extended gray number (EGN). We consider as a union of a set of closed or open intervals, while is an integer and , , and [33].
Theorem 1.
If is an EGN, then the following properties hold:
- (1)
- if and only if ( or n = 1.
- (2)
- is a discrete EGN if and only if .
- (3)
- is a mixed EGN if only some of its intervals integrate to crisp numbers and the others remain intervals.
Definition 4.
For two EGNs and , let , , , and . Then, the arithmetic operations can be defined as follows [34]:
where , , and (j=1,2,…,m).
Definition 5.
The length of a gray value is measured as
3.3. Gray-Based Combined Compromise Solution (CoCoSo)
For the first time in the literature related to MCDM methods, [6] proposed the CoCoSo method as an alternative ranking tool for multi-criteria problems. Since its introduction, the CoCoSo method was used for multiple problems in its initial form or in an extended form. In this paper, we use the gray-based CoCoSo method. The steps of the gray-based CoCoSo are described below.
Step 1. The decision-maker identifies decision factors and alternatives.
Step 2. In this step, the decision-maker constructs the initial gray-based decision matrix.
where represents the lower bound, while represents the upper bound, for ,
Step 3. The constructed initial decision matrix is normalized using Equations (18) and (19) considering benefit and cost criteria.
Step 4. The weighted normalized matrix and the sum of power weights of comparability sequences for each alternative are calculated using Equations (20) and (21).
Step 5. The relative weights of alternatives using three aggregation strategies are calculated in various ways. We use three appraisal score strategies to calculate the relative weights of other options using Equations (22)–(24).
The final preference order of the alternatives according to the CoCoSo-G method is calculated using Equation (25).
where λ (normally ) is chosen by the decision-makers. Different values of can have a significant effect on the flexibility and stability of the proposed CoCoSo.
Step 6. To rank the alternatives, we obtain the length of the gray values shown by the above equation (based on Definition 5).
4. Case Study
In big cities with high population, healthcare centers are very important facilities which are designed to deal with health issues. Location selection for healthcare centers, specifically hospitals, is a very important and very complicated decision for authorities and decision-makers, since multiple decision factors are involved in the decision-making process for this problem. The significance of location selection process for a hospital is implied by many direct or indirect relationships with economic, environmental, and social factors. Moreover, the location selection problem for a hospital is more important in critical time periods such as a disease outbreak. Starting in December 2019, COVID-19 became one of the biggest disease outbreaks of the last century. Soon after its emergence in China, COVID-19 became the most important issue to deal with for most countries in the world. In most countries, daily reports showed a sharp increasing trend in the number of infected patients. The high number of infected patients brought forward many problems in terms of the capacity of hospitals, such as hardware resources or specialized human resources to treat these patients. On the other hand, the presence of COVID-19-infected patients in hospitals increases the risk of its outbreak inside those hospitals, which would have a great effect on patients in other wards. In this matter, governments decided to construct well-resourced temporary hospitals to exclusively treat COVID-19-infected patients. As the first country affected, China constructed a hospital, with 1000 beds, for patients that were suspected to be infected by COVID-19. After construction of this special hospital by China, the necessity of constructing such hospitals was understood by other governments.
Istanbul is an international city with a population of more than 15 million people living on both Asian and European sides of the city. Istanbul is one of the biggest transportation and business hubs in the world, where more than hundreds of flights move people worldwide through Istanbul each day. The medical system in Turkey is divided into public and private sectors. Due to the population increase in Istanbul, many public and private hospitals were constructed in recent decades. Turkey remained one of the safest countries during the first days of the COVID-19 outbreak. However, a few months later, the COVID-19 outbreak happened very quickly with an increasing trend in most cities in Turkey, especially Istanbul, which has the highest number of infected patients. Istanbul can play a key role in treating and preventing infections in a pandemic circumstance. The first case in Turkey was officially confirmed on 11 March 2020, and, as of 29 April, based upon a Johns Hopkins university report [36], 4,673,809 people were infected and 312,646 people died due to this disease around the world. Furthermore, according to the health ministry of Turkey [37], the total number of tests administered was 991,613, of which 117,589 returned positive, with 3081 passing away, whereas the total number of intensive care patients is 1574 and 44,040 patients are recovered. In order to treat COVID-19-infected patients, as well as prevent its outbreak in other hospitals, there is a necessity to construct a temporary hospital which serves only clients that are suspected to be infected by COVID-19. With respect to the geographical features of Istanbul, selecting a suitable location for the establishment of a new hospital is a very complicated process.
To show the feasibility and applicability of the proposed decision-making framework, we applied the decision support framework to Istanbul in order to select a suitable location for a temporary hospital for COVID-19 patients. Istanbul is a very big city which is divided into Asian and European sides, where the population ratio is not the same on both sides. There are 25 districts on the European side and 14 districts on the Asian side, giving a total of 39 districts. The population of the European side is almost two times that of the Asian side, which is approximately 5.5 million. With this information in mind, five districts were selected as potential location alternatives for the hospital location selection problem. Due to the spread of the population and geographical features in Istanbul, three of these districts were located on the European side and the two other districts were located on the Asian side. As shown in Figure 1, the five districts of Beykoz (A1), Bakırköy (A2), Büyükçekmece (A3), Eyüp (A4), and Pendik (A5) were selected as potential locations for this case study.
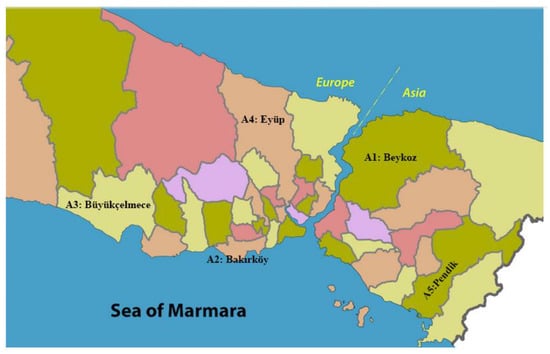
Figure 1.
Location alternatives in Istanbul.
Based on the characteristics of stakeholders, several criteria were identified and defined using the location selection studies in the literature. The identified criteria were categorized into three main groups of technological, economic, and social criteria. Firstly, we defined the technological criteria involved in the decision-making process. Traffic congestion (C1) was defined as a qualitative criterion to measure the level of traffic congestion in each district. Ease of transportation is very important when promptly delivering patients to a hospital. Accessibility via roads (C2) denotes how many different roadways are available in the district in order to deliver patients. Accessibility via airports (C3) measures the distance of the hospital to its closest international or local airport, which can be used to deliver patients in a critical situation. Health centers in the district (C4) measure how many hospitals are in the district that the hospital would be built in. The distance from populated residential areas (C5) measures how far the hospital is from areas with a high population density. Land price, transportation cost, and future expansion potential are considered as economic criteria. Land price (C6) measures the range of land cost for an infrastructure like a hospital. Transportation cost (C7) measures transportation cost in terms of transportation means available to deliver patients in different districts. Future expansion potential (8) denotes the possibility of expanding the temporary hospital to a permanent one with respect to financial indexes. We considered two criteria for environmental and social aspects. The distance from industrial areas (C9) measures how far the hospital is from industrial areas with respect to the fact that the emissions of factories in an industrial area can have a negative effect on the air quality level. Local regulation (10) represents a series of official and unofficial regulations related to each district with respect to its demography characteristics.
Table 2 shows a comparison among alternatives with respect to the defined criteria for Istanbul. In the first step, an initial decision matrix was constructed using gray values (Table 3). For each criterion, a gray value was indicated for each alternative with respect to expert experience, knowledge, etc. In Table 4, the initial decision matrix values were normalized using Equations (2) and (3) based on the benefit and cost criteria in step 2 of the CRITIC method. In the next step, the matrix of correlation was generated, as presented in Table 5, where the correlations of each pair of criteria are shown. Finally, we calculated the weights of criteria using Equations (4) and (5), as shown in the last row of Table 6. The distance from industrial areas (C9), future expansion potential (8), and land price (C6) were determined as the most important criteria.

Table 2.
Profile of experts.

Table 3.
Performance value matrix.

Table 4.
Transformations of performance values.

Table 5.
Correlation coefficient.

Table 6.
The weights of decision-making criteria.
After determining the weights of the criteria, we normalized the initial gray-based decision matrix using Equations (18) and (19), as presented in Table 7. In the next step of the gray-based CoCoSo method, we constructed the weighted decision matrix by multiplying the normalized decision matrix and weight vector using Equation (20), as presented in Table 7. Gray values were calculated for each alternative in Table 8. In Table 9, we calculated the power-weighted normalized decision matrix using Equation (21). Gray values were calculated for each alternative in Table 9. In order to prioritize the alternatives, three appraisal score strategies were used with respect to Equations (22)–(24). As shown in Table 10, we calculated the gray-based relative weights of alternatives, and the results were finally combined using Equation (25) as values. Using values, the ranking of alternatives was determined using gray lengths. As represented in Table 10, the Beykoz (A1) and Bakırköy (A2) districts were ranked as the first and second priorities to build a temporary hospital. Pendik (A5) and Eyüp (A4) were ranked as the third and fourth preferred locations. Büyükçekmece (A3) was the least preferred location to build a temporary hospital.

Table 7.
Normalized matrix for CoCoSo-G.

Table 8.
The weighted normalized matrix.

Table 9.
Power weighted normalized matrix.

Table 10.
The CoCoSo-G ranking for alternatives.
5. Managerial Insights and Conclusions
The hospital location selection problem is an important issue for big cities with respect to the fact that the location selection problem is influenced by various decision factors and dimensions in the context of technical, environmental, economic, and social aspects. Therefore, a logical analysis of location alternatives considering all criteria will enable policy-makers to better address the location selection problem. The importance of the hospital location selection problem relies on the fact that any consequences from the medical services directly affect the mortality rate in societies. On the other hand, the COVID-19 outbreak, as one of the biggest threats of the last century, spread to most countries in the world. The high number of infected patients and the limited medical resources to treat the patients resulted in healthcare sectors facing many issues. Thus, policy-makers in the healthcare sector suggested establishing temporary hospitals for only patients diagnosed with COVID-19. In this situation, the location selection problem becomes more important than ever due to the critical situation that the health sectors are in.
To show the efficiency of the proposed decision support framework, we performed a case study using Istanbul, which is one of the world’s biggest cities with more than 15 million people. Results indicated that the Beykoz and Bakırköy districts are the most suitable locations for the establishment of a temporary hospital for COVID-19 patients. The populations of Beykoz and Bakırköy districts are very close together. However, the population density in Bakırköy is 7734 per km2, whereas the same parameter for Beykoz is only 800 per km2. The distance from industrial and production areas is greater for Beykoz than Bakırköy. In addition, the traffic congestion in Beykoz is way lower than in Bakırköy. On the other hand, Bakırköy is one of the closest districts to local and international airports, which can be used to deliver patients that are being transported using air medical services. The establishment of a temporary hospital in Beykoz would also benefit this district in the future. With a high future expansion potential, a big hospital in this area would play a great role in its gentrification. In other words, transportation factors and the applicability of the area will improve, which would certainly bring more profit and satisfaction for all stakeholders in the healthcare sector.
In this paper, we addressed the location selection problem for a temporary hospital in the era of the COVID-19 outbreak. A gray-based decision support framework was presented for the decision-making process, considering the uncertain nature of the information related to location alternatives. The CRITIC and CoCoSo methods were implemented under gray values to determine the weights of criteria and to prioritize the location alternatives, respectively. For a case study in Istanbul, we selected five possible districts for the establishment of a temporary hospital in Istanbul.
Some future research directions can be identified. One may use the proposed decision support framework for the location selection problem in other industries such as waste management, hotels, power plants, airports, and so on. In another direction, one may implement the proposed decision-making approach with other uncertainty models such as fuzzy set theory, rough numbers, neutrosophic sets, etc.
Author Contributions
Main idea, conceptualization, supervision, editing, and writing-original by S.H.Z.; Methodology, supervision, editing, and writing-original by M.Y., main idea, case study, methodology, and writing-original by A.E.T., Literature review, general background review, and writing-original by A.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Simonovic, S.P. Approach to management of disasters—A missed opportunity? J. Integr. Disaster Risk Manag. 2015, 5, 70–83. [Google Scholar] [CrossRef]
- Pambuccian, S.E. The COVID-19 pandemic: Implications for the cytology laboratory. J. Am. Soc. Cytopathol. 2020, 9, 202–211. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Wang, Y.; Li, X.; Ren, L.; Zhao, J.; Hu, Y.; Zhang, J.; Fan, G.; Xu, J.; Gu, X.; et al. Clinical features of patients infected with 2019 novel coronavirus in Whuan, China. Lancet 2020, 395, 497–506. [Google Scholar] [CrossRef]
- WHO (World Health Organization). WHO Timeline—Covid-19. 2020. Available online: https://www.who.int/news-room/detail/27-04-2020-who-timeline---covid-19 (accessed on 25 April 2020).
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining objective weights in multiple criteria problems: The CRITIC method. Comput. Ops. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Yazdani, M.; Zarate, P.; Kazimieras Zavadskas, E.; Turskis, Z. A combined compromise solution (CoCoSo) method for multi-criteria decision-making problems. Manag. Decis. 2019, 57, 2501–2519. [Google Scholar] [CrossRef]
- Hashemkhani Zolfani, S.; Aghdaie, M.H.; Derakhti, A.; Zavadskas, E.K.; Morshed Varzandeh, M.H. Decision making on business issues with foresight perspective; An application of new hybrid MCDM model in shopping mall locating. Expert Syst. Appl. 2013, 40, 7111–7121. [Google Scholar] [CrossRef]
- Ijadi Maghsoodi, A.; Rasoulipanah, H.; Martínez López, L.; Liao, H.; Zavadskas, E.K. Integrating interval-valued multi-granular 2-tuple linguistic BWM-CODAS approach with target-based attributes: Site selection for a construction project. Comput. Ind. Eng. 2020, 139, 106147. [Google Scholar]
- Hashemkhani Zolfani, S.H.; Rezaeiniya, N.; Zavadskas, E.K.; Turskis, Z. Forest roads locating based on AHP and COPRAS-G methods: An empirical study based on Iran. E M Ekon. Manag. 2011, 14, 6–21. [Google Scholar]
- Rezaeiniya, N.; Zolfani, S.H.; Zavadskas, E.K. Greenhouse locating based on ANP-COPRAS-G methods—An empirical study based on Iran. Int. J. Strateg. Prop. Manag. 2012, 16, 188–200. [Google Scholar] [CrossRef]
- Haghnazar Kouchaksaraei, R.; Hashemkhani Zolfani, S.; Golabchi, M. Glasshouse locating based on SWARA-COPRAS approach. Int. J. Strateg. Prop. Manag. 2015, 19, 111–122. [Google Scholar] [CrossRef]
- Kahraman, C.; Keshavarz Ghorabaee, M.; Zavadskas, E.K.; Cevik Onar, S.; Yazdani, M.; Oztaysi, B. Intuitionistic fuzzy EDAS method: An application to solid waste disposal site selection. J. Environ. Eng. Landsc. Manag. 2017, 25, 1–12. [Google Scholar] [CrossRef]
- Krylovas, A.; Zavadskas, E.K.; Kosareva, N. Multiple criteria decision-making KEMIRA-M method for solution of location alternatives. Econ. Res. Ekon. Istraz. 2016, 29, 50–65. [Google Scholar] [CrossRef]
- Çevik Onar, S.; Büyüközkan, G.; Öztayşi, B.; Kahraman, C. A new hesitant fuzzy QFD approach: An application to computer workstation selection. Appl. Soft Comput. J. 2016, 46, 1–16. [Google Scholar] [CrossRef]
- Suder, A.; Kahraman, C. Minimizing Environmental Risks Using Fuzzy TOPSIS: Location Selection for the ITU Faculty of Management. Hum. Ecol. Risk Assess. 2015, 21, 1326–1340. [Google Scholar] [CrossRef]
- Kilci, F.; Kara, B.Y.; Bozkaya, B. Locating temporary shelter areas after an earthquake: A case for Turkey. Eur. J. Oper. Res. 2015, 243, 323–332. [Google Scholar] [CrossRef]
- Celik, E. A cause and effect relationship model for location of temporary shelters in disaster operations management. Int. J. Disaster Risk Reduct. 2017, 22, 257–268. [Google Scholar] [CrossRef]
- Iqbal, S.; Sardar, M.U.; Lodhi, F.K.; Hasan, O. Statistical model checking of relief supply location and distribution in natural disaster management. Int. J. Disaster Risk Reduct. 2018, 31, 1043–1053. [Google Scholar] [CrossRef]
- Hashemkhani Zolfani, S.; Ecer, F.; Pamucar, D.; Raslanas, S. Neighborhood selection for a newcomer via a novel BWM-based Reised MAIRCA integrated model: A case from the Coquimbo-La Serena conurbation, Chile. Int. J. Strateg. Prop. Manag. 2020, 24, 102–118. [Google Scholar] [CrossRef]
- Karasan, A.; Zavadskas, E.K.; Kahraman, C.; Keshavarz-Ghorabaee, M. Residential construction site selection through interval-valued hesitant fuzzy CODAS method. Informatica (Netherlands) 2019, 30, 689–710. [Google Scholar] [CrossRef]
- Hashemkhani Zolfani, S.; Mosharafiandehkordi, S.; Kutut, V. A pre-planning for hotel locating according to the sustainability perspective based on BWM-WASPAS approach. Int. J. Strateg. Prop. Manag. 2019, 23, 405–419. [Google Scholar] [CrossRef]
- Lin, C.T.; Tsai, M.C. Location choice for direct foreign investment in new hospitals in China by using ANP and TOPSIS. Qual. Quant. 2010, 44, 375–390. [Google Scholar] [CrossRef]
- Senvar, O.; Otay, I.; Bolturk, E. Hospital site selection via hesitant fuzzy TOPSIS. IFAC Pap. 2016, 49, 1140–1145. [Google Scholar] [CrossRef]
- Kutlu Gündoǧdu, F.; Kahraman, C.; Civan, H.N. A novel hesitant fuzzy EDAS method and its application to hospital selection. J. Intell. Fuzzy Syst. 2018, 35, 6353–6365. [Google Scholar] [CrossRef]
- Vafaeipour, M.; Hashemkhani Zolfani, S.; Morshed Varzandeh, M.H.; Derakhti, A.; Keshavarz Eshkalag, M. Assessment of regions priority for implementation of solar projects in Iran: New application of a hybrid multi-criteria decision making approach. Energy Convers. Manag. 2014, 86, 653–663. [Google Scholar] [CrossRef]
- Marques-Perez, I.; Guaita-Pradas, I.; Gallego, A.; Segura, B. Territorial planning for photovoltaic power plants using an outranking approach and GIS. J. Clean. Prod. 2020, 257, 120602. [Google Scholar] [CrossRef]
- Ekmekçioglu, M.; Can Kutlu, A.; Kahraman, C. A fuzzy multi-criteria swot analysis: An application to nuclear power plant site selection. Int. J. Comput. Intell. Syst. 2011, 4, 583–595. [Google Scholar] [CrossRef]
- Moradi, S.; Yousefi, H.; Noorollahi, Y.; Rosso, D. Multi-criteria decision support system for wind farm site selection and sensitivity analysis: Case study of Alborz Province, Iran. Energy Strategy Rev. 2020, 29, 100478. [Google Scholar] [CrossRef]
- Athawale, V.M.; Chatterjee, P.; Chakraborty, S. Decision making for facility location selection using PROMETHEE II method. Intern. J. Ind. Syst. Eng. 2012, 11, 16–30. [Google Scholar] [CrossRef]
- Yazdani, M.; Chatterjee, P.; Pamucar, D.; Chakraborty, S. Development of an integrated decision making model for location selection of logistics centers in the Spanish autonomous communities. Expert Syst. Appl. 2020, 148, 113208. [Google Scholar] [CrossRef]
- Ebadi Torkayesh, A.; Fathipoir, F.; Saidi-Mehrabd, M. Entropy-based multi-criteria analysis of thermochemical conversions for energy recovery from municipal solid waste using fuzzy VIKOR and ELECTRE III: Case of Azerbaijan Region. Iran. J. Energy Manag. Technol. 2019, 3, 17–29. [Google Scholar]
- Wu, Y.; Zhang, T.; Xu, C.; Zhang, B.; Li, L.; Ke, Y.; Yan, Y.; Xu, R. Optimal location selection for offshore wind-PV-seawater pumped storage power plant using a hybrid MCDM approach: A two-stage framework. Energy Convers. Manag. 2019, 199, 112066. [Google Scholar] [CrossRef]
- Yang, Y.J. Extended grey numbers and their operations. In Proceedings of the 2007 IEEE International Conference on Fuzzy Systems and Intelligent Services, Man and Cybernetics, Montreal, QC, Canada, 7–10 October 2017; pp. 2181–2186. [Google Scholar]
- Liu, S.F.; Dang, Y.G.; Fang, Z.G.; Xie, N.M. Grey Systems Theory and Its Applications; Science Press: Beijing, China, 2010. [Google Scholar]
- Zhou, H.; Wang, J.; Zhang, H. Grey Stochastic Multi-criteria Decision-making Approach Based on Prospect Theory and Distance Measures. J Grey Syst. 2017, 29, 15–33. [Google Scholar]
- Johns Hopkins University & Medicine. Corona Virus Resource Center. 2020. Available online: https://coronavirus.jhu.edu/map.html (accessed on 1 April 2020).
- The Ministry of Health. Türkiye’deki Güncel Durum. 2020. Available online: https://covid19.saglik.gov.tr/ (accessed on 1 April 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).