Abstract
Recently, hidden attractors with stable equilibria have received considerable attention in chaos theory and nonlinear dynamical systems. Based on discrete fractional calculus, this paper proposes a simple two-dimensional and three-dimensional fractional maps. Both fractional maps are chaotic and have a unique equilibrium point. Results show that the dynamics of the proposed fractional maps are sensitive to both initial conditions and fractional order. There are coexisting attractors which have been displayed in terms of bifurcation diagrams, phase portraits and a 0-1 test. Furthermore, control schemes are introduced to stabilize the chaotic trajectories of the two novel systems.
1. Introduction
Continuous-time and discrete-time chaotic dynamical systems have been extensively studied over the last years. Referring to discrete-time systems number of chaotic maps have been deeply analyzed. Researchers such as Hénon, Lozi and Arnold have attempted to provide different maps with different features. In [1], Hénon proposed the first map by employing the Poincaré section on the Lorenz system. In 1960, the Russian mathematician Vladimer I Arnold discovered a two-dimensional chaotic map using an image of cat [2]. More recently, Lozi developed a new discrete chaotic system by replacing the quadratic term in the Hénon map with quasi-linear term [3]. All of the chaotic attractors in these maps fall into the class of self-excited attractors, for which the initial conditions are located near the unstable fixed points. Recently, another type of attractors called hidden chaotic attractors have been discovered, referring to attractors whose basin of attraction does not intersect with any neighborhoods of any equilibrium of the systems [4]. They are generated by nonlinear systems without equilibrium points or with nonlinear systems with special equilibrium points, for example systems with stable equilibrium points [5]. The topic of chaotic maps with hidden attractors has been recently investigated. For example, in [6] a 1D chaotic discontinuous map without equilibria has been illustrated, whereas in [7] three-dimensional chaotic maps with different types of stable equilibria have been proposed by designing the simplest and most elegant difference systems. Moreover, in [8] 2D chaotic quadratic maps without equilibria and with no discontinuity in the right-hand equations have been introduced. On the basis of the famous Hénon map, some two-dimensional chaotic maps with no equilibrium point and with stable equilibrium have been illustrated in [9]. Some other examples of chaotic attractors with curve equilibrium were numerically presented in [10]. These studies have proven the significant role of hidden attractors in practical engineering applications.
Fractional calculus is a very interesting topic in mathematics with several potential applications in many fields of science and engineering [11]. Recently, several efforts have been devoted to the study of complex dynamics of fractional maps, i.e., maps described by fractional-order difference equations. Researchers have extensively examined the potential application of these maps in many fields such as, engineering, economics and other areas [12,13,14]. For this purpose, many fractional maps have been reported in the literature to show the different dynamical phenomena. For example, a fractional 3D generalized Hénon map has been studied [15], whereas the Stefanski, Rössler and Wang fractional maps have been illustrated in [16]. Moreover, in [17] the fractional-order version of the Grassi-Miller map is considered, whereas in [18] the dynamics of the fractional discrete double scroll are analyzed in detail. Results show that the dynamics of such systems are clearly dependent on the fractional-order and they are more complex because of their memory effect. Moreover, control and synchronization based on these fractional chaotic maps have also attracted lots of attention [19,20,21,22]
Up to the present day, most of the literature on the analysis of fractional maps is still limited to systems with self exited attractors. To our knowledge, fractional maps with hidden attractors have rarely been reported [23], which has inspired researchers to devote themselves to the design of new two and three-dimensional fractional discrete-time chaotic systems [24,25,26]. Based on the above considerations, new two and three-dimensional fractional chaotic maps with hidden coexisting attractors are developed. The conducted analysis highlights that hidden attractors are generated for some values of the fractional order in the difference equations. The presence of chaos is validated via the bifurcation diagrams and phase portraits. Furthermore, we apply the 0-1 test method to distinguish chaos from regular behavior [27]. The idea under the test is to transform the states of the fractional maps into plots. Generally, unbounded trajectories imply chaotic behavior whereas bounded trajectories imply regular behavior. We also propose two active controllers with the aim of stabilizing the chaotic dynamics of the two fractional maps.
2. Basic Concepts
Herein, some discrete fractional calculus background and theorems are introduced briefly. The definition of fractional Caputo-like difference operator will be given first.
Definition 1.
For a given function , the Caputo definition of the fractional difference operator of order is defined as:
where the symbol represents the Euler’s gamma function and. According to reference [28], the definition of ν-th fractional sum of is expressed in the following:
withand.
In the following, we need to define the discrete version of the proposed maps. For that, we introduce the following theorem:
Theorem 1.
[29] In particular, for the initial value problem
the solution turns out to the discrete integral equation as
in which, is a discrete kernel function, and is the initial condition.
Set and , Equation (4) can be transformed to:
Stability of Fractional Order Maps
The stability of equilibrium points for fractional maps can be analysed using the following theorem.
Theorem 2.
[30,31] Let be an equilibrium point of a nonlinear fractional difference system where , and is the Jacobian matrix at the equilibrium point . The equilibrium point is asymptotically stable when all the eigenvalues () of J verifies:
We recall the following lemma, which is a special case of Theorem 2.
Lemma 1.
[30] Two-dimensional fractional map is locally asymptotically stable if and
in which is the trace of the Jacobian matrix J and is the determinant of the matrix J.
We now present the following theorem, which identifies the asymptotic stability conditions of the zero solution to a linear fractional difference system.
Theorem 3.
[30] For a linear fractional difference system
where and the zero equilibrium is asymptotically stable if
for all the eigenvalues λ of .
3. New Two and Three-Dimensional Fractional Maps
3.1. Description of the New Two-Dimensional Fractional Map
An effective method for defining new integer order maps with quadratic nonlinearity terms was proposed by [32]. Motivated by this strategy, we removed and added some terms to obtain the following two-dimensional fractional map:
with state variables x and y, and system parameter A. denotes the fractional order. For calculating the equilibrium points of the fractional map (10), we assign its left hand side to zero:
from system of Equation (11) it follows:
It is easy to verify that the fractional map (10) has a unique equilibrium point when . The Jacobian matrix of the fractional map (10) at an arbitrary point , is given by:
The associated characteristic equation is defined in terms of the trace () and determinant () of the matrix J by:
where and . For , the fractional map has a unique equilibrium point . Based on Lemma 1 the equilibrium point E is stable when By simple calculation it is easy to verify that the equilibruim point E is asymptotically stable when the fractional order .
In order to investigate the variety of dynamics behavior that can be observed in the fractional map (10) near to the stable equilibrium point E, it is important to present at first the corresponding numerical formula. In view of Theorem 1, the fractional map (10) is changed to:
where and are the initial conditions. Numerical analysis are presented in the next subsection.
3.2. Bifurcation and 0-1 Test
In the following, the coexisting of hidden attractors in the fractional map are revealed by phase portraits, bifurcation diagrams and 0–1 test. The phase portrait is a geometric representation of the trajectories of a dynamical system. For the system parameter , fractional order and initial condition , a hidden strange attractor is numerically obtained as it observed in Figure 1. The Lyapunov exponents (LEs) of the fractional map (10) are . . Since the maximum Lyapunov exponent is larger than zero, we can determine that the hidden attractor is chaotic.
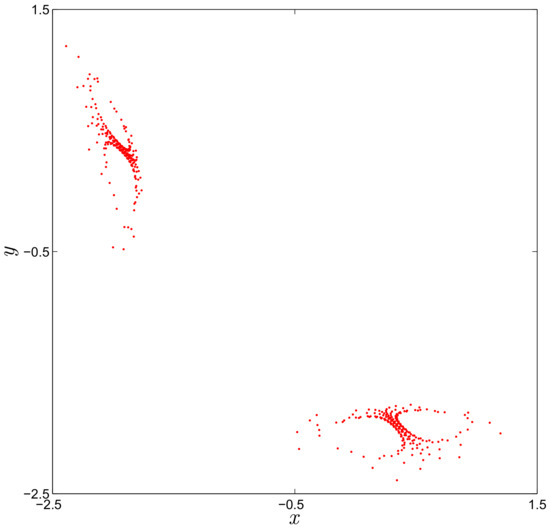
Figure 1.
Strange attractor of the two-dimensional fractional map (10) for and .
For , the dynamic evolution of the fractional map versus is given via plotting its bifurcation diagram (see Figure 2). The bifurcation diagram is obtained by plotting the local maximum value of the variable x for two sets of initial conditions. The blue diagram begins with the initial condition and the red diagram begins with the initial condition . When the fractional order varies from 1 to 0.999, our fractional system (10) generates chaos with transient states. As decreases further a coexisting periodic orbits are obtained. The coexisting attractors with different values of are shown in Figure 3. Two periodic attractors coexist for , , with initial values and as shown in Figure 3b–d. A hidden chaotic attractor is observed with order . It is noticed that the type of hidden attractors not only depend on the value of but also on the initial conditions.
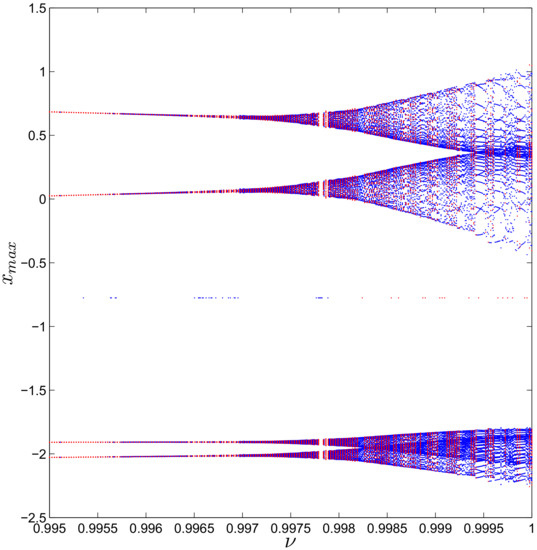
Figure 2.
Bifurcation diagrams of the two-dimensional fractional map (10) versus for .
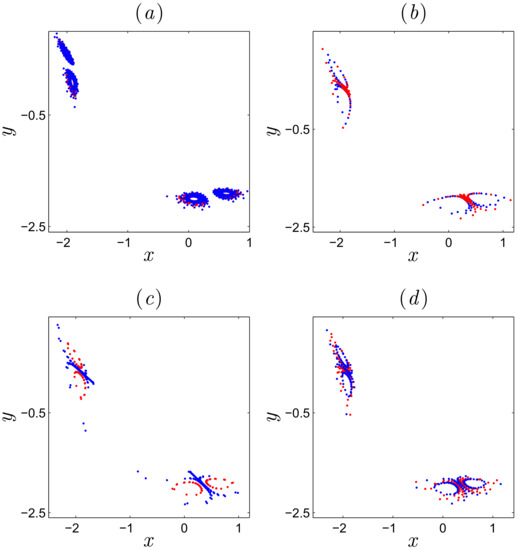
Figure 3.
The coexisting hidden attractors of the two-dimensional fractional map (10) for system parameter and initial condition for red attractors and for blue attractors, with fractional order varying: (a) , (b) , (c) , (d) .
Now, the plots of the 0-1 test are used to confirm the property of coexisting attractors. The 0-1 test is relatively new method that was proposed by Gottwald and Melbourne [27] to test the presence of chaos in a series of data which originate from deterministic systems. For the fractional map (10) consider a set of discrete points where For a randomly chosen constant , decompose the state into two components p and q as:
Generally, unbounded trajectories imply chaotic behavior whereas bounded trajectories imply regular behavior. As in Figure 3 we chose to fix the system parameter A to and vary the fractional order . Figure 4 shows the plots with and , where the blue plots are obtained for the initial values and the red plots are obtained for In particular, Figure 4a shows Brownian like trajectories in p versus q plan for both initial conditions, confirming that the dynamics of the fractional map (10) are chaotic for both initial values and fractional order . When , Figure 4b depicts bounded like trajectories in p versus q plane for both initial conditions, which confirms the coexisting of hidden periodic orbits.
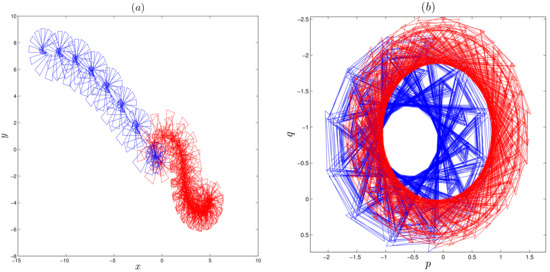
Figure 4.
The 0-1 test of the two-dimensional fractional map. (a) Brownian like trajectories for both initial conditions with , (b) bounded trajectories for both initial conditions with .
3.3. Description of the New Three-Dimensional Fractional Map
We introduce here a new three-dimensional fractional map with two nonlinearities:
where is the fractional order in which The equilibrium points of the fractional map (17) are found by:
from Equation (18) we have the simplified form
It is obvious that the point is the only equilibrium point and it is stable.
Similarly, the discrete version of system (17) is obtained by applying Theorem 1 as follows:
3.4. Bifurcation and 0-1 Test
To evaluate the dynamic properties of the new system, the initial condition need to set as . The three-dimensional fractional map (17) with stable equilibrium point display strange attractor for as shown in Figure 5. Here, the largest Lyapunove exponent () of the fractional map (17) is calculated as , so the strange attractor in Figure 5 is chaotic.
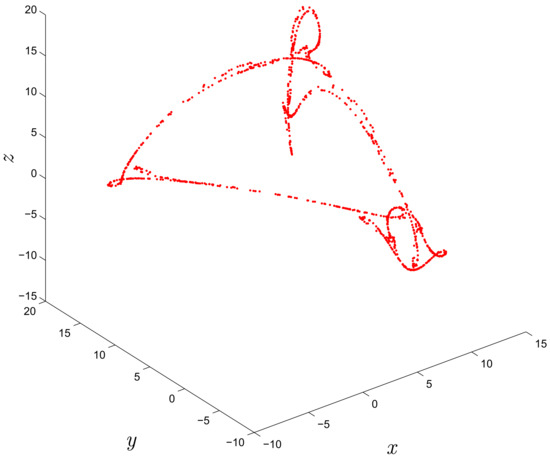
Figure 5.
Strange attractor of the three-dimensional fractional map (17).
The bifurcation diagram can help us to observe the dynamic behaviours of the fractional map (17). The fractional order is considered as the only bifurcation parameter in this subsection. Changing from to 1 and setting two different initial conditions we can obtain the bifurcation diagram in Figure 6, where the blue color diagram and the red color diagram are yielded from the initial conditions and , respectively. When coexisting fixed point attractors are observed. When the fractional order increases from to , we can observe coexisting periodic windows. For , the states of the fractional map go from periodic behavior to chaos. The coexistence of the different dynamic behaviours of the new fractional map (17) is confirmed with phase portrait and plots of the 0-1 test for different values of . Figure 7 shows the phase portraits of the system while Figure 8 shows the plots for the same fractional orders where the blue plots are obtained for the initial values and the red plots are obtained for Figure 8a depicts bounded like trajectories, which confirms the periodic phenomena of the hidden attractor in Figure 7a for For , a hidden attractor coexists as shown in Figure 7, whose Brownian-like trajectories can be seen in Figure 8.
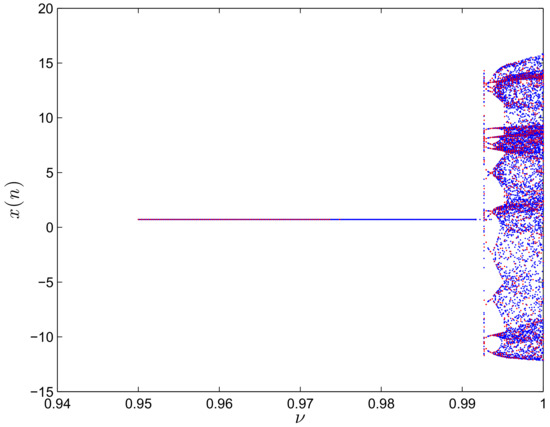
Figure 6.
Bifurcation diagram of the three-dimensional fractional map (15) versus .
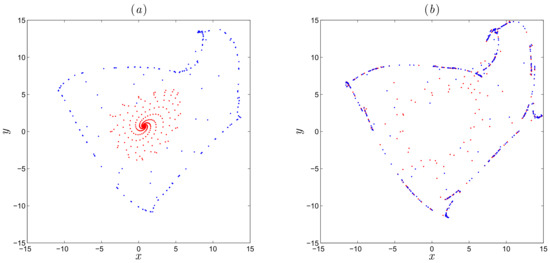
Figure 7.
Coexisting hidden attractors of the three-dimensional fractional map (17) with initial condition for red attractors and for blue attractors, (a) for fractional order , (b) for fractional order .
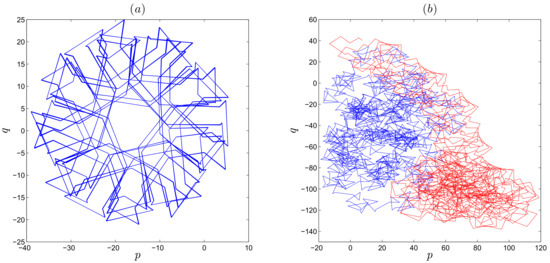
Figure 8.
The plots of the three-dimensional fractional map, (a) bounded trajectories for , (b) Brownian-like trajectories for both initial conditions with .
4. Chaos Control
In this section, adaptive controllers are designed to stabilize the chaotic trajectories of two-dimensional fractional map (10) as well as the three-dimensional fractional map (17) to zero asymptotically. The purpose of such controllers is to assure that all states of the proposed maps converge to zero, by adding an adaptive term into one of the systems states that forces the systems to become linear. A purely linear fractional difference system of the form has zero as its equilibrium. We use the stability theory of linear fractional difference systems to guarantee the asymptotic stability of the zero equilibrium.
The controlled two-dimensional fractional map (10) is given by
where denotes the one-dimensional controller. Our goal is to find a suitable one-dimensional controller such that both of states of system are stabilized towards zero asymptotically. For that, we propose the following theorem.
Theorem 4.
The two-dimensional fractional map (10) can be stabilized by the one-dimensional controller described by
Proof.
If we substitute the adaptive control law (26) to the second state of the fractional map we obtain the following set of equations:
So, the eigenvalues , of the matrix have been found that satisfies the condition of the Theorem 3:
Now, we give the evolution of states and phase space plots of the controlled system to confirm the above theoretical results. In Figure 9, the value parameter is taken as and the fractional order is chosen as . The simulation are done using the initial value . It is clear that the controller has compelled the states towards zeros.
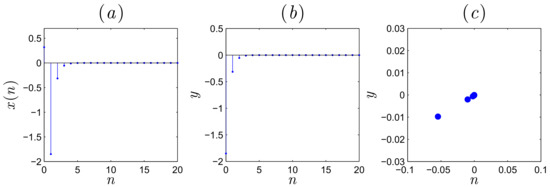
Figure 9.
(a) Stabilization of state , (b) stabilization of state , (c) attractor of the controlled system (10) for .
With the same procedure, we may state the following result regarding the chaos control of the three-dimensional fractional map (17).
Theorem 5.
The three-dimensional fractional map (17) can be stabilized by the one-dimensional controller described by
Again, assuming the fractional order value , the resulting states and phase plot are depicted in Figure 10. The results confirms the success of the proposed law in stabilizing the systems states asymptotically.
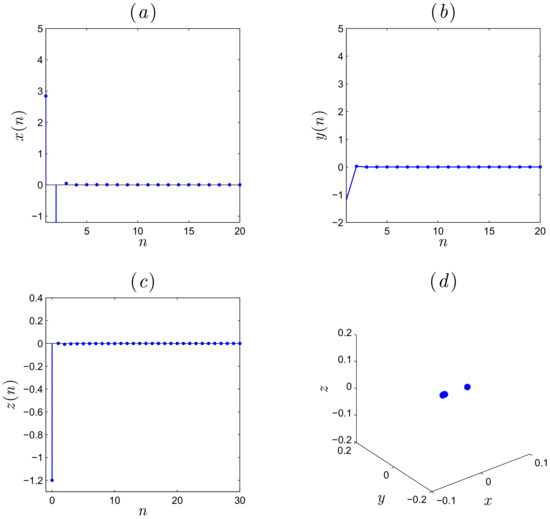
Figure 10.
(a) Stabilization of state , (b) stabilization of state , (c) stabilization of state , (d) attractor of the controlled system (17) for .
5. Conclusions
In this paper, two fractional maps with stable equilibrium points are developed. The complex dynamics of these fractional maps are discussed numerically with some changes in system parameters and fractional order . The presence of chaos and the property of coexisting attractors have been validated via the computation of a 0-1 test and bifurcation diagrams. The type of hidden attractors does not only depend on the value of fractional order but also on the initial condition. Finally, one-dimensional control laws have been designed, with the aim to stabilize at zero the dynamics of the two proposed maps. These novel maps are good candidates for engineering applications. We will focus on putting this claim to the test in a future study. An interesting question under investigation is that of developing a new type of fractional pseudo number generator based on the fractional maps with hidden attractors for potential cryptographic applications. It is our intention to investigate this issue further in future studies.
Author Contributions
Conceptualization, A.O. and D.B.; Data curation, O.A.A. and A.A.K.; formal analysis, O.A.A. and A.A.K.; funding acquisition, V.V.H.; investigation, A.O.; methodology, M.M.A. and D.B.; project administration, A.O.; resources, M.M.A. and V.-T.P.; software, V.-T.P.; supervision, D.B.; visualization, O.A.A., M.M.A. and V.V.H.; writing—original draft, A.A.K.; writing—review and editing, V.V.H. and V.-T.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
This work has been supported by Scientific Research Deanship at University of Ha’il, Saudi Arabia, though Project Number RG-191307. The author Adel Ouannas was supported by the Directorate General for Scientific Research and Technological Development of Algeria.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hénon, M. A two-dimensional mapping with a strange attractor. In The Theory of Chaotic Attractors; Springer: New York, NY, USA, 2004; pp. 94–102. [Google Scholar]
- Anton, H.; Rorres, C. Elementary Linear Algebra: Application Version, 7th ed.; Howard, Drexel Unversity: Philadelphia, PA, USA, 1994; pp. 571–572. [Google Scholar]
- Lozi, R. Un attracteur étrange du type attracteur de Hénon. J. Phys. Colloq. 1978, 39, C5-9. [Google Scholar]
- Leonov, G.A.; Kuznetsov, N.V. Hidden attractors in dynamical systems: From hidden oscillation in Hilbert–Kolmogorov, Aizerman and Kalman problems to hidden chaotic attractor in Chua circuits. Int. J. Bifurc. Chaos 2013, 23, 1330002. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J.C.; Nazarimehr, F. Recent new examples of hidden attractors. Eur. Phys. J. Spec. Top. 2015, 224, 1469. [Google Scholar] [CrossRef]
- Jafari, S.; Pham, V.T.; Golpayegani, S.M.R.H.; Moghtadaei, M.; Kingni, S.T. The relationship between chaotic maps and some chaotic systems with hidden attractors. Int. J. Bifurc. Chaos 2016, 26, 1650211. [Google Scholar] [CrossRef]
- Jiang, H.; Liu, Y.; Wei, Z.; Zhang, L. A new class of three-dimensional maps with hidden chaotic dynamics. Int. J. Bifurc. Chaos 2016, 26, 1650206. [Google Scholar] [CrossRef]
- Shabestari, P.S.; Panahi, S.; Hatef, B.; Jafari, S.; Sprott, J.C. Two simplest quadratic chaotic maps without equilibrium. Int. J. Bifurc. Chaos 2018, 28, 1850144. [Google Scholar]
- Jiang, H.; Liu, Y.; Wei, Z.; Zhang, L. Hidden chaotic attractors in a class of two-dimensional maps. Nonlinear Dyn. 2016, 85, 2719–2727. [Google Scholar]
- Jiang, H.; Liu, Y.; Wei, Z.; Zhang, L. A New Class of Two-Dimensional Chaotic Maps with Closed Curve Fixed Points. Int. J. Bifurc. Chaos 2019, 29, 1950094. [Google Scholar] [CrossRef]
- Wu, G.C.; Baleanu, D. Discrete fractional logistic map and its chaos. Nonlinear Dyn. 2014, 75, 283–287. [Google Scholar] [CrossRef]
- Khennaoui, A.A.; Ouannas, A.; Bendoukha, S.; Wang, X.; Pham, V.T. On chaos in the fractional-order discrete-time unified system and its control synchronization. Entropy 2018, 20, 530. [Google Scholar] [CrossRef]
- Kang, X.; Luo, X.; Zhang, X.; Jiang, J. Homogenized Chebyshev-Arnold map and its application to color image encryption. IEEE Access 2019, 7, 114459–114471. [Google Scholar] [CrossRef]
- Xin, B.; Peng, W.; Kwon, Y. A fractional-order difference Cournot duopoly game with long memory. arXiv 2019, arXiv:1903.0430. [Google Scholar]
- Jouini, L.; Ouannas, A.; Khennaoui, A.A.; Wang, X.; Grassi, G.; Pham, V.T. The fractional form of a new three-dimensional generalized Hénon map. Adv. Differ. Equ. 2019, 1, 122. [Google Scholar] [CrossRef]
- Khennaoui, A.A.; Ouannas, A.; Bendoukha, S.; Grassi, G.; Lozi, R.P.; Pham, V.T. On fractional–order discrete–time systems: Chaos, stabilization and synchronization. Chaos Solitons Fractals 2019, 119, 150–162. [Google Scholar] [CrossRef]
- Ouannas, A.; Khennaoui, A.A.; Grassi, G.; Bendoukha, S. On chaos in the fractional-order Grassi–Miller map and its control. J. Comput. Appl. Math. 2019, 358, 293–305. [Google Scholar] [CrossRef]
- Ouannas, A.; Khennaoui, A.A.; Bendoukha, S.; Grassi, G. On the dynamics and control of a fractional form of the discrete double scroll. Int. J. Bifurc. Chaos 2019, 29, 1950078. [Google Scholar] [CrossRef]
- Ouannas, A.; Khennaoui, A.A.; Odibat, Z.; Pham, V.T.; Grassi, G. On the dynamics, control and synchronization of fractional-order Ikeda map. Chaos Solitons Fractals 2019, 123, 108–115. [Google Scholar] [CrossRef]
- Ouannas, A.; Khennaoui, A.A.; Grassi, G.; Bendoukha, S. On the Q–S chaos synchronization of fractional-order discrete-time systems: General method and examples. Discret. Dyn. Nat. Soc. 2018, 2018, 2950357. [Google Scholar] [CrossRef]
- Khennaoui, A.A.; Ouannas, A.; Bendoukha, S.; Grassi, G.; Wang, X.; Pham, V.T. Generalized and inverse generalized synchronization of fractional-order discrete-time chaotic systems with non-identical dimensions. Adv. Differ. Equ. 2018, 2018, 1–14. [Google Scholar]
- Bendoukha, S.; Ouannas, A.; Wang, X.; Khennaoui, A.A.; Pham, V.T.; Grassi, G.; Huynh, V.V. The Co-existence of different synchronization types in fractional-order discrete-time chaotic systems with non–identical dimensions and orders. Entropy 2018, 20, 710. [Google Scholar] [CrossRef]
- Ouannas, A.; Wang, X.; Khennaoui, A.A.; Bendoukha, S.; Pham, V.T.; Alsaadi, F.E. Fractional form of a chaotic map without fixed points: Chaos, entropy and control. Entropy 2018, 20, 720. [Google Scholar]
- Khennaoui, A.A.; Ouannas, A.; Boulaaras, S.; Pham, V.T.; Taher Azar, A. A fractional map with hidden attractors: Chaos and control. Eur. Phys. J. Spec. Top. 2020, 229, 1083–1093. [Google Scholar]
- Ouannas, A.; Khennaoui, A.A.; Momani, S.; Grassi, G.; Pham, V.T. Chaos and control of a three-dimensional fractional order discrete-time system with no equilibrium and its synchronization. AIP Adv. 2020, 10, 045310. [Google Scholar]
- Ouannas, A.; Khennaoui, A.; Momani, S.; Pham, V.T.; El-Khazali, R. Hidden attractors in a new fractional-order discrete system: Chaos, complexity, entropy and control. Chin. Phys. B 2020, 29, 050504. [Google Scholar]
- Gottwald, G.A.; Melbourne, I. On the implementation of the 0–1 test for chaos. SIAM J. Appl. Dyn. Syst. 2009, 8, 129–145. [Google Scholar] [CrossRef]
- Atici, F.M.; Eloe, P.W. Discrete fractional calculus with the nabla operator. Electron. J. Qual. Theory Differ. Equ. 2009, 3, 1–12. [Google Scholar] [CrossRef]
- Anastassiou, G.A. Principles of delta fractional calculus on time scales and inequalities. Math. Comput. Model. 2010, 52, 556–566. [Google Scholar] [CrossRef]
- Cermak, J.; Gyori, I.; Nechvatal, L. On explicit stability conditions for a linear fractional difference system. Fract. Calc. Appl. Anal. 2015, 18, 651–672. [Google Scholar] [CrossRef]
- Mozyrska, D.; Wyrwas, M. Stability by linear approximation and the relation between the stability of difference and differential fractional systems. Math. Methods Appl. Sci. 2017, 40, 4080–4091. [Google Scholar] [CrossRef]
- Sprott, J.C. Strange Attractors: Creating Patterns in Chaos; M & T Books: New York, NY, USA, 1993. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).