Asymmetric Compensation of Reactive Power Using Thyristor-Controlled Reactors
Abstract
1. Introduction
- No one on the market offers the SVC, which is based on TSCs and TCRs, for smooth asymmetric compensation of reactive power in low-voltage grids.
- There are few publications dedicated to the SVC for smooth compensation of reactive power in low-voltage grids [5,6,7,8,9,44]. However, all these publications are dedicated to symmetric compensation of reactive power in all three phases, and in most of them, just the simulation results are presented.
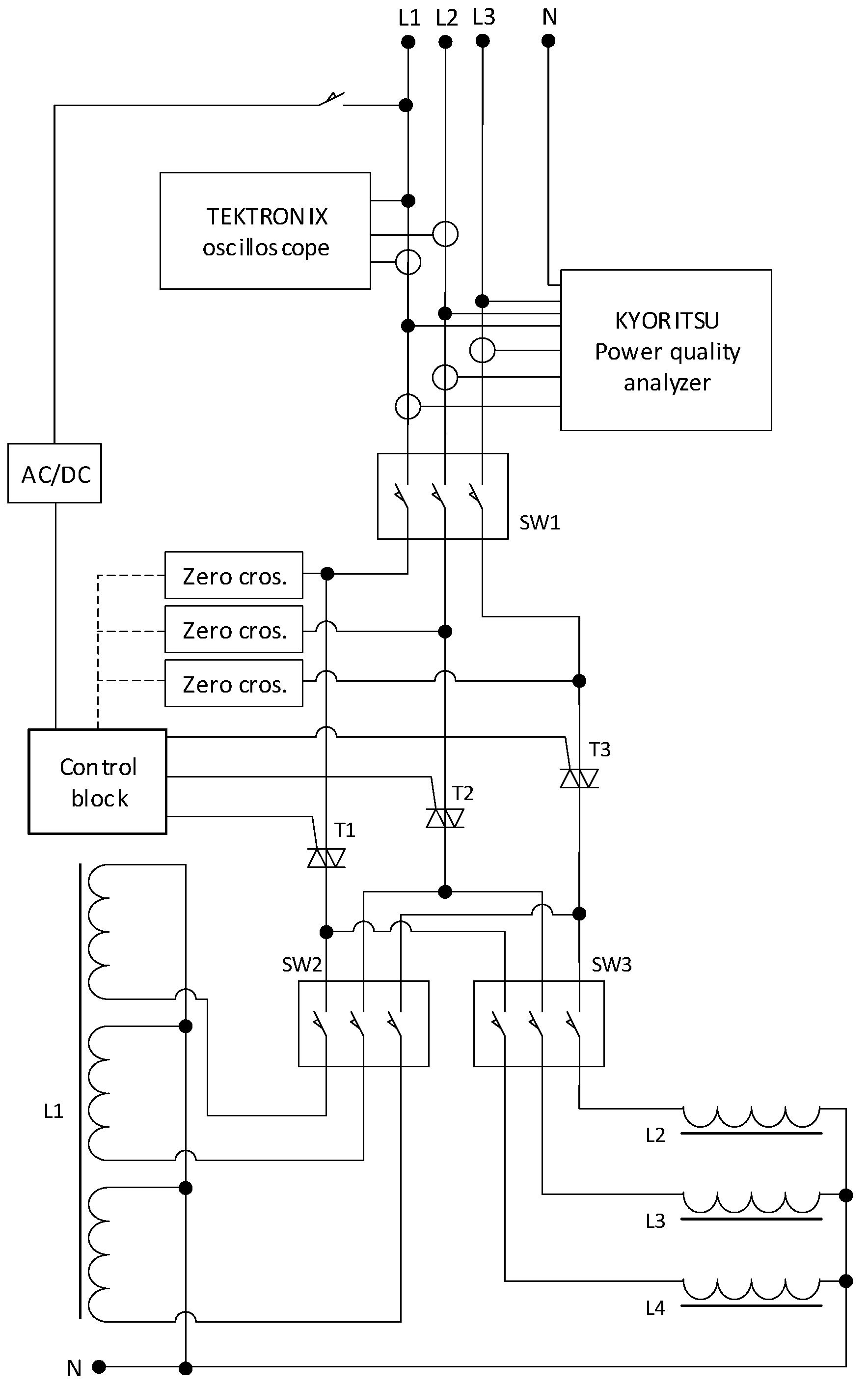
2. The Topology and Operation of the TCR Compensator
3. Investigation Results
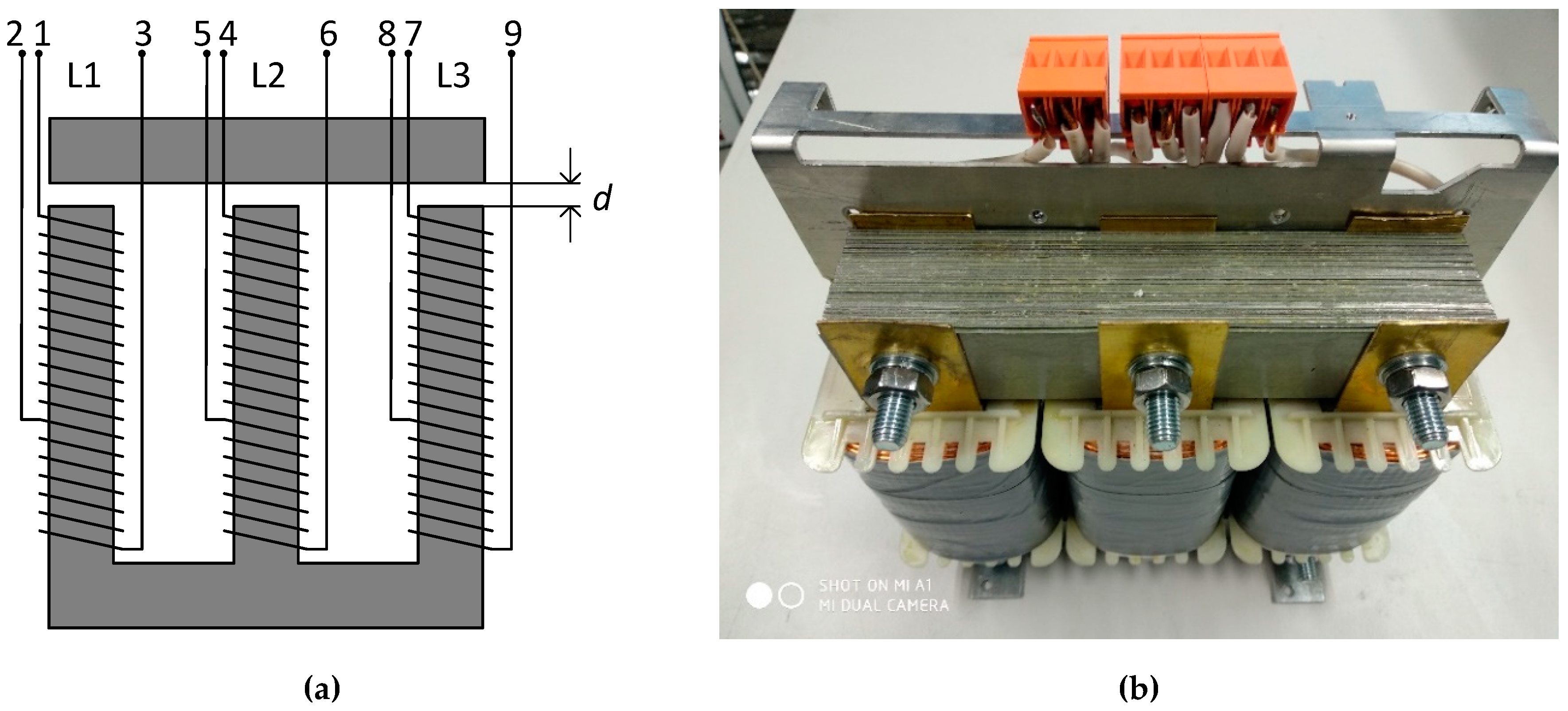
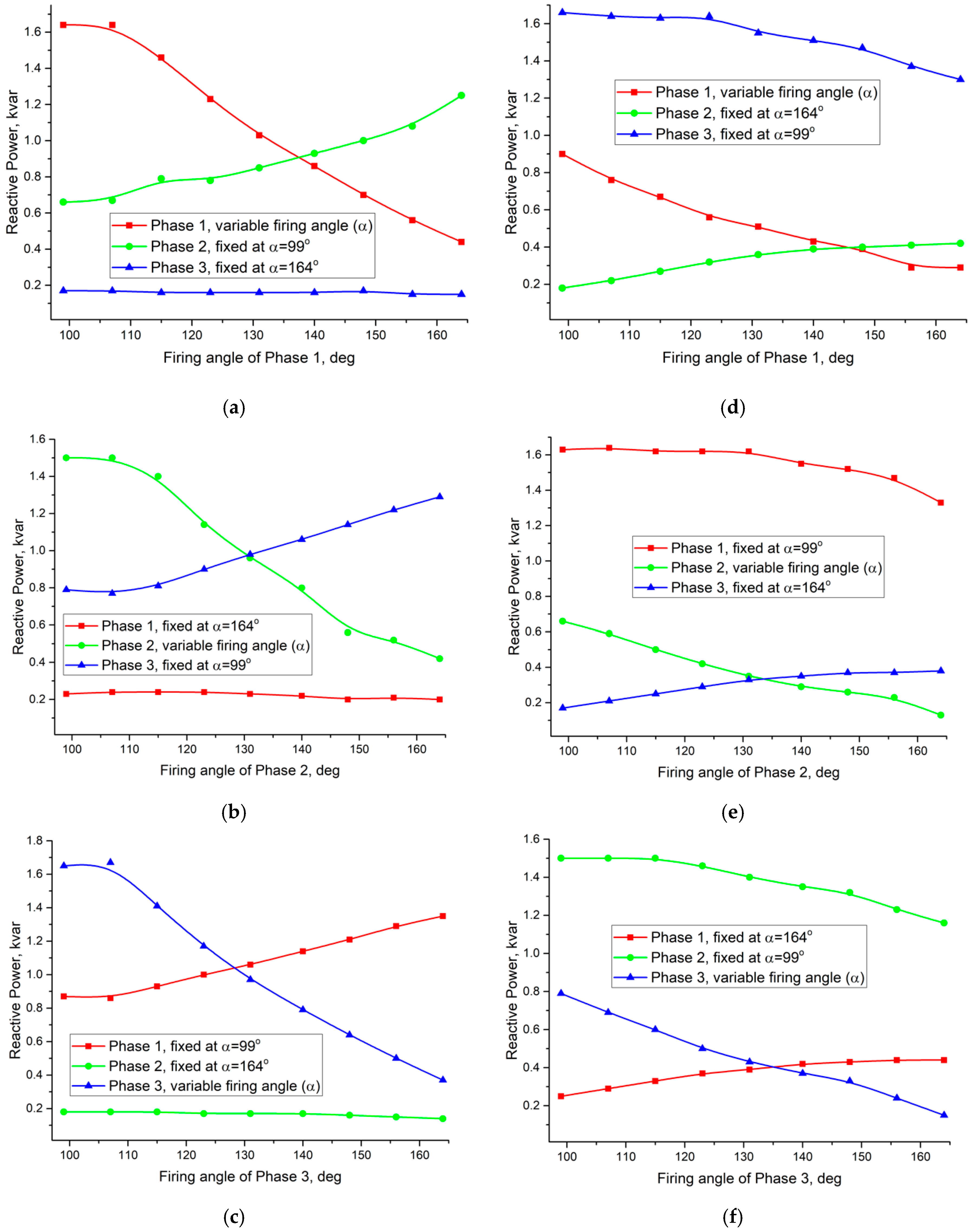
3.1. Investigation of the Compensator Based on a Single-Cored Three-Phase Reactor
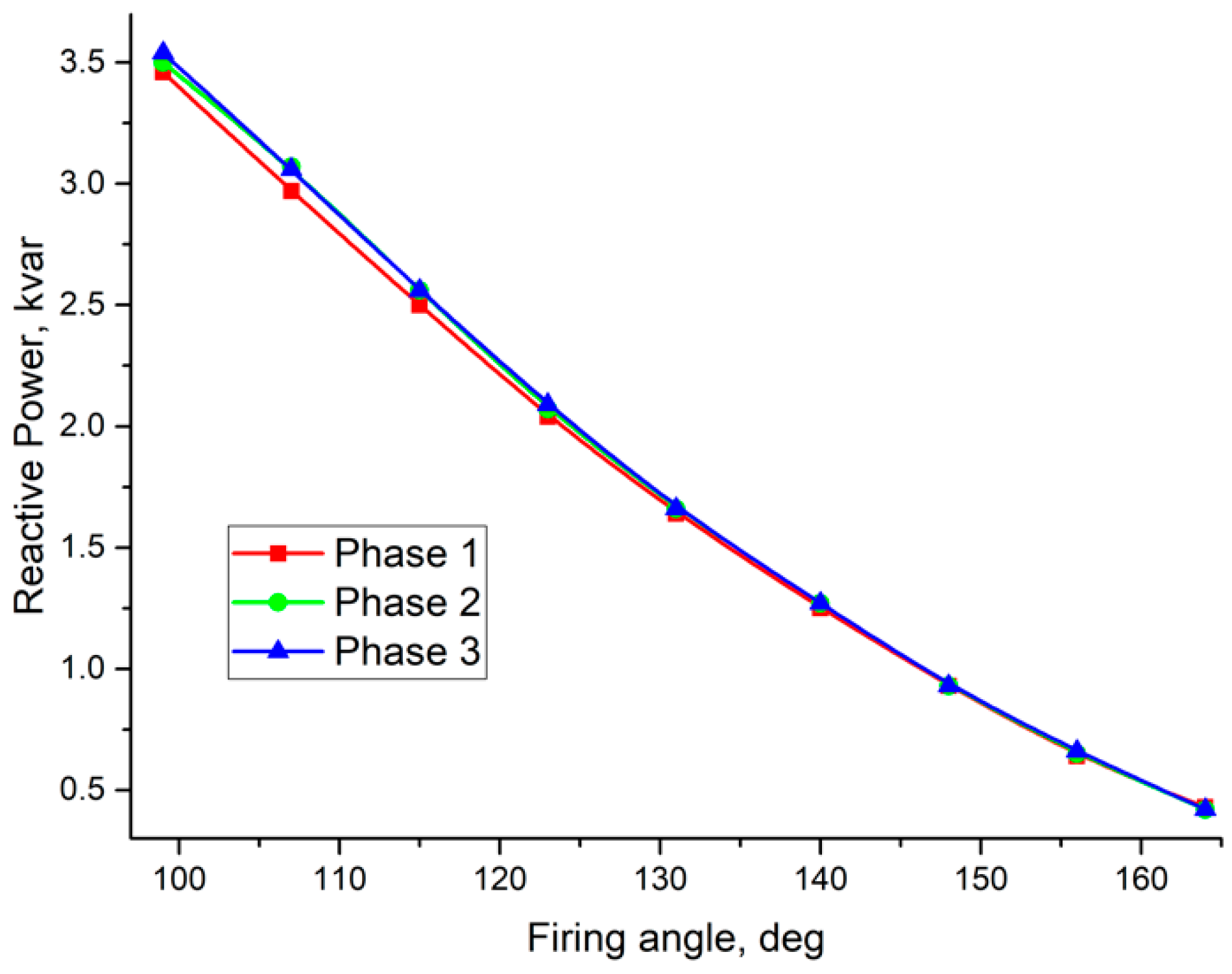
3.2. Investigation of the Compensator Based on Separate Reactors for Every Phase
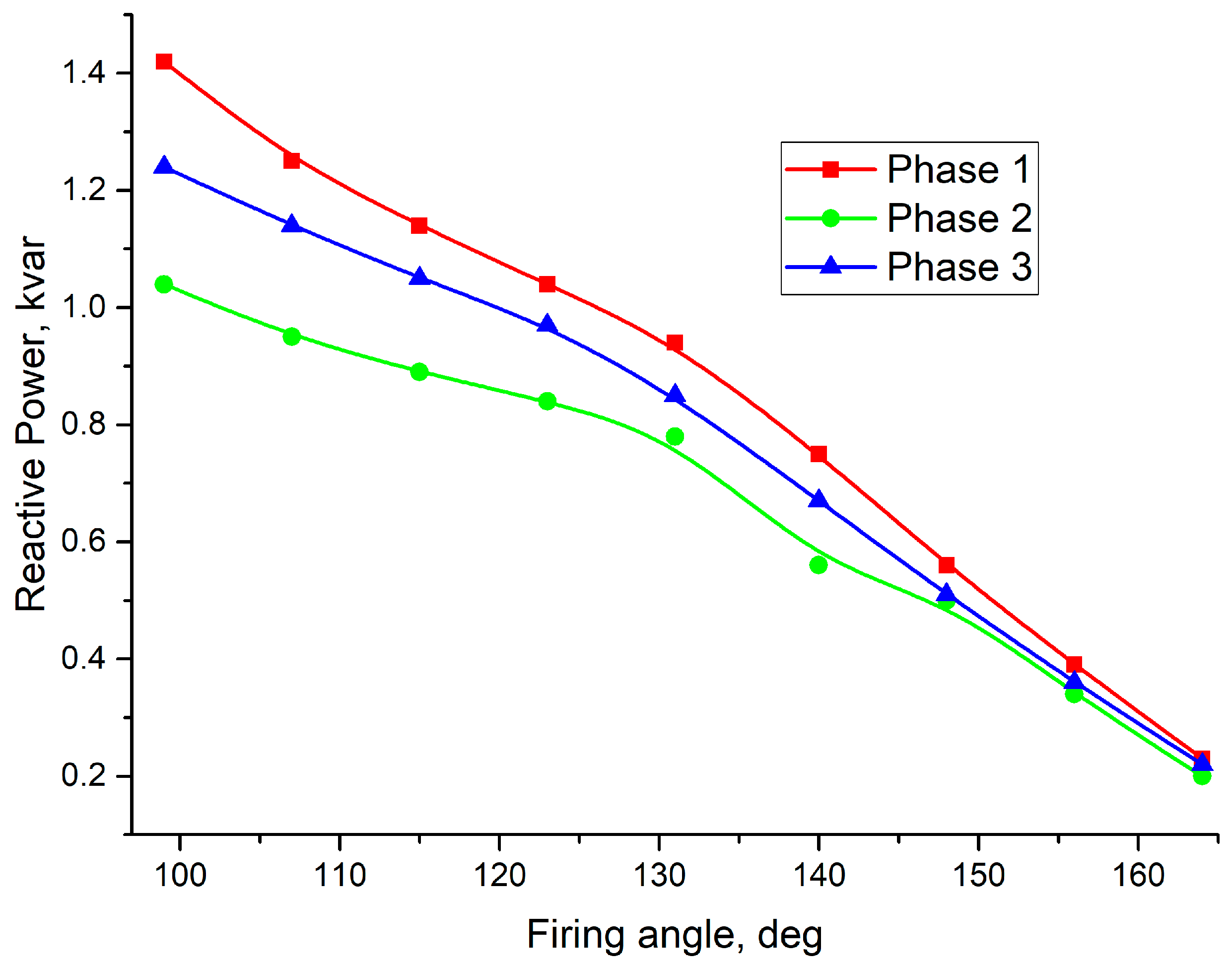
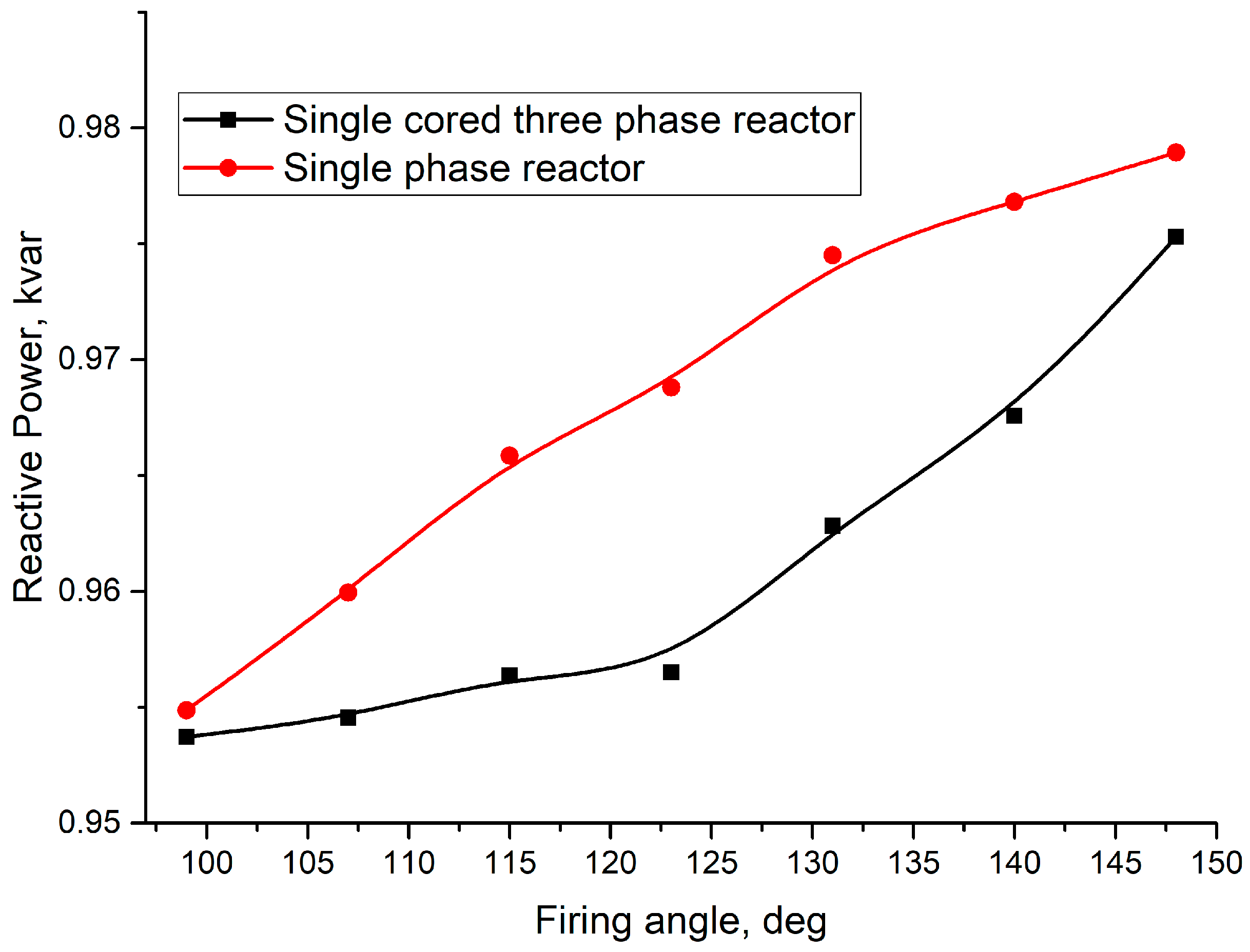
3.3. Efficiency of the TCR Compensator
4. Conclusions
- TCR compensators, which typically are used in high- and medium-voltage utility grids, can be implemented in a low-voltage utility grid employing air-gapped reactors using a Y-connection connected to the neutral midpoint.
- Variation of the thyristor firing angle of one phase of single-cored three-phase reactor does not just change the reactive power of the controlled phase but influences the reactive power of phases with fixed firing angles. This fact shows that it is impossible to control the reactive power in every phase independently using a TCR compensator based on a single-cored three-phase air-gaped reactor, i.e., a compensator with such a reactor is not suitable for the asymmetric compensation of reactive power.
- Employment of three single-phase air-gaped reactors allows us to control the reactive power in every phase independently; therefore, a developed TCR compensator based on three single-phase reactors is suitable for smooth and asymmetric compensation of reactive power in a low-voltage utility grid.
- Commutation of the reactor using thyristor switches does not introduce any high-frequency disturbances of the reactor current and grid voltage.
- TCR compensator topologies with ∆ connection of coils of single-phase reactors as well as Y-connection with unconnected midpoint are not suitable for asymmetric compensation of reactive power in a low-voltage utility grid.
- The developed single-cored three-phase reactor and single-phase reactors are characterized by 0.955–0.975 efficiency.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yong, X.; Jiamei, D.; Shuangbao, M. Power flow control of a distributed generation unit in micro-grid. In Proceedings of the 2009 IEEE 6th International Power Electronics and Motion Control Conference, Wuhan, China, 17–20 May 2009; pp. 2122–2125. [Google Scholar]
- Trentini, F.; Tasca, M.; Tomasin, S.; Erseghe, T. Reactive power compensation in smart micro grids: A prime-based testbed. In Proceedings of the 2012 IEEE International Energy Conference and Exhibition (ENERGYCON), Florence, Italy, 9–12 September 2012; pp. 909–914. [Google Scholar]
- Deblecker, O.; Stevanoni, C.; Vallée, F. Cooperative control of multi-functional inverters for renewable energy integration and power quality compensation in micro-grids. In Proceedings of the 2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Anacapri, Italy, 22–24 June 2016; pp. 1051–1058. [Google Scholar]
- Ilisiu, D.; Dinu, E.-D. Modern reactive power compensation for smart electrical grids. In Proceedings of the 2019 22nd International Conference on Control Systems and Computer Science (CSCS), Bucharest, Romania, 28–30 May 2019; pp. 353–357. [Google Scholar]
- Bogónez-Franco, P.; Balcells, J.; Junyent, O.; Jordà, J. SVC model for voltage control of a microgrid. In Proceedings of the 2011 IEEE International Symposium on Industrial Electronics, Gdansk, Poland, 27–30 June 2011; pp. 1645–1649. [Google Scholar]
- Balcells, J.; Bogónez-Franco, P. Voltage control in a LV microgrid by means of an SVC. In Proceedings of the IECON 2013-39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 6027–6030. [Google Scholar]
- Beck, Y.; Berkovich, Y.; Müller, Z.; Tlusty, J. A Matlab-Simulink model of network reactive power compensation based on binary switchable capacitors and thyristor-controlled reactor. In Proceedings of the 2016 IEEE International Conference on the Science of Electrical Engineering (ICSEE), Eilat, Israel, 16–18 November 2016; pp. 1–5. [Google Scholar]
- Beck, Y.; Berlovich, Y.; Braunstein, A. A Matlab-Simulink model of AC grid with a FC-TCR and invariant control system for reactive power compensation. In Proceedings of the 2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Anacapri, Italy, 22–24 June 2016; pp. 1292–1297. [Google Scholar]
- Dong, T.; Li, L.; Ma, Z. A combined system of APF and SVC for power quality improvement in microgrid. In Proceedings of the 2012 Power Engineering and Automation Conference, Wuhan, China, 18–20 September 2012; pp. 1–4. [Google Scholar]
- Ali, Z.; Christofides, N.; Hadjidemetriou, L.; Kyriakides, E. Photovoltaic reactive power compensation scheme: An investigation for the Cyprus distribution grid. In Proceedings of the 2018 IEEE International Energy Conference (ENERGYCON), Limassol, Cyprus, 3–7 June 2018; pp. 1–6. [Google Scholar]
- Arshad, A.; Lehtonen, M. Instantaneous active/reactive power control strategy for flicker mitigation under high PV penetration. In Proceedings of the 2018 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Sarajevo, Bosnia and Herzegovina, 21–25 October 2018; pp. 1–6. [Google Scholar]
- Stanelyte, D.; Radziukynas, V. Review of voltage and reactive power control algorithms in electrical distribution networks. Energies 2020, 13, 58. [Google Scholar] [CrossRef]
- Gayatri, M.T.L.; Parimi, A.M.; Kumar, A.V.P. A review of reactive power compensation techniques in microgrids. Renew. Sustain. Energy Rev. 2018, 81, 1030–1036. [Google Scholar] [CrossRef]
- Charalambous, A.; Hadjidemetriou, L.; Zacharia, L.; Bintoudi, A.D.; Tsolakis, A.C.; Tzovaras, D.; Kyriakides, E. Phase balancing and reactive power support services for microgrids. Appl. Sci. 2019, 9, 5067. [Google Scholar] [CrossRef]
- Li, B.; Tian, X.; Zeng, H. A grid-connection control scheme of PV system with fluctuant reactive load. In Proceedings of the 2011 4th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), Weihai, China, 6–9 July 2011; pp. 786–790. [Google Scholar]
- Santacana, E.; Rackliffe, G.; Tang, L.; Feng, X. Getting Smart. IEEE Power Energy Mag. 2010, 8, 41–48. [Google Scholar] [CrossRef]
- Bielskis, E.; Baskys, A.; Valiulis, G. Controller for the grid-connected microinverter output current tracking. Symmetry 2020, 12, 112. [Google Scholar] [CrossRef]
- Bielskis, E.; Baskys, A.; Sapurov, M. Single stage microinverter based on two-switch DC-DC flyback converter. Elektron. Ir Elektrotechnika 2017, 23, 29–32. [Google Scholar] [CrossRef][Green Version]
- Pană, A.; Băloi, A.; Molnar-Matei, F. From the balancing reactive compensator to the balancing capacitive compensator. Energies 2018, 11, 1979. [Google Scholar] [CrossRef]
- Pană, A.; Băloi, A.; Molnar-Matei, F. Iterative method for determining the values of the susceptances of a balancing capacitive compensator. Energies 2018, 11, 2742. [Google Scholar] [CrossRef]
- Xiang-Qian, T.; Keqing, X.; Ming, S.; Xianhong, M. Reactive power and unbalance compensation with DSTATCOM. In Proceedings of the 2005 International Conference on Electrical Machines and Systems, Nanjing, China, 27–29 September 2005; Volume 2, pp. 1181–1184. [Google Scholar]
- Fuchs, E.; Masoum, M.A.S. Power Quality in Power Systems and Electrical Machines; Academic Press: Cambridge, MA, USA, 2011; ISBN 978-0-08-055917-9. [Google Scholar]
- Igbinovia, F.; Fandi, G.; Svec, J.; Muller, Z.; Tlusty, J. Comparative review of reactive power compensation technologies. In Proceedings of the 2015 16th International Scientific Conference on Electric Power Engineering, Ostrava, Czech Republic, 20–22 May 2015; pp. 2–7. [Google Scholar] [CrossRef]
- Acha, E.; Agelidis, V.; Anaya-Lara, O.; Miller, T.J.E. Power Electronic Control in Electrical Systems; Newnes: Oxford, UK, 2002; ISBN 978-0-7506-5126-4. [Google Scholar]
- Dixon, J.; Moran, L.; Rodriguez, J.; Domke, R. Reactive power compensation technologies: State-of-the-art review. Proc. IEEE 2005, 93, 2144–2164. [Google Scholar] [CrossRef]
- Padiyar, R.K. Facts Controllers in Power Transmission and Distribution; New Age International (P) Ltd.: New Delhi, India, 2007; ISBN 978-81-224-2541-3. [Google Scholar]
- Mathur, R.M.; Varma, R.K. Thyristor-Based FACTS Controllers for Electrical Transmission Systems; John Wiley & Sons: Hoboken, NJ, USA, 2002; ISBN 978-0-470-54668-0. [Google Scholar]
- Tehrani, K.-A.; Capitaine, T.; Barrandon, L.; Hamzaoui, M.; Rafiei, S.M.R.; Lebrun, A. Current control design with a fractional-order PID for a three-level inverter. In Proceedings of the Proceedings of the 2011 14th European Conference on Power Electronics and Applications, Birmingham, UK, 30 August–1 September 2011; pp. 1–7. [Google Scholar]
- Xu, Y.; Tolbert, L.M.; Kueck, J.D.; Rizy, D.T. Voltage and current unbalance compensation using a static var compensator. IET Power Electron. 2010, 3, 977–988. [Google Scholar] [CrossRef]
- Chang, W.-N.; Liao, C.-H. Design and implementation of a STATCOM based on a multilevel FHB converter with delta-connected configuration for unbalanced load compensation. Energies 2017, 10, 921. [Google Scholar] [CrossRef]
- PQC-Statcon. Available online: https://library.e.abb.com/public/2b588b8dd20ce996c1257a37003639e4/PQC-STATCON_Flyer.pdf (accessed on 6 November 2019).
- Yan, J. Handbook of Clean Energy Systems, 1st ed.; John Wiley & Sons: Chichester, UK, 2015; Volume 6, ISBN 978-1-118-38858-7. [Google Scholar]
- Panfilov, D.I.; ElGebaly, A.E. Modified thyristor controlled reactor for static VAR compensators. In Proceedings of the 2016 IEEE International Conference on Power and Energy (PECon), Melaka, Malaysia, 28–29 November 2016; pp. 712–717. [Google Scholar]
- Khonde, R.S.; Palandurkar, M.V. Simulation model of thyristor controlled reactor. Int. J. Eng. Res. Technol. 2014, 3, 1692–1694. [Google Scholar]
- Panfilov, D.I.; ElGebaly, A.E.; Astashev, M.G. Design and evaluation of control system for static VAR compensators with thyristors switched reactors. In Proceedings of the 2017 IEEE 58th International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON), Riga, Latvia, 12–13 October 2017; pp. 1–6. [Google Scholar]
- Mahapatra, S.; Goyal, A.; Kapil, N. Thyristor controlled reactor for power factor improvement. Int. J. Eng. Res. Appl. 2014, 4, 55–59. [Google Scholar]
- Awad, F.; Mansour, A.; Elzahab, E. Thyristor controlled reactor with different topologies based on fuzzy logic controller. Int. J. Eng. Res. 2015, 4, 498–505. [Google Scholar] [CrossRef]
- Panfilov, D.I.; ElGebaly, A.E.; Astashev, M.G. Topologies of thyristor controlled reactor with reduced current harmonic content for static VAR compensators. In Proceedings of the 2017 IEEE International Conference on Environment and Electrical Engineering and 2017 IEEE Industrial and Commercial Power Systems Europe (EEEIC / I CPS Europe), Milan, Italy, 6–9 June 2017; pp. 1–6. [Google Scholar]
- Čerňan, M.; Tlustý, J. Study of the susceptance control of industrial static var compensator. In Proceedings of the 2015 16th International Scientific Conference on Electric Power Engineering (EPE), Kouty nad Desnou, Czech Republic, 20–22 May 2015; pp. 538–541. [Google Scholar]
- Hong, H.; Wenmei, W.; Shaohua, X.; Min, T.; Chuanjia, H. Summary on reactive power compensation technology and application. In Proceedings of the 2nd International Conference on Intelligent Computing and Cognitive Informatics (ICICCI 2015), Singapore, 8–9 September 2015. [Google Scholar]
- Farkoush, S.G.; Kim, C.-H.; Rhee, S.-B. THD reduction of distribution system based on ASRFC and HVC method for SVC under EV charger condition for power factor improvement. Symmetry 2016, 8, 156. [Google Scholar] [CrossRef]
- Alkayyali, M.; Ghaeb, J. Hybrid PSO–ANN algorithm to control TCR for voltage balancing. IET Gener. Transm. Distrib. 2020, 14, 863–872. [Google Scholar] [CrossRef]
- Panfilov, D.I.; Rozhkov, A.N.; Astashev, M.G.; Zhuravlev, I.I. Modern approaches to controlled static VAR compensators design. In Proceedings of the 2019 IEEE International Conference on Environment and Electrical Engineering and 2019 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I CPS Europe), Genova, Italy, 11–14 June 2019; pp. 1–5. [Google Scholar]
- Köse, A.; Irmak, E. Modeling and simulation of a static VAR compensator based on FC-TCR. In Proceedings of the 2016 IEEE International Conference on Renewable Energy Research and Applications (ICRERA), Birmingham, UK, 20–23 November 2016; pp. 924–927. [Google Scholar]
- Rahmani, S.; Hamadi, A.; Al-Haddad, K.; Dessaint, L.A. A Combination of shunt hybrid power filter and thyristor-controlled reactor for power quality. IEEE Trans. Ind. Electron. 2014, 61, 2152–2164. [Google Scholar] [CrossRef]
- Liberado, E.V.; Souza, W.A.; Pomilio, J.A.; Paredes, H.K.M.; Marafão, F.P. Design of static VAr compensator using a general reactive energy definition. In Proceedings of the International School on Nonsinusoidal Currents and Compensation 2013 (ISNCC 2013), Zielona Góra, Poland, 20–21 June 2013; pp. 1–6. [Google Scholar]
- Tokiwa, A.; Yamada, H.; Tanaka, T.; Watanabe, M.; Shirai, M.; Teranishi, Y. New hybrid static VAR compensator with series active filter. Energies 2017, 10, 1617. [Google Scholar] [CrossRef]
- Arab-Tehrani, K.; Colteu, A.; Rasoanarivo, I.; Michel-Sargos, F. Design a new high intensity magnetic separator with permanent magnets for industrial applications. Int. J. Appl. Electromagn. Mech. 2010, 32, 237–248. [Google Scholar] [CrossRef]
- Topaloglu, I. Air gap optimization of iron core shunt reactors with discretely disturbed air gaps for UHV systems. In Proceedings of the International conference on engineering and natural science (ICENS 2016), Sarajevo, Bosnia and Herzegovina, 24–28 May 2016; pp. 1–6. [Google Scholar]
- Wass, T.; Hörnfeldt, S.; Valdemarsson, S. The design and construction of a controllable reactor with a HTS control winding. J. Phys. Conf. Ser. 2006, 43, 873. [Google Scholar] [CrossRef]
- Bielskis, E.; Baskys, A.; Sapurov, M. Impact of transformer design on flyback converter voltage spikes. Elektron. Ir Elektrotechnika 2016, 22, 58–61. [Google Scholar] [CrossRef][Green Version]
- Šapurov, M.; Bielskis, E.; Bleizgys, V.; Dervinis, A. Stepless compensator of reactive power. Moksl. Liet. Ateitis Sci. Future Lith. 2020, 12. [Google Scholar] [CrossRef]



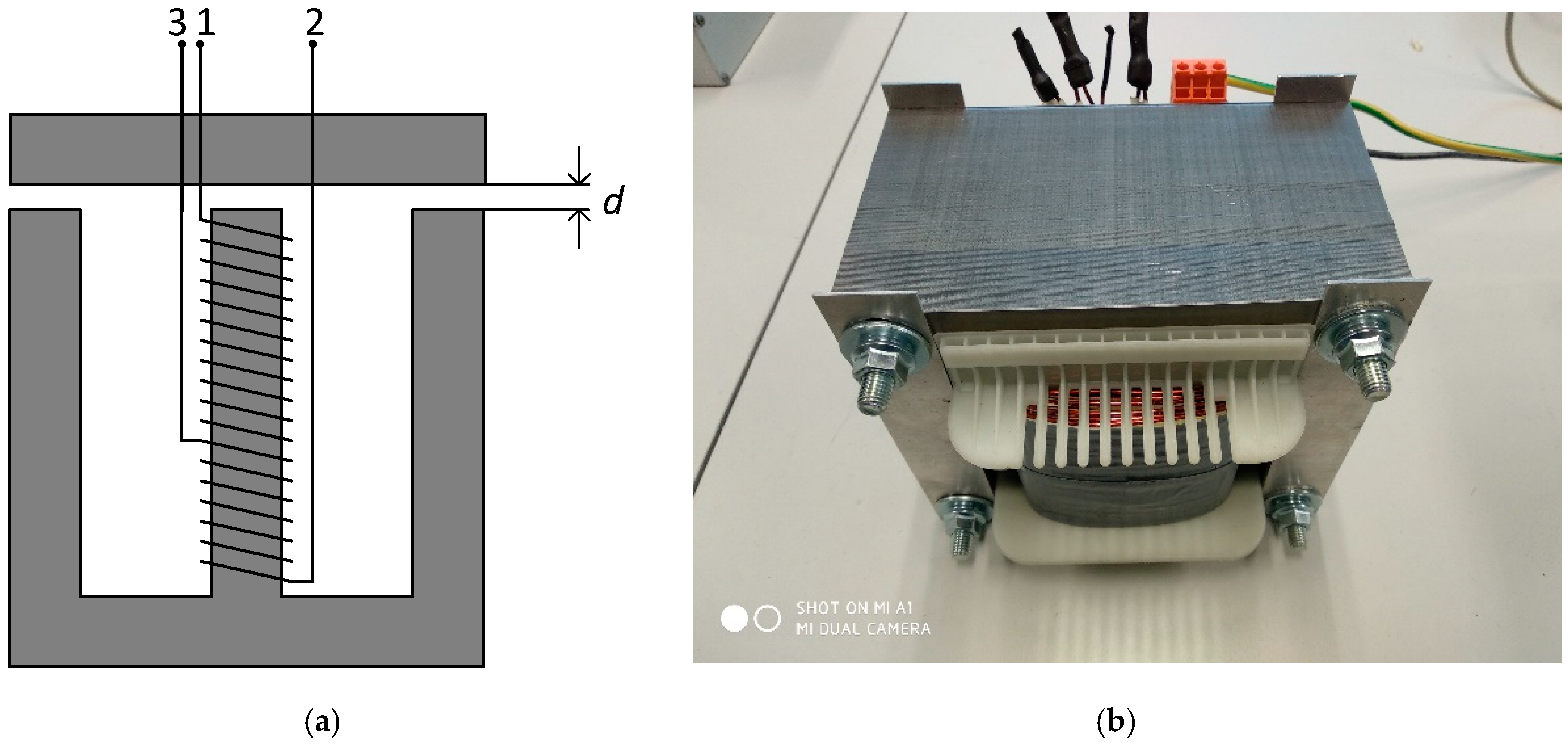


| Parameter | Value |
|---|---|
| Relative magnetic permeability of iron core (μI) | 100 |
| Number of turns of coil (N) | 510 |
| Winding area (S) | 17.6 cm2 |
| Length of coil (l) | 10.8 cm |
| Wire cross-section | 1.8 mm2 |
| Inductance of coil at core air gap length d = 0 | 530 mH |
| Inductance of coil at d = 6 mm | 100 mH |
| Inductance of coil at d = 10 mm | 37 mH |
| Inductance of coil without core | 5.3 mH |
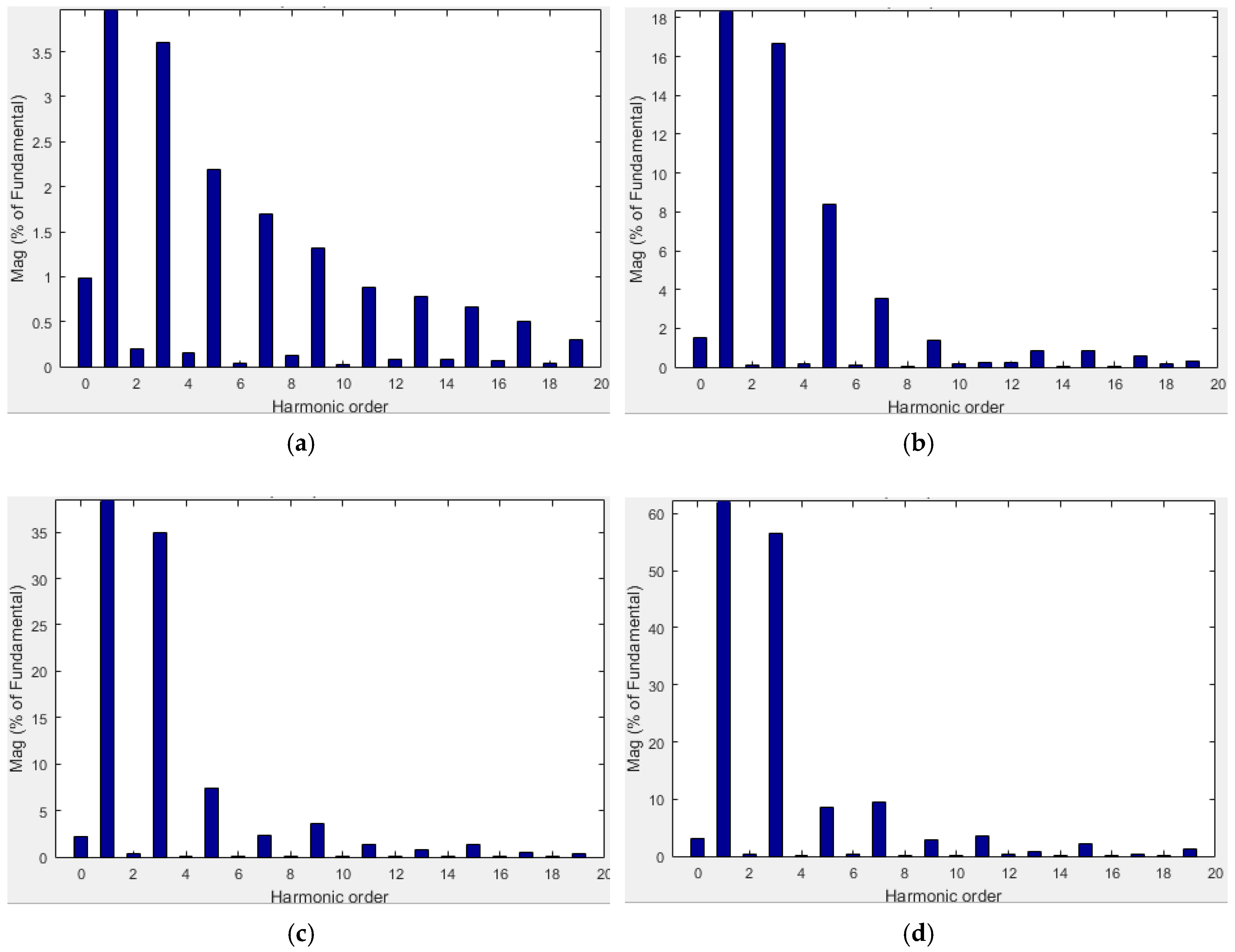
| Thyristor Firing Angle (α) | Total Harmonic Distortion (THD), % |
|---|---|
| 95° | 5.2 |
| 110° | 19.2 |
| 140° | 36.1 |
| 160° | 58.3 |
| Parameter | Value |
|---|---|
| Relative magnetic permeability of iron core (μI) | 100 |
| Number of turns of coil (N) | 160 |
| Winding area (S) | 71.5 cm2 |
| Length of coil (l) | 9.0 cm |
| Wire cross-section | 3.1 mm2 |
| Inductance of coil at core air gap length d = 0 | 256 mH |
| Inductance of coil at d = 5 mm | 40 mH |
| Inductance of coil at d = 10 mm | 18 mH |
| Inductance of coil without core | 2.6 mH |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Šapurov, M.; Bleizgys, V.; Baskys, A.; Dervinis, A.; Bielskis, E.; Paulikas, S.; Paulauskas, N.; Macaitis, V. Asymmetric Compensation of Reactive Power Using Thyristor-Controlled Reactors. Symmetry 2020, 12, 880. https://doi.org/10.3390/sym12060880
Šapurov M, Bleizgys V, Baskys A, Dervinis A, Bielskis E, Paulikas S, Paulauskas N, Macaitis V. Asymmetric Compensation of Reactive Power Using Thyristor-Controlled Reactors. Symmetry. 2020; 12(6):880. https://doi.org/10.3390/sym12060880
Chicago/Turabian StyleŠapurov, Martynas, Vytautas Bleizgys, Algirdas Baskys, Aldas Dervinis, Edvardas Bielskis, Sarunas Paulikas, Nerijus Paulauskas, and Vytautas Macaitis. 2020. "Asymmetric Compensation of Reactive Power Using Thyristor-Controlled Reactors" Symmetry 12, no. 6: 880. https://doi.org/10.3390/sym12060880
APA StyleŠapurov, M., Bleizgys, V., Baskys, A., Dervinis, A., Bielskis, E., Paulikas, S., Paulauskas, N., & Macaitis, V. (2020). Asymmetric Compensation of Reactive Power Using Thyristor-Controlled Reactors. Symmetry, 12(6), 880. https://doi.org/10.3390/sym12060880





